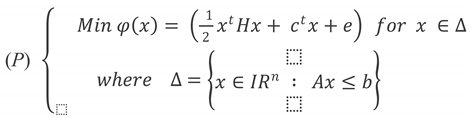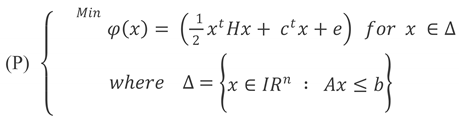Algorithm Based on the Modified Sufficient Conditions of Inertia-Controlling Method for Globally Solution of a General Quadratic Problem

1. Introduction

Currently, the domain of optimization is attracting considerable interest from the academic and industrial communities, see, for instances [1,2,3]. The various studies existing for solving a given problem in this domain and the efficient algorithmics implementations open up many perspectives and diverse applications. By many researchers in this field and whose objective is formed by several numerical methods [5,6,9] used in two ways; the first way is the essential principal of such a generally method consists of enumerating, often of implicitly manner the set of solutions of the optimization problem as well as has the techniques to detect the possible failures and the second way concerning the large size.

The quadratic programming problem in continuous time and the theory of the characterizations of its global solutions seem appropriate to the questions where the objective function is of the general form either convex, concave or indefinite form. However, the quadratic problem can be written in several forms equivalents, normally, which help us to simplify and find the good optimality conditions for this type of problems in the general case, but now, it’s only found for the general quadratic programming of optimization with equality constraints [10].

According to our long scientific research on the manner for solving our problem denoted in below, we have not found an effective method that will allow us to find the globally minimum in reasonable time and avoiding the numerical difficulties linked to the bad conditioning of the Hessian of problem.

With the new global sufficiently conditions that we propose, we can apply any iterative method converging towards the local solution of the problem (P) whose the goal is to compute the global solutions of the optimization problems (P). As in the indefinite case, the (P) problem, may had more than one global solution, this on the one hand, on the other hand, we avoid writing the equivalent forms to the optimization problem (P) which helps us to take directly the original problem. The analytic solution is computationally intense and numerical issues my occur, knowing, this solution exists especially when the domain is bounded, However it`s not the case with the not indefinite Hessian reduced matrix and the question is stay also posed about the globally solution which is noted by variable $x_G$.

In this study, we are interested on the global sufficiently conditions to solve the general quadratic problem of optimization, where the set of his constraints are linear:

Such as A is an (m∗n) matrix not necessarily full rank; H is a Hessian matrix of order n (not necessarily convex). The b and c are two given vectors, and e is a scalar.

Actually, the conditions which we help to solve the problem (P) are not found. By these conditions we can apply any iterative method converging to the local solution of problem (P), whose goal is to compute the global solution of the optimization problem of (P).

This analytic solution is computationally intense and numerical issues my occur, knowing, this solution exists especially when the domain of constraints is bonded, or not bonded with the reduced Hessian is not indefinite, but the question is stay also posed about the global solution in other cases, for example, in case of indefinite reduced Hessian matrix.

2. Notation and Glossary

We present in this paragraph the designation of the different symbols and variables used in our work:

Table 1. Notation and Glossary.

Ak	The active matrix at iteration k
m,mk	Number of rows in matrix A respectively Ak
$x_s$	Stationary point
$x_a$	Active point
$x_G$	Globally solution
q	Direction of minimization
$\mu$	Lagrange Multiplier vector’s
${\propto }_{q,c}$ and ${ \propto }_{q,i}$	denotes respectively the steep length in convex case c and in indefinite case i
Zk	Kernel matrix of Ak
nk	Number of columns in Zk
$\phi (x)$	The objective function
H	The Hessian matrix
I. C.M	Denotes the initials letters of Inertia Controlling Method
$g_k$	The gradient of objective function in point $x_k$ at iteration k
$∆$	The domain of linear constraints of problem (P)
Fr ($∆$)	denotes the domain border of$∆$
P.D	Denotes the initials letters of Positive Defined matrix

Table 1. Notation and Glossary.

Ak	The active matrix at iteration k
m,mk	Number of rows in matrix A respectively Ak
$x_s$	Stationary point
$x_a$	Active point
$x_G$	Globally solution
q	Direction of minimization
$\mu$	Lagrange Multiplier vector’s
${\propto }_{q,c}$ and ${ \propto }_{q,i}$	denotes respectively the steep length in convex case c and in indefinite case i
Zk	Kernel matrix of Ak
nk	Number of columns in Zk
$\phi (x)$	The objective function
H	The Hessian matrix
I. C.M	Denotes the initials letters of Inertia Controlling Method
$g_k$	The gradient of objective function in point $x_k$ at iteration k
$∆$	The domain of linear constraints of problem (P)
Fr ($∆$)	denotes the domain border of$∆$
P.D	Denotes the initials letters of Positive Defined matrix

3. Existence of Global Solution ${\mathbf{x}}_{\mathbf{G}}$

We consider the general quadratic problem (P) under the linear constraints Δ.

To show the existence of the global solution, we are stating and implementing two lemmas. The first concerns the determination of minimization direction q (negative direction of curvature, or direction of descent). The second concerns the steep of length ${\propto }_k$ which makes finite our algorithm.

3.1.

Lemma 1. Let $x_s$ a stationary point obtained at iteration k. Then the following linear system (1) obtained thanks KKT-matrix has a single solution in $x_s$

$$\left(\begin{array}{cc}H& A_k^t\\ A_k& 0\end{array}\right)\left(\begin{array}{c}q\\ u\end{array}\right)=\left(\begin{array}{c}0\\ -1\end{array}\right)$$

(1)

Note that this solution exists and unique if and only if $Z_k^{t}H{Z}_k \mathrm{i}\mathrm{s} \mathrm{a} \mathrm{D}.\mathrm{P}.$matrix, with Z_k is a kernel matrix of A_k such that $A_k{Z}_k=0_{m_k\times n_k}$

This single solution is a minimize direction of $\phi$ in the following cases:

Case1 $q^{t}Hq<0$ with $g_k^{t}q\le 0$

Case2 $q^{t}Hq>0$ with $g_k^{t}q<0$

Proof

Given that $Z_k^{t}H{Z}_k$ is D.P. matrix, then it is non-singular matrix and according to the expression referred to in [1], it comes to us that the K-matrix

$$\left(\begin{array}{cc}H& A_k^t\\ A_k& 0\end{array}\right) \text{is also nonsingular}.$$

Consequently, the linear system (1) has a single solution ${\left(q, u\right)}^t$.

Now, let’s distinguish the cases where the vector q represents the minimization direction of problem (P).

Let us recall that, among the important properties in general quadratic programming problem and iterates at the point $x_k$we have ${\phi }_{k+1}={\phi }_k+{\displaystyle \frac{{\alpha }_k^2}{2}}{q}^{t}Hq+{\alpha }_k{g}_k^{t}q$ [1] (2)

In case1: If $q^{t}Hq<0$ with ${\mathrm{g}}_{\mathrm{k}}^{\mathrm{t}}\mathrm{q}\le 0$. We have directly ${\phi }_{k+1}<{\phi }_k$.

This fits the negative curvature direction which is a minimization direction

In case2: if $q^{t}Hq>0$ with $g_k^{t}q<0$. It fits a descent direction at point $x_k$ and positive curvature. Here it results also ${\phi }_{k+1}<{\phi }_k$

$${\propto }_{\mathit{q},\mathit{c}}={\displaystyle \frac{-{\mathit{g}}_{\mathit{k}}^{\mathit{t}}\mathit{q}}{{\mathit{q}}^{\mathit{t}}\mathit{H}\mathit{q}}}(\mathbf{c}\mathbf{o}\mathbf{n}\mathbf{v}\mathbf{e}\mathbf{x} \mathbf{c}\mathbf{a}\mathbf{s}\mathbf{e})$$

(3)

3.2.

Lemma 2. We take the same data of lemma1 with the satisfaction once situation of these two following cases:

Case1 $q^{t}Hq\ge 0$ with $g_k^{t}q\ge 0$

Case2 $q^{t}Hq<0$ with $g_k^{t}q>0$ such that ${\propto }_k<{\propto }_{q,i}$

Where ${\propto }_{q,i}={\displaystyle \frac{{-2 g}_k^{t}q}{q^{t}Hq}}$ (4)

and ${\propto }_k=\begin{array}{c}Min\left({\displaystyle \frac{b_i-a_i^t{x}_k}{a_i^{t}q}}\right)\\ a_i^{t}q>0,fori=1,\dots ,m\end{array}$ (5)

Then $x_k$ is a globally solution of our problem (P).

Proof

Take the expression used in the proof of Lemma 1,

In case1: According the expression that we have considered in proof of lemma 1, it results that

$${\phi }_{k+1}\ge {\phi }_k$$

In case 2: As ${\propto }_k<{\propto }_{q, i}$ where

$${\propto }_{q,i}={\displaystyle \frac{{-2g}_k^{t}q}{q^{t}Hq}}$$

We multiply the expression (4) by ${\propto }_k$, it means

$-{\propto }_{\mathrm{k}}.{\displaystyle \frac{{\mathsf{\alpha }}_{\mathrm{k}}}{2}}{\mathrm{q}}^{\mathrm{t}}\mathrm{H}\mathrm{q}<{\mathrm{g}}_{\mathrm{k}}^{\mathrm{t}}\mathrm{q}$.${\propto }_{\mathrm{k}}$

and involve that ${\displaystyle \frac{-{\propto }_k^2{q}^{t}Hq}{2}}<{\displaystyle \frac{g_k^{t}q}{1}}.{\propto }_k,$ it results

$${\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq>-{\alpha }_k{g}_k^{t}q$$

This expression is always positive.

That is ${\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq+{\alpha }_k{g}_k^{t}q>0$ and according the expression that we have considered in proof of lemma 1

(${\phi }_{k+1}={\phi }_k+{\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq+{\alpha }_k{g}_k^{t}q)$ it results that

${\phi }_{k+1}\ge {\phi }_k$

and we can say that $x_k$ is a globally solution of problem (P).

4. New Sufficient Conditions Globally Solution of (P)

The new sufficient conditions globally solutions of the problem (P) that we propose are shown in the following steps:

• $g_k=A_k^t\mu$
• $Z_k^{T}H{Z}_k$ is a positive defined matrix
• In this third condition we propose the new following step. We replace the condition of Lagrange Multiplier $\mu >$0 by the following linear system obtained thanks to KKT-Matrix

  $$\left(\begin{array}{cc}H& A_k^t\\ A_k& 0\end{array}\right)\left(\begin{array}{c}q\\ u\end{array}\right)=\left(\begin{array}{c}0\\ -1\end{array}\right)$$

Which has the only increasing direction q with the steep length ${\propto }_k<{\propto }_q$

on all cases i.e. in convex case ${\propto }_k<{\propto }_{q,c}$ such that

$${\propto }_{q,c}={\displaystyle \frac{-g_k^{t}q}{q^{t}Hq}}$$

And in indefinite case ${\propto }_k<{\propto }_{q,i}$ such that

$${\propto }_{q,i}={\displaystyle \frac{-2g_k^{t}q}{q^{t}Hq}}$$

Where

$${\propto }_k={}_{\begin{array}{c}i=1,,m\\ a_i^{t}q>0\end{array}}{}^{min }( {\displaystyle \frac{b_i-a_i^t{x}_k}{a_i^{t}q}} )$$

Proof

Before showing this result, we will recall the sufficient conditions of the local solutions of the problems of type (P) which is given in the following theorem and use his results to find the globally solution:

Theorem [10]

We consider the quadratic problem (P), and let $x^{*}ϵ∆$ be the point obtained by minimizing the objective function ϕ after performing k iterations starting from the initial point $x_0$. We are given two matrices, $A_k$ and $Z_k$ , such that the columns of the latter constitute a basis for the kernel of the former. If there is a positive vector ${\gamma }_1^{*}>0$such that $\nabla \phi \left(x^{*}\right)-A_k^t{\gamma }_1^{*}=0_n$ ,

and if more the expression $Z^{t}HZ$ is positive for all $Z\ne 0:$

$$A_k{Z}_k=0_{m_k\times n_k}$$

Then $x^{*}$ is a local solution of the problem (P).

Now, we return to show the proof of the our original result by considering $q\ne 0_n$(because the case of $q=0_n$ is evidently $q^t{g}_k=q^{t}Hq=0 )$

We have $g_k=A_k^t\mu$

We multiply by q^t; we obtain:

$q^t{g}_k=-\sum _{I_k}{\mu }^{( i)}$ (6)

(who can be positive for a global solution)

We distinguish her two following cases:

Case1. If $q^t{g}_k<0$ then we obtain a decreasing direction q from the linear system (1), so the point $x_k$ is not a global solution of problem (P) we therefore continue the calculation until find the best solution.

Case2. If $q^t{g}_k\ge 0 \mathrm{t}\mathrm{h}\mathrm{e}\mathrm{n}$ as we have ${\phi }_{k+1}={\phi }_k+{\propto }_k.g_k^{t}q+{\displaystyle \frac{1}{2}}{\propto }_k^2{q}^{t}Hq$ and

$$q^{t}Hq<0$$

two situations appear:

The first: If${\propto }_{\mathrm{k}}<{\propto }_{\mathrm{q}}$, then $x_k$ point is a global solution of our (P) problem, where

$${\propto }_k={}_{\begin{array}{c}i=1..,m\\ { with a}_i^{t}q > 0\end{array}}{}^{min} ( {\displaystyle \frac{b_i-{ a}_i^t{x}_k}{a_i^{t}q}} ){\propto }_{q,c}={\displaystyle \frac{-g_k^{t}q}{q^{t}Hq}} \text{and} {\propto }_{q,i}={\displaystyle \frac{-{2 g}_k^{t}q}{q^{t}Hq}} .$$

The second: If${ \propto }_k\ge {\propto }_q$ then we continue to do the same technical of minimization at the $x_k$ point, until find the global solution $x_G$ .

5. Inertia Controlling Method (I.C.M)

We note that the researchers have abandoned this method, which I believe could be improved and applied to help us solve our problem by introducing some changes (see section 4 in above) to obtain better results, especially since it relies on second-order conditions, whether related to the nature of the reduced Hessian matrix or the nature of the minimization direction.

Definition 1. (Stationary Point) [1]

We say the point $x_k$= $x_s$ is stationary point of problem (P) if we have these two followings conditions are hold:

• $g_k=A_k^t\mu$
• $Z_k^{t}H{Z}_k is D.P.$ (Positive Defined matrix)

Definition 2. (Minimization Direction)[1]

We say vector q $\in {IR}^n$ is the minimization direction of problem (P) in the point $x_k$, if we have once of these followings conditions is hold:

1. $g_k^{t}q<0$

2. $q^{t}Hq<0$(Direction of negative curvature)

Now, we give some important assumptions of I.C.M [1] technique’s used in our work.

A1. The objective function $\phi$ is bounded from bellow in the feasible region.

A2. All active constraints in x point are in the working set.

A3. The working-set matrix A has full row rank.

A4. The point x satisfies the first-order necessarily conditions for optimality.

Theorem. Let $x_k$ is a point of k^th iteration defined by $x_{k+1}=x_k+{\alpha }_{k}q$ then the estimation ${\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq+ {\propto }_k{g}_k^t(-q)$ is always decreasing in all cases, where q is a direction which is resulted by solving the following linear system

$$\left(\begin{array}{cc}H& A_k^t\\ A_k& 0\end{array}\right)\left(\begin{array}{c}q\\ u\end{array}\right)=\left(\begin{array}{c}{g}_k\\ 0\end{array}\right)$$

(7)

And ${\propto }_k$ is a steep length of function $\phi$ at point $x_k$

Proof.

We distinguish three cases to show the decreasing of the objective function at the $x_{k+1}$ point as follows:

• Convex case

When we have $g_k^{t}q$ is a positive value, we can change a direction q by (-q) which is given a negative value $g_k^t(-q)$, therefore we compute the value of ${\propto }_k$ by using the following formula:

$${\alpha }_k\le Min\left({Min{\displaystyle \frac{b_i-a_i^t{x}_k}{a_i^t\left(-q\right)}}}_{a_i^t\left(-q\right)>0}, {\displaystyle \frac{-g_k^t\left(-q\right)}{q^{t}Hq}}, 1\right)$$

(8)

Thus we have ${\displaystyle \frac{{\propto }_k}{2}}{q}^{t}Hq+ g_k^t\left(-q\right)<0$. Multiply by ${\alpha }_k$ both terms, we obtain the result

$${\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq+ {\propto }_k{g}_k^t(-q)<0.$$

Now, when we have $g_k^{t}q$ is a negative value, we repeat the same process changing only the direction (-q) by direction (q) and we will have the same result.

2.

Indefinite case

When we have $g_k^{t}q$ is a positive value with ${\propto }_k\ne 0$ (if it is zero we can add a constraint associated to this ${\propto }_k$ ) we change the direction q by direction (-q) which is given a negative value $g_k^t(-q)$ therefore we compute the value of ${\propto }_k$ by using the following formula:

$${\alpha }_k\le Min\left({Min{\displaystyle \frac{b_i-a_i^t{x}_k}{a_i^t\left(-q\right)}}}_{a_i^t\left(-q\right)>0}, {\displaystyle \frac{2g_k^t\left(-q\right)}{q^{t}Hq}}\right)$$

(9)

Thus we have

$${\displaystyle \frac{{\propto }_k}{2}}{q}^{t}Hq+ g_k^t\left(-q\right)<0.$$

Multiply by ${\alpha }_k$ both terms, we obtain the result

$${\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq+ {\propto }_k{g}_k^t(-q)<0.$$

Now, when we have $g_k^{t}q$ is a negative value, we repeat the same process changing only the direction (-q) by direction (q) and we will have the same result.

3-singular case

When we have $g_k^{t}q$ is a positive value with ${\propto }_k\ne 0$ (if it is zero we add a constraint associated to this ${\propto }_k$ ) we change the direction q by direction (-q) which is given a negative value $g_k^t(-q)$ therefore we compute the value of ${\propto }_k$ by using the following formula:

$${\alpha }_k\le Min({\displaystyle \frac{b_i-a_i^t{x}_k}{a_i^t\left(-q\right)}} such that a_i^t\left(-q\right) )>0$$

Thus we have

$$g_k^t\left(-q\right)<0.$$

Multiply by${ \alpha }_k$, this directly implies the following result

$${\displaystyle \frac{{\propto }_k^2}{2}}{q}^{t}Hq+ {\propto }_k{g}_k^t(-q)<0.$$

Now, when we have $g_k^{t}q$ is negative value, we repeat the same process changing only the direction (-q) by direction (q) and we will have the same result.

6. Algorithm

Algorithm for Finding Global Solution

Step 1: Choose an arbitrary initial solution $x_0$ in ${IR}^n$.

Step 2: Use the algorithm of the active point [^1] which returns several results: the associated matrix $A_0$ to the active point $x_a$ at iteration k with its kernel matrix $Z_0$ and that satisfies the linear system:

$$A_0{Z}_O=0_{m_0\times n_0},$$

and the gradient $g_0$

Step 3: Call the “subroutine in below” to find a stationary point $x_s$​ that satisfies:

• $A_s{Z}_s=0_{m_s\times n_s}$
• $Z_s^{t}H{Z}_s$​ is a positive definite matrix,
• $x_s$∈Fr(Δ) (see Definition 5.1.).

Step 4: Find a minimization direction q and the steep length ${\alpha }_s$ which corresponds to $x_s$​.

Step 5: Stopping conditions:

• If $q^{t}Hq<0$ :

  ○

  If${ (g}_k^{t}q\le 0 \mathrm{o}\mathrm{r}{(\propto }_{q, i}<{\propto }_s\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}{g}_k^{t}q>0))$Return to step3

  ○

  Else ( $g_k^{t}q>0$ with${\propto }_s\le {\propto }_{q, i}$ ) Proceed to step6

• Else if $q^{t}Hq$ >0:

  ○

  If ${ (g}_k^{t}q$ ≥0): → Proceed to Step 6.

  ○

  Else If ${ (g}_k^{t}q$ <0 with with ${\propto }_{q,c}\le {\propto }_s$) ​: → Proceed to Step 7.

  ○

  Else If ${ (g}_k^{t}q$ <0): → Take Min ( ${\propto }_k , {\propto }_{q, c}$) and return to Step 3.

• Else If $q^{t}Hq$ =0:

  ○

  If ${ (g}_k^{t}q$<0 ): → Return to Step 3.

  ○

  Else (${ g}_k^{t}q$≥0): → Proceed to Step 6.

Step 6: $x_k$​ is the global solution of (P). Terminate.

Step 7: $x_{k+1}$​ is the global solution of (P).Terminate.

Subroutine to calculate the stationary point

1-To determine the stationary point $x_s$ we solve the following linear system after verified $Z_k^{t}H{Z}_k$ is positive defined matrix (D.P)

$$\left(\begin{array}{cc}H& A_k^t\\ A_k& 0\end{array}\right)\left(\begin{array}{c}q\\ u\end{array}\right)=\left(\begin{array}{c}{g}_k\\ 0\end{array}\right)$$

such that

$A_k$ is an associated matrix to active point $x_k$ obtained at iteration k

$g_k$ is the gradient obtained at iteration k from the active point algorithm

2- If (q=0) then the stationary point is

$$x_s=x_k$$

Else we change the active point k=k+1,

$$x_{l+1}=x_k+{\propto }_{k}q$$

and repeat End

* ${\propto }_k$ is the steep length of case2-Step5 of Algorithm. That is to say

$${\propto }_k={\displaystyle \frac{-g_k^{t}q}{q^{t}Hq}}\ast$$

Remarks. We note these two remarks

1-The case 3 is a singular type. So it accepts the linear constraints which has a border domain.

2- Each iteration based on the resolution of linear systems characterized by the simplicity of the programming aspect as well as by the nature of the reduced Hessian matrix $Z_k^{t}H{Z}_k$ and the steep length ${\propto }_k$ .

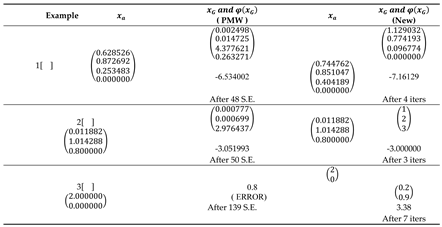
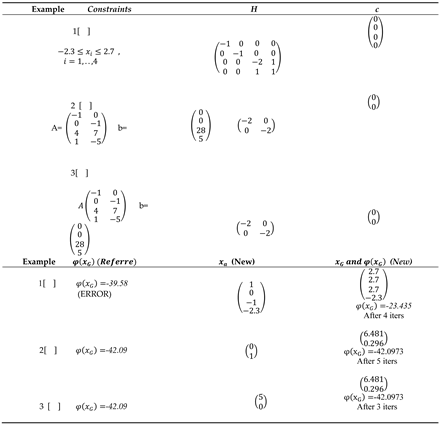
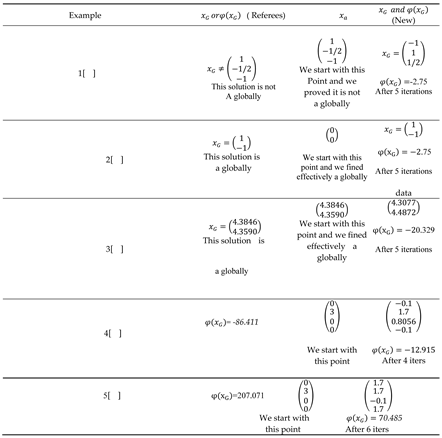
7. Numerical Results and Comparative Analysis

Our work is well justified by comparing it with some more recent methods with benchmarks used in the literature [7,13,14,15,16]. We note that the researchers left this track for a long time by used the Inertia-Controlling method, although with a small modification of this method, we managed to find good results.

In addition to the simplicity for verifying the global optimality conditions, the results have also been improved. In the concave case (Table 4).

However, in the indefinite case (Table 3) and convex cases (Table 2), our results are obtained with a minimal number of iterations and the determined solution is very better, which confirms the originality of our solving technique.

The results have also been improved. In the convex case (Table 1: Data for Convex Case Examples and Table 2: Results for Convex Case Examples). However, in the concave case (Table 3: Data for Concave Case

Examples and Table 4: results for Concave Case Examples) and indefinite case (Table 5: Data for Indefinite Case Examples and Table 6: Results for Indefinite Case Examples), our results are obtained with a minimal number of iterations and the determined solution is very better, which confirms the originality of our solving technique. 1-Convex case Results by using Path Method with Weight ( P.M.W. ) with depart point $x_0$. New Results with the same initial or depart point $x_0$.

Table 2. Data for Convex Case Examples.

Example A	H	B	c
1 [] $\left(\begin{array}{ccc}-1& \begin{array}{cc}0& 0\end{array}& 0\\ \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}\begin{array}{c}0\\ 1\end{array}\\ -1\end{array}\\ 1\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}-1\\ 0\end{array}\\ \begin{array}{c}\begin{array}{c}0\\ 1\end{array}\\ -1\end{array}\\ 5\end{array}& \begin{array}{c}0\\ \begin{array}{c}\begin{array}{c}-1\\ \begin{array}{c}0\\ 1\end{array}\end{array}\\ -1\end{array}\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}\begin{array}{c}-1\\ 0\end{array}\\ 0\end{array}\\ 1\end{array}\\ -1& \begin{array}{cc}-5& 0\end{array}& -1\end{array}\right)$	$\left(\begin{array}{ccc}4& \begin{array}{cc}-2& 0\end{array}& 0\\ -2& \begin{array}{cc}4& 0\end{array}& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\right)$	$\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\end{array}\\ 2\\ -2\end{array}\\ 5\\ -5\end{array}\right)$	$\left(\begin{array}{c}-4\\ \begin{array}{c}-6\\ 0\end{array}\\ 0\end{array}\right)$
2 [] $\left(\begin{array}{ccc}-1& 0& 0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 1\\ -1\end{array}\\ 1\end{array}& \begin{array}{c}-1\\ \begin{array}{c}0\\ 1\\ -1\end{array}\\ 1\end{array}& \begin{array}{c}0\\ \begin{array}{c}-1\\ 0\\ 0\end{array}\\ 1\end{array}\\ -1& -1& -1\end{array}\right)$	$\left(\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 0\end{array}\right)$	$\left(\begin{array}{c}0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 1\\ -1\end{array}\\ 2\end{array}\\ -2\end{array}\right)$	$\left(\begin{array}{c}-2\\ -4\\ 0\end{array}\right)$
3 [] $\left(\begin{array}{cc}-1& 0\\ \begin{array}{c}0\\ 1\\ -1\end{array}& \begin{array}{c}-1\\ 2\\ 2\end{array}\\ 1& -2\end{array}\right)$	$\left(\begin{array}{cc}1& 0\\ 0& 2.5\end{array}\right)$	$\left(\begin{array}{c}0\\ \begin{array}{c}0\\ 2\\ 2\end{array}\\ 2\end{array}\right)$	$\left(\begin{array}{c}-2\\ -5\end{array}\right)$

Table 2. Data for Convex Case Examples.

Example A	H	B	c
1 [] $\left(\begin{array}{ccc}-1& \begin{array}{cc}0& 0\end{array}& 0\\ \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}\begin{array}{c}0\\ 1\end{array}\\ -1\end{array}\\ 1\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}-1\\ 0\end{array}\\ \begin{array}{c}\begin{array}{c}0\\ 1\end{array}\\ -1\end{array}\\ 5\end{array}& \begin{array}{c}0\\ \begin{array}{c}\begin{array}{c}-1\\ \begin{array}{c}0\\ 1\end{array}\end{array}\\ -1\end{array}\\ 0\end{array}\end{array}& \begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ \begin{array}{c}\begin{array}{c}-1\\ 0\end{array}\\ 0\end{array}\\ 1\end{array}\\ -1& \begin{array}{cc}-5& 0\end{array}& -1\end{array}\right)$	$\left(\begin{array}{ccc}4& \begin{array}{cc}-2& 0\end{array}& 0\\ -2& \begin{array}{cc}4& 0\end{array}& 0\\ \begin{array}{c}0\\ 0\end{array}& \begin{array}{cc}\begin{array}{c}0\\ 0\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}& \begin{array}{c}0\\ 0\end{array}\end{array}\right)$	$\left(\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}0\\ 0\end{array}\\ 0\\ 0\end{array}\\ 2\\ -2\end{array}\\ 5\\ -5\end{array}\right)$	$\left(\begin{array}{c}-4\\ \begin{array}{c}-6\\ 0\end{array}\\ 0\end{array}\right)$
2 [] $\left(\begin{array}{ccc}-1& 0& 0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 1\\ -1\end{array}\\ 1\end{array}& \begin{array}{c}-1\\ \begin{array}{c}0\\ 1\\ -1\end{array}\\ 1\end{array}& \begin{array}{c}0\\ \begin{array}{c}-1\\ 0\\ 0\end{array}\\ 1\end{array}\\ -1& -1& -1\end{array}\right)$	$\left(\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 0\end{array}\right)$	$\left(\begin{array}{c}0\\ \begin{array}{c}0\\ \begin{array}{c}0\\ 1\\ -1\end{array}\\ 2\end{array}\\ -2\end{array}\right)$	$\left(\begin{array}{c}-2\\ -4\\ 0\end{array}\right)$
3 [] $\left(\begin{array}{cc}-1& 0\\ \begin{array}{c}0\\ 1\\ -1\end{array}& \begin{array}{c}-1\\ 2\\ 2\end{array}\\ 1& -2\end{array}\right)$	$\left(\begin{array}{cc}1& 0\\ 0& 2.5\end{array}\right)$	$\left(\begin{array}{c}0\\ \begin{array}{c}0\\ 2\\ 2\end{array}\\ 2\end{array}\right)$	$\left(\begin{array}{c}-2\\ -5\end{array}\right)$

Table 3. Results for Convex Case Examples.

Table 3. Results for Convex Case Examples.

Table 4. Data for Concave Case Examples.

Table 4. Data for Concave Case Examples.

Table 5. Data for Indefinite Case Examples.

Table 5. Data for Indefinite Case Examples.

Table 6. Results for Indefinite Case Examples.

Table 6. Results for Indefinite Case Examples.

8. Conclusion

In this article we have shown that it is possible to check the global optimization conditions to decide that completed point of the Inertia-Controlling method (I.C.M.)is a global solution or not.

In the fact that any optimization problem is solved by the necessary and sufficiently conditions of its solutions, when these conditions are satisfied at the point denoted in our (P) problem by$x_k$, this later becomes a solution to the considered problem.

However, if the relevant conditions are not found then we can’t obtain the exact solution.

Through these new sufficient conditions for global optimality we can apply any decreasing method converges to a local solution of problem (P) and we can also say that any point x of the field is a global solution of our mathematical problem or not, this is on the one hand.

On the other hand, the condition that we changed in this work depends on the solution of a linear system that is listed before in the local solution of objective function $\phi$, and in our theories, the given direction q is a best decreasing of the objective function$\phi$at$x_k$in terms of minimization, because all negative Eigen values of the matrix $Z_k^{t}H{Z}_k$ are taken, as we have also shown the decrease objective function at each active point in the convex, indefinite and singular case.

The results found provide high efficiency and reliability compared to the methods used (for example interior points) to resolve the quadratic programming problems at point of view of Accuracy and response times (a large number of iterations may be to find the solution).

Consequently, we recommend and ask that the method of I.C.M be seen again and used in many academic research which encourage university researchers to resort to this mathematical method to enrich their research in the scientific fields of applied mathematics and economics.