Convergence and Stability Improvement of Quasi-Newton Methods by Full-Rank Update of the Jacobian Approximates

1. Introduction

Root-finding methods are essential for solving a great class of numerical problems, such as data fitting problem with $\mathit{m}$ sampled data $\mathit{d}=\left[{\mathit{d}}_{\mathit{j}}\right]$ ($\mathit{j}=1,\dots ,\mathit{m}$) and $\mathit{n}$ adjustable parameters $\mathit{x}=\left[{\mathit{x}}_{\mathit{i}}\right]$ ($\mathit{i}=1,\dots ,\mathit{n}$) with $\mathit{m}\ge \mathit{n}$. It leads to the problem of least-squares solving of an overdetermined system of nonlinear equations

$$\mathit{f}\left(\mathit{x}\right)=\mathit{0}$$

(1.1)

($\mathit{x}\in$${\mathbb{R}}^{\mathit{n}}$ and $\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m$ ($\mathit{m}\ge \mathit{n}$)) where the solution ${\mathit{x}}^{*}$ minimizes the difference ${∥\mathit{f}\left(\mathit{x}\right)∥}_2=∥\varphi \left(\mathit{x}\right)-\mathit{d}∥$₂ between the data $\mathit{d}$ and a computational model function $\varphi \left(\mathit{x}\right)$. The system of simultaneous multi-variable nonlinear Equations (1.1) can be solved by the Newton’s method when the derivatives of $\mathit{f}\left(\mathit{x}\right)$ are available analitically and a new iterate

$${\mathit{x}}_{\mathit{p}+1}={\mathit{x}}_p-{\mathit{J}}_p^{-1}{\mathit{f}}_p$$

(1.2)

that follows ${\mathit{x}}_{\mathit{p}}$ can be determined, where ${\mathit{f}}_{\mathit{p}}=\mathit{f}\left({\mathit{x}}_p\right)$ is the function value and ${\mathit{J}}_{\mathit{p}}=\mathit{J}\left({\mathit{x}}_{\mathit{p}}\right)$ is the Jacobian matrix of $\mathit{f}$ at ${\mathit{x}}_{\mathit{p}}$ in the $p^{th}$ iteration step. It is well-known that the local convergence of Newton’s method is q-quadratic if the initial trial approximate ${\mathit{x}}_0$ is close enough to the solution ${\mathit{x}}^{*}$, $\mathit{J}\left({\mathit{x}}^{*}\right)$ is non-singular and $\mathit{J}\left(\mathit{x}\right)$ satisfies the Lipschitz condition

$$∥\mathit{J}\left(\mathit{x}\right)-\mathit{J}\left({\mathit{x}}^{*}\right)∥\le L∥\mathit{x}-{\mathit{x}}^{*}∥$$

(1.3)

for all $\mathit{x}$ close enough to ${\mathit{x}}^{*}$. However, in many cases, the function $\varphi \left(\mathit{x}\right)$ is not an analytical function, the partial derivatives are not known and Newton’s method cannot be applied. Quasi-Newton methods are defined as the generalization of Equation (1.2) as

$${\mathit{x}}_{\mathit{p}+1}={\mathit{x}}_p-{\mathit{B}}_p^{-1}{\mathit{f}}_p$$

(1.4)

and

$${\mathit{B}}_p▵{\mathit{x}}_{\mathit{p}}=-{\mathit{f}}_p$$

(1.5)

where

$$▵{\mathit{x}}_{\mathit{p}}={\mathit{x}}_{\mathit{p}+1}-{\mathit{x}}_{\mathit{p}}$$

(1.6)

is the iteration step length and ${\mathit{B}}_{\mathit{p}}$ is expected to be the approximate to the Jacobian matrix ${\mathit{J}}_{\mathit{p}}$ without computing derivatives in most cases. The new iterate is then given as

$${\mathit{x}}_{\mathit{p}+1}={\mathit{x}}_{\mathit{p}}+▵{\mathit{x}}_{\mathit{p}}$$

(1.7)

and ${\mathit{B}}_{\mathit{p}}$ is updated to ${\mathit{B}}_{\mathit{p}+1}$ according to the specific quasi-Newton method. Martinez [1] has been made a thorough survey on practical quasi-Newton methods. The iterative methods of the form 1.4 that satisfy the equation

$${\mathit{B}}_{p+1}▵{\mathit{x}}_{\mathit{p}}={\mathit{f}}_{p+1}-{\mathit{f}}_p$$

(1.8)

for all $\mathit{k}=0,1,2,\dots$ are called “quasi-Newton” methods and Equation (1.8) is called the fundamental equation of quasi-Newton methods (“quasi-Newton condition” or “secant equation”). However, the quasi-Newton condition doesn’t uniquely specify the updated Jacobian approximate ${\mathit{B}}_{\mathit{p}+1}$ and further constraints are needed. Different methods offer their own specific solution. One new quasi-Newton approximate ${\mathit{x}}_{\mathit{p}+1}$ will never allow full-rank update of ${\mathit{B}}_{\mathit{p}+1}$ because it is an $\mathit{n}\times \mathit{n}$ matrix and only $\mathit{n}$ components can be determined from the secant equation, making it an underdetermined system of equations for the elements $\left[B_{i,j,p+1}\right]$ $\left(\mathit{i},\mathit{j}=1,\dots \mathit{n}\right)$ if $\mathit{n}>1$.

The suggested new strategy is based on Wolfe’s [2] formulation of a generalized secant method. The function

$$\mathit{x}\to \mathit{f}\left(\mathit{x}\right),where\mathit{x}\in {\mathbb{R}}^{\mathit{n}}and\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^n,n>1$$

(1.9)

is locally replaced by linear interpolation through $\mathit{n}+1$ interpolation base points ${\mathit{A}}_{\mathit{p}}$, ${\mathit{B}}_{\mathit{p},\mathit{k}}$$\left(k=1,\dots ,n\right)$. The variables $\mathit{x}$ and the function values $\mathit{f}$ are separated into two equations and an auxiliary variable ${\mathit{q}}^A$ is introduced. Then the Jacobian approximate matrix ${\mathit{B}}_{\mathit{p}}$ is split into a variable difference $▵{\mathit{X}}_{\mathit{p}}$ and a function value difference $▵{\mathit{F}}_{\mathit{p}}$ matrix and the zero ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ of the ${\mathit{p}}^{\mathit{th}}$ interpolation plane is determined from the quasi-Newton condition 1.5 as

$$\left[\begin{array}{c}▵{\mathit{x}}_{p+1}^A\\ -{\mathit{f}}_p^A\end{array}\right]=\left[\begin{array}{c}▵{\mathit{X}}_p\\ ▵{\mathit{F}}_p\end{array}\right]{\mathit{q}}_p^A$$

(1.10)

where

$$▵{\mathit{x}}_{p+1}^A={\mathit{x}}_{p+1}^A-{\mathit{x}}_p^A$$

(1.11)

The auxiliary variable ${\mathit{q}}_p^A$ is determined from the 2^nd row of Equation (1.10) and the new quasi-Newton approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ comes from the 1^st row of this equation. Popper [3] made further generalization for functions

$$\mathit{x}\to \mathit{f}\left(\mathit{x}\right),where\mathit{x}\in {\mathbb{R}}^{\mathit{n}}and\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m,m\ge n>1$$

(1.12)

and suggested to use pseudo-inverse solution for the over determined system of linear equations (where $\mathit{n}$ is the number of unknowns and $\mathit{m}$ is the number of function values). The auxiliary variable ${\mathit{q}}_p^A$ is determined from the 2^nd row of Equation (1.10) as

$${\mathit{q}}_p^A=-▵{\mathit{F}}_{\mathit{p}}^{+}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(1.13)

where ${\left[.\right]}^{+}$ stands for the pseudo-inverse, and the new quasi-Newton approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ comes from the 1^st row of this equation as

$${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}_{\mathit{p}}^{\mathit{A}}-▵{\mathit{X}}_{\mathit{p}}▵{{\mathit{F}}_{\mathit{p}}}^{+}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(1.14)

The new iteration continues with $\mathit{n}+1$ new base points ${\mathit{A}}_{\mathit{p}+1}$, ${\mathit{B}}_{\mathit{p}+1,\mathit{k}}$ $\left(k=1,\dots ,n\right)$. Details are given in Section 3.

Ortega and Rheinboldt [4] stated that a necessary condition of convergence is that the interpolation base points should be linearly independent and they have to be “in general position” through the whole iteration process. Experiences show that the low-rank update procedures often lead to a dead end, because this condition is not satisfied. The purpose of the suggested new iteration strategy is to determine linearly independent base points providing that the Ortega and Rheinboldt condition is satisfied. The basic idea of the procedure is that another new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ is determined from the previous approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and a new system of $\mathit{n}$ linearly independent base points is generated. The basic equations of the Wolfe-Popper formulation (Equation (1.10)) were modified as

$$\left[\begin{array}{c}▵{\mathit{x}}_{p+1}\\ -{\mathit{f}}_p^A\end{array}\right]=\left[\begin{array}{cc}{\mathit{T}}_p^X& \mathit{0}\\ \mathit{0}& {\mathit{T}}_p^F\end{array}\right]\left[\begin{array}{c}▵{\mathit{X}}_p\\ ▵{\mathit{F}}_p\end{array}\right]{\mathit{q}}_p^B$$

(1.15)

where

$$▵{\mathit{x}}_{p+1}={\mathit{x}}_{p+1}^B-{\mathit{x}}_{p+1}^A$$

(1.16)

$${\mathit{T}}_p^X=diag\left({\mathit{t}}_{\mathit{p},\mathit{i}}^{\mathit{X}}\right)=\mathit{diag}\left(\frac{{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}}{{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}-{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}\right)$$

(1.17)

and

$${\mathit{T}}_{\mathit{p}}^{\mathit{F}}=\mathit{diag}\left(t_{p,j}^F\right)=diag\left(\frac{f_{p+1,j}^{\mathit{B}}-{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{f_{p+1,j}^{\mathit{A}}-{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)$$

(1.18)

The auxiliary variable ${\mathit{q}}_p^B$ is determined from the 2^nd row of Equation (1.15) as

$${\mathit{q}}_p^B=-▵{\mathit{F}}_p^{+}{\left({\mathit{T}}_p^F\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}=-\left[\sum _{\mathit{j}=1}^{\mathit{m}}\left(▵F_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)\right]$$

(1.19)

and the new quasi-Newton approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ comes from the 1^st row of Equation (1.15) as

$${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}+\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}{\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{B}}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}-\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}▵{\mathit{F}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(1.20)

$\left(i=1,\dots ,n\right)$. The details of the proposed new strategy (’T-Secant method’) is given in Section 4. It is different from the traditional secant method in a way, that all interpolation base points ${\mathit{A}}_{\mathit{p}}$ and $B_{p,k}$$\left(k=1,\dots ,n\right)$ are updated in each iteration (full-rank update) providing $\mathit{n}+1$ new base points ${\mathit{A}}_{\mathit{p}+\mathit{1}}$ and $B_{p+1,k}$ for the next iteration. The key idea of the method is very simple. The function value ${\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}$ (that can be determined from the new secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$) measures the ’distance’ of the approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ from the root ${\mathit{x}}^{*}$ (if ${\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}=\mathit{0}$, then the distance is zero and ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}^{*}$). The T-secant method uses this information so that the basic equations of the secant method are modified by a scaling transformation $\mathit{T}$ , and an additional new estimate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ is determined. Then the new approximates ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ are used to construct the $\mathit{n}+1$ new interpolation base points ${\mathit{A}}_{\mathit{p}+1}$ and $B_{p+1,k}$.

The T-secant procedure has been worked out for solving multi-variable problems, it can also be applied for solving single-variable ones, though. The geometrical representation of the latter one gives a good view to explain the mechanism of the procedure as shown in Section 5. It is a surprising result that the T-Secant modification corresponds to a hyperbolic function

$${\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)=\frac{a_p}{x-x_{p+1}^A}+f_p^A$$

(1.21)

the zero of which gives the second approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ in single variable case. A vector space interpretation is also given for the multvariable case in this section.

The general formulations of the proposed method are given in Section 6 and compared with the basic formula of classic quasi-Newton methods. It follows from Equation (1.14) that

$${\mathit{S}}_p▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(1.22)

where

$${\mathit{S}}_p=▵{\mathit{F}}_{\mathit{p}}▵{\mathit{X}}_{\mathit{p}}^{-\mathit{1}}=\left[\begin{array}{ccc}\frac{▵{\mathit{f}}_{1,1,\mathit{p}}}{▵{\mathit{x}}_1}& \dots & \frac{▵{\mathit{f}}_{\mathit{n},1,\mathit{p}}}{▵{\mathit{x}}_{\mathit{n}}}\\ ⋮& ⋮& ⋮\\ \frac{▵{\mathit{f}}_{1,\mathit{m},\mathrm{p}}}{▵{\mathit{x}}_1}& \cdots & \frac{▵{\mathit{f}}_{\mathit{n},\mathit{m},\mathrm{p}}}{▵{\mathit{x}}_{\mathit{n}}}\end{array}\right]=\left[\frac{▵{\mathit{f}}_{\mathit{k},,\mathit{j},\mathit{p}}}{▵{\mathit{x}}_{\mathit{i},\mathit{p}}}\right]$$

(1.23)

is the Jacobian approximate of the traditional secant method. It follows from the $1^{\mathit{st}}$ and $2^{\mathit{nd}}$ rows of Equation (1.15) of the T-Secant method and from the Definition 1.23 of ${\mathit{S}}_{\mathit{p}}$, that

$${\mathit{S}}_{\mathit{T},\mathit{p}}▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(1.24)

is the modified secant equation, where

$${\mathit{S}}_{T,p}={\mathit{T}}_p^F{\mathit{S}}_p{\left({\mathit{T}}_p^X\right)}^{-1}={\mathit{T}}_p^F▵{\mathit{F}}_{\mathit{p}}▵{\mathit{X}}_{\mathit{p}}^{-\mathit{1}}{\left({\mathit{T}}_p^X\right)}^{-1}=\left[\frac{{\mathit{t}}_{\mathit{j},\mathit{p}}^{\mathit{F}}}{t_{\mathit{i},\mathit{p}}^{\mathit{X}}}\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j},\mathit{p}}}{▵{\mathit{x}}_{\mathit{i},\mathit{p}}}\right]$$

(1.25)

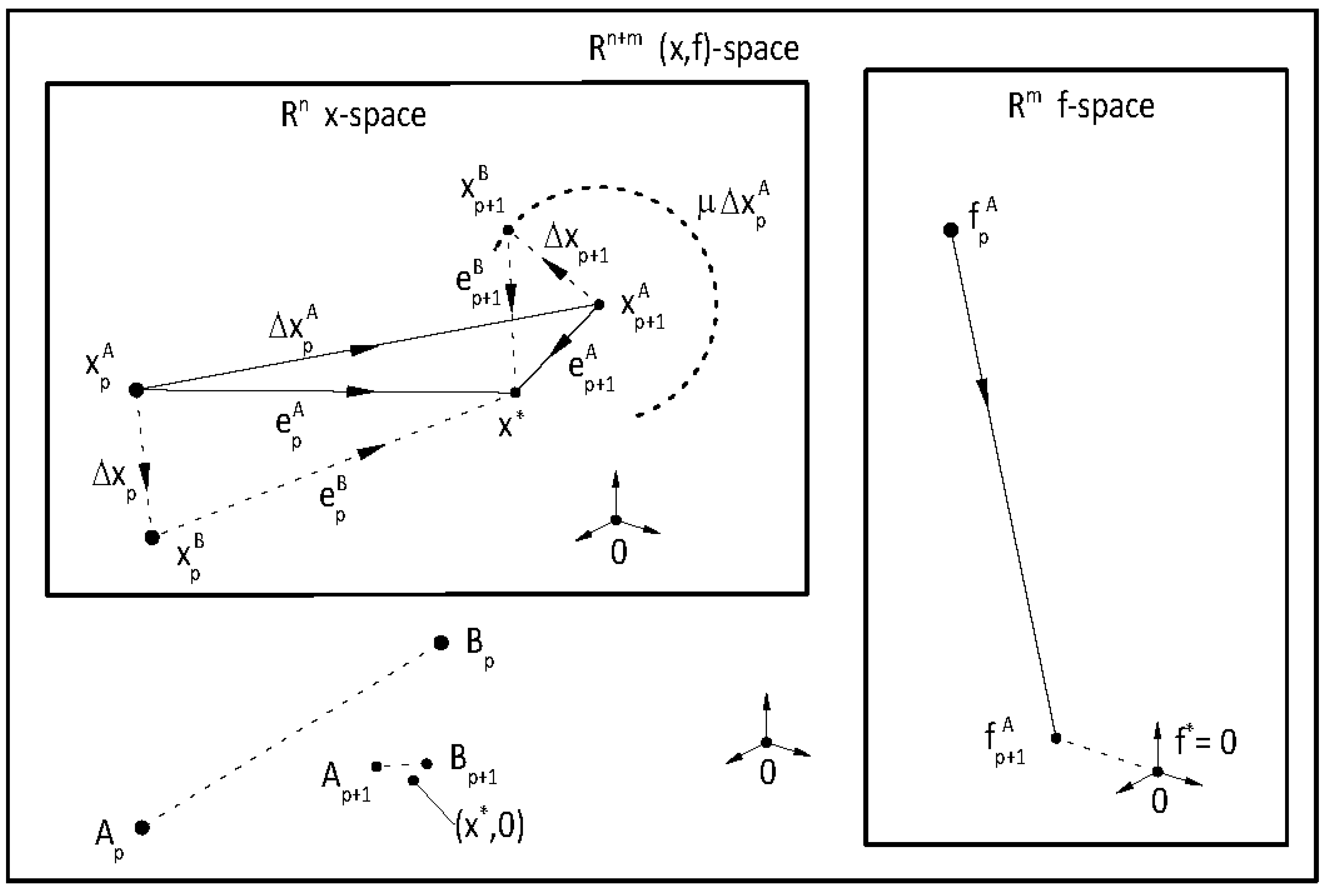
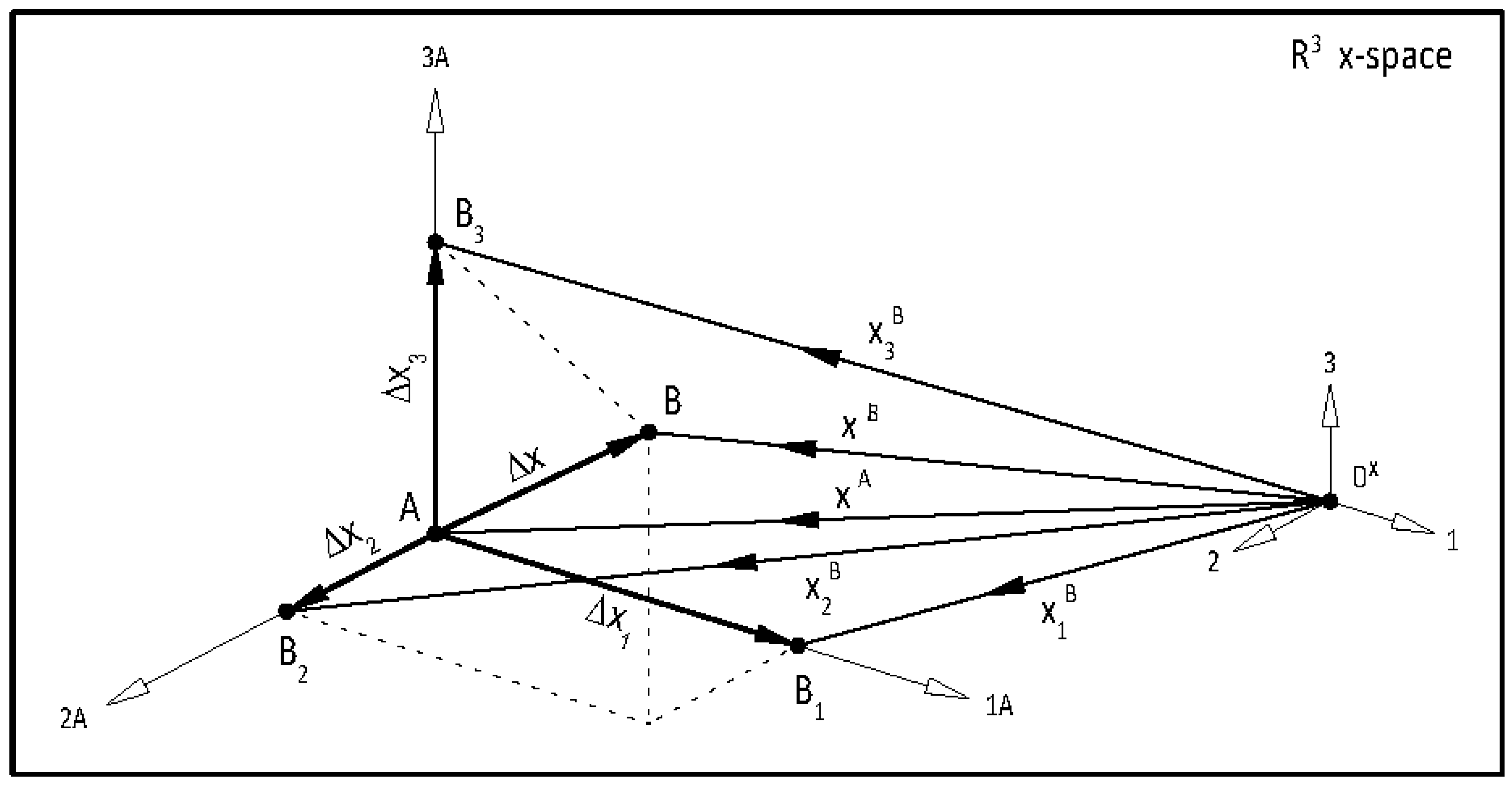
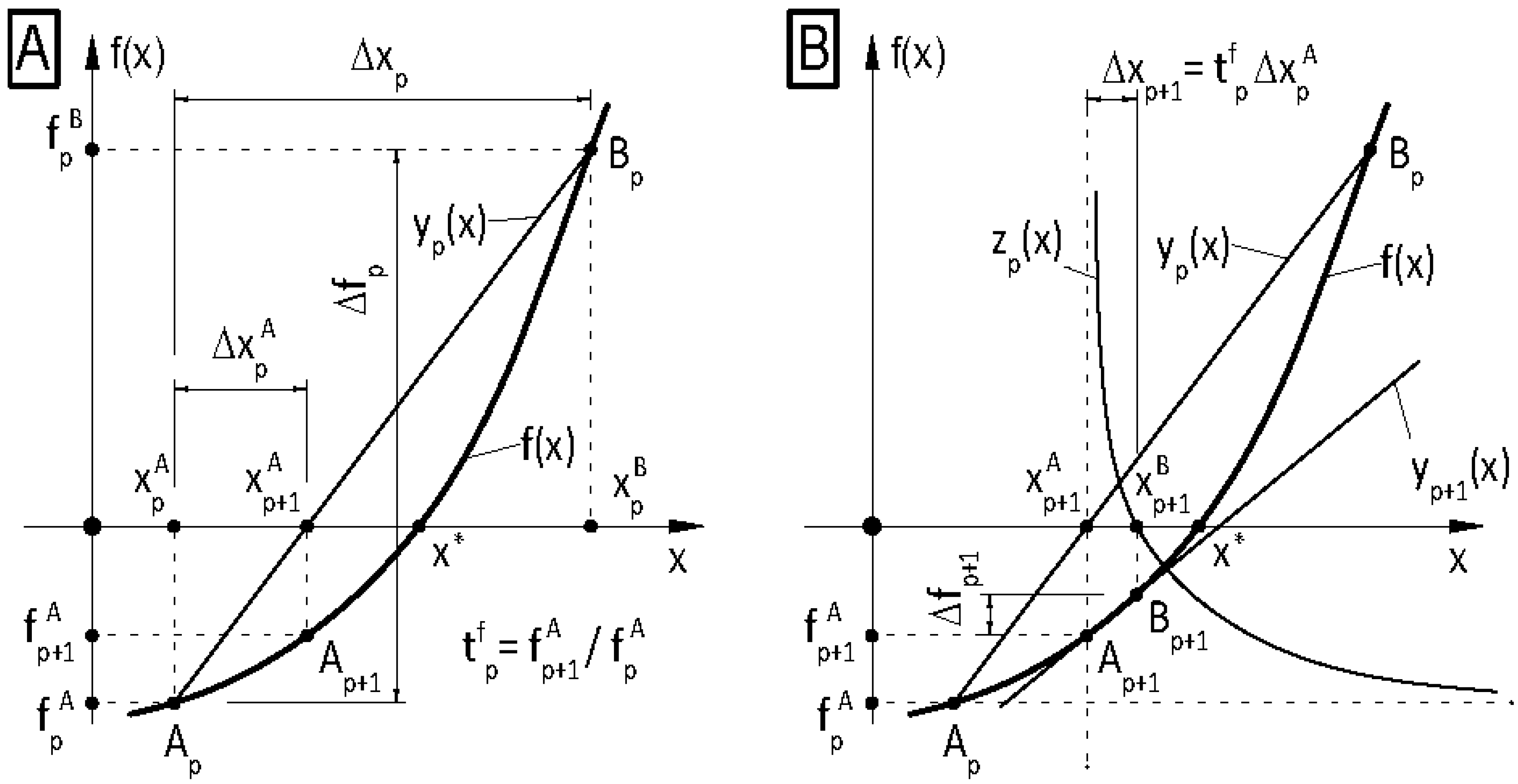
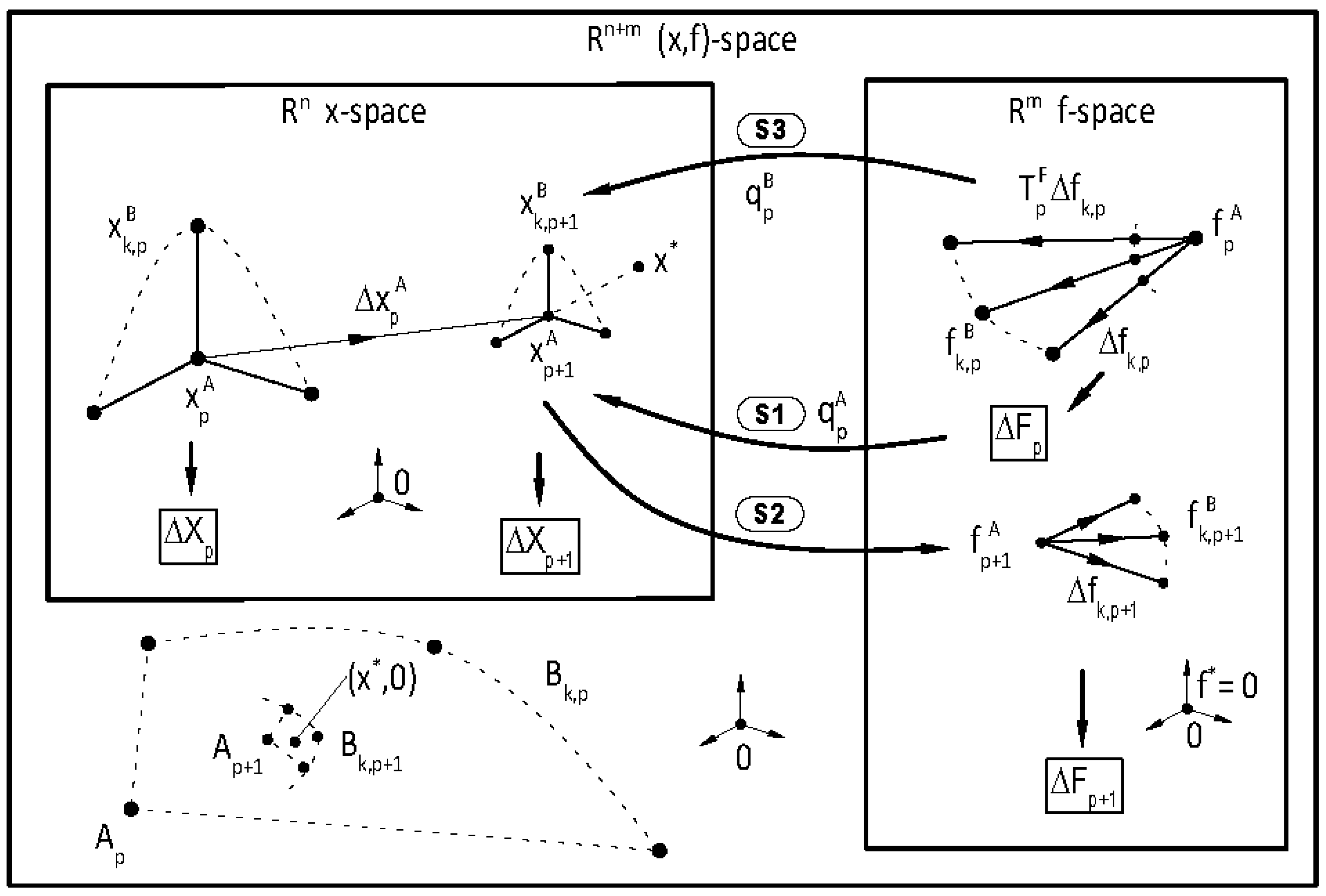
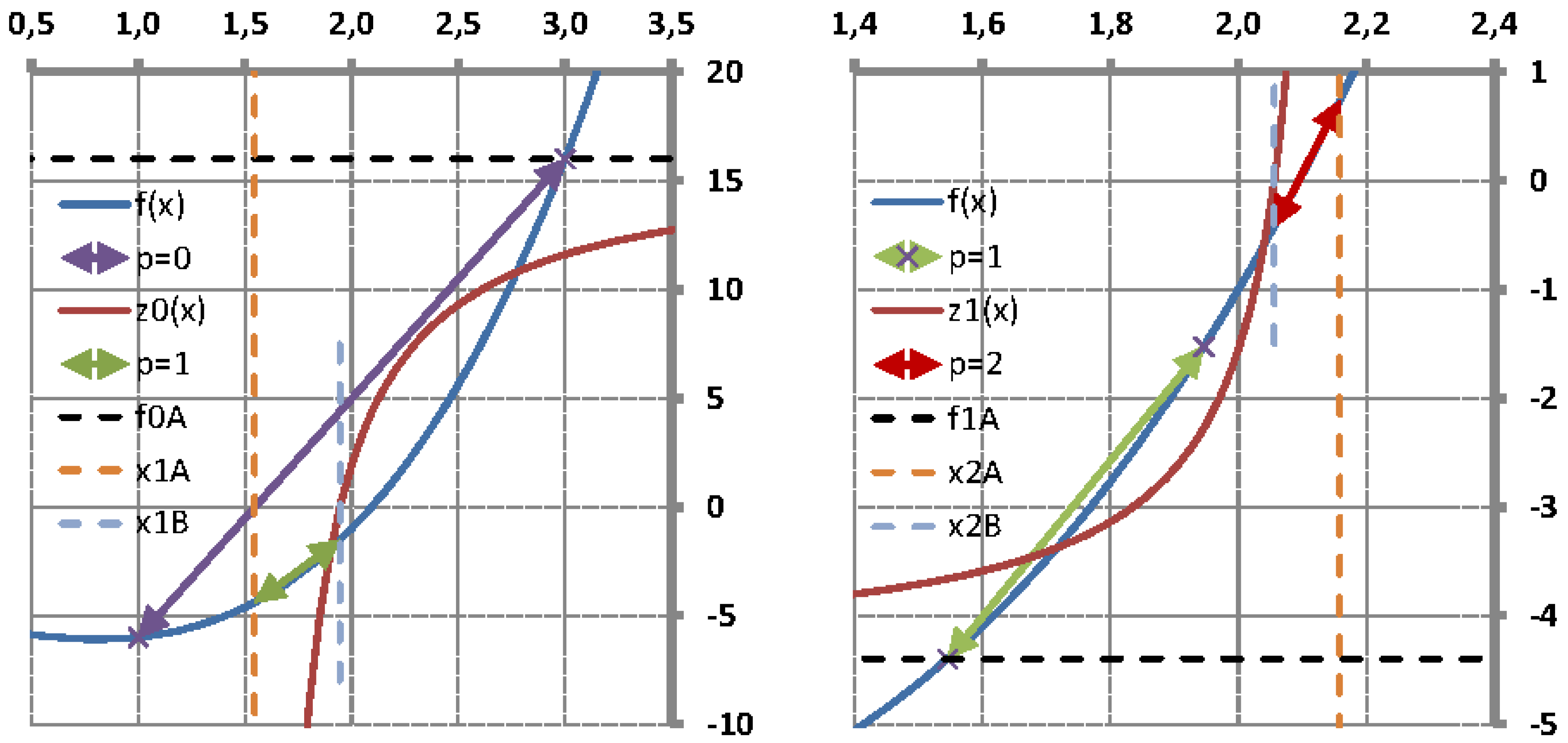
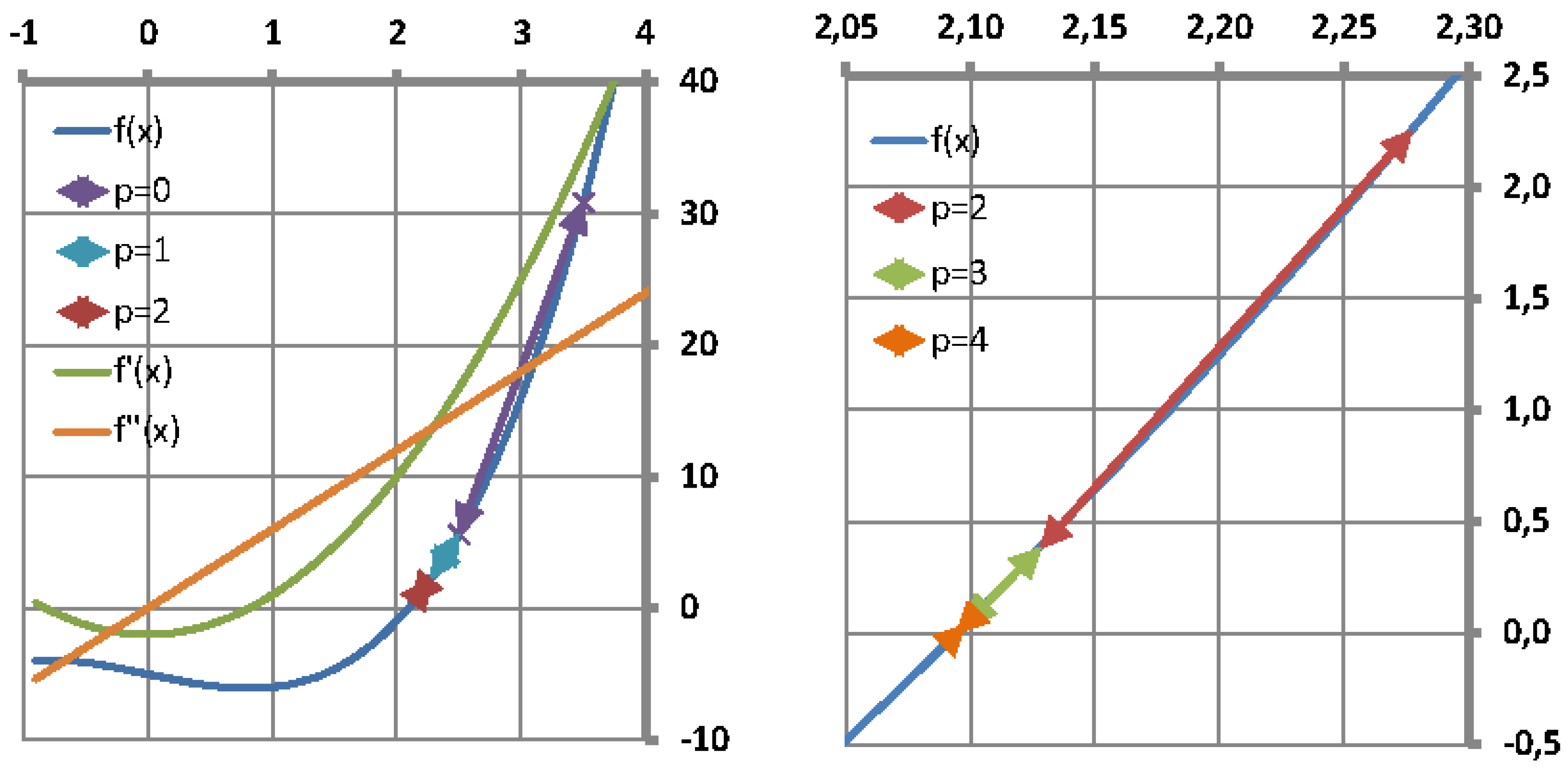
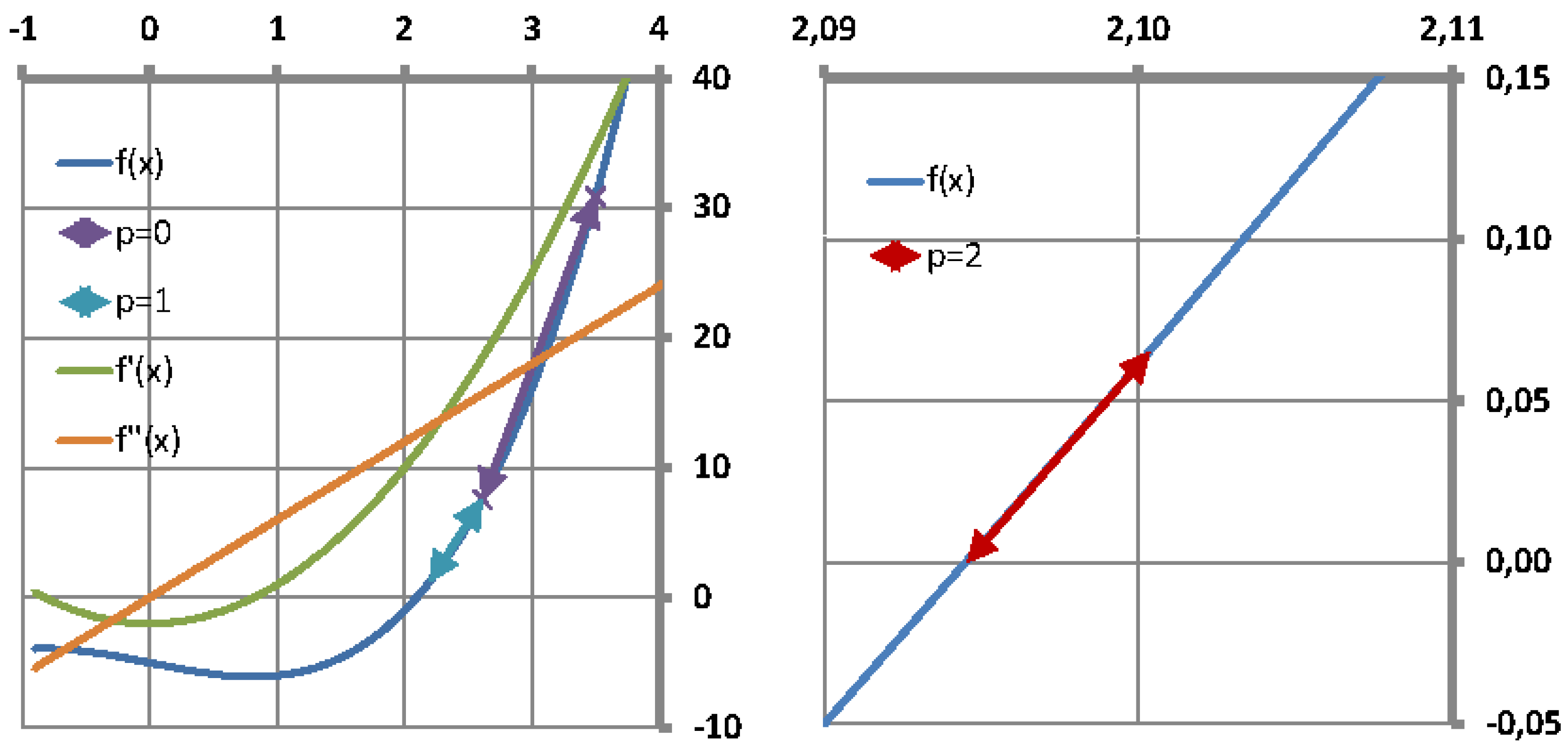
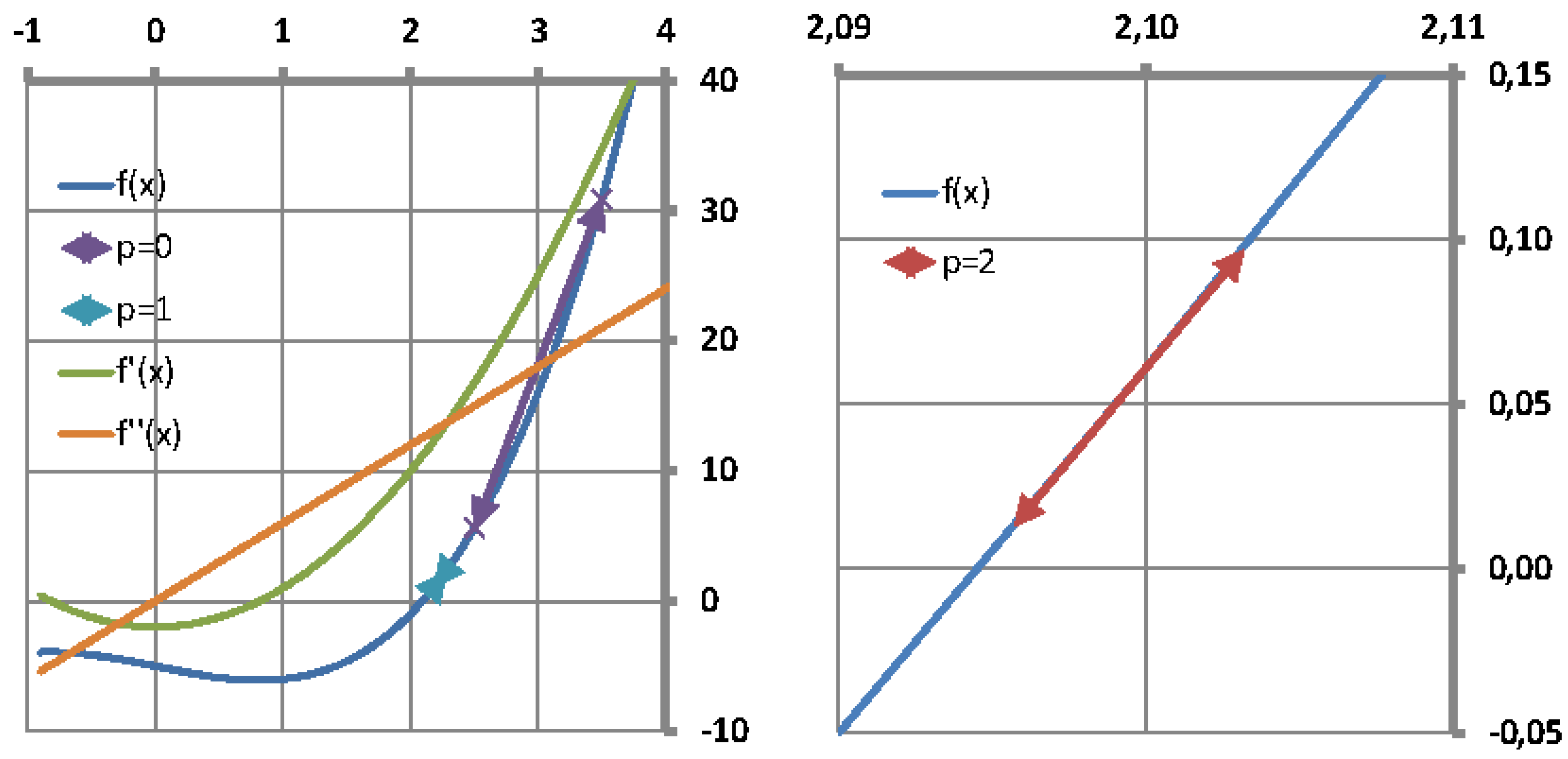
It is well known that the single-variable secant method has asymptotic convergence for sufficiently good initial approximates ${\mathit{x}}^{\mathit{A}}$ and ${\mathit{x}}^{\mathit{B}}$ if ${\mathit{f}}^{\prime }\left(\mathit{x}\right)$ doesn’t vanish in $\mathit{x}\in \left[\begin{array}{cc}{\mathit{x}}^{\mathit{A}}& {\mathit{x}}^{\mathit{B}}\end{array}\right]$ and ${\mathit{f}}^{″}\left(\mathit{x}\right)$ is continuous at least in a neighborhood of the zero ${\mathit{x}}^{*}$. The super-linear convergence property has been proved in different ways and it is known that the order of convergence is $\alpha =\left(1+\sqrt{5}\right)/2=\phi$ (where $\phi =1.618...$ is the golden ratio). The convergence order of the proposed method is determined in Section 7 and it is shown that it has super-quadratic convergence with rate ${\alpha }^{TS}=\phi +1={\phi }^2=2.618\dots$ in single variable case. It is also shown for the multi-variable case in this section, that the second approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ will always be in the vicinity of the classic secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$, providing that the solution ${\mathit{x}}^{*}$will evenly be surrounded by the $\mathit{n}+1$ new trial approximates, and matrix ${\mathit{S}}_{\mathit{p}+1}$ will be well-conditioned.

A step-by-step algorithm is given in Section 8 and the results of numerical tests with a Rosenbrock-type test function demonstrates the stability of the proposed strategy in Section 9 for up to 1000 unknown variables. The Broyden-type efficiency (mean convergence rate) of the proposed method is studied in multi-variable case in Section 10 and it is compared with other classic rank-one update and line-search methods on the basis of available test data. It is shown in Section 11 how the new procedure can be used to improve the convergence of other classic multi-variable root finding methods (Newton-Raphson and Broyden methods). Concluding remarks are summarized in Section 12. Among others, the method has been used for the identification of vibrating mechanical systems (foundation pile driving [5], percussive drilling [6]) and found to be very stable and efficient even in case of large number of unknowns.

The proposed method needs $\mathit{n}+1$ function value evaluations in each iteration and it is not using the derivative information of the function, like the Newton-Raphson method is doing. On the other hand, it needs $\mathit{n}$ more function evaluations than the traditional secant method needs in each iteration. However, it is an apparent disadvantage, as the convergence rate considerably increases (${\alpha }^{\mathrm{TS}}\cong 2.618...$), furthermore the stability and the efficiency of the procedure has been highly improved.

2. Notations

Vectors and matrices are denoted by bold-face letters. Subscripts refer to components of vectors and matrices, superscripts $\mathit{A}$ and $\mathit{B}$ refer to interpolation base points. Vectors and matrices may also be given by their general elements. $▵$ refers to a difference of two elements. $\mathit{x}$ and $\mathit{X}$ denotes unknown quantities, $\mathit{f}$ and $\mathit{F}$ denotes function values and matrices. $\mathit{q}$, $\mathit{q}$, $\mathit{t}$, and $\mathit{T}$ denotes multiplier scalars, vectors and matrices. $\mathit{e}$, $\epsilon$ and $\mathit{E}$ denotes approximate error, $\mathit{p}$ is iteration counter, $\alpha$ is convergence rate, ${\epsilon }^{*}$ is termination criterion. $\mathit{n}$ is the number of unknowns, $\mathit{m}$ is the number of function values, $\mathit{i}$, $\mathit{j}$, $\mathit{k}$ and l are running indexes of matrix columns and rows. Superscripts $\mathit{S}$ and $\mathit{TS}$ refer to the traditional Secant-method and to the proposed T-Secant method receptively.

3. Secant method

The history of the secant method in single variable case is several thousands years old, its origin was found in ancient time. The idea of finding the scalar root $x^{*}$of a scalar nonlinear function

$$x\to f\left(x\right)(where\mathit{x}\in {\mathbb{R}}^{1}andf:{\mathbb{R}}^1\to {\mathbb{R}}^1)$$

(3.1)

by successive local replacement of the function by linear interpolation (secant line) gives a simple and efficient numerical procedure. It has an advantage that it doesn’t need the calculation of function derivatives, it only uses function values and the order of asymptotic convergence is super-linear with convergence rate ${\alpha }^S\cong 1.618...$.

The function $\mathit{f}\left(\mathit{x}\right)$ is locally replaced by linear interpolation (secant line) through interpolation base points $\mathit{A}$ and $\mathit{B}$ and the zero ${\mathit{x}}^{\mathit{A}}$ of the secant line is determined as an approximate to the zero ${\mathit{x}}^{*}$ of the function. The next iteration continues with new base points, selected from available old ones. Wolfe [2] extended the scalar procedure to multidimensional

$$\mathit{x}\to \mathit{f}\left(\mathit{x}\right),where\mathit{x}\in {\mathbb{R}}^{\mathit{n}}and\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^n,n>1$$

(3.2)

and Popper [3] made further generalization

$$\mathit{x}\to \mathit{f}\left(\mathit{x}\right),where\mathit{x}\in {\mathbb{R}}^{\mathit{n}}and\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m,m\ge n>1$$

(3.3)

and suggested to use pseudo-inverse solution for the over determined system of linear equations (where $\mathit{n}$ is the number of unknowns and $\mathit{m}$ is the number of function values).

The zero ${\mathit{x}}^{*}$ of the nonlinear function $\mathit{x}\to \mathit{f}\left(\mathit{x}\right)$ has to be found, where $\mathit{x}\in$${\mathbb{R}}^{\mathit{n}}$ and $\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m$. Let ${\mathit{x}}^A$ be the initial trial for the zero ${\mathit{x}}^{*}$, and let the function $\mathit{f}\left(\mathit{x}\right)$ be linearly interpolated through $\mathit{n}+1$ interpolation base points $A\left(\begin{array}{cc}{\mathit{x}}^A& {\mathit{f}}^A\end{array}\right)$ and $B_k\left(\begin{array}{cc}{\mathit{x}}_k^B& {\mathit{f}}_k^B\end{array}\right)$$\left(k=1,\dots ,n\right)$ and be approximated / replaced by the interpolation “plane” $\mathit{y}\left(\mathit{x}\right)$ near ${\mathit{x}}^{*}$. One of the key ideas of the suggested numerical procedure is that interpolation base points $B_k\left(\begin{array}{cc}{\mathit{x}}_k^B& {\mathit{f}}_k^B\end{array}\right)$ are constructed by individually increment the coordinates ${\mathit{x}}_{\mathit{i}}^{\mathit{A}}$ of the initial trial ${\mathit{x}}^A$ by an “initial trial increment” value $▵{\mathit{x}}_{\mathit{i}}$$\left(i=1,\dots ,n\right)$ as

$$x_{k,i}^B=x_i^A+▵{\mathit{x}}_{\mathrm{i}}$$

(3.4)

or in vector form as

$${\mathit{x}}_k^B={\mathit{x}}^A+▵{\mathit{x}}_{\mathit{k}}{\mathit{d}}^k$$

(3.5)

where ${\mathit{d}}^{\mathit{k}}$ is the $k^{th}$ Cartesian unit vector as shown on Figure 1.

It follows from this special construction of the initial trials ${\mathit{x}}_{\mathit{k}}^{\mathit{B}}$ , that ${\mathit{x}}_{\mathit{k},\mathit{i}}^{\mathit{B}}-x_i^A=0$ for $\mathit{i}\ne \mathit{k}$ and ${\mathit{x}}_{\mathit{k},\mathit{i}}^{\mathit{B}}-x_i^A=▵x_i$ for $\mathit{i}=\mathit{k}$ providing that

$$▵\mathit{x}=\left[x_{i,i}^B-x_i^A\right]=\left[▵x_i\right]$$

(3.6)

is the “initial trial increment vector”. Let

$$▵{\mathit{f}}_k=\left[▵f_{k,j}\right]=\left[f_{k,j}^B-f_j^A\right]$$

(3.7)

$\left(j=1,\dots ,m\right)$. Any point on the $\mathit{n}$ dimensional interpolation plane $\mathit{y}\left(\mathit{x}\right)$ can be expressed as

$$\left[\begin{array}{c}\mathit{x}\\ \mathit{y}\left(\mathit{x}\right)\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}^A\\ {\mathit{f}}^A\end{array}\right]+\left[\begin{array}{c}▵\mathit{X}\\ ▵\mathit{F}\end{array}\right]{\mathit{q}}^A$$

(3.8)

where

$$▵\mathit{X}=\left[{\mathit{x}}_k^B-{\mathit{x}}^A\right]=\left[\begin{array}{ccc}{x}_{1,1}^B-x_1^A& \cdots & x_{n,1}^B-x_1^A\\ ⋮& \ddots & ⋮\\ x_{1,n}^B-x_n^A& \cdots & x_{n,n}^B-x_n^A\end{array}\right]$$

(3.9)

$$▵\mathit{F}=\left[{\mathit{f}}_k^B-{\mathit{f}}^A\right]=\left[\begin{array}{ccc}{f}_{1,1}^B-f_1^A& \cdots & f_{n,1}^B-f_1^A\\ ⋮& ⋮& ⋮\\ f_{1,m}^B-f_m^A& \cdots & f_{n,m}^B-f_m^A\end{array}\right]$$

(3.10)

$\left(k=1,\dots ,n\right)$, ${\mathit{q}}^{\mathit{A}}$ is a vector with $\mathit{n}$ scalar multipliers $q_i^A,\left(i=1,\dots ,n\right)$ and as a consequence of Equation (3.5)

$$▵\mathit{X}=\left[▵{\mathit{x}}_k\right]=\left[\begin{array}{ccc}▵x_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & ▵x_n\end{array}\right]=diag\left(▵x_i\right)$$

(3.11)

is a diagonal matrix that has great computational advantage. It also follows from Definition 3.7 that

$$▵\mathit{F}=\left[▵{\mathit{f}}_k\right]=\left[\begin{array}{ccc}▵f_{1,1}& \cdots & ▵f_{n,1}\\ ⋮& ⋮& ⋮\\ ▵f_{1,m}& \cdots & ▵f_{n,m}\end{array}\right]$$

(3.12)

Let ${\mathit{x}}_{p+1}^A$ be the zero of the n-dimensional interpolation plane ${\mathit{y}}_p\left(\mathit{x}\right)$ in the ${\mathit{p}}^{\mathit{th}}$ iteration with interpolation base points $A_p\left(\begin{array}{cc}{\mathit{x}}_p^A& {\mathit{f}}_p^A\end{array}\right)$ and $B_{k,p}\left(\begin{array}{cc}{\mathit{x}}_{k,p}^B& {\mathit{f}}_{k,p}^B\end{array}\right)$. Then it follows from the zero condition

$${\mathit{y}}_p\left({\mathit{x}}_{p+1}^A\right)=\mathit{0}$$

(3.13)

and from the $2^{\mathit{nd}}$ row of Equation (3.8) that

$$▵{\mathit{F}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(3.14)

and the vector ${\mathit{q}}_p^A$ of multipliers ${\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{A}}$ can be expressed as

$${\mathit{q}}_p^A=-▵{\mathit{F}}_{\mathit{p}}^{+}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(3.15)

where ${\left[.\right]}^{+}$ stands for the pseudo-inverse. Let

$$\left[\begin{array}{c}▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\\ ▵{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_{p+1}^A-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\\ {\mathit{f}}_{p+1}^A-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\end{array}\right]$$

(3.16)

be the iteration step-size of the secant method, then it follows from the $1^{\mathit{st}}$ row of Equation (3.8) and from Equation (3.15), that

$$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=▵{\mathit{X}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-▵{\mathit{X}}_{\mathit{p}}▵{\mathit{F}}_{\mathit{p}}^{+}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(3.17)

and from Definition 3.16 it follows that

$$\left[\begin{array}{c}{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}\\ {\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_p^A+▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\\ {\mathit{f}}_{\mathit{p}}^{\mathit{A}}+▵{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\end{array}\right]$$

(3.18)

and the new secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ can be expressed from Equation (3.17) as

$${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}_{\mathit{p}}^{\mathit{A}}+▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(3.19)

A base point ${\mathit{A}}_{\mathit{p}+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}\right)$ and base vector ${\mathit{v}}_{\mathit{p}+1}^{\mathit{A}}=\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}\right)$ can than be determined for the next iteration. In single variable case $\left(\mathit{m}=\mathit{n}=\mathit{k}=1\right)$ with interpolation base points $A_p\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}},{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\right)$ and $B_p\left({\mathit{x}}_{\mathit{p}}^{\mathit{B}},{\mathit{f}}_{\mathit{p}}^{\mathit{B}}\right)$, Equation (3.15) will have the form

$$q_p^A=-\frac{f_p^A}{f_p^B-f_p^A}=-\frac{f_p^A}{▵f_p}$$

(3.20)

and the new secant approximate

$$x_{p+1}^A=x_p^A+▵x_p{q}_p^A=x_p^A-\frac{▵x_p}{▵f_p}{f}_p^A=\frac{x_p^A{f}_p^B-x_p^B{f}_p^A}{f_p^B-f_p^A}$$

(3.21)

can be determined according to Equation (3.19). The procedure then continues with interpolation base points $A_{p+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}\right)$ and $B_{p+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{B}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{B}}\right)$.

4. T-Secant method

4.1. Single-variable case

The T-secant method is different from the traditional secant method in a way, that all interpolation base points ${\mathit{A}}_{\mathit{p}}$ and $B_{p,k}$$\left(k=1,\dots ,n\right)$ are updated in each iteration providing $\mathit{n}+1$ new base points ${\mathit{A}}_{\mathit{p}+\mathit{1}}$ and $B_{p+1,k}$ for the next iteration. The key idea of the method is very simple. The function value ${\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}$ (that can be determined from the new secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$) measures the ’distance’ of the approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ from the root ${\mathit{x}}^{*}$ (if ${\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}=\mathit{0}$, then the distance is zero and ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}^{*}$). The T-secant method uses this information to determine another approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$. In single variable case$\left(\mathit{m}=\mathit{n}=\mathit{k}=1\right)$ with interpolation base points $A_p$ and $B_p$, the basic equation

$$▵f_p{q}_p^A=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(4.1)

of the secant method (Equation (3.14) in multi-variable case) is modified by a factor

$$t_p^f=\frac{f_{p+1}^A}{f_p^A}$$

(4.2)

that expresses the ’improvement rate’ of the new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ to the original approximate ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$, providing the T-secant modified basic equation

$$t_p^f▵f_p{q}_p^B=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(4.3)

Then the T-secant multiplier

$$q_p^B=\frac{q_p^A}{t_p^f}=-\frac{{\left(f_p^A\right)}^2}{f_{p+1}^A▵f_p}$$

(4.4)

can be determined. The other basic equation

$$▵x_p^A=▵x_p{q}_p^A$$

(4.5)

of the secant method (Equation (3.17) in multi-variable case) with iteration step size

$$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(4.6)

is also modified in a similar way like in case of Equation (4.1) and Equation (4.3) by a factor

$${\mathit{t}}_{\mathit{p}}^{\mathit{x}}=\frac{{\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}}{{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}=\frac{▵{\mathit{x}}_{\mathit{p}+1}}{▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}$$

(4.7)

that expresses the ’improvement rate’ of the new ’T-secant approximate change’ $▵{\mathit{x}}_{\mathit{p}+1}$ to the previous ’secant iteration step size’ $▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ , providing a new basic equation

$$▵x_p^A=t_p^x▵x_p{q}_p^B$$

(4.8)

from which

$$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=\frac{▵{\mathit{x}}_{\mathit{p}+1}}{▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}▵x_p{q}_p^B$$

(4.9)

and

$${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-\frac{{\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}}{{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}\left({\mathit{x}}_{\mathit{p}}^{\mathit{B}}-x_p^A\right)\frac{{\left(f_p^A\right)}^2}{f_{p+1}^A\left(f_p^B-f_p^A\right)}$$

(4.10)

By re-ordering Equation (4.10), the T-secant approximate

$$x_{p+1}^{\mathit{B}}=x_{p+1}^A+\frac{{\left(▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p}}{q}_p^B}=x_{p+1}^A-\frac{{\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^2\left(f_p^B-f_p^A\right)f_{p+1}^A}{\left({\mathit{x}}_{\mathit{p}}^{\mathit{B}}-x_p^A\right){\left(f_p^A\right)}^2}$$

(4.11)

can be determined and it is used to update the original interpolation base point $B_p$ to $B_{p+1}$. The new iteration will then continue with new base points ${\mathit{A}}_{\mathit{p}+\mathit{1}}$ and $B_{p+1}$. Note, that it follows from Equations (4.4), (4.5) and (4.11) that

$$▵x_{p+1}=x_{p+1}^B-x_{p+1}^A=\frac{{\left(▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p}}{q}_p^B}=t_p^f\frac{{\left(▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p}}{q}_p^A}=t_p^f▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(4.12)

4.2. Multi-variable case

In multi-variable case $\left(\mathit{m}\ge \mathit{n}>\mathit{1}\right)$ with $\left(\mathit{n}+1\right)$ interpolation base points $A_p\left(\begin{array}{cc}{\mathit{x}}_p^A& {\mathit{f}}_p^A\end{array}\right)$ and $B_{p,k}\left(\begin{array}{cc}{\mathit{x}}_{p,k}^B& {\mathit{f}}_{p,k}^B\end{array}\right)$$\left(k=1,\dots ,n\right)$, the basic equations of the secant method (Equation (3.14) and 3.17) are modified as

$${\mathit{T}}_p^F▵{\mathit{F}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{B}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(4.13)

and

$$▵{\mathit{x}}_p^{\mathit{A}}={\mathit{T}}_p^X▵{\mathit{X}}_{\mathit{p}}{\mathit{q}}_p^{\mathit{B}}$$

(4.14)

Then a vector based equation can be formulated like in case of the traditional secant method (see Equation (3.8)) in a form

$$\left[\begin{array}{c}\mathit{x}-▵\mathit{x}\\ \mathit{z}\left(\mathit{x}\right)\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}^A\\ {\mathit{f}}^A\end{array}\right]+\left[\begin{array}{cc}{\mathit{T}}^X& \mathit{0}\\ \mathit{0}& {\mathit{T}}^F\end{array}\right]\left[\begin{array}{c}▵\mathit{X}\\ ▵\mathit{F}\end{array}\right]{\mathit{q}}^B$$

(4.15)

where $▵\mathit{X}$ and $▵\mathit{F}$ are defined in 3.9 and 3.10, $\mathit{z}\left(\mathit{x}\right)$ is a function with zero at ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{B}}$ and the diagonal transformation matrix in the ${\mathit{p}}^{\mathit{th}}$ iteration is

$${\mathit{T}}_p=\left[\begin{array}{cc}{\mathit{T}}_p^X& \mathit{0}\\ \mathit{0}& {\mathit{T}}_p^F\end{array}\right]$$

(4.16)

with ${\mathit{T}}_p^X$ and ${\mathit{T}}_p^F$ sub-diagonals, where

$${\mathit{T}}_p^X=diag\left({\mathit{t}}_{\mathit{p},\mathit{i}}^{\mathit{X}}\right)=\mathit{diag}\left(\frac{{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}}{{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}-{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}\right)=\mathit{diag}\left(\frac{▵{\mathit{x}}_{\mathit{p}+1,\mathit{i}}}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}\right)$$

(4.17)

$${\mathit{T}}_{\mathit{p}}^{\mathit{F}}=\mathit{diag}\left(t_{p,j}^F\right)=diag\left(\frac{f_{p+1,j}^{\mathit{B}}-{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{f_{p+1,j}^{\mathit{A}}-{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)$$

(4.18)

and ${\mathit{T}}_{\mathit{p}}^{\mathit{F}}$ is approximated with the assumption $\mathit{f}\left(\mathit{x}\right)\simeq {\mathit{y}}_{\mathit{p}}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}\right)\simeq {\mathit{z}}_{\mathit{p}}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}\right)$ and according to the conditions ${\mathit{y}}_{\mathit{p}}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}\right)=0$ and ${\mathit{z}}_p\left({\mathit{x}}_{p+1}^B\right)=0$ as

$${\mathit{T}}_{\mathit{p}}^{\mathit{F}}\simeq \mathit{diag}\left(\frac{{\mathit{z}}_{\mathit{p},\mathit{j}}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}\right)-{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{{\mathit{y}}_{\mathit{p},\mathit{j}}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}\right)-{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)=diag\left(\frac{{\mathit{f}}_{\mathit{p}+\mathit{1},\mathit{j}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)$$

(4.19)

$\left(i=1,\dots ,n\right)$, $\left(j=1,\dots ,m\right)$, where ${\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}\ne 0$. The vector of T-secant multipliers

$${\mathit{q}}_p^B=-▵{\mathit{F}}_p^{+}{\left({\mathit{T}}_p^F\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}=-\left[\sum _{\mathit{j}=1}^{\mathit{m}}\left(▵F_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)\right]$$

(4.20)

can be determined from Equation (4.13) , where ${\left[.\right]}^{+}$ stands for the pseudo-inverse ($▵{\mathit{F}}_p^{+}$ has already been calculated when ${\mathit{q}}_p^A$ was determined from Equation (3.15)). The ${\mathit{i}}^{\mathit{th}}$ element of the new approximate ${\mathit{x}}_{p+1}^B$ can be expressed from the ${\mathit{i}}^{\mathit{th}}$ row of Equation (4.14) as

$$▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}=\frac{▵{\mathit{x}}_{\mathit{p}+1,\mathit{i}}}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}▵x_{p,i}{q}_{p,i}^B=\frac{{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}▵x_{p,i}{q}_{p,i}^B$$

(4.21)

and the T-Secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ can be calculated as

$${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}+\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}{\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{B}}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}-\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}▵{\mathit{F}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(4.22)

where $▵{\mathit{x}}_{\mathit{p},\mathit{i}}\ne 0$ and ${\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{B}}\ne 0$ $\left(i=1,\dots ,n\right)$. Then the next iteration continues with the new trial increment vector

$$▵{\mathit{x}}_{p+1}={\mathit{x}}_{p+1}^B-{\mathit{x}}_{p+1}^A$$

(4.23)

and with $\mathit{n}+1$ new interpolation base points $A_{p+1}\left(\begin{array}{cc}{\mathit{x}}_{p+1}^A& {\mathit{f}}_{p+1}^A\end{array}\right)$$B_{k,p+1}\left(\begin{array}{cc}{\mathit{x}}_{k,p+1}^B& {\mathit{f}}_{k,p+1}^B\end{array}\right)$$\left(k=1,\dots ,n\right)$. Figure 1 shows the formulation of a set of new base vectors ${\mathit{x}}_{\mathit{k},\mathit{p}+\mathit{1}}^{\mathit{B}}$ from ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{A}}$ and ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{B}}$ in $n=3$ case.

Table 1. Summary of the basic equations (single- and multi-variable cases).

	Single-variable $\left(\mathit{m}=\mathit{n}=\mathit{1}\right)$	Multi-variable$\left(\mathit{m}\ge \mathit{n}>\mathit{1}\right)$	Equations
1	$x_p^A$	${\mathit{x}}_p^A$
2	$x_p^B$	${\mathit{x}}_{p,k}^B={\mathit{x}}_p^A+▵{\mathit{x}}_{\mathit{p},\mathit{k}}{\mathit{d}}^k$	3.5
3	$▵x_p={\mathit{x}}_{\mathit{p}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{X}}_{\mathit{p}}=\left[{\mathit{x}}_{p,k}^B-{\mathit{x}}_p^A\right]=diag\left(▵x_{p,i}\right)$	3.9, 3.11
4	$▵f_p={\mathit{f}}_{\mathit{p}}^{\mathit{B}}-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{F}}_p=\left[\begin{array}{ccc}▵f_{p,1,1}& \cdots & ▵f_{p,n,1}\\ ⋮& \ddots & ⋮\\ ▵f_{p,1,m}& \cdots & ▵f_{p,n,m}\end{array}\right]$	3.7, 3.10, 3.12
5	$▵f_p{q}_p^A=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{F}}_p{\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	4.1, 3.14
6	${\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-\frac{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}{▵{\mathit{f}}_{\mathit{p}}}$	${\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-▵{\mathit{F}}_{\mathit{p}}^{+}{\mathit{f}}_p^{\mathit{A}}$	3.20, 3.15
7	$x_{p+1}^A=x_p^A+▵x_p{q}_p^A$	${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}_p^A+▵{\mathit{X}}_p{\mathit{q}}_p^{\mathit{A}}$	3.21, 3.19
8	$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$	4.6
9	$t_p^f=\frac{f_{p+1}^A}{f_p^A}$	${\mathit{T}}_{\mathit{p}}^{\mathit{F}}=diag\left(\frac{{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)$	4.2, 4.19
10	${\mathit{t}}_{\mathit{p}}^{\mathit{f}}▵{\mathit{f}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{B}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	${\mathit{T}}_{\mathit{p}}^{\mathit{F}}▵{\mathit{F}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{B}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	4.3, 4.13
11	$q_p^B=\frac{q_p^A}{t_p^f}=-\frac{{\left(f_p^A\right)}^2}{f_{p+1}^A▵f_p}$	${\mathit{q}}_p^{\mathit{B}}=-▵{\mathit{F}}_{\mathit{p}}^{+}{\left({\mathit{T}}_{\mathit{p}}^{\mathit{F}}\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	4.4, 4.20
12	$t_p^x=\frac{{\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}}{x_{p+1}^A-x_p^A}=\frac{▵{\mathit{x}}_{\mathit{p}+1}}{▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}$	${\mathit{T}}_p^X=\mathit{diag}\left(\frac{▵{\mathit{x}}_{\mathit{p}+\mathit{1},\mathit{i}}}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}\right)$	4.7, 4.17
13	$▵x_p^A=t_p^x▵x_p{q}_p^B$	$▵{\mathit{x}}_p^A={\mathit{T}}_p^X▵{\mathit{X}}_{\mathit{p}}{\mathit{q}}_p^{\mathit{B}}$	4.8, 4.14
14	$x_{p+1}^{\mathit{B}}=x_{p+1}^A+\frac{{\left(▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p}}{q}_p^B}$	${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}+\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathrm{i}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}{\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{B}}}$	4.11, 4.22

Table 1. Summary of the basic equations (single- and multi-variable cases).

	Single-variable $\left(\mathit{m}=\mathit{n}=\mathit{1}\right)$	Multi-variable$\left(\mathit{m}\ge \mathit{n}>\mathit{1}\right)$	Equations
1	$x_p^A$	${\mathit{x}}_p^A$
2	$x_p^B$	${\mathit{x}}_{p,k}^B={\mathit{x}}_p^A+▵{\mathit{x}}_{\mathit{p},\mathit{k}}{\mathit{d}}^k$	3.5
3	$▵x_p={\mathit{x}}_{\mathit{p}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{X}}_{\mathit{p}}=\left[{\mathit{x}}_{p,k}^B-{\mathit{x}}_p^A\right]=diag\left(▵x_{p,i}\right)$	3.9, 3.11
4	$▵f_p={\mathit{f}}_{\mathit{p}}^{\mathit{B}}-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{F}}_p=\left[\begin{array}{ccc}▵f_{p,1,1}& \cdots & ▵f_{p,n,1}\\ ⋮& \ddots & ⋮\\ ▵f_{p,1,m}& \cdots & ▵f_{p,n,m}\end{array}\right]$	3.7, 3.10, 3.12
5	$▵f_p{q}_p^A=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{F}}_p{\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	4.1, 3.14
6	${\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-\frac{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}{▵{\mathit{f}}_{\mathit{p}}}$	${\mathit{q}}_{\mathit{p}}^{\mathit{A}}=-▵{\mathit{F}}_{\mathit{p}}^{+}{\mathit{f}}_p^{\mathit{A}}$	3.20, 3.15
7	$x_{p+1}^A=x_p^A+▵x_p{q}_p^A$	${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}_p^A+▵{\mathit{X}}_p{\mathit{q}}_p^{\mathit{A}}$	3.21, 3.19
8	$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$	$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$	4.6
9	$t_p^f=\frac{f_{p+1}^A}{f_p^A}$	${\mathit{T}}_{\mathit{p}}^{\mathit{F}}=diag\left(\frac{{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)$	4.2, 4.19
10	${\mathit{t}}_{\mathit{p}}^{\mathit{f}}▵{\mathit{f}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{B}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	${\mathit{T}}_{\mathit{p}}^{\mathit{F}}▵{\mathit{F}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{B}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	4.3, 4.13
11	$q_p^B=\frac{q_p^A}{t_p^f}=-\frac{{\left(f_p^A\right)}^2}{f_{p+1}^A▵f_p}$	${\mathit{q}}_p^{\mathit{B}}=-▵{\mathit{F}}_{\mathit{p}}^{+}{\left({\mathit{T}}_{\mathit{p}}^{\mathit{F}}\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$	4.4, 4.20
12	$t_p^x=\frac{{\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}}{x_{p+1}^A-x_p^A}=\frac{▵{\mathit{x}}_{\mathit{p}+1}}{▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}$	${\mathit{T}}_p^X=\mathit{diag}\left(\frac{▵{\mathit{x}}_{\mathit{p}+\mathit{1},\mathit{i}}}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}\right)$	4.7, 4.17
13	$▵x_p^A=t_p^x▵x_p{q}_p^B$	$▵{\mathit{x}}_p^A={\mathit{T}}_p^X▵{\mathit{X}}_{\mathit{p}}{\mathit{q}}_p^{\mathit{B}}$	4.8, 4.14
14	$x_{p+1}^{\mathit{B}}=x_{p+1}^A+\frac{{\left(▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p}}{q}_p^B}$	${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}+\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathrm{i}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}{\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{B}}}$	4.11, 4.22

5. Geometry

5.1. Single-variable case

The T-secant procedure has been worked out for solving multi-variable problems, it can also be applied for solving single-variable ones, though. The geometrical representation of the latter one gives a good view to explain the mechanism of the procedure.

Find the scalar root $x^{*}$of a nonlinear function $x\to f\left(x\right)$, where $\mathit{x}\in {\mathbb{R}}^1$ and $f:{\mathbb{R}}^1\to {\mathbb{R}}^1$. Let the function $f\left(x\right)$ be linearly interpolated through initial base points $A_p\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}},{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\right)$ and $B_p\left({\mathit{x}}_{\mathit{p}}^{\mathit{B}},{\mathit{f}}_{\mathit{p}}^{\mathit{B}}\right)$ providing a “secant” line $y_p\left(x\right)$ as shown on Figure 2, where $f_p^A=f\left({\mathit{x}}_p^{\mathit{A}}\right)$ and $f_p^B=f\left({\mathit{x}}_p^B\right)$ are the corresponding function values. An arbitrary point of the secant ${\mathit{y}}_{\mathit{p}}\left(\mathit{x}\right)$ can be expressed as

$$\left[\begin{array}{c}x\\ y_p\left(x\right)\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\\ {\mathit{f}}_{\mathit{p}}^{\mathit{A}}\end{array}\right]+\left[\begin{array}{c}▵x_p\\ ▵f_p\end{array}\right]q_p^A$$

(5.1)

where $q_p^A$ is a scalar multiplier. Let a new approximate $x_{p+1}^A$ be the root of the secant ${\mathit{y}}_{\mathit{p}}\left(\mathit{x}\right)$ and let

$$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(5.2)

be the iteration step size. It follows from condition

$$y_p\left(x_{p+1}^A\right)=0$$

(5.3)

and from the $2^{\mathit{nd}}$ row of Equation (5.1) that

$$▵f_p{q}_p^A=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(5.4)

and the scalar multiplier can be determined as

$$q_p^A=-\frac{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}{▵f_p}$$

(5.5)

From the $1^{\mathit{st}}$ row of Equation (5.1), the iteration step size is given as

$$▵x_{\mathit{p}}^{\mathit{A}}=▵{\mathit{x}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{A}}$$

(5.6)

and the new approximate can be expressed as

$$x_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}_{\mathit{p}}^{\mathit{A}}+▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(5.7)

A new base point $A_{p+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}\right)$ (see Figure 2) can than be determined for the next iteration. Two out of the three available base points $\left(\begin{array}{ccc}{A}_{\mathit{p}}& B_{\mathit{p}}& A_{\mathit{p}+\mathit{1}}\end{array}\right)$ are used for the next iteration by omitting either ${\mathit{A}}_{\mathit{p}}$ or ${\mathit{B}}_{\mathit{p}}$ in case of the traditional secant method. Decision is not obvious and it may cause that the iteration will be unstable and / or will not converge to the solution. Instead, an additional new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ is determined by the T-secant procedure as a root of the function ${\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)$ near the first secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$, and iteration continues with new base points $A_{p+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}\right)$ and $B_{p+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{B}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{B}}\right)$. An arbitrary point of the function ${\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)$ can be expressed as

$$\left[\begin{array}{c}x-▵x\\ {\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\\ {\mathit{f}}_{\mathit{p}}^{\mathit{A}}\end{array}\right]+\left[\begin{array}{cc}{t}^x& 0\\ 0& t^f\end{array}\right]\left[\begin{array}{c}▵x_p\\ ▵f_p\end{array}\right]q_p^B$$

(5.8)

where the transformation scalars for $▵{\mathit{x}}_{\mathit{p}}$ and $▵{\mathit{f}}_{\mathit{p}}$ at $\mathit{x}={\mathit{x}}_{\mathit{p}}^{\mathit{B}}$ are

$$t_p^x=\frac{▵x_{p+1}}{▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}=\frac{x_{p+1}^B-x_{p+1}^A}{{\mathit{x}}_{p+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}and{t}_p^f=\frac{{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}$$

(5.9)

Then it follows from condition

$$z_p\left(x_{p+1}^{\mathit{B}}\right)=0$$

(5.10)

and from the $2^{\mathit{nd}}$ row of Equation (5.8) that

$$t_p^f▵f_p{q}_p^B=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(5.11)

and

$$q_p^B=-\frac{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}{t_p^f▵f_p}=-\frac{{\left({\mathit{f}}_{\mathit{p}}^{\mathit{A}}\right)}^2}{f_{p+1}^A\left({\mathit{f}}_{\mathit{p}}^B-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\right)}$$

(5.12)

The new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ can then be expressed from the $1^{\mathit{st}}$ row of Equation 5.8, as

$${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}+\frac{{\left(▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)}^{\mathit{2}}}{▵{\mathit{x}}_{\mathit{p}}{\mathit{q}}_{\mathit{p}}^{\mathit{B}}}$$

(5.13)

The new base point $B_{p+1}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{B}},{\mathit{f}}_{\mathit{p}+1}^{\mathit{B}}\right)$ (see Figure 2) then can be determined. Interpolation base points $A_{p+1}$ and $B_{p+1}$ are used for the next iteration. The scalar multiplier $q_{\mathit{p}}^{\mathit{B}}$ can be expressed from Equation (5.13) as

$$q_{\mathit{p}}^{\mathit{B}}=\frac{{\left(x_{\mathit{p}+1}^{\mathit{A}}-x_{\mathit{p}}^A\right)}^2}{\left({\mathit{x}}_{\mathit{p}}^B-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)\left(x_{p+1}^B-x_{p+1}^{\mathit{A}}\right)}$$

(5.14)

By substituting it into the $2^{\mathit{nd}}$ row of Equation 5.8 and changing ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ to $\mathit{x}$, it turns to a hyperbolic function

$${\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)=\frac{a_p}{x-x_{p+1}^{\mathit{A}}}+{\mathit{f}}_p^{\mathit{A}}$$

(5.15)

with vertical and horizontal asymptotes ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and ${\mathit{f}}_{\mathit{p}}^{\mathit{A}}$, where

$$a_p={\left(x_{p+1}^{\mathit{A}}-x_p^A\right)}^2\frac{{\mathit{f}}_{\mathit{p}}^{\mathit{B}}-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}{{\mathit{x}}_{\mathit{p}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}}\frac{{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}$$

(5.16)

and the root ${\mathit{x}}_{p+1}^B$ of the function ${\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)$ will be in the vicinity of ${\mathit{x}}_{p+1}^{\mathit{A}}$ in “appropriate distance” that is regulated by the function value ${\mathit{f}}_{p+1}^{\mathit{A}}$ (see Figure 2). This virtue of the T-secant procedure ensures an automatic mechanism for having base vectors in general positions through the whole iteration process providing stable and efficient numerical performance.

5.2. Multi-variable case

Find the root ${\mathit{x}}^{*}$of a nonlinear function $\mathit{x}\to \mathit{f}\left(\mathit{x}\right)$, where $\mathit{x}\in {\mathbb{R}}^{\mathit{n}}$ and $f:{\mathbb{R}}^{\mathit{n}}\to {\mathbb{R}}^{\mathit{m}}$. Let the function $\mathit{f}\left(\mathit{x}\right)$ be linearly interpolated through $\mathit{n}+1$ base points $A_p\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}},{\mathit{f}}_{\mathit{p}}^{\mathit{A}}\right)$ and $B_{k,p}\left({\mathit{x}}_{\mathit{k},\mathit{p}}^{\mathit{B}},{\mathit{f}}_{\mathit{k},\mathit{p}}^{\mathit{B}}\right)$ in the ${\mathit{R}}^{\mathit{n}+\mathit{m}}$ space ($\mathit{f}\left(\mathit{x}\right)-$ space) in the ${\mathit{p}}^{\mathit{th}}$ iteration as shown on Figure 3, where $\mathit{k}=1,\dots ,\mathit{n}$ . Given a set of approximates ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ and

$${\mathit{x}}_{k,p}^B={\mathit{x}}_p^A+▵{\mathit{x}}_{\mathit{k},\mathit{p}}{\mathit{d}}^k$$

(5.17)

in the ${\mathbb{R}}^{\mathit{n}}$ space ($\mathit{x}-$ space) with $\mathit{k}=1,\dots ,\mathit{n}$, where ${\mathit{d}}^{\mathit{k}}$ is the $k^{th}$ Cartesian unit vector. Let the expression

$$▵{\mathit{F}}_p{\mathit{q}}_p^A=\left[\begin{array}{ccc}▵f_{1,1,p}& \cdots & ▵f_{n,1,p}\\ ⋮& ⋮& ⋮\\ ▵f_{1,m,p}& \cdots & ▵f_{n,m,p}\end{array}\right]{\mathit{q}}_p^A$$

(5.18)

represent the linear combination ${\mathit{q}}_{\mathit{p}}^{\mathit{A}}={\left[q_{p,k}^A\right]}^T$ of $\mathit{n}$ column vectors

$$\left[▵f_{k,j,p}\right]=\left[▵{\mathit{f}}_{k,p}\right]=\left[{\mathit{f}}_{k,p}^B-{\mathit{f}}_{k,p}^A\right]$$

in the ${\mathbb{R}}^{\mathit{m}}$ space ($\mathit{f}-$ space) with $\mathit{k}=1,\dots ,\mathit{n}$ column index and with $\mathit{j}=1,\dots ,\mathit{m}$ row index and the expression

$$▵{\mathit{X}}_p{\mathit{q}}_p^A=\left[\begin{array}{ccc}▵x_{1,1,p}& \cdots & ▵x_{n,1,p}\\ ⋮& ⋮& ⋮\\ ▵x_{1,n,p}& \cdots & ▵x_{n,n,p}\end{array}\right]{\mathit{q}}_p^A$$

(5.19)

represent the same linear combination of $\mathit{n}$ column vectors

$$\left[▵x_{k,j,p}\right]=\left[▵{\mathit{x}}_{p,k}\right]=\left[{\mathit{x}}_{p,k}^B-{\mathit{x}}_{p,k}^A\right]$$

(5.20)

with $\mathit{k}=1,\dots ,\mathit{n}$ column index and with $\mathit{j}=1,\dots ,\mathit{n}$ row index. The linear combination ${\mathit{q}}_{\mathit{p}}^{\mathit{A}}$ is determined from Equation (3.15) in step $\mathit{S}1$ (see Figure 3) providing a new approximate

$${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}=\left[x_{p+1,k}^{\mathit{A}}\right]={\mathit{x}}_{\mathit{p}}^{\mathit{A}}+▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(5.21)

for the solution ${\mathit{x}}^{*}$ as shown on Figure 3 and the corresponding ${\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}$ vector is also determined in step $\mathit{S}2$ (see Figure 3). The column vectors $▵{\mathit{f}}_{\mathit{k},\mathit{p}}$ of $▵{\mathit{F}}_{\mathit{p}}$ are then modified by a non-uniform scaling transformation

$${\mathit{T}}_{\mathit{p}}^{\mathit{F}}=diag\left(\frac{{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right)$$

(5.22)

and a new linear combination ${\mathit{q}}_{\mathit{p}}^{\mathit{B}}={\left[q_{p,k}^B\right]}^T$ is determined from Equation (4.20) in step $\mathit{S}3$ (see Figure 3) providing a new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ for the solution ${\mathit{x}}^{*}$ with elements

$${\mathit{x}}_{\mathit{p}+1,\mathit{k}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{k}}^{\mathit{A}}+\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{k}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p},\mathit{k}}{\mathit{q}}_{\mathit{p},\mathit{k}}^{\mathit{B}}}$$

(5.23)

A new set of $\mathit{n}+\mathit{1}$ approximates ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and

$${\mathit{x}}_{k,p+1}^B={\mathit{x}}_{p+1}^A+▵{\mathit{x}}_{\mathit{k},\mathit{p}+1}{\mathit{d}}^k$$

(5.24)

($\mathit{k}=1,\dots ,\mathit{n}$) can then be generated with

$$▵{\mathit{x}}_{p+1}=\left[▵{\mathit{x}}_{\mathit{k},\mathit{p}+1}\right]={\mathit{x}}_{p+1}^B-{\mathit{x}}_{p+1}^A$$

(5.25)

for the next iteration.

5.3. Single-variable example

An example is given with function $x\to f\left(x\right)$, where $x\in$ ${\mathbb{R}}^1$$f:{\mathbb{R}}^1\to {\mathbb{R}}^1$ and

$$f\left(x\right)=x^3-2x-5$$

(5.26)

with root ${\mathit{x}}^{*}\cong 2.09455...$ . Figure 4 summarizes the results of the first two iterations (left : ${\mathit{x}}_1^{\mathit{A}}$ is the zero of ${\mathit{y}}_0\left(\mathit{x}\right)$, ${\mathit{x}}_1^{\mathit{B}}$ is the zero of ${\mathit{z}}_0\left(\mathit{x}\right)$, right : ${\mathit{x}}_2^{\mathit{A}}$ is the zero of ${\mathit{y}}_1\left(\mathit{x}\right)$, ${\mathit{x}}_2^{\mathit{B}}$ is the zero of ${\mathit{z}}_1\left(\mathit{x}\right)$). Iterations were made with initial approximates ${\mathit{x}}_0^{\mathit{A}}=3.0$ and ${\mathit{x}}_0^{\mathit{B}}=1.0$ providing ${\mathit{f}}_0^{\mathit{A}}=16$ ($\mathit{p}=0$). The first secant approximate ${\mathit{x}}_1^{\mathit{A}}=1.545...$ is found as the zero of the first secant ${\mathit{y}}_0\left(\mathit{x}\right)$ and the first T-secant appropriate ${\mathit{x}}_1^{\mathit{B}}=1.945...$ is found as the zero of the first hyperbola function ${\mathit{z}}_0\left(\mathit{x}\right)$ (Figure 4, left). Iteration then goes on ($\mathit{p}=1$) with new interpolation base point ${\mathit{x}}_1^{\mathit{A}}=1.545...$ and ${\mathit{x}}_1^{\mathit{B}}=1.945...$ providing ${\mathit{f}}_1^{\mathit{A}}=-4.3997...$, and new approximates ${\mathit{x}}_2^{\mathit{A}}=2.158...$ and ${\mathit{x}}_2^{\mathit{B}}=2.0556...$ are found as the zeros of the second secant and the second hyperbola function ${\mathit{y}}_1\left(\mathit{x}\right)$ and ${\mathit{z}}_1\left(\mathit{x}\right)$ receptively (Figure 4, right). The next iteration ($\mathit{p}=2$) will then continue with interpolation base point ${\mathit{x}}_2^{\mathit{A}}=2.158......$ and ${\mathit{x}}_2^{\mathit{B}}=2.0556...$ and with ${\mathit{f}}_2^{\mathit{A}}=0.7367...$ . The iterated values of ${\mathit{f}}_{\mathit{p}}^{\mathit{A}}$${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ and ${\mathit{x}}_{\mathit{p}}^{\mathit{B}}$ are also indicated on the diagrams. Further diagrams of this example are shown in Section 7.3.

6. General formulations

Re-ordering Equation (3.17) gives the general equation

$$▵\mathit{F}▵{\mathit{X}}^{-1}▵{\mathit{x}}^{\mathit{A}}=-{\mathit{f}}^{\mathit{A}}$$

(6.1)

of the secant method. The initial trials are constructed according to Equation (3.5) providing that $▵\mathit{X}$ is a diagonal matrix with elements $\left(▵{\mathit{x}}_{\mathit{i}}\right)=\left({\mathit{x}}_{\mathit{i},\mathit{i}}^{\mathit{B}}-x_i^A\right)$ $\left(i=1,\dots ,n\right)$. Let the “Jacobean-type” matrix of the Secant-method be defined as

$$\mathit{S}=▵\mathit{F}▵{\mathit{X}}^{-\mathit{1}}$$

(6.2)

$$\mathit{S}=\left[\begin{array}{ccc}\frac{{\mathit{f}}_{1,1}^{\mathit{B}}-{\mathit{f}}_1^{\mathit{A}}}{{\mathit{x}}_{1,1}^{\mathit{B}}-{\mathit{x}}_1^{\mathit{A}}}& \cdots & \frac{f_{n,1}^B-{\mathit{f}}_1^{\mathit{A}}}{{\mathit{x}}_{\mathit{n},1}^{\mathit{B}}-{\mathit{x}}_1^{\mathit{A}}}\\ ⋮& ⋮& ⋮\\ \frac{{\mathit{f}}_{1,\mathit{m}}^{\mathit{B}}-{\mathit{f}}_{\mathit{m}}^{\mathit{A}}}{{\mathit{x}}_{1,1}^{\mathit{B}}-{\mathit{x}}_1^{\mathit{A}}}& \cdots & \frac{{\mathit{f}}_{\mathit{n},\mathit{m}}^{\mathit{B}}-{\mathit{f}}_{\mathit{m}}^{\mathit{A}}}{{\mathit{x}}_{\mathit{n},1}^{\mathit{B}}-{\mathit{x}}_1^{\mathit{A}}}\end{array}\right]=\left[\begin{array}{ccc}\frac{▵{\mathit{f}}_{1,1}}{▵{\mathit{x}}_1}& \dots & \frac{▵{\mathit{f}}_{\mathit{n},1}}{▵{\mathit{x}}_{\mathit{n}}}\\ ⋮& ⋮& ⋮\\ \frac{▵{\mathit{f}}_{1,\mathit{m}}}{▵{\mathit{x}}_1}& \cdots & \frac{▵{\mathit{f}}_{\mathit{n},\mathit{m}}}{▵{\mathit{x}}_{\mathit{n}}}\end{array}\right]=\left[\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]$$

(6.3)

$\left(\mathit{i}=1,\dots ,\mathit{n}\right)$, $\left(j=1,\dots ,m\right)$, $\left(\mathit{k}=1,\dots ,\mathit{n}\right)$ and

$${\mathit{S}}^{+}=▵\mathit{X}▵{\mathit{F}}^{+}$$

(6.4)

Then Equation (6.1) simplifies as

$$\mathit{S}▵{\mathit{x}}^{\mathit{A}}=-{\mathit{f}}^{\mathit{A}}$$

(6.5)

and

$$▵{\mathit{x}}^{\mathit{A}}=-{\mathit{S}}^{+}{\mathit{f}}^{\mathit{A}}$$

(6.6)

The ${\mathit{i}}^{\mathit{th}}$element of the new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ in the ${\mathit{p}}^{\mathit{th}}$ iteration will then be

$${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}={\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}+▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}={\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}-\sum _{\mathit{j}=1}^{\mathit{m}}\left({\mathit{S}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}\right)$$

(6.7)

$\left(i=1,\dots ,n\right)$. It follows from the 1st row of Equation 4.15 of the T-Secant method, from Equation 4.13 and from the Definition 6.4 of ${\mathit{S}}^{+}$, that the ${\mathit{p}}^{\mathit{th}}$ iteration step-size is

$$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{T}}_{\mathit{p}}^{\mathit{X}}{\mathit{S}}_{\mathit{p}}^{+}{\left({\mathit{T}}_{\mathit{p}}^{\mathit{F}}\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(6.8)

and

$${\mathit{T}}_{\mathit{p}}^{\mathit{F}}{\mathit{S}}_p{\left({\mathit{T}}_p^X\right)}^{-\mathit{1}}▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(6.9)

Let the modified “Jacobean-type” matrix of the T-Secant-method be defined as

$${\mathit{S}}_{\mathit{p},\mathit{T}}={\mathit{T}}_p^F{\mathit{S}}_p{\left({\mathit{T}}_p^X\right)}^{-\mathit{1}}$$

(6.10)

$${\mathit{S}}_{\mathit{p},\mathit{T}}=\left[\begin{array}{ccc}\frac{{\mathit{f}}_{\mathit{p}+1,1}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},1}^{\mathit{A}}}& 0& 0\\ 0& \ddots & 0\\ 0& 0& \frac{{\mathit{f}}_{\mathit{p}+1,\mathit{m}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{m}}^{\mathit{A}}}\end{array}\right]\left[\begin{array}{ccc}\frac{▵{\mathit{f}}_{\mathit{p},1,1}}{▵{\mathit{x}}_{\mathit{p},1}}& \dots & \frac{▵{\mathit{f}}_{\mathit{p},\mathit{n},1}}{▵{\mathit{x}}_{\mathit{p},\mathit{n}}}\\ ⋮& ⋮& ⋮\\ \frac{▵{\mathit{f}}_{\mathit{p},1,\mathit{m}}}{▵{\mathit{x}}_{\mathit{p},1}}& \cdots & \frac{▵{\mathit{f}}_{\mathit{p},\mathit{n},\mathit{m}}}{▵{\mathit{x}}_{\mathit{p},\mathit{n}}}\end{array}\right]\left[\begin{array}{ccc}\frac{▵{\mathit{x}}_{\mathit{p},1}^{\mathit{A}}}{▵{\mathit{x}}_{\mathit{p}+1,1}}& 0& 0\\ 0& \ddots & 0\\ 0& 0& \frac{▵{\mathit{x}}_{\mathit{p},\mathit{n}}^{\mathit{A}}}{▵{\mathit{x}}_{\mathit{p}+1,\mathit{n}}}\end{array}\right]$$

(6.11)

and in condensed form with general matrix elements (without the $\mathit{p}$ index) :

$${\mathit{S}}_{\mathit{T}}={\mathit{T}}^{\mathit{F}}\mathit{S}{\left({\mathit{T}}^{\mathit{X}}\right)}^{-\mathit{1}}=diag\left(t_j^{\mathit{F}}\right)\left[\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]diag\left(\frac{1}{t_{\mathit{i}}^{\mathit{X}}}\right)=\left[\frac{{\mathit{t}}_{\mathit{j}}^{\mathit{F}}}{t_{\mathit{i}}^{\mathit{X}}}\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]$$

(6.12)

$\left(\mathit{i}=1,\dots ,\mathit{n}\right)$, $\left(j=1,\dots ,m\right)$, $\left(\mathit{k}=1,\dots ,\mathit{n}\right)$ and

$${\mathit{S}}_{\mathit{T}}^{+}={\mathit{T}}^X{\mathit{S}}^{+}{\left({\mathit{T}}^F\right)}^{-\mathit{1}}$$

(6.13)

Equations (6.8) and (6.9) then can be re-written as

$$▵{\mathit{x}}^{\mathit{A}}=-{\mathit{S}}_{\mathit{T}}^{+}{\mathit{f}}^{\mathit{A}}$$

(6.14)

and

$${\mathit{S}}_T▵{\mathit{x}}^{\mathit{A}}=-{\mathit{f}}^{\mathit{A}}$$

(6.15)

in a similar form like in case of the traditional secant method (Equations 6.6 and 6.5). The ${\mathit{i}}^{\mathit{th}}$ element ${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}$ of the $2^{\mathit{nd}}$ new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ in the ${\mathit{p}}^{\mathit{th}}$ iteration will then be

$${\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}+▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}+1,\mathit{i}}^{\mathit{A}}-\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left({\mathit{S}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(6.16)

where ${\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}\ne 0$, $\left(j=1,\dots ,m\right)$ and $\left(i=1,\dots ,n\right)$. Note, that the T-secant modification in the secant method “Jacobean-type” matrix 6.3 is made with multipliers $t_{p,j}^{\mathit{F}}=\frac{{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}$ and $t_{p,i}^{\mathit{X}}=\frac{▵{\mathit{x}}_{\mathit{p}+1,\mathit{i}}}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}$ to the difference quantities $▵{\mathit{f}}_{\mathit{p},\mathit{k},\mathit{j}}$ and $▵{\mathit{x}}_{\mathit{p},\mathit{i}}$. The basic equations of the secant method and the T-secant method are summarized in Table 2 : rows 1-4 are the elements (matrix$\mathit{T}$) of the basic equations, row 5-6 are the explicit basic equations, row 7 : the Jacobean-type matrices, row 8-9 are the general formulations of the basic equations.

7. Convergence

7.1. Single-variable case

As it was shown in Section 4 (Equation (4.12)), the ${\mathit{p}}^{\mathit{th}}$ iteration step length of the $2^{\mathit{nd}}$ new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ is

$$▵{\mathit{x}}_{\mathit{p}+1}=t_p^f▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(7.1)

The secant method is super-linear convergent, so the new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ is expected to be a much better approximate to the solution $x^{*}$ then the previous one (${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$). Thus

$$\left|f_{p+1}^A\right|⋘\left|f_p^A\right|$$

(7.2)

and

$$\left|{\mathit{t}}_{\mathit{p}}^{\mathit{f}}\right|=\left|\frac{{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}\right|$$

(7.3)

is expected to be a “small positive number”. It means, that the T-secant approximate $x_{\mathit{p}+1}^{\mathit{B}}$ will always be in the vicinity of the classic secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and the approximate errors of the new approximates will be of similar order, providing that the solution $x^{*}$will evenly be surrounded by the 2 new trial approximates $x_{p+1}^A$ and $x_{p+1}^B$.

7.2. Convergence rate

It is well known that the single-variable secant method has asymptotic convergence for sufficiently good initial approximates ${\mathit{x}}^{\mathit{A}}$ and ${\mathit{x}}^{\mathit{B}}$ if ${\mathit{f}}^{\prime }\left(\mathit{x}\right)$ doesn’t vanish in $\mathit{x}\in \left[\begin{array}{cc}{\mathit{x}}^{\mathit{A}}& {\mathit{x}}^{\mathit{B}}\end{array}\right]$ and ${\mathit{f}}^{″}\left(\mathit{x}\right)$ is continuous at least in a neighborhood of the zero ${\mathit{x}}^{*}$. The super-linear convergence property has also been proved in different ways and it is known that the order of convergence ${\alpha }^S=\left(1+\sqrt{5}\right)/2$ with asymptotic error constant

$$C={\left(\frac{1}{2}\left|\frac{f^{″}\left(\xi \right)}{f^{\prime }\left(\xi \right)}\right|\right)}^{\frac{1}{\alpha }}$$

(7.4)

The order of convergence of the T-secant method is determined in this section. Let $\mathit{p}$ be the iteration counter and the approximate error be defined in the ${\mathit{p}}^{\mathrm{th}}$ iteration as

$$e_p={\mathit{x}}_{\mathit{p}}-{\mathit{x}}^{*}$$

(7.5)

It follows from Equation (3.21) and from Definition 7.5 that the error ${\mathit{e}}_{\mathit{p}+1}^{\mathit{A}}$ of the new secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ can be expressed as

$$e_{p+1}^A=\frac{e_p^A{f}_p^B-e_p^B{f}_p^A}{f_p^B-f_p^A}=\frac{x_p^B-x_p^A}{f_p^B-f_p^A}\frac{f_p^B/e_p^B-f_p^A/e_p^A}{x_p^B-x_p^A}{e}_p^A{e}_p^B$$

(7.6)

It follows from the mean value theorem, that the first factor of right side of Equation (7.6) can be replaced with $1/{\mathit{f}}^{\prime }\left({\eta }_p\right)$, where ${\eta }_p\in \left(x_p^A,x_p^B\right)$, if $\mathit{f}\left(\mathit{x}\right)$ is continuously differentiable on $\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}},{\mathit{x}}_{\mathit{p}}^{\mathit{B}}\right)$ and ${\mathit{f}}^{\prime }\left({\eta }_p\right)\ne 0$. Let the function $\mathit{f}\left(\mathit{x}\right)$ be approximated around the root ${\mathit{x}}^{*}$ by a $2^{\mathit{nd}}$ order Taylor series expansion as

$$f_p=f\left(e_p+x^{*}\right)=f\left(x^{*}\right)+e_p{f}^{\prime }\left(x^{*}\right)+\frac{1}{2}{\left(e_p\right)}^2{f}^{″}\left({\xi }_p\right)$$

(7.7)

where ${\xi }_p\in \left(x_p^A,x_p^B,x^{*}\right)$ in the remainder term. Since $\mathit{f}\left({\mathit{x}}^{*}\right)=0$, it follows from Equation (7.7) that

$$\frac{f_p}{e_p}=f^{\prime }\left(x^{*}\right)+\frac{1}{2}{f}^{″}\left({\xi }_p\right)e_p$$

(7.8)

Substituting this expression to Equation (7.6), and since ${\mathit{e}}_{\mathit{p}}^{\mathit{B}}-{\mathit{e}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ we get

$$e_{p+1}^A=\frac{1}{2}\frac{f^{″}\left({\xi }_p\right)}{{\mathit{f}}^{\prime }\left({\eta }_p\right)}\frac{e_p^B-e_p^A}{x_p^B-x_p^A}{e}_p^A{e}_p^B=C_p{e}_p^A{e}_p^B$$

(7.9)

and

$$C_p=\frac{1}{2}\frac{f^{″}\left({\xi }_p\right)}{{\mathit{f}}^{\prime }\left({\eta }_p\right)}$$

(7.10)

If the series $\left\{x_p^A\right\}$ converges to ${\mathit{x}}^{*}$, then ${\xi }_p$ and ${\eta }_p$$\to x^{*}$ with increasing iteration counter $\mathit{p}$, and

$$C_p\to \frac{1}{2}\frac{f^{″}\left(x^{*}\right)}{{\mathit{f}}^{\prime }\left(x^{*}\right)}=constant$$

(7.11)

It follows from Equation (4.11) with Definition 7.5 and from the mean value theorem (with ${\eta }_{p-1}\in \left(x_{p-1}^A,x_{p-1}^B\right)$, if $\mathit{f}\left(\mathit{x}\right)$ is continuously differentiable on $\left({\mathit{x}}_{\mathit{p}-1}^{\mathit{A}},{\mathit{x}}_{\mathit{p}-1}^{\mathit{B}}\right)$) that

$${\mathit{x}}_{\mathit{p}}^{\mathit{B}}={\mathit{x}}_{\mathit{p}}^{\mathit{A}}-{\left(\frac{{\mathit{x}}_{\mathit{p}}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}-1}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p}-1}^{\mathit{A}}}\right)}^2{f}^{\prime }\left({\eta }_{p-1}\right)f_p^A$$

(7.12)

and the error ${\mathit{e}}_{\mathit{p}}^{\mathit{B}}$ of the T-secant approximate ${\mathit{x}}_{\mathit{p}}^{\mathit{B}}$ can be expressed as

$$e_p^B=e_p^A-{\left(\frac{e_p^A-e_{p-1}^A}{f_{p-1}^A}\right)}^2{f}^{\prime }\left({\eta }_{p-1}\right)f_p^A$$

(7.13)

With the Taylor-series expansion 7.7 for ${\mathit{f}}_{\mathit{p}-1}^{\mathit{A}}$ and ${\mathit{f}}_{\mathit{p}}^{\mathit{A}}$, where ${\xi }_{p-1}\in \left(x_{p-1}^A,x_{p-1}^B,x^{*}\right)$ and ${\xi }_p\in \left(x_p^A,x_p^B,x^{*}\right)$ in the remainder term, we get

$$e_p^B=e_p^A-e_p^A{\left(\frac{e_p^A-e_{p-1}^A}{e_{p-1}^A}\right)}^2{\gamma }_p$$

(7.14)

where

$${\gamma }_p=\frac{\frac{f^{\prime }\left(x^{*}\right)}{f^{\prime }\left({\eta }_{p-1}\right)}+\frac{1}{2}\frac{f^{″}\left({\xi }_p\right)}{f^{\prime }\left({\eta }_{p-1}\right)}{e}_p^A}{{\left(\frac{f^{\prime }\left(x^{*}\right)}{f^{\prime }\left({\eta }_{p-1}\right)}+\frac{1}{2}\frac{f^{″}\left({\xi }_{p-1}\right)}{f^{\prime }\left({\eta }_{p-1}\right)}{e}_{p-1}^A\right)}^2}$$

(7.15)

and $f^{\prime }\left({\eta }_{p-1}\right)\ne 0$ . If the series $\left\{x_p^A\right\}$ converges to ${\mathit{x}}^{*}$, then with increasing iteration counter $\mathit{p}$, ${\xi }_p$, ${\xi }_{p-1}$, ${\eta }_{p-1}$$\to x^{*}$ and ${\mathit{e}}_{\mathit{p}}^{\mathit{A}}$, ${\mathit{e}}_{\mathit{p}-1}^{\mathit{A}}\to 0$, implies that

$$\frac{f^{\prime }\left(x^{*}\right)}{f^{\prime }\left({\eta }_{p-1}\right)}\to \frac{f^{\prime }\left(x^{*}\right)}{f^{\prime }\left(x^{*}\right)}=1$$

(7.16)

and ${\gamma }_p\to 1$. By substituting ${\mathit{e}}_{\mathit{p}}^{\mathit{B}}$ (Equation (7.14)) into Equation (7.9) gives

$$e_{p+1}^A=C_p{e}_p^A\left(e_p^A-e_p^A{\left(\frac{e_p^A-e_{p-1}^A}{e_{p-1}^A}\right)}^2{\gamma }_p\right)$$

(7.17)

and by re-arranging

$$e_{p+1}^A=C_p{e}_p^A\left({\gamma }_p{\left(e_p^A\right)}^2\frac{2e_{p-1}^A-e_p^A}{{\left(e_{p-1}^A\right)}^2}+\left(1-{\gamma }_p\right)e_p^A\right)$$

(7.18)

with $\left\{x_p^A\right\}$ converges to ${\mathit{x}}^{*}$, ${\gamma }_p\to 1$ and the above equation simplifies as

$$e_{p+1}^A=C_p{e}_p^A{\left(e_p^A\right)}^2\frac{2e_{p-1}^A-e_p^A}{{\left(e_{p-1}^A\right)}^2}$$

(7.19)

It means that ${\mathit{e}}_{\mathit{p}+1}^{\mathit{A}}$ depends on ${\mathit{e}}_{\mathit{p}}^{\mathit{A}}$ and ${\mathit{e}}_{\mathit{p}-1}^{\mathit{A}}$, and by assuming an asymptotic convergence, a power law relationship

$$\left|e_{p+1}^A\right|=C{\left|e_p^A\right|}^{\alpha }$$

(7.20)

can be established, where $\mathit{C}$ is the asymptotic error constant and $\alpha$ is the convergence rate or also called “convergence order” of the iterative method. It also follows from Equation (7.20), that

$$\left|e_p^A\right|=C{\left|e_{p-1}^A\right|}^{\alpha }$$

(7.21)

and

$$\left|e_{p-1}^A\right|={\left(\frac{\left|e_p^A\right|}{C}\right)}^{\frac{1}{\alpha }}$$

(7.22)

Let $\mathit{E}=\left|{\mathit{e}}_{\mathit{p}}^{\mathit{A}}\right|$ be introduced for simplifying purpose, then it follows from Equations (7.17), (7.20), (7.21) and (7.22) that

$$E^{\alpha }=\frac{C_p}{C}{E}^3\frac{2{\left(\frac{E}{C}\right)}^{\frac{1}{\alpha }}-E}{{\left(\frac{E}{C}\right)}^{\frac{2}{\alpha }}}$$

(7.23)

where ${\mathit{C}}_{\mathit{p}}$ and $\mathit{C}$ are constants and if the series $\left\{x_p^A\right\}$ converges to ${\mathit{x}}^{*}$, then with increasing iteration counter $\mathit{p}$, $E\to 0^{+}$. Taking the logarithms of both sides of Equation (7.23) and dividing by $\mathit{lnE}$ gives

$$\alpha =\frac{ln\frac{C_p}{C}}{lnE}+3-\frac{2}{\alpha }·\frac{ln\left(\frac{E}{C}\right)}{lnE}+\frac{ln(2{\left(\frac{E}{C}\right)}^{\frac{1}{\alpha }}-E)}{lnE}$$

(7.24)

If $\left\{x_p^A\right\}$ series converges to ${\mathit{x}}^{*}$, then with increasing iteration counter $\mathit{p}$, $E\to 0^{+}$, $ln\mathit{E}\to -\infty$ and

$$\underset{E\to 0^{+}}{lim}\frac{ln\frac{C_p}{C}}{lnE}=0$$

(7.25)

$$\underset{E\to 0^{+}}{lim}ln\left(\frac{E}{C}\right)=\underset{E\to 0^{+}}{lim}\left(lnE-lnC\right)=lnE$$

(7.26)

$$\underset{E\to 0^{+}}{lim}\frac{ln\left(2E^{\frac{1}{\alpha }}-E\right)}{lnE}=\frac{1}{\alpha }$$

(7.27)

and Equation (7.24) simplifies as

$$\alpha -3+\frac{1}{\alpha }=0$$

(7.28)

with root (convergence rate of the T-Secant method) :

$${\alpha }^{TS}=\frac{3+\sqrt{5}}{2}\cong 2.618033988\dots ={\alpha }^S+1={\phi }^2$$

(7.29)

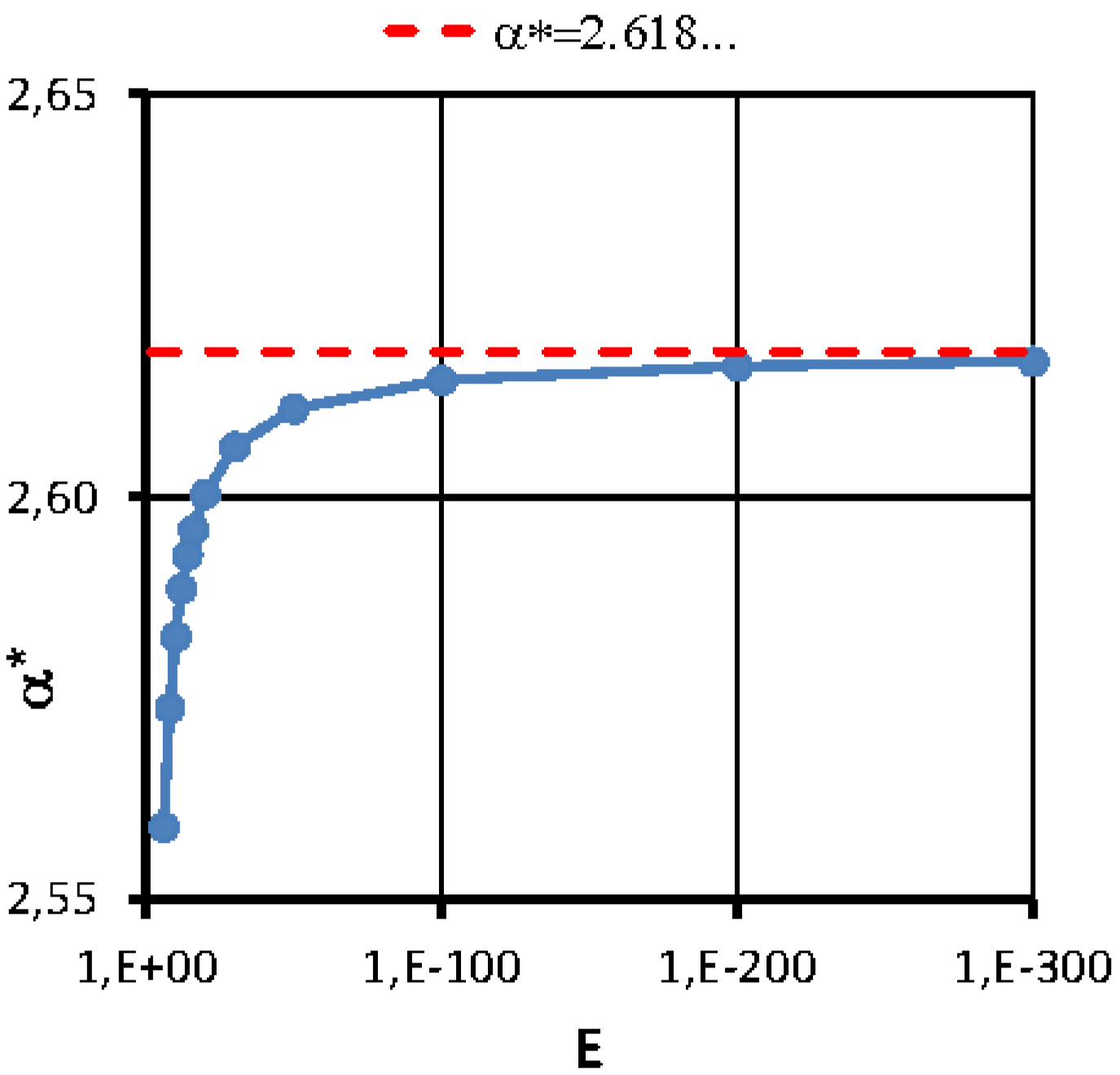
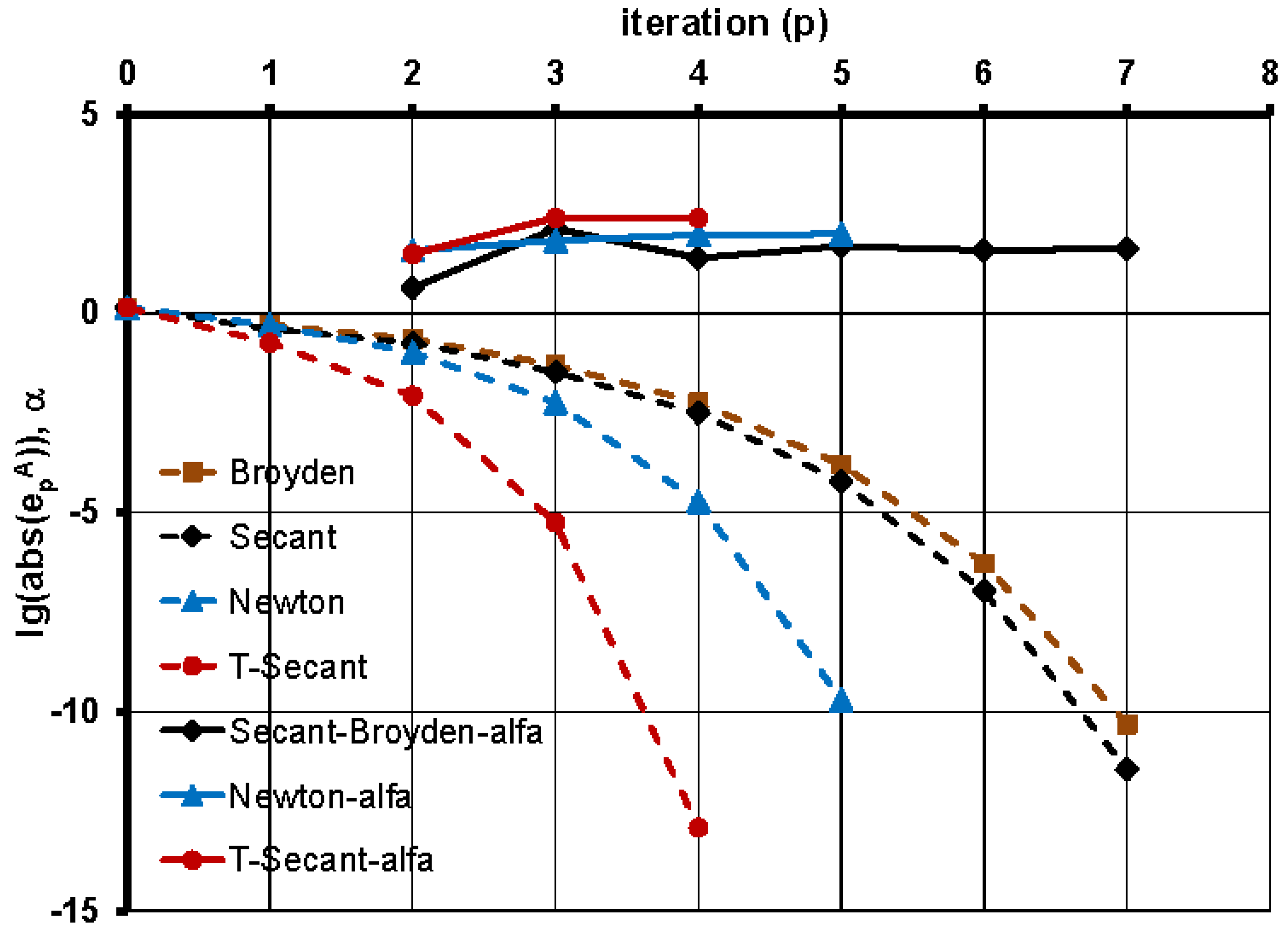
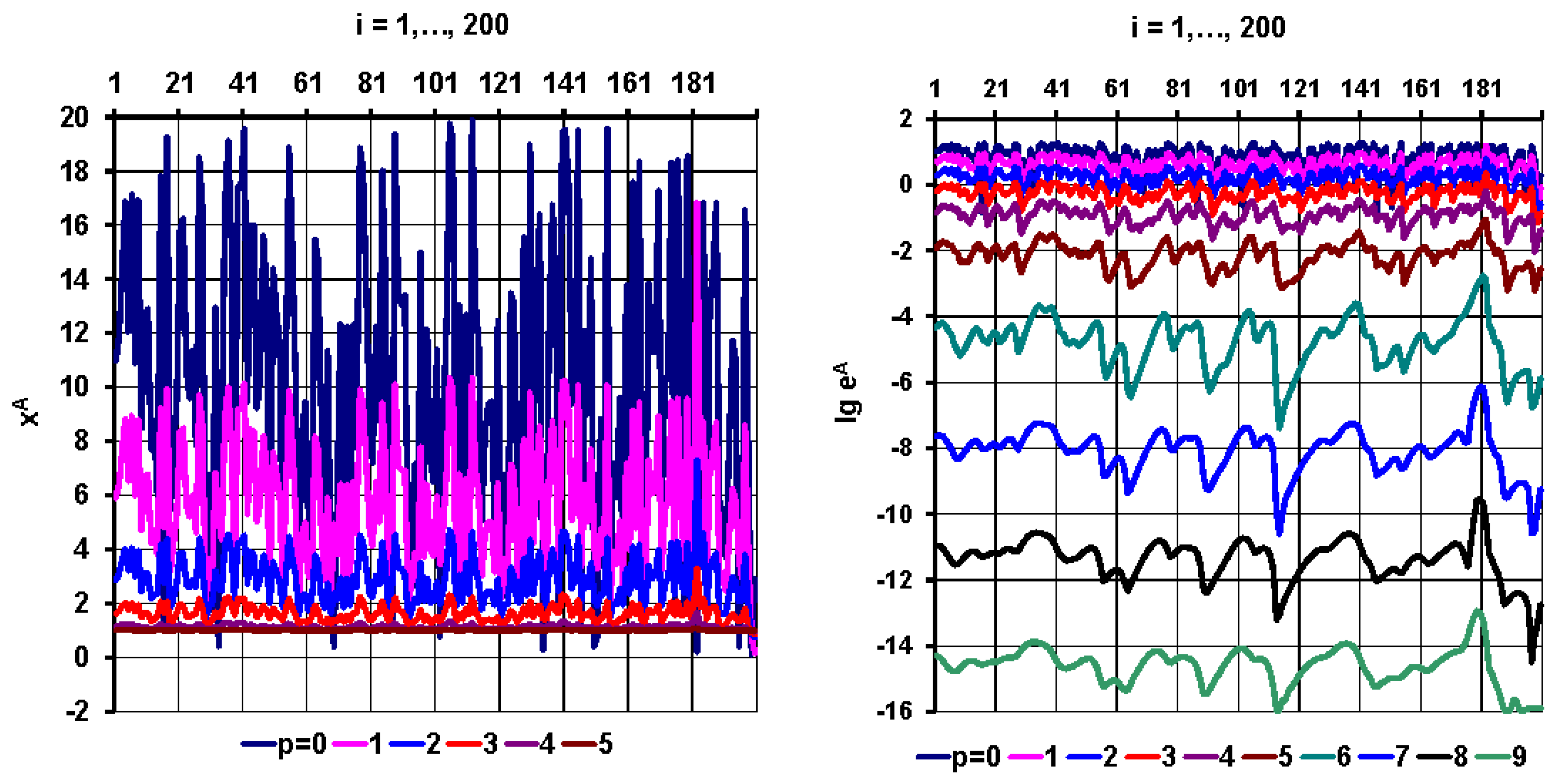
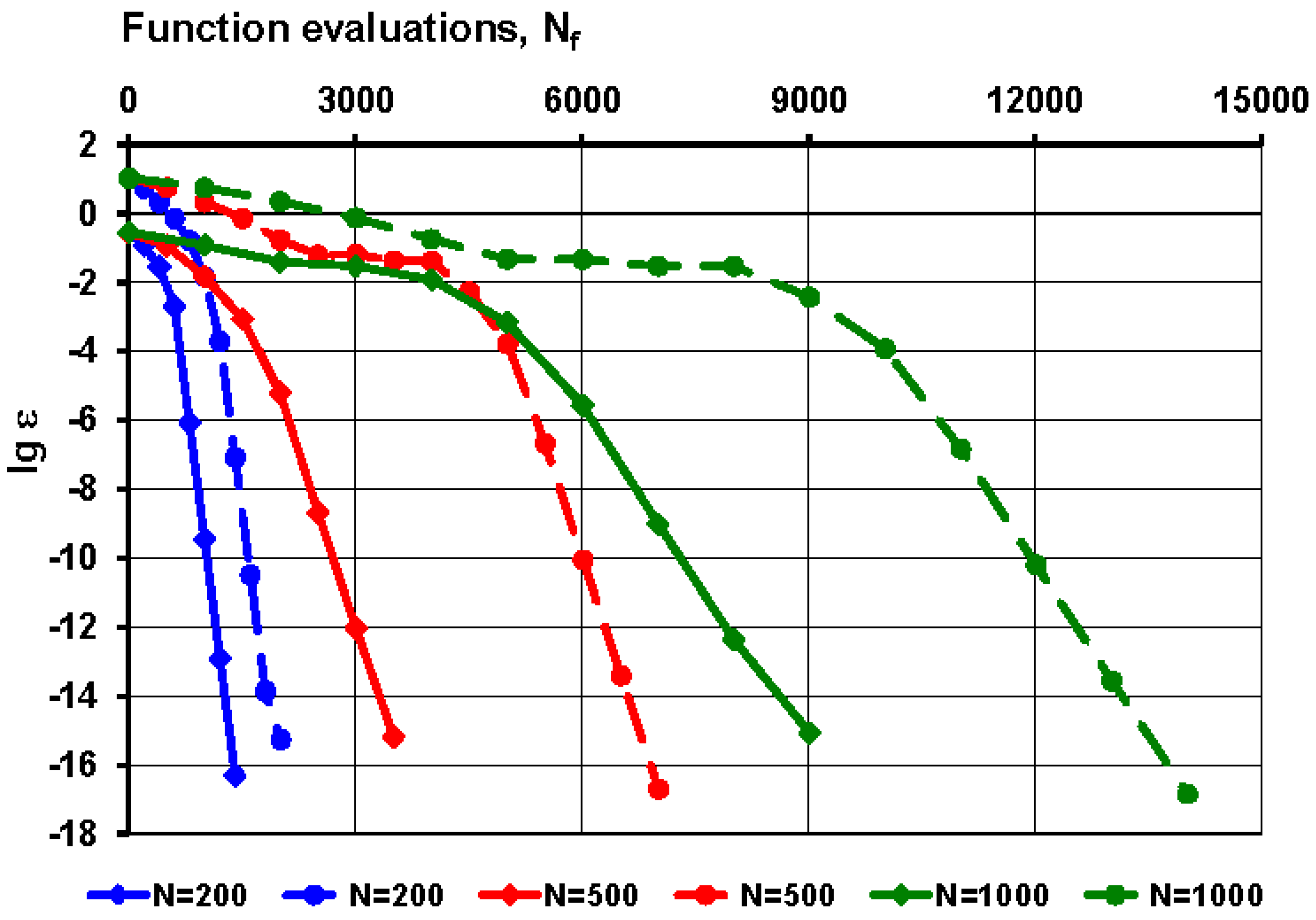
where ${\alpha }^S=\phi \cong 1.618033988\dots$ is the convergence rate of the traditional secant method and ’ is the well known golden ratio. It follows from Equation (7.24) that the actual values ${\alpha }^{*}$ of ${\alpha }^{TS}$ depend on the approximate error $\mathit{E}=\left|{\mathit{e}}^{\mathit{A}}\right|$. Convergence rates ${\alpha }^{*}\left(E\right)$ were determined for different $\mathit{E}$ values and shown on Figure 5. The upper bound ${\alpha }^{TS}={\alpha }^S+1=2.618\dots$ at $\mathit{E}\to {\mathit{0}}^{+}$ is also indicated (horizontal dashed red line).

7.3. Single-variable example

An example is given for demonstration purpose with a single-variable test function 5.26 with root ${\mathit{x}}^{*}\cong 2.09455...$. Iterations were made with initial approximates ${\mathit{x}}_0^{\mathit{A}}=3.5$ and ${\mathit{x}}_0^{\mathit{B}}=2.5$ and the convergence rates ${\alpha }^S$, ${\alpha }^N$ and ${\alpha }^{TS}$ were determined for the traditional secant method (Table 3, Figure 6), for the Newton-Raphson method (Table 4, Figure 7) and for the T-secant method (Table 5, Figure 8) respectively, the cumulative number of function value (${\mathit{N}}_{\mathit{f}}$) and derivative function value (${\mathit{N}}_{{\mathit{f}}^{\prime }}$) calculations are also indicated in the tables. Calculated convergence rates agree well with theoretical values ${\alpha }^S=1.62...$, ${\alpha }^N=2.0$ and ${\alpha }^{TS}=2.62...$. Figure 9 summarizes the results of iterations with three different methods (Secant, Newton-Raphson and T-Secant). Two groups of graphs show the absolute approximate error $\left|e_p^A\right|$ decrease and the calculated convergence rates $\alpha$ for the three compared methods. Results demonstrate that the convergence rate of the T-Secant method is higher than the convergence rate of the Newton-Raphson method.

7.4. Multi-variable convergence

Matrix $\mathit{S}$ corresponds to a divided difference approximation to the Jacobian. It is known (e. g. from Dennis-Schnabel [7]) that these values give a second order approximation to the derivative in the midpoint. When considering Newton’s iteration, it is assumed that the Jacobian has inverse in a neighbourhood of ${\mathit{x}}^{*}$. If that condition holds, than there are chances that the approximate Jacobian has also inverse in the same neighbourhood.

It follows from Equations (6.7) and (6.16), that the ${\mathit{i}}^{\mathit{th}}$ elements of the iteration step lengths of the new approximates ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ in the ${\mathit{p}}^{\mathit{th}}$ iteration are

$$▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}=-\sum _{\mathit{j}=1}^{\mathit{m}}\left({\mathit{S}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}\right)$$

(7.30)

and

$$▵{\mathit{x}}_{\mathit{p}+1,\mathit{i}}=-\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left({\mathit{S}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(7.31)

$\left(i=1\dots ,n\right)$. It is known, that the secant method is locally q-super-linear convergent, so the new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ is expected to be a much better approximate to the solution ${\mathit{x}}^{*}$ then the previous approximate ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$. Thus

$$∥{\mathit{f}}_{p+1}^A∥⋘∥{\mathit{f}}_p^A∥$$

(7.32)

and the diagonal elements

$$\left|{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}\right|=\left|\frac{{\mathit{f}}_{\mathit{p}+1,\mathit{j}}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}\right|⋘1$$

(7.33)

of the transformation matrix ${\mathit{T}}_{\mathit{p}}^{\mathit{F}}$$\left(j=1\dots ,m\right)$ are expected to be “small numbers”. Let the scalar multipliers ${\mu }_i$ be introduced so that

$${\mu }_i\left|\sum _{\mathit{j}=1}^{\mathit{m}}\left(S_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)\right|=\left|\sum _{\mathit{j}=1}^{\mathit{m}}\left(S_{p,i,j}^{+}{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}\right)\right|$$

(7.34)

Then Expression 7.31 for the ${\mathit{i}}^{\mathit{th}}$ element of the iteration step length $▵{\mathit{x}}_{\mathit{p}+1}$ of the new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ in the ${\mathit{p}}^{\mathit{th}}$ iteration simplifies as

$$▵{\mathit{x}}_{\mathit{p}+1,\mathit{i}}=-\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{\frac{1}{{\mu }_i}{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left({\mathit{S}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}\right)}={\mu }_i\frac{{\left(▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^2}{▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}}={\mu }_i▵{\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}$$

(7.35)

where

$${\mu }_i⋘1$$

(7.36)

$\left(i=1\dots ,n\right)$ and it follows from the above derivations that

$$∥▵{\mathit{x}}_{p+1}∥\le ∥\mathit{\mu }∥∥▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}∥$$

(7.37)

It means, that the T-secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ will always be in the vicinity of the classic secant approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and the approximate errors of the new approximates will be of similar order, providing that the solution ${\mathit{x}}^{*}$will evenly be surrounded by the $\mathit{n}+1$ new trial approximates ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and ${\mathit{x}}_{\mathit{k},\mathit{p}+1}^{\mathit{B}}$ $\left(k=1\dots ,n\right)$ and matrix ${\mathit{S}}_{\mathit{p}+1}$ will be well-conditioned.

Figure 10. Geometrical representation of the T-secant method convergence in multi-variable case (analogous to the convergence proof figure Dennis-Schnabel [7], p. 180.).

Figure 10. Geometrical representation of the T-secant method convergence in multi-variable case (analogous to the convergence proof figure Dennis-Schnabel [7], p. 180.).

8. Algorithm

Let $\mathit{p}$ be the iteration counter, ${\epsilon }^{*}$ be the error bound for termination criterion and

$${\mathit{e}}_p^A={\mathit{x}}_{\mathit{p}}^{\mathit{A}}-{\mathit{x}}^{*}$$

(8.1)

be the approximate error vector of approximate ${\mathit{x}}^{\mathit{A}}$ in the ${\mathit{p}}^{\mathit{th}}$ iteration with elements ${\mathit{e}}_{\mathit{p},\mathit{i}}^{\mathit{A}}$ $\left(i=1,\dots ,n\right)$. Let the scalar approximate error

$${\epsilon }_p=\frac{{∥{\mathit{e}}_p^A∥}_2}{n}=\frac{\sqrt{{\displaystyle \sum _{\mathit{i}=\mathit{1}}^{\mathit{n}}}{\left({\mathit{e}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)}^{\mathit{2}}}}{n}$$

(8.2)

be defined, where ${∥\dots ∥}_2$ is Euclidean norm and let the iteration be terminated when

$${\epsilon }_p<{\epsilon }^{*}$$

(8.3)

holds. Let ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ be the initial trial and $▵{\mathit{x}}_{\mathit{p}}$ be the trial increment in the ${\mathit{p}}^{th}$ iteration. Choose ${\mathit{T}}_{\mathit{min}}$ and ${\mathit{T}}_{\mathit{max}}$ as lower and upper bounds for $\left|t_{p,j}^F\right|$ $\left(j=1\dots ,m\right)$ and let ${\mathit{f}}_{\mathit{min}}$ and ${\mathit{q}}_{\mathit{min}}$ be lower bounds for $\left|{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}\right|$ $\left(j=1,\dots ,m\right)$ and $\left|q_{p,i}^{\mathit{B}}\right|$$\left(i=1,\dots ,n\right)$ respectively.

• Initial step
  Let $\mathit{p}=0$ and let the initial trial ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}=\left(\begin{array}{ccc}{\mathit{x}}_{\mathit{p},1}^{\mathit{A}}& \cdots & {\mathit{x}}_{\mathit{p},\mathrm{n}}^{\mathit{A}}\end{array}\right)$ and the initial trial increment $▵{\mathit{x}}_{\mathit{p}}=\left(\begin{array}{ccc}▵{\mathit{x}}_{\mathit{p},1}& \cdots & ▵{\mathit{x}}_{\mathit{p},\mathrm{n}}\end{array}\right)$ be given. Calculate the corresponding function values ${\mathit{f}}_{\mathit{p}}^{\mathit{A}}$ and assume that ${\mathit{f}}_{\mathit{min}}<\left|{\mathit{f}}_{\mathit{p},\mathrm{j}}^{\mathit{A}}\right|(j=1\dots ,m)$.
• Step 1 : Generate a set of $\mathrm{n}$ additional initial trials (interpolation base points)

  $${\mathit{x}}_{p,k}^B={\mathit{x}}_p^A+▵{\mathit{x}}_{\mathit{p},\mathit{k}}·{\mathit{d}}^k$$

  (8.4)

  and evaluate function values ${\mathit{f}}_{\mathit{p},\mathit{k}}^{\mathit{B}}$ $\left(k=1,\dots ,n\right)$.
• Step 2 (Secant) : Construct matrix

  $$▵{\mathit{F}}_p=\left[▵{\mathit{f}}_{p,k}^i\right]=\left[{\mathit{f}}_{p,k}^B-{\mathit{f}}_p^A\right]$$

  (8.5)

  then calculate ${\mathit{q}}_{\mathit{p}}^{\mathit{A}}$ from Equation 3.15. Let ${\mathit{q}}_{\mathit{min}}<\left|{\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right|$, and determine ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ from Equation (3.19) and ${\epsilon }_p$ from Equation 8.2.
• Step 3 : If ${\epsilon }_p$<${\epsilon }^{*}$ then terminate iteration, else continue with Step 4.
• Step 4 (T-secant) : Calculate ${\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}$ and ${\mathit{T}}_{\mathit{p}}^{\mathit{F}}$from Equation (4.19). Let ${\mathit{T}}_{\mathit{min}}<\left|{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}\right|<{\mathit{T}}_{\mathit{max}}$ and determine ${\mathit{q}}_{\mathit{p}}^{\mathit{B}}$ from Equation 4.20 ($▵{\mathit{F}}_p^{+}$ has already been calculated when ${\mathit{q}}_{\mathit{p}}^{\mathit{A}}$ was determined from Equation (3.15)). Let ${\mathit{q}}_{\mathit{min}}<\left|{\mathit{q}}_{\mathit{p},\mathit{i}}^{\mathit{B}}\right|$, calculate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ from Equation (4.22).
• Step 5 : Let the new initial trial be

  $${\mathit{v}}_{p+1}^A=\left[\begin{array}{c}{\mathit{x}}_{p+1}^A\\ {\mathit{f}}_{p+1}^A\end{array}\right]$$

  (8.6)

  and the new initial trial increment be

  $$▵{\mathit{x}}_{p+1}={\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$$

  (8.7)

  and continue iteration with Step 1.

Iteration constants $\left(\begin{array}{ccccc}{\delta }_{min}& f_{min}& q_{min}& T_{min}& T_{max}\end{array}\right)$ are necessary to avoid division by zero and to avoid computed values be near the numerical precision. If ${\mathit{p}}_{\mathit{max}}$ is the number of necessary iterations for satisfying the termination criterion ${\epsilon }_p<{\epsilon }^{*}$ and $\mathit{n}$ is the number of unknowns to be determined, then T-Secant method needs $\mathit{n}+\mathit{1}$ function evaluations in each iterations and altogether

$$N_f={\mathit{p}}_{\mathit{max}}\left(n+1\right)$$

(8.8)

function evaluations to reach the desired termination criterion. ${\mathit{p}}_{\mathit{max}}$ is depending on many circumstances such as the nature of the function $\mathit{f}\left(\mathit{x}\right)$, termination criteria (${\epsilon }^{*}$ or others), the distance of the initial trial ${\mathit{x}}^{\mathit{A}}$ from the solution ${\mathit{x}}^{*}$ and from the iteration constants $\left({\mathit{T}}_{\mathit{min}},{\mathit{q}}_{\mathit{min}}^{\mathit{A}},\dots \right)$.

9. Numerical tests results

9.1. Rosenbrock test function

A variant of the Rosenbrock function [8] has been used for testing the numerical performance of the new method. Determine the global minimum of the function

$$\mathit{R}\left(\mathit{x}\right)=\sum _{\mathit{i}=1}^{\mathit{N}-1}\left(100·{\left({\mathit{x}}_{\mathit{i}+1}-x_i^2\right)}^2+{\left(1-{\mathit{x}}_{\mathit{i}}\right)}^2\right)$$

(9.1)

where $\mathit{x}=\left(\begin{array}{ccc}{x}_1& \cdots & x_{\mathit{N}}\end{array}\right)\in {\mathbb{R}}^{\mathit{N}}$ and $\mathit{N}\ge \mathit{2}$. $\mathit{R}\left(\mathit{x}\right)$ has exactly one minimum for $\mathit{N}=\mathit{3}$ at ${\mathit{x}}^{*}=$$\left(\begin{array}{ccc}1& 1& 1\end{array}\right)$ and exactly two minima for $4\le N\le 7$ , a global minimum of all ones and a local minimum near $\widehat{\mathit{x}}=\left(\begin{array}{cccc}-1& 1& \cdots & 1\end{array}\right)$. The sum of squares $\mathrm{R}\left(\mathit{x}\right)$ will be minimum when all terms are zero, such that the minimization of the function $\mathrm{R}\left(\mathit{x}\right)$ is equivalent with finding the zero of a function $\mathit{x}\to \mathit{f}\left(\mathit{x}\right)$, where $\mathit{x}\in {\mathbb{R}}^{\mathrm{N}}$, $\mathit{f}:{\mathbb{R}}^N\to {\mathbb{R}}^{2(N-1)}$, and

$$\mathit{f}\left(\mathit{x}\right)=\left[\begin{array}{c}{\mathit{f}}_{2\mathrm{i}-1}\left(\mathit{x}\right)\\ {\mathit{f}}_{2\mathrm{i}}\left(\mathit{x}\right)\end{array}\right]=\left[\begin{array}{c}10·({\mathit{x}}_{\mathrm{i}+1}-{\mathit{x}}_{\mathrm{i}}^2)\\ 1-{\mathit{x}}_{\mathrm{i}}\end{array}\right]$$

(9.2)

$\left(i=1,\dots ,N-1\right)$. For $\mathrm{N}>7$ , the function $\mathrm{R}\left(\mathit{x}\right)$ has exactly one global minimum ${\mathit{x}}^{*}=\left(\begin{array}{ccc}1& \dots & 1\end{array}\right)$ and has some local minima with some ${\mathit{x}}_{\mathrm{j}}^{*}=-1$ and with ${\mathit{x}}_{\mathrm{i}}^{*}=1$ for all other unknowns. The results were obtained by least squares solving of the simultaneous system of nonlinear equations $\mathit{f}\left(\mathit{x}\right)=\mathit{0}$ by the T-Secant method.

9.2. $\mathit{N}=2$, $\mathit{N}=3$ and $\mathit{N}=10$ examples

In case $\mathit{N}=\mathit{n}=\mathit{m}=2$, iterations terminated after ${\mathit{N}}_{\mathit{f}}=6$ function evaluations (${\mathit{p}}_{\mathit{max}}=2$ iterations) in most cases. ${\mathit{f}}_2\left(\mathit{x}\right)=1-{\mathit{x}}_1$ is a linear function and the first T-secant iteration $\left(p=0\right)$ finds the exact value of ${\mathit{x}}_1$ in one step, then ${\mathit{f}}_1\left(\mathit{x}\right)=10\left({\mathit{x}}_2-{\mathit{x}}_1^2\right)$ also becomes linear. The exact value of ${\mathit{x}}_2$ was then determined in one additional step.

Let $\mathit{N}=\mathit{n}=3$ and $\mathit{m}=4$, ${\mathit{T}}_{\mathit{min}}=0.01$ and ${\epsilon }^{*}={10}^{-14}$. Let $\mathit{p}=0$ , and

$$▵x_{0,i}=0.05·x_{0,i}^A$$

(9.3)

$(\mathrm{i}=1\dots ,3)$. The number of necessary function evaluations ${\mathit{N}}_{\mathit{f}}$ varied between $20-36$ within ${\mathit{p}}_{\mathit{max}}=5-9$ iterations for different initial trials ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$. Iteration results are summarized in Table 6 and in Figure 11 with initial trial ${\mathit{x}}_0^{\mathit{A}}=\left({\mathit{x}}_{0,\mathit{i}}^{\mathit{A}}\right)=\left(\begin{array}{ccc}2.0& -1.5& -2.5\end{array}\right)$. Termination criterion ${\epsilon }_p<{”}^{*}$ was satisfied after ${\mathit{p}}_{\mathit{max}}=5$ iterations with ${\mathit{N}}_{\mathit{f}}=20$ function evaluations.

Let $\mathit{N}=\mathit{n}=10$ and $\mathit{m}=18$. Calculations were made with different, manually constructed initial trials ${\mathit{x}}_0^{\mathit{A}}=\left(x_{0,i}^A\right)$. Figure 12 (Left) shows the variation of ${\mathit{x}}_{\mathit{p},\mathit{i}}^{\mathit{A}}$ for initial trial ${\mathit{x}}_0^{\mathit{A}}=\left(\begin{array}{cccccccccc}\mathit{2}.\mathit{0}& -\mathit{1}.\mathit{5}& -\mathit{2}.\mathit{5}& \mathit{1}.\mathit{5}& -\mathit{1}.\mathit{2}& \mathit{3}.\mathit{0}& -\mathit{3}.\mathit{5}& \mathit{2}.\mathit{5}& -\mathit{2}.\mathit{0}& \mathit{3}.\mathit{5}\end{array}\right)$. Iteration terminated after ${\mathit{N}}_{\mathit{f}}=154$ function evaluations (${\mathit{p}}_{\mathit{max}}=14$ iterations) for ${\epsilon }_p<{\epsilon }^{*}={10}^{-14}$ condition. Table 7 shows a set of further initial trials for numerical tests. Test “3” failed probably due to the large distance from the global optimal solution. Test “4” found a local zero $x^{*}=\left(\begin{array}{cccccccccc}-1& 1& 1& 1& 1& 1& 1& 1& 1& 1\end{array}\right)$. Figure 12 (Right) summarizes the results of numerical tests “1-6”. Graphs show the iteration paths in the $lg\left|e_p^A\right|-R_p\left(x_p^A\right)$ plane. They have an initial part where the variation of $R_p\left(x_p^A\right)$ seems “chaotic”, while below $\left|e_p^A\right|\cong 0.01$ and ${\mathit{R}}_{\mathit{p}}\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)\cong$ 0.001 the iterations run on similar paths.

9.3. Large $N\left(2005001000\right)$ examples

A series of numerical test has been performed with large number of unknown variables. The values of the initial trials ${\mathit{x}}_0^{\mathit{A}}=\left(x_{0,i}^A\right),\left(i=1,\dots N\right)$ were generated as

$$x_{0,i}^A=x_i^{*}+L_1·\frac{Random-\frac{1}{2}}{5}+L_2$$

(9.4)

where “$\mathit{Random}$” is a random real number ($0\le \mathit{Random}<1$), ${\mathit{L}}_{\mathit{i}}\left(i=1,2\right)$ are parameters regulating the size and location of the interval in which the initial trial values are expected to variate. ${\mathit{x}}^{*}=\left(x_i^{*}\right)=\left(\begin{array}{ccc}1& \dots & 1\end{array}\right)\left(i=1,\dots N\right)$ is the known global optimal solution. Table 8 shows the results of T-Secant iterations with $\mathit{N}=200$ and with initial trials ${\mathit{x}}_0^{\mathit{A}}:0.1\le x_{0,i}^A\le 19.9$ (${\mathit{L}}_{\mathit{1}}=99,L_2=9$). Figure 13 (Left) shows the variation of variables ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ through T-Secant iterations. The iteration counter $\mathit{p}$ value is indicated below the graphs for iterations. Figure 13 (Right) shows the decrease of the approximate error ${\mathit{e}}_p^A=\left({\mathit{e}}_{\mathit{p},\mathit{i}}^{\mathit{A}}\right)$$\left(\mathit{i}=1,\dots ,200\right)$, with the $\mathit{p}$ iteration counter indication below the graphs. Table 9 shows the results of iterations with $\mathit{N}=1000$ and initial trials ${\mathit{x}}_0^{\mathit{A}}:0.5\le x_{0,i}^A\le 1.5$ (${\mathit{L}}_{\mathit{1}}=5,L_2=0$). Figure 14 summarizes the results of numerical tests with large number of unknowns $N=\left(\begin{array}{ccc}200& 500& 1000\end{array}\right)$. The norm ${\epsilon }_p$ of the approximate error ${\mathit{e}}_{\mathit{p}}^{\mathit{A}}$ decrease is shown and the number of function value evaluations ${\mathit{N}}_{\mathit{f}}$ is indicated for $N=\left(\begin{array}{ccc}200\left(blue\right)& 500\left(red\right)& 1000\left(green\right)\end{array}\right)$ and for initial trials ${\mathit{x}}_0^{\mathit{A}}:0.5\le x_{0,i}^A\le 1.5$ (solid line) and ${\mathit{x}}_0^{\mathit{A}}:0.1\le x_{0,i}^A\le 19.9$ (dashed line).

10. Efficiency

Very limited data are available to compare the performance of the T-secant method with other methods, especially for large number of unknowns. Broyden [9] suggested the mean convergence rate

$$L=\frac{1}{N_f}ln\frac{R\left({\mathit{x}}_0^A\right)}{R\left({\mathit{x}}_{p_{max}}^A\right)}$$

(10.1)

as a measure of efficiency of a method for solving a particular problem, where ${\mathit{N}}_{\mathit{f}}$ is the total number of function evaluations, ${\mathit{x}}_0^{\mathit{A}}$ is the initial trial, ${\mathit{x}}_{{\mathit{p}}_{\mathit{max}}}^{\mathit{A}}$ is the last trial for the solution ${\mathit{x}}^{*}$ when the termination criteria is satisfied after ${\mathit{p}}_{\mathit{max}}$ iterations. $\mathit{R}\left(\mathit{x}\right)$ is the Euclidean norm of $\mathit{f}\left(\mathit{x}\right)$. Efficiency results were given by Broyden [9] for the Rosenbrock function for $\mathit{N}=2$ and for ${\mathit{x}}_0^{\mathit{A}}=\left(\begin{array}{cc}-1.2& 1.0\end{array}\right)$. The calculated convergence rates for the two Broyden method variants [9], for the Powell’s method [10], for the adaptive coordinate descent method [11] and for the Nelder-Mead simplex method [12] were compared with the calculated values for the T-secant method in Table 10. Rows $1-5$ are data from referenced papers, rows $6-8$ are T-secant results with the referenced initial trials and rows 9-15 are calculated data for $\mathit{N}>2$. Results show that the mean convergence rate $\mathit{L}$ (Equation (10.1)) for $\mathit{N}=2$ is much higher for the T-secant method ($\simeq 5.5-6.9$) than for the other listed methods ( $\simeq 0.1-0.6$), however it is obvious that the convergence rate values decrease rapidly with increasing $\mathit{N}$ values (more unknowns need more function evaluations). A modified convergence rate

$$L_N=\mathit{N}\ast \mathit{L}=\frac{\mathit{N}}{{\mathit{N}}_{\mathit{f}}}ln\frac{\mathit{R}\left({\mathit{x}}_0^{\mathit{A}}\right)}{\mathit{R}\left({\mathit{x}}_{{\mathit{p}}_{\mathit{max}}}^{\mathit{A}}\right)}$$

(10.2)

can be used as a more $”\mathit{N}”$ independent measure of efficiency (see Table 10) than the quantity $\mathit{L}$. The values of $\mathit{L}$ and ${\mathit{L}}_{\mathit{N}}$ are at least 10 times larger for the T-secant method than for the other listed methods for $\mathit{N}=2$. Note that the efficiency measures ($\mathit{L}$ and ${\mathit{L}}_{\mathit{N}}$) are also depending on the initial conditions (distance of the initial trial set from the optimal solution, termination criterion). Results from large number of numerical tests indicate an average ${\mathit{L}}_{\mathit{N}}$ value around $7.4$ with standard deviation $3.7$ for the T-secant method even for large $\mathit{N}$ values. It has to be noted that if the value of $\mathit{R}\left({\mathit{x}}_{{\mathit{p}}_{\mathit{max}}}^{\mathit{A}}\right)$ is zero, then the mean convergence rates ($\mathit{L}$ and ${\mathit{L}}_{\mathit{N}}$) are not countable (zero in the denominator). A substitute value ${10}^{-25}$ was used when iteration ended with $\mathit{R}\left({\mathit{x}}_{{\mathit{p}}_{\mathit{max}}}^{\mathit{A}}\right)=0$ in the sample examples.

11. Discussions

11.1. General

The suggested new procedure needs the usual approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ be determined by any of a classic quasi-Newton iterative method (Wolfe-Popper-Secant, Broyden, etc.). By using the “information” $\mathit{f}\left({\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}\right)=f_{p+1}^A$, an additional and independent approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ is determined, that provides the possibility for a full-rank update of the exact or approximate derivatives (${\mathit{S}}_{\mathit{p}}$ for Secant or ${\mathit{B}}_{\mathit{p}}$ for Broyden). Results and experience show that the new procedure considerably accelerates the convergence and the efficiency of the classic methods, and the full-rank update technique increases the stability of the iterative procedure. In multi-variable-case, it follows from Equation (6.8) that

$${\left({\mathit{T}}_{\mathit{p}}^{\mathit{X}}\right)}^{-1}▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{S}}_{\mathit{p}}^{+}{\left({\mathit{T}}_{\mathit{p}}^{\mathit{F}}\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(11.1)

and in explicit form after re-arrangement

$$\left[\frac{{\left(▵x_{p,i}^A\right)}^2}{x_{p+1,i}^B-x_{p+1,i}^A}\right]=-\left[{\mathit{S}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}\right]\left[\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right]$$

(11.2)

Then the ${\mathit{i}}^{\mathit{th}}$ element of the new approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ can be expressed from the ${\mathit{i}}^{\mathit{th}}$ row of the above equation as

$$x_{p+1,\mathit{i}}^{\mathit{B}}=x_{p+1,i}^A-\frac{{\left(▵x_{p,i}^A\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left(S_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(11.3)

The mechanism of the procedure can be resembled to the mechanism of an engine’s turbocharger that is powered by the flow of exhaust gases (analogous to ${\mathit{f}}_{\mathit{p}+\mathit{1}}^{\mathit{A}}$ or ${\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}$).

11.2. Newton method

Matrix $\mathit{S}$ in the general formula 6.5 gives a direct connection between secant and Newton method, as differences go to differentials,

$$\mathit{S}=\left[\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]=\left[S_{i,j}\right]⟶\mathit{J}=\left[\frac{\partial {\mathit{f}}_{\mathit{k},\mathit{j}}}{\partial {\mathit{x}}_{\mathit{i}}}\right]=\left[J_{i,j}\right]$$

(11.4)

where $\mathit{J}$ is the Jacobian matrix the function $\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m$ ($\mathit{m}\ge \mathit{n}$) with $\mathit{k}$ and $\mathit{i}$ column and with $\mathit{j}$ row indeces respectively. It follows from formula 6.12 of matrix ${\mathit{S}}_{\mathit{T}}$ that the proposed full-rank update procedure can also be applied to the Newton method as

$${\mathit{S}}_{\mathit{T}}=\left[\frac{t_j^{\mathit{F}}}{t_{\mathit{i}}^{\mathit{X}}}\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]⟶{\mathit{J}}_T=\left[\frac{{\mathit{t}}_{\mathit{j}}^{\mathit{F}}}{t_{\mathit{i}}^{\mathit{X}}}\frac{\partial {\mathit{f}}_{\mathit{k},\mathit{j}}}{\partial {\mathit{x}}_{\mathit{i}}}\right]$$

(11.5)

where ${\mathit{J}}_{\mathit{T}}$ is the modified Jacobian matrix of the ’T-Newton’ method. In single-variable case, with approximate ${\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ in the ${\mathit{p}}^{\mathit{th}}$ iteration, with function value ${\mathit{f}}_{\mathit{p}}^{\mathit{A}}=f\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)$ and with derivative function value ${\mathit{f}}_{\mathit{p}}^{\prime \mathit{A}}=f^{\prime }\left({\mathit{x}}_{\mathit{p}}^{\mathit{A}}\right)$, the new Newton-Raphson approximate can be expressed as

$$x_{p+1}^A=x_p^A-\frac{\partial x_p}{\partial f_p}{f}_p^A=x_p^A-\frac{f_p^A}{{\mathit{f}}_{\mathit{p}}^{\prime \mathit{A}}}$$

(11.6)

and the iteration step size is

$$▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}={\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}-{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$$

(11.7)

With the hyperbolic function (Equation (5.15))

$${\mathit{z}}_{\mathit{p}}\left(\mathit{x}\right)=\frac{a_p}{x-x_{p+1}^{\mathit{A}}}+{\mathit{f}}_p^{\mathit{A}}$$

(11.8)

where

$$a_p={\left(x_{p+1}^{\mathit{A}}-x_p^A\right)}^2{\mathit{f}}_{\mathit{p}}^{\prime \mathit{A}}\frac{{\mathit{f}}_{\mathit{p}+1}^{\mathit{A}}}{{\mathit{f}}_{\mathit{p}}^{\mathit{A}}}$$

(11.9)

($▵{\mathit{f}}_{\mathit{p}}/▵{\mathit{x}}_{\mathit{p}}$ is replaced by ${\mathit{f}}_{\mathit{p}}^{\prime \mathit{A}}$), the new ’T-Newton’ approximate is

$$x_{p+1}^{\mathit{B}}=x_{p+1}^A-\frac{{\left(▵x_p^A\right)}^2{f}_p^{\prime A}{f}_{p+1}^A}{{\left(f_p^A\right)}^2}$$

(11.10)

($▵{\mathit{f}}_{\mathit{p}}/▵{\mathit{x}}_{\mathit{p}}$ is again replaced by ${\mathit{f}}_{\mathit{p}}^{\prime \mathit{A}}$) similarly like Equation (4.11) in case of the T-secant method. It can be seen from Table 11 and Table 12 that the convergence rate is be improved from ${\alpha }^N=2$ to ${\alpha }^{TN}=3$. In multi-variable case, it follows from Equation (6.8) (${\mathit{S}}_{\mathit{p}}^{+}$ is replaced by ${\mathit{J}}_{\mathit{p}}^{+}$) that

$${\left({\mathit{T}}_{\mathit{p}}^{\mathit{X}}\right)}^{-1}▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}=-{\mathit{J}}_{\mathit{p}}^{+}{\left({\mathit{T}}_{\mathit{p}}^{\mathit{F}}\right)}^{-1}{\mathit{f}}_{\mathit{p}}^{\mathit{A}}$$

(11.11)

and in explicit form after re-arrangement

$$\left[\frac{{\left(▵x_{p,i}^A\right)}^2}{x_{p+1,i}^B-x_{p+1,i}^A}\right]=-\left[{\mathit{J}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}\right]\left[\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right]$$

(11.12)

Then the ${\mathit{i}}^{\mathit{th}}$ element of the new the ’T-Newton’ approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ can be expressed from the ${\mathit{i}}^{\mathit{th}}$ row of the above equation as

$$x_{p+1,\mathit{i}}^{\mathit{B}}=x_{p+1,i}^A-\frac{{\left(▵x_{p,i}^A\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left(J_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(11.13)

similarly like with Equation (4.22) in case of the T-secant method. Thus the “hyperbolic” approximation accelerates the convergence of the Newton-Raphson method by only one additional function evaluation.

11.3. Broyden’s method

Broyden’s method is a special case of the secant method. In single variable case, the derivative of the function is approximated as

$$f_p^{\prime }\simeq B_p=B_{p-1}+\frac{▵f_p-B_{p-1}▵x_p}{{\left|▵x_p\right|}^2}▵x_p$$

(11.14)

in the ${\mathit{p}}^{\mathit{th}}$ iteration step, and with

$$\frac{▵x_p}{{\left|▵x_p\right|}^2}=\frac{1}{▵x_p}$$

(11.15)

it is simplified as

$$B_p=B_{p-1}+\frac{▵f_p-B_{p-1}▵x_p}{▵x_p}$$

(11.16)

The next Broyden-approximate is then determined as

$$x_{p+1}^A=x_p^A-\frac{f_p^A}{B_p}$$

(11.17)

The convergence can similarly be improved by the new hyperbolic approximation procedure as in cases of the secant and the Newton methods. An additional new approximate

$$x_{p+1}^{\mathit{B}}=x_{p+1}^A-\frac{{\left(▵x_p^A\right)}^2{B}_p{f}_{p+1}^A}{{\left(f_p^A\right)}^2}$$

(11.18)

can be determined, and the iteration continues with this value. Figure 16 demonstrates the effect of the hyperbolic approximation applied to the classic Broyden method. Not surprisingly, the convergence rate will be improved from ${ff}^{\mathit{B}}=\phi \simeq 1.618$ to ${ff}^{\mathit{TB}}={\phi }^2\simeq 2.618$ as in case of the Secant method. In multi-variable case, the ${\mathit{i}}^{\mathit{th}}$ element of the new the ’T-Broyden’ approximate ${\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}$ can be expressed as

$$x_{p+1,\mathit{i}}^{\mathit{B}}=x_{p+1,i}^A-\frac{{\left(▵x_{p,i}^A\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left(B_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(11.19)

similarly like from Equation (11.13) in case of the T-Newton method with ${\mathit{J}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}$ replaced by ${\mathit{B}}_{\mathit{p},\mathit{i},\mathit{j}}^{+}$. The new approximate ${\mathit{B}}_{\mathit{p}+\mathit{1}}$ to the Jacobian matrix can then fully be updated in a similar way as it was shown in case of the T-secant method.

12. Conclusions

A completely new iteration strategy has been worked out for solving simultaneous nonlinear equations

$$\mathit{f}\left(\mathit{x}\right)=0$$

(12.1)

$\mathit{x}\in$${\mathbb{R}}^{\mathit{n}}$ and $\mathit{f}:{\mathbb{R}}^n\to {\mathbb{R}}^m$ ($\mathit{m}\ge \mathit{n}$). It replaces the Jacobian matrix with finite-difference approximations. The step size $▵{\mathit{x}}_{\mathit{p}+1}$ was determined as the difference between two new approximates

$${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}={\mathit{x}}_p^A+▵{\mathit{x}}_p^A$$

(12.2)

and ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{B}}$ with elements

$$x_{p+1,\mathit{i}}^{\mathit{B}}=x_{p+1,i}^A+▵x_{p+1,i}=x_{p+1,i}^A-\frac{{\left(▵x_{p,i}^A\right)}^2}{{\displaystyle \sum _{\mathit{j}=1}^{\mathit{m}}}\left(S_{p,i,j}^{+}\frac{{\mathit{f}}_{\mathit{p},\mathit{j}}^{\mathit{A}}}{{\mathit{t}}_{\mathit{p},\mathit{j}}^{\mathit{F}}}\right)}$$

(12.3)

$\left(\mathit{i}=1,\dots ,n\right)$ as

$$▵{\mathit{x}}_{\mathit{p}+1}={\mathit{x}}_{\mathit{p}+1}^{\mathit{B}}-{\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$$

(12.4)

The first one is a classic quasi-Newton approximate with stepsize $▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$, while the second one was determined from a hyperbolic approximation governed by ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{A}}$ and ${\mathit{f}}_{\mathit{p}+\mathit{1}}^{\mathit{A}}$, such that the classic secant equation

$$\mathit{S}▵{\mathit{x}}^{\mathit{A}}=-{\mathit{f}}^{\mathit{A}}$$

(12.5)

was modified by a non-uniform scaling transformation

$$\mathit{T}=\left[\begin{array}{cc}{\mathit{T}}^X& \mathit{0}\\ \mathit{0}& {\mathit{T}}^F\end{array}\right]$$

(12.6)

with diagonal elements ${\mathit{t}}_{\mathit{j}}^{\mathit{F}}$$\left(\mathit{j}=1,\dots ,\mathit{m}\right)$, ${\mathit{t}}_{\mathit{i}}^{\mathit{X}}$$\left(\mathit{i}=1,\dots ,\mathit{n}\right)$ as

$${\mathit{S}}_T▵{\mathit{x}}^{\mathit{A}}=-{\mathit{f}}^{\mathit{A}}$$

(12.7)

where

$$\mathit{S}=\left[\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]\mathit{and}{\mathit{S}}_{\mathit{T}}=\left[\frac{{\mathit{t}}_{\mathit{j}}^{\mathit{F}}}{t_{\mathit{i}}^{\mathit{X}}}\frac{▵{\mathit{f}}_{\mathit{k},\mathit{j}}}{▵{\mathit{x}}_{\mathit{i}}}\right]$$

(12.8)

$\left(\mathit{k}=1,\dots ,\mathit{n}\right)$. It was shown, that the new step size $▵{\mathit{x}}_{\mathit{p}+1}$ is much smaller than the step size $▵{\mathit{x}}_{\mathit{p}}^{\mathit{A}}$ of the classic quasi-Newton approximate, providing that ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{B}}$ will always be in the vicinity of ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{A}}$. Having two new approximates, a set of $\mathit{n}+\mathit{1}$ new independent trial approximates ${\mathit{x}}_{\mathit{p}+\mathit{1}}^{\mathit{A}}$ and ${\mathit{x}}_{\mathit{k},\mathit{p}+1}^{\mathit{B}}$ $\left(\mathit{k}=1,\dots ,\mathit{n}\right)$ was constructed (see Equation (3.5)), providing that the new trial approximates are always in general positions, and ensures stable behavior of the iteration. According to the geometrical representation in single variable case, the suggested procedure corresponds to finding the root of a hyperbolic function with vertical and horizontal asymptotes ${\mathit{x}}_{\mathit{p}+1}^{\mathit{A}}$ and ${\mathit{f}}_{\mathit{p}}^{\mathit{A}}$. It was shown in Section 7 that the proposed method has super-quadratic convergence with rate ${\alpha }^{TS}=$${\phi }^2=2.618...$(where $\phi =1.618...$ is the well-known golden ratio) in single variable case. The proposed method needs two function evaluations in each iteration in single variable case and $\mathit{n} +$ 1 evaluations in multi-variable case. The efficiency of the proposed method was studied in Section 10 in multi-variable case and compared with other classic rank-one update and line-search methods on the basis of available test data. Results show, that the efficiency of the proposed full-rank update procedure is considerably better, then the efficiency of other classic low-rank update methods. A Rosenbrock test function (Equations (9.1) and (9.2)) with up to $\mathit{n}=1000$ variables was used to demonstrate the efficiency in Section 9.