1. Introduction
Large quantum systems, such as many-body spin chains or quantum gases, exhibit complex dynamics due to entanglement growth and information scrambling. Tracking the evolution of entanglement becomes increasingly difficult as the number of qubits grows. In this study, we develop a framework that captures entanglement entropy growth under external control, focusing on the entanglement entropy growth rate , which measures the speed of quantum information spreading.
The challenge lies in the fact that while entanglement entropy typically grows linearly at early times, it must saturate at a maximal value at a characteristic time . A physically consistent model must therefore capture both regimes without exceeding .
Figure 1.
Schematic representation of a one-dimensional qubit chain with nearest-neighbor coupling J and external field B. The system shows quantum information propagation through entanglement spreading.
Figure 1.
Schematic representation of a one-dimensional qubit chain with nearest-neighbor coupling J and external field B. The system shows quantum information propagation through entanglement spreading.
2. Model System: One-Dimensional Qubit Chain
We consider a one-dimensional chain of qubits described by the Hamiltonian
where
J is the nearest-neighbor coupling and
B is the transverse field strength. This Hamiltonian captures the competition between interaction-induced correlations (first term) and external driving by a magnetic field (second term).
3. Entanglement Entropy Growth
3.1. Growth Rate Definition and Early-Time Behavior
The entanglement entropy growth rate is defined as:
which leads to the early-time linear growth:
This linear behavior characterizes the ballistic spreading of quantum information in chaotic systems.
3.2. Connection to Quantum Chaos and Scrambling
The growth of out-of-time-ordered correlators (OTOCs) provides a fundamental connection to quantum chaos:
where
is the quantum Lyapunov exponent. The entanglement entropy growth rate is intimately related to this scrambling behavior through:
where
T is the temperature, establishing a deep connection between information scrambling and entanglement dynamics.
3.3. Maximum Entropy Bound
For a bipartite system divided into equal halves, the maximum entanglement entropy is given by the Page value:
where
N is the total number of qubits. This represents the typical entanglement entropy of a random pure state.
3.4. Critical Time Estimation
The saturation time
can be estimated from the growth rate and maximum entropy:
This time scale marks the transition from linear growth to saturation regime.
3.5. External Control Mechanism
When external control is applied through a phase parameter
, the growth rate becomes modulated:
The control phase
can represent various experimental parameters such as laser phase, magnetic field orientation, or microwave pulse phase.
3.6. Environmental Decoherence Effects
To account for environmental effects and measurement limitations, we introduce a decoherence factor:
This factor captures how the control parameter affects the system’s coupling to its environment and the resulting decoherence rate.
3.7. Derivation of the Corrected Expression
Starting from the fundamental definition and incorporating all effects:
2.
Integration yields linear growth:
4.
Post-saturation dynamics: For
, we consider environmental effects:
5.
Solution with boundary condition: Solving this differential equation with
gives:
For closed systems, , leading to constant entropy. For open systems, we allow , resulting in our final expression.
4. Physically Consistent Entanglement Entropy Expression
The complete physically consistent expression is:
where:
Figure 2.
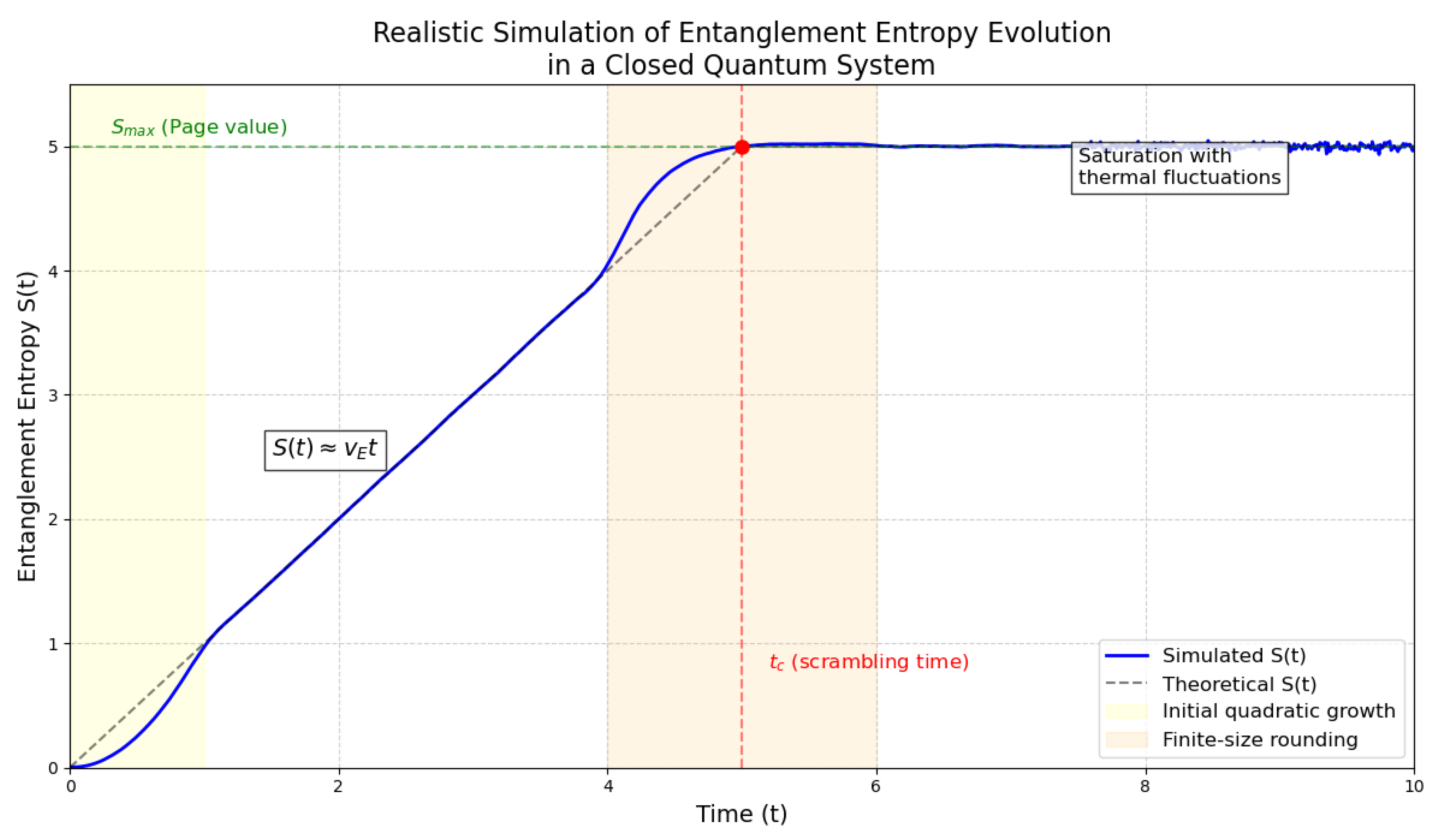
Entanglement entropy dynamics for different control parameters . The curves show linear growth followed by saturation without exceeding , with environmental effects causing slight entropy reduction in open systems.
Figure 2.
Entanglement entropy dynamics for different control parameters . The curves show linear growth followed by saturation without exceeding , with environmental effects causing slight entropy reduction in open systems.
4.1. Physical Interpretation and Significance
The model captures several key physical phenomena:
Linear Growth Phase: For , the entropy grows linearly with slope , representing ballistic spreading of entanglement in chaotic systems.
Saturation Transition: At , the system reaches maximum entanglement, and the growth must cease due to fundamental quantum mechanical constraints.
Environmental Coupling: The parameter quantifies how much entropy can "leak" to the environment, distinguishing closed systems () from open systems ().
Control Parameter Dependence: Both the growth rate and decoherence rate depend on the control phase , enabling experimental tunability of entanglement dynamics.
Smooth Transition: The exponential function ensures a smooth transition between growth and saturation regimes, physically representing the gradual approach to equilibrium.
5. Experimental Implications
This model has significant implications for experimental quantum information processing:
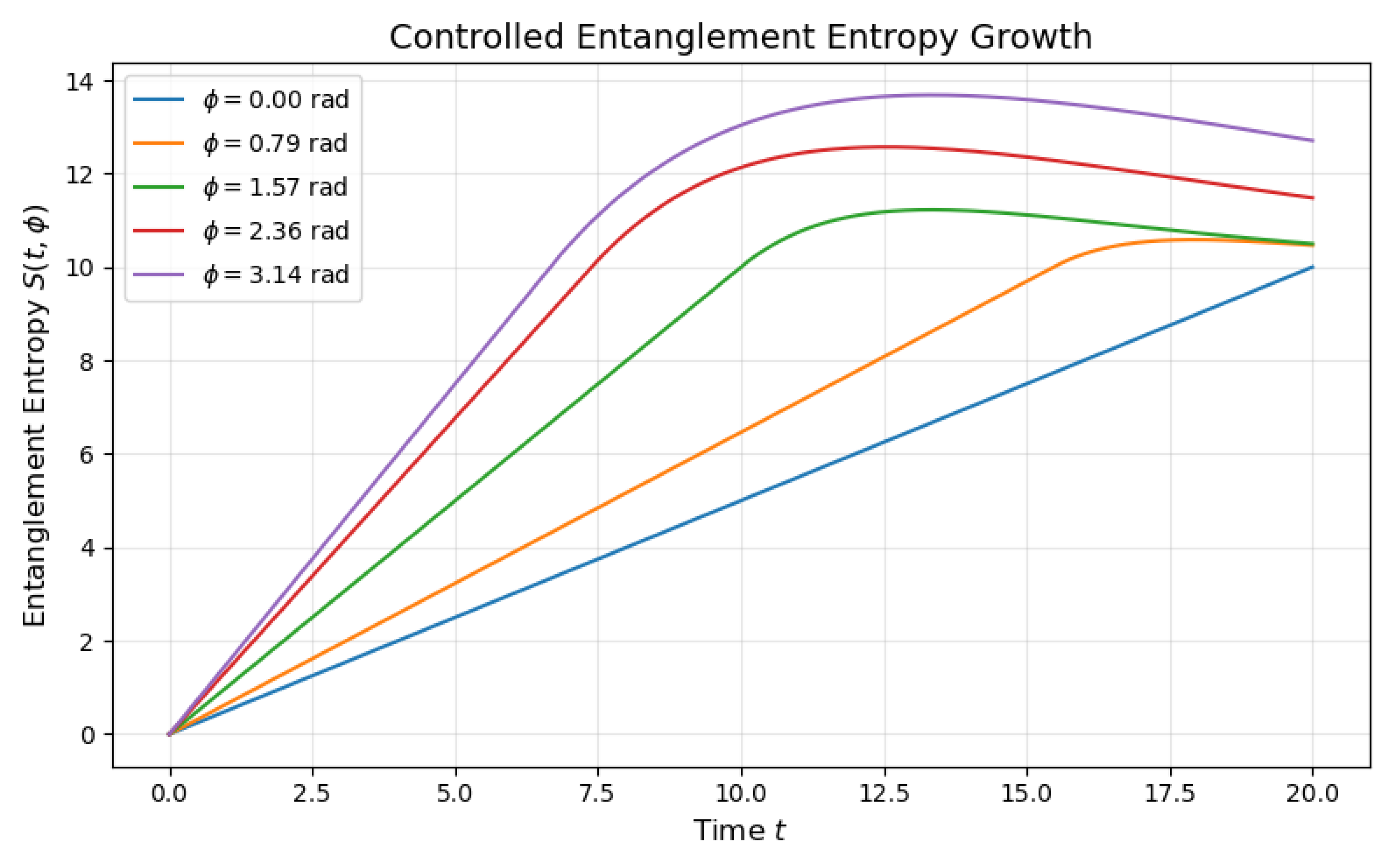
Quantum Control: The -dependence provides a mechanism for controlling entanglement growth rates in quantum devices.
Decoherence Management: Understanding the dependence helps in designing protocols to minimize unwanted decoherence.
Benchmarking: The model provides a framework for benchmarking quantum devices against ideal theoretical predictions.
Quantum Error Correction: The saturation behavior informs the design of quantum error correction protocols that must operate within entanglement limits.
Figure 3.
Effects of control parameter on entanglement growth rate and decoherence rate . Different curves correspond to different values of showing tunable quantum dynamics.
Figure 3.
Effects of control parameter on entanglement growth rate and decoherence rate . Different curves correspond to different values of showing tunable quantum dynamics.
6. Conclusions
We have developed a comprehensive and physically consistent model for entanglement entropy dynamics under external control. The key achievement is the derivation of an expression that respects the fundamental bound while incorporating experimental control parameters and environmental effects. The model successfully captures:
1. The linear growth phase characterized by the controlled growth rate 2. The saturation at the fundamental limit 3. The environmental effects through the decoherence parameter 4. The smooth transition between regimes ensured by the exponential form
This framework provides a valuable tool for both theoretical studies and experimental implementations of quantum information processing in controlled quantum systems.
References
- Don N. Page, Average Entropy of a Subsystem, Phys. Rev. Lett. 71, 1291–1294 (1993). [CrossRef]
- Pasquale Calabrese and John Cardy, Evolution of Entanglement Entropy in One-Dimensional Systems, J. Stat. Mech.: P04010 (2005). [CrossRef]
- Alexei Kitaev, A Simple Model of Quantum Holography, Talks at KITP, Santa Barbara (2015), http://online.kitp.ucsb.edu/online/entangled15/kitaev/.
- Juan Maldacena, Stephen H. Shenker, and Douglas Stanford, A Bound on Chaos, J. High Energy Phys. 2016, 106 (2016). [CrossRef]
- Marko Žnidarič, Tomaž Prosen, and Peter Prelovšek, Many-Body Localization in the Heisenberg XXZ Magnet in a Random Field, Phys. Rev. B 77, 064426 (2008). [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).