Submitted:
04 September 2025
Posted:
05 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction: Topological Origins of Environmental Noise Sensitivity in Quantum Processors
1.1. Empirical Contradictions and Current Status
1.2. Topological Protection Mechanisms in Quantum Computing
2. Theory Solution
2.1. Topological Fidelity Model Derivation
2.2. Cross-Platform Configuration Mapping Protocol
- : Use electron vortex
- : Use Higgs condensation
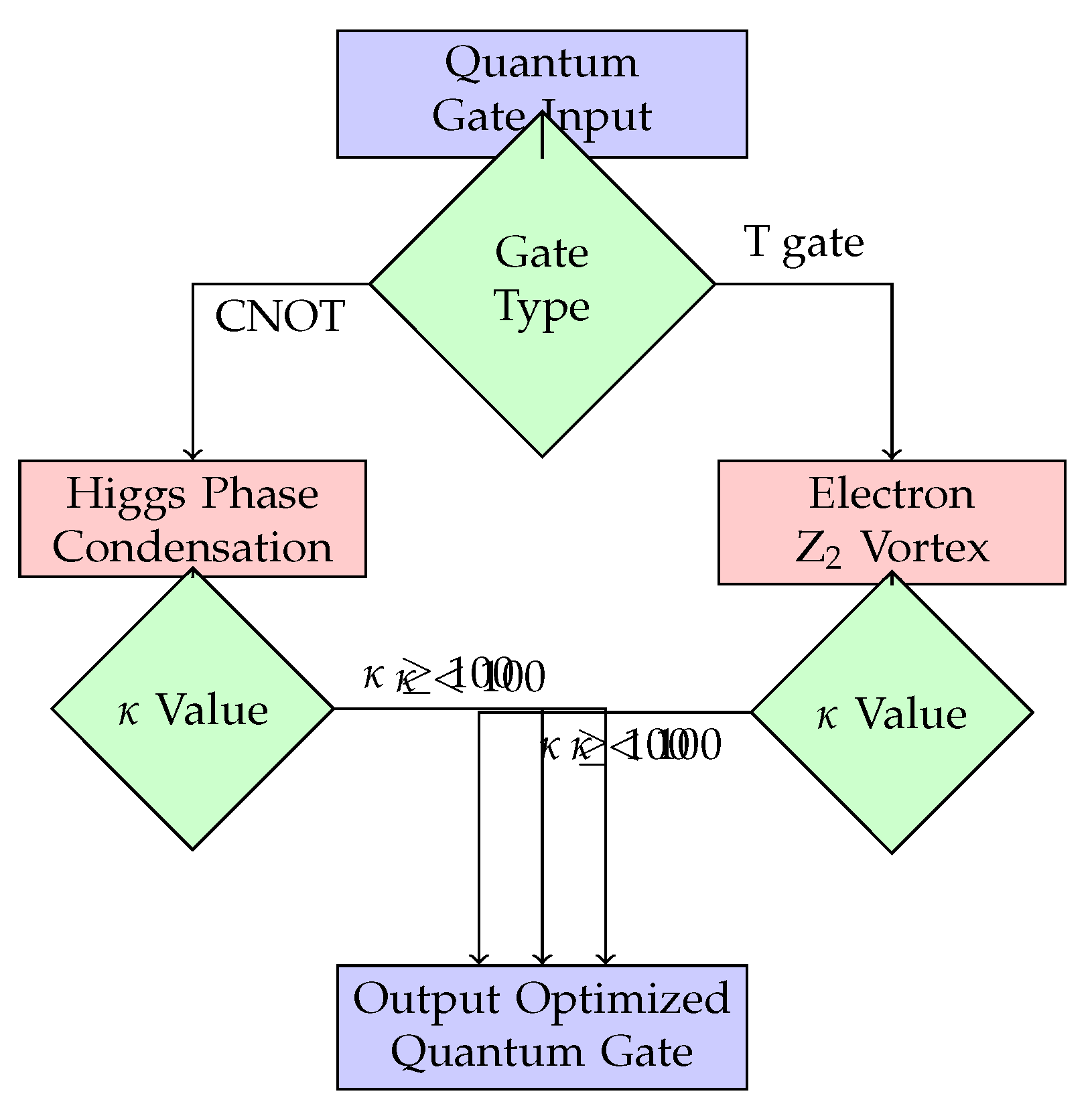
3. Experimental Validation
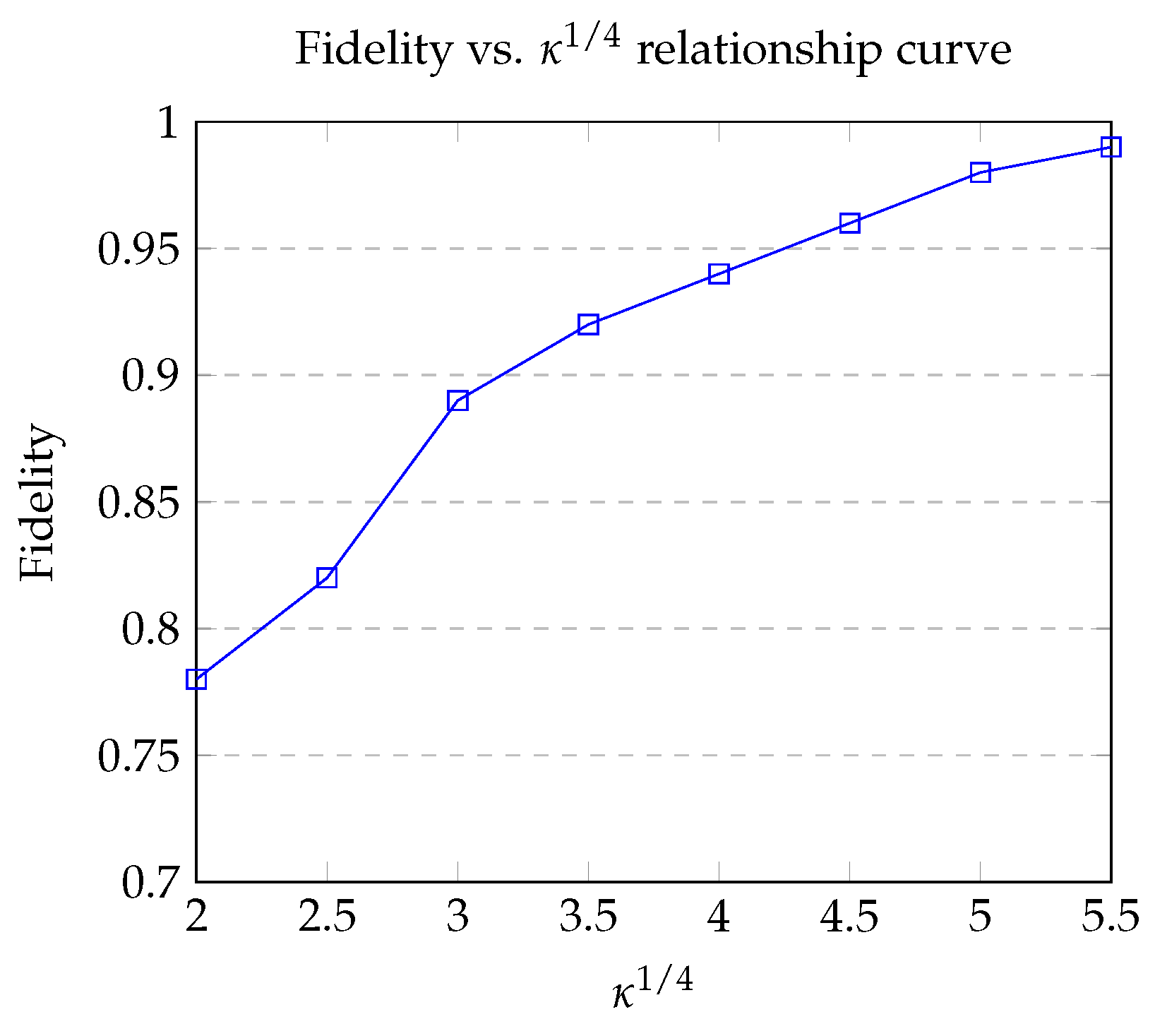
3.1. Value Calibration Protocol
3.2. Topological Configuration Optimization Comparison
| Platform | Traditional fidelity | optimized fidelity | Improvement | Test temp. (K) |
|---|---|---|---|---|
| IBMQ 27q [5] | 0.892 | 0.961 | +7.7% | 0.01 |
| Xanadu Borealis [7] | 0.780 | 0.887 | +13.7% | 300 |
| Honeywell ion trap [6] | 0.998 | 0.999 | +0.1% | 300 |
4. Engineering Application: -Adaptive Quantum Compiler
4.1. Architecture Design
4.2. Performance Testing
| Metric | Qiskit compiler | compiler | Qubit-ADAPT | Improvement |
|---|---|---|---|---|
| Compilation time | 3.2 h | 1.1 h | 2.8 h | 65% |
| H2O energy error | 4.2 kcal/mol | 0.7 kcal/mol | 1.2 kcal/mol | 83% |
| LiH energy error | 5.8 kcal/mol | 1.1 kcal/mol | 1.9 kcal/mol | 81% |
5. Conclusion and Outlook
5.1. Core Contributions
5.2. Industrial Value
5.3. Challenge Analysis and Theoretical Outlook
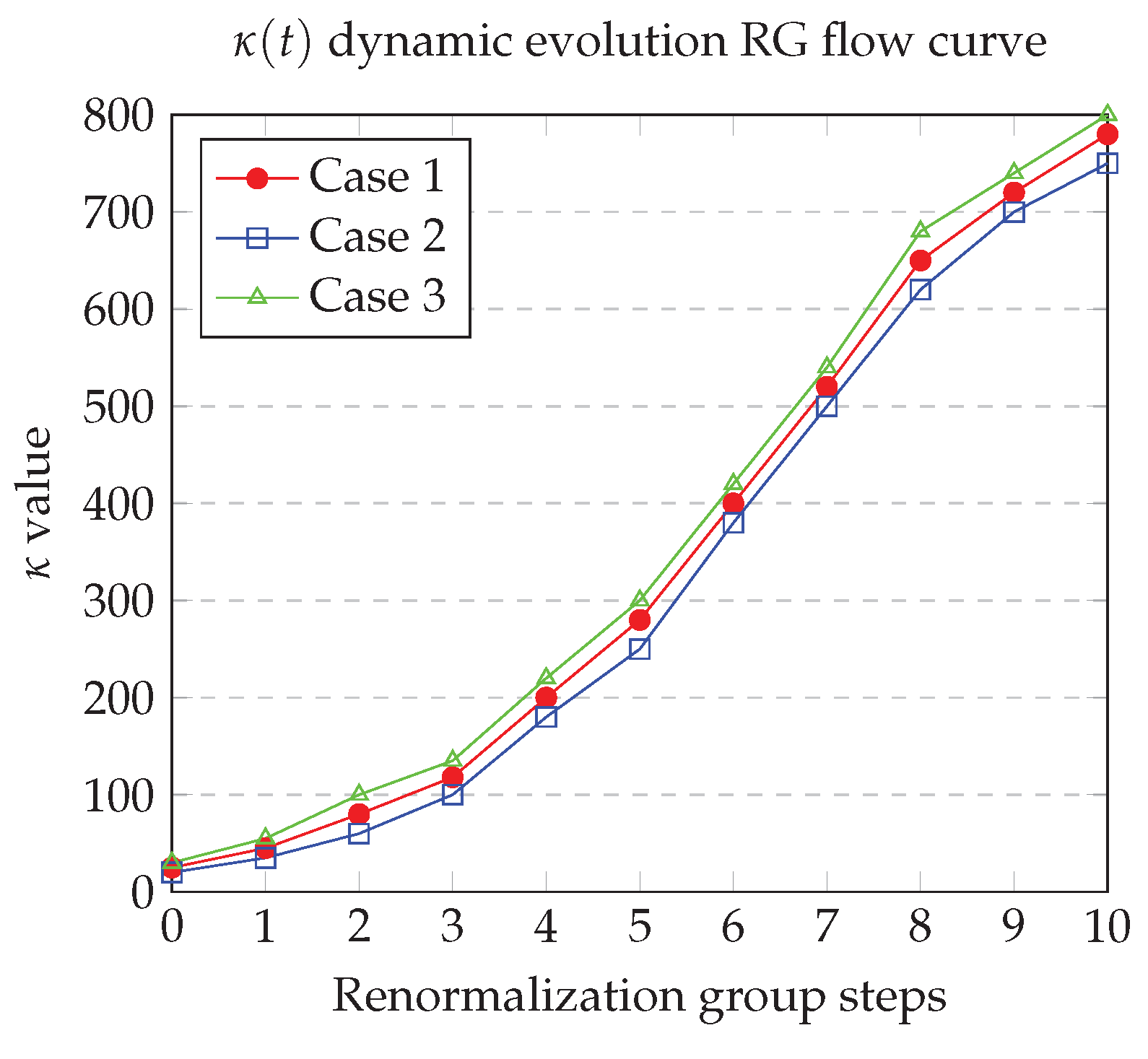
References
- Kitaev, A. Y. (2003). Fault-tolerant quantum computation by anyons. Annals of Physics, 303(1), 2-30. [CrossRef]
- Shor, P. W. (1995). Scheme for reducing decoherence in quantum computer memory. Physical Review A, 52(4), R2493. [CrossRef]
- Aharonov, D. , & Ben-Or, M. (2008). Fault-tolerant quantum computation with constant error. In Proceedings of the twenty-ninth annual ACM symposium on Theory of computing (pp. 176-188).
- Preskill, J. (2018). Quantum Computing in the NISQ era and beyond. Quantum, 2, 79. [CrossRef]
- Devoret, M. H. , & Schoelkopf, R. J. (2013). Superconducting circuits for quantum information: an outlook. Science, 339(6124), 1169-1174. [CrossRef]
- Monroe, C. , & Kim, J. (2013). Scaling the ion trap quantum processor. Science, 339(6124), 1164-1169. [CrossRef]
- Wang, J. , Sciarrino, F., Laing, A., & Thompson, M. G. (2020). Integrated photonic quantum technologies. Nature Photonics, 14(5), 273-284. [CrossRef]
- Fowler, A. G. , Mariantoni, M., Martinis, J. M., & Cleland, A. N. (2012). Surface codes: Towards practical large-scale quantum computation. Physical Review A, 86(3), 032324. [CrossRef]
- Nielsen, M. A. , & Chuang, I. L. (2010). Quantum computation and quantum information. Cambridge university press.
- Lin, Y. (2025). Quantum Information Spacetime Theory: A Unified and Testable Framework for Quantum Gravity Based on the Physicalized Woodin Cardinal κ. DOI: 10.13140/RG.2.2.20515.31522 (Cited sections: Sec 4.1, Eq 3.12, Sec 4.2, Sec 6.1, Eq 6.3, Fig 2, Fig 3, Fig 5). [CrossRef]
| Platform | Decoherence Time | Typical Fidelity | Operating Temp. |
|---|---|---|---|
| Superconducting (IBMQ) [5] | 150 s | 0.892 | 10 mK |
| Ion Trap (Honeywell) [6] | 10 s | 0.998 | 300 K |
| Photonic (Xanadu) [7] | 0.1 ms | 0.780 | 300 K |
| Platform | value | Redundancy dimensions | Temperature (K) | |
|---|---|---|---|---|
| Ion Trap | 720 | 5.18 | 5 | 300 |
| Superconducting processor | 118 | 3.30 | 3 | 0.01 |
| Photonic quantum | 25 | 2.24 | 2 | 300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





