New Thermodynamic Data for NH₄NO₃-Sucrose-Water Ternary System: Water Activity, Osmotic Coefficient, Activity Coefficient, Excess Gibbs Energy, Solubility and Transfer Gibbs Energy at 298.15 K

1. Introduction

Electrolyte and non-electrolyte solutions play a crucial role in numerous scientific and industrial fields, such as biology, pharmaceuticals, chemistry, and biochemistry, as well as in a wide range of practical applications.One notable example is atmospheric aerosol, which consists primarily of suspended solid particles, particularly electrolytes, and exerts a crucial influence on the environment. This impact encompasses aspects such as air quality, cloud formation, and the regulation of the climate system.

Ammonium nitrate (AN, NH₄NO₃) has emerged as a potential substitute for ammonium perchlorate as a solid propellant oxidizer [1,2]. This compound holds immense importance in both the chemical industry and agriculture, making it one of the most widely utilized ammonium compounds. Notably, it finds extensive application in nitrogen-based fertilizers and explosives. While it serves as a vital source of ammonia and nitrate ions, crucial for plant growth as a nitrogen fertilizer, its role in explosives and propellants lies in providing oxygen as an oxidizer.

Ammonium nitrate has garnered attention from researchers across various disciplines for several reasons. Firstly, its inherent phase transitions have been extensively investigated in the field of solid-state physics, aiming to unravel the intricacies of these transformations [3,4]. Secondly, ammonium nitrate is frequently employed as a fertilizer, but it often experiences undesired agglomeration. Researchers in the field of fertilizer technology are therefore interested in exploring methods to mitigate such phenomena, with a particular focus on the solid’s phase transitions occurring at or near ambient temperatures (20–30°C) [5,6]. Thirdly, due to its explosive nature, it is crucial to thoroughly examine and avoid the conditions that may lead to disastrous consequences, considering the large-scale production of ammonium nitrate [7,8,9].

Sucrose is a disaccharide composed of two monosaccharides, glucose and fructose, with a chemical formula of C₁₂H₂₂O₁₁. The connection between the fructose and glucose molecules in a C₁₂H₂₂O₁₁ molecule occurs through a glycosidic bond, which is a type of linkage for two monosaccharides. Sucrose possesses a monoclinic crystal structure and is highly soluble in water, exhibiting its characteristic sweet taste.

The term “sucrose” was coined by William Miller, an English chemist, in 1857. It is widely utilized as a sweetener in the food industry. C₁₂H₂₂O₁₁ can be obtained from sugar beets or sugar canes, but it requires refinement to ensure suitability for human consumption. Refined sucrose, commonly known as sugar, is a popular ingredient in various food recipes due to its sweet taste.

This study aims to investigate the physicochemical properties of a mixture system comprising ammonium nitrate, sucrose, and water using the hygrometric method [14,15,16] at a temperature of 298.15 K. The relative humidities of the mixture at 298.15 K were measured for different molalities of sucrose (0.1, 0.3, 0.5, 1.0, 2.0, 3.0 and 4.0 mol.kg^-1) and different molalities of NH₄NO₃ (0.10, 0.50, 1.00, 2.00, 3.00, 4.00, 5.00, 6.00 mol^.kg^-1). To ensure the reliability of the experimental results for the mixed system, additional measurements were conducted on pure solutions of NH₄NO₃ (aq) and compared to existing literature data. Osmotic coefficients for these solutions were determined based on water activities. The Pitzer-Simonson-Clegg model [17−21] was utilized to calculate solute activity coefficients and excess Gibbs energies using the experimental data obtained in this study.

The solubilities of a ternary aqueous solution of NH₄NO₃-sucrose-water were measured using the hygrometric method and correlated with the PSC model. Powder X-ray diffraction (XRPD) and attenuated total reflection Fourier-transform infrared (ATR-FTIR) spectroscopy were employed to identify the crystallized solids from the supersaturated NH₄NO₃-sucrose-water solution.

No literature data are currently available on the thermodynamic parameters addressed in this study.

2. Experimental Section

Water activity was determined using a hygrometric method based on the measurement of relative humidity above aqueous solutions containing non-volatile electrolytes. Experiments were carried at 298.15 K (with a standard uncertainty of ±0.02 K) and under an atmospheric pressure of 0.1 MPa (with a standard uncertainty of ±0.002 MPa).

For preparing the NaCl, NH₄NO₃, and sucrose solutions, anhydrous materials from Merck and Fluka (Table 1) were used, along with deionized distilled water with a conductivity of approximately 5.10^-6 S.cm^-1. The stock solutions were prepared by weighing and measuring volumes using pipettes. The uncertainty in the molality of the stock solution arises from the uncertainty in the analysis of the stock solution’s molality and the weighing error. The standard uncertainties were calculated using error propagation techniques and are at maximum u(m) = 0.01 mol.kg-1 (with a 0.68 level of confidence).

$${\displaystyle \frac{u\left(m\right)}{m}}=\sqrt{{\left({\displaystyle \frac{u\left(w\right)}{w}}\right)}^2+{\left({\displaystyle \frac{u\left(p\right)}{p}}\right)}^2+{\left({\displaystyle \frac{u\left(V\right)}{V}}\right)}^2+{\left({\displaystyle \frac{u\left(M\right)}{M}}\right)}^2+{\left({\displaystyle \frac{u\left(\right)}{}}\right)}^2},$$

(1)

The molality (m) of the solution and its standard uncertainty (u (m)) are defined as follows. The mass of the component initially weighed for the experiment is denoted as (w), with a standard uncertainty of (u(w)) equal to 24.5.10^-2 mg. The volume (V) of the solution and its standard uncertainty (u(V)) are 0.03 mL. The molar mass (M) of the component and its standard uncertainty (u(M)) are 18.10^-3 g·mol^-1 (The standard uncertainties for the molar masses of different elements can be found on the IUPAC website). The purity of the component is represented as (p), with a standard uncertainty of (u(p)) equal to 1.44 .10^-3. The specific volume of water (ρ) used is 998.20675 kg·m^-3, and its standard uncertainty (u(ρ)) is 8.10^-4 kg·m^-3.

The relative uncertainty (u_r (m)) in the calculated molality using Equation 1 is approximately 1.6 × 10^-3. To verification of the molalities, the refractive index (nr) was measured using the Chemical Handbook, with a standard uncertainty (u(nr)) of 2.10^-4.

2.1. Hygrometric Method

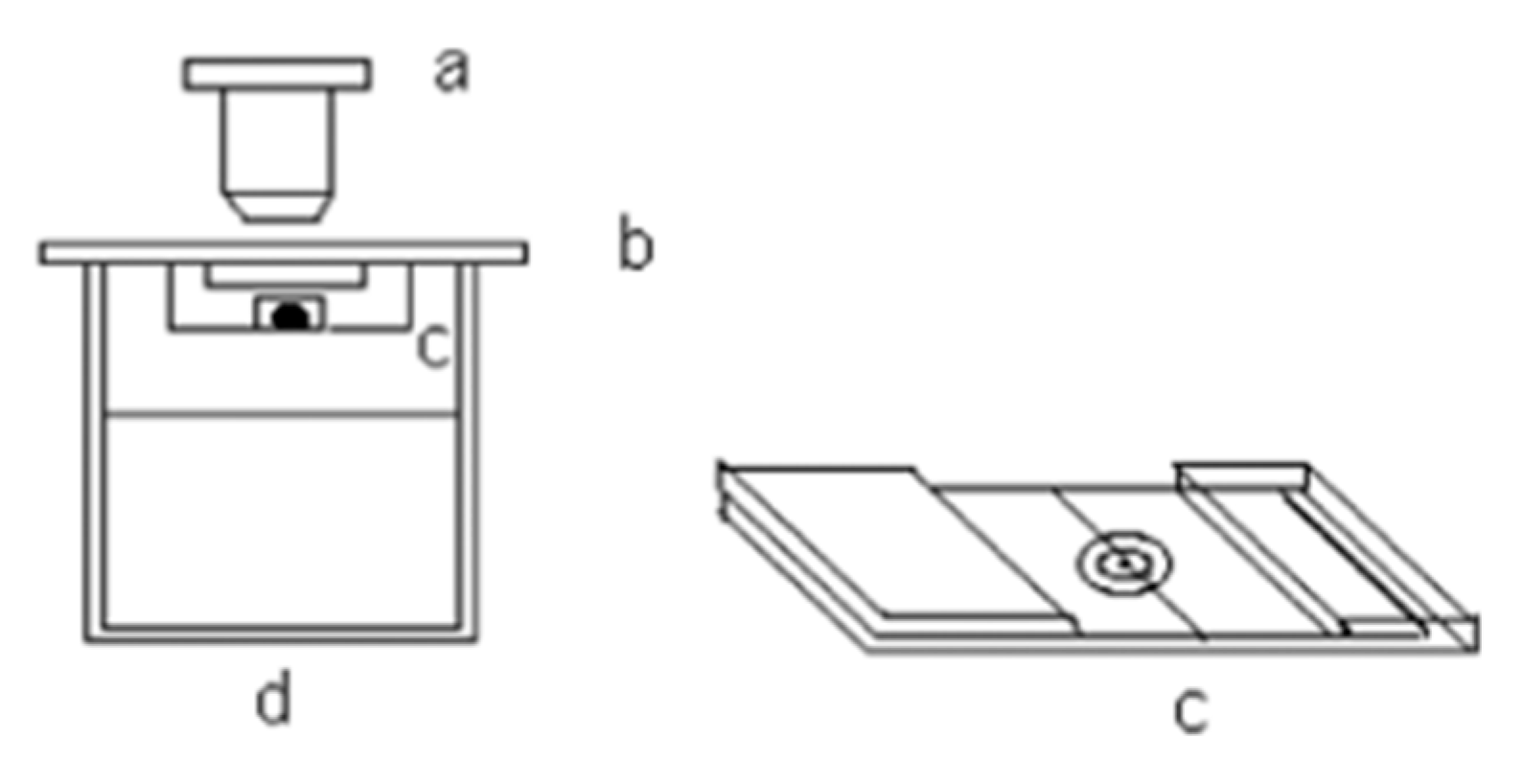
Water activity in electrolyte solutions can be evaluated by measuring the relative humidity above the solution. This is achieved by suspending a fine spider silk thread under tension above a container holding the test solution. Reference droplets—typically of aqueous NaCl or LiCl—are deposited onto the thread. The setup is placed in a temperature-regulated chamber, and a digital microscope is used to monitor the droplet diameter (see Figure 1).

Assuming thermodynamic equilibrium between the water in the liquid phase and its surrounding vapor, the water activity in the electrolyte solution can be expressed accordingly:

a_w = P_w/P_0w ,

(2)

The water partial pressure above the aqueous solution (P_w) and the saturation vapor pressure of pure water (P_0w) at the same temperature play a crucial role.

The practical identification of the relative humidity (h_r) of a salt solution is closely associated with the water activity of the solution.

h_r = a_w,

(3)

Thermodynamic properties for the reference solutions NaCl(aq) and LiCl(aq) are available in the literature. Using this data, we can calculate the relationship between relative humidity and molar concentration. Consequently, we can determine how the diameter of the drops in the reference solutions varies with the surrounding relative humidity.

We consider the drop formed by the reference solution as a sphere with a diameter D, its volume V is:

V = (4/3)π(D/2)³,

(4)

The volume of the solution’s drop undergoes changes due to the evaporation or condensation of water from or onto the solution, respectively. Consequently, the diameter of the drop increases or decreases during these processes.

Using a reference relative humidity value of 0.84, the growth ratio K can be introduced to account for the variation in droplet diameter relative to that of the reference solution. This ratio is defined as follows:

K = D(a_w)/D(a_ref),

(5)

Here, D(a_ref), and D(a_w) denote the diameters of the droplets at the reference relative humidity (typically 0.84 or 0.98) and at the unknown relative humidity a_w, respectively.

The growth ratio K is related to the solute concentration as follows:

C = n/V,

(6)

where n represents the number of moles of solute in the droplet, and C denotes the solute concentration in the droplet solution. Consequently, the following relationship is obtained:

K=[C(a_ref)/C(a_w)]^1/3 ,

(7)

C(a_ref) and C(a_w) represent the concentrations of solutions at the reference humidity level h_r=0.84 (or 0.98) and the unknown relative humidity a_w, respectively. The calibration procedure consists of correlating the droplet diameter of the reference solution with the relative humidity measured above the cup containing that same reference solution (D(0.84) or D(0.98)).

A droplet is placed above the cup containing the solution under investigation, and its diameter (D(a_w)) is measured. The water activity $a_w$ (or relative humidity) is then determined by calculating the growth ratio K, which is derived from the relationship between K and the relative humidity of the reference solutions, typically aqueous NaCl or LiCl.

If the relative humidity is above 0.75, the reference NaCl solution is used. Conversely, the reference LiCl solution is employed for relative humidities below 0.75.

Determination of the K ratioenables the determination of the water activity of the solution being studied in this research. This is achieved by using the graph that illustrates the variation of the K ratio with the relative humidity of the reference solution, or alternatively, by applying the correlation equations derived from these curves:

For a relative humidity reference of NaCl (h_r = 0.84):

h_r = –2,8835+ 9,3641 K – 9,0016 K² + 4,2497 K³ − 0,9799 K⁴ + 0,0881 K⁵,

(8)

for reference h_r =0,98:

h_r = - 0,8348 + 7,2209 K − 11,628 K² + 9,3913 K³ − 3,7676 K⁴ + 0,5975 K⁵,

(9)

The relative uncertainty in the measured droplet diameter is approximately ur=0.0025. Consequently, the relative uncertainty in the relative humidity measurements can be determined using error propagation 22 methods as follows:

$${\displaystyle \frac{∆a_w}{a_w}}=\sqrt{{\left({\displaystyle \frac{∆D{a}_w}{a_w}}\right)}^2+{\left({\displaystyle \frac{∆D{a}_{ref}}{a_{ref}}}\right)}^2},$$

(10)

Accurate relative humidity measurements require careful control of experimental conditions, including proper hygrometric calibration and stable temperature maintenance. The standard uncertainty (at a 0.68 confidence level) associated with these measurements depends on the water activity (a_w)value being measured. Specifically, the uncertainty ranges from u(a_w)=0.0002 for dilute solutions up to u(a_w)=0.005 for more concentrated solutions.

The saturation points of the water/D-sucrose/ammonium nitrate (NH₄NO₃) system were determined through the hygrometric technique.This approach involved gradually adding small amounts of D-Sucrose or NH₄NO₃ to pre-prepared mixtures of D-Sucrose-H₂O or NH₄NO₃-H₂O until the drop diameter variation became insignificant or constant. The solid phase was characterized using a LABXXRD-6100 Shimadzu powder X-ray diffractometer equipped with Cu radiation, operated at 40 kV and 25 mA. Diffraction patterns were recorded by scanning the samples over a 2θ range of 10° to 70°, with a scanning speed of 2.4° min⁻¹ and a step size of 0.02°.

The FT-IR-ATR spectra of the composites were collected at a resolution of 4 cm⁻¹ using a Jasco FT/IR 4600 spectrometer equipped with a Pro One type attenuated total reflectance (ATR) accessory.

3. Theory and Models

To facilitate the comparison of our findings with previously published data, we chose several well-established empirical equations and models that describe the thermodynamic properties of electrolyte solutions in aqueous mixtures. The selected models include the Lin et al, ECA, LS, and the Pitzer-Simonson-Clegg (PSC) model.

3.1. The Lin et al. Rule

Lin et al.²³ proposed a simple empirical equation for aqueous ternary systems, which can be expressed as follows:

$$a_w-1=\left(a_{w1}-1\right)+\left(a_{w2}-1\right)+C_{12}{m}_1{m}_2,$$

(11)

Here, $m_i$denotes the molality of species iii in the multicomponent solution, and $C_{12}$ is an adjustable coefficient determined from the ternary mixture. The terms $a_{w1}$and $a_{w2}$ represent the water activities of the binary aqueous solutions containing electrolyte 1 and non-electrolyte 2, respectively.

3.2. The ECA Rule

In a previous study, A. Dinane [24] introduced the “Extended Composed Additivity” (ECA) rule, which enables the prediction of water activity in mixed electrolyte solutions. In our current investigation, we employed this equation to calculate the water activities within the ternary system under examination: NH₄NO₃/D-Sucrose/Water. This equation gives a good approximation for mixtures of non-volatile electrolytes in aqueous solution and has been validated by our several experimental studies of mixtures of several electrolytes. The equation is as follows:

$$a_w=-1+a_{w\left(1\right)}+a_{w\left(2\right)}-m_1{m}_2\lambda -m_1{m}_{2}m\delta$$

(12)

where m₁, m₂

nd m are the molalities of solute 1, solute 2, and the total molality of the mixture, respectively. The terms a_w1 and a_w2 correspond to the water activities of electrolyte 1 and non-electrolyte 2 in their respective binary solutions. The parameters λ and δ characterize the deviation from ideality in the ternary mixture at higher concentrations. These parameters can be determined graphically using the derived Equation (12) as follows:

$${\displaystyle \frac{{∆a}_w}{m_1{m}_2}}=-\lambda -m\delta ,$$

(13)

The term Δa_wcorresponds to the discrepancy between the predicted and observed water activities. By plotting this difference against the total molality, the resulting best-fit line enables the extraction of the intercept λ and slope δ parameters.

3.2. The LS Model

The LS II model, developed by Lietzke and Stoughton [25,26], allows for the prediction of osmotic coefficients in mixtures containing two solutes, expressed as follows:

(ν₁m₁ + ν₂m₂)φ = ν₁m₁φ₁ + ν₂m₂φ_2,

(14)

In this context, m₁ and m₂ correspond to the molalities of electrolyte 1 and non-electrolyte 2, respectively. The parameters ν₁and ν₂ indicate the number of ions released upon complete dissociation of each solute. The osmotic coefficients for the binary solutions at the total molality are represented by φ₁,φ₂ whereas φdenotes the osmotic coefficient of the ternary mixture.

3.5. The Pitzer-Simonson-Clegg Model

Pitzer and Simonson [17,18,19,20,21] developed an alternative model based on mole fractions to describe mixtures containing ions with symmetrical charges at very high concentrations in aqueous solutions. Their model assumes that the excess Gibbs free energy of the mixture consists of two components: a long-range term based on Debye–Hückel theory and short-range interaction terms.

This model enables the determination of activity coefficients for both solvent and solutes in mixtures containing ionic and neutral species. In the present study, we employed the PSC model to calculate the osmotic coefficients, activity coefficients of the solvent and solutes, the system’s excess Gibbs free energy, as well as the solubilities of D-sucrose and NH₄NO₃ in the NH₄NO₃/D-sucrose/water system at 298.15 K.

3.6. Theoretical Development

Several thermodynamic models have been developed to describe the non-ideal behavior of aqueous electrolyte solutions with mixed solvents. Among these, the Pitzer–Simonson–Clegg (PSC) equations [20,21,22] are widely recognized as one of the most successful models for mixed electrolytes. In our previous work, we applied the PSC model to aqueous mixtures of electrolytes and non-electrolytes, effectively capturing the non-ideal behavior of ternary electrolyte–D-sucrose–water systems at 298.15 K over a broad range of electrolyte concentrations. The excess Gibbs free energy is considered as the sum of long-range($g_{PDH}^{ex}$) and short-range electrostatic($g_{PSC}^{ex}$) interactions:

$${\displaystyle \frac{g^{Ex}}{RT}}={\displaystyle \frac{g_{PDH}^{ex}}{RT}}+{\displaystyle \frac{g_{PSC}^{ex}}{RT}},$$

(15)

The universal gas constant is denoted by R, and T stands for the absolute temperature. The long-range interaction term for the water (1)/D-sucrose (2)/ammonium nitrate (AN) system can be written as follows:

$$\begin{array}{l}{\displaystyle \frac{g_{PSC}^{ex}}{RT}}=x_1\left(x_1\cdot W_{1.MX}+x_2{W}_{2.MX}\right)+x_I^2\left(x_1\cdot U_{1.MX}+x_2{U}_{2.MX}\right)+\\ x_I^2\left(x_1^2\cdot V_{1.MX}+x_2^2{V}_{2.MX}\right)+x_1{x}_2\left[w_{12}+u_{12}\left(x_1-x_2\right)+x_I\left(Y_{1,2,MX}^{\left(0\right)}+Y_{1,2MX}^{\left(1\right)}{\displaystyle \frac{x_I^2}{4}}\right)\right]\end{array}$$

(16)

The mole fractions of D-sucrose, water, and ions are denoted by x₁, x₂, and $x_I\left(x_I=1-x_1-x_2\right)$, respectively. Model parameters W_1.MX, U_1.MX and V_1.MX are obtained from experimental data for the NH₄NO₃/water binary system, whereas parameters w₁₂ and u₁₂ pertain to the D-sucrose/water system. The interaction parameters W_2.MX, U_2.MX,V_2.MX, $Y_{1.2.MX}^0$ and $Y_{1.2.MX}^1$ describe the behavior of mixtures containing both ionic and non-ionic species. The long-range Pitzer–Debye–Hückel term is expressed as follows:

$${\displaystyle \frac{g_{PDH}^{ex}}{RT}}=-\left({\displaystyle \frac{4A_x{I}_x}{\rho }}\right)\ln \left(1+\rho \cdot I_x^{1/2}\right)+\left({\displaystyle \frac{x_I^2}{4}}\right)\left[B_{MX}g\left(\alpha \cdot I_x^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right)\right]$$

(17)

A_x is the Debye–Hückel constant, with a value of 2.917. The symbol ρ denotes the closest approach parameter, set at 14.0292, and α\alphaα is the standard value, typically taken as 13.0. B_MX represents the Pitzer interaction parameter for the MX ion pair, while I_x refers to the ionic strength expressed on the mole fraction scale $\left(I_x={\displaystyle \frac{1}{2}}\sum _{i=1}{z}_i^2{x}_i\right)$. The function $g\left(y=\alpha \sqrt{I_x}\right)$ is done as:

$$g\left(y\right)={\displaystyle \frac{2}{y^2}}\left[1-\left(1+y\right)\exp \left(-y\right)\right]$$

(18)

The differentiation of Equations (16) and (17) permits us to obtain the corresponding expressions of activity and ionic mean coefficients of different components in aqueous solution. The water activity coefficient is expressed as:

$$\begin{array}{ll}\ln \left({\gamma }_1\right)& ={\displaystyle \frac{2\cdot A_X\cdot I_X^{3/2}}{1+\rho \cdot I_X^{1/2}}}-I_X^2{B}_{MX}\exp \left(-\alpha \cdot I_x^{1/2}\right)+x_I\left[\left(1-x_1\right)\cdot W_{1,MX}-x_2\cdot W_{2,MX}\right]\\ & +x_I^2\left[\left(1-2\cdot x_1\right)\cdot U_{1,MX}-2\cdot x_2\cdot U_{2,MX}\right]+x_I^2\left[x_1\left(2-3\cdot x_1\right)\cdot V_{1,MX}-3\cdot x_2^2\cdot V_{2,MX}\right]\\ & +\left[2x_2\cdot I_x\cdot \left(1-2\cdot x_1\right)\cdot Y_{1,2,MX}^0+\left({\displaystyle \frac{x_I^3}{4}}\right)\cdot x_2\cdot \left(1-4\cdot x_1\right)\cdot Y_{1,2,MX}^1\right]\\ & +x_2\cdot \left[\left(1-x_1\right)\cdot w_{12}+\left(2\cdot \left(x_1-x_2\right)\cdot \left(1-x_1\right)+x_2\right)\cdot u_{12}\right]\end{array},$$

(19)

The D-Sucrose activity coefficient is given as:

$$\begin{array}{ll}\ln \left({\gamma }_2\right)& ={\displaystyle \frac{2\cdot A_X\cdot I_X^{3/2}}{1+\rho \cdot I_X^{1/2}}}-I_X^2{B}_{MX}\exp \left(-\alpha \cdot I_x^{1/2}\right)+x_I\left[\left(1-x_2\right)\cdot W_{2,MX}-x_1\cdot W_{1,MX}\right]\\ & +x_I^2\left[\left(1-2\cdot x_2\right)\cdot U_{2,MX}-2\cdot x_1\cdot U_{1,MX}\right]+x_I^2\left[x_2\left(2-3\cdot x_2\right)\cdot V_{2,MX}-3\cdot x_1^2\cdot V_{1,MX}\right]\\ & +\left[2x_1\cdot I_x\cdot \left(1-2\cdot x_2\right)\cdot Y_{1,2,MX}^0+\left({\displaystyle \frac{x_I^3}{4}}\right)\cdot x_1\cdot \left(1-4\cdot x_2\right)\cdot Y_{1,2,MX}^1\right]\\ & +x_1\cdot \left[\left(1-x_2\right)\cdot w_{12}+\left(2\cdot \left(x_1-x_2\right)\cdot \left(1-x_2\right)-x_1\right)\cdot u_{12}\right]-\left[w_{12}+u_{12}\right]\end{array},$$

(20)

The ionic mean activity coefficient of AN in D-Sucrose/Water system is

$$\begin{array}{ll}\ln \left({\gamma }_{\pm }\right)& =-A_X\left[\left({\displaystyle \frac{2}{\rho }}\right)\ln \left(1+\rho \cdot I_x^{1/2}\right)+{\displaystyle \frac{I_x^{1/2}\left(1-2\cdot I_x\right)}{1+\rho \cdot I_x^{1/2}}}\right]\\ & +\left({\displaystyle \frac{I_x}{2}}\right)B_{MX}\left[g\left(\alpha \cdot I_x^{1/2}\right)+\exp \left(-\alpha \cdot I_x^{1/2}\right)\left(1-x_I\right)\right]\\ & +\left(1-x_I\right)\left[x_1\cdot W_{1,MX}+x_2\cdot W_{2,MX}\right]+2\cdot x_I\left(1-x_I\right)\left[x_1\cdot U_{1,MX}+x_2\cdot U_{2,MX}\right]\\ & +x_I\left(2-3\cdot x_I\right)\left[x_1^2\cdot V_{1,MX}+x_2^2\cdot V_{2,MX}\right]\\ & +x_1\cdot x_2\left[\left(1-4\cdot I_x\right)\cdot Y_{1,2,MX}^0+\left(3\cdot I_x^2-\cdot x_I^3\right)\cdot Y_{1,2,MX}^1\right]\\ & -x_1\cdot x_2\cdot \left[w_{12}+2\cdot \left(x_1-x_2\right)\cdot u_{12}\right]-W_{1,MX}\end{array},$$

(21)

3.7. Thermodynamic Properties Calculation

3.7.1. Excess Gibbs Energy

The excess Gibbs free energy of the ternary water/D-sucrose/ammonium nitrate (AN) system was determined using the following expression:

$${\displaystyle \frac{g^{ex}}{RT}}={\displaystyle \sum _{i=1}{x}_i\ln \left({\gamma }_i\right)=x_1\cdot \ln \left({\gamma }_1\right)}+x_2\cdot \ln \left({\gamma }_2\right)+x_I\cdot \ln \left({\gamma }_{\pm }\right)$$

(22)

in this expression, R is the universal gas constant and T is the absolute temperature.$g^{ex}$represents the excess Gibbs free energy per mole of particles. The mole fractions of water, D-sucrose, and the total ionic species (from NH₄NO₃) are denoted by $x_1$, $x_2$, and $x_I$, respectively. The activity coefficients of water, D-sucrose, and the mean ionic activity coefficient of NH₄NO₃ in the D-sucrose/water system are represented by ${\gamma }_1$, ${\gamma }_2$, and ${\gamma }_{\pm }$, respectively.

The total excess Gibbs energy $G^{ex}$ for any amount of material is given by:

$$G^{ex}={\displaystyle \sum _i{n}_i}{g}^{ex}$$

(23)

where n_i is the mole number of component i.

3.7.2. Transfer Gibbs Energy

The standard Gibbs free energy of transfer is a key parameter, as it reflects the interactions between the ions present in the mixed aqueous solution and the surrounding solvent molecules. The Gibbs energy of transfer of ammonium nitrate (AN) from pure water (W) to D-sucrose/water (W + S) mixtures, denoted as $G_{tr}^{AN}$, is calculated as follows [30]:

$$G_{tr}^{AN}\left(W\to W+S\right)=\upsilon RT\mathrm{l}\mathrm{n}\left({\displaystyle \frac{f_{AN}}{f_{AN}^0}}\right)$$

(24)

Here, υ denotes the number of ions produced upon complete dissociation of the electrolyte. $f_{AN}$ and $f_{AN}^0$, represent the mole fraction activity coefficients of NH₄NO₃ in the ternary water/D-sucrose/AN system and in the binary NH₄NO₃/water system, respectively.

3.7.3. D-Sucrose Solubility

The solubility of D-sucrose$m_s$ in an aqueous solution containing an electrolyte can be determined based on its saturation molality $m_s^0$ in pure water, i.e., in the absence of electrolyte. Accordingly, the equilibrium expression is given as follows:

$$m_s{\gamma }_s=m_s^0\gamma {}_s{}^0$$

(25)

$m_s^0$ and $m_s$ represent the molalities of D-sucrose in the binary D-sucrose/water system and in the ternary water/D-sucrose/ammonium nitrate (AN) system, respectively. Similarly, ${\gamma }_s^0$ and ${\gamma }_s$ denote the activity coefficients of D-sucrose in the binary and ternary systems, respectively. The values of molality and activity coefficient for the D-sucrose/water system at 25 °C were taken from the literature [31].

3.7.4. Electrolyte Solubility

The dissolution of NH₄NO₃ in the ternary water/D-sucrose/ammonium nitrate(AN) system can be represented by the following equilibrium:

$$k_{sp}=m_{N{H}_4^{+}}{\gamma }_{N{H}_4^{+}}{m}_{\mathrm{N}{O}_3^{-}}{\gamma }_{\mathrm{N}{O}_3^{-}}=m_{N{H}_4{NO}_3}^2{\gamma }_{\pm ,N{H}_4{NO}_3}^2$$

(26)

The mean ionic activity coefficient of NH₄NO₃ is represented by ${\gamma }_{\pm N{H}_{4}N{O}_3}$, while $m_{N{H}_{4}N{O}_3}$ denotes its molality. The solubility product $k_{sp}$ was determined in this study based on standard thermodynamic data [32].

3.7.5. Parameters Optimization

Experimental data for osmotic coefficients and/or mean ionic activity coefficients of the binary AN/water and D-sucrose/water subsystems, as well as the ternary water/D-sucrose/AN system, were employed for optimizing interaction parameters. The Maquardt algorithm [33] was applied to minimize the difference between calculated and experimental osmotic coefficients, by minimizing the sum of squared deviations $S_{\phi }$:

$$s_{\phi }={\displaystyle \frac{1}{N-p}}{\displaystyle \sum _{i=1}^{\mathrm{N}}{\left({\phi }_{\mathrm{i}}^{\exp }-{\phi }_{\mathrm{i}}^{\mathrm{cal}}\right)}^2}$$

(27)

N corresponds to the total number of experimental measurements employed, while p is the count of fitted parameters.

4. Results and Discussion

Experimental determinations were carried out to evaluate the water activities and osmotic coefficients of D-Sucrose and NH₄NO₃ at various molalities. The molalities investigated for D-Sucrose included 0.1, 0.3, 0.5, 1, 2, 3 and 4, whereas for NH₄NO₃, the tested molalities ranged from 0.1 to 6 mol.kg^-1. The relationship between water activities and osmotic coefficients can be expressed as follows:

$$\phi =-\left[{\displaystyle \frac{1000}{M_w.{\displaystyle \sum _i{\nu }_i{m}_i}}}\right]ln\left(a_w\right)$$

(28)

where ${\mathrm{M}}_w$is the molar mass of water, ${\nu }_i$is the number of ions released upon dissociation (with $=1$for non-electrolytes), and ${\mathrm{m}}_i$is the molality of solute i. The uncertainty ${\mu }_{\phi }$ can be estimated using the error propagation law, expressed as:

$${\mu }_{\phi }=\sqrt{\left[{\left({\displaystyle \frac{\partial \phi }{\partial a_w}}\right)}_{m_{1,}{m}_2}^2{\mu }_{a_w}^2+{\left({\displaystyle \frac{\partial \phi }{\partial m_1}}\right)}_{m_{2,}{a}_w}^2{\mu }_{m_1}^2+{\left({\displaystyle \frac{\partial \phi }{\partial m_2}}\right)}_{m_{1,}{a}_w}^2{\mu }_{m_2}^2\right]}$$

(29)

Assuming that the uncertainties ${\mu }_{m_1}$and ${\mu }_{m_2}$ are negligible, the uncertainty ${\mu }_{\phi }$can be determined using the following equation:

$${\mu }_{\phi }=\sqrt{\left[{\left({\displaystyle \frac{\partial \phi }{\partial a_w}}\right)}_{m_{1,}{m}_2}^2{\mu }_{a_w}^2\right]}=\sqrt{{\displaystyle \frac{1000}{M_w\cdot {\displaystyle \sum _i{\nu }_i{m}_i}\cdot a_w}}{\mu }_{a_w}^2}$$

(30)

The estimated uncertainty in the osmotic coefficients is u(φ) = 0.009.

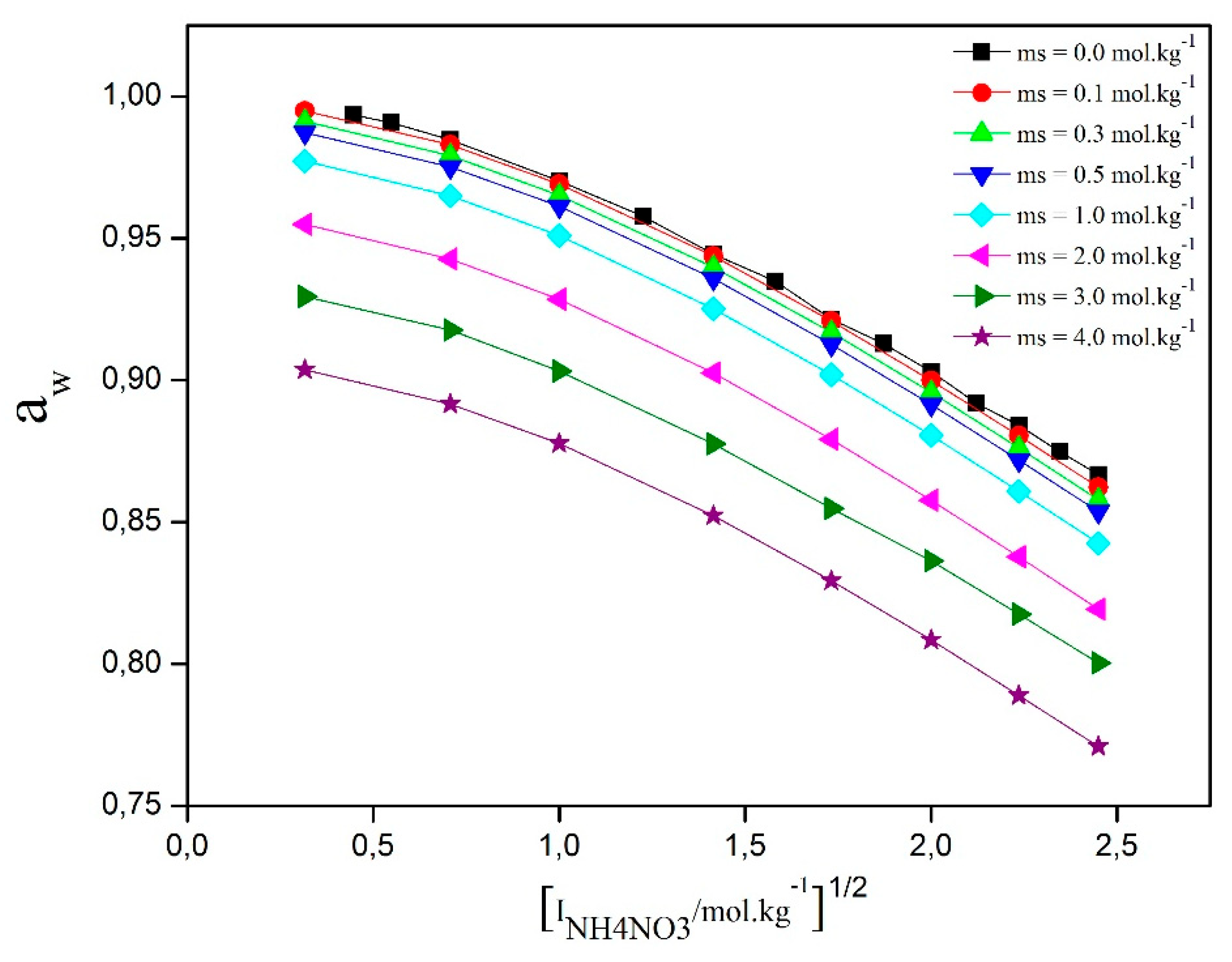
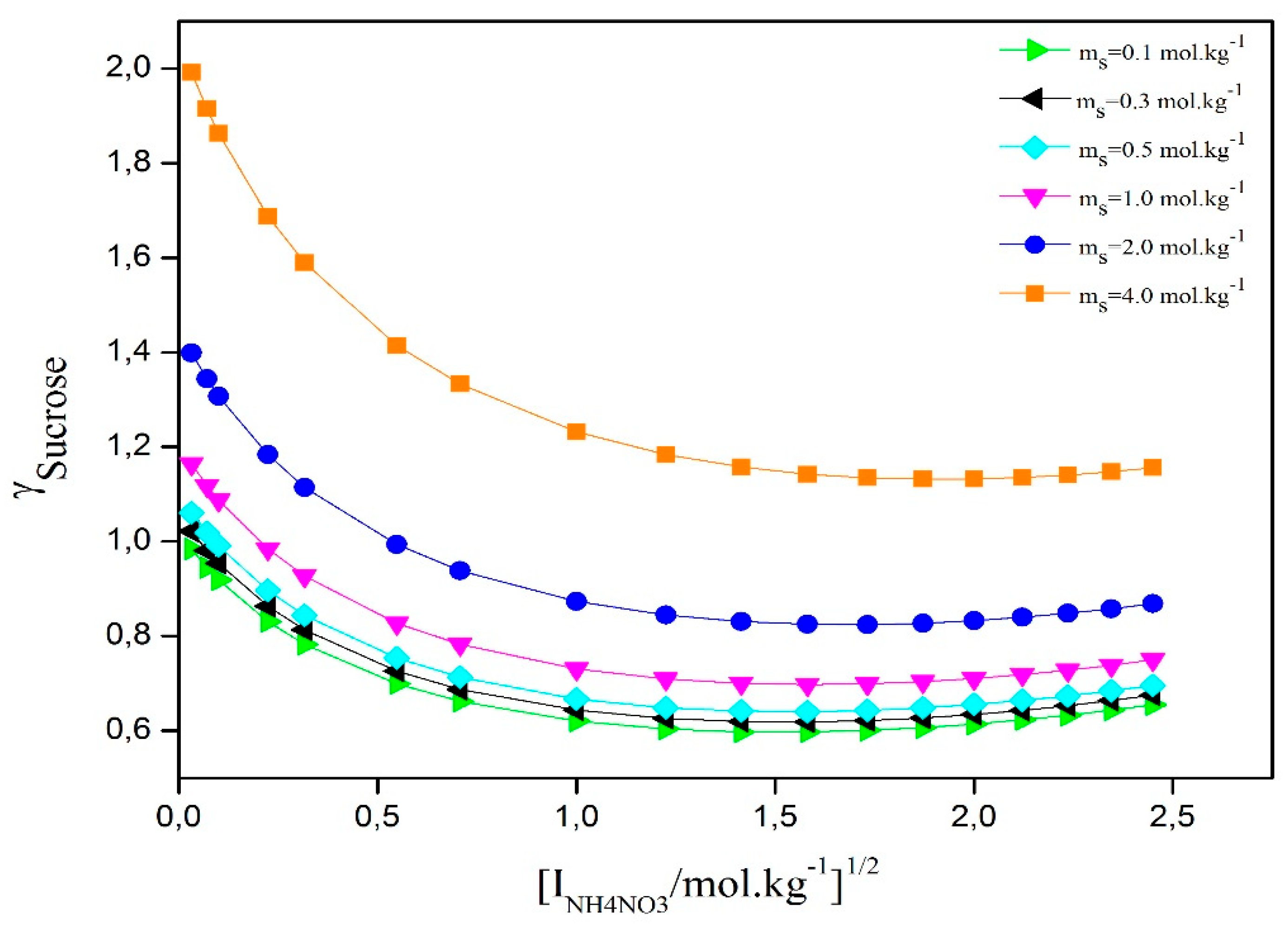
Table 2 presents the experimental data of osmotic coefficients (φ) and water activities (aw). Figure 2 illustrates the variation of water activity as a function of the square root of ionic strength for different D-sucrose concentrations. For all D-sucrose contents, water activity decreases with increasing molality—a behavior commonly observed in aqueous solutions of non-volatileelectrolytes. The addition of NH₄NO₃ to the D-sucrose/water system significantly influences its thermodynamic properties. These changes result from the specific interactions between water and D-sucrose, NH₄NO₃ and water, and NH₄NO₃ and D-sucrose, as well as from the ternary interactions among all three components. This implies that the presence of NH₄NO₃ substantially disrupts the hydration structure of the sugar solution. These interactions are governed by the hydration degree of each species, which directly affects the system’s activity.

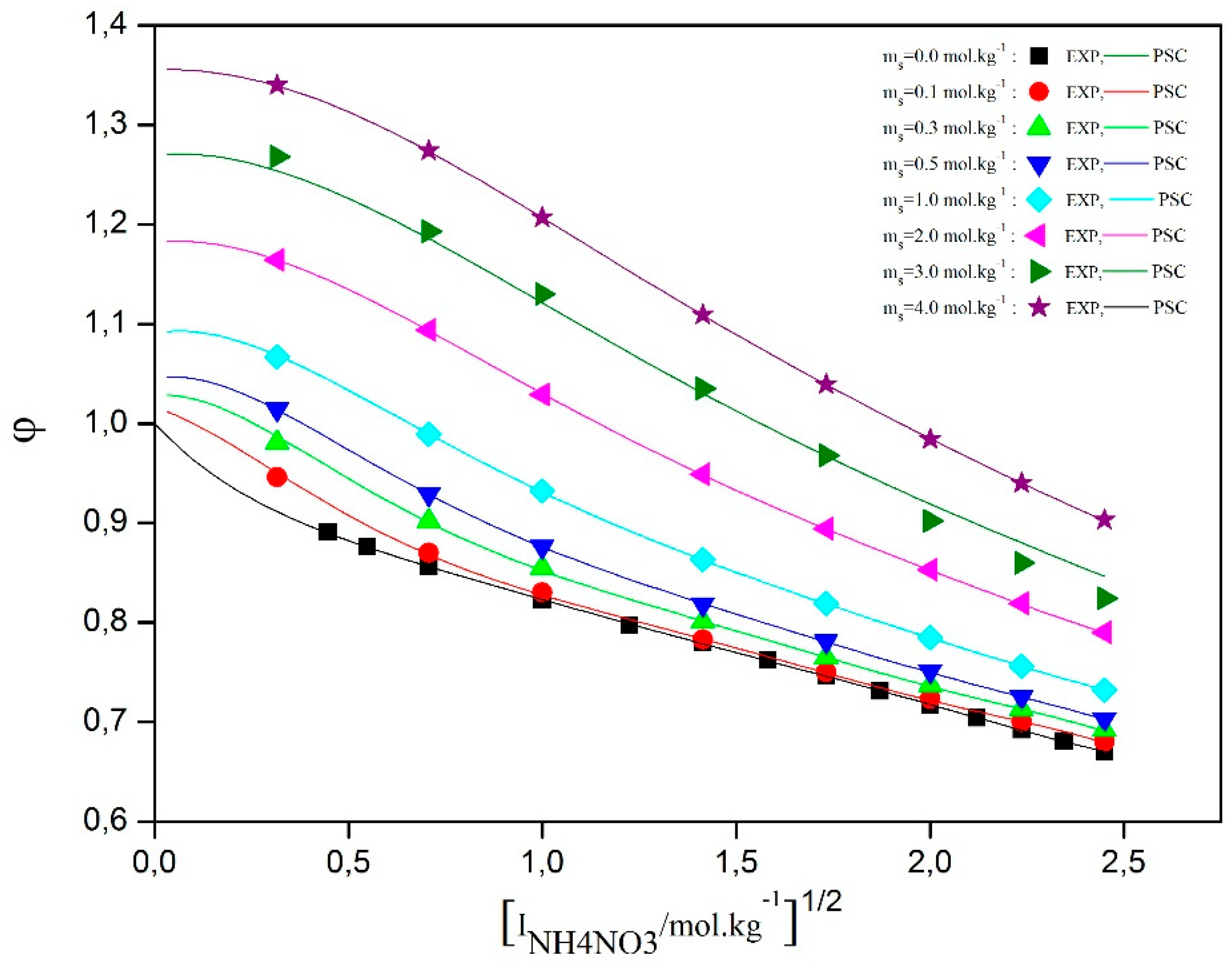
Figure 3 shows the osmotic coefficients derived from water activity measurements for the studied water/D-sucrose/ammonium nitrate (AN) system. The graph indicates that, at constant NH₄NO₃ concentration, the osmotic coefficient increases with rising D-sucrose content. However, the curves do not follow a uniform trend as a function of D-sucrose molality. Additionally, a slight decrease in the osmotic coefficient is observed with increasing NH₄NO₃ concentration.

These observations highlight the influence of molecular interactions within the solution. Ammonium ions (NH₄⁺) and nitrate ions (NO₃^-) ions interact electrostatically with sucrose molecules (C₁₂H₂₂O₁₁). More specifically, ammonium ions can form hydrogen bonds with the hydroxyl groups (OH^-) of sucrose. Such interactions may disrupt sucrose–sucrose associations, thereby affecting the solution’s structure and thermodynamic properties, including viscosity and solubility.

Water activities were calculated using three models: the ECA equation [24], the Lietzke and Stoughton (LS II) equation [25,26], and the Lin et al. correlation, all of which are provided in the appendix. The thermodynamic data used in these models were taken from Robinson and Stokes [28] for aqueous D-sucrose and from reference [29] for aqueous NH₄NO₃. For the water/D-sucrose/AN system, the parameter values used are:

• For the ECA model: λ=0, 00438 (mol.kg^-1)^-2 and δ=0,000758 (mol.kg^-1)^-3.
• For the Lin et al. model: C₁₂=0,0000418.

The calculated values of water activity ($a_w$) and osmotic coefficient using the parameter sets from the ECA and Lin et al. equations show good agreement with the experimental data. In contrast, predictions obtained using the LS II equation exhibit significant deviations from the measured values. This discrepancy can be attributed to the inherent limitation of the LS model, which treats the behavior of the mixture as a simple sum of the behaviors of its individual components, thereby neglecting specific interactions present in the ternary system.

To calculate the unknown parameters of the PSC model for the water/D-sucrose/NH₄NO₃ system, a minimization method is used. The parameters B_MX, W_1.MX, U_1.MX, and V_1.MX are determined from experimental data on osmotic coefficients(φ) and mean ionic activity coefficients (γ_AN) for the water–NH₄NO₃ system [29]. For the water/D-sucrose system, the Margules parameters w₁₂ and u₁₂ are taken from the data reported by Robinson et al. [28].

The interaction parametersW_2.MX, U_2.MX, V_2.MX,Y⁰_1.2.MX and Y¹_1.2.MXwere calculated using osmotic coefficient data from the ternary water–D-sucrose–ammonium nitrate system measured in this study. Table 3 shows these parameters and their standard deviations.

The estimated standard deviations show that the activity and osmotic coefficients are more reliable for the D-sucrose/water and NH₄NO₃/water systems. This work focused on studying the optimized parameters of the mixing model for the water/D-sucrose/ammonium nitrate system. The results revealed important details about the interactions between the different substances in the solution.

The developed model was used to predict the activity coefficients of NH₄NO₃ and D-sucrose, as well as the excess Gibbs free energy, in the ternary water/D-sucrose/ammonium nitrate system at 298.15 K. The results are shown in Table 4, and graphs are given in Figure 4, Figure 5 and Figure 6.

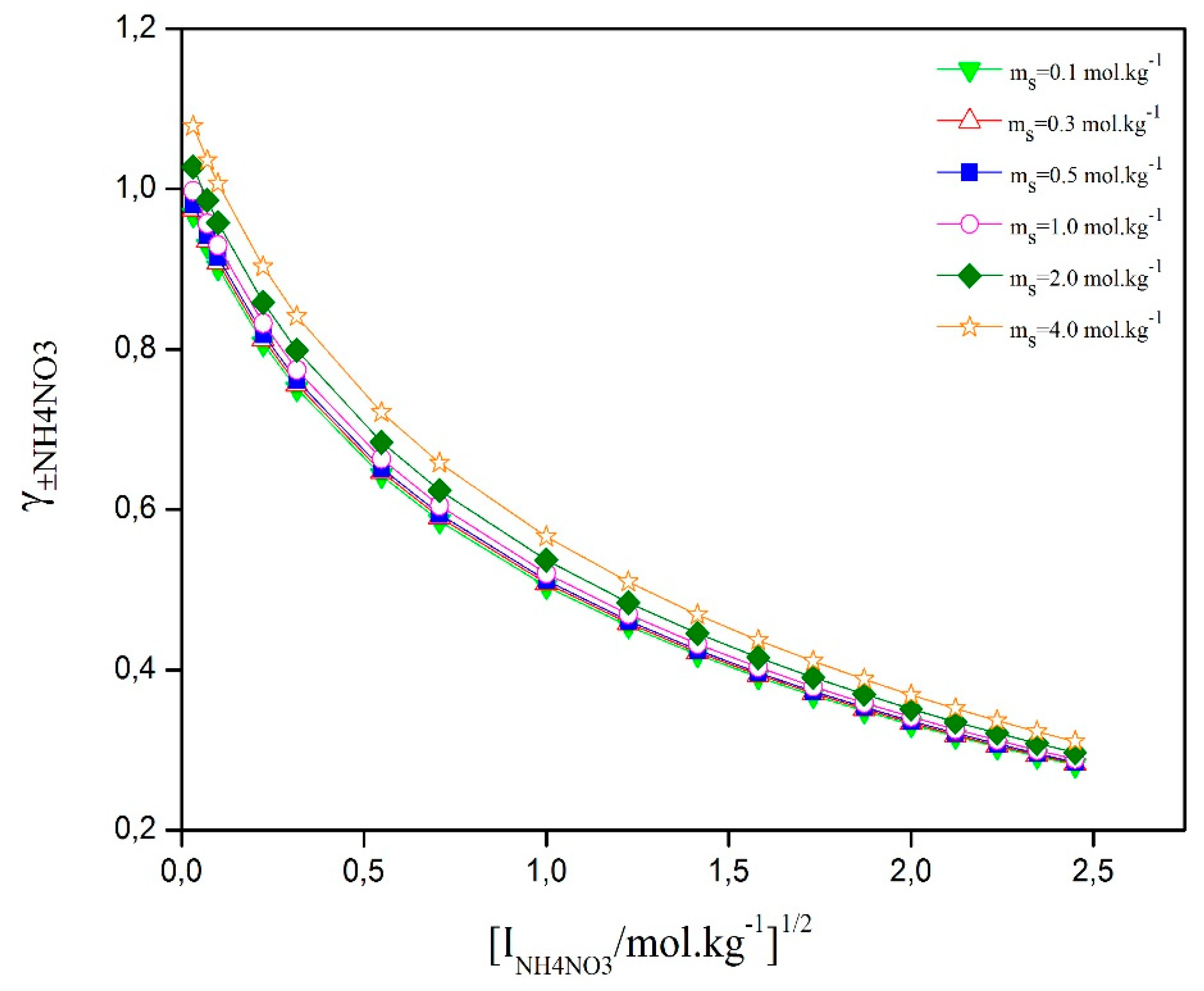
Figure 4 shows how the activity coefficient of ammonium nitrate (AN) changes with the square root of ionic strength in a ternary solution. The graph shows that the curves follow a clear pattern influenced by interactions between ions, ion-water solvation, and water-D-sucrose. In solutions with high AN concentration and less than about 1 mol·kg⁻¹ of D-sucrose, the activity coefficient of ammonium nitrate is very close to that of pure aqueous NH₄NO₃. However, when D-sucrose concentration exceeds 1 mol·kg⁻¹, the activity coefficient ${\gamma }_{{NH}_4{NO}_3}$ decreases as ammonium nitrate concentration increases, but it slightly rises with more D-sucrose. This behavior is due to interactions between ions and D-sucrose, and between water and D-sucrose, which affect the solution’s thermodynamics.

Figure 5 shows how the activity coefficient of D-sucrose changes with the square root of ionic strength in a ternary solution. All curves follow a similar trend depending on the amounts of D-sucrose and ammonium nitrate. The data indicate that the activity coefficient of D-sucrose in the ternary solutions is higher than in pure D-sucrose aqueous solutions. This suggests that NH₄NO₃ strongly affects the D-sucrose activity coefficient and causes a salting-out effect. Moreover, as ammonium nitrate concentration increases, both the D-sucrose activity coefficient and the salting-out effect become stronger.

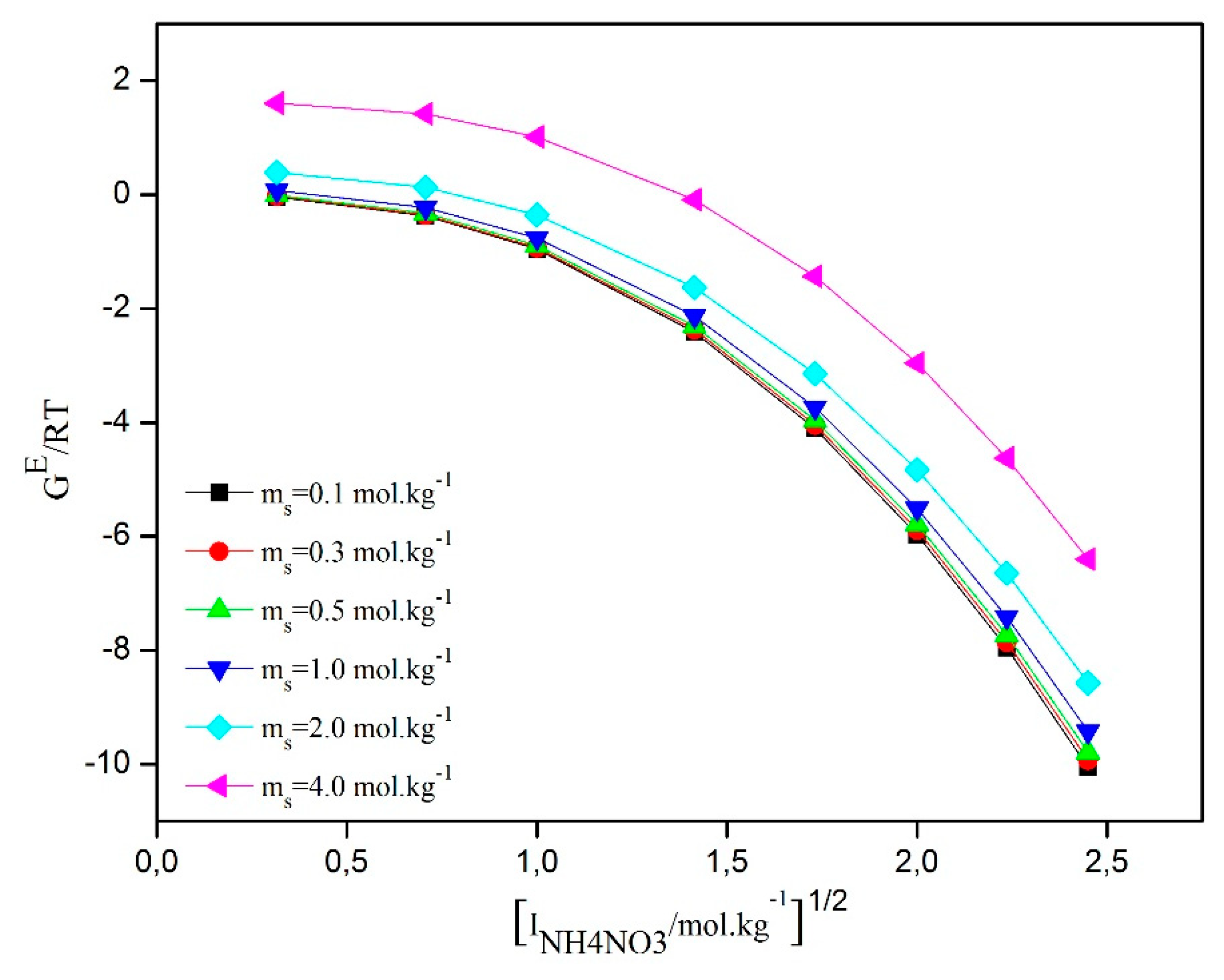
The data regarding the excess Gibbs free energies (g^E) have been determined for the entire range of molalities studied for NH₄NO₃ and D-Sucrose using the estimated parameters of the model and Equation (23). In Table 4, the trends of excess Gibbs free energies are presented as a function of the square root of the ionic strength for the ternary system water/D-Sucrose/AN at different concentrations of D-Sucrose. The results show similar trends for this system. Specifically, as the concentration of D-Sucrose increases, the excess Gibbs free energy also increases. This suggests an increased interaction between D-Sucrose molecules and the other components of the system. On the other hand, as the ionic strength increases, the excess Gibbs free energy decreases. This indicates that the presence of ions has a reducing effect on the interaction of D-Sucrose molecules with other species present in the system. These observations are consistent with the data presented in the Figure 6.

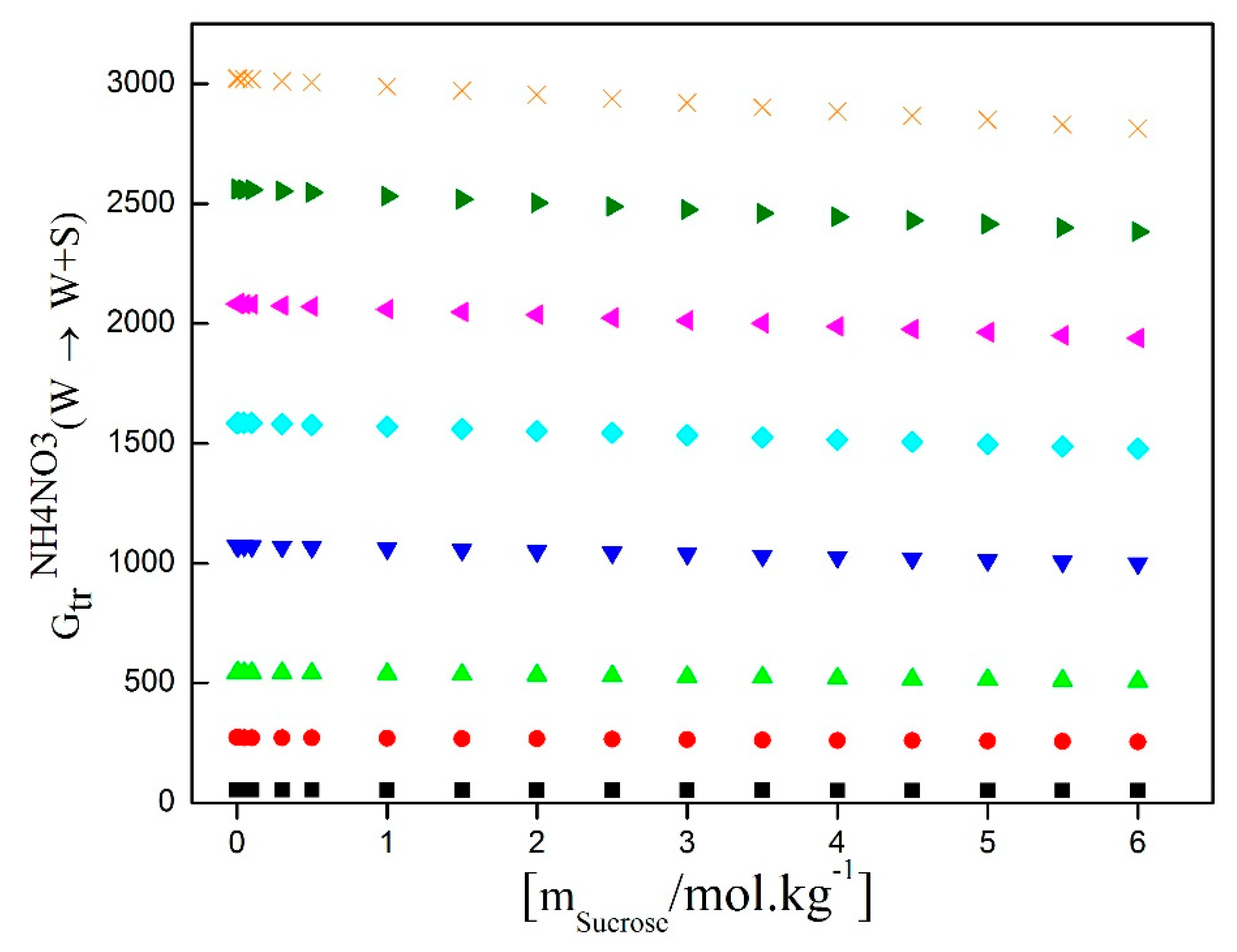
Figure 7 presents the calculated results of the AN transfer Gibbs energies from water to water/D-Sucrose mixtures as a function of salt molality and at various D-Sucrose molalities. This figure illustrates a positive correlation between the AN transfer Gibbs energy and the D-Sucrose content, indicating an increasingly unfavorable interaction between D-Sucrose and AN with higher D-Sucrose concentrations. However, it is important to note that the transfer Gibbs energy of ammonium nitrate remains constant for a single molality of sucrose, due to the establishment of a chemical equilibrium between ammonium nitrate and sucrose in the solution.

In the presence of a constant molality of sucrose, the hydration of ammonium nitrate is not directly affected. Upon dissolution of ammonium nitrate in water, NH₄⁺ and NO₃^- ions hydrate through electrostatic interactions with water molecules. Simultaneously, sucrose dissolves by forming dipole-dipole interactions with water molecules. Although solute-solvent interactions can be altered in the presence of sucrose, the hydration of NH₄⁺ and NO₃^- ions remains relatively constant. Therefore, the transfer Gibbs energy of ammonium nitrate remains unchanged, as the compensating effects of solute-solvent interactions maintain a dynamic equilibrium between the dissolved chemical species and water molecules.

The free energy parameters for the pairwise interaction g_NE (where E and N are assigned to the electrolyte and non-electrolyte, respectively) describe how the electrolyte interacts with D-sucrose in aqueous media. These values reflect the overall average of all individual interactions between D-sucrose molecules and the ions present in a specific salt. Based on the McMillan–Mayer solution theory, the Gibbs transfer energies of NH₄NO₃ from pure water to water/D-sucrose mixtures, under constant temperature and pressure conditions, can be determined using the following relationship:

$$G_{tr}^{N{H}_{4}N{O}_3}\left(W\to W+S\right)=2\upsilon m_N{g}_{EN}+6\upsilon m_E{m}_N{g}_{EEN}+3{\upsilon }^2{m}_N^2{g}_{ENN}$$

(31)

where $m_N$ and $m_E$ are the molality of Nonelectrolyte (D-Sucrose) and Electrolyte (NH₄NO₃), respectively. $g_{EN}$, $g_{EEN}$ and $g_{ENN}$ are the pair interaction and the triplet interaction parameters. The data of transfer Gibbs energy of NH₄NO₃from water to mixture water/D-Sucrose were used for optimization of $g_{EN}$, $g_{EEN}$ and $g_{ENN}$.

When both the electrolyte and non-electrolyte are present at low concentrations, triplet interaction terms can be neglected. Under these conditions, the salting coefficient can be evaluated from the pair interaction parameter using the following expression:

$$RT{\eta }_s=2\upsilon g_{EN}$$

(32)

Table 5. Interaction parameters of Gibbs energies of transfer of NH₄NO₃ from water to mixture water+D-Sucrose and salting constants η_s at 298.15 K.

	gEN/J.kg.mol-2	gEEN/J.kg.mol-3	gENN/J.kg.mol-3	ηs
This work	137.894	0.48253	-0.64843	0.2225

Table 5. Interaction parameters of Gibbs energies of transfer of NH₄NO₃ from water to mixture water+D-Sucrose and salting constants η_s at 298.15 K.

	gEN/J.kg.mol-2	gEEN/J.kg.mol-3	gENN/J.kg.mol-3	ηs
This work	137.894	0.48253	-0.64843	0.2225

The hygrometric method can be employed to determine the saturation limit of an aqueous solution. Once the solution reaches saturation, both its relative humidity and the solute concentration in the liquid phase remain constant [14,19]. In this work, the saturation limit was measured for an aqueous mixture composed of water, D-sucrose, and ammonium nitrate (AN). To identify the solid phases formed, ATR-FTIR spectroscopy and powder X-ray diffraction (PXRD) analyses were performed. The PXRD patterns of the obtained crystals are shown in Figure 8, while the ATR-FTIR spectra are presented in Figure 9. For comparison, crystallization results for sucrose and ammonium nitrate in pure water are also included in these figures.

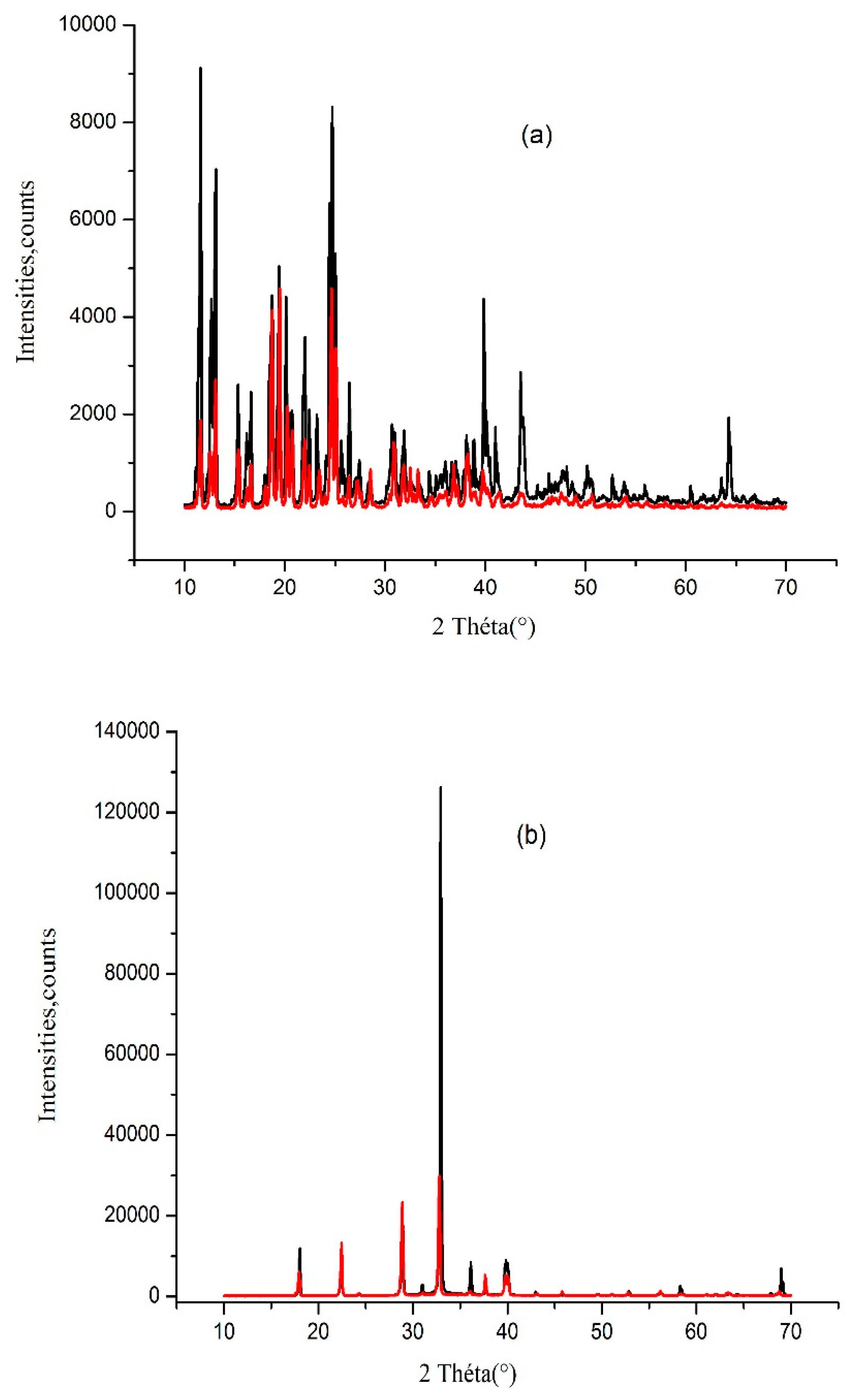
As illustrated in Figure 8a, PXRD analyses of solids crystallized from supersaturated sucrose–water mixtures and from water/D-sucrose/AN mixtures at high sucrose concentrations yielded identical diffraction patterns. The PXRD profile of crystalline sucrose (Figure 8a) matches very well with reference data reported in the literature. Figure 8b presents the PXRD patterns of crystals obtained from supersaturated water/D-sucrose/AN solutions with high ammonium nitrate content. These results indicate that dry AN crystals are formed both in the crystallization of ammonium nitrate from pure water and from supersaturated ammonium nitrate–sucrose–water systems at elevated AN concentrations. 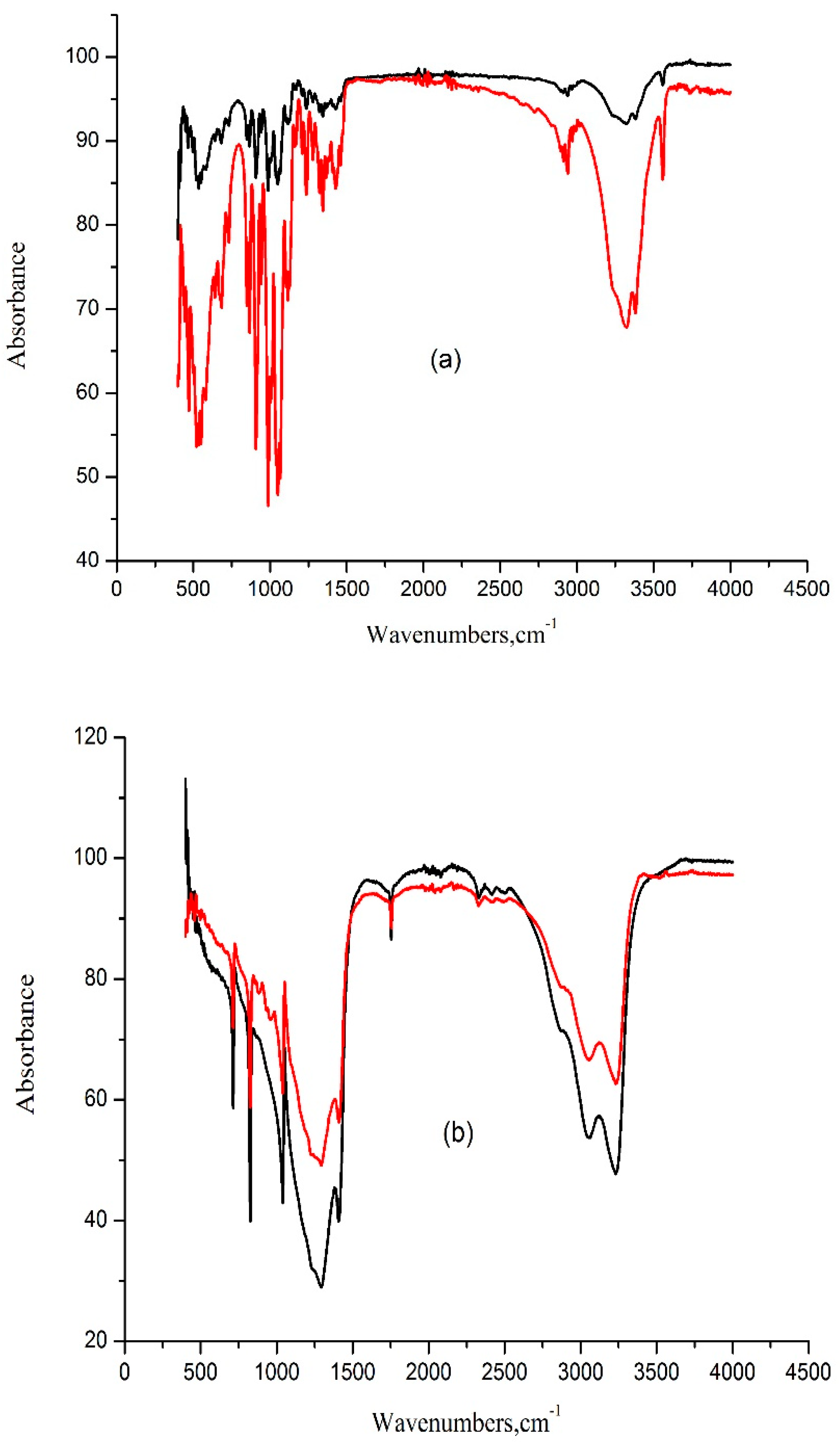Figure 9 displays the ATR-FTIR spectra of solids recovered from supersaturated mixtures of ammonium nitrate, sucrose, and water, alongside the spectra of pure sucrose and pure ammonium nitrate crystallized from water for comparison.

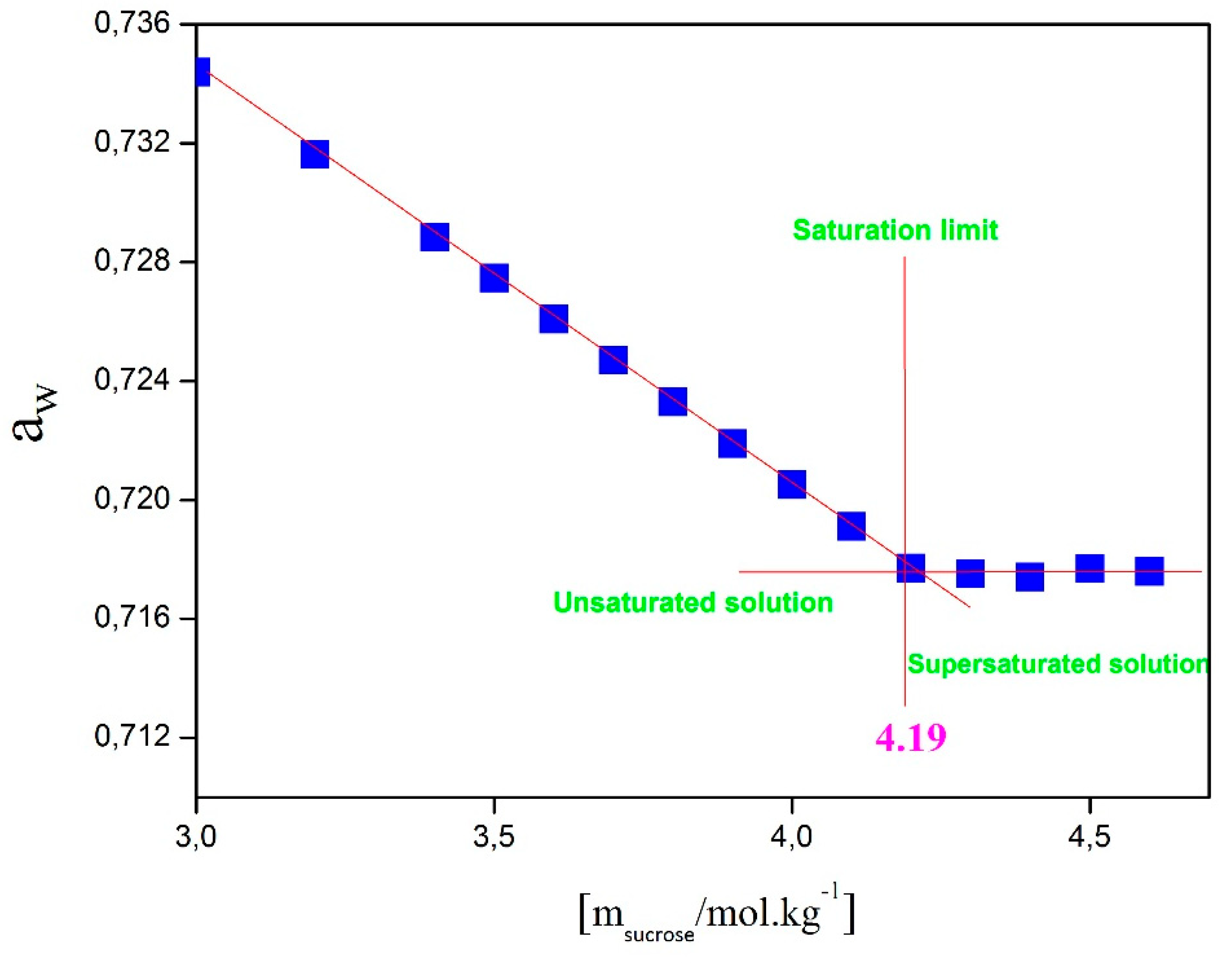
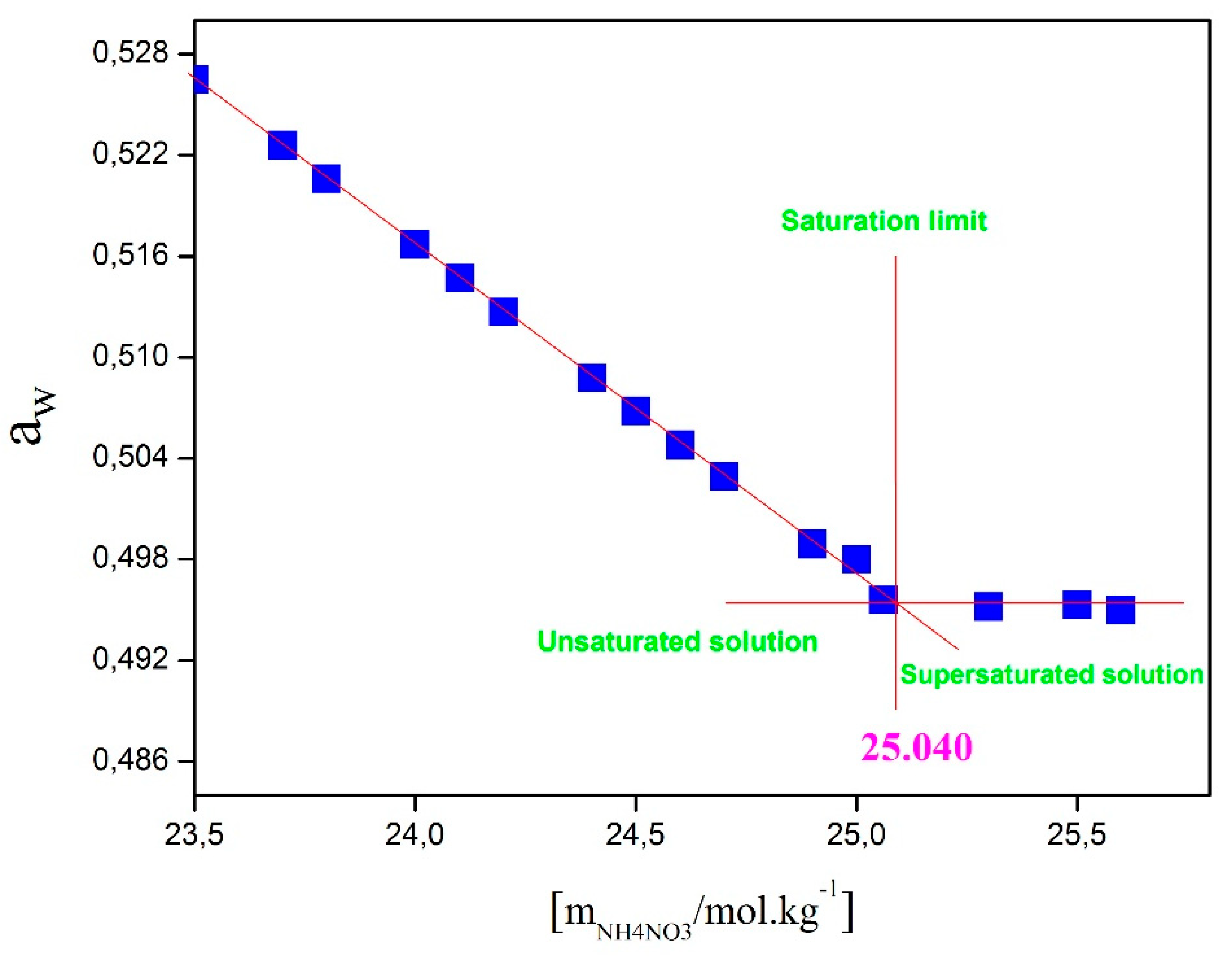
Figure 10 shows the variation of water activity in the NH₄NO₃-Sucrose-H₂O system as a function of sucrose molality, with a fixed NH₄NO₃ concentration set at 18.7 mol.kg⁻¹ and at a temperature of 25°C. In this graph, it is observed that water activity remains stable once the saturation limit is reached. The approximate value of this limit, extracted from Figure IV.8, is around 4.19 mol.kg⁻¹, corresponding to the solubility of sucrose in the aqueous solution of the NH₄NO₃-Sucrose-H₂O system containing 18.7 mol.kg⁻¹ of NH₄NO₃. The same methodology was applied to determine the solubility of sucrose at different NH₄NO₃ concentrations and the solubility of NH₄NO₃ at different sucrose concentrations (see Figure 11).

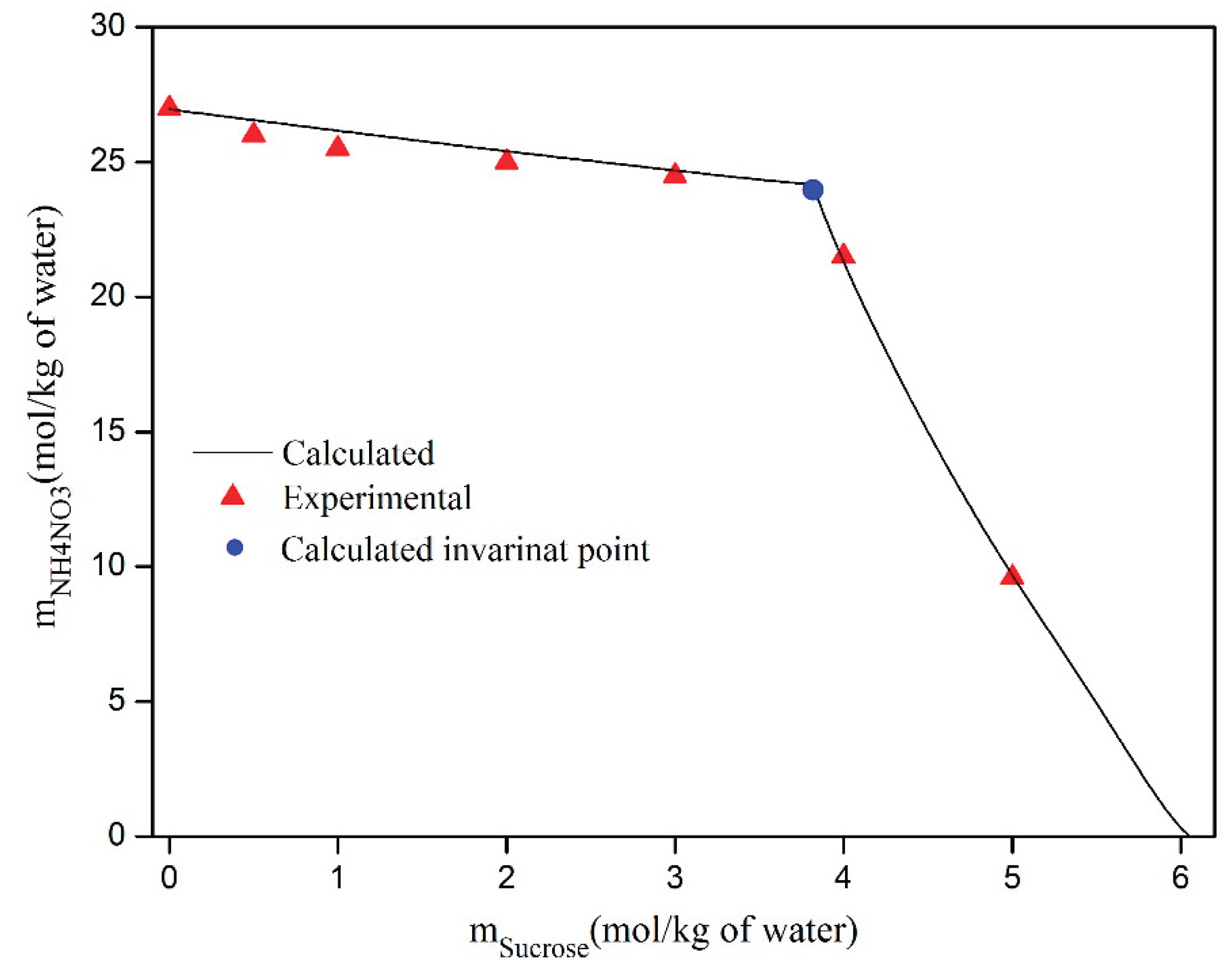
The calculated and experimental saturated aqueous solutions of mixtures of water, D-sucrose, and NH₄NO₃ at 298.15 K are presented in Table 6 and shown in Figure 12. This table clearly demonstrates the good agreement between the solubility measurements obtained in this study and those calculated. However, Figure 12 reveals a significant disparity between the calculated and experimental values for the NH₄NO₃/D-sucrose/water saturated aqueous solutions at 298.15 K. The graphical determination of the inflection point can lead to a deviation in the measurement of the saturation point. From this figure, it is evident that the solubility of D-sucrose in the NH₄NO₃/D-sucrose/water system decreases slightly as the salt content increases. Similarly, the solubility of NH₄NO₃ decreases as the concentration of D-sucrose increases.

5. Conclusions

Sucrose is of considerable importance to scientific research in a variety of fields. Its importance stems from its role in biochemistry and molecular biology, where it serves as a crucial molecule for the study of carbohydrate metabolism and energy storage. In the field of plant biology and physiology, sucrose plays the role of primary transport carbohydrate, making it possible to understand the growth and development of plants and their reactions to the environment. In addition, in the field of food science and nutrition, the impact of sucrose on human health and its applications in the food industry are being studied in depth. Moreover, sucrose has applications in biotechnology and industrial processes, serving as a carbon source for microbial fermentation and contributing to the production of various valuable compounds. The unique chemical and physical properties of sucrose make it a fascinating subject of study.

The importance of sucrose in scientific research lies in its multiple roles and its potential to advance knowledge and applications in many disciplines. In this study, we are interested in the influence of the presence of an electrolyte salt on the thermodynamic properties of sucrose. NH₄NO₃, or ammonium nitrate, is of great importance in scientific research. It is widely used as a nitrogen fertilizer in agriculture, contributes to explosive formulations, and plays a significant role in atmospheric chemistry and air pollution.

The aim of this work is therefore to study the aqueous sucrose and ammonium nitrate electrolyte/non-electrolyte system. This ternary system was studied using the hygrometric method at a temperature of 298.15 K. Relative humidity measurements were carried out at 298.15 K to obtain water activities and osmotic coefficients for the water-sucrose/NH₄NO₃ system. This system was tested in a wide range of NH₄NO₃ molality, from 0.1 to 6 mol.kg^-1, and for different sucrose contents from 0.1 to 4 mol.kg^-1.

Three predictive equations for the properties of aqueous mixed electrolytes were applied to the system under investigation, and their outputs were compared with experimental water activity data. The Dinane ECA rule, the Lin et al. equation, and the Lietzke–Stoughton equation (LS II) were found to be well suited to the studied system. Overall, the predicted values showed excellent agreement with the measurements, with deviations remaining within experimental uncertainty. The obtained results were further used to determine the activity coefficients and solubilities of sucrose and ammonium nitrate in the ternary aqueous system, as well as the excess Gibbs free energy of the D-sucrose/NH₄NO₃mixture, using the PSC model. Complementary characterization was performed through X-ray powder diffraction and spectroscopic analyses.

Thermodynamic studies of electrolyte and non-electrolyte solutions enhance our understanding of the complex interactions between ions and water molecules. Their findings have broad implications in natural, industrial, biological, medical, water treatment, and mineral processing fields, improving our knowledge and ability to optimize a variety of processes.

List of symbols

a	Activity
Ax	Debye–Huckel parameter
$B_{MX}$	Parameter of single electrolyte
D	Diameter of the drop
gex	Excess Gibbs energy per mole of particles
Gex	Excess Gibbs energy
hr	Relative humidity
K	Ratio of drops
Ks	Solubility product
M	Molality
n	Mole number
nr	Index of refraction
R	Gas constant, J.mol-1.K-1
T	Absolute temperature
P	Pressure
X	Mole fraction
u(p)	Standard uncertainty of parameter p
W12, U12	Parameters of PSC model
$W_{j,MX}$, $U_{j,MX}$and $V_{j,MX}$	Short-range parameters between molecule j and salt MX
$Y_{1,2,MX}^0$and $Y_{1,2,MX}^1$	Short-range ternary parameters molecule-molecule-Salt MX
Greek letters
α	Constant
ρ	Closest approach distance
φ	Osmotic coefficient
γ	Activity coefficient
σaw	Uncertainty of measured water activity
σφ	Uncertainty of measured osmotic coefficient
Subscripts
Calc	Calculated
Exp	Experimental
ref	Reference
i, 1, 2	Indicate component
PSC	Pitzer-Simonson-Clegg
PDH	Pitzer-Debye-Hückel
Superscripts
Ex		Excess