Theory & Medical Applications of DNA and RNA Helices as Antennae for Sonic & Electromagnetic Communication

1. Introduction

There is a substantial literature describing the long wavelength excitations of long chain organic polymer biomolecules by quantum field theories in one spatial dimension. The applications of quantum field theoretic statistical thermodynamics[1] to the biological mantra that proteins are fabricated and controlled by mathematical computational programs contained within DNA and RNA macro-molecules[2] has thus far still been limited. Ultimately the methods of quantum field theory should be applicable to medicinal practice such as the development of alternatives to standard vaccines applied to the maladies of some DNA molecules within bacteria and some RNA molecules within viruses. Our purpose is to provide some initial stages towards studying field theoretical models. Applications to the avatars of RNA of the COVID-19 virus would have some immediate importance.

The microscopic theory of the condensed matter physics that can be used for understanding forces in biological matter must be based on the quantum electrodynamic interaction in continuous media[3]. At the classical level, the Lagrangian method employed for describing photons and collective electromagnetic field configurations is fairly well known[4]. Field quantization follows the canonical rules. For weak excitations in long chain biomolecules, the effective Lagrangians describe bosons computed by functionally integrating out Fermion electron interactions. Purely electron charge transport can then be described by boson fields of the effective Lagrangian employing topologically charged soliton excitations. The mathematical properties of such soliton solutions of the boson equations of motion are very well established[5]. In what follows, we consider electronic charge transport along DNA and RNA long chain molecules responsible for inducing electromagnetic antenna processes wherein very low frequency radio and acoustic frequency phonons and photons[6,7] can be emitted and absorbed[8].

For the case of bacteria, there exist electronic communications within large communities because within a single community different cells are biologically wired to one another and circuit electrons pass through the biological mesh wiring through cell walls. A single bacterium with one or more connection wires allowing electrons to pass across the cell wall is often called an electrogenic bacterium. Studies of electrogenic bacteria communities abound[9,10,11,12] and engineering applications are beginning. For example, one may produce chemical batteries with electromotive forces induced by bacteria[13]. However, the electricity in this case is maintained by wiring some bacteria to other bacteria and/or by wiring bacteria to chemical cell electrode surfaces.

Of central interest in this work is the wireless electrodynamic connections between bacteria and/or viruses. And some practical applications of their sonic & EM radiation for medical purposes are discussed in Sec.(6)

In wireless connections, information is emitted or detected in antennae that can radiate and absorb respectively electrodynamic radiation from a distance. In particular, our purpose is to further elaborate the antennae emission and absorption properties of long DNA and RNA molecules. In fact work has already started on wireless bacterial/virus communication, both experimentally[14] and theoretically, quantum mechanically[6,7] through the RNA and DNA molecules and more recently from a more classical perspective via amyloid fibrils[15]. Since these long polymer molecules are quasi- one dimensional, the electrical currents that emit or absorb radiation photons may be adequately described by one dimensional quantum electrodynamic models, and these shall be essential to our general approach. In addition to photon excitations in the DNA and RNA molecules, there exist boson mechanical phonon oscillations, i.e., acoustic vibrations. The phonon-photon interaction thereby describes a piezoelectric effect in DNA and RNA molecules that occurs due to the chiral or handedness symmetry breaking, of the helical molecules that are double stranded for DNA and single stranded for RNA. The symmetry breaking must thereby be included in the one spatial dimensional field theoretical models employed to describe biological piezoelectricity[16,17]. Ultimately this requires Dirac electron matrices that have dimension four, i.e., two spin states times two chiral states. Employing one spatial dimensional Dirac spinors, these four states can be handled two states at a computational time.

The notion of describing electron charged currents in one spatial dimensional models with boson fields is very well known and constitutes the physical basis of Tomonaga-Luttinger fermion liquid models[18,19,20]. A central physical point is that a locally conserved charge in a model in one space plus one time dimension obeys the local charge conservation law ${\partial }_{\mu }{J}^{\mu }=0$. In field theories with one spatial dimension

$${\displaystyle \frac{\partial \lambda (z,t)}{\partial t}}+{\displaystyle \frac{\partial I(z,t)}{\partial z}}=0,$$

(1)

wherein $\lambda (z,t)$ and $I(z,t)$ represent, respectively, the charge density per unit length and the current. For the problem of wireless communication between different DNA or RNA long polymer helical molecules, Eq.(1) represents the antennae current along the molecule emitting and absorbing radiation. The general solution to the local charge conservation Eq.(1) involves the dipole moment per unit length $Q(z,t)$ defined to obey

$$I(z,t)={\displaystyle \frac{\partial Q(z,t)}{\partial t}}\mathrm{and}\lambda (z,t)=-{\displaystyle \frac{\partial Q(z,t)}{\partial z}}.$$

(2)

Thus, the electrical currents in one plus one dimensional field theories can be described by a single scalar Boson field $Q(z,t)$ having physical dimension of charge regardless of the fermion field dynamics that may be at the root of the physical motions.

1.1. Cable Photons in DNA and RNA Chains

Short ranged heavy massive Boson exchange can lead in the vacuum to a point-like Fermion interaction between currents. Boson masses in biological matter are here considered massive if $M_{\left(\mathrm{heavy}\mathrm{boson}\right)}{c}^2/e\gg 1$ millivolt. The semiconducting electrons in electrodynamic coherent water[21] domains set the voltage scale of millivolts for the electronic semiconducting energy gaps in biology. For quantum field theories in one spatial dimension, the photons can travel along the molecules as E waves or TM cable modes or as B waves or TE cable modes. TE and TM modes along one dimensional cables are massive and exchange of such photons in one spatial dimension lead the Fermi electronic point like or at least short ranged interaction. The vacuum interaction depends on the square of the current $J_{\mu }{J}^{\mu }=I^2-c^2{\lambda }^2$.

Since the long DNA or RNA chains reside in solution there is a capacitance per unit chain length $\epsilon$ and an inductance per unit chain length µ. The condensed matter Fermi current-current interaction is a simple TEM massless photon. In Gaussian electromagnetic units, there is a zero mass TEM cable mode Lagrangian as grown out of the biological matter point-like Fermi interaction in one spatial dimension

$$\begin{array}{ccc}& & L_{TEM}={\displaystyle \frac{1}{2}}{\int }_{\mathcal{L}}\left[{\displaystyle \frac{\mu }{c^2}}{I}^2-{\displaystyle \frac{1}{\epsilon }}{\lambda }^2\right]dz,\hfill \\ & & L_{TEM}={\displaystyle \frac{1}{2}}{\int }_{\mathcal{L}}\left[{\displaystyle \frac{\mu }{c^2}}{\left({\displaystyle \frac{\partial Q}{\partial t}}\right)}^2-{\displaystyle \frac{1}{\epsilon }}{\left({\displaystyle \frac{\partial Q}{\partial z}}\right)}^2\right]dz,\hfill \\ & & v={\displaystyle \frac{c}{\sqrt{\mu \epsilon }}}\mathrm{wherein}v=\mathrm{TEM}\mathrm{photon}\mathrm{velocity}.\hfill \end{array}$$

(3)

The quantum electrodynamic zero mass photon quantization from the Lagrangian Eq.(3) is canonical and describes the Goldstone boson for the ordered Tomonaga-Luttinger liquid of electrons.

1.2. Polymer Chain Thermodynamics

In Section 2 the statistical thermodynamics of a long polymer molecule having energy $\mathcal{U}$, entropy $\mathcal{S}$, length $\mathcal{L}$, dipole moment $\mathcal{P}$ and chemical composition particle numbers ${\mathcal{N}}_1,\dots ,{\mathcal{N}}_f$ will be discussed in terms of the complete extensive scaling thermodynamic function

$$\begin{array}{ccc}& & \mathcal{U}=\mathcal{U}(\mathcal{S},\mathcal{L},\mathcal{P},{\mathcal{N}}_1,\dots ,{\mathcal{N}}_f),\hfill \\ & & \lambda \mathcal{U}=\mathcal{U}(\lambda \mathcal{S},\lambda \mathcal{L},\lambda \mathcal{P},\lambda {\mathcal{N}}_1,\dots ,\lambda {\mathcal{N}}_f),\hfill \\ & & d\mathcal{U}=Td\mathcal{S}+\tau d\mathcal{L}+Ed\mathcal{P}+\sum _{a=1}^f{\mu }_{a}d{\mathcal{N}}_a,\hfill \\ & & \mathcal{U}=T\mathcal{S}+\tau \mathcal{L}+E\mathcal{P}+\sum _{a=1}^f{\mu }_a{\mathcal{N}}_a,\hfill \end{array}$$

(4)

wherein $T,\tau ,E,\mathrm{and}{\mu }_1\dots ,{\mu }_f$ represent respectively the temperature, long molecule tension (negative compression), electric field tangent to the molecule axis and chemical potentials. In terms of intensive quantities per unit length

$$\begin{array}{ccc}& & \mathcal{U}=u\mathcal{L},\mathcal{S}=s\mathcal{L},\mathcal{P}=Q\mathcal{L},{\mathcal{N}}_a={\mathrm{\Gamma }}_a\mathcal{L},\hfill \\ & & u=Ts+\tau +EQ+\sum _{a=1}^f{\mu }_a{\mathrm{\Gamma }}_a,\hfill \\ & & -d\tau =sdT+QdE+\sum _{a=1}^f{\mathrm{\Gamma }}_{a}d{\mu }_a,\hfill \\ & & du=Tds+EdQ+\sum _{a=1}^f{\mu }_{a}d{\mathrm{\Gamma }}_a.\hfill \end{array}$$

(5)

The complete thermodynamic intensive energy per unit length function $u(s,Q,{\mathrm{\Gamma }}_1,\dots ,{\mathrm{\Gamma }}_f)\equiv u(s,Q,\mathrm{\Gamma })$ determines the dipole moment per unit length function $Q(s,E,\mathrm{\Gamma })$,

$$\begin{array}{ccc}& & Q=-{\left({\displaystyle \frac{\partial \tau }{\partial E}}\right)}_{T,\mu }=-{\left({\displaystyle \frac{\partial w}{\partial E}}\right)}_{s,\mathrm{\Gamma }}\hfill \\ & & w(s,E,\mathrm{\Gamma })=\underset{Q}{inf}\left(u(s,Q,\mathrm{\Gamma })-EQ\right)\hfill \\ & & dw=Tds-QdE+\sum _{a=1}^f{\mu }_{a}d{\mathrm{\Gamma }}_a.\hfill \end{array}$$

(6)

The thermodynamic equations of state may be computed from field theoretical models in one spatial z plus one temporal t dimension wherein the spatial coordinate z represents the distance along the axis of the molecule. The current Eqs.(1,2) along the molecular axis is completely determined by Q obeying in thermodynamics Eq.(6). Finally, the full Lagrangian for molecular polymer antennae currents read

$$\begin{array}{ccc}& & L_{electronic}\left[Q\right]=\hfill \\ & & {\int }_{\mathcal{L}}\left\{{\displaystyle \frac{1}{2\epsilon }}\left[{\displaystyle \frac{1}{v^2}}{\left({\displaystyle \frac{\partial Q}{\partial t}}\right)}^2-{\left({\displaystyle \frac{\partial Q}{\partial z}}\right)}^2\right]-u(s,Q,\mathrm{\Gamma })\right\}dz.\hfill \end{array}$$

(7)

The quantum electrodynamic antenna photon quantization from the Lagrangian Eq.(7) is canonical. Eq.(7) holds true in virtue of Eqs.(3) and (5). The above Lagrangian, Eq.(7), is a central result of this work on DNA and RNA antennae.

Ordinary Helmholtz linear electric dipole antennae or loop magnetic dipole antennae are designed employing the physics of linear electromagnetic equations in matter as in the Lagrangian Eq.(3). Nature’s biological antennae design has been more inventive than Helmholtz’s, employing nonlinear effects and yielding electronic currents for emitting and absorbing photons described by soliton transport. Previously, this approach has proved successful in describing polyacetylene and magnetic dipole rings of ${\left(CH\right)}_n$ of the benzene ring (n=6) type.

Finally, additional dissipation processes increasing entropy (s) in the antennae will give rise to finite lifetime effects for the non-linear collective photon solitons. However, these lifetimes become limited to large times by the semiconductor soliton topological stability which amounts to identifying soliton fundamental homotopy group kinks as physical electronic charges. Some discussion of photon and phonon absorption is given in Section 4.

1.3. Field Theoretical Models

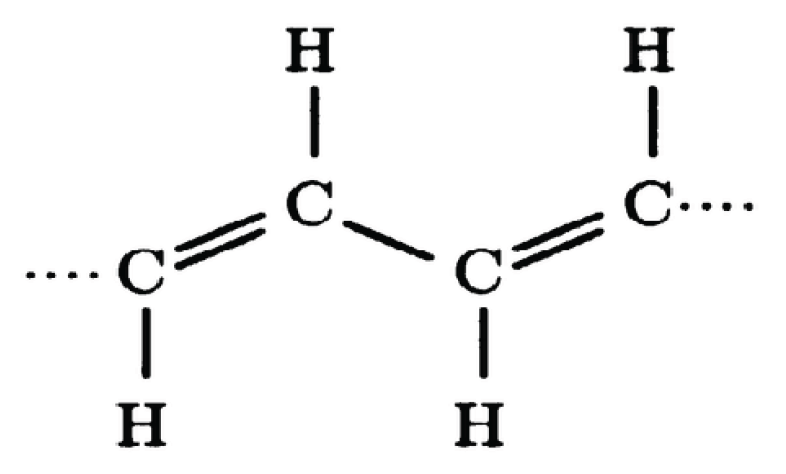
The simplest example of the field theoretical models applied to a long organic polymer molecule involved trans-polyacetylene whose chain of n links has the chemical formula ${\left(CH\right)}_n$ is discussed in Section 2 and pictured in Figure 1.

The fermion electronic model in one spatial dimension involves the massive Thirring model with a Dirac spinor band kinetic energy plus the Fermi pointwise current-current electron interaction. This point-like Fermi interaction can be renormalized only in a one spatial dimension field theory. Such a Fermion model can also be “bosonized” as noted by Tomonaga[18], Luttinger[19] and Mattis and Lieb[20]. A relativistic view of the renormalized massive Thirring model in one spatial dimension was discussed in great mathematical detail by Coleman[22] who proved the “bosonized” equivalence to the sine-Gordon field theory in one spatial dimension. The connection between the soliton in the quantum field theoretical sine-Gordon model and electronic charge transport in polyacetylene polymer chains was discussed in the work on the SSH model[23,24] (Su, Schrieffer, Heeger).

The nature of the soliton Fermion number was explored by Jackiw and Rebbi[25]. In our work the soliton has the charge of one electronic charge as demanded by the connection between local charge conservation and gauge invariance. The soliton structure has been reported observed[26]. The Coleman sine-Gorden equivalence is discussed in Section 3.

1.4. The Mechanics of Damped Slinky Modes

The two helix DNA model and the single helix RNA model mechanically act similarly to a quantum mechanical molecular toy helical slinky. The known mechanical modes of motion of such a slinky is usually called wormlike in conventional studies[27] of long polymer chains. The statistical mechanics[28] of the slinky or wormlike motions wherein the long helical biological molecules clump into balls of string or are knitted and folded into sheets of polymer protein material is well studied. These have long been applied to describe biological compaction essential for the central biological mantra of how DNA and RNA produce proteins. These compaction modes are discussed in Section 4.

The differential geometry of the path of a long spatial winding polymer chain is described by giving the points on a polymer path[29] as a function of arclength s,

$$\mathbf{r}=\mathbf{r}\left(s\right)\mathrm{wherein}d{s}^2=d\mathbf{r}·d\mathbf{r}.$$

(8)

A triad of unit vectors, one tangent $\mathbf{t}$ and two normal $\mathbf{n}$ and $\mathbf{b}=\mathbf{t}\times \mathbf{n}$, creates a moving reference frame triad of unit vectors $(\mathbf{t},\mathbf{n},\mathbf{b})$ along the curved molecular path. The rotation of the unit orthonormal vector triad obeys the equations of Frenet and Serret,

$${\displaystyle \frac{d}{ds}}\left(\begin{array}{c}\mathbf{t}\\ \mathbf{n}\\ \mathbf{b}\end{array}\right)=\left(\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right)\left(\begin{array}{c}\mathbf{t}\\ \mathbf{n}\\ \mathbf{b}\end{array}\right),$$

(9)

wherein $\kappa$ is the curvature of the molecule and $\tau$ is the torsion of the molecule. In order to understand the meaning of curvature and torsion, consider the case wherein the curvature and torsion are uniform along the curve,

i.e.,

$$\kappa ={\displaystyle \frac{R}{R^2+{[h/\left(2\pi \right)]}^2}},\tau ={\displaystyle \frac{[h/(2\pi \left)\right]}{R^2+{[h/\left(2\pi \right)]}^2}}$$

(10)

for the case that R = const. and h = const. generates a helix as shown in Figure 2.

In the Kratky-Porod model, also known as the wormlike chain model[27,30,31], the DNA and/or RNA the polymer helices wiggle about like worms in the fluid solute environment. The energy of a worm-like chain or more briefly a deformed slinky-wormlike polymer is described by the energy

$$\begin{array}{ccc}& & {\mathcal{U}}_{deformation}=\tilde{\tau }\mathcal{L}+\hfill \\ & & {\displaystyle \frac{\mathcal{Y}}{2}}{\int }_{\mathcal{L}}\left[{\xi }_1^4\kappa {\left(s\right)}^2+{\xi }_2^4{(\tau \left(s\right)-{\tau }_0)}^2\right]ds,\hfill \end{array}$$

(11)

wherein the tension, $\tilde{\tau }>0$, or compression, $\tilde{\tau }<0$, in the first term on the right hand side of Eq.(11) has an overhang $\tilde{\tau }$ only to distinguish it from torsion $\tau$. This first term treats the wormlike slinky motions as in string theory with the long chain molecular “string” embedded in the physical three spatial dimensions. The second two terms on the right hand side of Eq.(11) give rise to rigidity in transverse mechanical vibrations and in torsional (or angular) mechanical vibrations that affect the mechanical vibrations, giving rigidity to the polymer chain. The Young’s modulus is denoted by $\mathcal{Y}$ and the Poisson ratio is denoted by $\sigma$. Finally, the persistence lengths of the polymer rigidity will be denoted by ${\xi }_j$. Here we are applying classical elasticity theory[32]. In bulk solids, there is one longitudinal sound wave velocity and two modes of transverse sound velocity as given by

$$\begin{array}{ccc}& & v_{long}=\sqrt{{\displaystyle \frac{\mathcal{Y}(1-\sigma )}{\rho (1-\sigma )(1-2\sigma )}}}\mathrm{Bulk}\mathrm{Longitudinal}\hfill \\ & & v_{trans}=\sqrt{{\displaystyle \frac{\mathcal{Y}}{2\rho (1+\sigma )}}}\mathrm{Bulk}\mathrm{Transverse}.\hfill \end{array}$$

(12)

Finally, the persistence lengths of the polymer rigidity will be denoted by ${\xi }_j$.

There are four modes of mechanical waves on helical polymer molecules in a worm-like chain as shown in Figure 3. There exist four kinds of mechanical waves of interest: (i) There are two longitudinal modes with a straight line z-axis as the center of the coils. There is compressional sound in a cylinder, and rotational sound due to torsion. (ii) There are two transverse degrees of freedom for the now curved central axis of the coil as in Eq.(11).

Associated with bulk polymer mass density $\rho$ is a longitudinal persistence length ${\xi }_l$ defined thermodynamically by

$${\rho }_1\equiv \left(\sum _{a=1}^f{m}_a{\mathrm{\Gamma }}_a\right)=\rho {\xi }_l^2,$$

(13)

wherein $m_a$ is the mass of chemical species a on the polymer chain, and ${\rho }_1$ is the mass per unit length of the chain.

For small oscillations in the elastic strain, the first longitudinal compressional mode in a thin straight worm slinky has a sound velocity spectrum

$$\omega =v_{l}k\mathrm{compressional}{v}_l=\sqrt{{\displaystyle \frac{\mathcal{Y}}{\rho }}}.$$

(14)

The second straight central axis mode is torsional with spectrum

$$\omega =D_l{k}^2\mathrm{torsional}{D}_l=v_l{\xi }_l.$$

(15)

Typically, longitudinal compressional mode velocities $v_l\sim 2\times {10}^5$ cm/sec, while persistence lengths are approximately the coherent domain sizes in water[21,33], $\xi \sim 5\times {10}^{-6}$ cm. Thus, $D_l\sim 1{\mathrm{cm}}^2/\sec$. Note the electron quantum of circulation $D_{el}=(\hslash /m)\approx 1.16{\mathrm{cm}}^2/\sec$ contributing to the free electron spectrum $E={\hslash }^2{k}^2/\left(2m\right)$. The agreement $D_{el}\sim D_l$ is not fortuitous. Finally, the transverse bending modes for the wormlike-slinky have the spectrum

$$\omega =D_t{k}^2\mathrm{transverse}{D}_l=v_t{\xi }_t,$$

(16)

which is degenerate if the straight-line axis does not sense an asymmetry in the rotational moments of inertia. Here ${\xi }_t$ is the transverse persistence length. These frequencies, quadratic in the wave number k, are comparable to free electron Bohr transition frequencies, $\hslash {\omega }_{fi}=E_f-E_i$, wherein $E={\hslash }^2{k}^2/\left(2m\right)$ and obey

$${\omega }_{fi}={\displaystyle \frac{1}{2}}{D}_{el}\left[(k_f+k_i)(k_f-k_i)\right]\mathrm{with}{D}_{el}={\displaystyle \frac{\hslash }{m}}.$$

(17)

The similar orders of magnitude $D_l\sim D_{el}$ are not fortuitous. Young’s modulus describes the internal pressure-energy as determined by the electron Pauli exclusion principle required for stable matter when Coulomb forces are of microscopic importance.

1.5. Electric and Magnetic Dipole Antennae

In Section 3 the electric dipole antenna that constitutes a linear axis DNA or RNA chain polymer molecule subject to an electric field is described by the massive Thirring sine Gordon Lagrangian in a driving electric E field

$$\begin{array}{ccc}& & L_{electronic}\left[Q\right]=\left({\displaystyle \frac{1}{2\epsilon }}\right)\times \hfill \\ & & {\int }_{\mathcal{L}}\left[{\displaystyle \frac{1}{v^2}}{\left({\displaystyle \frac{\partial Q}{\partial t}}\right)}^2-{\left({\displaystyle \frac{\partial Q}{\partial z}}\right)}^2\right]dz-\hfill \\ & & {\int }_{\mathcal{L}}\left[\hslash \overline{\omega }\left(1-cos\left(2\pi {\displaystyle \frac{Q}{e}}\right)\right)-EQ\right]dz,\hfill \end{array}$$

(18)

corresponding to the equation of motion

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{\epsilon }}\left[{\displaystyle \frac{1}{v^2}}{\left({\displaystyle \frac{\partial }{\partial t}}\right)}^2-{\left({\displaystyle \frac{\partial }{\partial z}}\right)}^2\right]Q+\hfill \\ & & \left({\displaystyle \frac{2\pi \hslash \overline{\omega }}{e}}\right)sin\left(2\pi {\displaystyle \frac{Q}{e}}\right)=E.\hfill \end{array}$$

(19)

If the driving electric field depends only on time,

$$E\left(t\right)=-{\displaystyle \frac{1}{c}}\dot{A}\left(t\right)\mathrm{and}\mathcal{P}=\mathcal{L}Q\left(t\right),$$

(20)

then only the total electric dipole moment $\mathcal{P}$ comes into the equations of motion. In the electric dipole limit we thereby have the ordinary differential equation corresponding to a voltage $V\left(t\right)$ driven pendulum with a current output $I\left(t\right)=\dot{Q}\left(t\right)$,

$${\displaystyle \frac{L}{c^2}}\ddot{Q}\left(t\right)+V_{c}sin\left(2\pi {\displaystyle \frac{Q\left(t\right)}{e}}\right)=V\left(t\right),$$

(21)

wherein the antenna inductance $L=\mu \mathcal{L}$, the driving voltage $V\left(t\right)=E\left(t\right)\mathcal{L}$ and the critical voltage is defined $V_c=(2\pi \hslash \overline{\omega }/e)\mathcal{L}$. If the electron oscillations on the straight axis of the antenna have a finite dissipation, increasing the molecular entropy by heating, then phenomenologically a resistance R may be added to the electric dipole antenna model according to $I\left(t\right)=\dot{Q}\left(t\right)$,

$${\displaystyle \frac{L}{c^2}}\ddot{Q}\left(t\right)+R\dot{Q}\left(t\right)+V_{c}sin\left(2\pi {\displaystyle \frac{Q\left(t\right)}{e}}\right)=V\left(t\right).$$

(22)

For the moment, neglecting resistance, the driven electric dipole antenna acts as a quantum electrodynamic circuit described by the ordinary Lagrangian

$$\begin{array}{c}\hfill \mathrm{\Lambda }(\dot{Q},Q)={\displaystyle \frac{L}{2c^2}}{\dot{Q}}^2+{\displaystyle \frac{\mathcal{L}A\dot{Q}}{c}}-\\ \hfill \left({\displaystyle \frac{e{V}_c}{2\pi }}\right)\left[1-cos\left(2\pi {\displaystyle \frac{Q}{e}}\right)\right]\end{array}$$

(23)

in virtue of Eq.(21). The Hamiltonian operator corresponding to the Lagrangian Eq.(23) is canonical,

$$\begin{array}{ccc}& & \mathcal{H}\left({\mathrm{\Phi }}_{ext}\right)={\displaystyle \frac{1}{2L}}{\left(-i\hslash c{\displaystyle \frac{\partial }{\partial Q}}-{\mathrm{\Phi }}_{ext}\right)}^2\hfill \\ & & +\left({\displaystyle \frac{e{V}_c}{2\pi }}\right)\left[1-cos\left(2\pi {\displaystyle \frac{Q}{e}}\right)\right].\hfill \end{array}$$

(24)

Here the driving vector potential is $A={\mathrm{\Phi }}_{ext}/\mathcal{L}$. By wrapping up the linear electric dipole antenna into a loop one obtains the magnetic dipole antennae with a total magnetic moment given by a current area product.

In detail, the external magnetic flux through the loop is given by

$${\mathrm{\Phi }}_{ext}=\oint \mathbf{A}·d\mathbf{r}={\int }_{\mathcal{L}}Ads.$$

(25)

The Schrödinger equation for the loop is given by

$$i\hslash {\displaystyle \frac{\partial \varphi (Q,t)}{\partial t}}=\mathcal{H}\left({\mathrm{\Phi }}_{ext}\right)\varphi (Q,t),$$

(26)

wherein the Hamiltonian is identical to the electric dipole antenna Hamiltonian Eq.(24). However, the magnetic dipole antennae boundary condition defining the geometrical meaning of “loop” is the magnetic dipole boundary periodic condition

$$\varphi (Q+e,t)=\varphi (Q,t)\mathrm{magnetic}\mathrm{dipole}\mathrm{loop}.$$

(27)

In particular, as a consequence of Eq.(27), the energy eigenvalues are periodic in external magnetic flux, i.e.,

$$\begin{array}{c}\hfill \mathcal{H}\left({\mathrm{\Phi }}_{ext}\right){\varphi }_n\left(Q\right)=E_n\left({\mathrm{\Phi }}_{ext}\right){\varphi }_n\left(Q\right),\\ \hfill {\varphi }_n(Q+e)={\varphi }_n\left(Q\right),\\ \hfill E_n({\mathrm{\Phi }}_{ext}+{\mathrm{\Phi }}_0)=E_n\left({\mathrm{\Phi }}_{ext}\right),\end{array}$$

(28)

wherein the flux quantum is given by

$${\mathrm{\Phi }}_0={\displaystyle \frac{2\pi \hslash c}{e}}.$$

(29)

According to present international agreements on SI units, where the electromagnetic charge conversion is exactly 1 emu $\equiv 10$ Coulomb and 1 Tesla $\equiv {10}^4$ Gauss, we have the exact three-unit definitions

$$\begin{array}{ccc}& & c\equiv 2.99792458\times {10}^{10}\mathrm{cm}/\sec ,\hfill \\ & & 2\pi \hslash \equiv 6.62607015\times {10}^{-27}\mathrm{erg}\sec ,\hfill \\ & & {\displaystyle \frac{e}{c}}\equiv 1.602176634\times {10}^{-20}\mathrm{emu}.\hfill \end{array}$$

(30)

The flux quantum is then

$${\mathrm{\Phi }}_0\approx 4.135667697\times {10}^{-7}\mathrm{Gauss}{\mathrm{cm}}^2.$$

(31)

Many distinctive properties of DNA or RNA molecular antennae follow from the periodicities of the circulating currents

$$I_n\left({\mathrm{\Phi }}_{ext}\right)=I_n({\mathrm{\Phi }}_{ext}+{\mathrm{\Phi }}_0).$$

(32)

Eq.(32) follows from

$$I_n\left({\mathrm{\Phi }}_{ext}\right)=-c{\displaystyle \frac{d{E}_n\left({\mathrm{\Phi }}_{ext}\right)}{d{\mathrm{\Phi }}_{ext}}}$$

(33)

in virtue of Eq.(29). The magnetic flux periodicity of circulating currents in molecular dipole antennae arises out of electrodynamic gauge invariance and the Bohm Aharonov effect and is likely to surpass the accuracy of a particular model Hamiltonian such as ours and play a strong role in wireless transmission of information between DNA and/or RNA molecules.

2. Statistical Thermodynamics

Of interest here are electrical and mechanical vibrations that quantize into photons and phonons in the usual manner. Photon-phonon conversions can and do take the form of piezoelectricity that go into the design of ultrasound emitters and absorbers[34]. A simple understanding of piezoelectricity can be obtained by the general principles of statistical thermodynamics. The role of this reasoning is of use for understanding biological piezoelectricity as it occurs in long strands of DNA and RNA due to the lack of chiral (handed) symmetry in helical molecules.

2.1. Quartz Crystal Ultrasound

To get ultrasound generators from a quartz crystal it is sufficient to cleave the crystal so that a given crystal plane appears parallel on two sides of the quartz sample. Then deposit two metallic films, one on each of the opposite flat sides of the quartz sample, forming a circuit capacitor and add equal and opposite charges on the two metallic plates. The thermodynamic equations of state of the capacitor follow from the fundamental law

$$d\mathcal{U}=Td\mathcal{S}+\mathcal{V}dQ+\mathcal{F}dX,$$

(34)

wherein $\mathcal{S}$, Q and X represent, respectively, the capacitor entropy, charge and quartz crystal plane displacement and T, $\mathcal{V}$ , and $\mathcal{F}$ represent, respectively, the capacitor temperature, voltage and force component parallel to the plane displacement that the metallic film exerts on the quartz crystal. Alternatively, one may employ the capacitor enthalpy

$$\begin{array}{ccc}& & \mathcal{W}(\mathcal{S},\mathcal{V},X)=\underset{Q}{min}[\mathcal{U}(\mathcal{S},Q,X)-\mathcal{V}Q],\hfill \\ & & dW=Td\mathcal{S}-Qd\mathcal{V}+\mathcal{F}dX.\hfill \end{array}$$

(35)

The capacitances at constant displacement X and at constant force $\mathcal{F}$ are defined respectively as

$$C_X={\left({\displaystyle \frac{\partial Q}{\partial V}}\right)}_{\mathcal{S},X}\mathrm{and}{C}_{\mathcal{F}}={\left({\displaystyle \frac{\partial Q}{\partial \mathcal{V}}}\right)}_{\mathcal{S},\mathcal{F}}.$$

(36)

Employing the thermodynamic derivative identities

$$\begin{array}{ccc}& & {\left({\displaystyle \frac{\partial Q}{\partial \mathcal{V}}}\right)}_{\mathcal{S},\mathcal{F}}={\left({\displaystyle \frac{\partial Q}{\partial \mathcal{V}}}\right)}_{\mathcal{S},X}+{\left({\displaystyle \frac{\partial Q}{\partial X}}\right)}_{\mathcal{S},\mathcal{V}}{\left({\displaystyle \frac{\partial X}{\partial \mathcal{V}}}\right)}_{\mathcal{S},\mathcal{F}},\hfill \\ & & C_{\mathcal{F}}=C_X-{\left({\displaystyle \frac{\partial Q}{\partial X}}\right)}_{\mathcal{S},\mathcal{V}}{\left({\displaystyle \frac{\partial X}{\partial \mathcal{F}}}\right)}_{\mathcal{S},\mathcal{V}}{\left({\displaystyle \frac{\partial \mathcal{F}}{\partial \mathcal{V}}}\right)}_{\mathcal{S},X},\hfill \\ & & C_{\mathcal{F}}=C_X+{\displaystyle \frac{{\mathrm{\Lambda }}_{\mathcal{S}}^2}{K_{\mathcal{S}}}},\hfill \end{array}$$

(37)

wherein the adiabatic piezoelectric coefficient is defined by a Maxwell relation for the enthalpy Eq.(35)

$${\mathrm{\Lambda }}_{\mathcal{S}}={\left({\displaystyle \frac{\partial Q}{\partial X}}\right)}_{\mathcal{S},\mathcal{V}}=-{\left({\displaystyle \frac{\partial \mathcal{F}}{\partial \mathcal{V}}}\right)}_{\mathcal{S},X}.$$

(38)

The thermodynamic adiabatic static Hook’s law spring constant for the vibrational quartz mode is defined as

$${\mathcal{K}}_{\mathcal{S}}={\left({\displaystyle \frac{\partial \mathcal{F}}{\partial X}}\right)}_{\mathcal{S},\mathcal{V}}.$$

(39)

The central result of this section is that a measured capacitance of the quartz filled capacitor is a circuit parallel connection between two capacitors: (i) a capacitance $C_X$ wherein the position of the vibrational mode is clamped and (ii) an elastic capacitance

$$\begin{array}{ccc}& & C_{\mathcal{F}}=C_X+C_{\mathrm{elastic}},\hfill \\ & & C_{\mathrm{elastic}}={\displaystyle \frac{{\mathrm{\Lambda }}_{\mathcal{S}}^2}{{\mathcal{K}}_{\mathcal{S}}}},\hfill \end{array}$$

(40)

adding capacitance for the parallel circuit connection. Using a damped harmonic oscillator model for the quartz vibrational phonon mode, yields a complex frequency dependent elastic electrical engineering capacitance

$$\begin{array}{ccc}& & \mathcal{M}\delta \ddot{X}\left(t\right)+\mathcal{R}\delta \dot{X}\left(t\right)+{\mathcal{K}}_{\mathcal{S}}\delta X\left(t\right)=\delta \mathcal{F}\left(t\right),\hfill \\ & & C_{\mathrm{elastic}}\left(\omega \right)={\displaystyle \frac{{\mathrm{\Lambda }}_{\mathcal{S}}^2}{{\mathcal{K}}_{\mathcal{S}}-i\omega \mathcal{R}-{\omega }^2\mathcal{M}}},\hfill \\ & & C_{\mathrm{elastic}}\left(\omega \right)={\displaystyle \frac{{\omega }_0^2{C}_{\mathrm{elastic}}}{{\omega }_0^2-i\mathrm{\Gamma }\omega -{\omega }^2}}.\hfill \end{array}$$

(41)

wherein $\mathcal{M}$ is the mass of the vibrational mode and $\mathcal{R}$ is the mechanical acoustic impedance of the vibrational mode. The frequency ${\omega }_0$ of the quartz phonon mode and the inverse phonon lifetime ${\tau }_{phonon}^{-1}=\mathrm{\Gamma }$ are determined in mechanical engineering terms by

$${\omega }_0=\sqrt{{\displaystyle \frac{{\mathcal{K}}_{\mathcal{S}}}{\mathcal{M}}}}\mathrm{and}\mathrm{\Gamma }={\displaystyle \frac{\mathcal{R}}{\mathcal{M}}}.$$

(42)

The frequency dependent circuit admittance of the fixed displacement capacitance connected in parallel with the elastic mode capacitance is

$$\begin{array}{ccc}& & Y\left(\omega \right)=-i\omega \left[C_X+C_{\mathrm{elastic}}\left(\omega \right)\right],\hfill \\ & & Y\left(\omega \right)=-i\omega \left[C_X+{\displaystyle \frac{{\omega }_0^2{C}_{\mathrm{elastic}}}{{\omega }_0^2-i\mathrm{\Gamma }\omega -{\omega }^2}}\right],\hfill \\ & & \Re eY\left(\omega \right)={\omega }_0^2\mathrm{\Gamma }\left[{\displaystyle \frac{\omega }{{({\omega }^2-{\omega }_0^2)}^2+{\omega }^2{\mathrm{\Gamma }}^2}}\right]C_{\mathrm{elastic}}.\hfill \end{array}$$

(43)

If a voltage source ${\mathcal{V}}_{\omega }$ at frequency $\omega$ is placed across the quartz crystal filled capacitor, then the dissipated power $P\left(\omega \right)=|{\mathcal{V}}_{\omega }{|}^2\Re eY\left(\omega \right)$ is mostly due to a sharp phonon peak as described by Eq.(43). The dissipative power mostly goes into phonon radiation from the quartz mechanical oscillator that becomes a source of ultrasound at a sharp frequency. Let us now apply similar thermodynamic arguments to long DNA and RNA molecules as we have above reviewed for standard ultrasonic crystal sources.

2.2. DNA and RNA Piezoelectricity

For describing the piezoelectric effect in DNA and RNA molecules, start from the dipole moment enthalpy

$$\begin{array}{ccc}& & \tilde{\mathcal{W}}=\underset{Q}{min}\left[\mathcal{U}(S,\mathcal{L},\mathcal{P},{\mathcal{N}}_1,\dots ,{\mathcal{N}}_f)-E\mathcal{P}\right],\hfill \\ & & \tilde{\mathcal{W}}=\tilde{\mathcal{W}}(S,\mathcal{L},E,{\mathcal{N}}_1,\dots ,{\mathcal{N}}_f),\hfill \\ & & d\tilde{\mathcal{W}}=Td\mathcal{S}+\tau d\mathcal{L}-\mathcal{P}dE+\sum _{a=1}^f{\mu }_{a}d{\mathcal{N}}_a,\hfill \\ & & \tilde{\mathcal{W}}=T\mathcal{S}+\tau \mathcal{L}+\sum _{a=1}^f{\mu }_a{\mathcal{N}}_a.\hfill \end{array}$$

(44)

With $\mathcal{N}={\sum }_{a=1}^f{\mathcal{N}}_a$. The intensive per constituent particles are defined as

$$\begin{array}{ccc}& & x_a={\displaystyle \frac{{\mathcal{N}}_a}{\mathcal{N}}},\sum _{a=1}^f{x}_a=1,\hfill \\ & & \tilde{w}={\displaystyle \frac{\tilde{\mathcal{W}}}{\mathcal{N}}},\tilde{s}={\displaystyle \frac{\tilde{\mathcal{S}}}{\mathcal{N}}},l={\displaystyle \frac{\tilde{\mathcal{L}}}{\mathcal{N}}},\tilde{p}={\displaystyle \frac{\tilde{\mathcal{P}}}{\mathcal{N}}}=lQ,\hfill \\ & & \tilde{w}=T\tilde{s}+\tau l+\sum _{a=1}^f{\mu }_a{x}_a,\hfill \end{array}$$

(45)

in vitue of which

$$d\tilde{w}=Td\tilde{s}+\tau dl-\tilde{p}dE+\sum _{a=1}^f{\mu }_{a}d{x}_a.$$

(46)

2.2.1. Static Piezoelectricity

The static adiabatic piezoelectric coefficient of a long polymer molecule is defined as

$${\lambda }_{\tilde{s}}={\left({\displaystyle \frac{\partial \tau }{\partial E}}\right)}_{\tilde{s},l,\mathbf{x}}=-{\left({\displaystyle \frac{\partial \tilde{p}}{\partial l}}\right)}_{\tilde{s},E,\mathbf{x}},$$

(47)

wherein a Maxwell relation implicit in Eq.(46) has been employed. Two molecular polarizability coefficients may be defined (i) at constant molecular tension $\tau$ and (ii) at constant molecular length l; They are, respectively,

$${\alpha }_{\tau }={\left({\displaystyle \frac{\partial \tilde{p}}{\partial E}}\right)}_{\tilde{s},\tau ,\mathbf{x}}\mathrm{and}{\alpha }_l={\left({\displaystyle \frac{\partial \tilde{p}}{\partial E}}\right)}_{\tilde{s},l,\mathbf{x}}.$$

(48)

The difference in partial differentials is evidently

$$\begin{array}{ccc}& & {\alpha }_{\tau }={\alpha }_l+{\left({\displaystyle \frac{\partial \tilde{p}}{\partial l}}\right)}_{\tilde{s},l,\mathbf{x}}{\left({\displaystyle \frac{\partial l}{\partial E}}\right)}_{\tilde{s},\tau ,\mathbf{x}},\hfill \\ & & {\alpha }_{\tau }={\alpha }_l-{\left({\displaystyle \frac{\partial \tilde{p}}{\partial l}}\right)}_{\tilde{s},l,\mathbf{x}}{\left({\displaystyle \frac{\partial l}{\partial \tau }}\right)}_{\tilde{s},E,\mathbf{x}}{\left({\displaystyle \frac{\partial \tau }{\partial E}}\right)}_{\tilde{s},l,\mathbf{x}},\hfill \\ & & {\alpha }_{\tau }={\alpha }_l+{\displaystyle \frac{{\lambda }_{\tilde{s}}^2}{{\kappa }_{\tilde{s}}}},\hfill \end{array}$$

(49)

wherein the Hooke law adiabatic spring constant ${\kappa }_{\tilde{s}}$ per molecule for a long molecule is defined by

$${\kappa }_{\tilde{s}}={\left({\displaystyle \frac{\partial \tau }{\partial l}}\right)}_{\tilde{s},E,\mathbf{x}}.$$

(50)

The fundamental thermodynamics for piezoelectricity in long DNA or RNA molecular polarizability,

$${\alpha }_{\tau }={\alpha }_l+{\alpha }_{\mathrm{elastic}}\mathrm{wherein}{\alpha }_{\mathrm{elastic}}={\displaystyle \frac{{\lambda }_{\tilde{s}}^2}{{\kappa }_{\tilde{s}}}},$$

(51)

plays the same role in long polymer piezoelectric physics that Eq. (40) plays for quartz piezoelectricity.

Classical thermal fluctuations in the molecular tension obey

$$\begin{array}{ccc}& & \overline{\Delta {\tau }^2}={\displaystyle \frac{k_{B}T}{\mathcal{N}}}{\left({\displaystyle \frac{\partial \tau }{\partial l}}\right)}_{\tilde{s},E,\mathbf{x}}=k_{B}T\left({\displaystyle \frac{{\kappa }_{\tilde{s}}}{\mathcal{N}}}\right),\hfill \\ & & \overline{\Delta {\tau }^2}=k_{B}T{\left({\displaystyle \frac{\partial \tau }{\partial \mathcal{L}}}\right)}_{\mathcal{S},E,{\mathcal{N}}_1,\dots ,{\mathcal{N}}_f}=k_{B}T{\mathcal{K}}_{\mathcal{S}},\hfill \end{array}$$

(52)

wherein the overall adiabatic spring constant of the molecule is inversely proportional to the number of constituent molecules ${\mathcal{K}}_{\mathcal{S}}={\kappa }_{\tilde{s}}/\mathcal{N}$. On the other hand, the mode mass for a homogeneous slinky-worm oscillation is extensive, $\mathcal{M}=\mathcal{N}{m}_0$, where $m_0$ is the order of the mean molecular mass. This means that the frequency of the homogeneous compression mode is given by

$$\mathrm{\Omega }=\sqrt{{\displaystyle \frac{{\mathcal{K}}_{\mathcal{S}}}{\mathcal{M}}}}={\displaystyle \frac{{\omega }_0}{\mathcal{N}}}\to 0\mathrm{as}\mathcal{N}\to \infty .$$

(53)

Given the virtually zero frequency of the homogeneous longitudinal dissipation, the mode is completely dissipative.

2.2.2. Vibrational Dissipation

For mechanical vibrations coupling into antennae currents via piezoelectric coefficients, an engineering approach may generalize the static quartz oscillator coupling Eq.(40) that in dynamic situations reads as Eq.(41). The close analogy is that the dynamic engineering dynamical version of Eq.(51) is given by

$${\alpha }_{\tau }={\alpha }_l+{\alpha }_{\mathrm{elastic}}\sum _j\left[{\displaystyle \frac{f_j{\omega }_j^2}{{\omega }_j^2-i{\mathrm{\Gamma }}_j-{\omega }^2}}\right],$$

(54)

wherein the sum is over mechanical modes described by damped harmonic oscillators with oscillator strengths $f_j>0$ that sum to unity, i.e., ${\sum }_j{f}_j=1$. In Eq.(54), ${\omega }_j$ represents the mechanical resonance frequency of the phonon and ${\mathrm{\Gamma }}_j$ represents the transition rate per unit time that the phonon is absorbed as heat energy into other degrees of freedom. One may introduce a damping force correlation time ${\tau }_j$ of the random force from these other degrees of freedom that damp the mechanical oscillation according to Fermi’s golden rule

$$\begin{array}{ccc}& & {\mathrm{\Gamma }}_j={\displaystyle \frac{2\pi }{\hslash }}{|\hslash {\omega }_j|}^2\left({\displaystyle \frac{{\tau }_j}{2\pi \hslash }}\right),\hfill \\ & & {\mathrm{\Gamma }}_j={\omega }_j^2{\tau }_j\Rightarrow {\displaystyle \frac{{\mathrm{\Gamma }}_j}{{\omega }_j}}={\omega }_j{\tau }_j.\hfill \end{array}$$

(55)

Eq.(54 describes how the mechanical modes enter into the electrodynamic properties of DNA and RNA antennae only if the modes are lightly damped, ${\omega }_j{\tau }_j\ll 1$. If the phonon modes are very highly damped by viscous forces then Eq.(54) is not adequate. The physical principles follow below.

Consider the original Stokes problem i.e., damping from a solid surface in contact with a viscous fluid. Consider the formally infinite surface problem wherein the solid is in the half space $z<0$, the viscous fluid is in the half space $z>0$, and the oscillation of the solid surface is in the x-direction. If $v_x(z,t)$ is the only non-zero fluid velocity component in the fluid mechanical Navier Stokes equations, then the velocity $V\left(t\right)$ and the force per unit area that the fluid exerts on the solid surface $F\left(t\right)$ obey, respectively,

$$\begin{array}{ccc}& & V\left(t\right)=\underset{z\to 0^{+}}{lim}{v}_x(z,t)\mathrm{and}\hfill \\ & & F\left(t\right)=-\eta \underset{z\to 0^{+}}{lim}\left({\displaystyle \frac{\partial v_x(z,t)}{\partial z}}\right).\hfill \end{array}$$

(56)

The velocity diffusion equation with viscosity $\eta$ and mass density $\rho$ is here written within the fluid as

$$\rho {\displaystyle \frac{\partial v_x(z,t)}{\partial t}}=\eta {\displaystyle \frac{{\partial }^2{v}_x(z,t)}{\partial z^2}}.$$

(57)

In virtue of the fractional derivative identities[35] one may take the “operator square root” of Eq.(57)

$$\sqrt{\rho {\displaystyle \frac{\partial }{\partial t}}}{v}_x(z,t)=\sqrt{\eta }{\displaystyle \frac{\partial v_x(z,t)}{\partial z}},$$

(58)

yielding the force per unit area as a functional of the sliding surface velocity,

$$\begin{array}{ccc}& & F\left(t\right)=-\sqrt{\rho \eta }\left[\sqrt{{\displaystyle \frac{\partial }{\partial t}}}\right]V\left(t\right),\hfill \\ & & F\left(t\right)=-\sqrt{\rho \eta }\left[\sqrt{{\displaystyle \frac{1}{\pi }}}{\int }_0^{\infty }{\displaystyle \frac{ds}{\sqrt{s}}}{e}^{-s\partial /\partial t}\right]V\left(t\right),\hfill \\ & & {\displaystyle \frac{F\left(t\right)}{\rho }}=-\sqrt{{\displaystyle \frac{\nu }{\pi }}}{\int }_0^{\infty }{\displaystyle \frac{ds}{\sqrt{s}}}V(t-s),\hfill \end{array}$$

(59)

wherein $\eta =\rho \nu$ in virtue of Eq.(56) and the evaluation of the integral $\sqrt{\pi a}={\int }_0^{\infty }{e}^{-as}ds/\sqrt{s}$.

The drag force per unit surface area [$F\left(t\right)]$ is a nonlocal in time functional of the surface velocity $V\left(t\right)$ for an incompressible fluid with kinematic viscosity $\nu$. The kinematic viscosity represents the diffusion of liquid vorticity at a rate in water of

$$\nu \approx {10}^{-2}{\displaystyle \frac{{\mathrm{cm}}^2}{\sec }}={10}^4\mathrm{Hz}\times {\left(10\mathrm{micron}\right)}^2\left(\mathrm{water}\right).$$

(60)

For a distance $\sim 10$ micron say within a biological cell, for many types of cells, the mechanical modes exhibit strongly viscous damping for frequencies $\omega <$ 10 kHz. The strong damping leads to fractional exponent in the imaginary part of the dielectric response $\sim {\omega }^{-1/2}$ as $\omega \to 0$. Confinement geometries more generally lead to dynamic fractional exponents $\sim {\omega }^{-z}$ as $\omega \to 0$, even in pure water wherein the extremely high dielectric response as $\omega \to 0$ has a domain size scale of ordered water[21,33].

3. Massive QED Thirring Model

The mass term employing Dirac spinors yields the invariant energy density

$$u_{\mathrm{mass}}=-m_{\mathrm{electron}}{c}^2\overline{\psi }\psi ,$$

(61)

wherein $\psi$ is the electron wave function. If the Dirac matrices are written in the representation in which the left and right chiral matrix is diagonal, then the notion of mass comes from matrix elements that connect right to left chirality. In one spatial dimension, fix the spin and consider the two-element electron wave function for left- and right-handed electrons,

$$\psi =\left(\begin{array}{c}{\psi }_R\\ {\psi }_L\end{array}\right)\mathrm{where}\overline{\psi }\psi ={\psi }_R^{*}{\psi }_L+{\psi }_L^{*}{\psi }_R.$$

(62)

If the left and right amplitudes have phases,

$$\begin{array}{ccc}& & {\psi }_{R,L}=\left|{\psi }_{R,L}\right|e^{i{\theta }_{L,R}}\equiv \sqrt{{\displaystyle \frac{n_{\mathrm{pair}}}{2}}}{e}^{i{\theta }_{L,R}},\hfill \\ & & {\psi }_R^{*}{\psi }_L+{\psi }_L^{*}{\psi }_R=n_{\mathrm{pair}}cos({\theta }_R-{\theta }_L),\hfill \end{array}$$

(63)

where $n_{\mathrm{pair}}=(1/2)\left|{\psi }_R{\psi }_L\right|$ denotes the number of bound particle-hole pairs per unit length. Then the phase difference implicit in Eq.(62)

$${\theta }_R-{\theta }_L=2\pi {\displaystyle \frac{Q}{e}},$$

(64)

yields the energy density

$$u_{\mathrm{mass}}=-\hslash \overline{\omega }cos\left(2\pi {\displaystyle \frac{Q}{e}}\right)$$

(65)

in virtue of quantum phase interference between the left- and right-handed chirality states. In Eq.(65), $m_{\mathrm{electron}}{c}^2{n}_{\mathrm{pair}}=\hslash \overline{\omega }$. A convention adds a constant to this energy to make a model energy density $u\left(Q\right)$,

$$u\left(Q\right)=\hslash \overline{\omega }\left[1-cos\left(2\pi {\displaystyle \frac{Q}{e}}\right)\right],$$

(66)

to employ in the Coleman sine Gordon Lagrangian Eq.(18). This completes our derivation of Coleman’s result that a massive Thirring Fermion model of electrons in a quasi-linear system is equivalent to a sine Gordon Boson model.

4. Slinky Damped Mechanics of the Longitudinal Sound Mode

Here we consider the viscous damping of a pure longitudinal wave in a slinky helix. The viscous damping is mainly due to the electronic viscosity that is in turn caused by the electrical conductivity. The molecular ultrasonic phonon absorption is thereby due to the electronic Landau-Fermi liquid conductivity in a bulk metal[36] but is here is due to the Tomonoga-Luttinger[18,19,20] liquid in DNA or RNA long helical slinky polymer molecules. Thermodynamics, as dictated by Section 2.2.1, is determined by

$$\begin{array}{ccc}& & d\tilde{u}=Td\tilde{s}+Ed\tilde{p}+\sum _{a=1}^f{\mu }_{a}d{x}_a,\hfill \\ & & d\tilde{w}=Td\tilde{s}+\tau dl-\tilde{p}dE+\sum _{a=1}^f{\mu }_{a}d{x}_a,\hfill \end{array}$$

(67)

yielding the thermodynamics identity

$$\begin{array}{ccc}& & {\kappa }_{\tilde{s}}={\left({\displaystyle \frac{\partial \tau }{\partial l}}\right)}_{\tilde{s},E,\mathbf{x}},\hfill \\ & & {\kappa }_{\tilde{s}}={\left({\displaystyle \frac{\partial \tau }{\partial l}}\right)}_{\tilde{s},\tilde{p},\mathbf{x}}+{\left({\displaystyle \frac{\partial \tilde{p}}{\partial l}}\right)}_{\tilde{s},E,\mathbf{x}}{\left({\displaystyle \frac{\partial \tau }{\partial \tilde{p}}}\right)}_{\tilde{s},l,\mathbf{x}},\hfill \\ & & {\kappa }_{\tilde{s}}={\kappa }_{\tilde{s}l}+{\left({\displaystyle \frac{\partial \tilde{p}}{\partial l}}\right)}_{\tilde{s},E,\mathbf{x}}{\left({\displaystyle \frac{\partial \tau }{\partial E}}\right)}_{\tilde{s},l,\mathbf{x}}{\left({\displaystyle \frac{\partial E}{\partial \tilde{p}}}\right)}_{\tilde{s},l,\mathbf{x}},\hfill \\ & & {\kappa }_{\tilde{s}}={\kappa }_{\tilde{s}l}-{\left({\displaystyle \frac{\partial \tau }{\partial E}}\right)}_{\tilde{s},l,\mathbf{x}}^2{\left({\displaystyle \frac{\partial E}{\partial \tilde{p}}}\right)}_{\tilde{s},l,\mathbf{x}},\hfill \\ & & {\kappa }_{\tilde{s}}={\kappa }_{\tilde{s}l}-\left({\displaystyle \frac{{\lambda }_{\tilde{s}}^2}{{\alpha }_l}}\right).\hfill \end{array}$$

(68)

To get the frequency dependent Hooke’s law force constant for a uniform compression or extension in electrical engineering terms, one extends Eq.(68) to the upper half complex frequency plane $\zeta =\omega +i\overline{\omega }$ wherein $\overline{\omega }>0$,

$$\kappa \left(\zeta \right)={\kappa }_{\tilde{s}l}-\left({\displaystyle \frac{{\lambda }_{\tilde{s}}^2}{{\alpha }_l\left(\zeta \right)}}\right).$$

(69)

In terms of the electrical engineering intensive impedance $\mathcal{Z}\left(\zeta \right)$ of the polymer DNA or RNA chain,

$$\begin{array}{c}\hfill \mathcal{Z}\left(\zeta \right)={\displaystyle \frac{i}{\zeta n_{\mathrm{el}}\alpha \left(\zeta \right)}},\\ \hfill \kappa \left(\zeta \right)={\kappa }_{\tilde{s}l}+i\zeta n_{\mathrm{el}}{\lambda }_{\tilde{s}}^2\mathcal{Z}\left(\zeta \right),\end{array}$$

(70)

where $n_{\mathrm{el}}$ is the electron density per unit length of the chain. The ultrasonic attenuation of the thin molecule is determined by

$$\Im m\kappa (\omega +i{0}^{+})=\left(n_{\mathrm{el}}{\lambda }_{\tilde{s}}^2\right)\omega \Re e\mathcal{Z}(\omega +i{0}^{+})$$

(71)

that constitutes the mathematical expression of the physical fact that the piezoelectric coupling allows one to see in the longitudinal sound attenuation, observable by the electrical antenna impedance $\mathcal{Z}(\omega +i{0}^{+})$.

5. Microbe Community Antennae

Microbial communities in the form of films adsorbed on solid substrates live much longer on insulating surfaces than on conducting metallic substances. For example, a community of COVID-19 viruses live typically for a few days on an insulator surface but only a few hours on a metallic surface. This fact makes metallic material insertions of for example copper into cloth hospital face masks of some utility. Microbial communities of electrogenic bacteria adsorbed on a chemical battery cathode employ an insulating adsorption surface although the battery lead cables are eventually metallic. A working hypothesis is that the community of microbes require for healthy living that DNA and RNA antennae within the community constitute a coherent phased array. The dissipative eddy currents within a metal surface will lessen the coherence of the array of antennae. Since the art of experimental biochemistry is closely entwined with the art of fine cooking, those experienced in baking bread should take note that baking yeast has DNA antennae of comparable size to bacteria. Spectroscopic measurements with a radio frequency spectrum analyzer while living processes are under way would be of interest as would other standard Josephson array measurements long understood for superconducting arrays.

Finally, we note the possibility for large electrically connected bacteria communities (say, of millimeters or centimeter scales) of a creation of classical resonating antenna in the order of ($30-300$) GHz (upper end of radio wave frequencies), depending upon the exact size & shape of the community as well as nature of electrical connections within it. See, also the query raised in reference [6].

6. Some Practical Applications

All (past and present) therapeutic methods aimed at the detection or treatment of coronavirus are based on chemicals. We test for it (positive or negative) chemically and hope to cure it with a future vaccine (a chemical/genetic preparation yet to be universally tested).

If and when the virus mutates, another set of chemical protocols for its testing and a hunt for new chemicals as a vaccine shall begin: again and again. But the history of modern medicine tells us that our bio-technology is not so limited.

As discussed here, copious scientific evidence for sonic and low energy electromagnetic signals produced by all biological elements (virus, DNA, bacteria, parasites, cells, etc.) exist; in turn the biological elements are affected by these non-chemical signals as well. A focussed research on distinct sonic & EM signals emitted by life forms can be an important non-invasive weapon in tracing unwanted life forms and a knowledge of their intensity and frequency providing important clues towards their removal. Hence, the objective of the present proposal that is stated below:

Measurements and a catalogue of the intensity and spectrum of these non-chemical signals (along with their careful analysis) is proposed here as a unique biophysical signature of the particular life form. Also, if and when a life form mutates, both the intensity and the frequency of the emitted signal change. Hence, such measurements would provide a dynamic real time recording of the status of the life form. Depending upon the intensity and their frequency, appropriate strategies can be defined for their removal. The relevance of the proposal for the past Covid CV-19 pandemic and its future avatars is obvious.

The sonic frequency of the virus (along with its intensity) can provide its heartbeat and act as a tracing device regarding the nature of the virus in a patient (even if judged asymptomatic through bio-chemical analyses). Ideally, just as the present day pulse and the heartbeat chart (typically between $0.6-2$ Hertz) or the brain wave chart ($\delta ,\vartheta ,\beta ,\alpha$)- waves, spanning between ($3-30$) Hertz and slightly above for gamma- waves) inform a clinician about the status of the general regulatory system of the patient, so can the intensity & the frequency spectrum of a virus (at much higher radio frequencies, in kilo, mega or giga Hertz range), provide yet another useful tool of clear benefit for the clinician and hopefully the patient.

Methodology for measurements of sonic & EM signals -discussed in the present paper- are three fold: (i) absorption of EM radiation by the life form tells us where the peak in frequency is; after which employment of resonant absorption can reduce by a factor of ($2-15$) the amount of radiation required for the removal of unwanted life forms to fall within safety standards; (ii) a designed digital impedance device to cross check against data in (i) above; (iii) in vitro and in vivo animal testing models in collaboration with a company specializing in preparation of vaccines in several locations around the world.

7. Conclusions

Electrogenic micro-organisms live within environments wherein they are wired to one another or are wired to the environmental surfaces. Electronic currents can flow through these wires into and out of biological cells through the cell walls. Of interest in the work described above was the wireless communication that can be radiated from a distance into and out of biological cells wherein the DNA or the RNA molecules can act as antennae that receive or emit radio frequency electromagnetic signals. Alternative to the chemical information carried in the DNA or RNA letter coding, communication information can be carried from a distance in the form of thermodynamic radiation signal entropy. Due to biological piezoelectricity, the electromagnetic radiation is appreciably coupled into ultrasonic acoustic radiation. Thus, electromagnetic as well as acoustic spectroscopy is evidently possible.

The helices or double helices, respectively, within RNA and DNA exhibit chiral symmetry breaking (handedness) as must the electronic energy structure. The electronic structure must also properly require chiral symmetry breaking. The electron as an elementary particle carries two possible spin states ↑ or ↓ as well as two chiral states right R or left L. Thus, we argued, as discovered by Dirac, the electron requires a four-component spinor for its description. These four components are required for describing chiral symmetry breaking even if the electrons have kinetic energies small on the scale of the electron rest mass energy.

DNA and RNA as long polymer molecules are quasi one dimensional. This, coupled with the chiral symmetry breaking, suggested that the electronic structure has the structure of a Tomonaga-Luttinger liquid wherein the particle-hole bound states. The bound state of an electron particle-hole pair is a Boson and the Tomonaga-Luttinger liquid is a condensation of these Bosons in a manner closely analogous to the Bose condensation of particle-particle or hole-hole bound states in a superconductor. In a superconductor the phase of the Bose pairing field gives rise to Josephson effects. In the biological Tomonaga-Luttinger electron liquid we employed the phase difference between right- and left-handed electron components to describe the quantum coherence leading to Josephson effects. In both cases the Josephson effects lead to a quantum pendulum, i.e., a sine Gordon boson field model as first demonstrated by Coleman. The physical principle involved is that Josephson effects occur whenever the coherent quantum liquid is forced to flow through weak links, quantum pendulum dynamics holds sway.

We have begun what we hope will be the beginning of the study of wireless electrodynamic communication between biological cells starting with (say) bacteria or viruses that have DNA or RNA within the cell nucleus. The basic DNA and RNA microbe antennae must be wired in nature as a biological community of coherent phased antenna arrays for appreciable communication information bit-rates radiated through large distances. Arrays of biological weak links might serve that purpose.