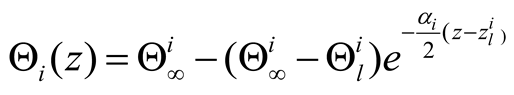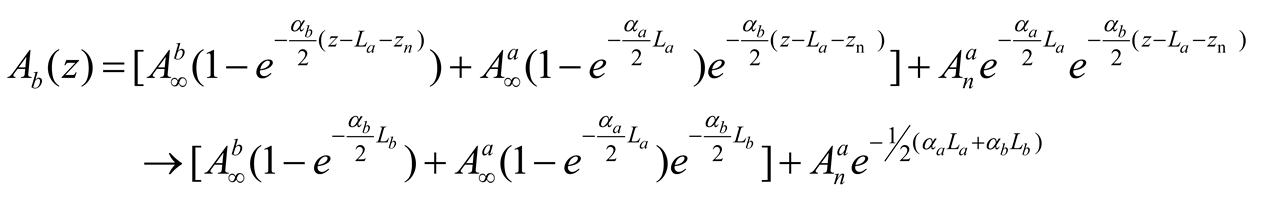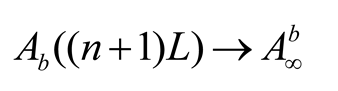Solitons Propagation in Heterogeneous Periodic Media by Tandem Arrangement of Nonlinear Materials

1. Introduction

Nonlinear pulse dynamics has proven itself as a significant area of physics, particularly in the optical regime, where it has found a sensible experimental test bed and practical applications, due to the ready availability of intense coherent light sources and nonlinear materials. The landmarks go from resonant pulse propagation, optical fibers, and self-guiding of light [1,2]. The first optical Solitons in Optics and Photonics were the resonant Temporal Solitons in Self self-induced transparency [3], and that became one of the mainstreams of physical optics. They introduced fundamental concepts such as the area theorem, which is a description of the convergence to the actual soliton eigenvalue, and a thorough analysis of the variety, behavior, and interaction of solitons. Complex coupled soliton systems were also introduced, such as the simultons [4], ancestors of the current quantum security. Since then, most of the attention has been focused on non-resonant solitons such as those produced by intensity nonlinearities. One of their most essential and visible applications, to the ordinary people, has been long-distance optical fiber communications. In these systems, interaction, loss, and periodic amplification of temporal solitons have been thoroughly studied and experimentally demonstrated [5]. A parallel development in spatial solitons has led to a new realm of optical information on self-guiding light, where the interaction between spatial solitons and more complex structures has garnered renewed attention [6,7,8,9,10,11], typically under the ideal conditions of a homogeneous, unlimited medium.

The amplification and loss of temporal solitons, and in general, intense pulse propagation, have received a great deal of attention, particularly for optical communication applications. There, the recovery of the original signal is a priority. To obtain the initial pulse, we can consider that the amplification process is adiabatic [12]. Pulse reshaping, then, is a purely internal nonlinear process that arises from the convergence of the pulse to specific eigenvalues of the nonlinear equation, reaching it as a steady state, characteristic of a given medium. However, the soliton consideration is at a long-distance limit. Therefore, the actual reshaping process has received limited attention. Thus, a periodic array of nonlinear media may freeze such transient behavior into a periodic one. There is an increasing interest in the study of propagation through heterogeneous media, in particular, in periodic arrays or Tandems of media sections larger than the wavelength, or Bragg reflectors [13,14]. On the one hand, this sets the problem beyond the scope of photonic crystals and their coherent reflection and transmission process; therefore, we limit ourselves to the transmission. These periodic heterogeneous systems have garnered significant attention in Nonlinear optics due to their consideration of tandems of quadratic nonlinearities and linear media sections [15], resonant [16,17], including split-step fiber links where Kerr nonlinearities${ \chi }_3$ alternate with linear segments [18]. Some other works included fully nonlinear tandems around a mean value [19] or in the extreme of opposite signs [20,21]. In these tandems, we can find focusing and defocusing effects, a different profile for each nonlinearity [22], or study the solitons as a result of a coupled NLSE [23]. Even when these works refer to a pulsating soliton [24], they do not refer to the essential process of reshaping, other than the tandem modulation. There are also some reviews on the general aspects of this topic [25,26,27,28], and there is a promising experimental potential that still has to be explored more thoroughly [29].

We will describe our tandem as a structure with a period $L=L_a+L_b$, where $L_a$ and $L_b$ are the lengths of each medium are both much larger than a wavelength. Therefore, we disregard the reflected signal. The interaction of a soliton with interfaces has been analyzed [30]; however, the propagation of solitons in different media is becoming increasingly important.

We show in the second section of this work that optical solitons propagate through a nonlinear, periodically stratified medium, where reshaping from medium to medium results in a nonlinear modulation. We also show that it can be locally linearized as a perturbation near a soliton and analytically studied in a two-level atom (TLA) medium. The area theorem is also a straightforward description of the evolution of the resonant eigenvalue, even in the case of more than one medium, and therefore will be the guiding topic of this section. Our idea is to lay the groundwork for understanding more complex, intensity-dependent cases. The third section uses the previous results to describe the soliton continuous reshaping process that occurs in Kerr and photorefractive materials. The pulse amplitude is related to the Kerr eigenvalue, although we do not have an additional description such as the area theorem. Therefore, we should present our findings graphically, and we based our discussion on our results in the resonant case. The reader will corroborate that these graphs are essential to understanding this case. Finally, in the fourth section, we present our conclusions.

2. Resonant Pulse Analysis

The Maxwell-Bloch Equations describe the lossless propagation of near-resonant light pulse propagation in a Two-Level Atoms (TLA) atomic medium, given by:

$$\dot{u}=-\Delta v,$$

(1)

$$\dot{v}=\Delta u+k{}_{E}w,$$

(2)

$$\dot{w}=-k{}^{E}v,$$

(3)

$${\displaystyle \frac{{\partial }^{2}E}{\partial z^2}}-{\displaystyle \frac{1}{c^2}}{\displaystyle \frac{{\partial }^{2}E}{\partial t^2}}=-{\mu }_0{\displaystyle \frac{{\partial }^{2}P}{\partial t^2}},$$

(4)

where $u$ and $v$ are the in and out of quadrature dipole terms, $w$ is the atomic inversion. Δ is the atomic detuning, Ω = 2dE is the Rabi Frequency. Θ usually express the area of the pulse, but in fact, it corresponds to the area of the Rabi frequency area, and in this work, this will be a substantial difference.

$$\Theta \left(z,t\right)={}^{{\displaystyle {\int }_{-\infty }^t\Omega \left(z,t\text{'}\right)dt\text{'}=}}2dA\left(z,t\right),$$

(5)

there $A\left(z,t\right)={\displaystyle {\int }_{-\infty }^{t}E\left(z,t\text{'}\right)dt\text{'}}$ is the actual area of the pulse, which satisfies the equation:

$${\displaystyle \frac{d\Theta }{dz}}=-{\displaystyle \frac{\alpha }{2}}Sen\Theta ,$$

(6)

where both $d$ and the absorption coefficient α depend on the material. The well-known area theorem describes the solution of Equation (5) depicted in Figure 1 as a function of z and Θ for that material.

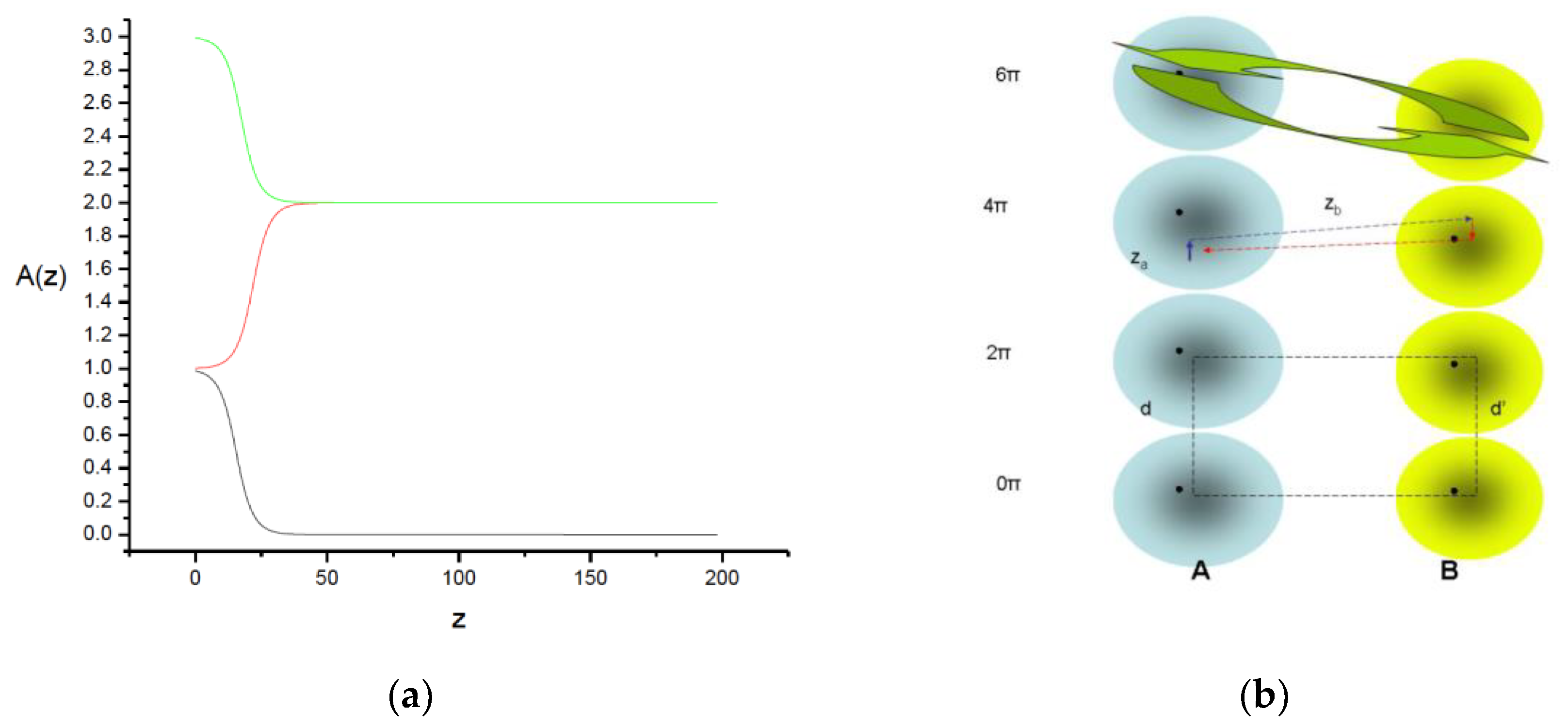
The soliton spectrum behaves as a collection of equally spaced attractors surrounded by their basins of attraction, without any overlap, which also corresponds to the corresponding branches of the area theorem. The propagation of two Different TLA materials, A and B, is shown pictorially in Figure 1b. While their spectra are the same, they are not identical. Their scaling is different because of the different dipole constant; however, they still will correspond to 0π, 2π, 4π, … attractors. The pulse-reshaping that occurs in material A depends on its initial value. This fact restricts its evolution to an attractor or branch in the area diagram. The evolution through a distance$L_a$ (thick arrow in A) results in a value Θ when it is interrupted by the change of materials, and then it turns into a new initial value for the material B (broken arrow). There, the new material coefficients produce a new reshaping process through a distance $L_b$, starting all over again. The continuous process, back and forth between the two spectra, corresponds to a periodic propagation in two different TLA materials, and corresponds to the solution of the equations:

$${\displaystyle \frac{d{\Theta }_a}{dz}}=-{\displaystyle \frac{{\alpha }_a}{2}}Sen{\Theta }_a, \mathrm{ }\mathrm{z}\mathrm{n}=\mathrm{ }\mathrm{n}\mathrm{L}\mathrm{ }<\mathrm{ }\mathrm{z}\mathrm{ }\le \mathrm{ }\mathrm{n}\mathrm{L}\mathrm{ }+\mathrm{ }\mathrm{L}\mathrm{a},\mathrm{ }\mathrm{ }\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\mathrm{ }\mathrm{L}\mathrm{ }=\mathrm{ }\mathrm{L}\mathrm{a}\mathrm{ }+\mathrm{ }\mathrm{L}\mathrm{b}.$$

(7)

$${\displaystyle \frac{d{\Theta }_b}{dz}}=-{\displaystyle \frac{{\alpha }_b}{2}}Sen{\Theta }_b,\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{n}\mathrm{L}\mathrm{ }+\mathrm{ }\mathrm{L}\mathrm{a}\mathrm{ }<\mathrm{ }\mathrm{z}\mathrm{ }\le \mathrm{ }(\mathrm{n}+1)\mathrm{L}.$$

(8)

In the $n+1$ period. If both areas’ initial values are such that ${\mathsf{\Theta }}_a$, ${\mathsf{\Theta }}_b$ << π, then both can be linearized and both will satisfy Beers law ${\Theta }_a={\Theta }_a^0{\mathrm{e}}^{-{\displaystyle \frac{{\alpha }_a}{2}}z}$and ${\Theta }_b={\Theta }_b^0{\mathrm{e}}^{-{\displaystyle \frac{{\alpha }_b}{2}}z}$, where ${\Theta }_b^0={\Theta }_a^0{\mathrm{e}}^{-{\displaystyle \frac{{\alpha }_a}{2}}{L}_a}$. This decay discontinuity produces a stepwise exponential decay that converges to the single identical attractor 0π.

In the case of propagation near a higher-order attractor, we can linearize these equations, which represents an attractive problem of perturbation near a soliton eigenvalue. Then it is simplified by the description of the eigenvalue provided by Equations (7) and (8). We can rewrite the soliton solution for the media $i = a,b$ in the slab $L$ as

$${\Theta }_i={\Theta }_{\infty }^i+{\theta }_i$$

(9)

$${\displaystyle \frac{\partial }{\partial z}}{\theta }_i=-{\displaystyle \frac{\alpha }{2}}\sin {\theta }_i\simeq -{\displaystyle \frac{\alpha }{2}}{\theta }_i\mathrm{for}{\theta }_{\mathrm{i}}<<{\Theta }_{\infty }$$

The solution for Equation (9) is given by:

(10)

where we can quickly recognize that the sign of the term ${(\mathsf{\Theta }}_{\infty }^i-{\mathsf{\Theta }}_l^i)$ corresponds, in the positive case, to the convergence of the steady state from below in the graphical representation of the area theorem. In the negative case, to an analog of the decay of the Beers law. If the description considers the terms of the pulse area that is continuous between the different media, for a specific period, we can rewrite it as:

$$A^a(z)=A_{\infty }^a(1-e^{-{\displaystyle \frac{{\alpha }_i}{2}}(z-z_n)})+A_n^a{e}^{-{\displaystyle \frac{{\alpha }_i}{2}}(z-z_n)}$$

(11)

The solution in the first medium, where ${\Theta }_{\infty }^i=2\pi =2d_i{A}_i$ and $i = a,b$. $A_n$ is the initial value in the $nth$ period and $z_n=nL$ is the previous distance in $n$ number of periods. In the second medium $z=z_n+L_a$, the corresponding expression is given by:

(12)

In the second line, we have written the expression at the end of that period. Suppose we consider long material conditions; i.e., ${\alpha }_i{L}_i>>1$ y ${\alpha }_j{L}_j>>1$, we are describing a sequence that selectively oscillates, without mixing the information of the two solitons, and its behavior will be strictly periodic, as depicted in Figure 2.

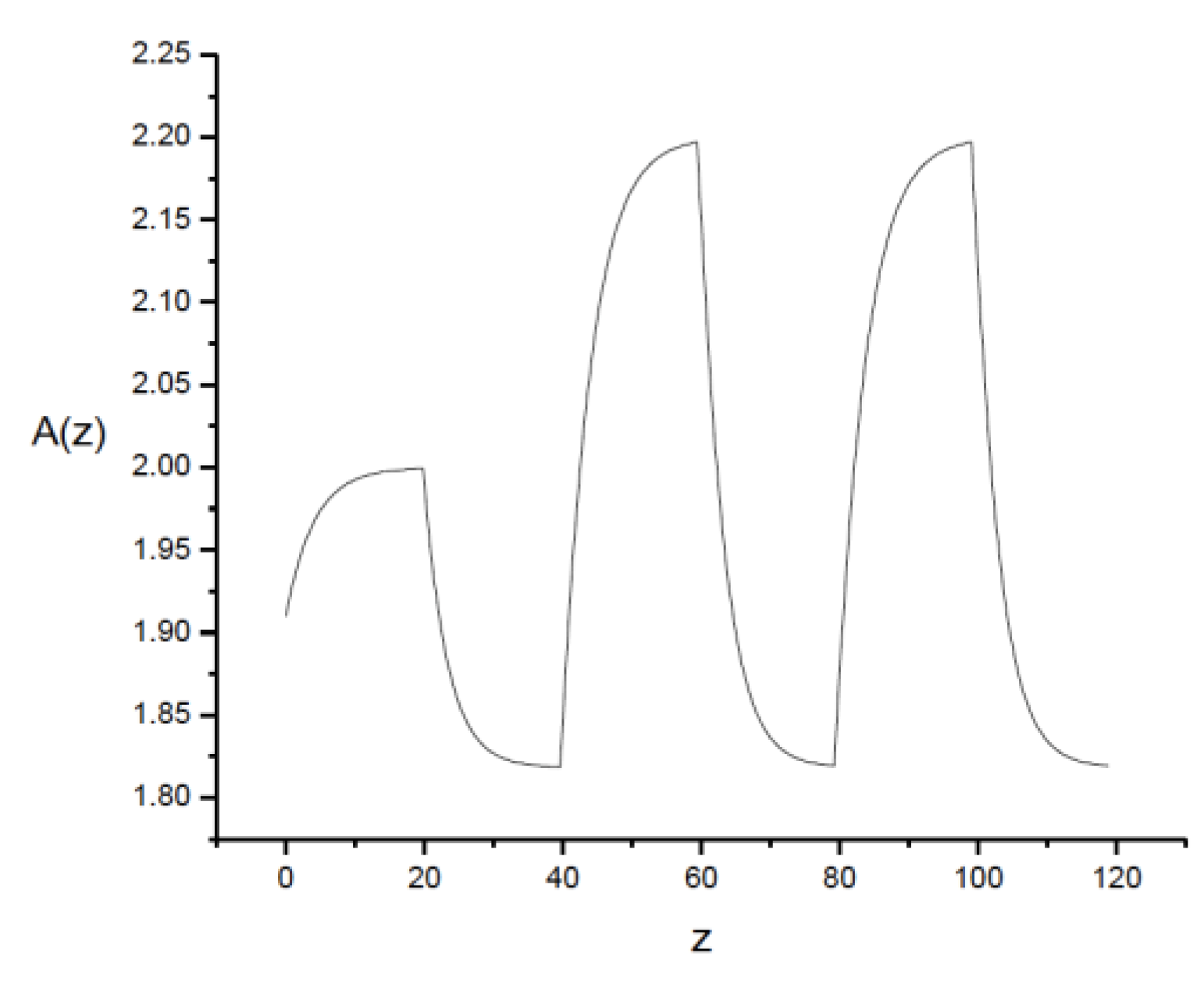
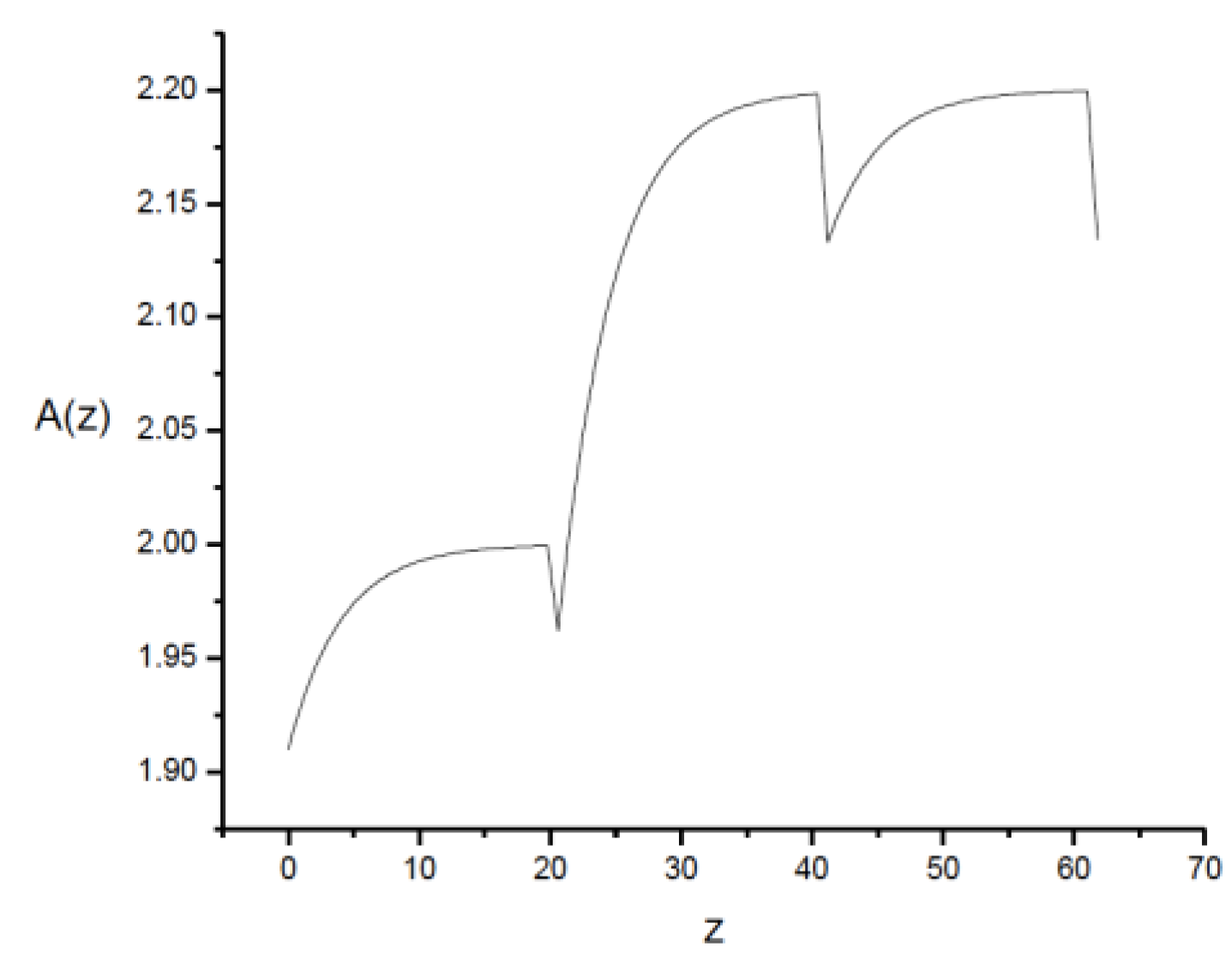
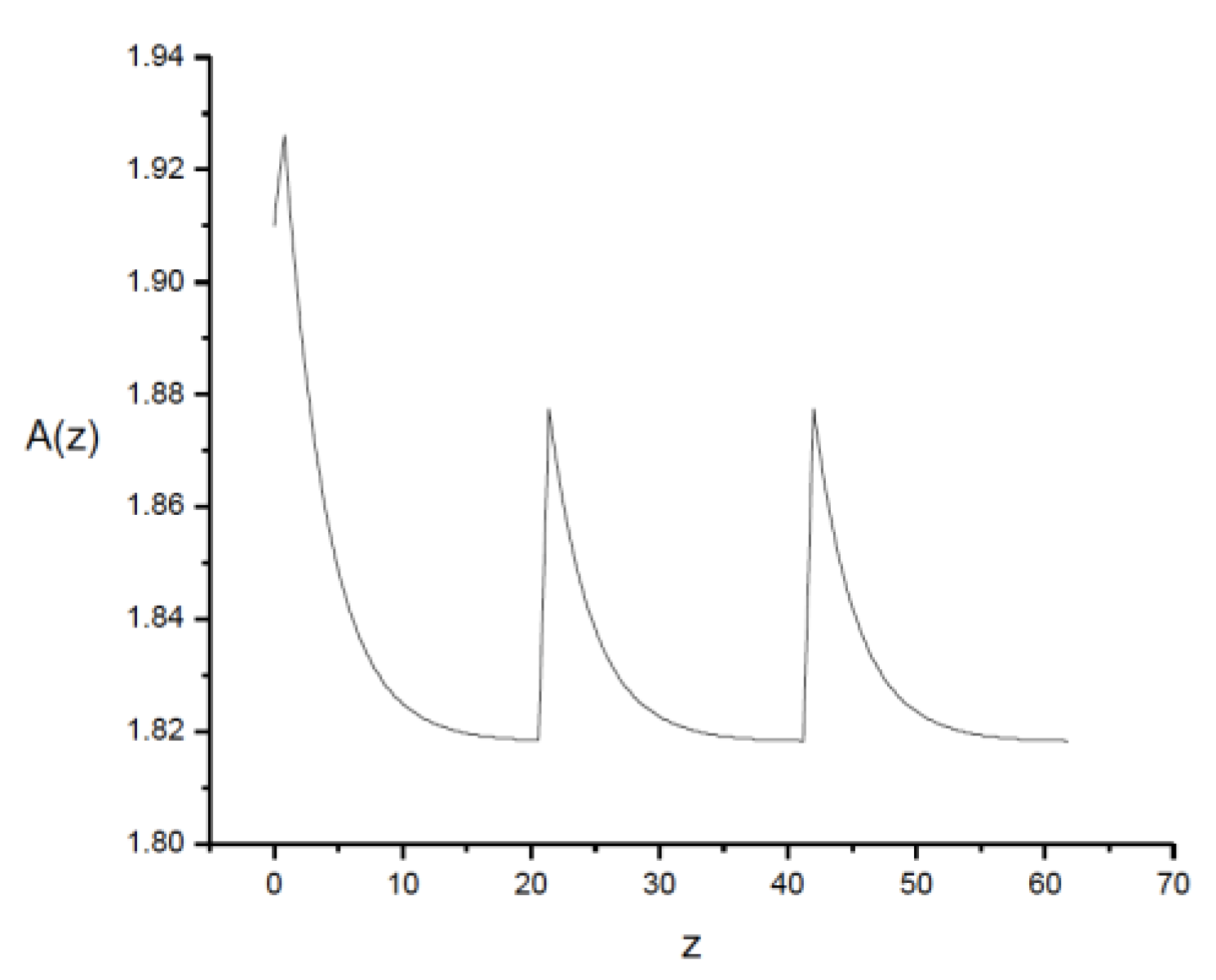
At the end of each period, the area will reach a value of $A_{\infty }^b$. However, if one medium is small, the enunciated conditions are not satisfied for that medium, although they are satisfied by the other one, which will lead to a periodic behavior, as can be seen in Figure 3 and Figure 4.

If ${\alpha }_a{L}_a>>1$ and ${\alpha }_b{L}_b\le 1$

$$A_b((n+1)L)\to [A_{\infty }^b(1-e^{-{\displaystyle \frac{{\alpha }_b}{2}}{L}_b})+A_{\infty }^a{e}^{-{\displaystyle \frac{{\alpha }_b}{2}}{L}_b}]$$

(13)

If ${\alpha }_b{L}_b>>1$ and ${\alpha }_a{L}_a\le 1$

(14)

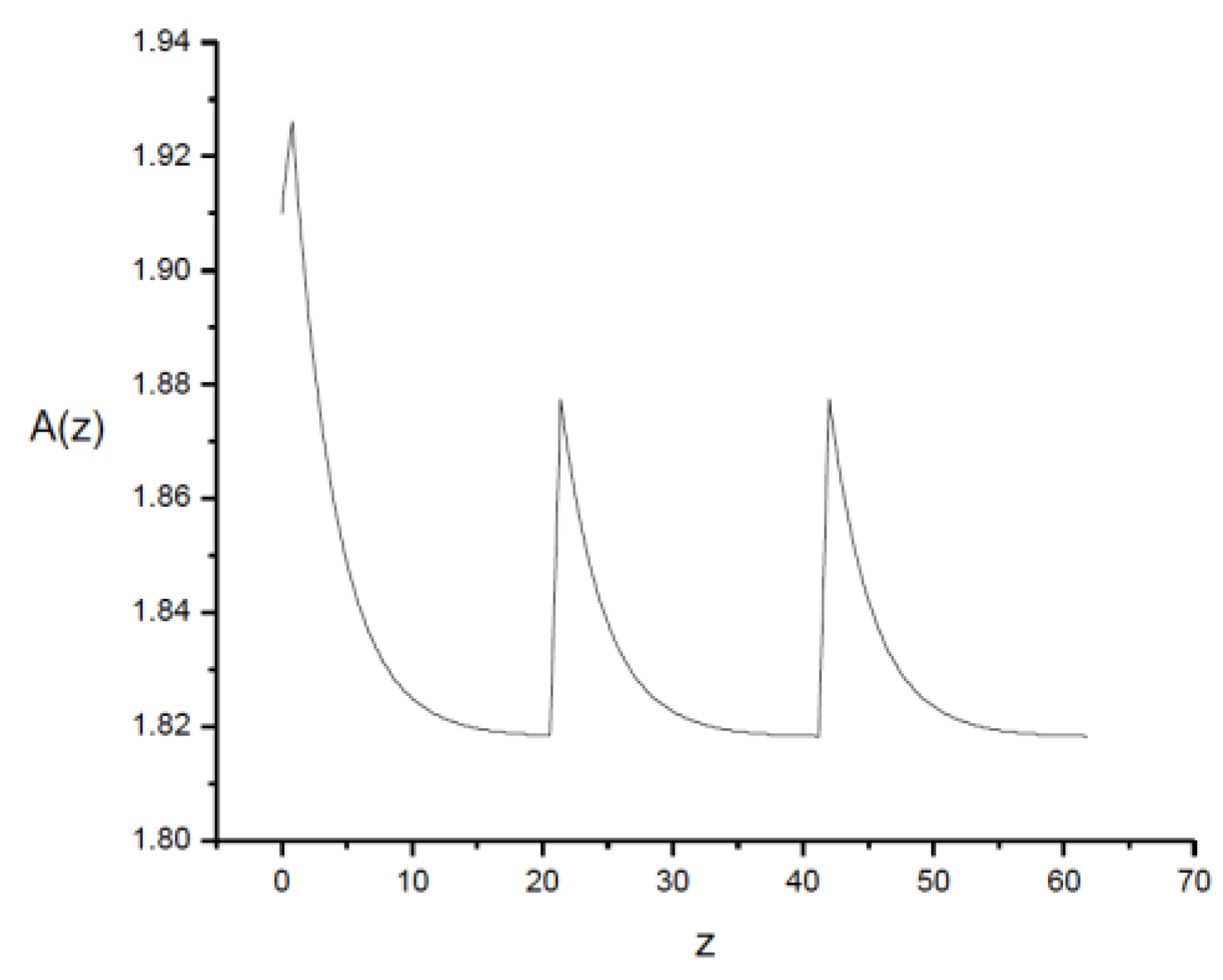
Finally, if both media are small, i.e., if ${\alpha }_a{L}_a<<1$ and ${\alpha }_b{L}_b<<1$ then, there is a clear memory of the initial conditions in the period, losing the periodicity, Figure 5,

We take Equation (15) to perform numerical simulations, setting the following: ${\alpha }_a=1g$ values, ${\alpha }_b=1.21{\alpha }_a (d_a=1), d_b=1.1d_a$. We also want to remark that we changed only the width of the slab. The input area has been set to six rad for all sequences.

$$A_b(nL)\approx A_0^a+{\displaystyle \frac{n}{2}}({\alpha }_b{L}_b{A}_{\infty }^b+{\alpha }_a{L}_a{A}_{\infty }^a)$$

(15)

We explored the oscillation near the same soliton eigenvalues, and we can rely on the stability of the propagation. However, there are a large number of possibilities where these conditions will not be satisfied and where we will need to consider in detail the resonant solitons behavior. For example, the case of 4π solitons tends to break into two 2π solitons, and those are somewhat sturdy, as well as there is a rich collection of 0π pulses, whose coupling will add additional features worth exploring by the adequate atomic systems. That may include the current interest in V and Λ atomic systems. We can find different works showing the behavior of the pulse itself, such as amplitude, width, and energy.

3. Photorefractive-Kerr Analysis

In this section, we numerically study the behavior of a soliton subject to a periodic sudden profile reshaping due to the change of the propagation material. The nonlinear materials involved here were photorefractive and Kerr nonlinearity type, where we had studied the photorefractive-photorefractive, photorefractive-Kerr, and Kerr-Kerr cases. The evolution into the corresponding soliton is a possibility if we provide a sufficient distance in each region. However, the Kerr soliton is much more complicated. The interference of the reshaping with this behavior leads to a much more complex dynamics, and we present here only the results for the case of Kerr-Kerr periodic media.

Because of space, we will assume that the two media have the same dimension, i.e., $L=2L_a$ and $L_a=L_b$. The sudden changes of material correspond to a step-like distribution of the Kerr constant. The equation we must solve for each material is the well-known Nonlinear Schrödinger Equation, given by:

$$i{\displaystyle \frac{\partial E}{\partial Z}}={\displaystyle \frac{1}{4}}{\displaystyle \frac{{\partial }^{2}E}{\partial X^2}}+{\eta }_a{\left|E\right|}^{2}E, z=nL<z\le nL+L_a \mathrm{where} L=L_a+L_b$$

(16)

$$i{\displaystyle \frac{\partial E}{\partial Z}}={\displaystyle \frac{1}{4}}{\displaystyle \frac{{\partial }^{2}E}{\partial X^2}}+{\eta }_b{\left|E\right|}^{2}E, nL+L_a<z\le (n+1)L$$

(17)

where ${\omega }_o$ represents the original width of the beam and, $A_o$ is the initial amplitude of the complex envelope of the field. We normalize the propagation variable Z regarding the diffraction length, $L_D=k{\omega }_o^2/2$ by $z=L_{D}Z$ and assigned the normalized transverse variable, and X, regarding the initial beam width, ${\omega }_o$ , by ${x=\omega }_{o}X$, the field amplitude $A$ was also normalized in terms of the initial field amplitude $A=A_{o}E$, using diffraction lengths as $z=k{\omega }_o^{2}Z/2$. Furthermore, we can write the nonlinear length as a function of initial field intensity and the nonlinear refraction index for “ith” media; then this length takes the form$L_{n{L}_i}=n_o/k{n}_{2i}{\left|A_o\right|}^2$ , where finally the nonlinear constant for the i-media is given by $n_i=k^2{\omega }_o^2{n}_{2i}{\left|A_o\right|}^2/{2n}_0=L_D/L_{NL}=P_0/P_c$, where $i=a,b$.

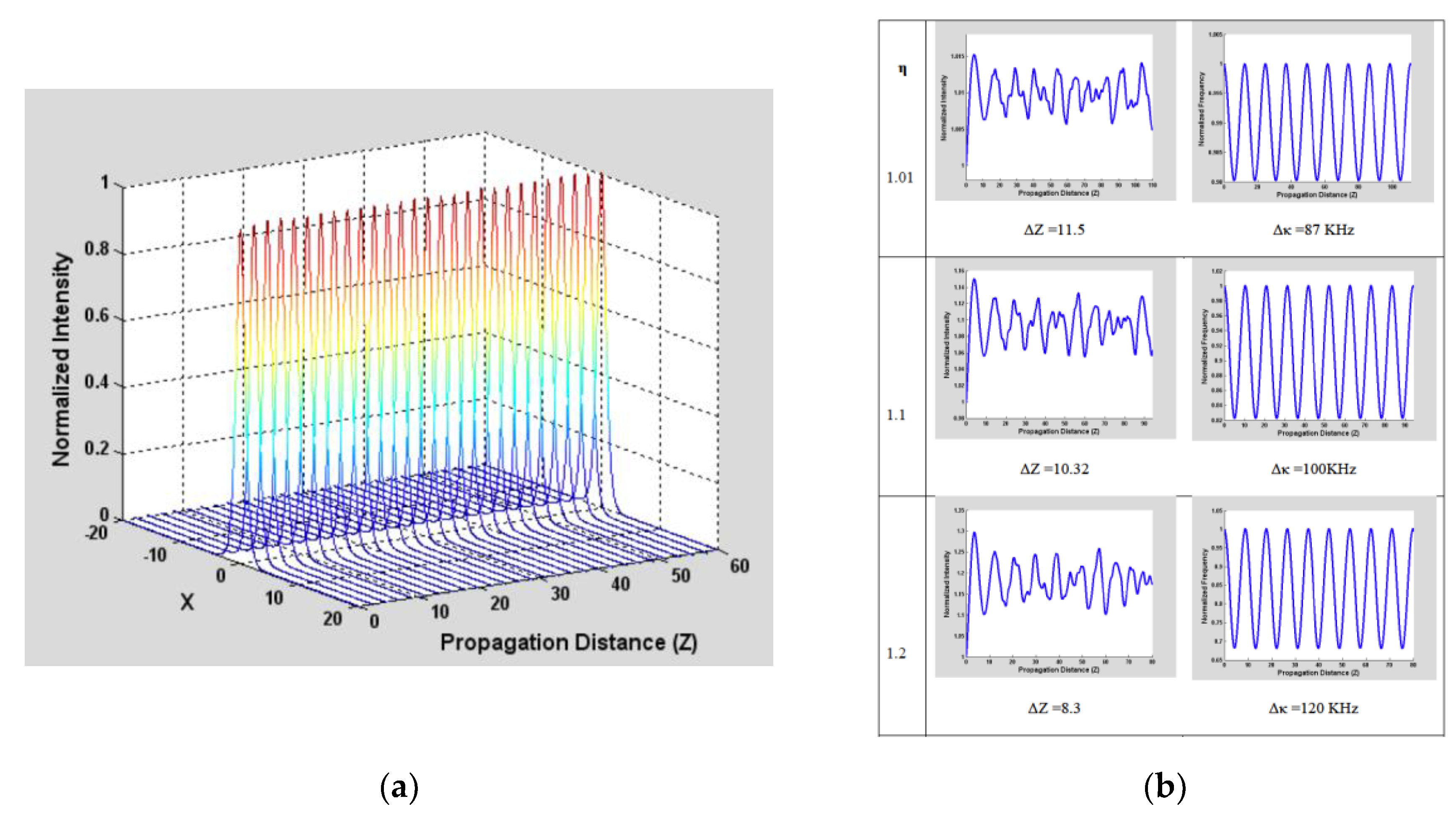
The solution of Equations (16) and (17) are well-known solitons, shown in Figure 6a, where the central peak amplitude provides the Soliton eigenvalue of the NLS. Therefore, in the absence of an equivalent to the area theorem of resonant pulse propagation, the convergence of the eigenvalues could be described by the central peak amplitude evolution, and we rely on numerical simulations. The peak amplitude exhibits a slight but perceptible fluctuation, as illustrated in Figure 6b, whose Fourier transform reveals that it is a cosenoidal modulation with a period dependent on the Kerr nonlinearity. We can characterize the peak by a relation of the form:

$$P_o=p_o+\mathsf{\Phi }\left(z\right),$$

(18)

where the Fourier transform of $\mathsf{\Phi }\left(z\right)$ is

$$\overline{\mathsf{\phi }}\left(k\right)\approx {\overline{\mathsf{\phi }}}_{o}Cos\mathsf{\Lambda }k,$$

(19)

and this spatial characteristic length $\mathsf{\Lambda }\left(\mathsf{\eta }\right)$ is central to our description.

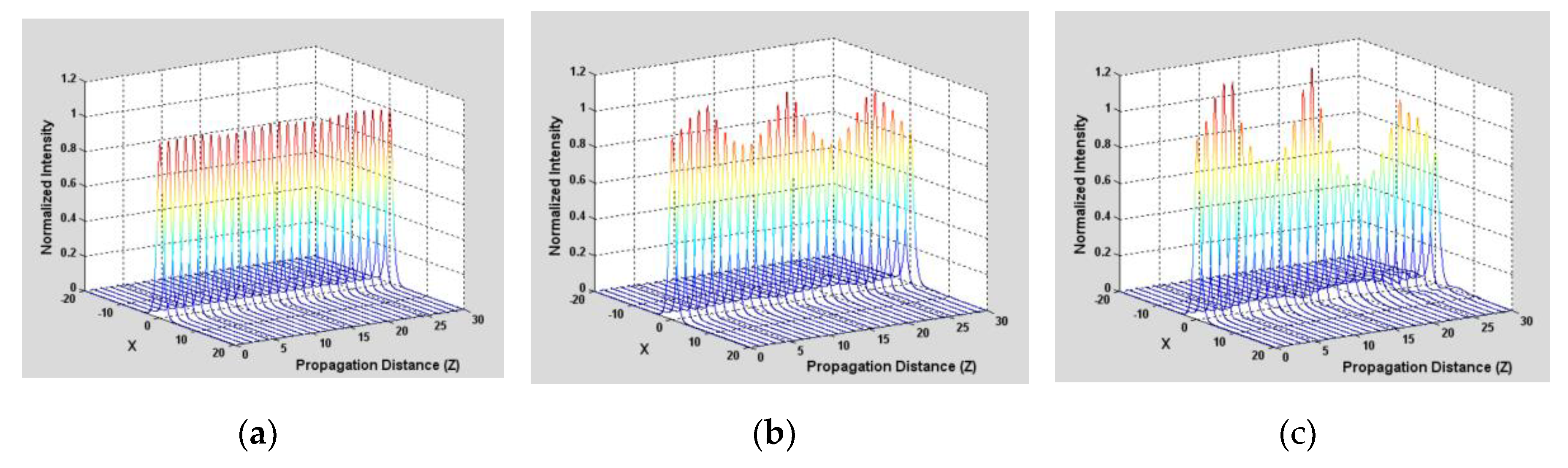
Figure 6b shows the linear frequency dependence on the nonlinearity, where the higher-order modulation is quite faint. Figure 7 illustrates the consideration of two different nonlinear media, showing an increase in fluctuations as the difference in nonlinearities increases.

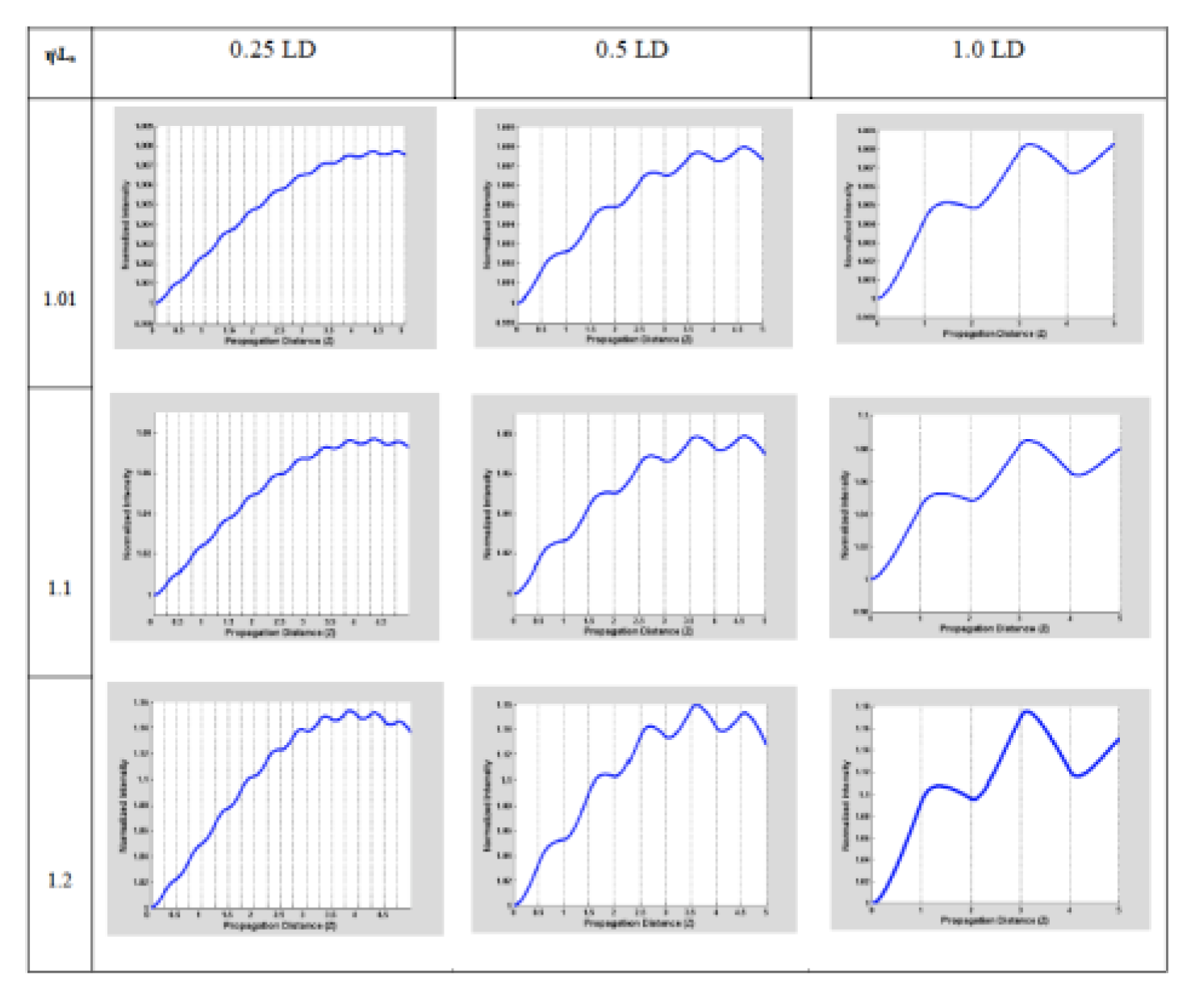
Suppose the material period is smaller than $\mathsf{\Lambda }\left(\mathsf{\eta }\right)$. In that case, its changes will superimpose on this modulation, Figure 8. But if the frequency is of similar dimension, then it would modulate the fluctuations, Figure 9. From Figure 6b, we can notice that in our simulation, the period of the variation is in the range of $10L_D$, that will prove a critical relative parameter to define those domains.

If the length of the media is small, i.e., in the range of an $L_D$, the frequencies of the changes due to the lengths of the media and those of the fluctuations are entirely different. We can see them as their superposition on the fluctuations, Figure 8. It is clear that the reshaping introduced by the change of materials is just a perturbation on the regular soliton oscillation and share features with the corresponding resonant case that we have already studied in the resonant case.

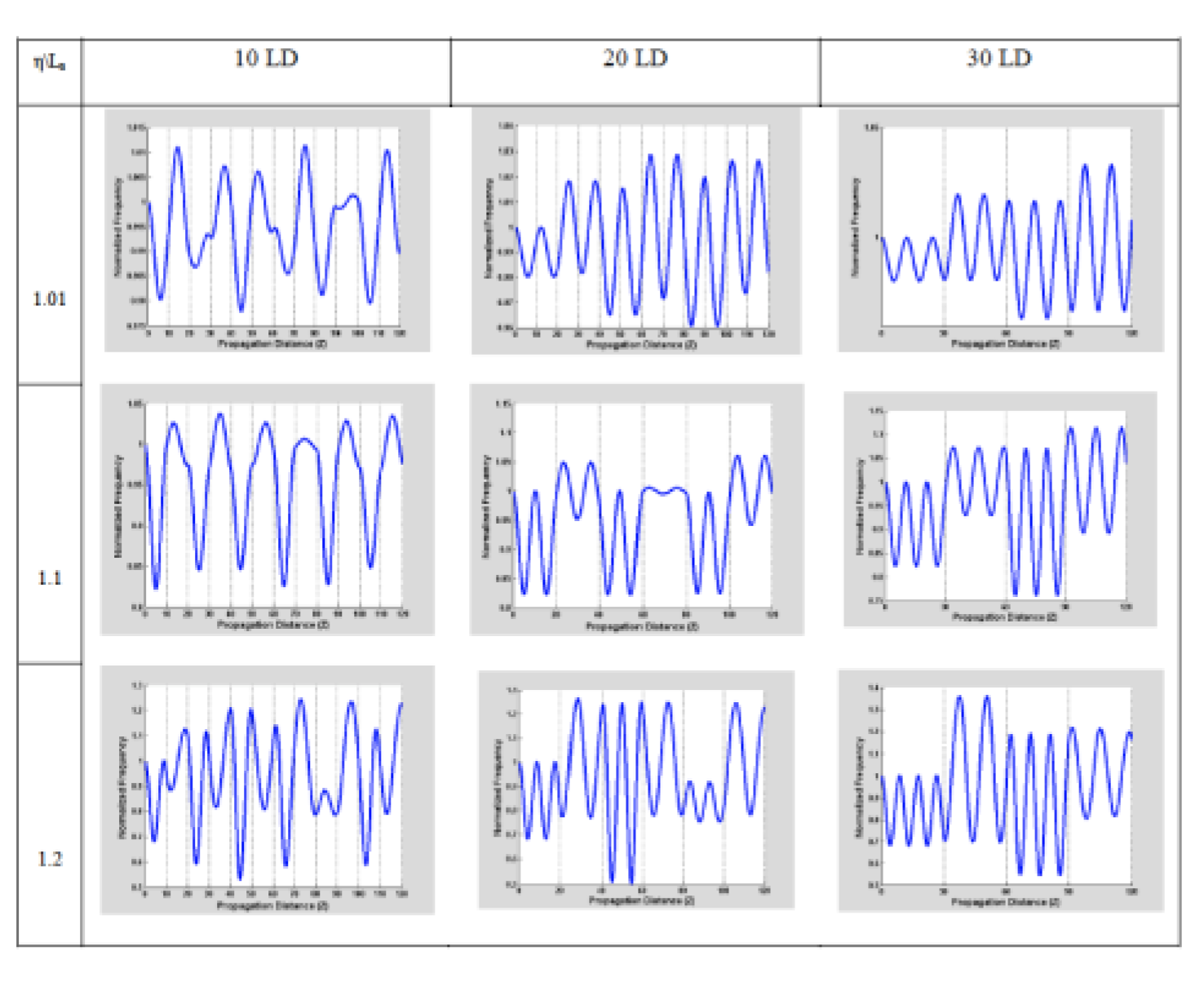
On the other hand, if the length of the media is in the range of the fluctuation’s characteristics length $\mathsf{\Lambda }\left(\mathsf{\eta }\right)$, i.e., larger than $L_D$, then both frequencies are similar. The modulation is related with their superposition, as is depicted in Figure 9. However, we can not consider it as a perturbation anymore, but apparently as a distinguishable modulation as shown in the last column, where we recover the original oscillations of the corresponding soliton, Figure 6 with an envelope produced by the media, resembling the long-distance result in the resonant case.

4. Conclusions

We have discussed the temporal and spatial propagation of Optical solitons through a nonlinear material Tandem from a different perspective. We have focused our attention on the reshaping transients of two particular nonlinear systems, that of a resonant TLA medium and a Kerr medium. We have demonstrated that, depending on the dimensions of the Tandem sections, we can freeze the transient features of the reshaping in a Tandem process. Where the reshaping from media to media results in a nonlinear modulation, which can be locally linearized as a perturbation near a soliton and analytically studied in a TLA medium. This claim sets the basis for the understanding of the much more complicated intensity-dependent cases, where such a handy description of the evolution of the soliton eigenvalue is not available. This nonlinear modulation overlaps with the natural nonlinear modulation and depends on the interplay between the dimensions of the media and the lengths of the nonlinear processes.

The detailed analysis of the pulse itself, governed by this behavior of the corresponding eigenvalue variable, still offers a vast number of opportunities. In particular, we will find elsewhere the consideration of nonlinearities of different characteristics, such as the quadratic and the intensity-dependent, such as those that describe Kerr and photorefractive materials, quite crucial for self-guiding of light. On its own, this soliton continuous reshaping process raises exciting questions. Indeed, the practical experience of resonant pulse propagation has not required such a detailed analysis as extensively as intensity-dependent nonlinearities. That calls for a comprehensive analysis of the pulse propagation to find out stable solutions and a transient solution made stable by the stratified medium.