Submitted:
06 July 2023
Posted:
06 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. BEC Model and Similarity transformation
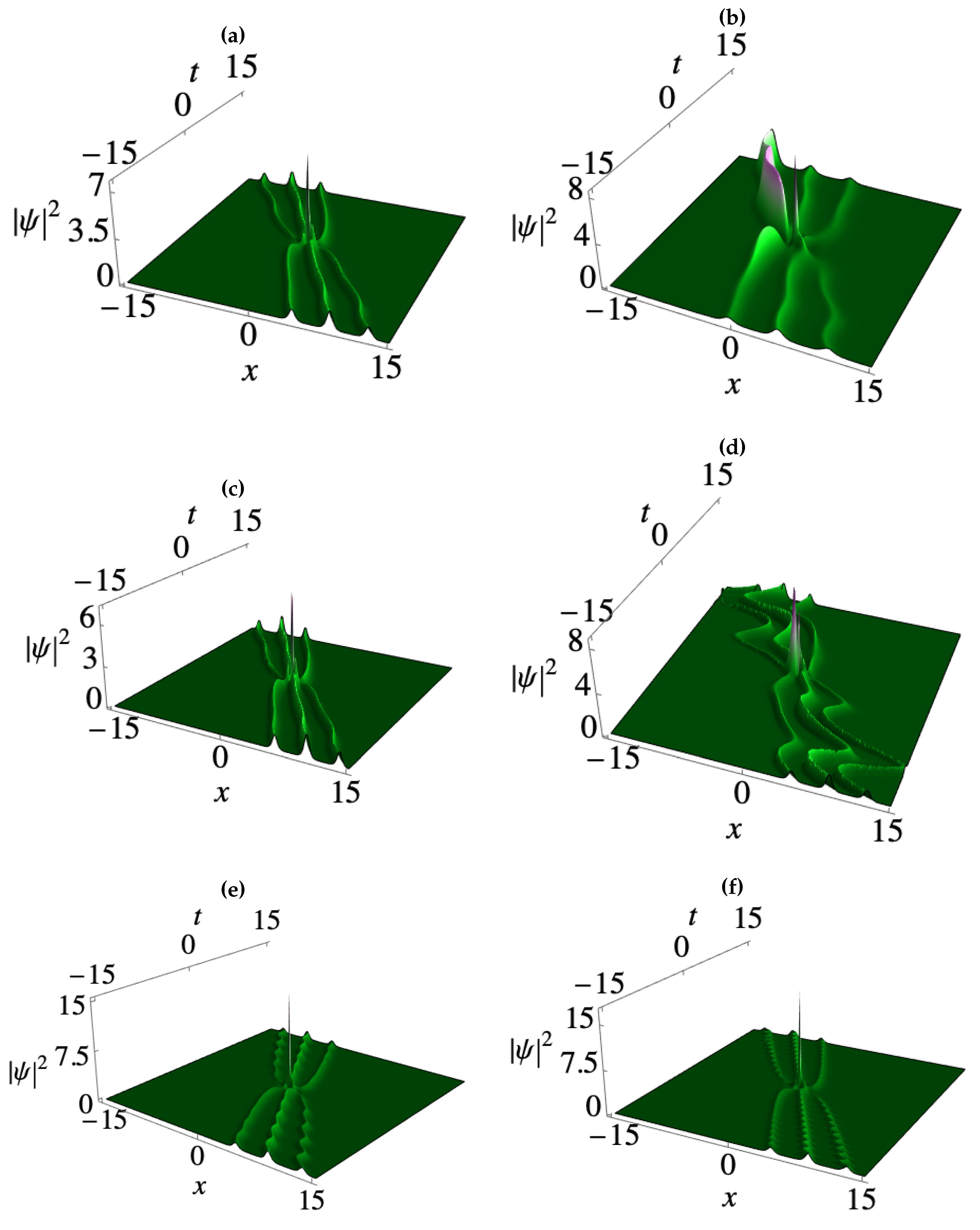
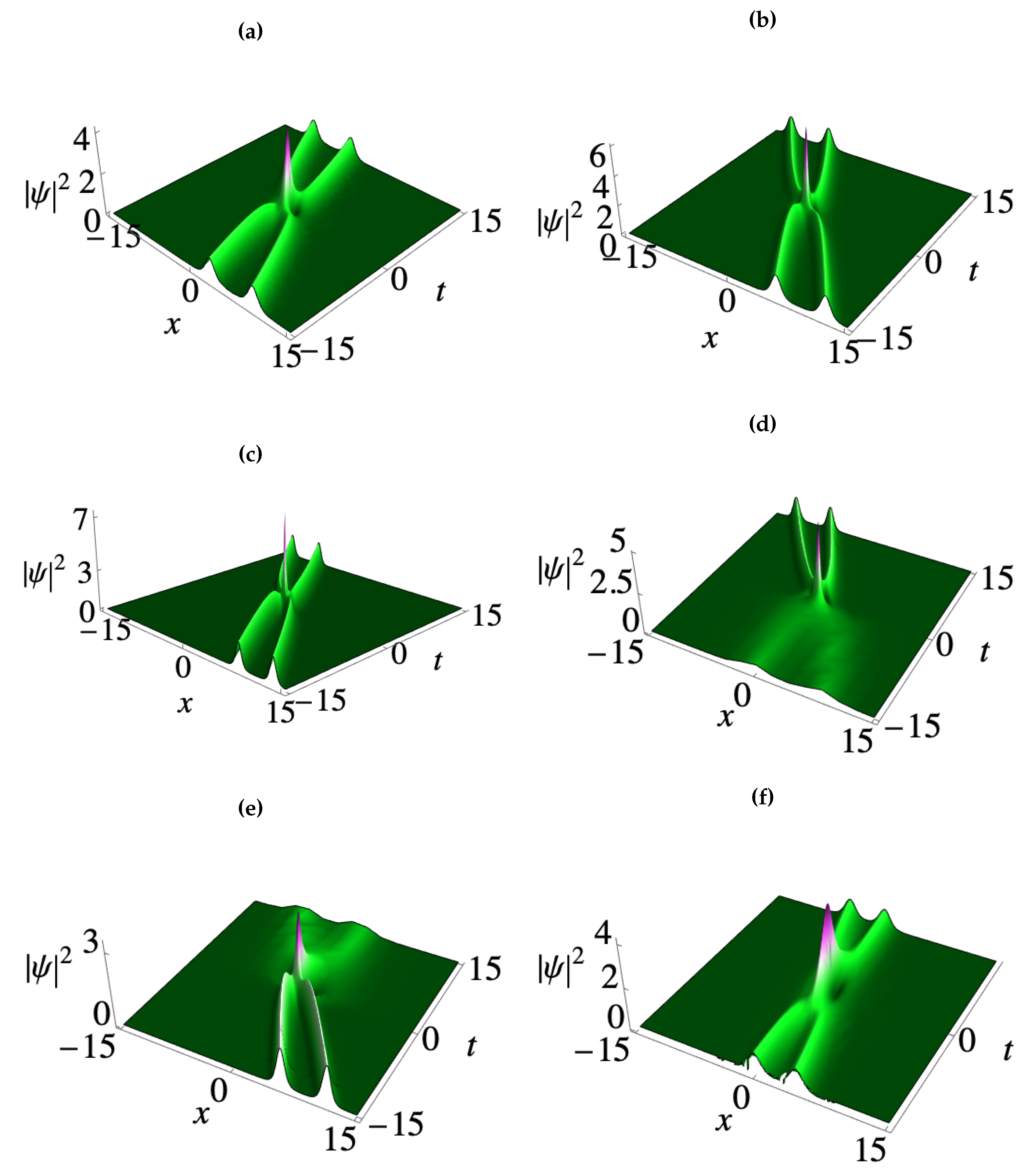
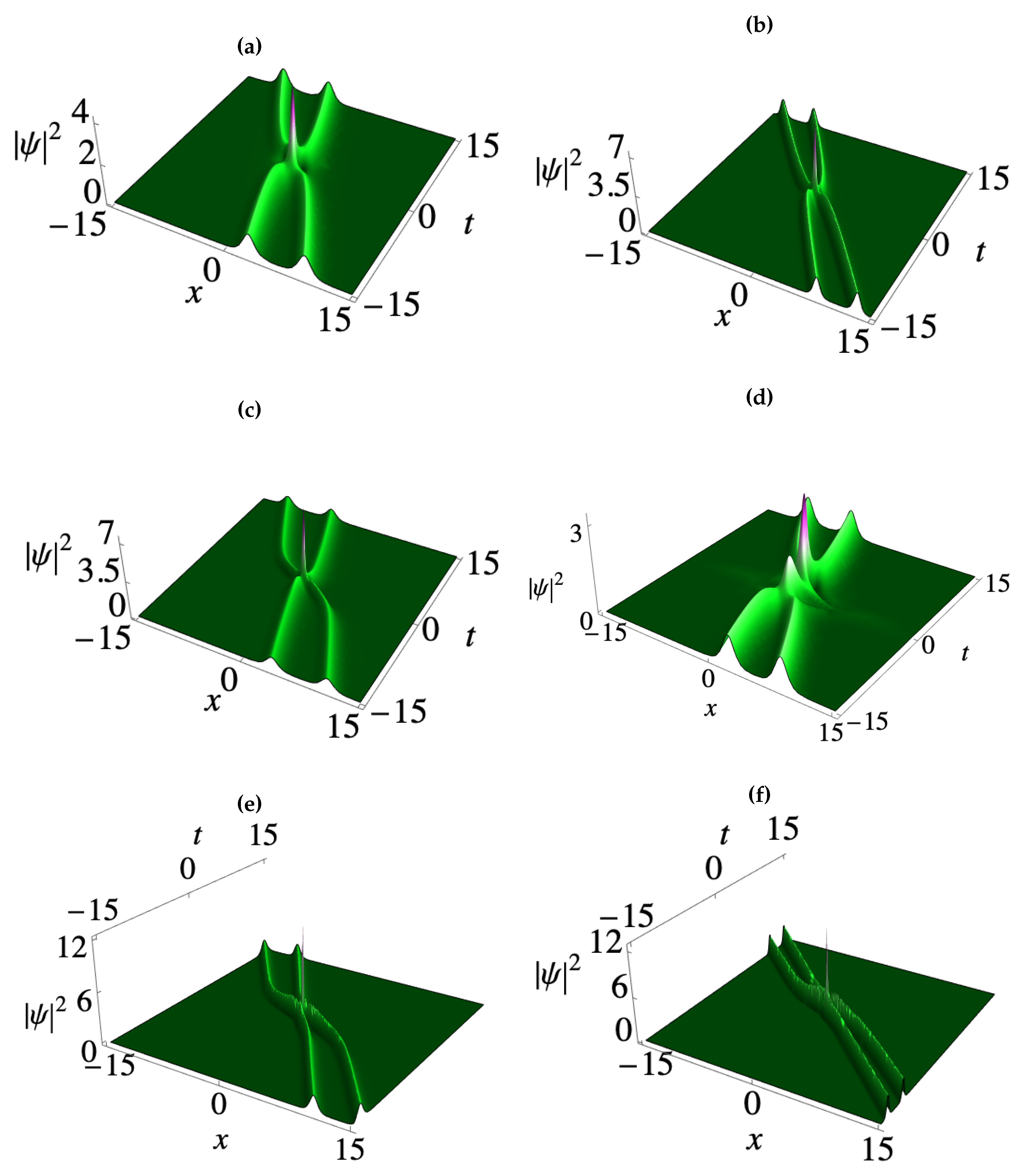
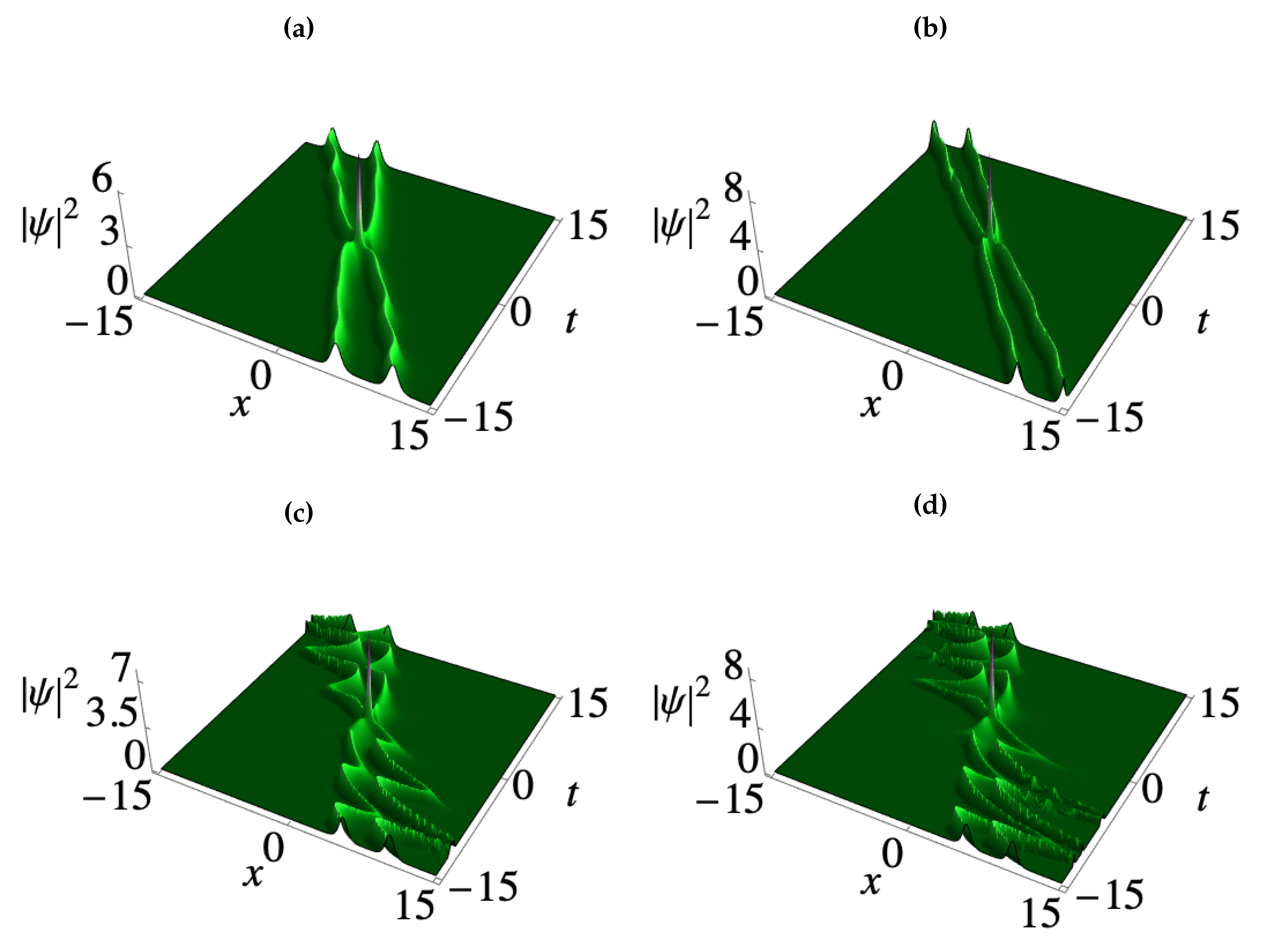
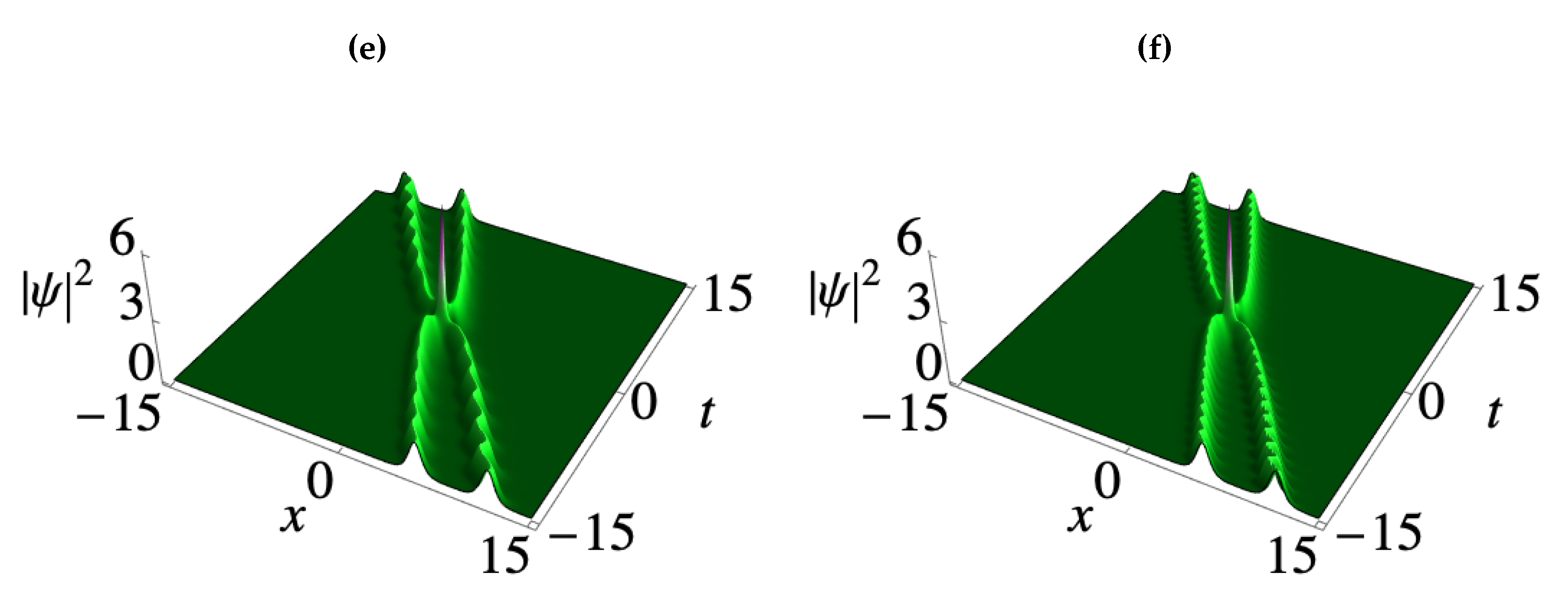
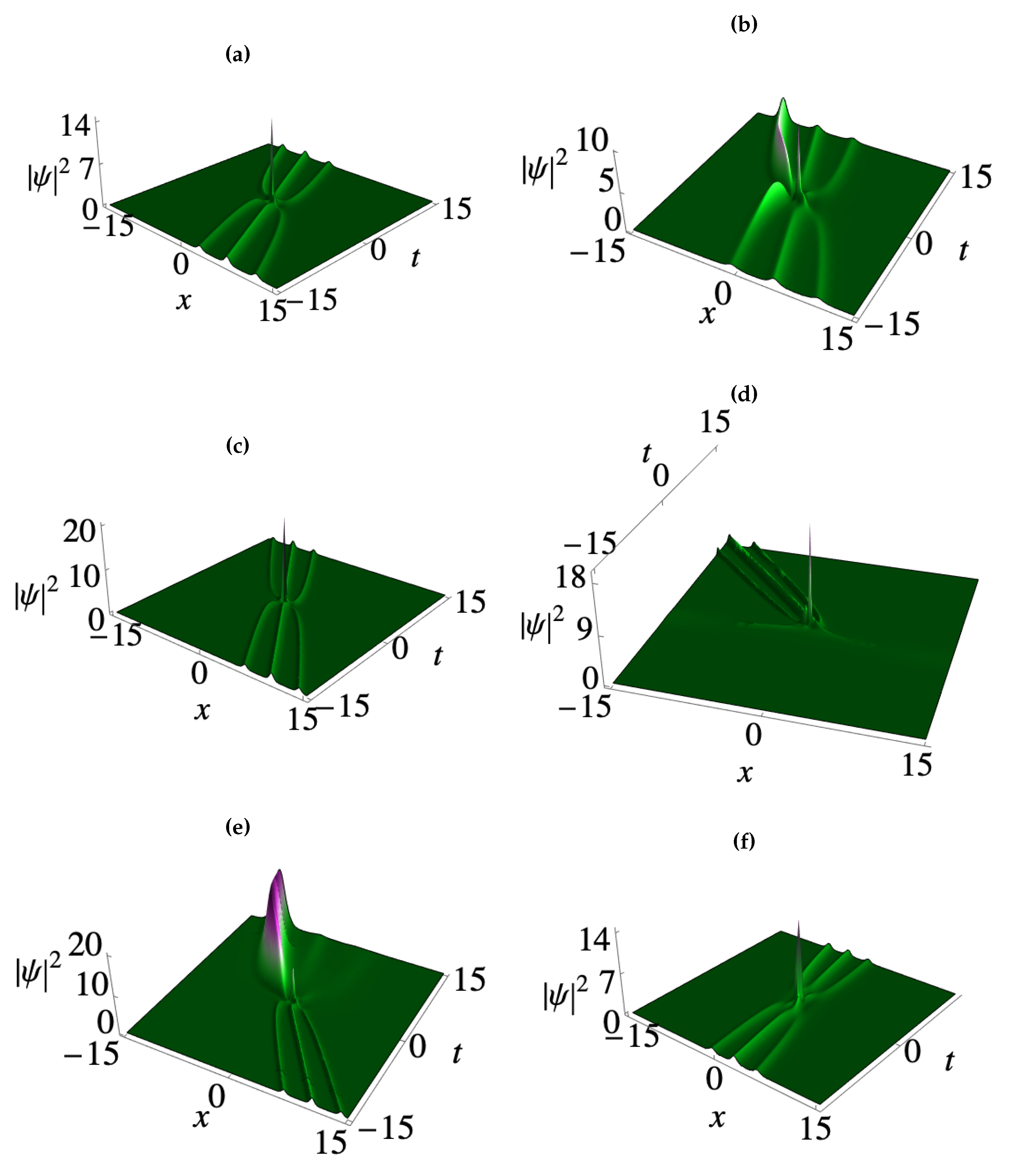
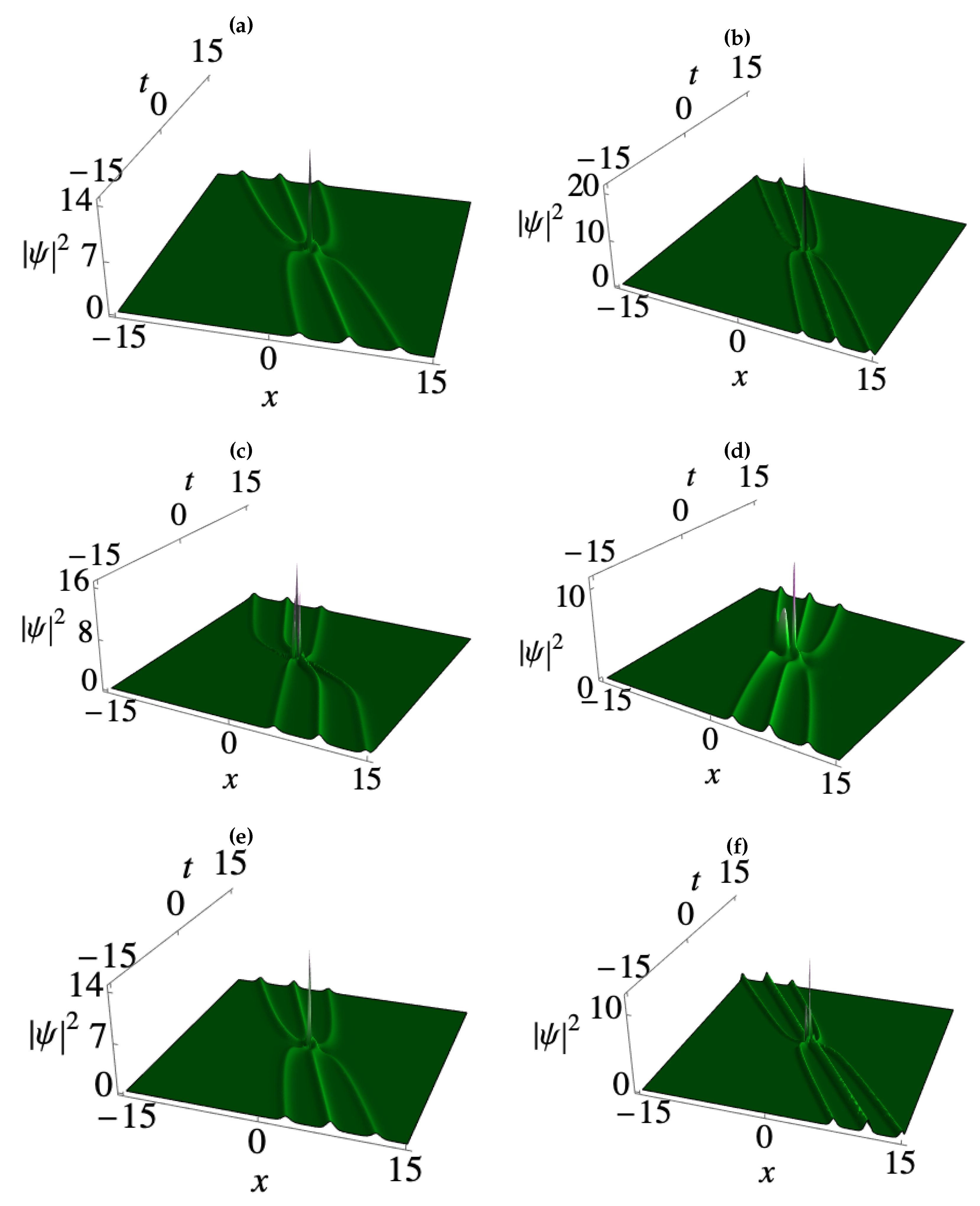
3. Deformation of matter wave positons in BECs
3.1. Second-order smooth matter wave positons
3.2. Third-order smooth matter wave positons
4. Conclusion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pitaevskii, L.P.; Stringari, S. Bose-Einstein condensation; Clarendon: Oxford, UK, 2003. [Google Scholar]
- Kevrekidis, P. G.; Frantzeskakis, D. J. R.; Carretero-González. Emergent Nonlinear Phenomena in Bose-Einstein Condensates; Springer: Berlin, Germany, 2008. [Google Scholar]
- Lakshmanan, M.; Rajasekar., S. Nonlinear Dynamics: Integrablity, Chaos and Patterns; Springer: Heidelberg, Germany, 2003. [Google Scholar]
- Yang, J. Nonlinear Waves in Integrable and Nonintegrable Systems; SIAM: Philadelphia, 2010. [Google Scholar]
- Serkin, V.N.; Hasegawa, A.; Belyaeva, T.L. Solitary waves in nonautonomous nonlinear and dispersive systems: nonautonomous solitons. J. Mod. Opt. 2010, 57, 1456–1472. [Google Scholar] [CrossRef]
- Luo, H.G.; Zhao, D.; He, X.G. Exactly controllable transmission of nonautonomous optical solitons. Phys. Rev. A. 2009, 79, 063802. [Google Scholar] [CrossRef]
- Shats, M.; Punzmann, H.; Xia, H. Capillary rogue waves. Phys Rev Lett. 2010, 104, 104503. [Google Scholar] [CrossRef] [PubMed]
- Ganshin, A.N.; Efimov, V.B.; Kolmakov, G.V. et al. Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett. 2008, 101, 065303. [Google Scholar] [CrossRef] [PubMed]
- El-Tantawy, S.A.; Salas, A.H.; Albalawi, W. New Localized and Periodic Solutions to a Korteweg-de Vries Equation with Power Law Nonlinearity: Applications to Some Plasma Models. Symmetry. 2022, 14, 197. [Google Scholar] [CrossRef]
- Vudragović, D.; Balaž, A. Faraday and Resonant Waves in Dipolar Cigar-Shaped Bose-Einstein Condensates. Symmetry. 2019, 11, 1090. [Google Scholar] [CrossRef]
- Inouye, S.; Andrews, M.R.; Stenger, J.; Miesner, H.J.; Stamper-Kurn, D.M.; Ketterle, W. Observation of Feshbach resonances in a Bose-Einstein condensate. Nature. 1998, 392, 151. [Google Scholar] [CrossRef]
- Theis, M.; Thalhammer, G.; Winkler, K.; Hellwig, M.; Ruff, G.; Grimm, R.; Denschlag, J.H. Tuning the scattering length with an optically induced Feshbach resonance. Phys. Rev. Lett. 2004, 93, 123001. [Google Scholar] [CrossRef]
- Malomed, B.A. Soliton Management in Periodic Systems; Springer: New York, 2006. [Google Scholar]
- Wang, D.S.; Liu, J.; Wang, L. Non-autonomous matter-wave solitons in hybrid atomic-molecular Bose-Einstein condensates with tunable interactions and harmonic potential. Phys. Lett. A. 2018, 382, 799–805. [Google Scholar] [CrossRef]
- Halder, B.; Ghosh, S.; Basu, P.; Bera, J.; Malomed, B.; Roy, U. Exact Solutions for Solitary Waves in a Bose-Einstein Condensate under the Action of a Four-Color Optical Lattice. Symmetry. 2022, 14, 49. [Google Scholar] [CrossRef]
- Bludov, Y.V.; Konotop, V.V.; Akhmediev, N. Matter rogue waves. Phys. Rev. A . 2009, 80, 033610. [Google Scholar] [CrossRef]
- Manikandan, K.; Muruganandam, P.; Senthilvelan, M.; Lakshmanan, M. Manipulating matter rogue waves and breathers in Bose-Einstein condensates. Phys Rev E. 2014, 90, 062905. [Google Scholar] [CrossRef] [PubMed]
- Wen, L.; Li, L.; Li, Z.-D.; Song, S.-W.; Zhang, X.-F.; Liu, W. M. Matter rogue wave in Bose-Einstein condensates with attractive atomic interaction. Eur. Phys. J. D. 2011, 64, 473. [Google Scholar] [CrossRef]
- Hacker, N.; Malomed, B.A. Nonlinear Dynamics of Wave Packets in Tunnel-Coupled Harmonic-Oscillator Traps. Symmetry. 2021, 13, 372. [Google Scholar] [CrossRef]
- Triki, H.; Choudhuri, A.; Qin, Z.; Biswas, A.; Alshomrani, A.S. Nonautonomous matter wave bright solitons in a quasi-1D Bose-Einstein condensate system with contact repulsion and dipole-dipole attraction. Applied Mathematics and Computation. 2020, 371, 124951. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Malomed, B. Nonlinear Management of Topological Solitons in a Spin-Orbit-Coupled System. Symmetry. 2019, 11, 388. [Google Scholar] [CrossRef]
- Yan, Z.Y. Nonautonomous rogons in the inhomogeneous nonlinear Schrödinger equation with variable coefficients. Phys. Lett. A. 2010, 374, 672. [Google Scholar] [CrossRef]
- Zhao, L.C. Dynamics of nonautonomous rogue waves in Bose-Einstein condensate. Ann. Phys. 2013, 73, 329. [Google Scholar] [CrossRef]
- Wu, X.F.; Hua, G.S.; Ma, Z. Y. Novel rogue waves in an inhomogenous nonlinear medium with external potentials. Commun. Nonlinear Sci. Num. Simulat. 2013, 18, 3325. [Google Scholar] [CrossRef]
- He, J.S.; Charalampidis, E.G.; Kevrekidis, P.G.; Frantzeskakis, D.J. Rogue waves in nonlinear Schrödinger models with variable coefficients: application to Bose–Einstein condensates. Phys. Lett. A. 2014, 378, 577. [Google Scholar] [CrossRef]
- Konotop, V.V.; Yang, J.; Zezyulin, D.A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
- Zezyulin, D.A.; Konotop, V.V. Nonlinear mode in the harmonic PT-symmetric potential. Phys. Rev. A. 2012, 85, 043840. [Google Scholar] [CrossRef]
- Manikandan, K.; Sudharsan, J.B.; Senthilvelan, M. Nonlinear tunneling of solitons in a variable coefficients nonlinear Schrödinger equation with PT-symmetric Rosen–Morse potential. Eur. Phys. J. B 2021, 94, 122. [Google Scholar] [CrossRef]
- Oliinyk, A.; Yatsuta, I.; Malomed, B.; Yakimenko, A. Symmetry Breaking in Interacting Ring-Shaped Superflows of Bose-Einstein Condensates. Symmetry. 2019, 11, 1312. [Google Scholar] [CrossRef]
- Matveev, V.B. Generalized Wronskian formula for solutions of the KdV equations: first applications. Phys. Lett. A. 1992, 166, 205–208. [Google Scholar] [CrossRef]
- Matveev, V.B. Positon-positon and soliton-positon collisions: KdV case. Phys. Lett. A. 1992, 166, 209–212. [Google Scholar] [CrossRef]
- Matveev, V.B. Positons: Slowly Decreasing Analogues of Solitons. Theor. Math. Phys. 2002, 131, 483. [Google Scholar] [CrossRef]
- Kedziora, D.J.; Ankiewicz, A.; Akhmediev, N. Second-order nonlinear Schrödinger equation breather solutions in the degenerate and rogue wave limits. Phys. Rev. E 2012, 85, 066601. [Google Scholar] [CrossRef]
- Chow, K.W.; Lai, W.C.; Shek, C.K.; Tso, K. Positon-like Solutions of Nonlinear Evolution Equations in (2+1) Dimensions. Chaos Solitons Fractals 1998, 9, 1901–1912. [Google Scholar] [CrossRef]
- Dubard, P.; Gaillard, P.; Klein, C.; Matveev, V.B. On multi-rogue wave solutions of the NLS equation and positon solutions of the KdV equation. Eur. Phys. J. Spec. Top. 2010, 185, 247–258. [Google Scholar] [CrossRef]
- Stahlhofen, A.A. Positons of the modified Korteweg-de Vries equation. Ann. Phys. 1992, 504, 554–569. [Google Scholar] [CrossRef]
- Maisch, H.; Stahlhofen, A.A. Dynamic properties of positons. Phys. Scr. 1995, 52, 228–236. [Google Scholar] [CrossRef]
- Beutler, R. Positon solutions of the sine-Gordon equation. J. Math. Phys. 1993, 34, 3081–3109. [Google Scholar] [CrossRef]
- Stahlhofen, A.A.; Matveev, V.B. Positons for the Toda lattice and related spectral problems. J. Phys. A. 1995, 28, 1957–1965. [Google Scholar] [CrossRef]
- Hu, H.C.; Liu, Y. New positon, negaton and complexiton solutions for the Hirota–Satsuma coupled KdV system. Phys. Lett. A. 2008, 372, 5795–5798. [Google Scholar] [CrossRef]
- Cen, J.; Correa, F.; Fring, A. Time-delay and reality conditions for complex solitons. J. Math. Phys. 2017, 58, 032901. [Google Scholar] [CrossRef]
- Cen, J.; Correa, F.; Fring, A. Degenerate multi-solitons in the sine-Gordon equation. J. Phys. A. 2017, 50, 435201. [Google Scholar] [CrossRef]
- Xing, Q.; Wu, Z.; Mihalache, D.; He, J.S. Smooth positon solutions of the focusing modified Korteweg-de Vries equation. Nonlinear Dyn. 2017, 89, 2299–2310. [Google Scholar] [CrossRef]
- Liu, S.Z.; Zhang, Y.S.; He, J.S. Smooth positons of the second-type derivative nonlinear Schrödinger equation. Commun. Theor. Phys. 2019, 71, 357–361. [Google Scholar] [CrossRef]
- Song, W.; Xu, S.; Li, M.; He, J. Generating mechanism and dynamic of the smooth positons for the derivative nonlinear Schrödinger equation. Nonlinear Dyn. 2019, 97, 2135–2145. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Y.S.; He, J.S. Dynamics of the smooth positons of the complex modified KdV equation. Waves Random Complex 2018, 28, 203–214. [Google Scholar] [CrossRef]
- Yuan, F. The dynamics of the smooth positon and b-positon solutions for the NLS-MB equations. Nonlinear Dyn. 2020, 102, 1761–1771. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Li, B. Soliton molecules and dynamics of the smooth positon for the Gerdjikov–Ivanov equation. Appl. Math. Lett. 2020, 103, 106168. [Google Scholar] [CrossRef]
- Hu, A.; Li, M.; He, J. Dynamic of the smooth positons of the higher-order Chen–Lee–Liu equation. Nonlinear Dyn. 2021, 104, 4329–4338. [Google Scholar] [CrossRef]
- Vishnu Priya, N.; Monisha, S.; Senthilvelan, M.; Rangarajan, G. Nth-order smooth positon and breather-positon solutions of a generalized nonlinear Schrödinger equation. Eur. Phys. J. Plus. 2022, 137, 646. [Google Scholar] [CrossRef]
- Monisha, S.; Vishnu Priya, N.; Senthilvelan, M.; Rajasekar, S. Higher order smooth positon and breather positon solutions of an extended nonlinear Schrödinger equation with the cubic and quartic nonlinearity. Chaos, Solitons and Fractals 2022, 162, 112433. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).