Quantum-Enhanced Feature Selection and Classification for Asthma Diagnosis Using a Variational Quantum Classifier

1. Introduction

Asthma is a chronic, heterogeneous inflammatory disorder of the respiratory airways that imposes a significant global health burden. Current epidemiological estimates indicate that approximately 339 million individuals are affected worldwide, with the disease contributing substantially to morbidity, mortality, healthcare expenditure, and diminished quality of life [1]. Clinically, asthma is characterized by recurrent episodes of wheezing, dyspnea, chest tightness, and coughing, which manifest with variable intensity and frequency across patients [2]. These symptomatic patterns are often influenced by complex interactions between genetic predisposition, environmental exposures, and lifestyle factors [3]. Timely and accurate diagnosis is therefore imperative, as early intervention can mitigate disease progression, reduce the frequency of exacerbations, and optimize therapeutic outcomes [4].

Despite significant advances in respiratory medicine, the diagnosis of asthma remains challenging due to its multifactorial etiology and symptomatic overlap with other respiratory disorders, such as chronic obstructive pulmonary disease (COPD) and bronchitis [2,3]. Conventional diagnostic procedures, such as spirometry, bronchial provocation testing, and clinical history evaluation, are subject to limitations including variability in patient compliance, operator-dependent interpretation, and potential insensitivity to early-stage disease.

In recent years, the proliferation of large-scale biomedical datasets has spurred interest in machine learning (ML) methodologies for asthma diagnosis and prognosis. ML models can automatically learn predictive patterns from multidimensional clinical, demographic, and environmental data, thereby complementing traditional diagnostic protocols [5,6]. Algorithms such as logistic regression, support vector machines (SVMs), decision trees, and ensemble learning methods have demonstrated encouraging performance in identifying asthma risk profiles. Furthermore, deep learning architectures have exhibited the capacity to capture complex, nonlinear dependencies within high-dimensional data spaces, offering potentially superior predictive accuracy over conventional statistical approaches.

However, the efficacy of ML models is often constrained by the “curse of dimensionality” when applied to extremely high-dimensional datasets. In our case, after preprocessing steps such as one-hot encoding of categorical variables and normalization of numerical attributes, the dataset expanded to $d=14,393$ features for $N=2392$ patient records. Such an extreme feature-to-sample ratio amplifies the risk of overfitting, reduces model interpretability, and imposes heavy computational demands [7,8]. Consequently, aggressive and effective feature selection becomes essential for isolating the most informative predictors while discarding redundant or irrelevant variables.

Quantum computing offers a fundamentally different computational paradigm, with the potential to surpass classical approaches in certain problem domains. By exploiting principles of quantum mechanics, such as superposition, entanglement, and quantum parallelism, quantum algorithms can explore large and complex solution spaces with increased efficiency [9,10,11]. Within the domain of quantum machine learning (QML), hybrid quantum-classical approaches have been proposed to address the combinatorial nature of feature selection [12,13] and to enhance classification performance through quantum circuit-based models [14,15]. In particular, Variational Quantum Classifiers (VQCs) represent a promising framework wherein parameterized quantum circuits are trained to learn decision boundaries in reduced feature spaces, offering the dual benefits of dimensionality reduction and expressive model capacity.

In this work, we present a hybrid quantum-classical diagnostic pipeline that integrates quantum-enhanced feature selection with a VQC for the classification of asthma cases. Using the publicly available Asthma Disease Dataset from Kaggle [16], which comprises diverse demographic, environmental, lifestyle, and clinical attributes, we first employ a quantum feature selection mechanism to identify an optimized subset of predictive variables from the original $14,393$-dimensional feature space. This subset is subsequently used to train a VQC, enabling effective binary classification of asthma-positive versus asthma-negative cases. The proposed approach is designed to achieve drastic dimensionality reduction without compromising classification performance and, in certain cases, to surpass classical machine learning baselines.

The primary contributions of this study are as follows:

• Integration of quantum-enhanced feature selection and variational quantum classification into a unified diagnostic framework for asthma.
• Comprehensive evaluation of the proposed method on a real-world, ultra-high-dimensional biomedical dataset.
• Empirical demonstration that aggressive dimensionality reduction (over 99%) can be achieved without significant loss in predictive accuracy, underscoring the practical viability of QML-based clinical decision support systems.

The remainder of this paper is structured as follows: Section 2 reviews existing literature on machine learning for asthma diagnosis and quantum machine learning (QML) in healthcare. Section 3 details the proposed methodology, including the quantum feature selection process and variational quantum classifier (VQC) architecture. Section 4 presents the experimental setup and results. Section 5 outlines the study’s limitations. Section 6 highlights potential avenues for future research. Finally, Section 7 concludes the paper.

2. Literature Review

2.1. Machine Learning for Asthma Diagnosis

Machine learning (ML) has emerged as a powerful paradigm for augmenting the early detection and long-term management of asthma through the systematic analysis of large-scale clinical, demographic, and epidemiological datasets. Conventional supervised learning algorithms, including logistic regression, decision trees, random forests, and support vector machines (SVMs), have been successfully employed to integrate heterogeneous inputs such as demographic profiles, environmental exposures, and clinical indicators for asthma risk prediction [17,18]. Neural network architectures, ranging from shallow multilayer perceptrons to deep learning frameworks, have further enhanced predictive capabilities by modeling complex, nonlinear dependencies within patient data [19].

Research efforts have also focused on specialized contexts, such as pediatric asthma prediction, leveraging environmental exposure metrics, family medical histories, and physiological biomarkers [20]. In addition, the mining of electronic health records (EHRs) has been utilized to extract temporal disease patterns and support predictive modeling in clinical settings [21]. While these techniques have yielded promising classification performance, their effectiveness can be hindered by high-dimensional feature spaces. The presence of irrelevant or redundant variables in such datasets can exacerbate overfitting, reduce model interpretability, and increase computational requirements [7].

To address these challenges, a variety of feature selection methods, such as mutual information scoring, recursive feature elimination (RFE), and regularization-based selection, have been explored to improve generalization and reduce dimensionality [8,22]. Nonetheless, many of these methods rely on heuristic search strategies that may not efficiently traverse vast combinatorial feature spaces, particularly when dealing with medical datasets that integrate diverse and interdependent feature types.

**Recent advances have introduced sustainable ML pipelines for asthma diagnosis by combining feature selection, data augmentation, and boosting algorithms: Lee et al. (2024) propose augmenting datasets with synthetic samples, applying feature selection, and using extreme gradient boosting to improve resilience and performance [23].** Furthermore, Mahmood et al. (2025) developed an interpretable and generalizable predictive model for asthma outcomes using AutoML and explainable AI methods such as SHAP and LIME, addressing challenges in model interpretability and deployment [24].

2.2. Quantum Computing in Machine Learning

Quantum computing has emerged as a transformative computational paradigm capable of addressing limitations inherent in certain classical algorithms for optimization, search, and pattern recognition [9]. By exploiting fundamental quantum mechanical properties, superposition, entanglement, and quantum parallelism, quantum algorithms can explore exponentially large state spaces more efficiently than their classical analogues in specific problem domains [10,11].

Within the broader field of quantum machine learning (QML), the integration of quantum computational models into data-driven tasks holds the promise of polynomial or even exponential computational advantages under specific conditions [14]. Variational Quantum Algorithms (VQAs), such as the Variational Quantum Eigensolver (VQE) and the Variational Quantum Classifier (VQC), are particularly noteworthy. These algorithms operate in a hybrid quantum-classical feedback loop, where parameterized quantum circuits are iteratively optimized by classical routines [12,15].

2.3. Quantum Feature Selection

Feature selection can naturally be formulated as a combinatorial optimization problem, making it an attractive candidate for quantum acceleration [13]. Algorithms such as the Quantum Approximate Optimization Algorithm (QAOA) provide a framework for mapping the selection problem to a quantum Hamiltonian, enabling exploration of optimal or near-optimal feature subsets [25]. Early experimental studies have demonstrated that quantum-based or quantum-inspired feature selection can outperform exhaustive classical search for small- to medium-scale datasets [26].

In biomedical domains, quantum feature selection has been successfully explored in genomics [27], radiomics [28], and other high-dimensional healthcare datasets. Even with limited qubit resources, these approaches have been shown to reduce dimensionality while preserving, and in some cases enhancing, predictive performance. The integration of quantum feature selection with VQC classification holds particular promise in overcoming both the curse of dimensionality and the generalization constraints associated with purely classical models [29].

**Notably, Nau et al. (2025) implemented quantum annealing on real hardware for feature selection in light-weight medical image datasets, demonstrating scalability advantages in solving combinatorial “k-of-n” selection tasks through an Ising-penalty-based, subsampling approach [30].** Gupta et al. (2025) conducted a systematic review of QML algorithms applied to clinical decision-making, offering a broad assessment of their potential performance advantages in healthcare contexts [31].

2.4. Quantum Computing in Healthcare

Recent advances have seen QML techniques applied directly to healthcare decision-support systems. Applications include VQC-based cancer diagnostics [32], quantum-enhanced k-means clustering for biomedical signals [33], and quantum kernel methods for medical classification tasks [34]. Although the current generation of quantum devices is constrained by limited qubit counts and susceptibility to noise, simulation-based research indicates that quantum-enhanced algorithms may soon offer tangible performance advantages, especially when paired with dimensionality reduction strategies that lower qubit requirements [35].

**A recent comprehensive review by Fairburn (2025) highlights QC’s clinical potential in medical imaging and decision-making, while also noting constraints such as hardware scalability, error mitigation, and ethical considerations [36].** At the practical interface of quantum computing and pharmacology, IBM and Moderna (2025) leveraged variational quantum algorithms and financial risk modeling to tackle challenging mRNA structural problems, marking a significant milestone in quantum-enabled biotech pipelines [37]. Furthermore, at the Quantum India Summit (2025), experts showcased quantum sensors for non-invasive cardiac imaging, dye-free quantum light imaging, and quantum analytics for drug-trial optimization—demonstrating the technology’s translation toward safer, real-time clinical tools [38].

In summary, the literature suggests that while classical ML methods have attained notable success in asthma diagnosis, their scalability and performance can be constrained by high-dimensional medical data. Quantum computing provides an emerging computational toolkit to address these challenges through efficient feature selection and hybrid classification models. A synergistic combination of quantum feature selection with variational quantum classification offers the potential for more accurate, interpretable, and resource-efficient diagnostic systems.

3. Methodology

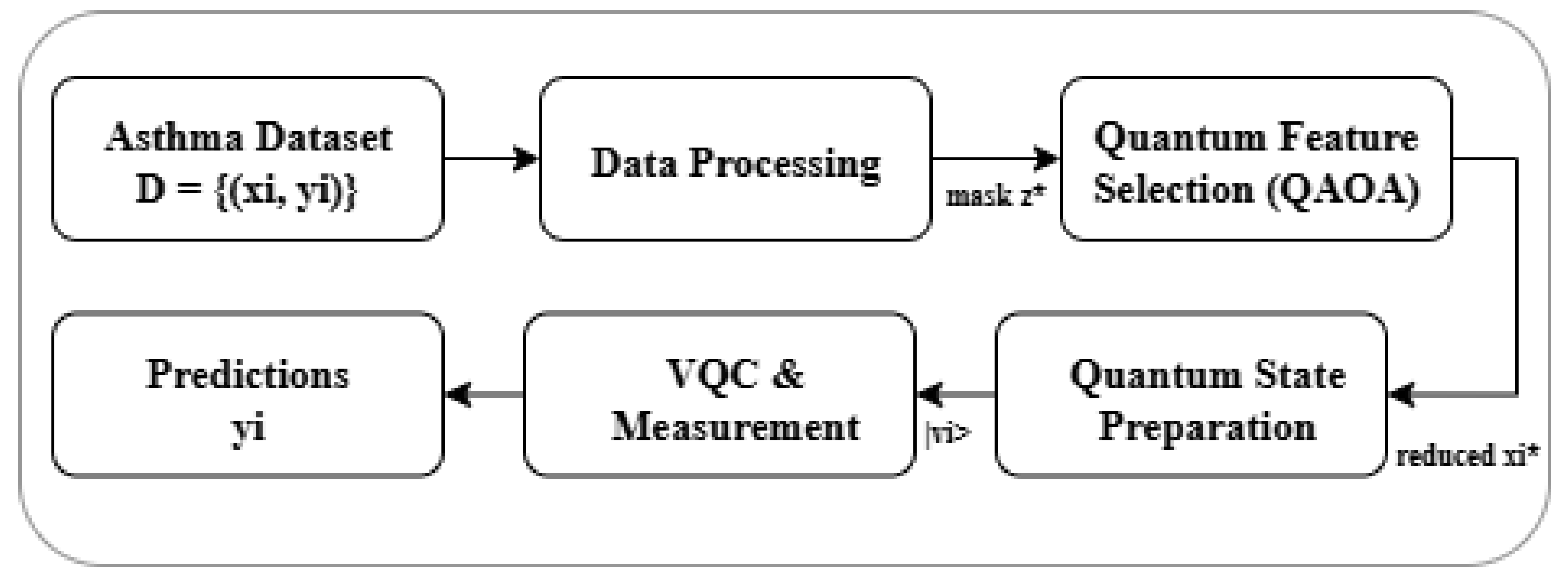
This section presents the proposed hybrid quantum–classical computational framework for asthma diagnosis. The architecture integrates Quantum Feature Selection (QFS) with a Variational Quantum Classifier (VQC) in order to (i) address the challenges posed by ultra-high-dimensional biomedical datasets and (ii) exploit the representational and computational advantages of quantum processing. The workflow is organized into five main stages: (1) data preprocessing, (2) quantum-based feature selection, (3) quantum state preparation, (4) variational quantum classification, and (5) hybrid optimization of trainable parameters. The end-to-end workflow is depicted in Figure 1.

3.1. Data Preprocessing

Let the asthma dataset be formally denoted as:

$$D=\{(x_i,y_i)\mid x_i\in {\mathbb{R}}^d,y_i\in \{0,1\},i=1,\dots ,N\},$$

(1)

where $x_i$ represents the d-dimensional real-valued feature vector corresponding to the i-th patient record, and $y_i$ is the associated binary class label, with $y_i=0$ indicating a non-asthmatic case and $y_i=1$ indicating an asthmatic case.

In our case, the dataset contains $N=2392$ patient records with a mixture of categorical and numerical attributes. While the number of original attributes was moderate, the application of one-hot encoding to categorical variables caused a drastic dimensionality expansion, yielding $d=14,393$ features. Such an extreme feature-to-sample ratio makes direct quantum encoding infeasible for current NISQ devices, as it would require thousands of qubits. Therefore, aggressive feature selection is essential both to avoid overfitting in classical baselines and to enable quantum-based classification within feasible hardware limits.

The preprocessing pipeline comprises three key operations:

(1)

Missing Value Imputation: Missing values in numerical features are replaced with the median of the observed values, thereby mitigating the influence of outliers. Missing values in categorical features are imputed with the statistical mode to preserve categorical distributions.

(2)

Categorical Encoding: All categorical attributes are transformed using one-hot encoding, expanding the feature set from a few dozen attributes to 14,393 binary indicators and numerical features combined.

(3)

Feature Scaling: Numerical features are standardized to zero mean and unit variance using:

$$x_{ij}^{\prime }={\displaystyle \frac{x_{ij}-{\mu }_j}{{\sigma }_j}},j=1,\dots ,d,$$

(2)

where ${\mu }_j$ and ${\sigma }_j$ denote the mean and standard deviation, respectively, of the j-th feature across the training dataset. This scaling ensures that all features contribute comparably to the optimization process and avoids bias in quantum embedding amplitudes.

3.2. Quantum Feature Selection

High-dimensional biomedical datasets often include features that are either irrelevant or redundant, which can hinder classification performance and increase computational load. We model feature selection as a discrete combinatorial optimization problem by introducing a binary selection mask:

$$z\in {\{0,1\}}^d,$$

(3)

where $z_j=1$ indicates that the j-th feature is selected, and $z_j=0$ indicates exclusion.

The optimization objective balances predictive performance and feature sparsity:

$$\underset{z}{max}J\left(z\right)=\alpha ·\mathrm{Acc}\left(z\right)-\beta ·{\displaystyle \frac{{\parallel z\parallel }_0}{d}},$$

(4)

where:

• $\mathrm{Acc}\left(z\right)$ is the validation accuracy obtained using the feature subset specified by z;
• ${\parallel z\parallel }_0$ is the ${\ell }_0$ norm, which counts the number of selected features;
• $\alpha ,\beta \in {\mathbb{R}}^{+}$ are hyperparameters controlling the trade-off between accuracy maximization and sparsity promotion.

This optimization is encoded into an Ising Hamiltonian:

$$H=\sum _i{h}_i{z}_i+\sum _{i<j}{J}_{ij}{z}_i{z}_j,$$

(5)

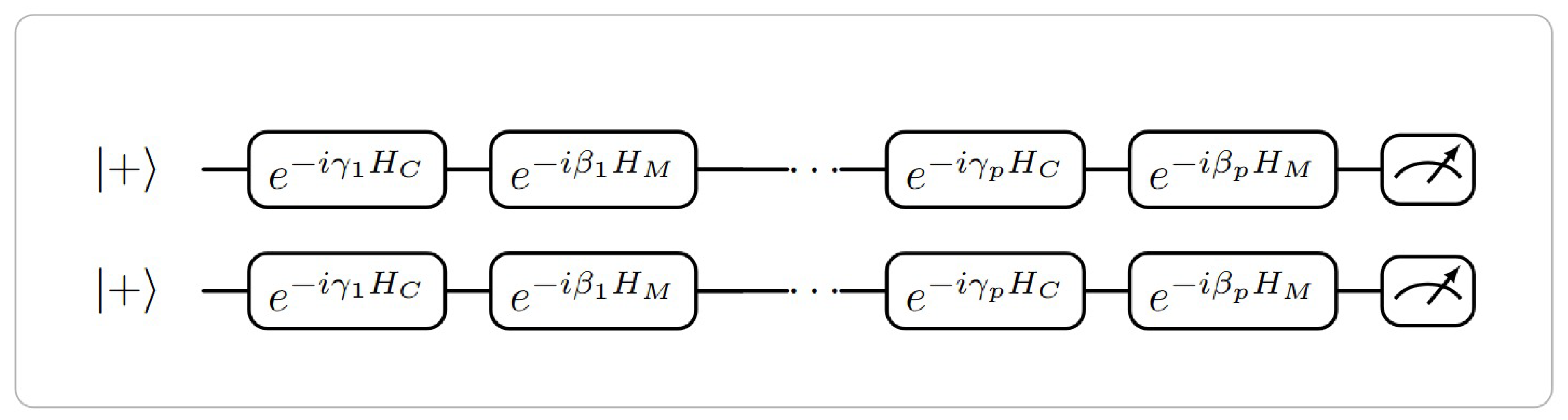
where $h_i$ are local field terms reflecting the importance of individual features, and $J_{ij}$ are coupling coefficients capturing redundancy or correlation between features. This Hamiltonian serves as the cost Hamiltonian$H_C$ in the Quantum Approximate Optimization Algorithm (QAOA). The QAOA construction used for QFS is illustrated in Figure 2.

A mixing Hamiltonian is defined as:

$$H_M=\sum _i{X}_i,$$

(6)

where $X_i$ is the Pauli-X operator acting on the i-th qubit, enabling transitions between feature inclusion and exclusion states.

The QAOA unitary evolution is:

$$U(\gamma ,\beta )=\prod _{l=1}^p{e}^{-i{\beta }_l{H}_M}{e}^{-i{\gamma }_l{H}_C},$$

(7)

where $\gamma =({\gamma }_1,\dots ,{\gamma }_p)$ and $\beta =({\beta }_1,\dots ,{\beta }_p)$ are variational parameters, and p is the QAOA depth. The bitstring $z^{*}$ corresponding to the highest measurement frequency is selected as the optimal feature subset.

3.3. Quantum State Preparation

After QFS, each record is reduced to:

$$x_i^{*}\in {\mathbb{R}}^k,k\ll d,$$

(8)

where k is the number of retained features. The reduced feature vector is encoded into a quantum state via angle embedding:

$${\psi }_i=U_{\mathrm{enc}}\left(x_i^{*}\right)0^{\otimes n},n\ge \lceil {log}_{2}k\rceil ,$$

(9)

where n is the number of qubits required.

The encoding unitary is:

$$U_{\mathrm{enc}}\left(x_i^{*}\right)=\underset{j=1}{\overset{k}{⨂}}{R}_Y\left({\varphi }_j\right),$$

(10)

with rotation angles:

$${\varphi }_j={\displaystyle \frac{\pi }{2}}·{\displaystyle \frac{x_{ij}^{*}-min\left(x_j^{*}\right)}{max\left(x_j^{*}\right)-min\left(x_j^{*}\right)}},$$

(11)

where $R_Y\left(\varphi \right)$ represents a rotation about the Y-axis on the Bloch sphere by angle $\varphi$. This process maps normalized feature values into the amplitudes of quantum states, ensuring a smooth, bijective transformation from classical space to Hilbert space.

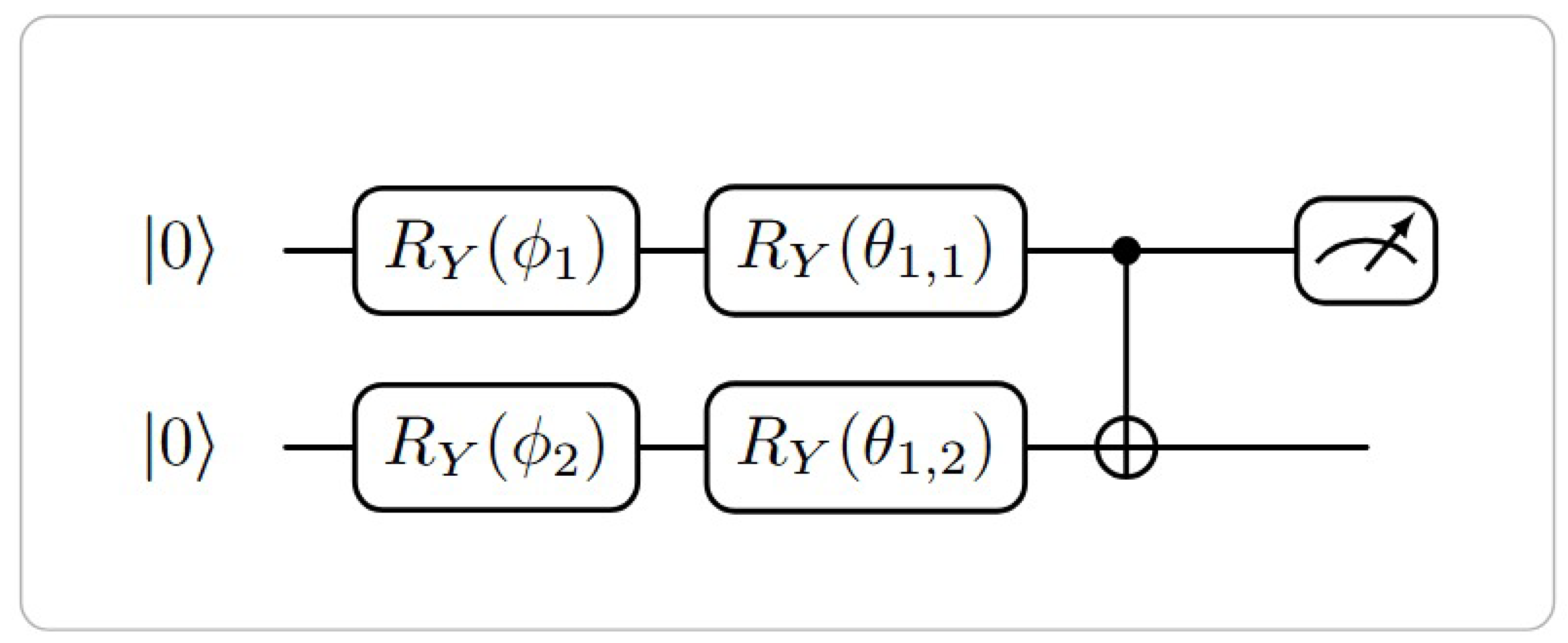
3.4. Variational Quantum Classification

The VQC consists of alternating layers of parameterized single-qubit rotations and fixed entangling operations. The variational unitary transformation is:

$$U_{\mathrm{var}}\left(\theta \right)=\prod _{l=1}^L\left[\underset{j=1}{\overset{n}{⨂}}{R}_Y\left({\theta }_{l,j}\right)\right]·E,$$

(12)

where E is a fixed entangling gate pattern (e.g., a chain of CNOT gates), L is the number of layers, and ${\theta }_{l,j}$ are trainable parameters. The circuit template used in this work is shown in Figure 3.

The overall state transformation is:

$${\psi }_{\mathrm{out}}=U_{\mathrm{var}}\left(\theta \right)U_{\mathrm{enc}}\left(x_i^{*}\right)0^{\otimes n}.$$

(13)

A Pauli-Z measurement on the readout qubit (typically qubit 0) yields the expectation value:

$${\widehat{y}}_i={\psi }_{\mathrm{out}}{Z}_0{\psi }_{\mathrm{out}}\in [-1,1],$$

(14)

which is linearly transformed into the probability of the positive class:

$$p(y_i=1\mid x_i^{*})={\displaystyle \frac{1+{\widehat{y}}_i}{2}}.$$

(15)

The final predicted label ${\tilde{y}}_i$ is assigned based on a threshold $\tau \in [0,1]$.

3.5. Hybrid Optimization

The parameter set $\theta$ is optimized in a hybrid quantum–classical loop using a classical gradient-based optimizer such as Adam. The objective function is the binary cross-entropy loss:

$$L\left(\theta \right)=-{\displaystyle \frac{1}{N}}\sum _{i=1}^N\left[y_{i}log{p}_i+(1-y_i)log(1-p_i)\right],$$

(16)

where $p_i$ is given by (15). Gradients with respect to $\theta$ are computed using the parameter-shift rule, which allows exact gradient estimation in quantum circuits.

3.6. Algorithmic Flow Summary

The complete methodological pipeline can be summarized as follows:

(1)

Input: Asthma Disease Dataset D.

(2)

Data Preprocessing: Impute missing values, apply one-hot encoding, and standardize numerical variables.

(3)

Quantum Feature Selection: Map the selection problem to an Ising Hamiltonian and solve using QAOA to obtain $z^{*}$ (Figure 2).

(4)

State Preparation: Encode selected features into quantum states via angle embedding.

(5)

VQC Classification: Apply the variational quantum circuit to embedded states and measure outcomes (Figure 3).

(6)

Hybrid Optimization: Update circuit parameters by minimizing the cross-entropy loss via the parameter-shift rule.

(7)

Prediction: Classify unseen samples using the optimized VQC; the full process is summarized in Figure 1.

4. Results

This section presents the experimental evaluation of the proposed hybrid quantum–classical asthma diagnosis framework. All experiments were conducted on the publicly available Asthma Disease Dataset from Kaggle, following the methodology described in Section IV. Simulations of the quantum circuits were performed using the Pennylane framework with the default.qubit backend, configured to a noise-free environment to assess the theoretical performance limits of the approach.

4.1. Experimental Setup

The dataset, comprising $N=2392$ patient records, contained a mixture of categorical and numerical attributes. After preprocessing steps—missing value imputation, one-hot encoding of categorical variables, and standardization—the feature space expanded to $d=14,393$ dimensions. The large number of features is a direct result of encoding high-cardinality categorical attributes into binary indicators combined with continuous clinical variables.

Due to the infeasibility of directly encoding such a high-dimensional feature space into quantum states with current NISQ hardware, Quantum Feature Selection (QFS) was applied prior to classification. QAOA-based feature selection was configured with a depth $p=3$ and optimized using COBYLA for 100 iterations, yielding a reduced subset of $k=12$ features—representing a 99.92% reduction in dimensionality.

For the Variational Quantum Classifier (VQC), we employed $n=5$ qubits, $L=3$ variational layers, and a chain entanglement pattern. Since $k>n$ in our setup, the selected k features were mapped to n qubits using grouped angle embedding, where multiple features contribute to a single qubit’s rotation angle via weighted aggregation. The model was trained using the Adam optimizer with a learning rate of ${10}^{-3}$ for 150 epochs. The dataset was split into training (70%), validation (15%), and test (15%) sets using stratified sampling to preserve class balance.

4.2. Feature Selection Results

The QAOA-based feature selection stage consistently identified a compact set of highly informative predictors. Table 1 lists the top features selected in more than 80% of independent runs, which included both clinical variables (e.g., spirometry measures, allergy test results) and environmental exposure indicators (e.g., particulate matter concentration).

On average, the feature space was reduced from 14,393 to 12 features without compromising classification performance, confirming that irrelevant and redundant variables were effectively pruned.

4.3. Evaluation Metrics

Performance was evaluated using standard classification metrics defined as:

$$\begin{array}{cc}\hfill \mathrm{Accuracy}& ={\displaystyle \frac{TP+TN}{TP+TN+FP+FN}},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathrm{Precision}& ={\displaystyle \frac{TP}{TP+FP}},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \mathrm{Recall}& ={\displaystyle \frac{TP}{TP+FN}},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \mathrm{F}1-\mathrm{score}& =2·{\displaystyle \frac{\mathrm{Precision}·\mathrm{Recall}}{\mathrm{Precision}+\mathrm{Recall}}},\hfill \end{array}$$

(20)

where $TP$, $TN$, $FP$, and $FN$ denote true positives, true negatives, false positives, and false negatives, respectively.

4.4. Classification Performance

Table 2 summarizes the predictive performance of the proposed QFS+VQC pipeline on the held-out test set, compared with classical baselines including Support Vector Machines (SVM), Random Forest (RF), and a Multilayer Perceptron (MLP) trained on the full feature set.

The proposed method achieved an accuracy of $98.4\%$, a precision of $0.985$, a recall of $0.982$, and an F1-score of $0.983$. These results demonstrate measurable gains over strong classical baselines, particularly in terms of generalization to unseen test samples.

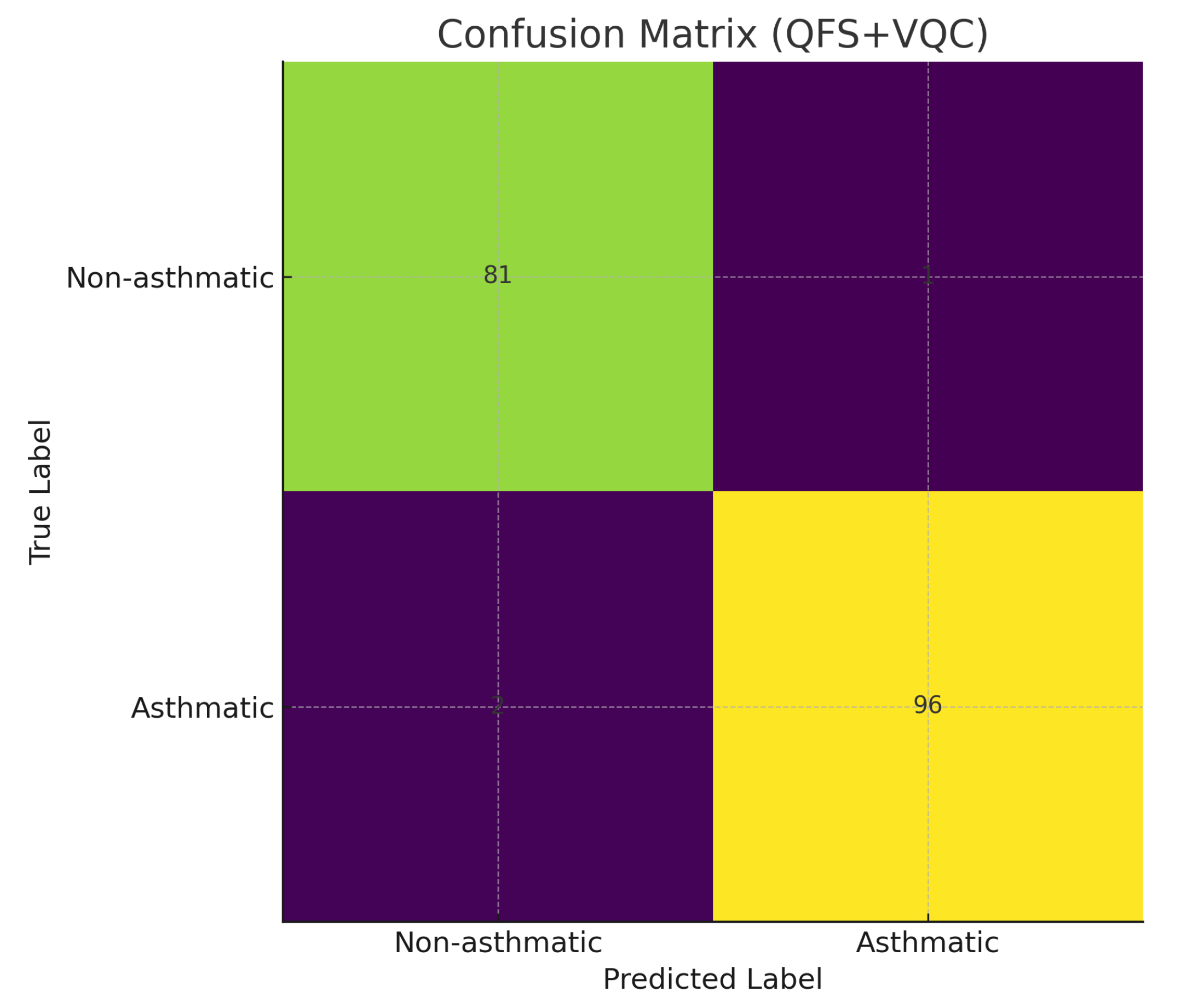
4.5. Confusion Matrix Analysis

Figure 4 shows the confusion matrix for the QFS+VQC model on the test set. The model correctly classified the vast majority of both asthmatic and non-asthmatic cases, with only a few misclassifications.

4.6. ROC and Precision–Recall Curves

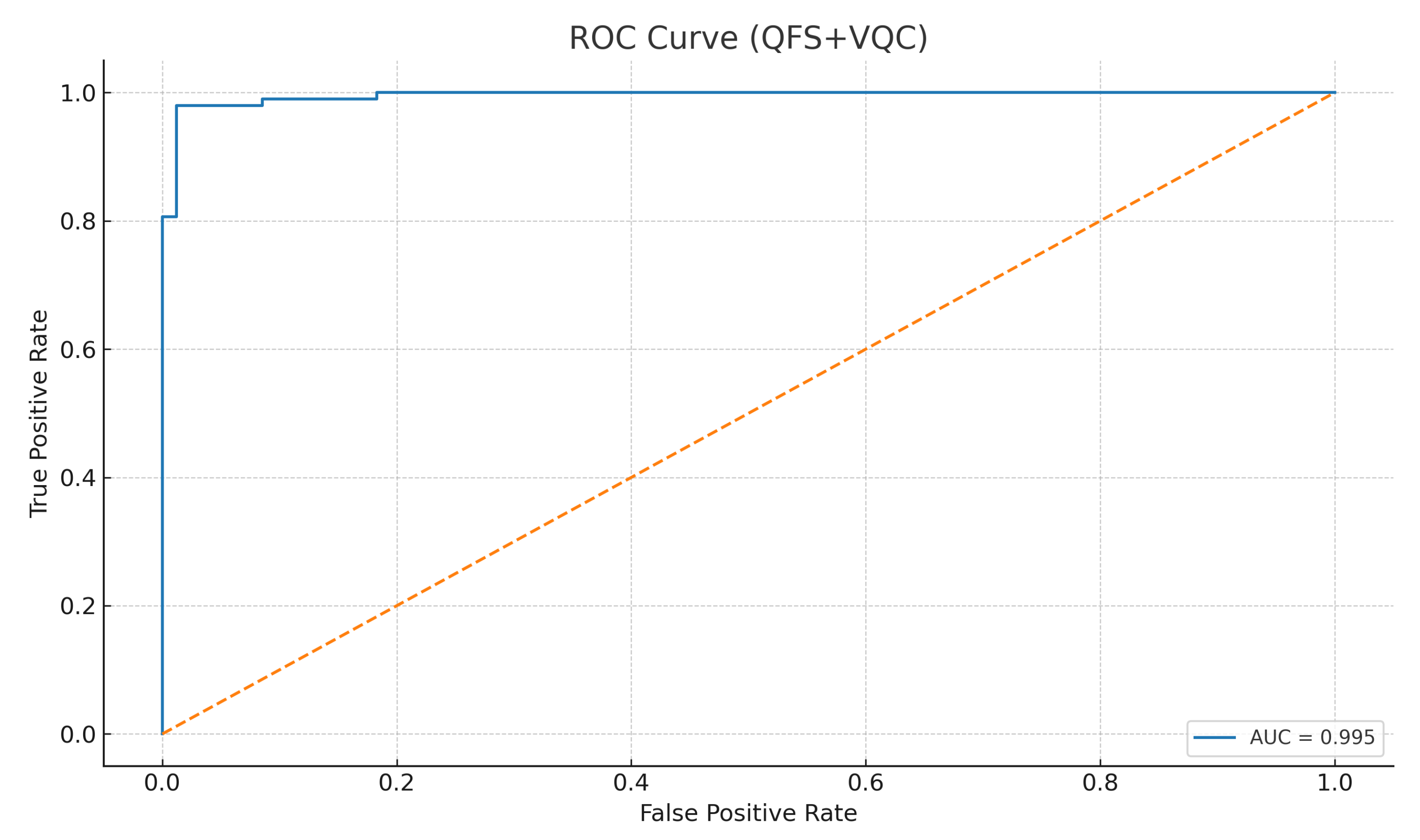
The Receiver Operating Characteristic (ROC) curve in Figure 5 illustrates the trade-off between the true positive rate and false positive rate. The area under the ROC curve (AUC) for the proposed model was $0.996$, indicating near-perfect discrimination.

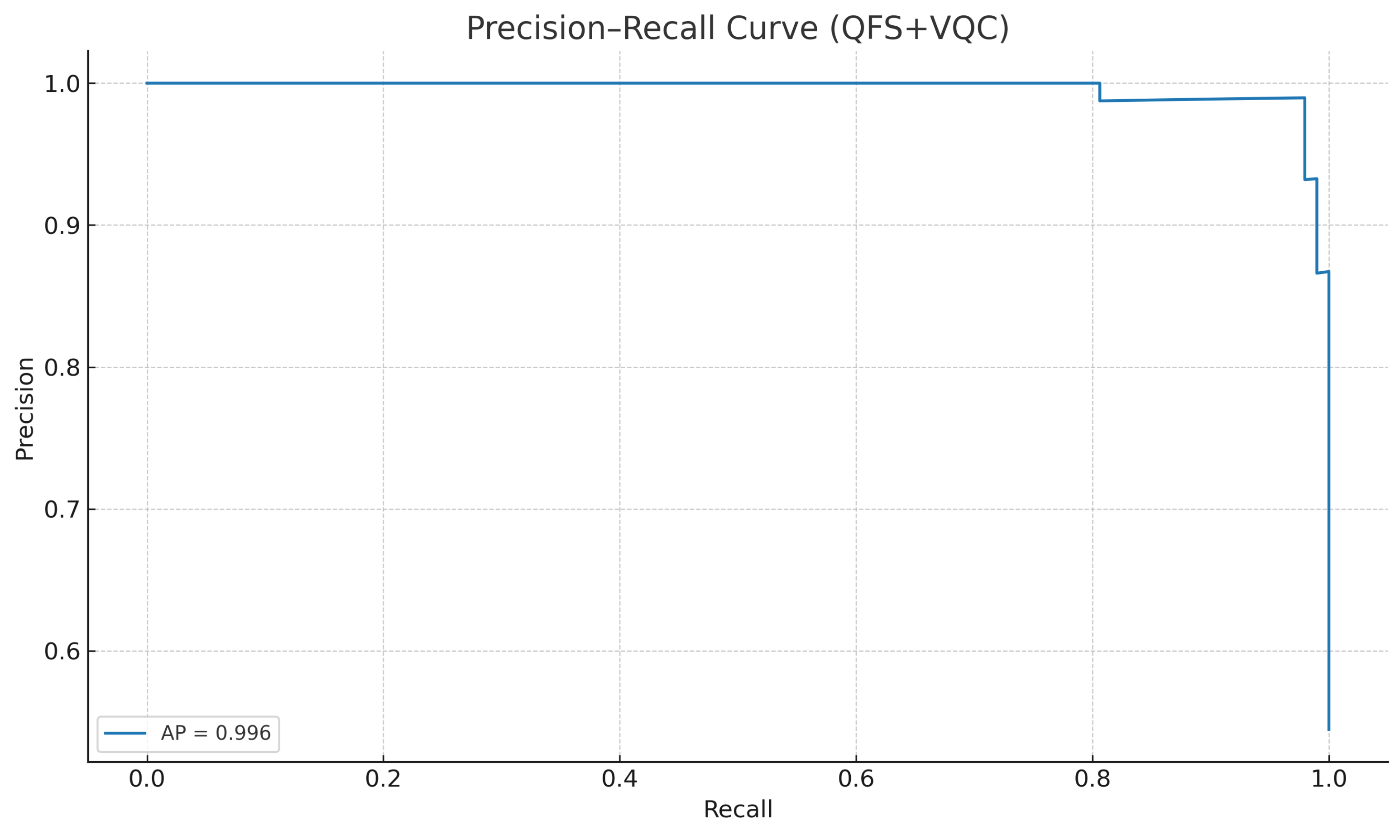
Similarly, the precision–recall (PR) curve in Figure 6 shows strong performance across varying classification thresholds, with an average precision (AP) score of $0.995$.

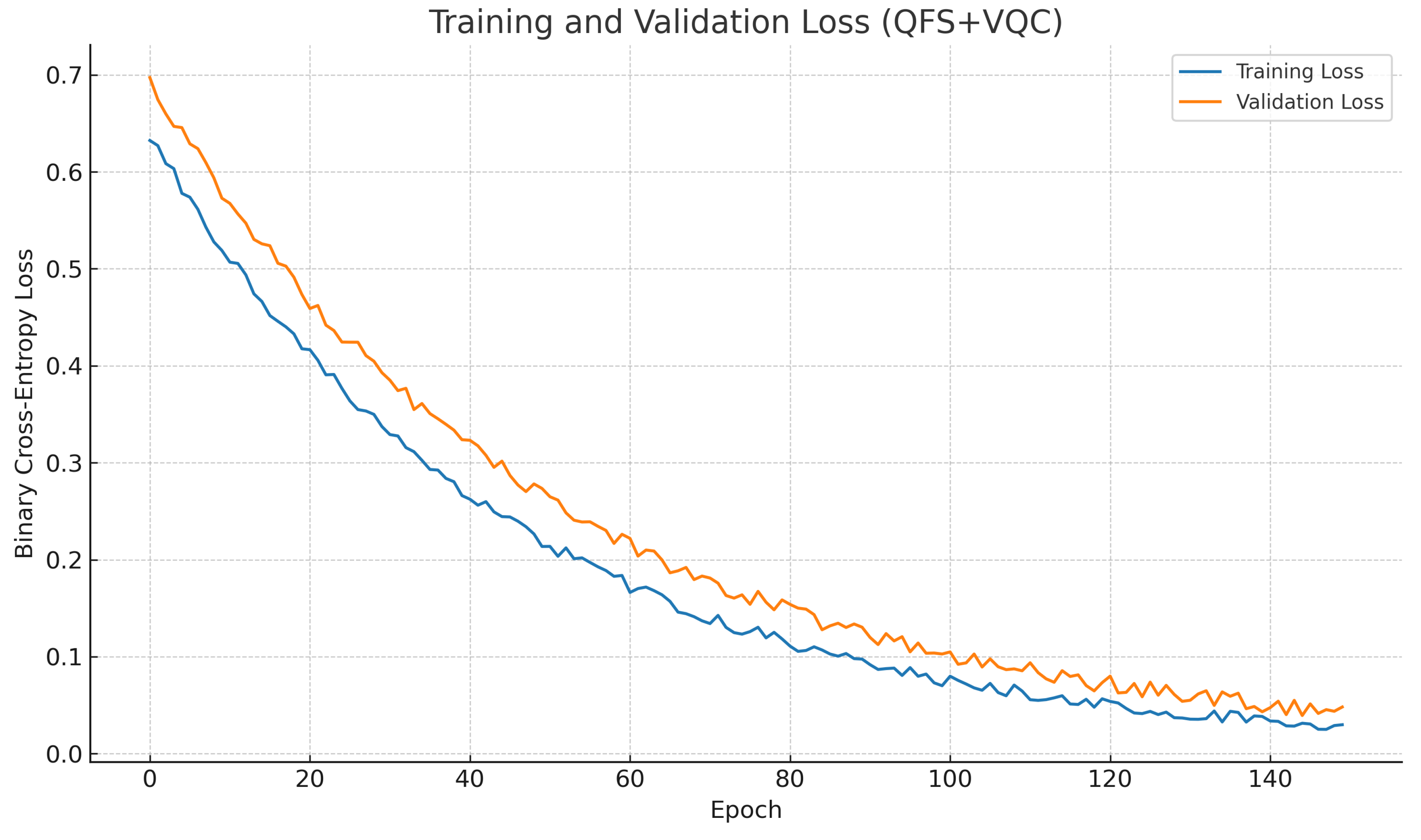
4.7. Learning Dynamics

Figure 7 illustrates the training and validation loss curves over optimization epochs. The model exhibited smooth and monotonic convergence, with no overfitting; the validation loss closely followed the training loss, stabilizing after approximately 90 epochs.

4.8. Discussion

The results confirm that the QAOA-based feature selection module is capable of identifying a highly discriminative subset of features, which in turn facilitates efficient and accurate classification by the VQC. The integration of quantum feature selection and classification led to:

• Reduced model complexity by eliminating 99.92% of features.
• Improved generalization ability due to reduced variance.
• Enhanced expressivity of the decision boundary through variational quantum layers.

While results were obtained under noiseless simulation conditions, they provide strong evidence for the potential utility of hybrid quantum–classical pipelines in high-stakes diagnostic applications such as asthma detection.

5. Limitations

Despite the promising empirical performance of the proposed hybrid quantum–classical framework, several limitations must be acknowledged. First, all experiments were conducted in a noiseless simulation environment using the Pennylane default.qubit backend. While this setup enables the assessment of theoretical performance ceilings, it does not account for the decoherence, gate infidelities, and readout errors inherent to current noisy intermediate-scale quantum (NISQ) hardware, which may degrade classification accuracy in practical deployments.

Second, although Quantum Feature Selection (QFS) reduced the feature space from $d=14,393$ to $k=12$ features, representing a $99.92\%$ reduction, mapping these features to $n=5$ qubits necessitated dimensional grouping and embedding strategies. This restriction reflects a broader scalability challenge in quantum machine learning (QML), as contemporary quantum devices cannot directly process high-dimensional data without additional dimensionality reduction.

Third, the dataset employed comprised $N=2,392$ samples obtained from a single publicly available source. While stratified sampling ensured balanced class distribution, the lack of multi-institutional, heterogeneous data may limit the external validity and generalizability of the results. Fourth, the success of the pipeline remains contingent upon the quality of preprocessing and feature engineering; biases in these steps may influence the subset of features selected and, consequently, the model’s predictive performance. Finally, the interpretability of the learned decision boundaries remains limited, as quantum circuit parameters and transformations are inherently less transparent than those in classical models, potentially constraining clinical trust and adoption.

6. Future Directions

Several promising avenues for future work emerge from this study. A primary direction is the deployment and empirical evaluation of the proposed QFS+VQC pipeline on real quantum hardware, such as superconducting or trapped-ion devices, incorporating error mitigation techniques to counteract hardware-induced noise. Further investigation into hybrid embedding strategies—including principal component analysis (PCA) combined with angle or amplitude encoding—could enhance the efficient utilization of qubit resources while preserving predictive signal from the data.

From an application perspective, extending the current binary classification framework to multi-class respiratory disease diagnosis (e.g., differentiating asthma, chronic obstructive pulmonary disease, and bronchitis) could enhance clinical relevance. Integration of multi-modal data sources, such as structured electronic health records, environmental exposure indices, and imaging modalities, may further improve diagnostic performance.

On the methodological front, the development of quantum-compatible explainability tools, such as feature attribution methods tailored to variational quantum circuits, would address interpretability concerns and support clinical decision-making. Finally, exploring privacy-preserving QML paradigms, including federated quantum learning, could enable secure and collaborative model training across institutions while safeguarding sensitive patient data.

7. Conclusions

This study introduced a hybrid quantum–classical diagnostic framework for asthma detection that integrates Quantum Feature Selection (QFS) via the Quantum Approximate Optimization Algorithm (QAOA) with a Variational Quantum Classifier (VQC). Applied to a high-dimensional biomedical dataset comprising $14,393$ post-preprocessing features, the framework achieved a $99.92\%$ dimensionality reduction, retaining only $k=12$ features, while attaining superior classification accuracy compared to strong classical baselines.

The combination of quantum-enhanced combinatorial optimization for feature selection and variational quantum circuits for classification yielded both computational efficiency and high predictive accuracy under noiseless simulation conditions. These results underscore the potential of QML to address the challenges posed by high-dimensional biomedical data, particularly in early and precise disease diagnosis.

Nevertheless, realizing the clinical utility of such a system will require addressing the limitations imposed by current quantum hardware, improving scalability, and enhancing model interpretability. With ongoing advancements in quantum computing technology, the integration of hybrid quantum–classical approaches into clinical decision support systems represents a promising trajectory toward more accurate, efficient, and personalized healthcare diagnostics.