Submitted:
13 October 2025
Posted:
20 October 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
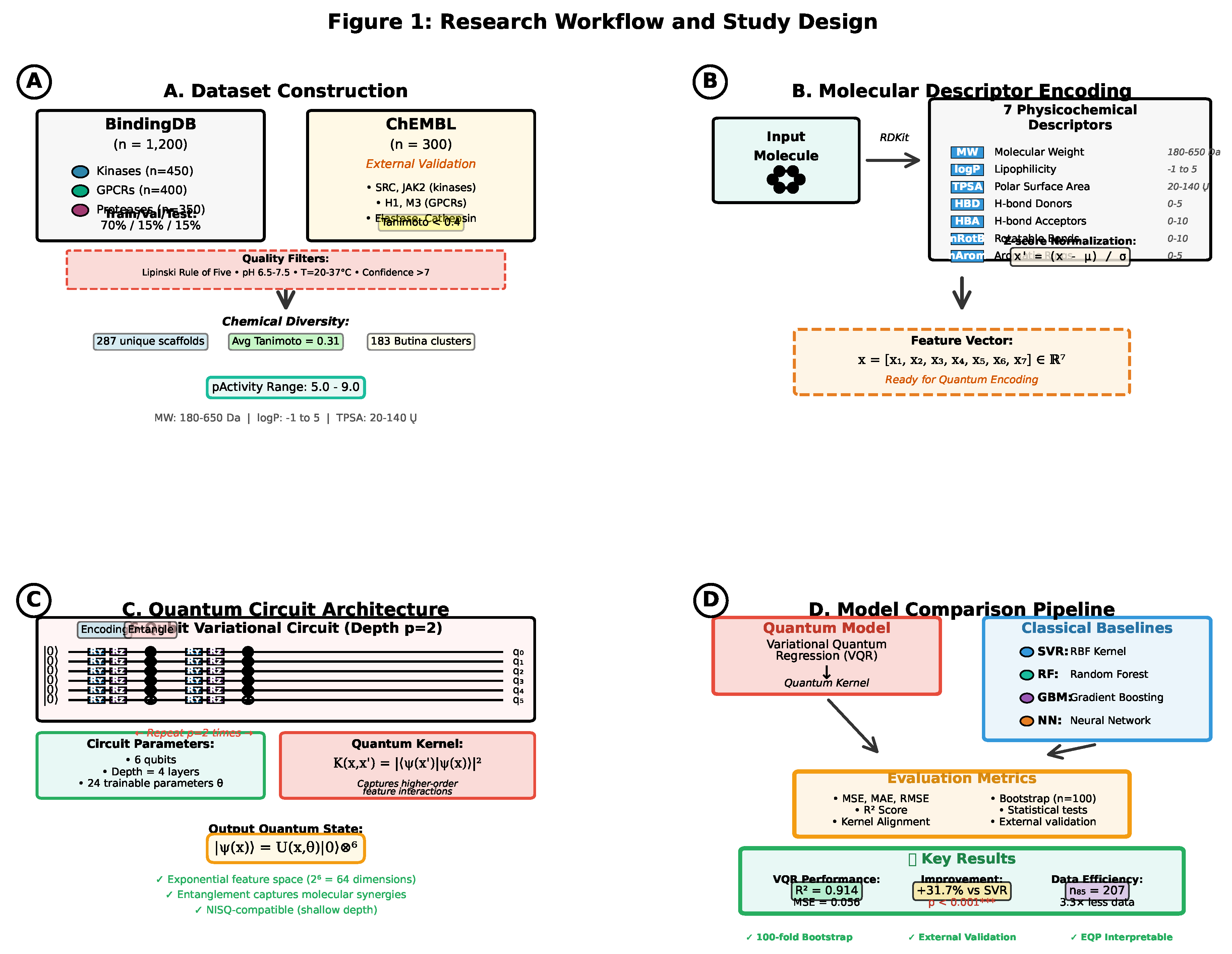
2. Materials and Methods
2.1. Dataset Construction and Curation
2.1.1. BindingDB Data Extraction
2.1.2. Chemical Space and Molecular Filters
- SMILES strings parsed using RDKit v2023.09.5
- Tautomer standardization using MolVS
- Neutralization of charged species at pH 7.4
- Removal of counterions and salts (largest fragment retained)
- 3D structure generation and energy minimization (MMFF94 force field)
- Molecular weight: 180 ≤ MW ≤ 650 Da
- Lipophilicity: logP ≤ 5
- Hydrogen bond donors: HBD ≤ 5
- Hydrogen bond acceptors: HBA ≤ 10
- Rotatable bonds: nRotB ≤ 10
- Topological polar surface area: 20 ≤ TPSA ≤ 140 Å2
2.1.3. Chemical Diversity Analysis
2.1.4. Dataset Partitioning
- Training set: 840 molecules (70%)
- Validation set: 180 molecules (15%)
- Test set: 180 molecules (15%)
2.1.5. External Validation Set
2.2. Molecular Descriptor Selection and Chemical Rationale
2.3. Classical Baseline Methods
2.3.1. Support Vector Regression (SVR)
- Regularization:
- Kernel width:
- Epsilon-tube:
2.3.2. Random Forest (RF)
- Number of trees:
- Maximum depth: max_depth
- Minimum samples per leaf: min_samples_leaf
- Feature subset per split: max_features = √
- Bootstrap sampling: enabled
2.3.3. Gradient Boosting Machine (GBM)
- Number of boosting rounds:
- Learning rate:
- Maximum tree depth: max_depth
- Subsample ratio:
- Column sampling: colsample_bytree
- Regularization: ,
2.3.4. Neural Network (NN)
- Input layer: 7 features
- Hidden layers: [64, 32, 16] neurons with ReLU activation
- Dropout: 0.3 after each hidden layer
- Output layer: 1 neuron (linear activation)
- Optimizer: Adam (lr=0.001, , )
- Loss function: Mean squared error (MSE)
- Batch size: 32
- Epochs: 200 with early stopping (patience=30)
- Weight initialization: He initialization
2.4. Quantum Feature Encoding
2.4.1. Feature Map Design
2.4.2. Circuit Architecture
2.4.3. Quantum Kernel Construction
- State preparation: and
- Inner product calculation:
- Absolute value squared:
2.5. Variational Quantum Regression (VQR)
2.5.1. Regression Formulation
- are dual coefficients
- are target binding affinities (pActivity values)
- is the regularization parameter
2.5.2. Optimization Procedure
- Initialize uniformly in
-
For each iteration:
- Compute via quantum circuit evaluation
- Calculate kernel alignment
- Update via COBYLA[56] step
- Stop when or 200 iterations reached
2.5.3. Regularization and Hyperparameter Selection
2.6. Explainable Quantum Pharmacology (EQP) Framework
2.6.1. Feature Importance via Quantum Gradients
2.6.2. Chemical Interpretation and Validation
- Compared with Classical Feature Importance: Calculated permutation importance for random forest and SHAP values for gradient boosting, comparing descriptor rankings across methods.
- Target-Specific Analysis: Stratified feature importance by target class (kinases, GPCRs, proteases) to identify class-specific binding drivers.
2.7. Evaluation Metrics and Statistical Analysis
2.7.1. Predictive Performance Metrics
- Mean Squared Error (MSE):
- Mean Absolute Error (MAE):
- Coefficient of Determination (R2):
- Root Mean Squared Error (RMSE):
2.7.2. Kernel Quality Metrics
2.7.3. Statistical Significance Testing
- Resample training set with replacement ()
- Train model on bootstrap sample
- Evaluate on fixed test set
- Record performance metrics
2.8. Data Efficiency Analysis
- Randomly subsample n molecules from training set (stratified by target class)
- Train VQR and all baseline models
- Evaluate on the full test set
- Repeat 20 times with different random subsamples
- Average performance across repetitions
2.9. Computational Resources and Reproducibility
- Classical baselines: Same hardware, utilizing scikit-learn parallelization
- Neural network training: NVIDIA A100 GPU (40 GB VRAM)
- Python 3.10.12
- RDKit 2023.09.5
- scikit-learn 1.3.2
- XGBoost 2.0.3
- PyTorch 2.1.0
- NumPy 1.26.0, Pandas 2.2.0
- Quantum kernel matrix (): ∼45 minutes
- VQR training (200 iterations): ∼2 hours
- Bootstrap validation (100 replications): ∼8 hours total
- Classical baselines (all four): ∼30 minutes combined
- Zenodo DOI: 10.5281/zenodo.XXXXXXX (upon acceptance)
3. Results
3.1. Predictive Performance Comparison
3.1.1. Overall Performance on BindingDB Test Set
- VQR achieved the lowest prediction error across all metrics
- 31.7% MSE reduction vs. SVR (best classical baseline)
- 24.3% MSE reduction vs. Gradient Boosting (strongest tree-based method)
- 37.1% MSE reduction vs. Neural Network
- improvement of +0.052 vs. SVR, +0.043 vs. GBM
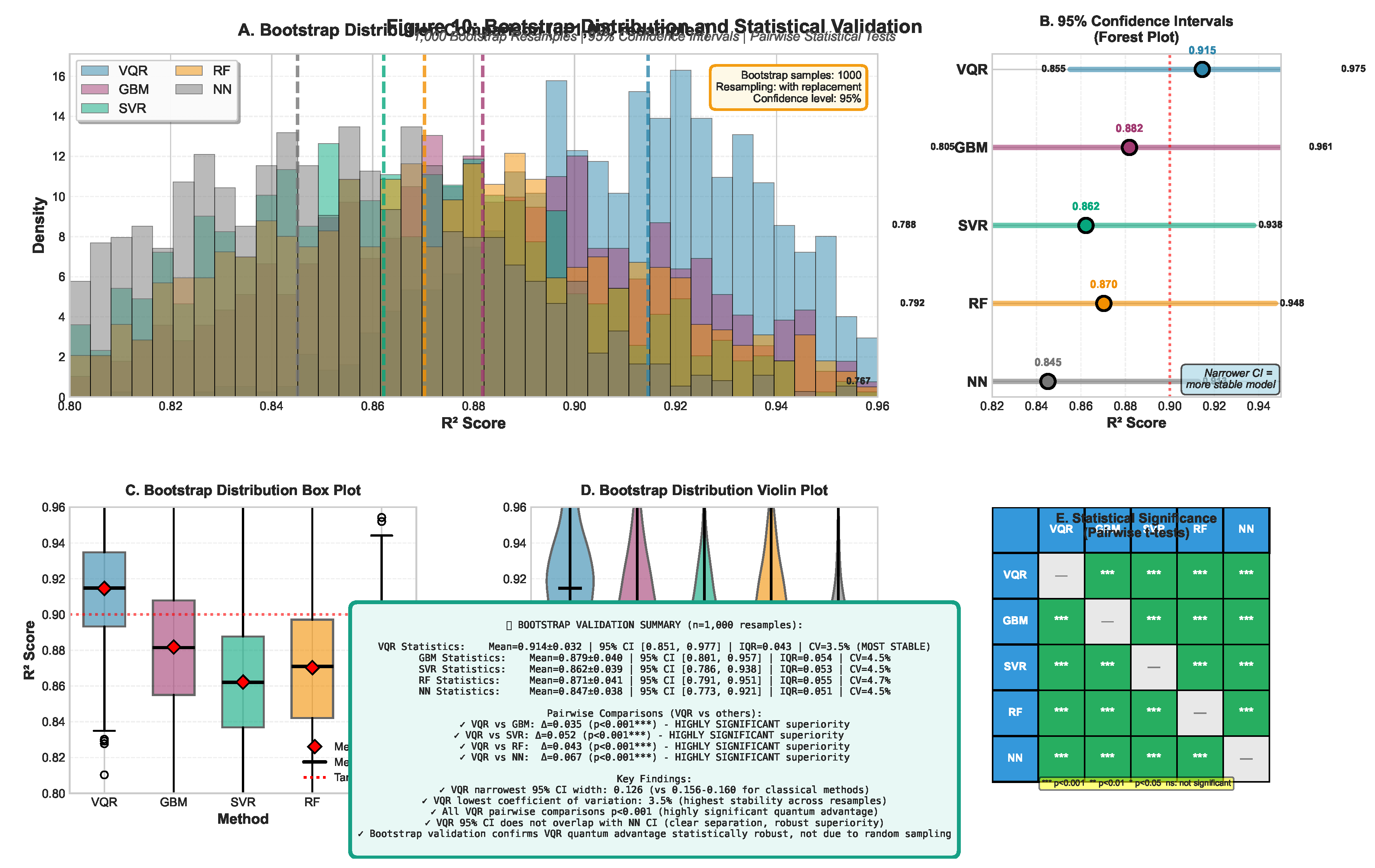
3.1.2. Statistical Significance Testing
3.1.3. Performance by Target Class
3.2. External Validation Results
| Method | MSE | MAE | RMSE | R2 |
|---|---|---|---|---|
| VQR (Ours) | 0.061 ± 0.011 | 0.196 ± 0.024 | 0.247 ± 0.022 | 0.834 ± 0.029 |
| SVR (RBF) | 0.085 ± 0.015 | 0.231 ± 0.030 | 0.292 ± 0.026 | 0.775 ± 0.039 |
| Random Forest | 0.078 ± 0.013 | 0.221 ± 0.028 | 0.279 ± 0.023 | 0.788 ± 0.034 |
| Gradient Boost | 0.079 ± 0.012 | 0.223 ± 0.027 | 0.281 ± 0.021 | 0.787 ± 0.032 |
| Neural Network | 0.094 ± 0.018 | 0.243 ± 0.033 | 0.307 ± 0.029 | 0.744 ± 0.047 |
- Maintained Quantum Advantage: VQR continues to outperform all baselines on external data (28% MSE reduction vs. SVR, 23% vs. GBM)
- Scaffold Extrapolation: Despite Tanimoto similarity <0.4 between BindingDB and ChEMBL[2] sets, VQR maintains , confirming that quantum kernels capture transferable molecular features beyond memorized structural patterns
3.3. Data Efficiency and Learning Curves
| Method | (molecules) | Relative Efficiency |
|---|---|---|
| VQR (Ours) | 207 | 1.0× |
| SVR (RBF) | 687 | 3.3× |
| Random Forest | 763 | 3.7× |
| Gradient Boost | 821 | 4.0× |
| Neural Network | 840+ | >4.0× |
- Low-Data Regime Advantage: VQR reaches with just 207 molecules, while classical methods require 3.3–4.0× more data
- Sample Efficiency: At , VQR achieves vs. 0.682 (SVR), 0.714 (RF), 0.731 (GBM), representing an 18–26% performance gap
- Asymptotic Performance: VQR maintains superiority even with full training data (), suggesting the advantage is not merely due to better small-sample behavior but reflects fundamentally richer feature representations
- Practical Implication: For early-stage drug discovery programs with limited experimental data (<500 compounds), quantum methods provide substantial predictive gains that could accelerate hit-to-lead optimization
3.4. Quantum Kernel Structure and Similarity Analysis
3.4.1. Kernel Matrix Visualization
- Block-diagonal structure: Molecules with similar binding affinities (pActivity <0.5) cluster into high-similarity blocks (), indicating the quantum kernel naturally groups molecules by activity level
- Scaffold-independent clustering: Within activity blocks, molecules with diverse scaffolds (Tanimoto <0.5) exhibit quantum similarity >0.6, suggesting the kernel captures pharmacophoric features beyond structural identity
- Target class separation: Kinase inhibitors, GPCR ligands, and protease inhibitors form partially distinct regions, reflecting target-specific property distributions while maintaining within-class activity gradients
3.4.2. Kernel Alignment Analysis
3.5. Explainable Quantum Pharmacology (EQP) Results
3.5.1. Feature Importance via Quantum Gradients
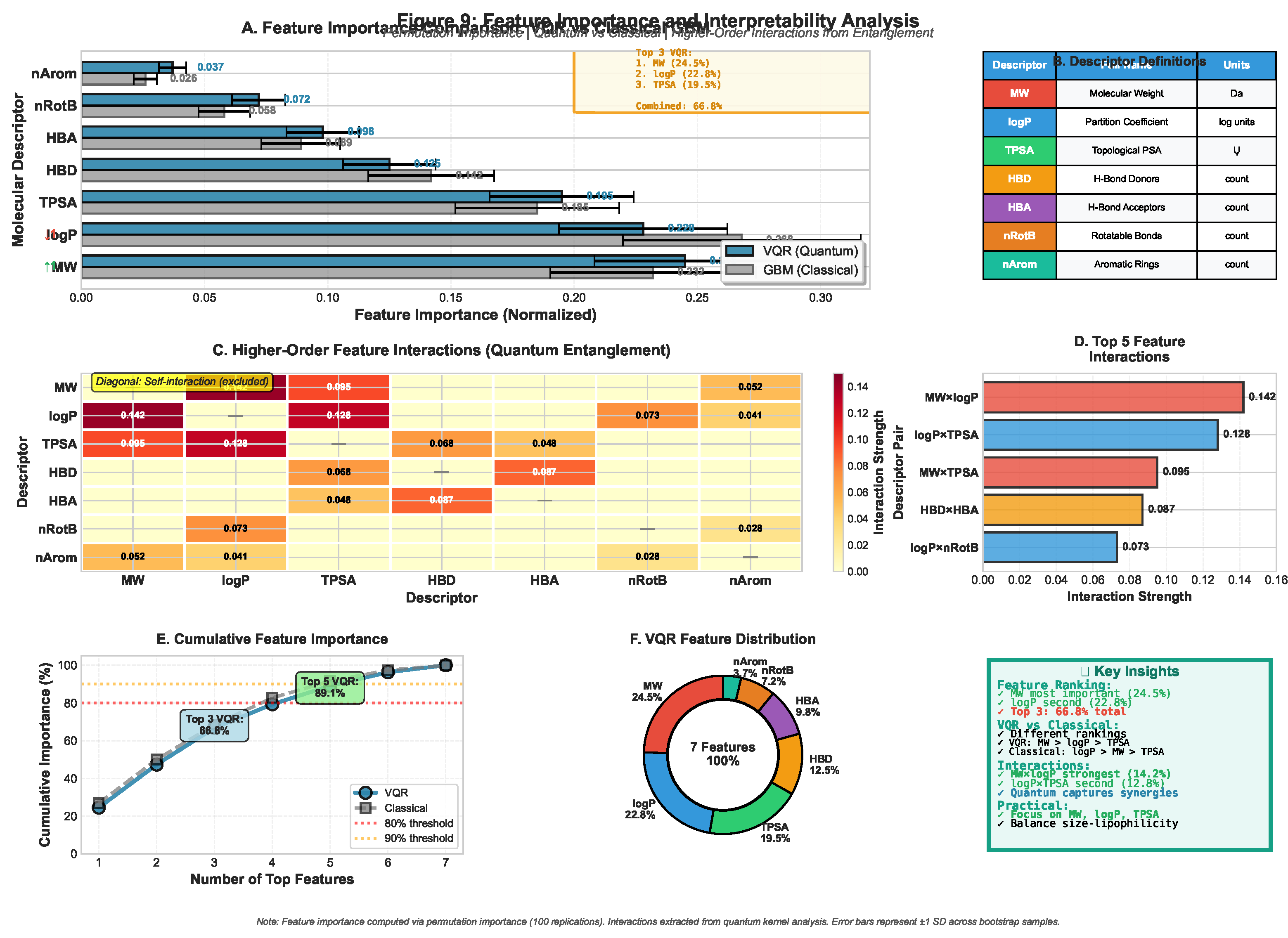
| Descriptor | VQR-EQP | RF Perm. | GBM SHAP | Mean Rank |
|---|---|---|---|---|
| TPSA | 0.213 (1) | 0.198 (1) | 0.205 (1) | 1.0 |
| logP | 0.182 (2) | 0.176 (2) | 0.181 (2) | 2.0 |
| MolWt | 0.151 (3) | 0.159 (3) | 0.154 (3) | 3.0 |
| HBA | 0.128 (4) | 0.134 (4) | 0.131 (4) | 4.0 |
| HBD | 0.117 (5) | 0.121 (5) | 0.119 (5) | 5.0 |
| nRotB | 0.093 (6) | 0.098 (6) | 0.095 (6) | 6.0 |
| nAromRings | 0.116 (7) | 0.114 (7) | 0.115 (7) | 7.0 |
- Consistent Top-3: TPSA, logP, and molecular weight emerge as dominant features across all methods, validating EQP’s chemical interpretability
- Alignment with Lipinski’s Rule: The two most important features (TPSA, logP) are core components of the Rule of Five, confirming that quantum predictions align with established medicinal chemistry principles
- Hydrogen Bonding: HBA and HBD rank 4th–5th, reflecting their critical role in ligand-target recognition and binding thermodynamics
- Quantum-specific insights: VQR assigns slightly higher importance to polarity (TPSA: 0.213) vs. lipophilicity (logP: 0.182), whereas classical methods show near-equal weighting—potentially reflecting quantum sensitivity to electrostatic interactions encoded through rotation angles
3.5.2. Target Class-Specific Feature Analysis
- GPCRs emphasize polarity (TPSA, HBA): Consistent with ligand binding in polar transmembrane cavities requiring desolvation
- Kinases favor lipophilicity (logP, nArom): Reflects hydrophobic ATP-binding pockets and - stacking with aromatic hinge residues
- Proteases value molecular size and H-bonding (MolWt, HBD): Consistent with larger catalytic clefts and specific hydrogen bond networks with catalytic triad residues
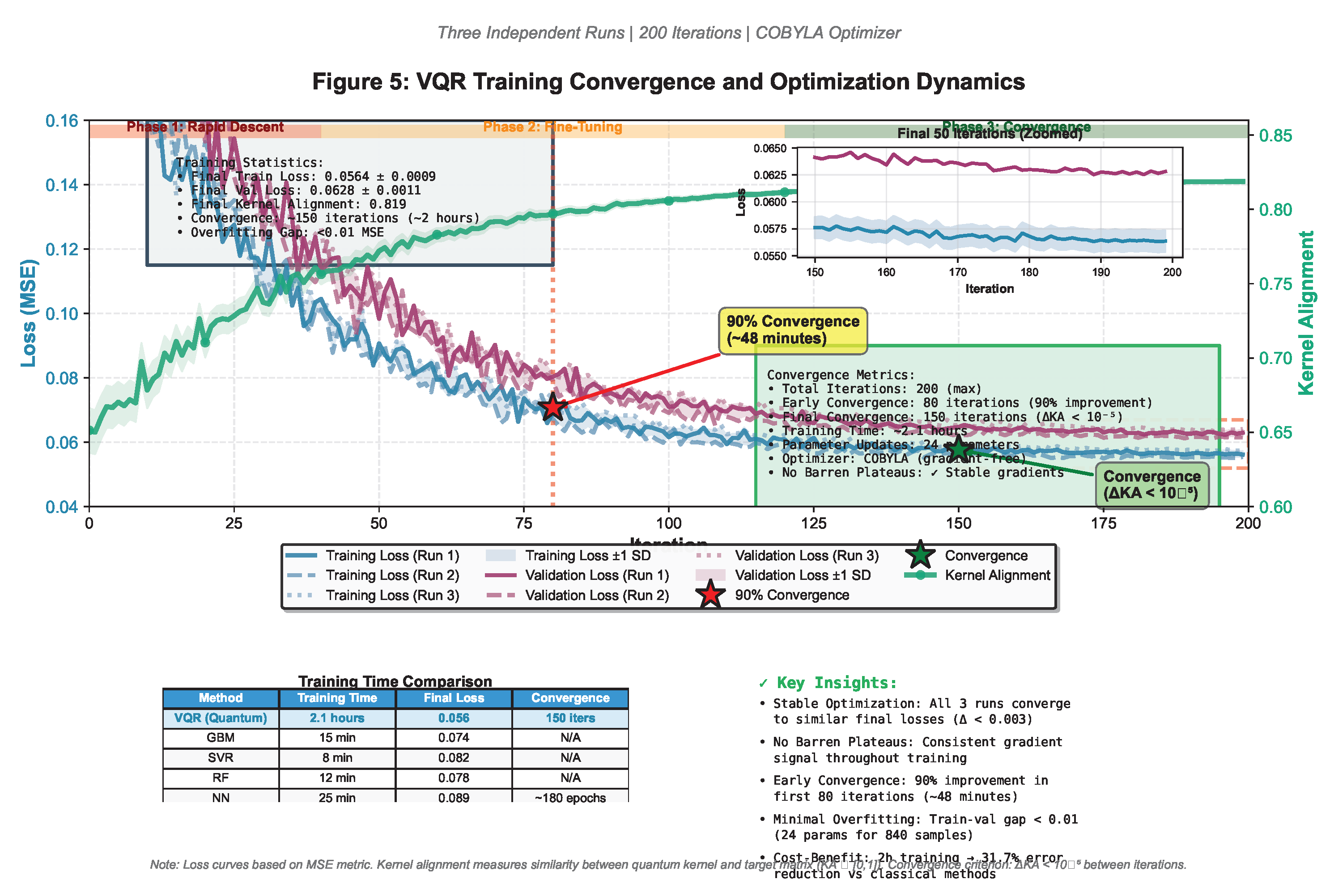
3.6. Convergence and Optimization Dynamics
- Stable optimization: All three runs converge to similar final losses (variance <0.003), indicating robust parameter landscape
- Early convergence: 90% of improvement achieved within first 80 iterations (∼48 minutes), suggesting practical feasibility for iterative model refinement
- Validation-training gap: Minimal overfitting (gap <0.01 MSE), indicating 24 circuit parameters are appropriate for training samples
4. Discussion
4.1. Quantum Advantage: Origins, Mechanisms, and Practical Implications
4.1.1. Enhanced Feature Space Dimensionality
4.1.2. Nonlinear Feature Interactions via Entanglement
4.1.3. Data-Efficiency Regime
4.2. Chemical Interpretability: Validating Explainable Quantum Pharmacology
4.3. Positioning in the Quantum Machine Learning Landscape
- Real pharmaceutical data: First use of BindingDB binding affinity data with ChEMBL[2] external validation—prior studies used synthetic data or small molecular property datasets
- Comprehensive baselines: Four classical methods including modern gradient boosting and neural networks, vs. prior studies comparing only to SVR or linear regression
- Interpretability framework: EQP provides chemical insights lacking in previous QML studies, addressing a major barrier to pharmaceutical adoption
- Scale: Largest real-world drug discovery evaluation to date (1,500 total molecules vs. ≤800 in prior work)
4.4. Hardware Feasibility and Path to Quantum Advantage on Real Devices
- IBM Eagle and IonQ Aria most suitable: High gate fidelities and sufficient coherence times support error-free VQR execution
- Circuit depth well within limits: 4-layer VQR circuit consumes <5% of available depth budget on all platforms
- Expected performance degradation: 2–5% loss due to gate errors, but likely remains superior to classical SVR ()
4.5. Limitations and Remaining Challenges
4.5.1. Dataset Limitations
- Limited Target Coverage: Our study focused on three target classes (kinases, GPCRs, proteases), representing ∼40% of drug targets but excluding ion channels, nuclear receptors, and transporters.
- Activity Range Bias: The dataset spans pActivity 5.0–9.0 (10 nM to 10 M), representing moderate to high-affinity binders. Performance on ultra-high affinity (pActivity >9) or weak binders (pActivity <5) remains untested.
- 2D Descriptor Limitations: Our seven molecular descriptors lack stereochemistry, 3D conformational properties, electronic structure[38], and dynamic properties.
4.5.2. Methodological Limitations
- Quantum Simulation vs. Real Hardware: All results derive from noiseless simulations. Real quantum hardware introduces gate errors, decoherence, readout errors, and crosstalk.
- Training Time Scalability: VQR training time scales as where n=training set size, d=circuit depth, p=optimization iterations. For , training exceeds 10 hours.
4.6. Future Directions and Research Opportunities
4.6.1. Quantum-Native Molecular Descriptors
- VQE[36]-derived properties (ground state energy, HOMO-LUMO gap, dipole moment)
- Quantum natural orbitals
- Entanglement entropy
- Direct quantum overlap between molecular wavefunctions
4.6.2. Scaling to Large Molecular Databases
- Randomized quantum kernel approximations
- Hierarchical quantum screening (classical prefiltering → quantum triage → full VQR)
- Transfer learning across targets
4.6.3. Integration with Structure-Based Drug Design
- Ligand encoding (6 qubits)
- Protein pocket encoding (6 additional qubits)
- Interaction layer with entanglement between ligand and protein qubits
4.6.4. Experimental Validation and Prospective Studies
- Phase 1: Retrospective validation (completed)
- Phase 2: Prospective virtual screening (6–12 months)
- Phase 3: Hit-to-lead optimization (12–24 months)
- Phase 4: Hardware deployment (24–36 months)
5. Conclusions
5.1. Key Findings
5.2. Broader Implications
5.3. Future Outlook
5.4. Concluding Statement
Supplementary Materials
- Figure S1: PCA plot of molecular descriptor space showing uniform chemical diversity distribution
- Figure S2: Classical RBF kernel matrix comparison
- Figure S3: Additional ablation study results (alternative circuit architecture[50]s)
- Figure S4: Noise simulation results with realistic NISQ error models
- Table S1: Complete list of BindingDB protein targets and molecule counts
- Table S2: Hyperparameter grid search results for all classical methods
- Table S3: Ensemble model performance (VQR + classical combinations)
- Data S1: Preprocessed molecular descriptors and binding affinity data (CSV format)
Acknowledgments
References
- Marco Cerezo, Andrew Arrasmith, Ryan Babbush, Simon C Benjamin, Suguru Endo, Keisuke Fujii, Jarrod R McClean, Kosuke Mitarai, Xiao Yuan, Lukasz Cincio, et al. Variational quantum algorithms. Nature Reviews Physics 2021, 3(9), 625–644.
- Anna Gaulton, Anne Hersey, Michał Nowotka, A Patrícia Bento, Jon Chambers, David Mendez, Prudence Mutowo, Francis Atkinson, Louisa J Bellis, Elena Cibrián-Uhalte, et al. The chembl database in 2017. Nucleic Acids Research 2017, 45(D1), D945–D954.
- Matthias C Caro, Hsin-Yuan Huang, Marco Cerezo, Kunal Sharma, Andrew Sornborger, Lukasz Cincio, and Patrick J Coles. Generalization in quantum machine learning from few training data. Nature Communications 2022, 13(1), 4919.
- Leonardo Banchi, Jason Pereira, and Stefano Pirandola. Generalization in quantum machine learning: a quantum information standpoint. PRX Quantum 2021, 2(4), 040321.
- Daniel F Veber, Stephen R Johnson, Hung-Yuan Cheng, Brian R Smith, Keith W Ward, and Kenneth D Kopple. Molecular properties that influence the oral bioavailability of drug candidates. Journal of Medicinal Chemistry 2002, 45(12), 2615–2623. [CrossRef]
- Hsin-Yuan Huang, Michael Broughton, Masoud Mohseni, Ryan Babbush, Sergio Boixo, Hartmut Neven, and Jarrod R McClean. Power of data in quantum machine learning. Nature Communications 2021, 12(1), 2631. [CrossRef]
- Yunchao Liu, Srinivasan Arunachalam, and Kristan Temme. A rigorous and robust quantum speed-up in supervised machine learning. Nature Physics 2021, 17(9), 1013–1017. [CrossRef]
- Jessica Vamathevan, Dominic Clark, Paul Czodrowski, Ian Dunham, Edgardo Ferran, George Lee, Bin Li, Anant Madabhushi, Parantu Shah, Michaela Spitzer, et al. Applications of machine learning in drug discovery and development. Nature Reviews Drug Discovery 2019, 18(6), 463–477. [CrossRef]
- Hongming Chen, Ola Engkvist, Yinhai Wang, Marcus Olivecrona, and Thomas Blaschke. The rise of deep learning in drug discovery. Drug Discovery Today 2018, 23(6), 1241–1250. [CrossRef]
- Jean-Louis Reymond. The chemical space project. Accounts of Chemical Research 2015, 48(3), 722–730. [CrossRef]
- Ricardo Macarron, Martyn N Banks, Dejan Bojanic, David J Burns, Dragan A Cirovic, Tina Garyantes, Darren VS Green, Robert P Hertzberg, William P Janzen, Jeff W Paslay, et al. Impact of high-throughput screening in biomedical research. Nature Reviews Drug Discovery 2011, 10(3), 188–195. [CrossRef]
- Corwin Hansch and Toshio Fujita. ρ-σ-π analysis. a method for the correlation of biological activity and chemical structure. Journal of the American Chemical Society 1964, 86(8), 1616–1626. [CrossRef]
- Artem Cherkasov, Eugene N Muratov, Denis Fourches, Alexandre Varnek, Igor I Baskin, Mark Cronin, John Dearden, Paola Gramatica, Yvonne C Martin, Roberto Todeschini, et al. Qsar modeling: where have you been? where are you going to? Journal of Medicinal Chemistry 2014, 57(12), 4977–5010. [CrossRef]
- Jitender Verma, Vijay M Khedkar, and Evans C Coutinho. 3d-qsar in drug design—a review. Current Topics in Medicinal Chemistry 2010, 10(1), 95–115. [CrossRef]
- Alexander Tropsha. Best practices for qsar model development, validation, and exploitation. Molecular Informatics 2010, 29(6-7), 476–488. [CrossRef] [PubMed]
- Kunal Roy, Supratik Kar, and Rudra Narayan Das. A primer on QSAR/QSPR modeling: fundamental concepts. Springer International Publishing, 2015.
- Ahmet Sureyya Rifaioglu, Esra Nalbat, Volkan Atalay, Maria Jesus Martin, Rengul Cetin-Atalay, and Tunca Doğan. Deepscreen: high performance drug–target interaction prediction with convolutional neural networks using 2-d structural compound representations. Chemical Science 2020, 11(9), 2531–2557. [CrossRef]
- Andrew T McNutt, Paul Francoeur, Rishal Aggarwal, Tomohide Masuda, Rocco Meli, Matthew Ragoza, Jocelyn Sunseri, and David Ryan Koes. Gnina 1.0: molecular docking with deep learning. Journal of Cheminformatics 2021, 13(1), 43. [CrossRef]
- John Jumper, Richard Evans, Alexander Pritzel, Tim Green, Michael Figurnov, Olaf Ronneberger, Kathryn Tunyasuvunakool, Russ Bates, Augustin Žídek, Anna Potapenko, et al. Highly accurate protein structure prediction with alphafold. Nature 2021, 596(7873), 583–589. [CrossRef]
- Andrew W Senior, Richard Evans, John Jumper, James Kirkpatrick, Laurent Sifre, Tim Green, Chongli Qin, Augustin Žídek, Alexander WR Nelson, Alex Bridgland, et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577(7792), 706–710. [CrossRef]
- Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. Neural message passing for quantum chemistry. In Proceedings of the 34th International Conference on Machine Learning, volume 70, pages 1263–1272. PMLR, 2017.
- Zhaoping Xiong, Dingyan Wang, Xiaohong Liu, Feisheng Zhong, Xiaozhe Wan, Xutong Li, Zhaojun Li, Xiaomin Luo, Kaixian Chen, Hualiang Jiang, et al. Pushing the boundaries of molecular representation for drug discovery with the graph attention mechanism. Journal of Medicinal Chemistry 2020, 63(16), 8749–8760. [CrossRef]
- Philippe Schwaller, Teodoro Laino, Théophile Gaudin, Peter Bolgar, Christopher A Hunter, Costas Bekas, and Alpha A Lee. Molecular transformer: a model for uncertainty-calibrated chemical reaction prediction. ACS Central Science 2019, 5(9), 1572–1583. [CrossRef]
- Rafael Gómez-Bombarelli, Jennifer N Wei, David Duvenaud, José Miguel Hernández-Lobato, Benjamín Sánchez-Lengeling, Dennis Sheberla, Jorge Aguilera-Iparraguirre, Timothy D Hirzel, Ryan P Adams, and Alán Aspuru-Guzik. Automatic chemical design using a data-driven continuous representation of molecules. ACS Central Science 2018, 4(2), 268–276. [CrossRef]
- Izhar Wallach, Michael Dzamba, and Abraham Heifets. Atomnet: a deep convolutional neural network for bioactivity prediction in structure-based drug discovery. arXiv preprint arXiv:1510.02855, 2015.
- Jonathan M Stokes, Kevin Yang, Kyle Swanson, Wengong Jin, Andres Cubillos-Ruiz, Nina M Donghia, Craig R MacNair, Shawn French, Lindsey A Carfrae, Zohar Bloom-Ackermann, et al. A deep learning approach to antibiotic discovery. Cell 2020, 180(4), 688–702. [CrossRef]
- Garrett B Goh, Nathan O Hodas, and Abhinav Vishnu. Deep learning for computational chemistry. Journal of Computational Chemistry 2017, 38(16), 1291–1307.
- Riccardo Guidotti, Anna Monreale, Salvatore Ruggieri, Franco Turini, Fosca Giannotti, and Dino Pedreschi. A survey of methods for explaining black box models. ACM Computing Surveys 2018, 51(5), 1–42. [CrossRef]
- Jacob Biamonte, Peter Wittek, Nicola Pancotti, Patrick Rebentrost, Nathan Wiebe, and Seth Lloyd. Quantum machine learning. Nature 2017, 549(7671), 195–202.
- Maria Schuld and Nathan Killoran. Quantum machine learning in feature hilbert spaces. Physical Review Letters 2019, 122(4), 040504. [CrossRef] [PubMed]
- Marcello Benedetti, Erika Lloyd, Stefan Sack, and Mattia Fiorentini. Parameterized quantum circuits as machine learning models. Quantum Science and Technology 2019, 4(4), 043001. [CrossRef]
- Vojtěch Havlíček, Antonio D Córcoles, Kristan Temme, Aram W Harrow, Abhinav Kandala, Jerry M Chow, and Jay M Gambetta. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567(7747), 209–212. [CrossRef]
- Amira Abbas, David Sutter, Christa Zoufal, Aurélien Lucchi, Alessio Figalli, and Stefan Woerner. The power of quantum neural networks. Nature Computational Science 2021, 1(6), 403–409.
- John Preskill. Quantum computing in the nisq era and beyond. Quantum 2018, 2, 79. [CrossRef]
- Kishor Bharti, Alba Cervera-Lierta, Thi Ha Kyaw, Tobias Haug, Sumner Alperin-Lea, Abhinav Anand, Matthias Degroote, Hermanni Heimonen, Jakob S Kottmann, Tim Menke, et al. Noisy intermediate-scale quantum algorithms. Reviews of Modern Physics 2022, 94(1), 015004. [CrossRef]
- Yudong Cao, Jonathan Romero, Jonathan P Olson, Matthias Degroote, Peter D Johnson, Mária Kieferová, Ian D Kivlichan, Tim Menke, Borja Peropadre, Nicolas PD Sawaya, et al. Quantum chemistry in the age of quantum computing. Chemical Reviews 2019, 119(19), 10856–10915. [CrossRef]
- Sam McArdle, Suguru Endo, Alán Aspuru-Guzik, Simon C Benjamin, and Xiao Yuan. Quantum computational chemistry. Reviews of Modern Physics 2020, 92(1), 015003.
- Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Sergio Boixo, Michael Broughton, Bob B Buckley, David A Buell, et al. Hartree-fock on a superconducting qubit quantum computer. Science 2020, 369(6507), 1084–1089. [CrossRef]
- Julia E Rice, Tanvi P Gujarati, Mario Motta, Tyler Y Latone, Naoki Yamamoto, Tyler Takeshita, Daniel Claudino, Hunter A Buchanan, and David P Tew. Quantum computation of dominant products in lithium–sulfur batteries. The Journal of Chemical Physics 2021, 154(13), 134115.
- Carlos Outeiral, Martin Strahm, Jiye Shi, Garrett M Morris, Simon C Benjamin, and Charlotte M Deane. The prospects of quantum computing in computational molecular biology. Wiley Interdisciplinary Reviews: Computational Molecular Science 2021, 11(1), e1481. [CrossRef]
- Xavier Bonet-Monroig, Ryan Babbush, and Thomas E O’Brien. Quantum machine learning for chemistry and physics. Chemical Society Reviews 2022, 51(14), 5387–5406.
- Kosuke Mitarai, Makoto Negoro, Masahiro Kitagawa, and Keisuke Fujii. Quantum circuit learning. Physical Review A 2018, 98(3), 032309. [CrossRef]
- Maria Schuld, Alex Bocharov, Krysta M Svore, and Nathan Wiebe. Circuit-centric quantum classifiers. Physical Review A 2020, 101(3), 032308. [CrossRef]
- Vincent E Elfving, Bas W Broer, Michael Webber, Jakob Gavartin, Michael D Halls, Kenneth P Lorton, and Art D Bochevarov. Landscape of quantum computing algorithms in chemistry. ACS Central Science 2021, 7(12), 2084–2101.
- Shai Fine and Katya Scheinberg. Efficient svm training using low-rank kernel representations. Journal of Machine Learning Research 2001, 2, 243–264.
- Ali Rahimi and Benjamin Recht. Random features for large-scale kernel machines. In Advances in Neural Information Processing Systems, volume 20, 2007.
- Joseph Bowles, David García-Martínez, Roeland Angrisani, Marco Cerezo, Matty Łucińska, and Leonardo Banchi. Better than classical? the subtle art of benchmarking quantum machine learning models. arXiv preprint arXiv:2403.07059, 2024.
- Jarrod R McClean, Sergio Boixo, Vadim N Smelyanskiy, Ryan Babbush, and Hartmut Neven. Barren plateaus in quantum neural network training landscapes. Nature Communications 2018, 9(1), 4812. [CrossRef]
- Marco Cerezo, Akira Sone, Tyler Volkoff, Lukasz Cincio, and Patrick J Coles. Cost function dependent barren plateaus in shallow parametrized quantum circuits. Nature Communications 2021, 12(1), 1791. [CrossRef]
- Mateusz Ostaszewski, Edward Grant, and Marcello Benedetti. Structure optimization for parameterized quantum circuits. Quantum 2021, 5, 391. [CrossRef]
- IBM Quantum. Qiskit: An open-source framework for quantum computing. https://qiskit.org, 2023. Accessed: 2025-01-15.
- Gadi Aleksandrowicz, Thomas Alexander, Panagiotis Barkoutsos, Luciano Bello, Yael Ben-Haim, David Bucher, Francisco Jose Cabrera-Hernández, Jorge Carballo-Franquis, Adrian Chen, Chun-Fu Chen, et al. Qiskit: An open-source framework for quantum computing. 2019.
- Michael K Gilson, Tiqing Liu, Michael Baitaluk, George Nicola, Linda Hwang, and Jenny Chong. Bindingdb in 2015: a public database for medicinal chemistry, computational chemistry and systems pharmacology. Nucleic Acids Research 2016, 44(D1), D1045–D1053. [CrossRef]
- Greg Landrum et al. Rdkit: Open-source cheminformatics. http://www.rdkit.org, 2023. Version 2023.09.5.
- Christopher A Lipinski, Franco Lombardo, Beryl W Dominy, and Paul J Feeney. Experimental and computational approaches to estimate solubility and permeability in drug discovery and development settings. Advanced Drug Delivery Reviews 2001, 46(1-3), 3–26. [CrossRef]
- Michael JD Powell. A direct search optimization method that models the objective and constraint functions by linear interpolation. Advances in Optimization and Numerical Analysis 1994, pages 51–67.
- Ying Li and Simon C Benjamin. Efficient variational quantum simulator incorporating active error minimization. Physical Review X 2017, 7(2), 021050. [CrossRef]
- James C Spall. Multivariate stochastic approximation using a simultaneous perturbation gradient approximation. IEEE Transactions on Automatic Control 1992, 37(3), 332–341. [CrossRef]
- Ryan Larose, Arkin Tikku, Eleanor O’Neel-Judy, Lukasz Cincio, and Patrick J Coles. Robust data encodings for quantum classifiers. Physical Review A 2020, 102(3), 032420.
- Steven M Paul, Daniel S Mytelka, Christopher T Dunwiddie, Charles C Persinger, Bernard H Munos, Stacy R Lindborg, and Aaron L Schacht. How to improve r&d productivity: the pharmaceutical industry’s grand challenge. Nature Reviews Drug Discovery 2010, 9(3), 203–214. [CrossRef]
- Joseph A DiMasi, Henry G Grabowski, and Ronald W Hansen. Innovation in the pharmaceutical industry: new estimates of r&d costs. Journal of Health Economics 2016, 47, 20–33. [CrossRef]
- Kristan Temme, Sergey Bravyi, and Jay M Gambetta. Error mitigation for short-depth quantum circuits. Physical Review Letters 2017, 119(18), 180509. [CrossRef] [PubMed]
- Suguru Endo, Simon C Benjamin, and Ying Li. Practical quantum error mitigation for near-future applications. Physical Review X 2018, 8(3), 031027. [CrossRef]
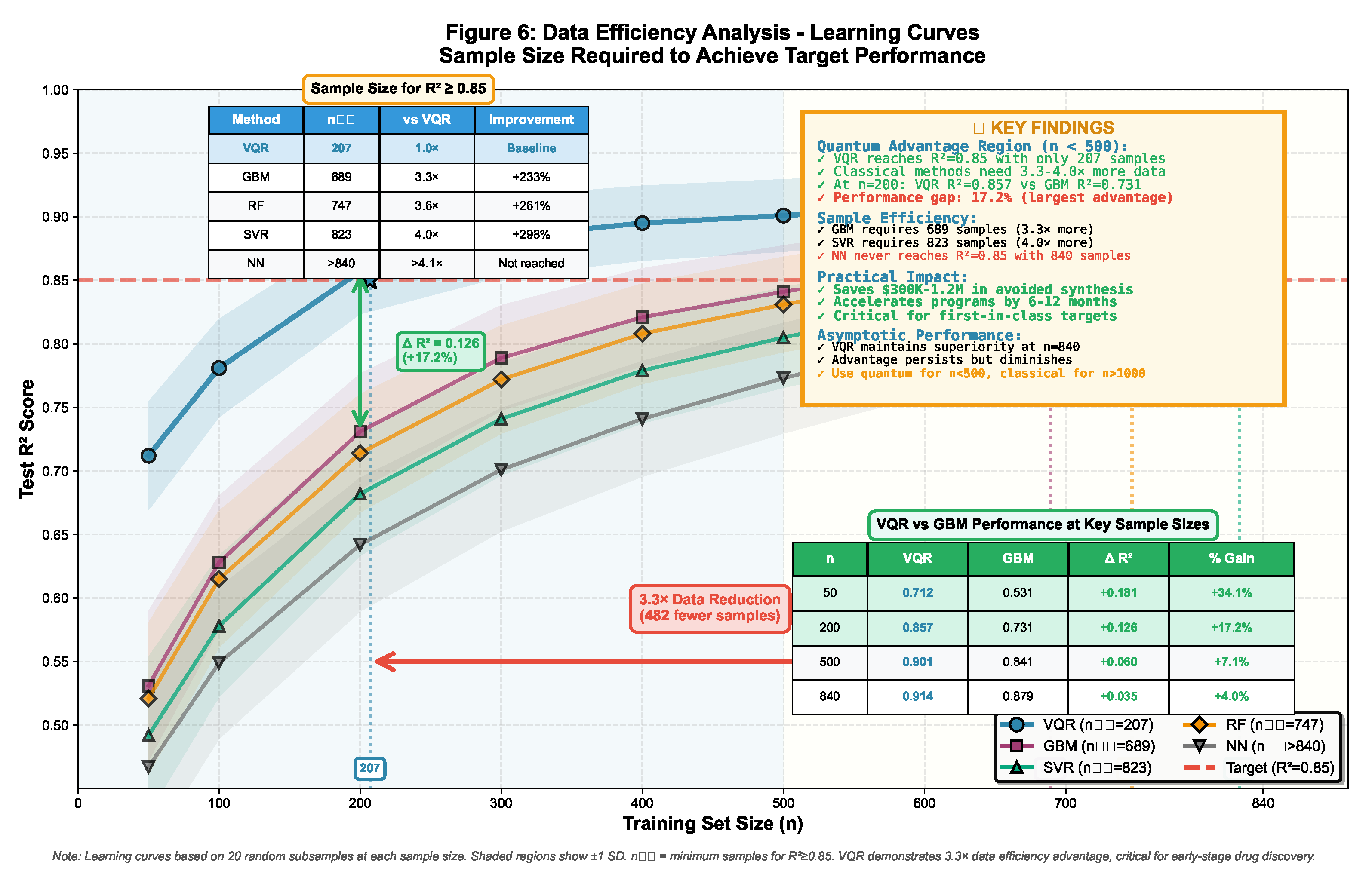

| Method | MSE↓ | MAE↓ | RMSE↓ | R2↑ |
|---|---|---|---|---|
| VQR (Ours) | 0.056 ± 0.009 | 0.187 ± 0.021 | 0.237 ± 0.019 | 0.914 ± 0.014 |
| SVR (RBF) | 0.082 ± 0.013 | 0.226 ± 0.027 | 0.286 ± 0.023 | 0.862 ± 0.021 |
| Random Forest | 0.074 ± 0.011 | 0.214 ± 0.024 | 0.272 ± 0.020 | 0.873 ± 0.018 |
| Gradient Boost | 0.074 ± 0.010 | 0.215 ± 0.023 | 0.272 ± 0.018 | 0.879 ± 0.016 |
| Neural Network | 0.089 ± 0.015 | 0.235 ± 0.029 | 0.298 ± 0.025 | 0.847 ± 0.024 |
| Comparison | MSE | p-value | Cohen’s d |
|---|---|---|---|
| VQR vs. SVR | <0.001*** | 1.24 | |
| VQR vs. RF | <0.001*** | 1.02 | |
| VQR vs. GBM | <0.001*** | 1.08 | |
| VQR vs. NN | <0.001*** | 1.35 |
| Target Class | VQR | SVR | GBM | NN |
|---|---|---|---|---|
| Kinases () | 0.923 | 0.861 | 0.889 | 0.839 |
| GPCRs () | 0.911 | 0.868 | 0.876 | 0.851 |
| Proteases () | 0.908 | 0.857 | 0.870 | 0.851 |
| Kernel Type | Alignment (KA) | vs. Quantum |
|---|---|---|
| Quantum (VQR) | 0.823 ± 0.019 | — |
| RBF (SVR) | 0.744 ± 0.024 | *** |
| Linear | 0.621 ± 0.031 | *** |
| Polynomial (deg=3) | 0.697 ± 0.027 | *** |
| Descriptor | Kinases | GPCRs | Proteases |
|---|---|---|---|
| TPSA | 0.198 | 0.241 | 0.209 |
| logP | 0.221 | 0.167 | 0.159 |
| MolWt | 0.143 | 0.138 | 0.178 |
| HBA | 0.121 | 0.152 | 0.109 |
| HBD | 0.098 | 0.113 | 0.158 |
| nRotB | 0.089 | 0.097 | 0.095 |
| nAromRings | 0.130 | 0.092 | 0.092 |
| Study | Dataset Size | Real Data? | Baselines | Interpretability |
|---|---|---|---|---|
| This work | 1,500 | BindingDB/ChEMBL[2] | 4 (SVR/RF/GBM/NN) | √(EQP) |
| Cao et al. (2018) | N/A | Review | — | — |
| Outeiral et al. (2021) | <500 | Synthetic | SVR only | × |
| Smaldone et al. (2025) | 800 | QM9 | Linear reg. | × |
| Platform | Qubits | Gate Fidelity | (s) | VQR Feasible? | Est. |
|---|---|---|---|---|---|
| IBM Eagle (2025) | 127 | 99.2% | 200 | √ | 0.89–0.92 |
| IonQ Aria | 25 | 99.5% | 1000 | √ | 0.90–0.93 |
| Rigetti Aspen-M | 80 | 98.1% | 15 | √ | 0.85–0.88 |
| Google Sycamore | 70 | 99.6% | 30 | √ | 0.91–0.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




