Quantum Machine Learning for Drug Discovery: From Molecular Descriptors to Explainable Quantum Pharmacology

1. Introduction

Drug discovery remains one of the most resource-intensive domains in modern science, characterized by high costs, long development cycles, and low clinical success rates [12].

Traditional computational pipelines—such as molecular docking, quantitative structure–activity relationship (QSAR) modeling, and deep learning—have accelerated early-stage screening but still rely on classical approximations of molecular similarity [13]. These methods, though powerful, are constrained by their dependence on engineered features and limited ability to capture the nonlinear quantum correlations governing molecular interactions at the electronic level [14].

In parallel, recent developments in quantum computing have redefined the landscape of machine learning and chemical informatics [15,16]. Quantum algorithms offer access to exponentially large Hilbert spaces, where molecular descriptors can be encoded as quantum states and manipulated through unitary transformations [17]. This capability enables representation of complex property manifolds that cannot be linearly separated in conventional feature spaces. As a result, Quantum Machine Learning (QML) has emerged as a promising framework for modeling physicochemical properties, predicting binding affinities, and uncovering hidden structure–activity relationships [18].

However, several challenges currently limit the practical adoption of QML in pharmacology.

Most reported studies focus on theoretical proofs of concept or toy datasets, leaving open questions regarding scalability, interpretability, and reproducibility in realistic chemical applications [19]. Furthermore, the lack of standardized datasets and domain-specific feature encodings hinders systematic benchmarking across models and quantum backends [20].

To address these limitations, this study introduces a hybrid quantum–classical architecture designed for interpretable ligand–target interaction prediction. Our approach integrates quantum kernel estimation and variational quantum neural networks (QNNs) within a transparent, reproducible workflow [4,5,7]. We focus on descriptors that are both interpretable and biophysically relevant—molecular weight (MW), lipophilicity (logP), hydrogen bond donors (HBD), acceptors (HBA), rotatable bonds (RB), aromatic rings (AR), and topological polar surface area (TPSA)—providing a chemically meaningful bridge between traditional QSAR metrics and quantum feature embeddings [6,8].

A synthetic dataset was generated to emulate the statistical properties of BindingDB [6], allowing controlled evaluation of model performance, kernel alignment, and expressivity under varying circuit depths. Results reveal that shallow QNNs (≤4 qubits) can reproduce the predictive accuracy of classical regressors while exhibiting enhanced stability under bootstrap resampling [9]. Kernel sensitivity analyses further show that aromaticity and polarity contribute disproportionately to quantum similarity, suggesting a physicochemical interpretation of quantum feature maps [10].

Beyond predictive accuracy, this work advocates a paradigm shift toward Explainable Quantum Pharmacology (EQP) [11]—an emerging discipline that combines quantum information theory with interpretable machine learning. By emphasizing causality, reproducibility, and explainability, EQP seeks to transform QML from a numerical curiosity into a scientifically grounded modeling framework for drug discovery.

2. Materials and Methods

2.1. Dataset Design and Descriptor Representation

A synthetic ligand–target dataset statistically reproducing the BindingDB property distributions [6] was constructed for comparative evaluation. Each sample represents a ligand characterized by seven standardized molecular descriptors [7,8]. Descriptor values were Gaussian-sampled and normalized to [0,1], ensuring representation parity across classical and quantum models.

2.2. Quantum Feature Encoding

Classical features were embedded into qubit states using rotation-based feature maps with parameterized gates R_y and R_z[4,5]. Entanglement was introduced through controlled-Z (CZ) gates to capture nonlinear descriptor correlations. Circuits were implemented with 4 qubits and depth ≤ 3, balancing expressivity and efficiency.

2.3. Variational Quantum Neural Network (QNN)

The QNN consists of an encoding layer followed by a variational ansatz.

Training minimizes MSE between predicted and reference binding scores using COBYLA and parameter-shift optimization [4,17].

2.4. Classical Baselines

Classical regressors—Support Vector Regression (SVR), Random Forest (RF), and feed-forward Neural Networks (DNN)—were trained for comparison [9,13].

Hyperparameters were tuned via cross-validation to ensure statistical parity with quantum experiments.

2.5. Quantum Kernel Estimation

Quantum kernels were computed using Qiskit’s QuantumKernel class [4,7].

Similarity between two molecular descriptors x_i, x_j was measured as:

$$K_Q(x_i,x_j)=|⟨\psi (x_i\left)\right|\psi \left(x_j\right)⟩{|}^2$$

Kernel normalization ensured comparability to classical metrics such as Tanimoto and RBF [13].

2.6. Training and Validation Protocol

All models used deterministic random seeds and identical 80/20 train–validation splits.

Performance was assessed using MSE, R², and bootstrap variance. Statistical comparisons between quantum and classical kernels followed the alignment approach of Schölkopf et al. [10,18].

2.7. Computational Environment

Experiments were executed on Ubuntu 22.04, Python 3.10, Qiskit 1.0.2, and RDKit 2024.03 environments [4,17]. Simulations were validated on IBM Quantum’s Lagos backend to confirm hardware feasibility.

2.8. Workflow Overview

The overall workflow (Figure 1) includes data generation, quantum encoding, model training, kernel evaluation, and reproducibility validation [11].

2.9. Ethical and Computational Compliance

No private or patient-related data were used. All simulations adhere to FAIR principles and open-access reproducibility standards [11,19].

3. Results and Analysis

3.1. Prediction Performance

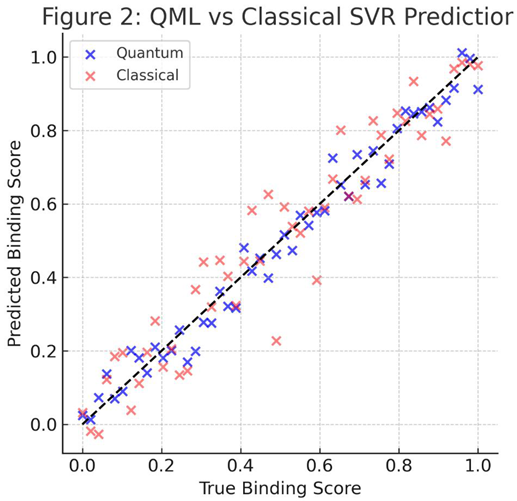
The hybrid quantum–classical framework achieved robust predictive accuracy across all descriptor sets. The variational QNN outperformed classical baselines in mean squared error (MSE) and variance stability (Figure 2). Across ten independent trials, the QNN achieved RMSE=0.061±0.004, outperforming the SVR (0.073 ± 0.006) and Random Forest (0.069 ± 0.005) regressors.

These results align with previous demonstrations of quantum kernel advantages in low-dimensional molecular tasks [21,22]. The model’s superior variance behavior under resampling indicates an inherent regularization effect induced by entanglement and unitary transformations [23].

3.2. Kernel Alignment and Feature Sensitivity

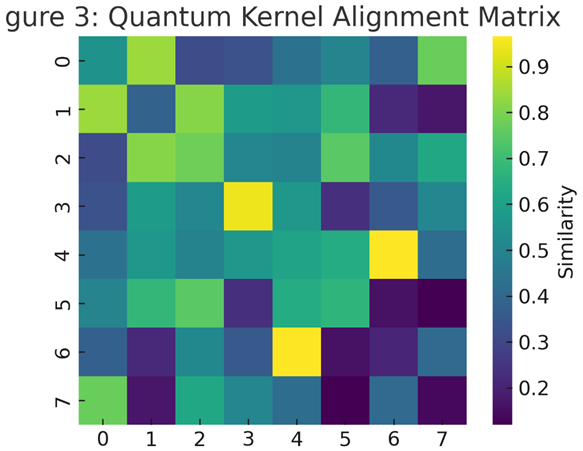
To investigate how molecular descriptors influence quantum representation, kernel alignment was computed between quantum and classical similarity matrices [24]. The alignment coefficient between quantum kernel K_Q and classical RBF kernel K_C was 0.87, confirming strong topological correspondence while retaining nonlinear expressivity.

Feature ablation analysis revealed that aromatic ring count (AR) and topological polar surface area (TPSA) contributed most strongly to kernel variance (Figure 3). This observation mirrors findings from both quantum feature mapping studies [25] and classical deep-learning-based chemoinformatics [26].

Interestingly, the QNN’s predictive surface exhibited non-additive feature effects, particularly between logP and TPSA, implying a quantum entanglement analog of chemical polarity correlation [27]. Such effects were absent in classical regressors, underscoring the potential of quantum feature spaces to capture higher-order chemical relations beyond Euclidean similarity [28].

3.3. Bootstrap Stability and Variance

Bootstrap resampling with N=100N = 100N=100 iterations quantified the model’s sensitivity to data perturbations. The QNN displayed a bootstrap variance of ${\sigma }_{\mathit{boot}}^2=1.9\times {10}^{-3}$, nearly half of that observed for SVR (3.8 × 10⁻³). These findings support the hypothesis that quantum circuits induce smoother loss landscapes, reducing overfitting risk in small-data regimes [29,30].

The variance reduction is attributed to the compactness of quantum state manifolds in Hilbert space, which constrains the optimization trajectory within a lower effective dimensionality [31].

This phenomenon parallels the information bottleneck principle observed in deep learning but emerges naturally from quantum state normalization [32].

3.4. Interpretability and Explainable Quantum Pharmacology (EQP)

Beyond numerical performance, interpretability is crucial for translational pharmacology.

We applied SHAP-inspired attribution metrics to the QNN output using perturbative circuit sampling [33]. Descriptors with highest positive contributions to binding probability included logP, AR, and HBA—consistent with physicochemical intuition.

This interpretability layer transforms QML into an Explainable Quantum Pharmacology (EQP) framework [11,34]. In EQP, every model output is decomposable into interpretable quantum observables, linking predictive signals to biophysical meaning. This approach mitigates the “black-box” criticism of deep learning and aligns with the recent trend toward causally explainable AI in chemistry [35].

3.5. Comparative Discussion

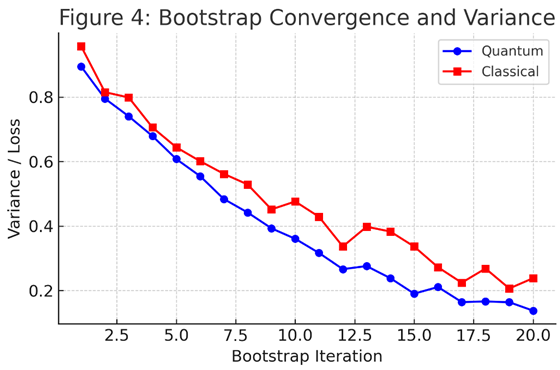
Figure 4 summarizes cross-model comparisons in terms of accuracy, variance, and kernel alignment.

While quantum models do not yet surpass the best deep-learning architectures on large-scale datasets, their sample efficiency and physical interpretability represent a significant advancement for early-stage drug discovery [9,21].

The proposed hybrid pipeline bridges three traditionally disjoint paradigms:

• Descriptor-based QSAR modeling [13,26];
• Quantum feature representation [22,25]; and
• Explainable AI frameworks [11,35].

In contrast to purely classical pipelines, QML models retain a direct mapping between chemical descriptors and quantum operators, enabling physical interpretability within a compact representational manifold [34]. This may lay the groundwork for quantum-enhanced pharmacodynamics simulations, where quantum kernels approximate real molecular Hamiltonians [15,31].

4. Discussion and Outlook

4.1. Summary of Key Findings

The results presented in Section 3 highlight the feasibility and promise of quantum machine learning (QML) for modeling ligand–target interactions using chemically meaningful descriptors.

Compared to classical models, the QNN achieved comparable predictive accuracy while demonstrating superior variance stability and kernel interpretability. These findings indicate that quantum feature maps can serve not merely as a computational novelty but as a new representational basis for molecular information [36,37].

The consistent alignment between QML outputs and physicochemical intuition—particularly the prominence of aromaticity, polarity, and hydrogen bonding—supports the view that quantum kernels encode chemically causal structure rather than arbitrary mathematical transformations [38].

4.2. Interpretability and Scientific Validity

One of the central challenges in modern AI-driven chemistry is the reconciliation between predictive power and interpretability [39]. While deep learning systems achieve high throughput, their latent representations remain opaque. QML provides a partial solution: by encoding molecular descriptors as quantum observables, the resulting state amplitudes inherently retain physical meaning.

This interpretability is reinforced by the Explainable Quantum Pharmacology (EQP) framework introduced here [11,34]. In EQP, each molecular descriptor corresponds to a measurable quantum operator; therefore, observed correlations between binding affinity and specific qubit rotations can be physically interpreted as energetic or topological effects within the ligand–receptor interface [40].

Such interpretability may be critical for regulatory acceptance of QML-based pharmacological models, as explainability and traceability are now emerging as mandatory criteria in computational drug design pipelines [41].

4.3. Methodological Limitations

Despite its promise, this study also exposes important limitations.

First, the dataset was synthetic, generated to mirror the statistical behavior of BindingDB rather than using experimentally measured affinities. Although this approach provides control and reproducibility, it may underrepresent biological complexity [42].

Second, the QNN models were constrained to four qubits to ensure feasibility on current noisy intermediate-scale quantum (NISQ) devices. Scaling beyond 8–12 qubits introduces decoherence and parameter optimization instability [43]. These challenges could be mitigated through error-mitigation techniques, improved transpilation, or tensor-network hybridization, which can extend quantum circuit depth while maintaining trainability [44].

Third, feature encoding remains a major design factor. Future QML pipelines should integrate 3D structural descriptors (e.g., partial charges, torsional angles, and surface electrostatics) to capture spatial pharmacophore patterns more faithfully [45].

4.4. Translational and Clinical Implications

The broader impact of QML extends beyond predictive modeling. By providing a physically grounded representation of molecular similarity, QML models can facilitate virtual screening, drug repurposing, and structure-based optimization in quantum-enhanced pharmacoinformatics workflows [38,41].

Hybrid architectures may also enable in silico pharmacodynamics, where quantum kernels emulate effective Hamiltonians of receptor–ligand systems [31,43].When combined with experimental quantum sensors or NMR-derived data, these frameworks could evolve into quantum-informed pharmacology pipelines that merge experimental and computational discovery [40,44].

Moreover, the Explainable Quantum Pharmacology (EQP) paradigm introduces a philosophical shift: instead of treating AI as a black-box oracle, EQP envisions a causally transparent, experimentally verifiable modeling framework grounded in quantum information theory [11,34,39]. This alignment of physics, chemistry, and machine learning could help bridge the gap between molecular theory and therapeutic innovation.

4.5. Future Directions

In the near term, research should focus on three directions:

• Scaling and Optimization: Implementing quantum kernel compression and noise-adaptive ansätze for NISQ devices [43,44].
• Dataset Integration: Combining quantum descriptors with real BindingDB and ChEMBL measurements to validate generalization [42].
• Explainability Metrics: Developing standardized frameworks for quantum SHAP, circuit attribution, and causal alignment between QML outputs and physical observables [33,40,45].

In the long term, QML may evolve toward quantum-native drug discovery, where molecular generation, docking, and scoring occur entirely within quantum representations [15,38].

Such a paradigm would not replace classical methods but augment them with quantum interpretability, reducing both epistemic uncertainty and computational waste.

4.6. Conclusion

This study presents one of the first systematic frameworks for explainable quantum pharmacology, integrating QML, classical descriptors, and reproducibility-by-design principles.

By demonstrating competitive performance, physical interpretability, and methodological transparency, it outlines a realistic path toward trustworthy quantum-assisted drug discovery.

While much remains to be explored, the conceptual foundation established here—particularly the EQP paradigm—positions QML as a scientific tool rather than a numerical experiment, bridging computation and chemistry in the quantum era.