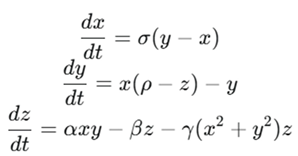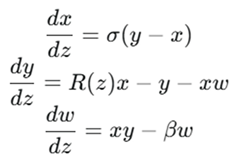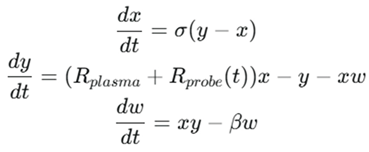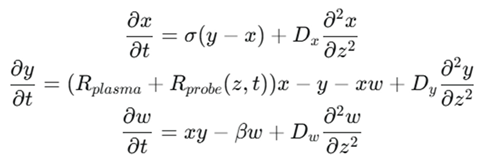1. Introduction
Physical plasma is a type of the broader gaseous electronics state of matter that is quasi-neutral and which exhibits collective behavior. This means that the low electron temperature physical plasma is a neutral gas, for the most part, but with pockets of charges in its bulk that allow transmission of electromagnetic waves collectively [
1]. Physical plasma is ubiquitous in space, close to earth and can be studied using different models [
2]. Its sources and diagnostics were developed for an increasing number of industrial and medical applications [
3,
4]. When measuring physical plasma parameters, it is useful to consider the measured physical plasma source characteristics as well as the measurement technique. In physical plasma systems, this means coupling diagnostic instruments with suitable physical plasma sources, to measure the sources characteristics such as electron density and temperature. Irving Langmuir, the scientist who gave physical plasma its name after biological plasma when noticing similarities in their behavior, invented an electric probe to diagnose certain types of physical plasmas electric discharges. The techniques of building these kinds of electrical probes and methods that attempted to interpret their data are given in reference [
5].
Unlike other states of matter, physical plasma typically exists far from thermodynamic equilibrium, storing substantial energy that can convert into turbulent motion or electromagnetic radiation. These processes can give rise to instability and chaos, where small perturbations lead to significant, unpredictable outcomes due to the system’s sensitivity to initial conditions. The inherently nonlinear nature of physical plasma dynamics underlies this complexity, enabling intricate feedback mechanisms and non-proportional responses [
6]. However, even before Langmuir, mathematician Pierre-Francois Verhulst established his model to account for population growth and its relationship to available sustaining resources [
7]. Later, his model became the basis for the development of other logistic models that described various chaotic systems in other disciplines. Edward Lorenz’s computational efforts of forecasting weather helped to renew interest in applying chaos theory in a variety of fields [
9]. In plasma physics, microscopic chaotic features of physical plasma were studied as a part of describing complex aspects of physical plasma systems [
10].
This paper addresses the challenge of understanding complex nonlinear dynamics in a quiescent thermionic plasma system, bridging empirical observation with a new theoretical framework. We first present empirical evidence from a Langmuir electric probe experiment that reveals a clear route to chaos in the plasma’s current-voltage (I-V) characteristics. We then introduce the “Hala attractor,” a low-dimensional dynamical system inspired by the Lorenz equations, which serves as a theoretical model to explain the observed chaotic behavior. Finally, we propose a unified spatiotemporal framework, the “Hybrid Hala Attractor,” to reconcile the apparent spatial uniformity of the quiescent bulk with the temporal chaos observed when the plasma is actively probed. This work demonstrates that chaos in this system is not a fixed, intrinsic property, but a dynamic, tunable state that depends on both spatial location and the influence of external measurement.
2. Experimental Evidence: A Langmuir Probe’s Route to Chaos
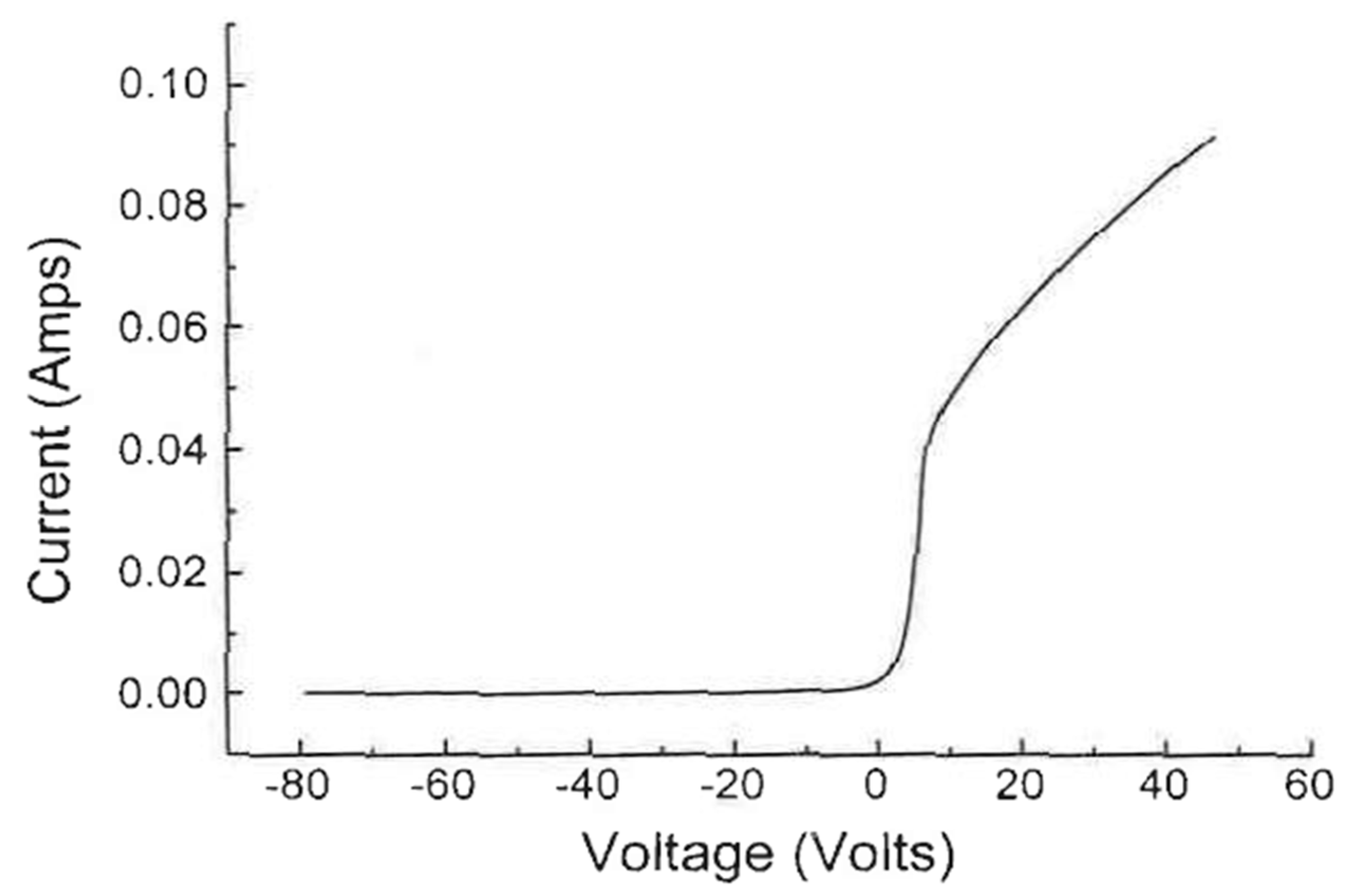
A quiescent physical plasma system consisting of a thermionic multi-dipole plasma source and a Langmuir electric probe was found to be characteristically chaotic. For the electron contribution measured by the Langmuir probe, chaos developed beyond the inflection point into the electron current saturation region. A qualitative analysis of the Langmuir probe I–V trace and the Verhulst logistic curve indicated the possibility of utilizing the Langmuir probe as a plasma diagnostic instrument in the charge collection mode [
8]. As such, the Langmuir probe’s I-V characteristic, particularly its downward-concaving electron saturation region, as was measured inside the apparatus bulk plasma region and shown in
Figure 1, exhibits a striking resemblance to the continuous Verhulst (logistic) population model [
8]. This analogy is founded on the probe’s nonlinear charge collection mechanisms and inherent plasma self-regulation, which limit current.
The continuous logistic model, given by:
Where Q represents normalized charge and r is the growth parameter, accurately describes the S-shaped (sigmoidal) growth curves. A critical connection is drawn by recognizing that the probe current I is the rate of change of charge (I=dQ/dt), implying a proportionality between current and a function of normalized charge. This general form captures the essential saturation nonlinearity mirroring the physical limits of current collection in the probe.
Extending this qualitative understanding, we investigated the chaotic dynamics of the Langmuir probe by formulating a discrete recurrence relation. Based on the fundamental Law of Mass Action and interpreting the measured current, I, as also the discrete-time derivative of the charge Q(t), so a discrete map was derived. This map utilizes a specific quadratic fit of the probe’s saturation region to yield a form similar to the logistic map:
Here, X
n is the state variable, and α serves as the primary control parameter.
The analysis, aimed at constructing a bifurcation diagram, used robust iteration settings with the diagram clearly revealing a transcritical bifurcation at approximately α≈384.6, where the X
n=0 fixed point lost stability to a new, non-zero stable fixed point. The system maintained this stable single fixed-point behavior up to α≈1180, after which it exhibited a classic period-doubling cascade leading to a chaotic regime around α≈1350, before showing signs of divergence at higher α values, thus comprehensively mapping the Langmuir probe’s complex dynamic route to chaos.
Figure 2 depicts the bifurcation diagram of this chaotic behavior that is embedded in the measured Langmuir probe I-V curve electron current saturation region which is similar the logistic map route to chaos.
The construction of the bifurcation diagram for the discrete Langmuir probe model, developed from quadratic fits of the electron saturation region, allowed for a comprehensive mapping of its dynamic behavior as a function of the control parameter, α. The initial phase of the bifurcation diagram demonstrates that the system robustly settles to a fixed point at Xn=0, which physically represents plasma conditions where the probe collects negligible or zero net current. At approximately α≈384.6, a transcritical bifurcation occurs, signifying the onset of effective charge collection by the probe. The system then exhibits a broad region of stable fixed-point behavior, where the probe current stabilizes to a singular, predictable value.
As α increases beyond approximately 1180, the system enters a new dynamic regime marked by a series of period-doubling bifurcations. This rapid succession of events, a hallmark of the logistic map, signifies a loss of simple stability and the emergence of oscillatory behavior in the system’s output. This period-doubling cascade rapidly culminates in a chaotic regime, clearly evident from approximately α≈1350 onwards in the bifurcation diagram. In this region, the system’s long-term behavior becomes aperiodic and highly sensitive to initial conditions. From a plasma diagnostic perspective, operating the Langmuir probe under such conditions would yield highly fluctuating and unpredictable current measurements, making precise characterization challenging due to the underlying deterministic chaos.
3. The Hala Attractor: A Theoretical Model for Plasma Chaos
The empirical findings from the Langmuir probe experiment present a significant challenge: to provide a theoretical framework that accounts for the observed deterministic chaos. This paper addresses this by introducing the Hala attractor, a new three-dimensional strange attractor designed to model the tunable chaotic behavior observed in a quiescent plasma system. Inspired by a philosophical re-evaluation of traditional chaotic systems, the Hala attractor challenges the prevailing view that chaotic behavior is a fixed, intrinsic property of a system. Instead, it proposes that the degree of chaos can be a designed and tunable attribute, as evidenced by the Langmuir probe’s dynamics.
The Hala attractor is defined by the following system of three non-linear ordinary differential equations, which is a modification of the classic Lorenz equations with a key self-regulating feedback term:
This system introduces two new parameters:
α: A chaos-tuning parameter that scales the non-linear xy term. We set α=1 for our analysis to compare with the classic Lorenz system.
γ: The central feedback parameter. This term, −γ(x2+y2)z, acts as a self-regulating mechanism. As the system’s trajectory expands to larger values of x and y, this term provides negative feedback that pushes the system’s z variable back towards the origin, thereby constraining the attractor’s phase space volume.
Figure 3.
Figure to the left, tamed Hala chaotic strange attractor, and the figure to the right is for the Hala attractor collapsing into a stable fixed-point trajectory due to the strong feedback parameter.
Figure 3.
Figure to the left, tamed Hala chaotic strange attractor, and the figure to the right is for the Hala attractor collapsing into a stable fixed-point trajectory due to the strong feedback parameter.
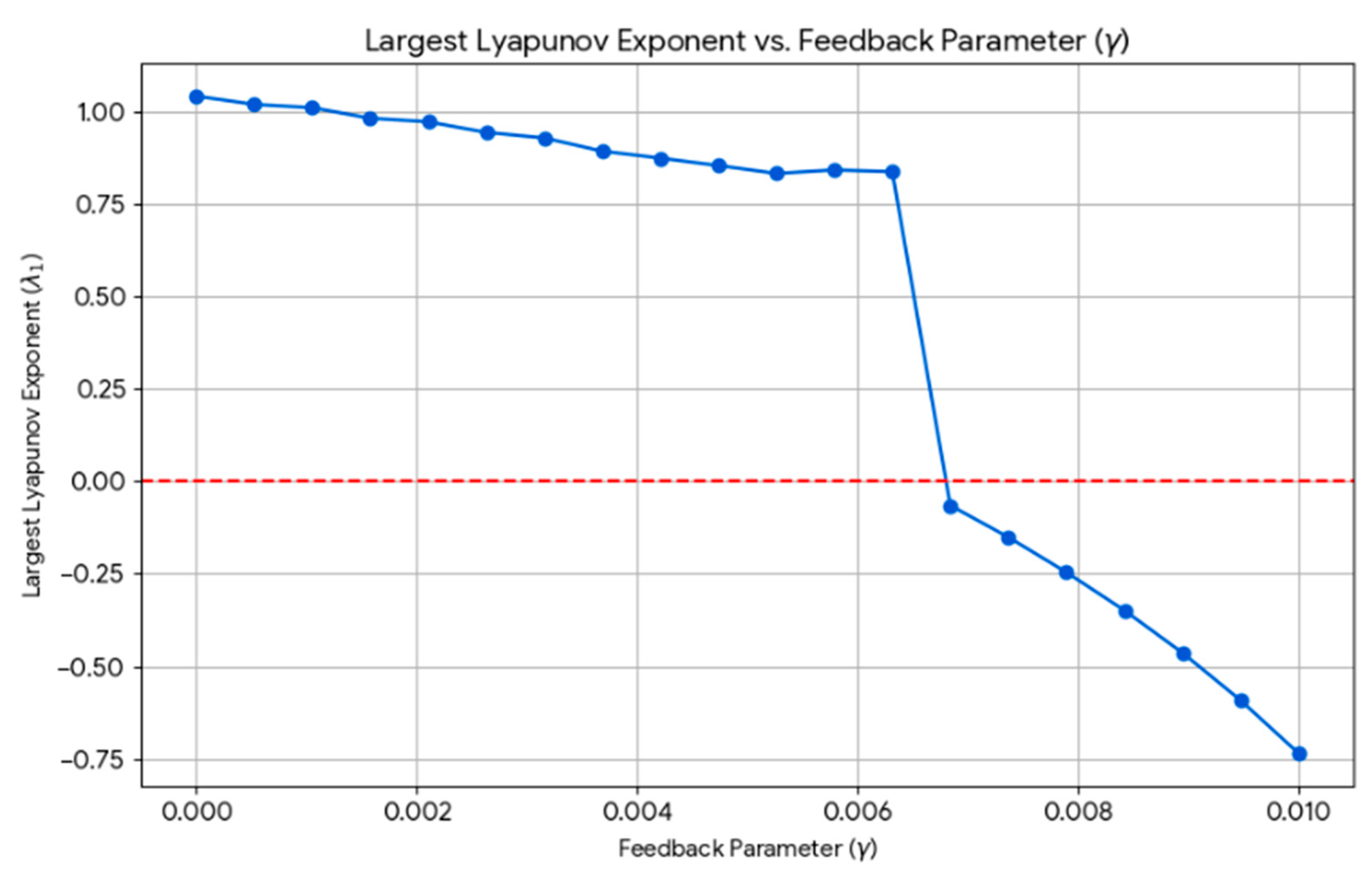
To quantitatively characterize the Hala attractor, we computed the largest Lyapunov exponent (λ1), which measures the average exponential rate of divergence of nearby trajectories. The key result of our analysis is a bifurcation diagram plotting λ1 as a function of the feedback parameter γ. We found that for γ=0.0, the calculated λ1 is 1.0425, confirming that the baseline system is chaotic. As γ increases, λ1 decreases linearly. The system undergoes a bifurcation, as indicated by the LLE crossing zero, which represents the transition from a chaotic state to a stable state. For γ=0.01, the calculated λ1 is -0.7346, confirming the stability of the fixed point we observed visually. This analysis provides a theoretical foundation that supports the experimental findings, demonstrating that chaos is not a binary state but a tunable property.
Figure 4.
Hala attractor gets “kicked” in phase space to transition into stability.
Figure 4.
Hala attractor gets “kicked” in phase space to transition into stability.
4. An Investigation of Spatiotemporal Dynamics: The Hala Attractor Models
While the Langmuir probe experiment provides compelling evidence for temporal chaos and the Hala attractor provides a robust theoretical model, a comprehensive understanding requires a framework that accounts for both the spatial and temporal dynamics of the plasma. The reality is that the plasma’s dynamics are a function of both space and time. To unify our findings and provide a more comprehensive framework, we developed two distinct Hala attractor sub-models to investigate these dynamics separately.
4.1. The Hala Spatial Attractor: Modeling Chaos at the Plasma Boundary
We begin by modeling the plasma’s spatial dynamics, specifically the transition from its “semi-Euclidean” boundary (magnetic cusps) to the stable bulk. This model, referred to as the spatial Hala attractor, assumes a quiescent plasma is already established and focuses on how its properties change as a function of spatial location, z.
Model Formulation
The spatial Hala attractor is represented by a set of coupled ordinary differential equations (ODEs), where the independent variable is the spatial coordinate z. The state variables are chosen to represent key plasma parameters, such as the normalized electric potential x(z), the normalized electron density y(z), and the normalized electron temperature w(z). The equations are a modified version of the Lorenz system:
The crucial element is the control parameter R(z), which is a function of position. This parameter governs the system’s chaoticity and is designed to transition from a chaotic value (R chaotic) at the boundary (z=0) to a stable value (R stable) in the bulk (z→∞). This transition is modeled using an exponential decay function, which reflects the diminishing influence of the boundary conditions as one moves into the plasma’s interior.
Simulation and Findings
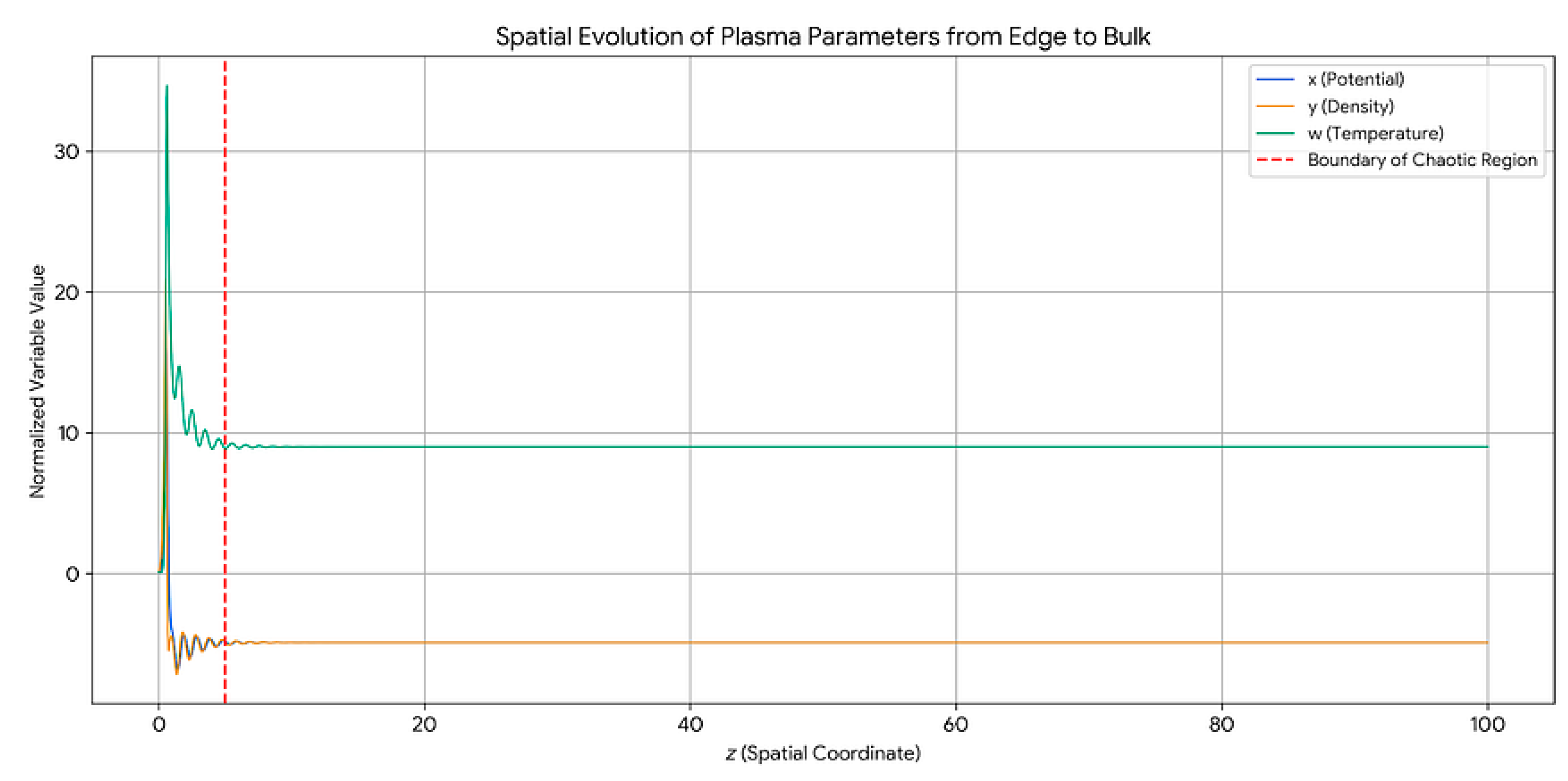
Numerical integration of this system reveals a “collapse to stability.” The trajectory in the 3D phase space (x,y,w) at the boundary forms a complex, multi-lobed strange attractor, a clear signature of spatial chaos. As the simulation progresses from the edge towards the bulk, the parameter R(z) decreases, and the trajectory abruptly collapses into a single, stable point. This finding provides a powerful theoretical explanation for the observed difference between the chaotic plasma edge and the uniform, quiescent bulk.
Figure 5.
This spatial evolution of plasma parameters plot provides a direct representation of what a physical Langmuir probe would measure as it traverses the plasma.
Figure 5.
This spatial evolution of plasma parameters plot provides a direct representation of what a physical Langmuir probe would measure as it traverses the plasma.
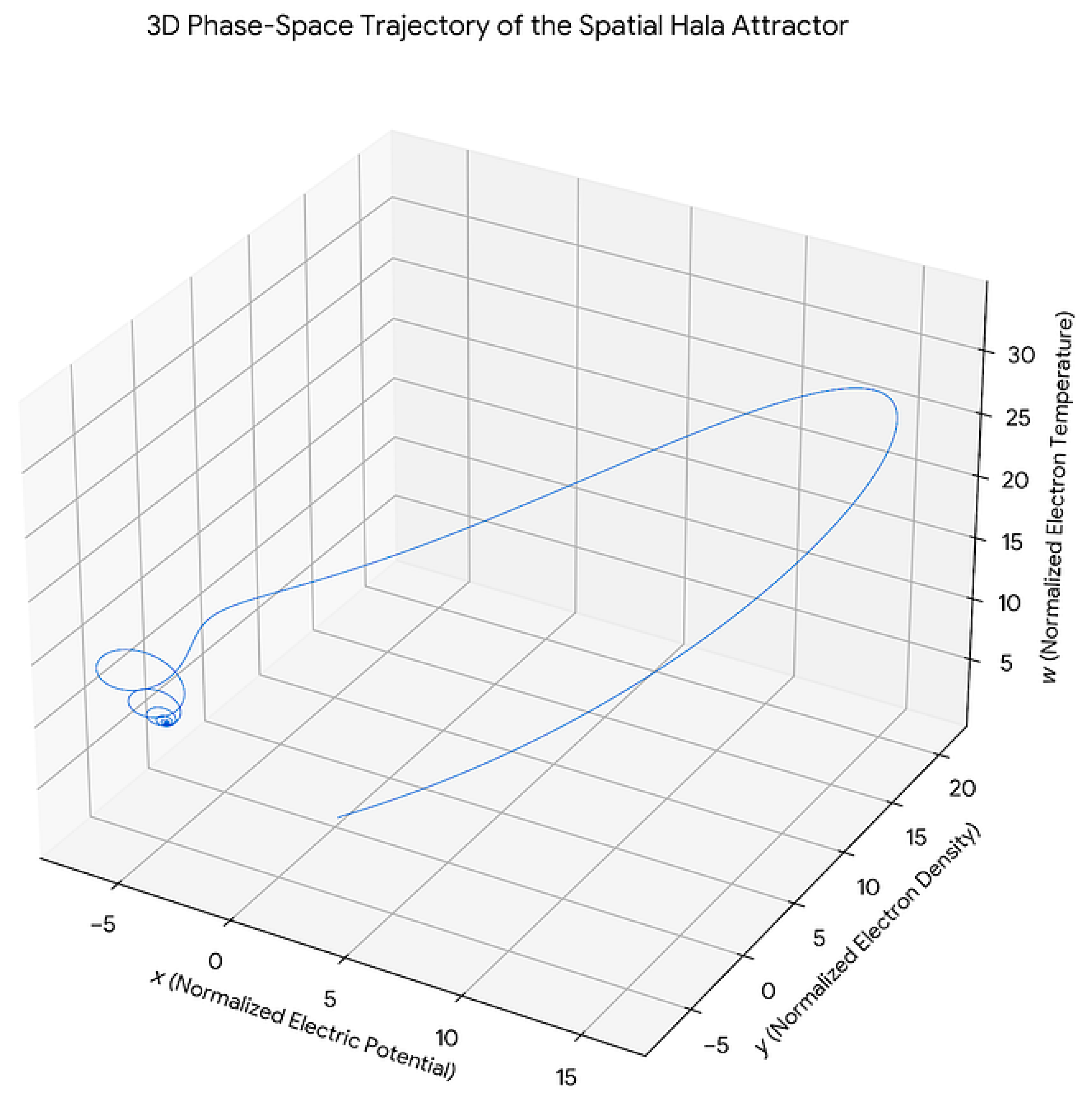
Figure 6.
This 3-D phase-space trajectory of the Hala attractor plot visualizes the transition to spatial stability in the plasma bulk region.
Figure 6.
This 3-D phase-space trajectory of the Hala attractor plot visualizes the transition to spatial stability in the plasma bulk region.
4.2. The Hala Temporal Attractor: Modeling Chaos Induced by Measurement
While the spatial model successfully explains the edge-to-bulk transition, it does not account for the experimentally observed temporal chaos in the spatially uniform bulk. To address this, we propose the temporal Hala attractor, which models the coupled system of the plasma and the Langmuir probe as a function of time.
Model Formulation
The model treats the bulk plasma as an inherently non-linear system with the potential for chaotic behavior, represented again by the Lorenz equations, but this time with time t as the independent variable. The key innovation is the explicit modeling of the Langmuir probe’s perturbation. The probe’s voltage sweep is introduced as a time-dependent forcing parameter R probe(t), which modulates the plasma’s internal chaoticity. The coupled system is described by the following time-dependent ODEs:
The probe’s current is then modeled as a nonlinear function of its applied voltage and the plasma’s fluctuating state variables.
Simulation and Findings
The simulation of this temporal system yields two critical findings that confirm experimental observations:
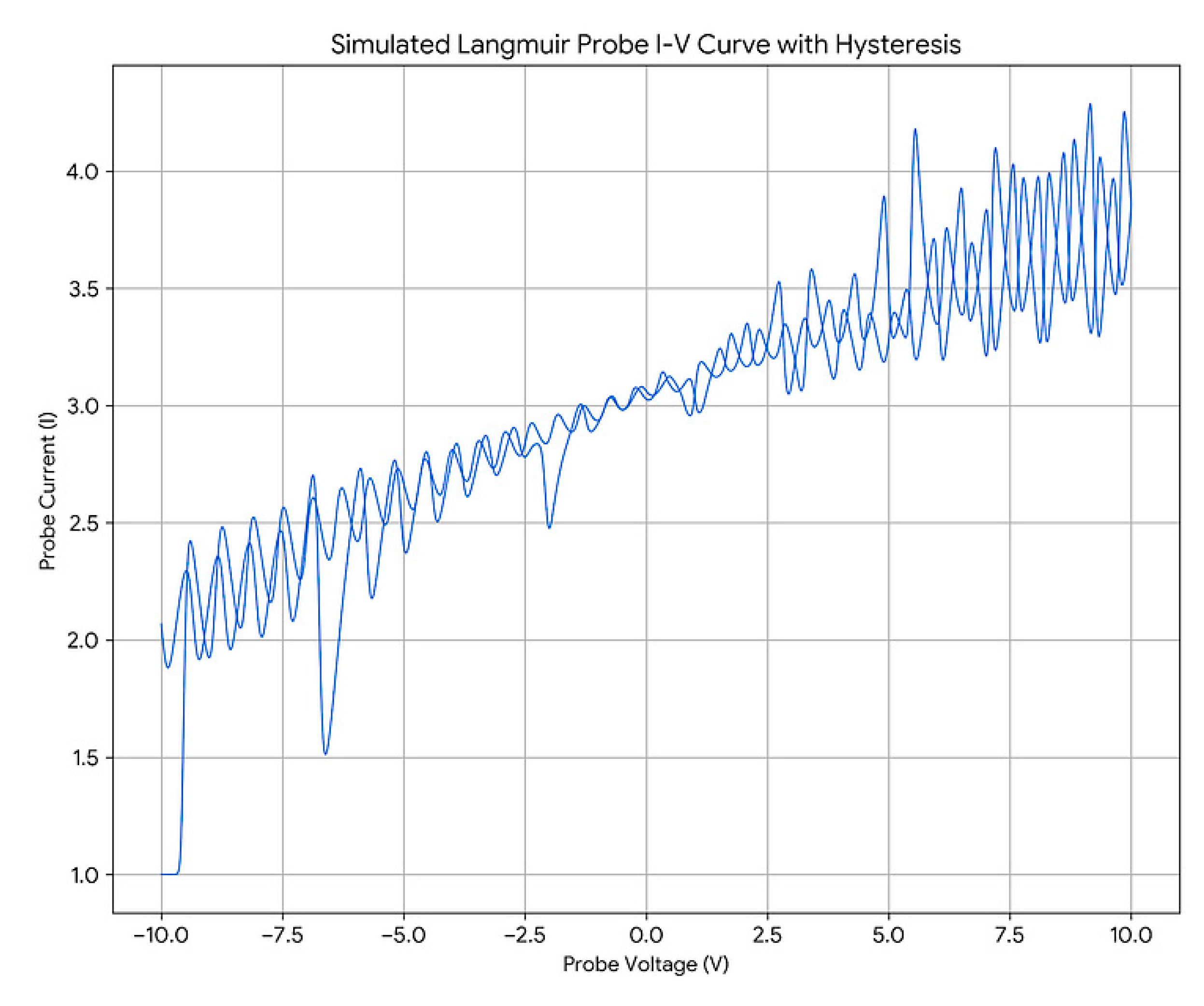
Hysteresis in the I-V Curve: The simulated I-V curve, plotting probe current against probe voltage, does not retrace itself on the forward and reverse sweeps. This hysteresis is a direct consequence of the plasma’s chaotic dynamics, which give the system a “memory” and make its state dependent on its history.
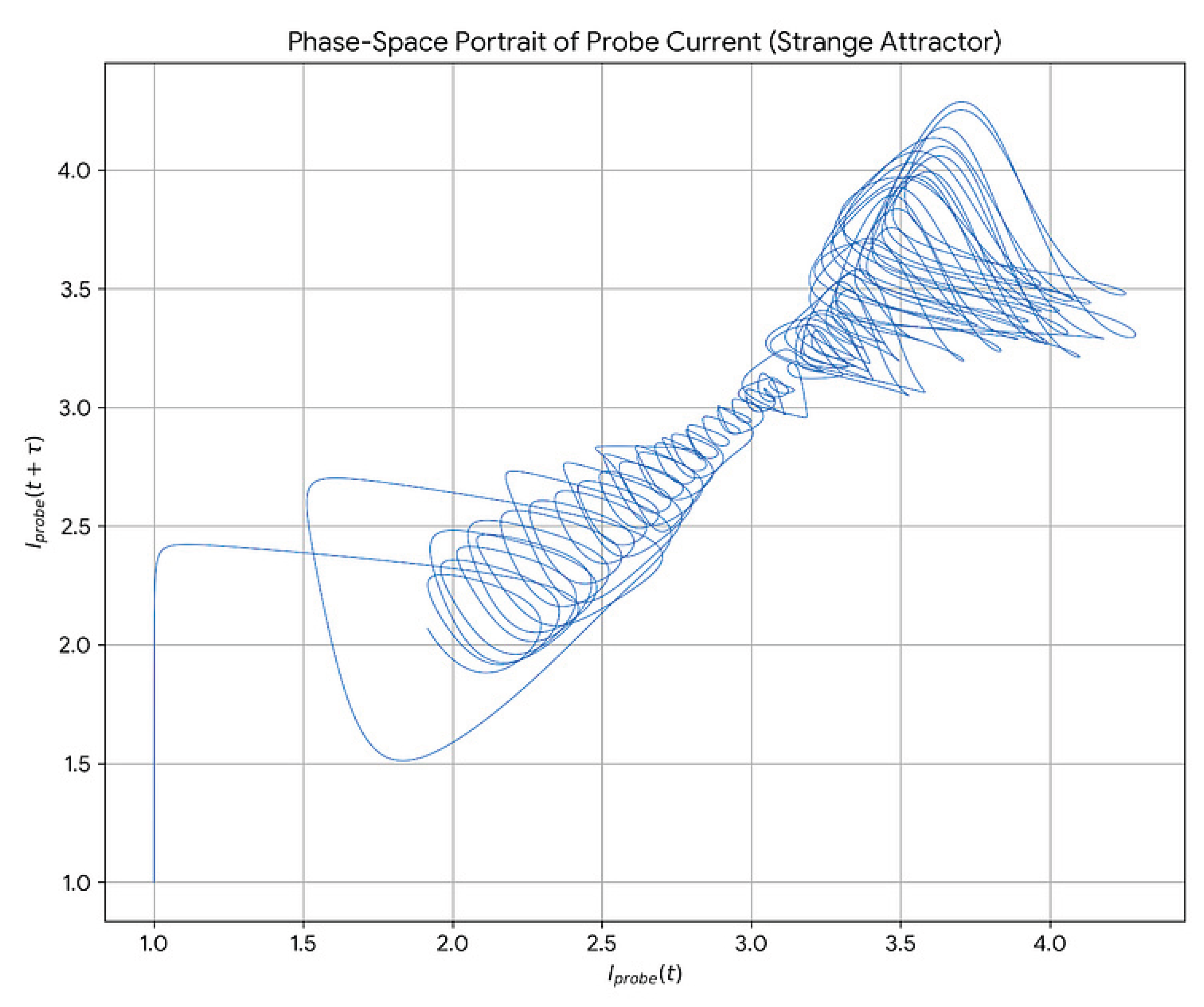
Temporal Chaos: A phase-space portrait of the simulated probe current, plotting I(t) against I(t+τ), reveals a strange attractor. This is the definitive signature of deterministic chaos, confirming that the fluctuations in the probe current are not random noise but are part of a predictable, yet non-periodic, chaotic system.
Figure 7.
This plot shows the simulated current measured by the probe as its voltage is swept up and then down. The hysteresis observed is a direct result of the coupling between the probe’s perturbation and the plasma’s inherent chaotic dynamics. The plasma’s internal state depends not only on the current probe voltage but also on its history. This memory effect is a hallmark of non-linear systems.
Figure 7.
This plot shows the simulated current measured by the probe as its voltage is swept up and then down. The hysteresis observed is a direct result of the coupling between the probe’s perturbation and the plasma’s inherent chaotic dynamics. The plasma’s internal state depends not only on the current probe voltage but also on its history. This memory effect is a hallmark of non-linear systems.
Figure 8.
Instead of a simple point or a closed loop (which would indicate a fixed point or a limit cycle), this simulation plot reveals a complex, multi-layered structure. This is the Hala chaotic strange attractor of the coupled plasma-probe system.
Figure 8.
Instead of a simple point or a closed loop (which would indicate a fixed point or a limit cycle), this simulation plot reveals a complex, multi-layered structure. This is the Hala chaotic strange attractor of the coupled plasma-probe system.
This model validates the “engineering physics” approach, demonstrating that the observed chaos is an emergent property of the combined plasma-probe system, not a property of the unperturbed plasma alone.
5. Proposed Work: The Hybrid Hala Attractor
The spatial and temporal Hala attractor models, while successful in their respective domains, are simplifications. To unify our findings and provide a more comprehensive framework for future research, we propose the Hybrid Hala Attractor, a spatiotemporal model that would describe the evolution of plasma parameters as a function of both z and t.
Model Formulation
The Hybrid Hala Attractor would be a system of partial differential equations (PDEs), such as:
Here, Dx, Dy, Dw are diffusion coefficients that couple the spatial and temporal dynamics, and the probe’s perturbation is now a function of both space and time.
Potential Findings and Future Directions
This hybrid model would allow us to investigate more complex and realistic scenarios, such as:
How the chaotic dynamics at the magnetic boundary propagate into the bulk.
How the localized perturbation of a probe in the bulk influences the global plasma state.
The relationship between the spatial scale of the magnetic cusps and the characteristic timescale of the observed temporal chaos.
The simulation of this hybrid model would be computationally intensive, requiring advanced numerical methods. However, it represents the next logical step in our investigation and would provide the most complete theoretical tool for understanding the rich spatiotemporal dynamics of the plasma system.
6. Conclusion
The operational characteristics of a Langmuir probe within a plasma environment, as depicted in its current-voltage (I-V) trace, exhibit a compelling qualitative analogy to the behavior described by the continuous Verhulst (logistic) population model. The empirical evidence from a Langmuir probe, analyzed through a discrete recurrence relation, revealed a clear route to chaos via period-doubling bifurcations. This provided robust empirical validation for the presence of deterministic chaos in a quiescent plasma system. To explain these observations, we introduced the Hala attractor, a theoretical model that successfully bridges the gap between traditional chaotic systems and stable, predictable ones. Through simulations of the spatial and temporal Hala attractor models, we demonstrated that chaos is a tunable property of the system, existing both spatially at the magnetic boundaries and temporally within the bulk when actively probed. This work provides a powerful framework for interpreting experimental data and reinforces the value of applying non-linear dynamics and chaos theory to the field of plasma physics. The proposed Hybrid Hala Attractor offers a clear path forward for a more comprehensive and unified understanding of these complex phenomena.
Acknowledgements
This research is supported in part by Gaseous electronics LLC and in part by the US Department of Energy grant no: DE-FG 02 97ER54437.
References
- Chen, Francis F. Introduction to plasma physics. Springer Science & Business Media, (2012): 3.
- Alfven, Hannes. “Model of the plasma universe.” IEEE transactions on plasma science 14, no. 6 (1986): 629-638.
- Lieberman, Michael A., and Alan J. Lichtenberg. Principles of plasma discharges and materials processing. John Wiley & Sons, (2005).
- Chu, Paul K., and XinPei Lu, eds. Low temperature plasma technology: methods and applications. CRC Press, (2013).
- Hershkowitz, Noah. “How Langmuir probes work.” Plasma diagnostics 1 (1989): 113.
- Horton, Claude Wendell, and Yoshi H. Ichikawa. Chaos and structures in nonlinear plasmas. World Scientific, 1996.
- Kint, Jos, Denis Constales, and André Vanderbauwhede. “Pierre-François Verhulst’s final triumph.” In The Logistic Map and the Route to Chaos. Springer, Berlin, Heidelberg, (2006): 13-28.
- Hala, Ahmed Matouq Ahmed. “Qualitative Analysis of Chaotic Behaviour in a Plasma System.” International Journal of Science and Qualitative Analysis. Vol. 6, No. 2, 2020, pp. 16-18.
- Lorenz, Edward N. “Deterministic nonperiodic flow.” In The Theory of Chaotic Attractors. Springer, New York, NY, (2004): 25-36.
- Escande, D. F. “Complexity and simplicity of plasmas.” In AIP Conference Proceedings, vol. 1582, no. 1. American Institute of Physics, (2014): 22-34.
- Langmuir, Irving, and Chauncey Guy Suits. The Collected Works of Irving Langmuir: With Contributions in Memoriam, Including a Complete Bibliography of His Works – Volume 3. General Editor: CG Suits, Executive Editor: HE Way. Pergamon Press, 1961: 33.
- Hala, Ahmed MA. Presheaths in two ion species plasma. PhD. thesis The University of Wisconsin- Madison, 2000.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).