Avogadro’s Number: History, Scientific Role, State-of-the-Art, and Frontier Computational Perspectives

1. Introduction

The unassuming appearance of Avogadro’s number, $N_A$, in physical and chemical equations belies its monumental role. It provides the essential bridge between the atomic and the macroscopic, making possible the conversion between moles, masses, atom counts, and molecular scales. The journey of Avogadro’s number—from conjecture, to experimental pursuit, to precise definition—parallels the rise of modern science’s ability to measure, define, and compute with extraordinary precision. It may be noted that, the Avogadro number—approximately 6.022 × 10²³—is indispensable for connecting atomic-scale counting with laboratory-scale measurements [1]. Yet, unlike certain fundamental constants etched deep into the framework of physical law, Avogadro’s number owes its existence and magnitude to historical conventions and pragmatic decisions about measurement. Rather than reflecting an underlying principle or symmetry of the universe, its value emerges from how scientists have chosen to define the mole, the gram, and related units over time.

This origin sets Avogadro’s number apart from constants such as the speed of light or Planck’s constant, whose roles flow directly from the very bedrock of physics and embody universal symmetry or necessity. In contrast, Avogadro’s number is a human-defined bridge: its magnitude reflects our need for a practical conversion between the microscopic world, where particles are individually counted, and the macroscopic quantities used in everyday laboratory practice.

Importantly, this contingent nature is rarely emphasized in mainstream educational materials. More often, the Avogadro number is simply presented as a fixed constant, with little discussion of how its value ultimately traces back to historical and practical choices in metrology, rather than a dictate of nature. Experimental efforts, such as the precise counting of atoms in silicon spheres, allow us to measure Avogadro’s number to many decimal places, but no theoretical law specifies that it must take its particular value.

Thus, Avogadro’s number subtly illustrates a gap in our physical understanding: while it is fundamental for scientific calculations and theories, its specific value is not demanded by the laws of nature but by the conventions and practicalities of measurement. This arbitrariness is seldom directly addressed in mainstream scientific discourse, often leaving a mistaken impression of inevitability or deeper significance where, in reality, there is a product of human-defined convention [2,3].

2. Historical Evolution of Avogadro’s Number

2.1. Origins: Concepts and Challenges

• Amedeo Avogadro (1811): Proposed that equal volumes of any gas, at equal temperature and pressure, contain equal numbers of molecules—an assertion that paved the way for atomic and molecular quantification, but without specifying a numerical value or mole concept.
• Nineteenth Century Progress: Advances in kinetic theory and gas laws (notably by Loschmidt in 1865) produced the first numerical estimates—originally the number of molecules per cubic centimetre, now called the Loschmidt constant.
• Jean Perrin (Early 1900s): Named the constant in honour of Avogadro and, through Brownian motion studies, provided the first values near those accepted today.
• Mole Concept: Only solidified with Stanislao Cannizzaro’s advocacy at the Karlsruhe Congress (1860), integrating Avogadro’s hypothesis into chemical atomic weights and equations.

2.2. From Experiment to Definition

The 20th century witnessed remarkable advances:

• Millikan’s Oil Drop: Linked the electron charge with Faraday’s constant, providing an indirect path to $N_A$.
• X-ray Crystallography: Measuring densities and unit cells of crystals (notably silicon-28 spheres) allowed precise atom counts per unit mass [4,5,6].
• Modern SI System: Culminated in the 2019 SI redefinition, which fixes $N_A$ at a stipulated value: $N_A\cong 6.02214076\times {10}^{23} {\mathrm{mol}}^{-1}$. This is now an exact number [1], anchoring the mole and providing the metric for “amount of substance.”

3. Current Scientific Status

3.1. The SI Mole and Avogadro Number

The 2019 SI redefinition resolves the mole’s conceptual ambiguity:

• Definition: One mole contains exactly 6.02214076 × 10²³ specified elementary entities.
• Interpretation: This value is not subject to revision by further experiment; improvements now affect implementations, not the SI constant itself.

3.2. Dimensionality and Educational Nuances

Avogadro’s number is formally dimensioned “per mole”, but:

• Historically and pedagogically, “atoms per gram” or “atoms per kilogram” have also been used, corresponding to “gram-mole” or “kg-mole.”
• Modern SI disambiguates, but educational material often benefits from clarifying such usage for students and practitioners.

4. Scientific Significance

4.1. Why Avogadro’s Number Matters

• Chemical Quantification: Enables precise mass–molecule conversion, underpins stoichiometry, and defines fundamental units in chemistry and biology.
• Physics and Beyond: Links atomic mass unit to kilogram, allowing direct comparison of micro and macro scales. Without $N_A$, the “bridge” between atomic mass (u) and macroscopic mass simply does not exist.
• Measurement and Metrology: Permits construction and realization of standards for mass, amount, and associated constants.

4.2. Educational and Conceptual Impact

• Teaching and understanding moles, atomic/molecular scale, and macroscopic phenomena are impossible without grasping Avogadro’s number.
• Clarifies large number concepts and demonstrates the unity of measurement across scales.

5. Computational Determination of Avogadro Number from Nuclear Physics: State-of-the-Art

5.1. Traditional Experimental Approaches

• Crystallographic Methods: Silicon-28 sphere experiments measure dimensions and masses at exquisite precision [4,5,6].
• Electrochemical Methods: Combine electron charge and Faraday constant.
• These have yielded $N_A$ values agreed upon to many significant digits—at or below parts per billion uncertainty.

5.2. Recent Computational Innovations

Nuclear Binding Energy-Based Computation

We have proposed a fundamentally different, theory-driven estimate of Avogadro’s number [7]:

• Logic: Avogadro’s number emerges as the inverse of the average atomic mass unit as computed from first-principles of nuclear mass and binding energy models.
• Procedure:
  • Compute average nucleon rest energy (mean of neutron and proton rest masses).
  • Subtract average nuclear binding energy per nucleon (from models such as the SEMF or SEWMF).
  • Add the electron rest mass energy.
  • Convert the total energy to mass (via $E=m{c}^2$), defining the unified atomic mass unit (UAMU).
  • Take the reciprocal of UAMU (with mass expressed in kg or gram) to yield Avogadro’s number with units “atoms per kg” or “atoms per gram.”
• Nuclear Mass Formulae Used:
  • Semi-Empirical Mass Formula (SEMF): Incorporates volume, surface, Coulomb, asymmetry, and shell terms using refined coefficients [8,9,10,11,12,13,14,15,16,17,18].
  • Strong and Electroweak Mass Formula (SEWMF): A simplified, innovative model emphasizing volume and electroweak contributions with fewer parameters.
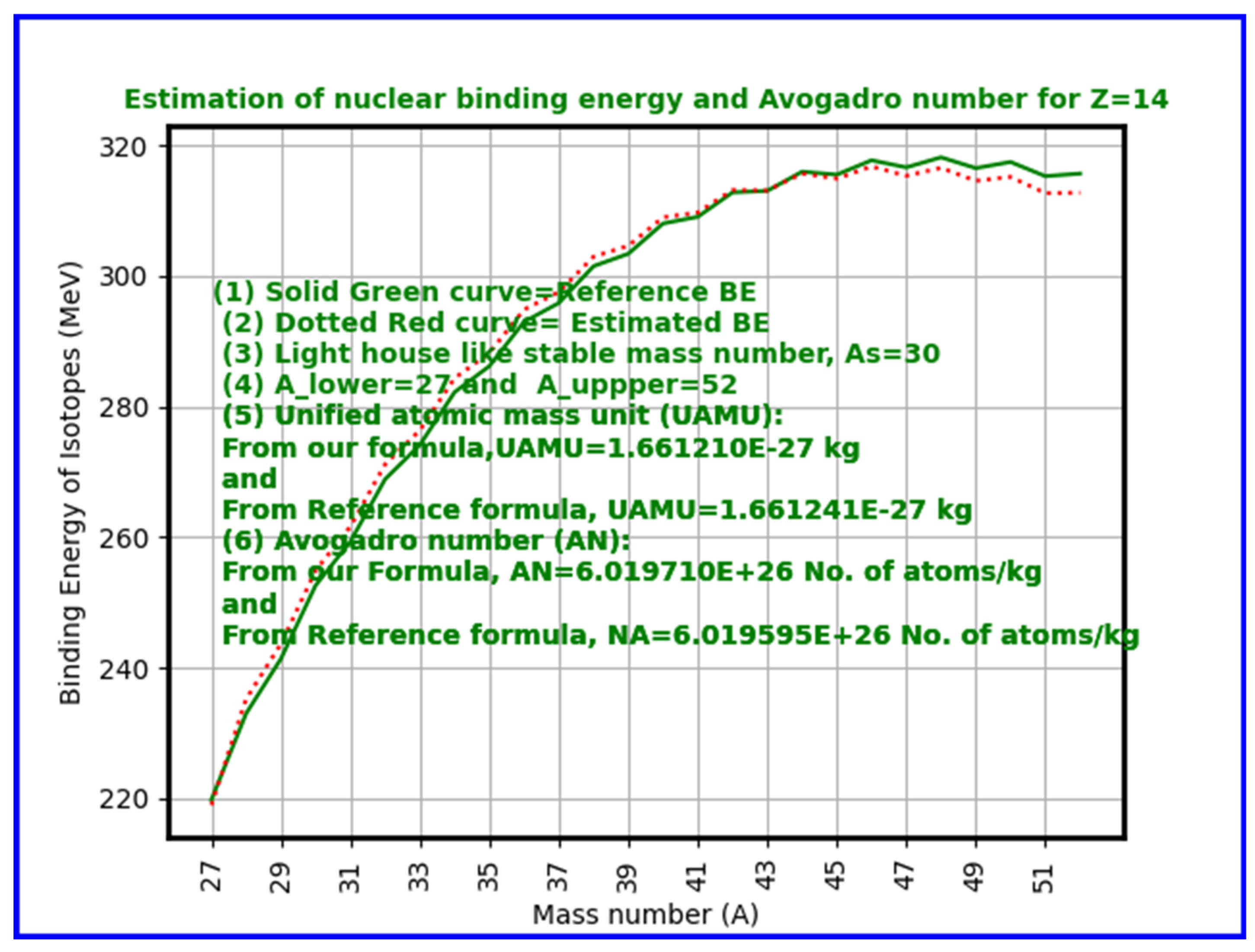
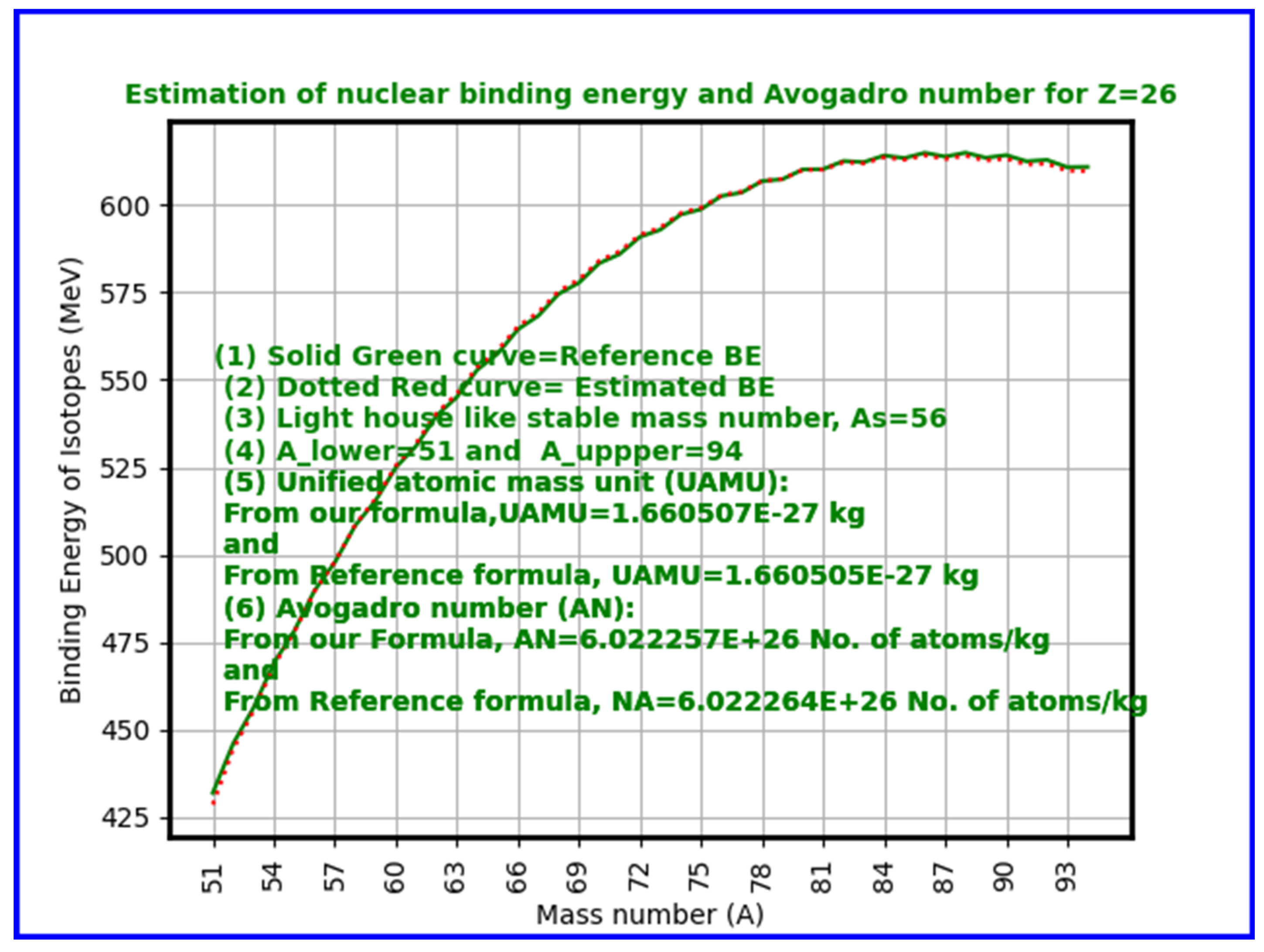
  • Key Results: Computed Avogadro values closely match accepted constants, particularly near iron (Z=26), where nuclear binding energy per nucleon peaks.
  • Averaging across Z = 6 to 118 illustrates robustness and the physical role of nuclear binding saturation in determining Avogadro's number.

6. Special Features of Our Approach

Our approach stands out distinctly among methods for deriving Avogadro’s number. Key special features include:

6.1. Nuclear Binding Energy–Centric Physical Framework

Rooted in first-principles of nuclear physics, our method relates the unified atomic mass unit and Avogadro number directly to nuclear binding energies [19,20,21,22,23,24,25,26,27,28], bypassing dependence on macroscopic bulk measurements like crystal densities. This bridges fundamental subatomic properties with macroscopic constants.

6.2. Explicit Inverse Relation Between Avogadro Number and Atomic Mass Unit

We emphasize and concretely operationalize the relation: $N_A\cong {\displaystyle \frac{1}{UAMU}}.$This direct link clarifies the origin and computation of Avogadro’s number in a straightforward manner, instead of relying solely on phenomenological or empirical approximations.

6.3. Comprehensive Coverage Across the Nuclear Landscape

Applied systematically over proton numbers from $Z=6\mathrm{to}118,$ encompassing stable and unstable isotopes, method provides averaged values across wide mass number intervals, giving insights into trends, uncertainties, and highlighting particularly stable regions such as around iron.

6.4. Dual-Formula Testing and Model Flexibility

By employing both a refined semi-empirical mass formula (SEMF) and our own Strong and Electroweak Mass Formula (SEWMF), we demonstrate the adaptability and consistency of our approach—even as different nuclear physics models are considered.

6.5. Clear Dimensional and Unit Treatment

A noteworthy pedagogical advancement is our careful discussion on units: showing how expressing atomic mass units in grams vs. kilograms leads to Avogadro numbers with units “atoms per gram” or “atoms per kilogram.” This resolves historical ambiguities and clarifies distinctions between gram-mole and kg-mole concepts.

6.6. Computational Transparency and Pedagogical Potential

Our calculations are implemented openly in Python, promoting reproducibility and accessibility. The approach serves as a powerful educational tool — capable of enhancing curricula and enabling students to explore fundamental physics with modern computational means.

6.7. Forward-Looking Integration with Artificial Intelligence

We explicitly propose incorporating AI and machine learning to refine nuclear binding energy parameters and hence improve accuracy. Our dynamic model invites continuous improvement as new nuclear data emerges.

6.8. Unifying Conceptual Framework for the Mole and Avogadro Number

Our model provides a fresh perspective unifying traditional “number of atoms per unit mass” viewpoints with SI conventions, enhancing conceptual clarity about the mole and its realizations.

7.3. Future Prospects

• AI and machine learning promise better nuclear mass models, potentially increasing computational accuracy.
• Web-based educational tools could expand accessibility.
• Further exploration of nuclear physics at the limits (superheavy elements, drip lines) can deepen understanding.

8. Our Nuclear-Computational Approach with a Unified 6 Term Semi Empirical Mass Formula

In contrast to experimental measurement, we have developed a theoretically driven and computational approach, bridging fundamental nuclear physics and macroscopic constants.

8.1. Physical and Computational Framework

• Starting Point: We consider the basic nuclear constituents — protons and neutrons — and their rest energies, combined with nuclear binding energies which represent the energy saving (mass deficit) due to nuclear forces holding the nucleons together.
• Key Steps in our Calculation:
  • Average Nucleon Rest Energy (ANRE): Calculate the mean rest energy of a nucleon, i.e., the average of proton and neutron rest masses multiplied by c².
  • Average Binding Energy per Nucleon (ABEPN): Across the periodic table (Z=1 to 118), and considering isotopes with mass numbers from approximately 2Z to 3.5Z, compute the average nuclear binding energy per nucleon using nuclear mass formulae.
  • Average Nuclear Energy Unit (ANEU): Subtract the average binding energy per nucleon from the mean nucleon rest energy to get the effective nuclear mass-energy contribution.
  • Add Electron Rest Energy: Incorporate the electron rest mass energy, acknowledging the electrons associated with atoms.
  • Calculate Unified Atomic Mass Unit (UAMU): Use the relation $E=m{c}^2$ to convert the nuclear and electron energy sum to a mass unit.
  • Calculate Avogadro Number: Consider the inverse of this mass unit (adjusted for units in grams or kilograms) to estimate the Avogadro number:

    $$N_A\cong {\displaystyle \frac{1}{UAMU}}$$
• Nuclear Models Used:
  • The classical Semi-Empirical Mass Formula (SEMF), including volume, surface, Coulomb, asymmetry, pairing and other microscopic terms.
  • Our Strong and Electroweak Mass Formula (SEWMF) connected with 4G model of final unification [20,21,22,23,24,25,26,27,28]—a simplified and elegant model emphasizing nuclear and electroweak contributions with 4 terms and single energy coefficient [29].
  • Our unified 6 term SEMF [30] applicable from Z=1 to 140.

    $$\left.\begin{array}{l}BE\cong \left[16.0\times A\right]-\left[\gamma \times 19.4\times A^{2/3}\right]\\ -\left[{\displaystyle \frac{0.71\times Z^2}{{\gamma }^x{A}^{1/3}}}\right]-\left\{\left(1-{\displaystyle \frac{1}{A}}\right){\displaystyle \frac{{\left(A-2Z\right)}^2}{A}}\right\}24.5\\ \pm \left[{\displaystyle \frac{10.0}{\sqrt{A}}}\right]+\left[10.0\times \exp \left(-4.2{\displaystyle \frac{\left|\mathrm{N}-\mathrm{Z}\right|}{\mathrm{A}}}\right)\right]\end{array}\right\}\mathrm{MeV}$$

    (3)

    where, $\gamma \cong 1-{\left({\displaystyle \frac{N-Z}{A}}\right)}^2\mathrm{and}x\cong 0.75-\left({\displaystyle \frac{Z}{2A}}\right)$
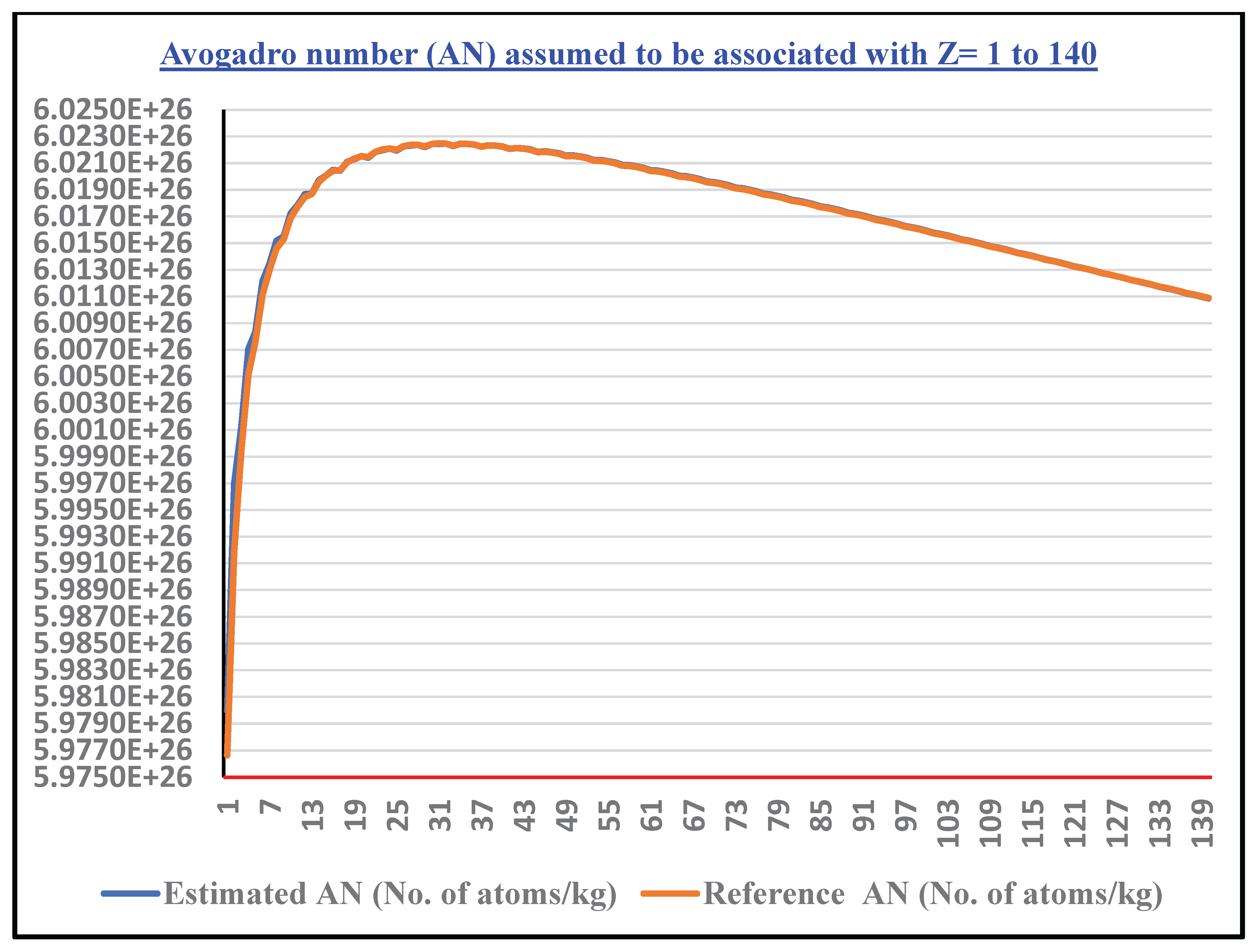
  • Following this unified SEMF applicable from Z= (1 to 140) and considering $A_{lower}\cong 2Z-1$ and $A_{upper}\cong \left(3.5Z\right)+3$, as the lower and upper mass limits, there is a scope for estimating the Avogadro number.
  • Considering proton drip lines and neutron drip lines and by fixing the lower and upper mass limits for Z=1 to 140, in a systematic way, for each and every element, corresponding Avogadro number can be estimated by considering average binding energy per nucleon for all of the isotopes under consideration.
  • Applying the statistical approach for all the elements, one unique value of $N_A$can be obtained.
  • In a collective approach and by considering the average binding energy effects of the revolving electrons, value of the Avogadro number can be tuned further.
  • See Figure 1 and Figure 2 for the isotopic binding energy curves of Z=14 and 26 and the estimated values of the Avogadro number.
  • See Figure 3 for the estimated Avogadro number assumed to be associated with Z=1 to 140.

• Results and Trends:
  • Our calculations show excellent agreement near iron (Z=26), the nucleus with peak binding energy per nucleon and thus greatest stability. The approach naturally explains why Avogadro’s number emerges as it does — as a function of nuclear binding energy saturation effects associated with strong interaction. Starting from Z = (1 to 140), for a total number of 15504 atomic nuclides, estimated $N_A\cong \left(6.017052\mathrm{to}6.017185\right)\times {10}^{26}\mathrm{atoms}/\mathrm{kg}.$
  • We recognize that our proposed computational procedure for deriving Avogadro’s number from nuclear binding energies represents a new perspective and methodology in the field. We look forward to the scientific community’s thorough understanding, critical evaluation, and constructive feedback on its validity, applicability, and potential refinements. Such collective scrutiny and collaboration are vital for advancing knowledge and integrating nuclear theory innovations with metrological constants.

8.2. Conceptual and Practical Differences

• The method is entirely computational and theoretical, relying on nuclear physics models rather than material bulk measurements [6,8,31].
• By averaging over wide ranges of nuclei—both stable and unstable—it provides a global survey of nuclear structure’s impact on atomic mass units and, consequently, Avogadro’s number.
• The dimensionality of the computed Avogadro number (atoms per gram or kilogram) is made explicit, aiding conceptual clarity around “gram mole” versus “kg mole.”
• We make Python code openly available, underscoring transparency and reproducibility.

9. Reframing the Mole Concept: Distinguishing Between Gram Mole and Kilogram Mole in Understanding Avogadro’s Number

In our approach, as we delve deeper into resolving the fundamental origin and underlying mystery of the Avogadro number, the traditional mole concept increasingly reveals its inherent arbitrariness—particularly when considered in relation to the number of atoms per unit mass, such as per gram or per kilogram. Conventionally viewed as a fixed count of particles, the mole [32,33,34,35] is often regarded as a universal and absolute quantity. However, closer scrutiny shows this is not strictly the case. Rather, the mole’s definition is deeply intertwined with specific, historically contingent choices about mass units that have shifted over time—initially anchored to the gram and more recently tied to the kilogram. These shifts highlight that the mole, as a concept, is not independent of the measurement scale it references but instead depends on the unit of mass against which the number of constituent particles is counted.

This understanding inevitably leads us to propose that the mole should always be explicitly qualified as either a “gram mole” or a “kilogram mole” (and potentially other variants if other mass units become relevant), depending on the mass scale under consideration. Doing so more honestly reflects the relationship between atomic-scale quantities and macroscopic measurements, and it prevents the implicit assumption that the mole is a unit-less, immutable constant. By explicitly denoting the mole relative to a specific mass unit, such as "gram mole" or “kilogram mole”, we clarify the underlying linkage: the numerical scale relating atoms or molecules to bulk mass is fundamentally a function of our chosen mass standard.

Making such distinctions carries several important conceptual and practical implications. Firstly, it demystifies the mole by situating its value within a framework of human-defined conventions rather than presenting it as a natural absolute. This demystification is crucial in both educational and research contexts, fostering clearer understanding and avoiding misconceptions that the mole is a fundamental constant of nature on the same footing as physical constants like the speed of light or Planck’s constant. Instead, it underscores that the mole is a pragmatic and highly useful construct devised for bridging microscopic and macroscopic worlds, shaped by measurement choices that have evolved historically.

Secondly, qualifying the mole relative to mass units enhances transparency and precision in communication of scientific measurements. It reduces ambiguity for chemists, physicists, and engineers who may work with different mass conventions or who may transition between older and newer SI definitions. For example, before the 2019 redefinition of the SI base units, the mole was defined based on 12 grams of carbon-12. Now, the mole is defined as containing an exact number of elementary entities, independent of a reference mass, yet in practice, laboratory-scale measurements inevitably refer to mass standards such as grams or kilograms. The explicit terminology of “gram mole” or “kilogram mole” thus harmonizes conceptual clarity with practical realities.

Furthermore, this reframing brings to light the historical and metrological context in which the mole emerged. It draws attention to how our unit systems and constants are shaped by the technological capabilities, standards, and needs of scientific communities rather than discovered “a priori” in nature. Recognizing that Avogadro’s number and the mole are products of human-defined measurement systems enhances scientific literacy and encourages a more critical perspective on how fundamental constants are established and applied.

Finally, by embracing the qualifiers “gram mole” and “kilogram mole”, scientists and educators invite a more nuanced dialogue about units and constants that may be extended to other areas where unit conventions exert strong influence on scientific understanding. This approach promotes transparency, reduces confusion, and ultimately strengthens the foundation of quantitative science by emphasizing clarity about the assumptions and definitions underlying critical measurements.

In summary, by explicitly contextualizing the mole as a “gram mole” or “kilogram mole”, we not only address the arbitrariness exposed by the evolving relationship between particle counts and mass units but also promote conceptual clarity, historical awareness, and precision in scientific communication. This perspective makes it clear that the mole is a practical tool shaped by human convention—a profound insight when striving to unravel the basic physical origin and meaning of Avogadro’s number.

11. Conclusion

Our innovative computational framework offers a fresh and physically grounded perspective on determining Avogadro’s number. By leveraging nuclear binding energy formulae and implementing transparent Python-based calculations, our approach uniquely ties the unified atomic mass unit and Avogadro number directly to fundamental nuclear properties across the entire nuclear chart (Z = 1 to 140). This method’s strengths lie in:

• Its explicit physical logic, highlighting the inverse relationship between Avogadro’s number and the unified atomic mass unit,
• Its capacity to incorporate and compare multiple nuclear mass models, including both advanced semi-empirical mass formulae and our novel Strong and Electroweak Mass Formula,
• The identification of nuclear binding energy saturation—especially near iron—as a principal factor determining Avogadro’s number’s precise value,
• The clarification of dimensional and unit conventions, elucidating “atoms per gram” versus “atoms per kilogram” and reconciling these with SI mole definitions,
• Its transparent, reproducible computational implementation and pedagogical value,
• The openness to future refinements driven by AI and machine learning methods applied to nuclear mass and binding energy data.

While current experimental methods maintain superior absolute precision for metrological applications, our approach enriches conceptual and educational understanding of Avogadro’s number, offering an independent and adaptable computational paradigm. It also provides promising pathways for integrating nuclear physics advances and data science techniques to further improve nuclear mass models and fundamental constants.

In light of these contributions, this approach deserves recognition as both a significant research endeavour and a versatile teaching tool. Future directions include refining the nuclear mass coefficients with large-scale data, exploring nuclear stability boundaries, creating interactive computational platforms for education, and deepening the quantum–macroscopic linkage embodied by Avogadro’s constant.

Thus, the constant named after Avogadro continues not only to unify dimensions of matter and measurement but also to inspire innovative integration of atomic-scale precision with macroscopic standards, driving advancements in fundamental metrology and shaping the redefinition of SI units in modern science.