Submitted:
06 May 2025
Posted:
07 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Three Assumptions of 4G Model of Final Unification
- 1)
- There exists a characteristic electroweak fermion of rest energy, . It can be considered as the zygote of all elementary particles.
- 2)
- There exists a nuclear elementary charge in such a way that, = Strong coupling constant and .
- 3)
- Each atomic interaction is associated with a characteristic large gravitational coupling constant. Their fitted magnitudes are,
- 1)
- 2)
- In a unified approach, most important point to be noted is that [10],
2.1. Understanding the Electroweak Coefficient and Nuclear Stability
2.2. Revised Strong and Electroweak Mass Formula
3. Revised 6 Term Semi Empirical Mass Formula
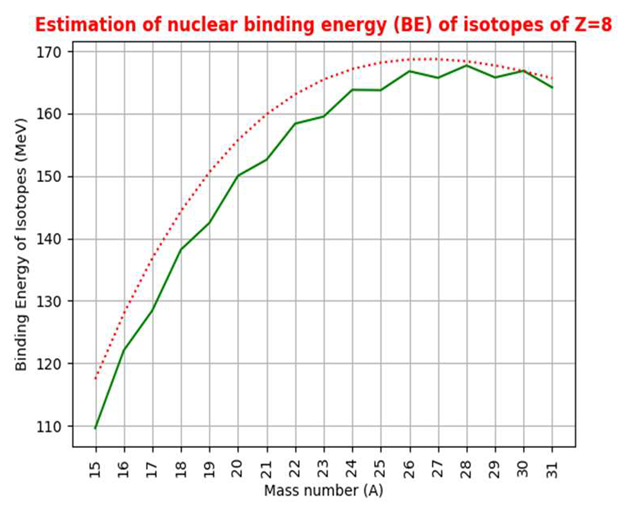
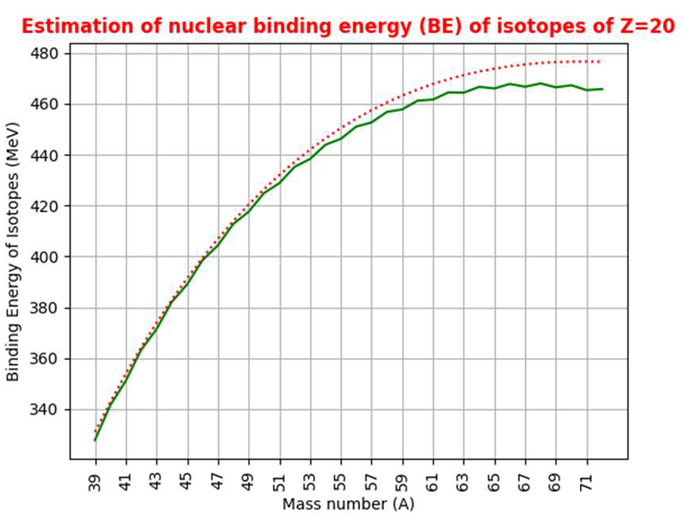
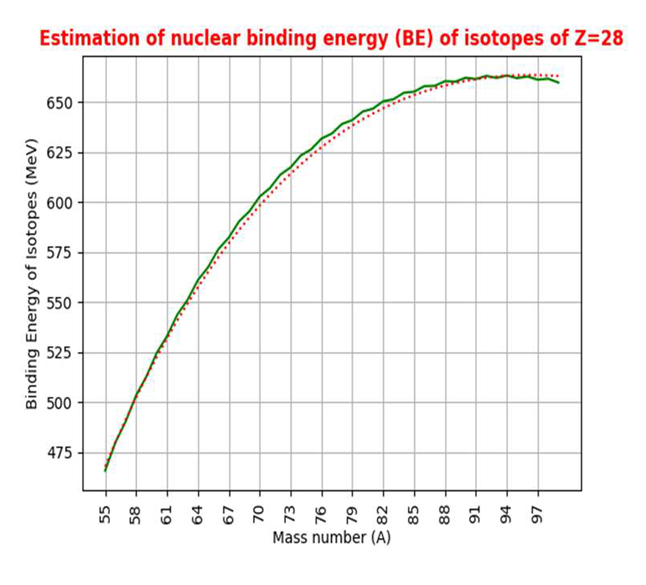
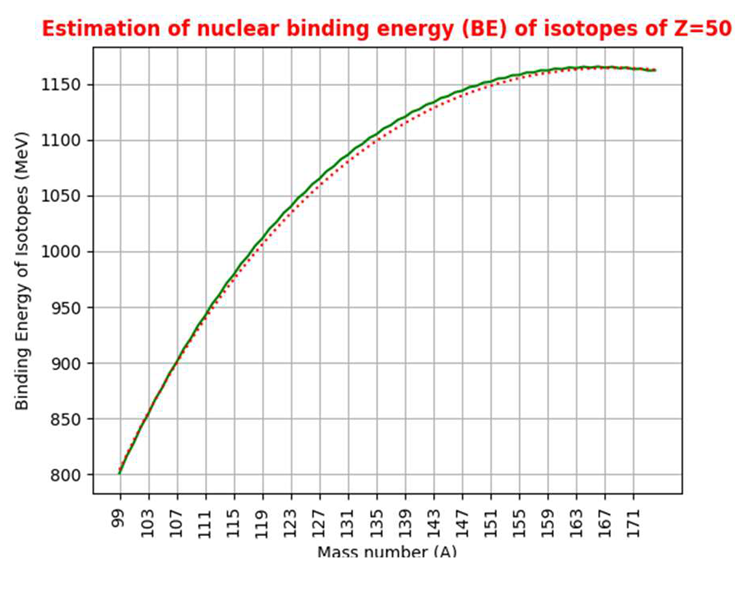
4. Nuclear Binding Energy Linked with Fermi Gas Model, Beta Stability, Strong Coupling Constant and Root Mean Square Radius of Proton
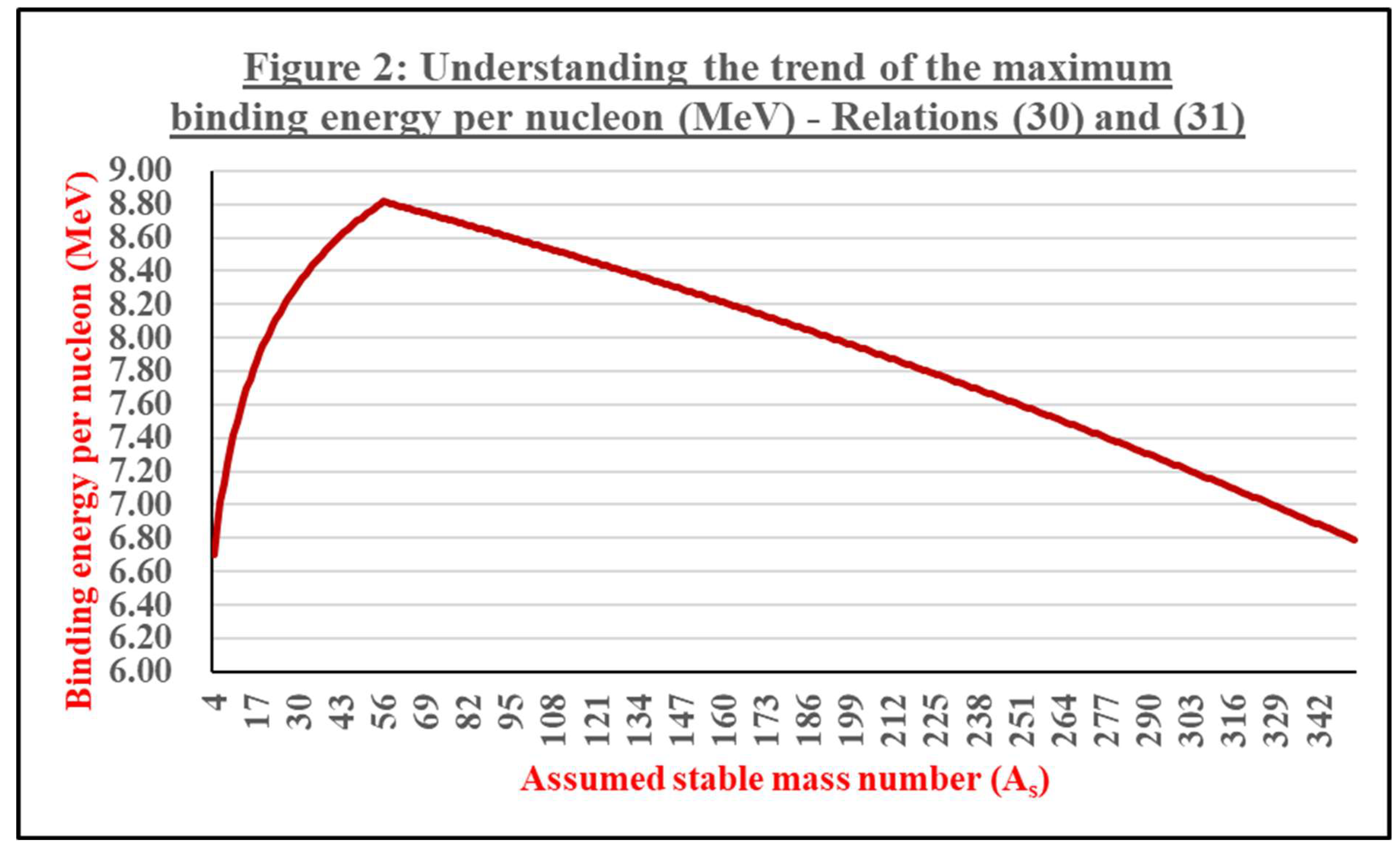
| Assumed stable mass number | Estimated maximum binding energy (MeV) | Estimated maximum binding energy per nucleon (MeV) | Assumed stable mass number | Estimated maximum binding energy (MeV) | Estimated maximum binding energy per nucleon (MeV) | |||
| 4 | 0.00642 | 26.80 | 6.70 | 179 | 0.287295 | 1448.19 | 8.09 | |
| 5 | 0.008025 | 34.35 | 6.87 | 180 | 0.2889 | 1455.11 | 8.08 | |
| 6 | 0.00963 | 42.08 | 7.01 | 181 | 0.290505 | 1462.02 | 8.08 | |
| 7 | 0.011235 | 49.94 | 7.13 | 182 | 0.29211 | 1468.91 | 8.07 | |
| 8 | 0.01284 | 57.93 | 7.24 | 183 | 0.293715 | 1475.79 | 8.06 | |
| 9 | 0.014445 | 66.03 | 7.34 | 184 | 0.29532 | 1482.65 | 8.06 | |
| 10 | 0.01605 | 74.22 | 7.42 | 185 | 0.296925 | 1489.50 | 8.05 | |
| 11 | 0.017655 | 82.49 | 7.50 | 186 | 0.29853 | 1496.33 | 8.04 | |
| 12 | 0.01926 | 90.85 | 7.57 | 187 | 0.300135 | 1503.15 | 8.04 | |
| 13 | 0.020865 | 99.28 | 7.64 | 188 | 0.30174 | 1509.95 | 8.03 | |
| 14 | 0.02247 | 107.77 | 7.70 | 189 | 0.303345 | 1516.73 | 8.03 | |
| 15 | 0.024075 | 116.33 | 7.76 | 190 | 0.30495 | 1523.50 | 8.02 | |
| 16 | 0.02568 | 124.94 | 7.81 | 191 | 0.306555 | 1530.26 | 8.01 | |
| 17 | 0.027285 | 133.61 | 7.86 | 192 | 0.30816 | 1537.00 | 8.01 | |
| 18 | 0.02889 | 142.32 | 7.91 | 193 | 0.309765 | 1543.73 | 8.00 | |
| 19 | 0.030495 | 151.08 | 7.95 | 194 | 0.31137 | 1550.44 | 7.99 | |
| 20 | 0.0321 | 159.89 | 7.99 | 195 | 0.312975 | 1557.13 | 7.99 | |
| 21 | 0.033705 | 168.73 | 8.03 | 196 | 0.31458 | 1563.81 | 7.98 | |
| 22 | 0.03531 | 177.62 | 8.07 | 197 | 0.316185 | 1570.47 | 7.97 | |
| 23 | 0.036915 | 186.54 | 8.11 | 198 | 0.31779 | 1577.12 | 7.97 | |
| 24 | 0.03852 | 195.50 | 8.15 | 199 | 0.319395 | 1583.76 | 7.96 | |
| 25 | 0.040125 | 204.49 | 8.18 | 200 | 0.321 | 1590.37 | 7.95 | |
| 26 | 0.04173 | 213.51 | 8.21 | 201 | 0.322605 | 1596.98 | 7.95 | |
| 27 | 0.043335 | 222.56 | 8.24 | 202 | 0.32421 | 1603.56 | 7.94 | |
| 28 | 0.04494 | 231.64 | 8.27 | 203 | 0.325815 | 1610.13 | 7.93 | |
| 29 | 0.046545 | 240.75 | 8.30 | 204 | 0.32742 | 1616.69 | 7.92 | |
| 30 | 0.04815 | 249.88 | 8.33 | 205 | 0.329025 | 1623.23 | 7.92 | |
| 31 | 0.049755 | 259.04 | 8.36 | 206 | 0.33063 | 1629.75 | 7.91 | |
| 32 | 0.05136 | 268.22 | 8.38 | 207 | 0.332235 | 1636.26 | 7.90 | |
| 33 | 0.052965 | 277.43 | 8.41 | 208 | 0.33384 | 1642.75 | 7.90 | |
| 34 | 0.05457 | 286.65 | 8.43 | 209 | 0.335445 | 1649.22 | 7.89 | |
| 35 | 0.056175 | 295.90 | 8.45 | 210 | 0.33705 | 1655.68 | 7.88 | |
| 36 | 0.05778 | 305.17 | 8.48 | 211 | 0.338655 | 1662.13 | 7.88 | |
| 37 | 0.059385 | 314.46 | 8.50 | 212 | 0.34026 | 1668.56 | 7.87 | |
| 38 | 0.06099 | 323.76 | 8.52 | 213 | 0.341865 | 1674.97 | 7.86 | |
| 39 | 0.062595 | 333.08 | 8.54 | 214 | 0.34347 | 1681.36 | 7.86 | |
| 40 | 0.0642 | 342.42 | 8.56 | 215 | 0.345075 | 1687.74 | 7.85 | |
| 41 | 0.065805 | 351.78 | 8.58 | 216 | 0.34668 | 1694.11 | 7.84 | |
| 42 | 0.06741 | 361.15 | 8.60 | 217 | 0.348285 | 1700.46 | 7.84 | |
| 43 | 0.069015 | 370.53 | 8.62 | 218 | 0.34989 | 1706.79 | 7.83 | |
| 44 | 0.07062 | 379.93 | 8.63 | 219 | 0.351495 | 1713.10 | 7.82 | |
| 45 | 0.072225 | 389.34 | 8.65 | 220 | 0.3531 | 1719.40 | 7.82 | |
| 46 | 0.07383 | 398.77 | 8.67 | 221 | 0.354705 | 1725.68 | 7.81 | |
| 47 | 0.075435 | 408.21 | 8.69 | 222 | 0.35631 | 1731.95 | 7.80 | |
| 48 | 0.07704 | 417.66 | 8.70 | 223 | 0.357915 | 1738.20 | 7.79 | |
| 49 | 0.078645 | 427.12 | 8.72 | 224 | 0.35952 | 1744.43 | 7.79 | |
| 50 | 0.08025 | 436.59 | 8.73 | 225 | 0.361125 | 1750.65 | 7.78 | |
| 51 | 0.081855 | 446.07 | 8.75 | 226 | 0.36273 | 1756.85 | 7.77 | |
| 52 | 0.08346 | 455.56 | 8.76 | 227 | 0.364335 | 1763.04 | 7.77 | |
| 53 | 0.085065 | 465.07 | 8.77 | 228 | 0.36594 | 1769.20 | 7.76 | |
| 54 | 0.08667 | 474.58 | 8.79 | 229 | 0.367545 | 1775.35 | 7.75 | |
| 55 | 0.088275 | 484.10 | 8.80 | 230 | 0.36915 | 1781.49 | 7.75 | |
| 56 | 0.08988 | 493.63 | 8.81 | 231 | 0.370755 | 1787.61 | 7.74 | |
| 57 | 0.091485 | 502.14 | 8.81 | 232 | 0.37236 | 1793.71 | 7.73 | |
| 58 | 0.09309 | 510.64 | 8.80 | 233 | 0.373965 | 1799.79 | 7.72 | |
| 59 | 0.094695 | 519.12 | 8.80 | 234 | 0.37557 | 1805.86 | 7.72 | |
| 60 | 0.0963 | 527.60 | 8.79 | 235 | 0.377175 | 1811.91 | 7.71 | |
| 61 | 0.097905 | 536.07 | 8.79 | 236 | 0.37878 | 1817.94 | 7.70 | |
| 62 | 0.09951 | 544.52 | 8.78 | 237 | 0.380385 | 1823.96 | 7.70 | |
| 63 | 0.101115 | 552.97 | 8.78 | 238 | 0.38199 | 1829.96 | 7.69 | |
| 64 | 0.10272 | 561.40 | 8.77 | 239 | 0.383595 | 1835.94 | 7.68 | |
| 65 | 0.104325 | 569.82 | 8.77 | 240 | 0.3852 | 1841.91 | 7.67 | |
| 66 | 0.10593 | 578.23 | 8.76 | 241 | 0.386805 | 1847.86 | 7.67 | |
| 67 | 0.107535 | 586.63 | 8.76 | 242 | 0.38841 | 1853.79 | 7.66 | |
| 68 | 0.10914 | 595.01 | 8.75 | 243 | 0.390015 | 1859.70 | 7.65 | |
| 69 | 0.110745 | 603.39 | 8.74 | 244 | 0.39162 | 1865.60 | 7.65 | |
| 70 | 0.11235 | 611.75 | 8.74 | 245 | 0.393225 | 1871.48 | 7.64 | |
| 71 | 0.113955 | 620.10 | 8.73 | 246 | 0.39483 | 1877.34 | 7.63 | |
| 72 | 0.11556 | 628.45 | 8.73 | 247 | 0.396435 | 1883.19 | 7.62 | |
| 73 | 0.117165 | 636.77 | 8.72 | 248 | 0.39804 | 1889.01 | 7.62 | |
| 74 | 0.11877 | 645.09 | 8.72 | 249 | 0.399645 | 1894.82 | 7.61 | |
| 75 | 0.120375 | 653.40 | 8.71 | 250 | 0.40125 | 1900.62 | 7.60 | |
| 76 | 0.12198 | 661.69 | 8.71 | 251 | 0.402855 | 1906.39 | 7.60 | |
| 77 | 0.123585 | 669.98 | 8.70 | 252 | 0.40446 | 1912.15 | 7.59 | |
| 78 | 0.12519 | 678.25 | 8.70 | 253 | 0.406065 | 1917.89 | 7.58 | |
| 79 | 0.126795 | 686.51 | 8.69 | 254 | 0.40767 | 1923.62 | 7.57 | |
| 80 | 0.1284 | 694.75 | 8.68 | 255 | 0.409275 | 1929.32 | 7.57 | |
| 81 | 0.130005 | 702.99 | 8.68 | 256 | 0.41088 | 1935.01 | 7.56 | |
| 82 | 0.13161 | 711.21 | 8.67 | 257 | 0.412485 | 1940.68 | 7.55 | |
| 83 | 0.133215 | 719.42 | 8.67 | 258 | 0.41409 | 1946.33 | 7.54 | |
| 84 | 0.13482 | 727.62 | 8.66 | 259 | 0.415695 | 1951.97 | 7.54 | |
| 85 | 0.136425 | 735.81 | 8.66 | 260 | 0.4173 | 1957.58 | 7.53 | |
| 86 | 0.13803 | 743.99 | 8.65 | 261 | 0.418905 | 1963.18 | 7.52 | |
| 87 | 0.139635 | 752.15 | 8.65 | 262 | 0.42051 | 1968.76 | 7.51 | |
| 88 | 0.14124 | 760.31 | 8.64 | 263 | 0.422115 | 1974.33 | 7.51 | |
| 89 | 0.142845 | 768.45 | 8.63 | 264 | 0.42372 | 1979.87 | 7.50 | |
| 90 | 0.14445 | 776.57 | 8.63 | 265 | 0.425325 | 1985.40 | 7.49 | |
| 91 | 0.146055 | 784.69 | 8.62 | 266 | 0.42693 | 1990.91 | 7.48 | |
| 92 | 0.14766 | 792.80 | 8.62 | 267 | 0.428535 | 1996.40 | 7.48 | |
| 93 | 0.149265 | 800.89 | 8.61 | 268 | 0.43014 | 2001.87 | 7.47 | |
| 94 | 0.15087 | 808.97 | 8.61 | 269 | 0.431745 | 2007.33 | 7.46 | |
| 95 | 0.152475 | 817.04 | 8.60 | 270 | 0.43335 | 2012.76 | 7.45 | |
| 96 | 0.15408 | 825.09 | 8.59 | 271 | 0.434955 | 2018.18 | 7.45 | |
| 97 | 0.155685 | 833.13 | 8.59 | 272 | 0.43656 | 2023.58 | 7.44 | |
| 98 | 0.15729 | 841.17 | 8.58 | 273 | 0.438165 | 2028.96 | 7.43 | |
| 99 | 0.158895 | 849.18 | 8.58 | 274 | 0.43977 | 2034.32 | 7.42 | |
| 100 | 0.1605 | 857.19 | 8.57 | 275 | 0.441375 | 2039.67 | 7.42 | |
| 101 | 0.162105 | 865.18 | 8.57 | 276 | 0.44298 | 2044.99 | 7.41 | |
| 102 | 0.16371 | 873.17 | 8.56 | 277 | 0.444585 | 2050.30 | 7.40 | |
| 103 | 0.165315 | 881.14 | 8.55 | 278 | 0.44619 | 2055.59 | 7.39 | |
| 104 | 0.16692 | 889.09 | 8.55 | 279 | 0.447795 | 2060.86 | 7.39 | |
| 105 | 0.168525 | 897.04 | 8.54 | 280 | 0.4494 | 2066.11 | 7.38 | |
| 106 | 0.17013 | 904.97 | 8.54 | 281 | 0.451005 | 2071.35 | 7.37 | |
| 107 | 0.171735 | 912.89 | 8.53 | 282 | 0.45261 | 2076.56 | 7.36 | |
| 108 | 0.17334 | 920.80 | 8.53 | 283 | 0.454215 | 2081.76 | 7.36 | |
| 109 | 0.174945 | 928.69 | 8.52 | 284 | 0.45582 | 2086.93 | 7.35 | |
| 110 | 0.17655 | 936.57 | 8.51 | 285 | 0.457425 | 2092.09 | 7.34 | |
| 111 | 0.178155 | 944.44 | 8.51 | 286 | 0.45903 | 2097.23 | 7.33 | |
| 112 | 0.17976 | 952.30 | 8.50 | 287 | 0.460635 | 2102.35 | 7.33 | |
| 113 | 0.181365 | 960.14 | 8.50 | 288 | 0.46224 | 2107.45 | 7.32 | |
| 114 | 0.18297 | 967.97 | 8.49 | 289 | 0.463845 | 2112.53 | 7.31 | |
| 115 | 0.184575 | 975.79 | 8.49 | 290 | 0.46545 | 2117.59 | 7.30 | |
| 116 | 0.18618 | 983.59 | 8.48 | 291 | 0.467055 | 2122.64 | 7.29 | |
| 117 | 0.187785 | 991.39 | 8.47 | 292 | 0.46866 | 2127.66 | 7.29 | |
| 118 | 0.18939 | 999.17 | 8.47 | 293 | 0.470265 | 2132.67 | 7.28 | |
| 119 | 0.190995 | 1006.93 | 8.46 | 294 | 0.47187 | 2137.65 | 7.27 | |
| 120 | 0.1926 | 1014.69 | 8.46 | 295 | 0.473475 | 2142.62 | 7.26 | |
| 121 | 0.194205 | 1022.43 | 8.45 | 296 | 0.47508 | 2147.57 | 7.26 | |
| 122 | 0.19581 | 1030.16 | 8.44 | 297 | 0.476685 | 2152.50 | 7.25 | |
| 123 | 0.197415 | 1037.87 | 8.44 | 298 | 0.47829 | 2157.41 | 7.24 | |
| 124 | 0.19902 | 1045.57 | 8.43 | 299 | 0.479895 | 2162.29 | 7.23 | |
| 125 | 0.200625 | 1053.26 | 8.43 | 300 | 0.4815 | 2167.16 | 7.22 | |
| 126 | 0.20223 | 1060.94 | 8.42 | 301 | 0.483105 | 2172.01 | 7.22 | |
| 127 | 0.203835 | 1068.60 | 8.41 | 302 | 0.48471 | 2176.85 | 7.21 | |
| 128 | 0.20544 | 1076.25 | 8.41 | 303 | 0.486315 | 2181.66 | 7.20 | |
| 129 | 0.207045 | 1083.89 | 8.40 | 304 | 0.48792 | 2186.45 | 7.19 | |
| 130 | 0.20865 | 1091.51 | 8.40 | 305 | 0.489525 | 2191.22 | 7.18 | |
| 131 | 0.210255 | 1099.12 | 8.39 | 306 | 0.49113 | 2195.97 | 7.18 | |
| 132 | 0.21186 | 1106.72 | 8.38 | 307 | 0.492735 | 2200.70 | 7.17 | |
| 133 | 0.213465 | 1114.30 | 8.38 | 308 | 0.49434 | 2205.42 | 7.16 | |
| 134 | 0.21507 | 1121.87 | 8.37 | 309 | 0.495945 | 2210.11 | 7.15 | |
| 135 | 0.216675 | 1129.43 | 8.37 | 310 | 0.49755 | 2214.78 | 7.14 | |
| 136 | 0.21828 | 1136.97 | 8.36 | 311 | 0.499155 | 2219.43 | 7.14 | |
| 137 | 0.219885 | 1144.50 | 8.35 | 312 | 0.50076 | 2224.06 | 7.13 | |
| 138 | 0.22149 | 1152.01 | 8.35 | 313 | 0.502365 | 2228.68 | 7.12 | |
| 139 | 0.223095 | 1159.52 | 8.34 | 314 | 0.50397 | 2233.27 | 7.11 | |
| 140 | 0.2247 | 1167.01 | 8.34 | 315 | 0.505575 | 2237.84 | 7.10 | |
| 141 | 0.226305 | 1174.48 | 8.33 | 316 | 0.50718 | 2242.39 | 7.10 | |
| 142 | 0.22791 | 1181.94 | 8.32 | 317 | 0.508785 | 2246.92 | 7.09 | |
| 143 | 0.229515 | 1189.39 | 8.32 | 318 | 0.51039 | 2251.43 | 7.08 | |
| 144 | 0.23112 | 1196.83 | 8.31 | 319 | 0.511995 | 2255.92 | 7.07 | |
| 145 | 0.232725 | 1204.25 | 8.31 | 320 | 0.5136 | 2260.39 | 7.06 | |
| 146 | 0.23433 | 1211.66 | 8.30 | 321 | 0.515205 | 2264.84 | 7.06 | |
| 147 | 0.235935 | 1219.05 | 8.29 | 322 | 0.51681 | 2269.27 | 7.05 | |
| 148 | 0.23754 | 1226.43 | 8.29 | 323 | 0.518415 | 2273.68 | 7.04 | |
| 149 | 0.239145 | 1233.80 | 8.28 | 324 | 0.52002 | 2278.07 | 7.03 | |
| 150 | 0.24075 | 1241.15 | 8.27 | 325 | 0.521625 | 2282.44 | 7.02 | |
| 151 | 0.242355 | 1248.49 | 8.27 | 326 | 0.52323 | 2286.78 | 7.01 | |
| 152 | 0.24396 | 1255.81 | 8.26 | 327 | 0.524835 | 2291.11 | 7.01 | |
| 153 | 0.245565 | 1263.12 | 8.26 | 328 | 0.52644 | 2295.42 | 7.00 | |
| 154 | 0.24717 | 1270.42 | 8.25 | 329 | 0.528045 | 2299.70 | 6.99 | |
| 155 | 0.248775 | 1277.70 | 8.24 | 330 | 0.52965 | 2303.96 | 6.98 | |
| 156 | 0.25038 | 1284.97 | 8.24 | 331 | 0.531255 | 2308.21 | 6.97 | |
| 157 | 0.251985 | 1292.22 | 8.23 | 332 | 0.53286 | 2312.43 | 6.97 | |
| 158 | 0.25359 | 1299.46 | 8.22 | 333 | 0.534465 | 2316.63 | 6.96 | |
| 159 | 0.255195 | 1306.69 | 8.22 | 334 | 0.53607 | 2320.81 | 6.95 | |
| 160 | 0.2568 | 1313.90 | 8.21 | 335 | 0.537675 | 2324.97 | 6.94 | |
| 161 | 0.258405 | 1321.10 | 8.21 | 336 | 0.53928 | 2329.10 | 6.93 | |
| 162 | 0.26001 | 1328.28 | 8.20 | 337 | 0.540885 | 2333.22 | 6.92 | |
| 163 | 0.261615 | 1335.45 | 8.19 | 338 | 0.54249 | 2337.32 | 6.92 | |
| 164 | 0.26322 | 1342.61 | 8.19 | 339 | 0.544095 | 2341.39 | 6.91 | |
| 165 | 0.264825 | 1349.75 | 8.18 | 340 | 0.5457 | 2345.44 | 6.90 | |
| 166 | 0.26643 | 1356.87 | 8.17 | 341 | 0.547305 | 2349.47 | 6.89 | |
| 167 | 0.268035 | 1363.99 | 8.17 | 342 | 0.54891 | 2353.48 | 6.88 | |
| 168 | 0.26964 | 1371.08 | 8.16 | 343 | 0.550515 | 2357.47 | 6.87 | |
| 169 | 0.271245 | 1378.17 | 8.15 | 344 | 0.55212 | 2361.44 | 6.86 | |
| 170 | 0.27285 | 1385.23 | 8.15 | 345 | 0.553725 | 2365.38 | 6.86 | |
| 171 | 0.274455 | 1392.29 | 8.14 | 346 | 0.55533 | 2369.30 | 6.85 | |
| 172 | 0.27606 | 1399.33 | 8.14 | 347 | 0.556935 | 2373.21 | 6.84 | |
| 173 | 0.277665 | 1406.35 | 8.13 | 348 | 0.55854 | 2377.09 | 6.83 | |
| 174 | 0.27927 | 1413.36 | 8.12 | 349 | 0.560145 | 2380.94 | 6.82 | |
| 175 | 0.280875 | 1420.36 | 8.12 | 350 | 0.56175 | 2384.78 | 6.81 | |
| 176 | 0.28248 | 1427.34 | 8.11 | 351 | 0.563355 | 2388.59 | 6.81 | |
| 177 | 0.284085 | 1434.30 | 8.10 | 352 | 0.56496 | 2392.39 | 6.80 | |
| 178 | 0.28569 | 1441.25 | 8.10 | 353 | 0.566565 | 2396.16 | 6.79 |
5. Conclusions
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seshavatharam, U.V. S and Lakshminarayana S. Radius, surface area and volume dependent electroweak term and isospin dependent asymmetry term of the strong and electroweak mass formula. Int. J. Phys. Appl. 2025, 7, 122–134. [Google Scholar] [CrossRef]
- Seshavatharam, U.V. S and Lakshminarayana S. Understanding the Origins of Quark Charges, Quantum of Magnetic Flux, Planck’s Radiation Constant and Celestial Magnetic Moments with the 4G Model of Nuclear Charge. Current Physics. 2024, 1, e090524229812. [Google Scholar] [CrossRef]
- Seshavatharam, U.V. S and Lakshminarayana S. Exploring condensed matter physics with refined electroweak term of the strong and electroweak mass formula. World Scientific News. 2024, 193, 105–113. [Google Scholar]
- Seshavatharam U., V. S, Gunavardhana Naidu T and Lakshminarayana S. Nuclear evidences for confirming the physical existence of 585 GeV weak fermion and galactic observations of TeV radiation. International Journal of Advanced Astronomy. 2025, 13, 1–17. [Google Scholar] [CrossRef]
- Seshavatharam U. V., S. , Gunavardhana Naidu T and Lakshminarayana S. To confirm the existence of heavy weak fermion of rest energy 585 GeV. AIP Conf. Proc. 2022, 2451, 020003. [Google Scholar]
- Seshavatharam U V S and Lakshminarayana, S. 4G model of final unification – A brief report. Journal of Physics: Conference Series 2022, 2197, 012029. [Google Scholar]
- Seshavatharam U., V. S and Lakshminarayana S., H. K. Cherop and K. M. Khanna, Three Unified Nuclear Binding Energy Formulae. World Scientific News 2022, 163, 30–77. [Google Scholar]
- Seshavatharam, U.V. S and Lakshminarayana, S., On the Combined Role of Strong and Electroweak Interactions in Understanding Nuclear Binding Energy Scheme. Mapana Journal of Sciences 2021, 20, 1–18. [Google Scholar]
- Seshavatharam, U.V. S and Lakshminarayana S., Strong and Weak Interactions in Ghahramany’s Integrated Nuclear Binding Energy Formula. World Scientific News 2021, 161, 111–129. [Google Scholar]
- Seshavatharam, U.V. S and Lakshminarayana S. Is reduced Planck’s constant - an outcome of electroweak gravity? Mapana Journal of Sciences. 2020, 19, 1–13. [Google Scholar]
- Seshavatharam, U.V. S and Lakshminarayana S. A very brief review on strong and electroweak mass formula pertaining to 4G model of final unification. Proceedings of the DAE Symp. on Nucl. Phys. 2023, 67, 1173. [Google Scholar]
- Seshavatharam, U.V. S and Lakshminarayana S. Computing unified atomic mass unit and Avogadro number with various nuclear binding energy formulae coded in Python. Int. J. Chem. Stud. 2025, 13, 24–30. [Google Scholar] [CrossRef]
- Bethe H., A. Thomas-Fermi Theory of Nuclei. Phys. Rev. 1968, 167, 879–907. [Google Scholar] [CrossRef]
- Myers W., D. and Swiatecki W. J. Nuclear Properties According to the Thomas-Fermi Model. LBL-36557 Rev. UC-413, 1995.
- Myers W., D. and Swiatecki W. J. Table of nuclear masses according to the 1994 Thomas-Fermi model. United States: N. p., 1994. Web.
- P. R. Chowdhury, C. Samanta, D.N. Basu, Modified Bethe– Weizsacker mass formula with isotonic shift and new driplines. Mod. Phys. Lett. A 2005, 20, 1605–1618. [Google Scholar] [CrossRef]
- G. Royer, On the coefficients of the liquid drop model mass formulae and nuclear radii. Nuclear Physics A 2008, 807, 105–118. [Google Scholar] [CrossRef]
- Djelloul Benzaid, Salaheddine Bentridi, Abdelkader Kerraci, Naima Amrani. Bethe–Weizsa¨cker semiempirical mass formula coefficients 2019 update based on AME2016. NUCL. SCI. TECH. 2020, 31, 9. [Google Scholar] [CrossRef]
- Gao, Z.P. , Wang, YJ., Lü, HL. et al., Machine learning the nuclear mass. NUCL. SCI. TECH. 2021, 32, 109. [Google Scholar] [CrossRef]
- Peng Guo, et. al. (DRHBc Mass Table Collaboration), Nuclear mass table in deformed relativistic Hartree-Bogoliubov theory in continuum, II: Even-Z nuclei. Atomic Data and Nuclear Data Tables 2024, 158, 101661. [Google Scholar]
- Cht. Mavrodiev S, Deliyergiyev M.A. Modification of the nuclear landscape in the inverse problem framework using the generalized Bethe-Weizsäcker mass formula. Int. J. Mod. Phys. E 2018, 27, 1850015. [Google Scholar] [CrossRef]
- Ghahramany N, Gharaati, S. , & Ghanaatian, M. New approach to nuclear binding energy in integrated nuclear model. Journal of Theoretical and Applied Physics 2012, 6, 3. [Google Scholar]
- Ghahramany N, Sh Gharaati, Ghanaatian M, Hora H. New scheme of nuclide and nuclear binding energy from quark-like model. Iranian Journal of Science & Technology A3.
- N. Ghahramany M. Ghanaatian and M. Hooshmand. Quark-Gluon Plasma Model and Origin of Magic Numbers. Iranian Physical Journal 2007, 1-2, 35–38. [Google Scholar]
- C. Grojean. Higgs Physics. Proceedings of the 2015 CERN–Latin-American School of High-Energy Physics, 143-157, 2016, CERN-2016-005 (CERN, Geneva, 2016).
- Ahmed Abokhalil. The Higgs Mechanism and Higgs Boson: Unveiling the Symmetry of the Universe. arXiv:2306. 0101.
- Einstein, B. Podolsky, and N. Rosen. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- N. Bohr. Can quantum mechanical description of physical reality be considered complete? Phys. Rev. 1935, 480, 696. [Google Scholar]
- J.S. Bell. On the Einstein Podolsky Rosen paradox. Physics 1, 195, 1964.
- J. Bell, On the problem of hidden variables in quantum mechanics. Reviews of Modern Physics. 1966, 38, 447. [Google Scholar] [CrossRef]
- Seshavatharam, U.V. S, Lakshminarayana S. EPR argument and mystery of the reduced Planck’s constant. Algebras, Groups, and Geometries. 2020, 36, 801–822. [Google Scholar]
- Sunil Mukhi. String theory: a perspective over the last 25 years. Class. Quantum Grav. 2011, 28, 153001. [Google Scholar] [CrossRef]
- Sachdev, Subir. Strange and stringy. Scientific American. 2013, 308, 44–51. [Google Scholar]
- Blumenhagen, R. , Lüst D., Theisen S. Basic Concepts of String Theory. Theoretical and Mathematical Physics Springer Heidelberg, Germany, 2013.
- Arnab Priya Saha and Aninda Sinha Phys. Field Theory Expansions of String Theory Amplitudes. Rev. Lett. 2024, 132, 221601. [Google Scholar] [CrossRef]
- Seshavatharam, U.V.S. and Lakshminarayana S. On the compactification and reformation of string theory with three large atomic gravitational constants. International Journal of Physical Research 2021, 9, 42–48. [Google Scholar] [CrossRef]
- D, d’Enterria; et al. The strong coupling constant: state of the art and the decade ahead. J. Phys. G: Nucl. Part. Phys. 2024, 51, 090501. [Google Scholar]
- S. Navas et al. Quarks. (Particle Data Group). Phys. Rev. D 2024, 110, 030001. [Google Scholar]
- Seshavatharam, U.V.S. and Lakshminarayana S. Understanding the Role of Nuclear Elementary Charge and Its Potential in Estimating Nuclear Binding Energy and Strong Coupling Constant. Preprints 2025, 2025042431. [Google Scholar] [CrossRef]
- M. Ismail1, W. M. Seif, and A. Abdurrahman. Relative stability and magic numbers of nuclei deduced from behavior of cluster emission half-lives. Phys. Rev. C 94, 024316.
- Maruhn, J.A. , Reinhard, PG., Suraud, E. The Fermi-Gas Model. In: Simple Models of Many-Fermion Systems. Springer, Berlin, Heidelberg. 2010.
- Seshavatharam, U.V.S.; et al. On the Role of Fermi Gas Model in Understanding the Binding Energy of Stable Atomic Nuclides. Prespacetime Journal 2015, 6. [Google Scholar]
- Seshavatharam, U.V.S. and Lakshminarayana S. Super symmetry in strong and weak interactions. Int. J. Mod. Phys. E 2010, 19, 263–280. [Google Scholar] [CrossRef]
- Deur Alexandre, Brodsky Stanley J, De Téramond, Guy F. The QCD running coupling. Progress in Particle and Nuclear Physics. 2016, 90, 1–74. [Google Scholar] [CrossRef]
- Seshavatharam, U.V.S. and Lakshminarayana S. Simplified & Unified Picture of Nuclear Binding Energy. Prespacetime journal 2015, 6, 1261–1273. [Google Scholar]
- H. Gao M. Vanderhaeghen, The proton charge radius. Rev. Mod. Phys. 2022, 94, 015002. [Google Scholar] [CrossRef]
| S.No | Interaction | String Tension | String energy |
| 1 | Weak | ||
| 2 | Strong | ||
| 3 | Electromagnetic |
| S.No | Interaction | String Tension | String energy |
| 1 | Weak | ||
| 2 | Strong | ||
| 3 | Electromagnetic |
 |
 |
 |
 |
 |
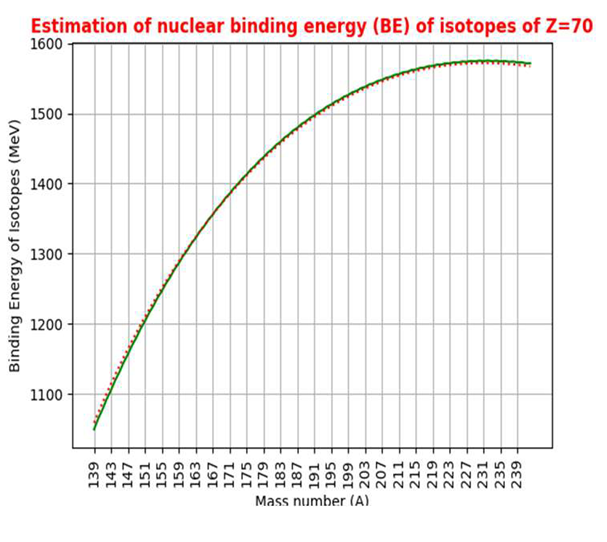 |
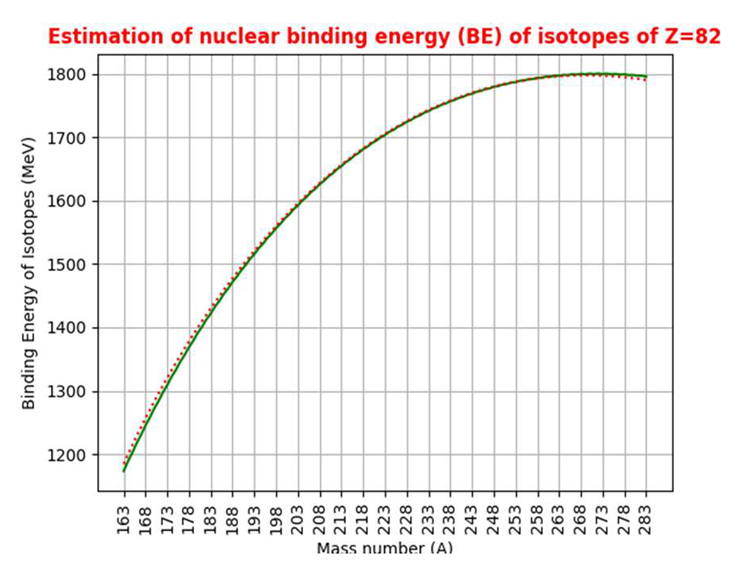 |
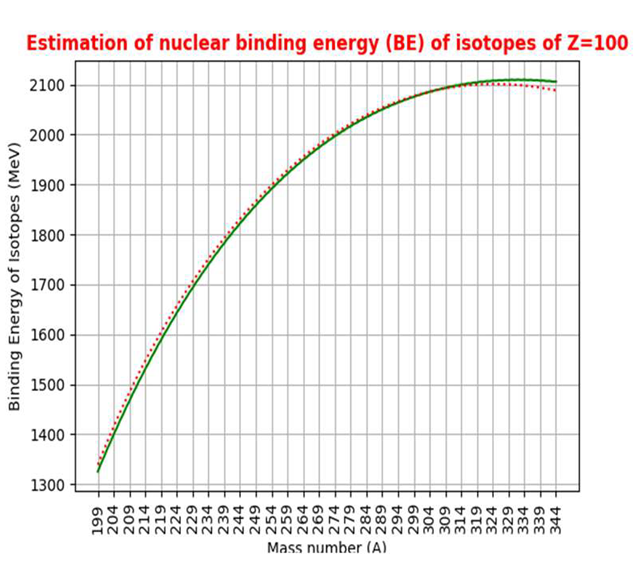 |
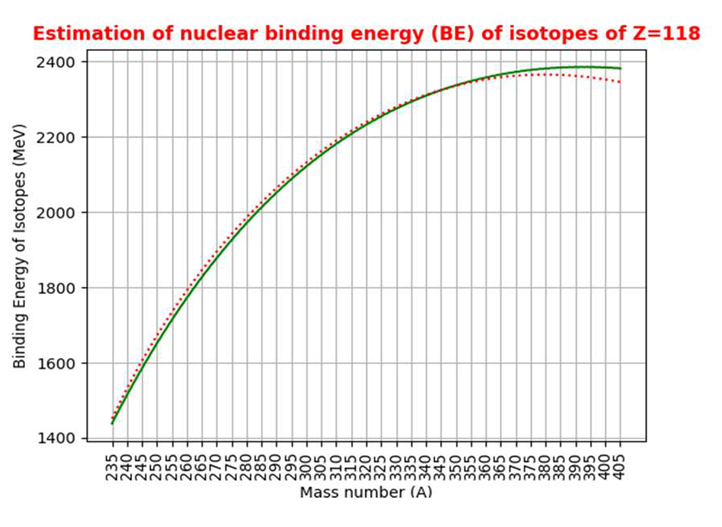 |
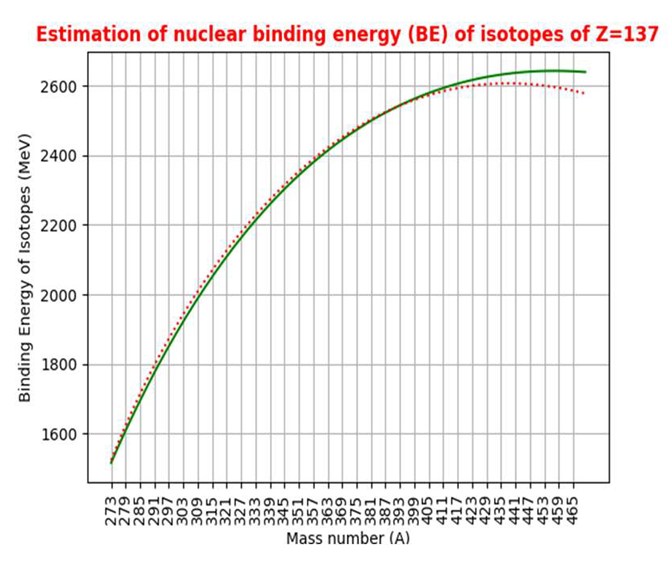 |
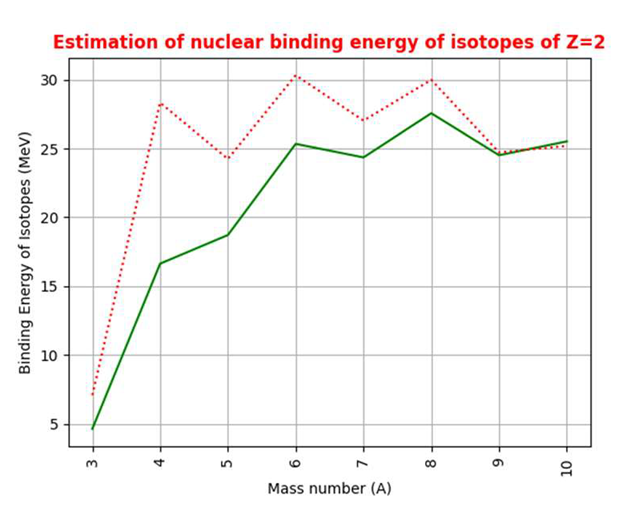 |
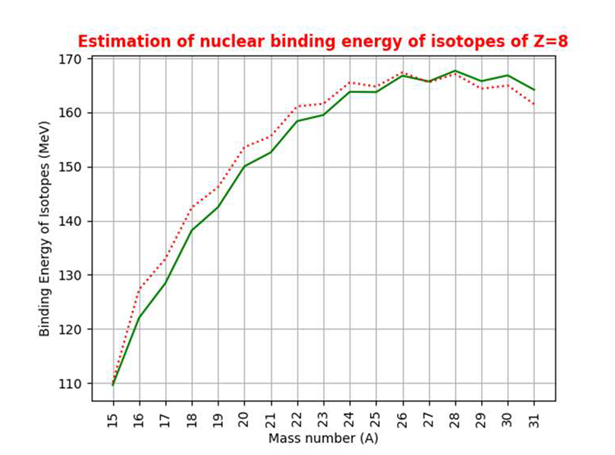 |
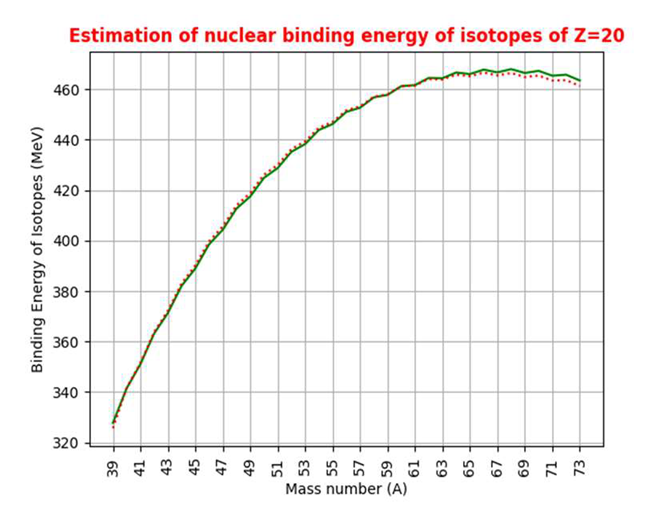 |
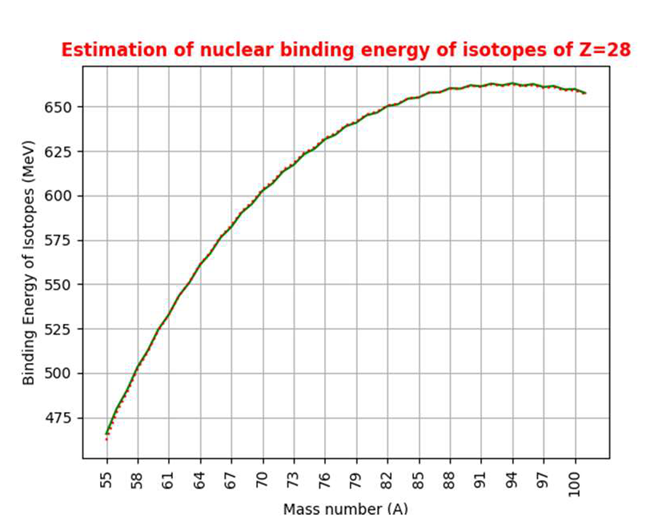 |
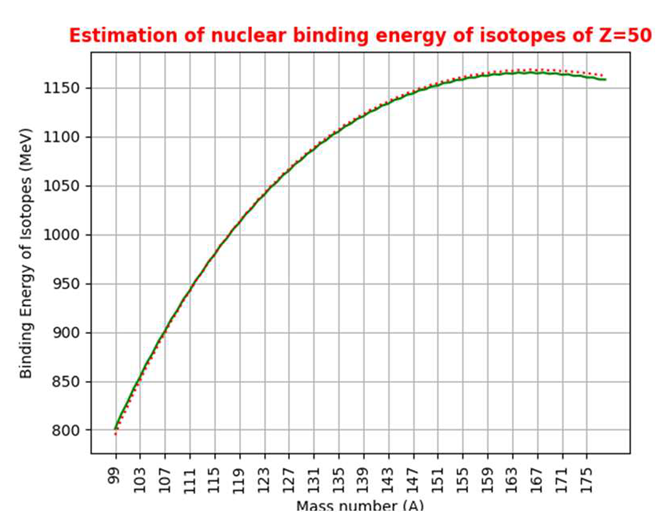 |
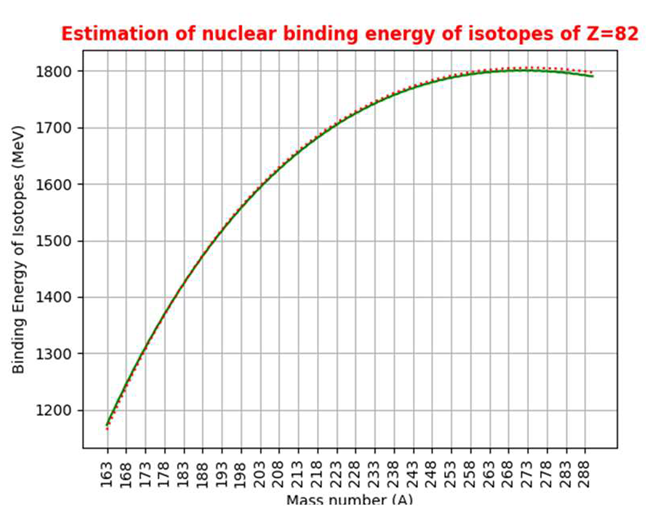 |
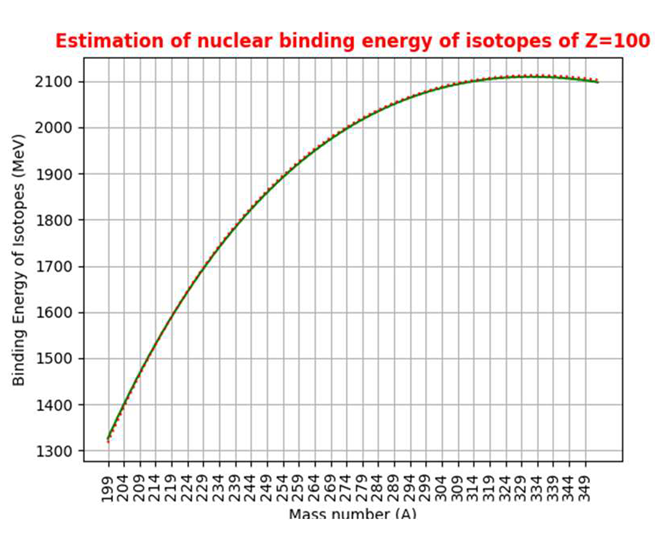 |
 |
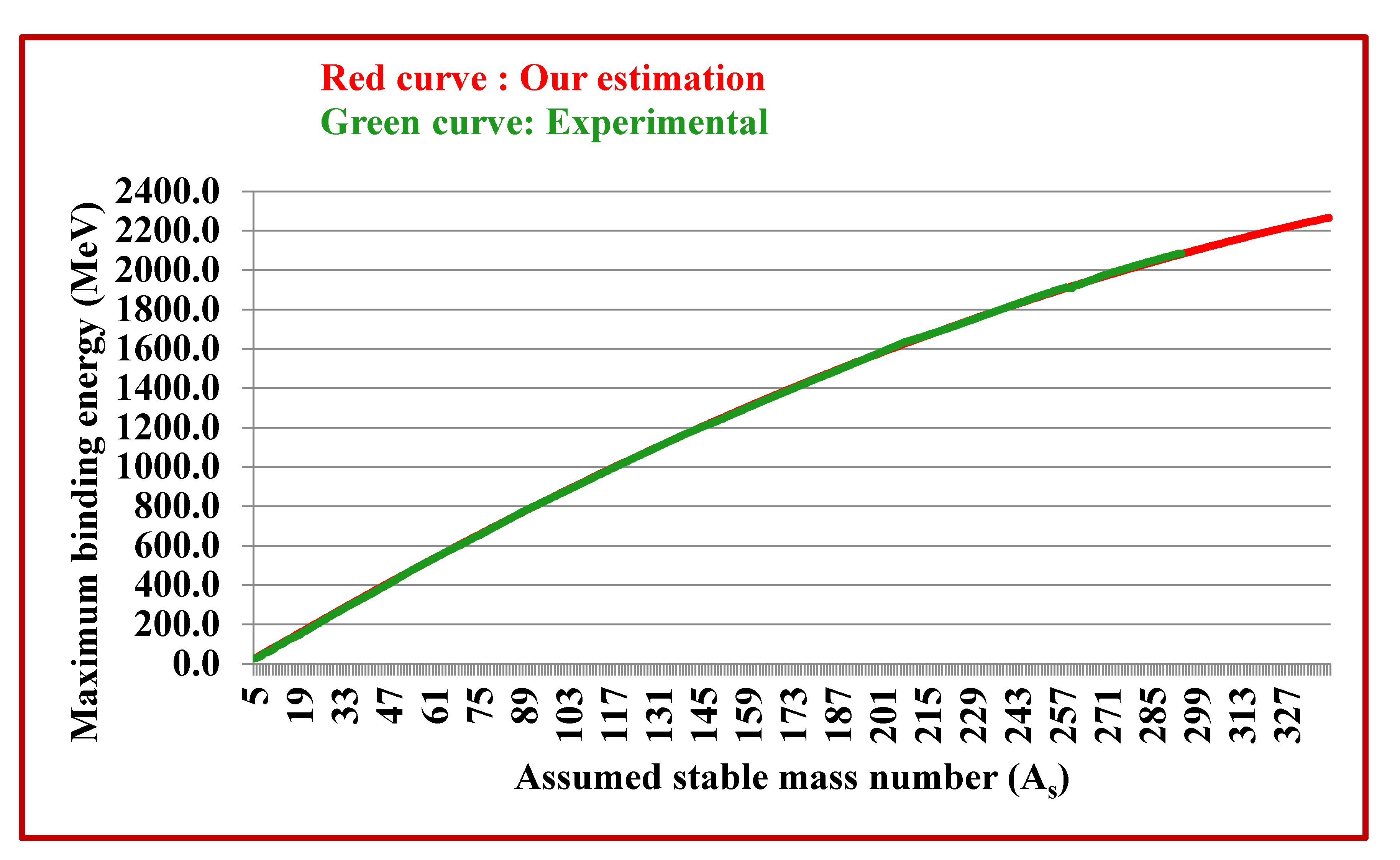
| Assumed stable mass number As | Estimated Max. Binding energy of As (MeV) Relation (32) |
Experimental Max. Binding energy of As(MeV) | (Exp.- Est.) Binding energy(MeV) | Estimated Binding energy per nucleon (MeV) |
Experimental Binding energy per nucleon(MeV) |
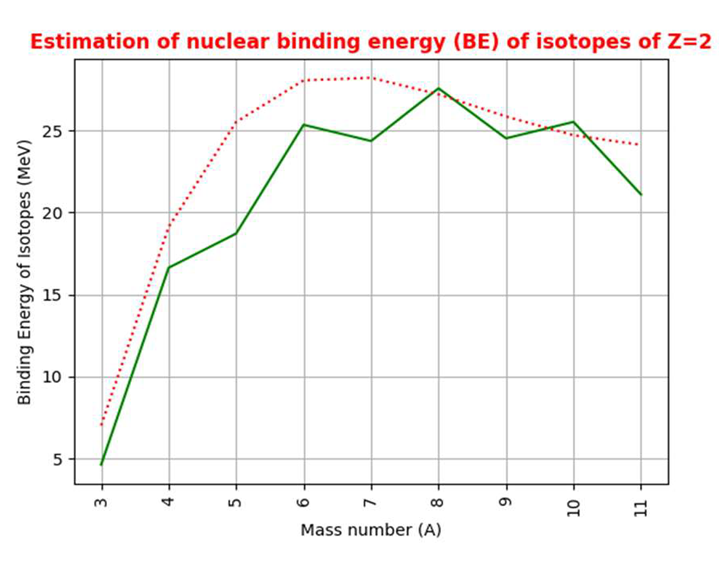
| 5 | 27.94 | 27.56 | -0.38 | 5.59 | 5.51 |
| 6 | 36.86 | 31.99 | -4.86 | 6.14 | 5.33 |
| 7 | 45.87 | 39.25 | -6.62 | 6.55 | 5.61 |
| 8 | 54.95 | 56.50 | 1.55 | 6.87 | 7.06 |
| 9 | 64.08 | 58.16 | -5.91 | 7.12 | 6.46 |
| 10 | 73.25 | 64.98 | -8.27 | 7.32 | 6.50 |
| 11 | 82.45 | 76.20 | -6.24 | 7.50 | 6.93 |
| 12 | 91.67 | 92.16 | 0.49 | 7.64 | 7.68 |
| 13 | 100.91 | 97.11 | -3.80 | 7.76 | 7.47 |
| 14 | 110.16 | 105.28 | -4.87 | 7.87 | 7.52 |
| 15 | 119.42 | 115.49 | -3.92 | 7.96 | 7.70 |
| 16 | 128.68 | 127.62 | -1.06 | 8.04 | 7.98 |
| 17 | 137.95 | 131.76 | -6.19 | 8.11 | 7.75 |
| 18 | 147.22 | 139.81 | -7.41 | 8.18 | 7.77 |
| 19 | 156.49 | 147.80 | -8.69 | 8.24 | 7.78 |
| 20 | 165.76 | 160.64 | -5.11 | 8.29 | 8.03 |
| 21 | 175.02 | 167.41 | -7.61 | 8.33 | 7.97 |
| 22 | 184.28 | 177.77 | -6.51 | 8.38 | 8.08 |
| 23 | 193.53 | 186.56 | -6.97 | 8.41 | 8.11 |
| 24 | 202.78 | 198.26 | -4.52 | 8.45 | 8.26 |
| 25 | 212.02 | 205.59 | -6.43 | 8.48 | 8.22 |
| 26 | 221.24 | 216.68 | -4.56 | 8.51 | 8.33 |
| 27 | 230.47 | 224.95 | -5.51 | 8.54 | 8.33 |
| 28 | 239.68 | 236.54 | -3.14 | 8.56 | 8.45 |
| 29 | 248.88 | 245.01 | -3.87 | 8.58 | 8.45 |
| 30 | 258.07 | 255.62 | -2.45 | 8.60 | 8.52 |
| 31 | 267.25 | 262.92 | -4.33 | 8.62 | 8.48 |
| 32 | 276.41 | 271.78 | -4.63 | 8.64 | 8.49 |
| 33 | 285.57 | 280.96 | -4.61 | 8.65 | 8.51 |
| 34 | 294.71 | 291.84 | -2.87 | 8.67 | 8.58 |
| 35 | 303.84 | 298.82 | -5.02 | 8.68 | 8.54 |
| 36 | 312.96 | 308.71 | -4.25 | 8.69 | 8.58 |
| 37 | 322.07 | 317.10 | -4.97 | 8.70 | 8.57 |
| 38 | 331.16 | 327.34 | -3.81 | 8.71 | 8.61 |
| 39 | 340.24 | 333.94 | -6.29 | 8.72 | 8.56 |
| 40 | 349.30 | 343.81 | -5.49 | 8.73 | 8.60 |
| 41 | 358.35 | 351.62 | -6.73 | 8.74 | 8.58 |
| 42 | 367.38 | 361.90 | -5.49 | 8.75 | 8.62 |
| 43 | 376.40 | 369.83 | -6.58 | 8.75 | 8.60 |
| 44 | 385.41 | 380.96 | -4.45 | 8.76 | 8.66 |
| 45 | 394.40 | 388.37 | -6.03 | 8.76 | 8.63 |
| 46 | 403.38 | 398.77 | -4.61 | 8.77 | 8.67 |
| 47 | 412.34 | 407.26 | -5.08 | 8.77 | 8.67 |
| 48 | 421.29 | 418.70 | -2.58 | 8.78 | 8.72 |
| 49 | 430.22 | 426.85 | -3.37 | 8.78 | 8.71 |
| 50 | 439.13 | 437.78 | -1.35 | 8.78 | 8.76 |
| 51 | 448.03 | 445.85 | -2.19 | 8.78 | 8.74 |
| 52 | 456.92 | 456.35 | -0.57 | 8.79 | 8.78 |
| 53 | 465.78 | 464.29 | -1.50 | 8.79 | 8.76 |
| 54 | 474.64 | 474.01 | -0.63 | 8.79 | 8.78 |
| 55 | 483.47 | 482.08 | -1.40 | 8.79 | 8.77 |
| 56 | 492.29 | 492.26 | -0.03 | 8.79 | 8.79 |
| 57 | 501.10 | 499.91 | -1.19 | 8.79 | 8.77 |
| 58 | 509.89 | 509.95 | 0.06 | 8.79 | 8.79 |
| 59 | 518.66 | 517.31 | -1.34 | 8.79 | 8.77 |
| 60 | 527.41 | 526.85 | -0.57 | 8.79 | 8.78 |
| 61 | 536.15 | 534.67 | -1.49 | 8.79 | 8.77 |
| 62 | 544.87 | 545.26 | 0.39 | 8.79 | 8.79 |
| 63 | 553.58 | 552.10 | -1.48 | 8.79 | 8.76 |
| 64 | 562.27 | 561.76 | -0.51 | 8.79 | 8.78 |
| 65 | 570.94 | 569.21 | -1.73 | 8.78 | 8.76 |
| 66 | 579.60 | 578.14 | -1.46 | 8.78 | 8.76 |
| 67 | 588.24 | 585.41 | -2.83 | 8.78 | 8.74 |
| 68 | 596.86 | 595.39 | -1.47 | 8.78 | 8.76 |
| 69 | 605.46 | 602.00 | -3.47 | 8.77 | 8.72 |
| 70 | 614.05 | 611.09 | -2.97 | 8.77 | 8.73 |
| 71 | 622.62 | 618.95 | -3.67 | 8.77 | 8.72 |
| 72 | 631.18 | 628.69 | -2.49 | 8.77 | 8.73 |
| 73 | 639.71 | 635.47 | -4.25 | 8.76 | 8.71 |
| 74 | 648.23 | 645.66 | -2.57 | 8.76 | 8.73 |
| 75 | 656.74 | 652.57 | -4.17 | 8.76 | 8.70 |
| 76 | 665.22 | 662.07 | -3.15 | 8.75 | 8.71 |
| 77 | 673.69 | 669.59 | -4.10 | 8.75 | 8.70 |
| 78 | 682.14 | 679.99 | -2.15 | 8.75 | 8.72 |
| 79 | 690.58 | 686.95 | -3.62 | 8.74 | 8.70 |
| 80 | 698.99 | 696.87 | -2.13 | 8.74 | 8.71 |
| 81 | 707.39 | 704.37 | -3.02 | 8.73 | 8.70 |
| 82 | 715.77 | 714.27 | -1.50 | 8.73 | 8.71 |
| 83 | 724.14 | 721.74 | -2.39 | 8.72 | 8.70 |
| 84 | 732.48 | 732.27 | -0.22 | 8.72 | 8.72 |
| 85 | 740.81 | 739.38 | -1.43 | 8.72 | 8.70 |
| 86 | 749.12 | 749.23 | 0.11 | 8.71 | 8.71 |
| 87 | 757.42 | 757.86 | 0.44 | 8.71 | 8.71 |
| 88 | 765.70 | 768.47 | 2.77 | 8.70 | 8.73 |
| 89 | 773.95 | 775.54 | 1.59 | 8.70 | 8.71 |
| 90 | 782.20 | 783.90 | 1.70 | 8.69 | 8.71 |
| 91 | 790.42 | 791.09 | 0.67 | 8.69 | 8.69 |
| 92 | 798.63 | 799.73 | 1.10 | 8.68 | 8.69 |
| 93 | 806.81 | 806.46 | -0.35 | 8.68 | 8.67 |
| 94 | 814.98 | 814.68 | -0.30 | 8.67 | 8.67 |
| 95 | 823.14 | 821.63 | -1.51 | 8.66 | 8.65 |
| 96 | 831.27 | 830.78 | -0.49 | 8.66 | 8.65 |
| 97 | 839.39 | 837.60 | -1.79 | 8.65 | 8.64 |
| 98 | 847.49 | 846.25 | -1.24 | 8.65 | 8.64 |
| 99 | 855.57 | 852.75 | -2.82 | 8.64 | 8.61 |
| 100 | 863.63 | 861.93 | -1.70 | 8.64 | 8.62 |
| 101 | 871.68 | 868.73 | -2.95 | 8.63 | 8.60 |
| 102 | 879.71 | 877.95 | -1.76 | 8.62 | 8.61 |
| 103 | 887.72 | 884.19 | -3.53 | 8.62 | 8.58 |
| 104 | 895.71 | 893.09 | -2.62 | 8.61 | 8.59 |
| 105 | 903.69 | 900.13 | -3.55 | 8.61 | 8.57 |
| 106 | 911.64 | 909.48 | -2.16 | 8.60 | 8.58 |
| 107 | 919.58 | 916.02 | -3.57 | 8.59 | 8.56 |
| 108 | 927.50 | 925.24 | -2.26 | 8.59 | 8.57 |
| 109 | 935.41 | 931.72 | -3.68 | 8.58 | 8.55 |
| 110 | 943.29 | 940.64 | -2.65 | 8.58 | 8.55 |
| 111 | 951.16 | 947.62 | -3.54 | 8.57 | 8.54 |
| 112 | 959.01 | 957.01 | -2.00 | 8.56 | 8.54 |
| 113 | 966.84 | 963.55 | -3.29 | 8.56 | 8.53 |
| 114 | 974.65 | 972.59 | -2.06 | 8.55 | 8.53 |
| 115 | 982.44 | 979.40 | -3.04 | 8.54 | 8.52 |
| 116 | 990.22 | 988.68 | -1.54 | 8.54 | 8.52 |
| 117 | 997.98 | 995.62 | -2.35 | 8.53 | 8.51 |
| 118 | 1005.72 | 1004.95 | -0.77 | 8.52 | 8.52 |
| 119 | 1013.44 | 1011.43 | -2.01 | 8.52 | 8.50 |
| 120 | 1021.15 | 1020.54 | -0.61 | 8.51 | 8.50 |
| 121 | 1028.83 | 1026.71 | -2.12 | 8.50 | 8.49 |
| 122 | 1036.50 | 1035.52 | -0.98 | 8.50 | 8.49 |
| 123 | 1044.15 | 1042.10 | -2.05 | 8.49 | 8.47 |
| 124 | 1051.78 | 1050.69 | -1.10 | 8.48 | 8.47 |
| 125 | 1059.40 | 1057.27 | -2.12 | 8.48 | 8.46 |
| 126 | 1066.99 | 1066.37 | -0.62 | 8.47 | 8.46 |
| 127 | 1074.57 | 1072.66 | -1.91 | 8.46 | 8.45 |
| 128 | 1082.13 | 1081.44 | -0.69 | 8.45 | 8.45 |
| 129 | 1089.67 | 1088.24 | -1.42 | 8.45 | 8.44 |
| 130 | 1097.19 | 1096.91 | -0.29 | 8.44 | 8.44 |
| 131 | 1104.69 | 1103.51 | -1.19 | 8.43 | 8.42 |
| 132 | 1112.18 | 1112.45 | 0.27 | 8.43 | 8.43 |
| 133 | 1119.65 | 1118.88 | -0.77 | 8.42 | 8.41 |
| 134 | 1127.10 | 1127.43 | 0.34 | 8.41 | 8.41 |
| 135 | 1134.53 | 1134.18 | -0.35 | 8.40 | 8.40 |
| 136 | 1141.94 | 1142.77 | 0.83 | 8.40 | 8.40 |
| 137 | 1149.34 | 1149.68 | 0.34 | 8.39 | 8.39 |
| 138 | 1156.71 | 1158.29 | 1.58 | 8.38 | 8.39 |
| 139 | 1164.07 | 1164.55 | 0.47 | 8.37 | 8.38 |
| 140 | 1171.41 | 1172.69 | 1.27 | 8.37 | 8.38 |
| 141 | 1178.74 | 1178.12 | -0.62 | 8.36 | 8.36 |
| 142 | 1186.04 | 1185.28 | -0.75 | 8.35 | 8.35 |
| 143 | 1193.32 | 1191.26 | -2.06 | 8.34 | 8.33 |
| 144 | 1200.59 | 1199.08 | -1.51 | 8.34 | 8.33 |
| 145 | 1207.84 | 1204.83 | -3.01 | 8.33 | 8.31 |
| 146 | 1215.07 | 1212.40 | -2.67 | 8.32 | 8.30 |
| 147 | 1222.28 | 1217.80 | -4.48 | 8.31 | 8.28 |
| 148 | 1229.47 | 1225.39 | -4.09 | 8.31 | 8.28 |
| 149 | 1236.65 | 1231.26 | -5.39 | 8.30 | 8.26 |
| 150 | 1243.81 | 1239.24 | -4.56 | 8.29 | 8.26 |
| 151 | 1250.95 | 1244.84 | -6.11 | 8.28 | 8.24 |
| 152 | 1258.07 | 1253.10 | -4.97 | 8.28 | 8.24 |
| 153 | 1265.17 | 1258.99 | -6.18 | 8.27 | 8.23 |
| 154 | 1272.25 | 1266.93 | -5.32 | 8.26 | 8.23 |
| 155 | 1279.32 | 1273.58 | -5.73 | 8.25 | 8.22 |
| 156 | 1286.36 | 1281.59 | -4.77 | 8.25 | 8.22 |
| 157 | 1293.39 | 1287.95 | -5.44 | 8.24 | 8.20 |
| 158 | 1300.40 | 1295.89 | -4.51 | 8.23 | 8.20 |
| 159 | 1307.39 | 1302.02 | -5.37 | 8.22 | 8.19 |
| 160 | 1314.37 | 1309.45 | -4.92 | 8.21 | 8.18 |
| 161 | 1321.32 | 1316.09 | -5.23 | 8.21 | 8.17 |
| 162 | 1328.26 | 1324.10 | -4.16 | 8.20 | 8.17 |
| 163 | 1335.17 | 1330.37 | -4.80 | 8.19 | 8.16 |
| 164 | 1342.07 | 1338.03 | -4.05 | 8.18 | 8.16 |
| 165 | 1348.95 | 1344.25 | -4.71 | 8.18 | 8.15 |
| 166 | 1355.82 | 1351.56 | -4.25 | 8.17 | 8.14 |
| 167 | 1362.66 | 1358.00 | -4.66 | 8.16 | 8.13 |
| 168 | 1369.49 | 1365.77 | -3.71 | 8.15 | 8.13 |
| 169 | 1376.29 | 1371.78 | -4.52 | 8.14 | 8.12 |
| 170 | 1383.08 | 1379.03 | -4.05 | 8.14 | 8.11 |
| 171 | 1389.85 | 1385.42 | -4.43 | 8.13 | 8.10 |
| 172 | 1396.60 | 1392.76 | -3.85 | 8.12 | 8.10 |
| 173 | 1403.34 | 1399.13 | -4.21 | 8.11 | 8.09 |
| 174 | 1410.05 | 1406.59 | -3.46 | 8.10 | 8.08 |
| 175 | 1416.75 | 1412.41 | -4.34 | 8.10 | 8.07 |
| 176 | 1423.43 | 1419.28 | -4.15 | 8.09 | 8.06 |
| 177 | 1430.09 | 1425.46 | -4.62 | 8.08 | 8.05 |
| 178 | 1436.73 | 1432.80 | -3.92 | 8.07 | 8.05 |
| 179 | 1443.35 | 1438.90 | -4.45 | 8.06 | 8.04 |
| 180 | 1449.95 | 1446.29 | -3.66 | 8.06 | 8.03 |
| 181 | 1456.54 | 1452.24 | -4.30 | 8.05 | 8.02 |
| 182 | 1463.11 | 1459.33 | -3.77 | 8.04 | 8.02 |
| 183 | 1469.65 | 1465.52 | -4.13 | 8.03 | 8.01 |
| 184 | 1476.18 | 1472.94 | -3.25 | 8.02 | 8.01 |
| 185 | 1482.70 | 1478.69 | -4.01 | 8.01 | 7.99 |
| 186 | 1489.19 | 1485.88 | -3.31 | 8.01 | 7.99 |
| 187 | 1495.66 | 1491.88 | -3.78 | 8.00 | 7.98 |
| 188 | 1502.12 | 1499.09 | -3.03 | 7.99 | 7.97 |
| 189 | 1508.56 | 1505.01 | -3.55 | 7.98 | 7.96 |
| 190 | 1514.98 | 1512.80 | -2.17 | 7.97 | 7.96 |
| 191 | 1521.38 | 1518.56 | -2.82 | 7.97 | 7.95 |
| 192 | 1527.76 | 1526.12 | -1.64 | 7.96 | 7.95 |
| 193 | 1534.12 | 1532.06 | -2.06 | 7.95 | 7.94 |
| 194 | 1540.47 | 1539.58 | -0.89 | 7.94 | 7.94 |
| 195 | 1546.79 | 1545.68 | -1.11 | 7.93 | 7.93 |
| 196 | 1553.10 | 1553.60 | 0.50 | 7.92 | 7.93 |
| 197 | 1559.39 | 1559.45 | 0.06 | 7.92 | 7.92 |
| 198 | 1565.66 | 1567.00 | 1.34 | 7.91 | 7.91 |
| 199 | 1571.91 | 1573.48 | 1.57 | 7.90 | 7.91 |
| 200 | 1578.14 | 1581.18 | 3.03 | 7.89 | 7.91 |
| 201 | 1584.36 | 1587.41 | 3.05 | 7.88 | 7.90 |
| 202 | 1590.56 | 1595.16 | 4.61 | 7.87 | 7.90 |
| 203 | 1596.73 | 1601.16 | 4.42 | 7.87 | 7.89 |
| 204 | 1602.89 | 1608.65 | 5.76 | 7.86 | 7.89 |
| 205 | 1609.03 | 1615.07 | 6.04 | 7.85 | 7.88 |
| 206 | 1615.16 | 1622.32 | 7.17 | 7.84 | 7.88 |
| 207 | 1621.26 | 1629.06 | 7.80 | 7.83 | 7.87 |
| 208 | 1627.34 | 1636.43 | 9.09 | 7.82 | 7.87 |
| 209 | 1633.41 | 1640.37 | 6.96 | 7.82 | 7.85 |
| 210 | 1639.46 | 1645.55 | 6.09 | 7.81 | 7.84 |
| 211 | 1645.49 | 1649.97 | 4.48 | 7.80 | 7.82 |
| 212 | 1651.50 | 1655.77 | 4.27 | 7.79 | 7.81 |
| 213 | 1657.49 | 1660.13 | 2.64 | 7.78 | 7.79 |
| 214 | 1663.46 | 1666.01 | 2.55 | 7.77 | 7.79 |
| 215 | 1669.42 | 1670.16 | 0.74 | 7.76 | 7.77 |
| 216 | 1675.35 | 1675.90 | 0.55 | 7.76 | 7.76 |
| 217 | 1681.27 | 1680.58 | -0.69 | 7.75 | 7.74 |
| 218 | 1687.17 | 1687.05 | -0.12 | 7.74 | 7.74 |
| 219 | 1693.05 | 1691.51 | -1.55 | 7.73 | 7.72 |
| 220 | 1698.91 | 1697.79 | -1.12 | 7.72 | 7.72 |
| 221 | 1704.76 | 1702.42 | -2.34 | 7.71 | 7.70 |
| 222 | 1710.58 | 1708.66 | -1.92 | 7.71 | 7.70 |
| 223 | 1716.39 | 1713.82 | -2.56 | 7.70 | 7.69 |
| 224 | 1722.17 | 1720.30 | -1.87 | 7.69 | 7.68 |
| 225 | 1727.94 | 1725.21 | -2.74 | 7.68 | 7.67 |
| 226 | 1733.69 | 1731.60 | -2.09 | 7.67 | 7.66 |
| 227 | 1739.42 | 1736.71 | -2.72 | 7.66 | 7.65 |
| 228 | 1745.14 | 1743.08 | -2.06 | 7.65 | 7.65 |
| 229 | 1750.83 | 1748.33 | -2.50 | 7.65 | 7.63 |
| 230 | 1756.51 | 1755.13 | -1.38 | 7.64 | 7.63 |
| 231 | 1762.16 | 1760.25 | -1.92 | 7.63 | 7.62 |
| 232 | 1767.80 | 1766.69 | -1.12 | 7.62 | 7.62 |
| 233 | 1773.42 | 1771.93 | -1.49 | 7.61 | 7.60 |
| 234 | 1779.02 | 1778.57 | -0.46 | 7.60 | 7.60 |
| 235 | 1784.61 | 1783.86 | -0.74 | 7.59 | 7.59 |
| 236 | 1790.17 | 1790.41 | 0.24 | 7.59 | 7.59 |
| 237 | 1795.71 | 1795.53 | -0.18 | 7.58 | 7.58 |
| 238 | 1801.24 | 1801.69 | 0.45 | 7.57 | 7.57 |
| 239 | 1806.75 | 1806.97 | 0.23 | 7.56 | 7.56 |
| 240 | 1812.24 | 1813.45 | 1.21 | 7.55 | 7.56 |
| 241 | 1817.71 | 1818.69 | 0.98 | 7.54 | 7.55 |
| 242 | 1823.16 | 1825.00 | 1.84 | 7.53 | 7.54 |
| 243 | 1828.59 | 1830.03 | 1.44 | 7.53 | 7.53 |
| 244 | 1834.01 | 1836.05 | 2.04 | 7.52 | 7.52 |
| 245 | 1839.40 | 1841.36 | 1.96 | 7.51 | 7.52 |
| 246 | 1844.78 | 1847.82 | 3.04 | 7.50 | 7.51 |
| 247 | 1850.14 | 1852.98 | 2.83 | 7.49 | 7.50 |
| 248 | 1855.48 | 1859.19 | 3.71 | 7.48 | 7.50 |
| 249 | 1860.80 | 1864.02 | 3.22 | 7.47 | 7.49 |
| 250 | 1866.11 | 1869.99 | 3.88 | 7.46 | 7.48 |
| 251 | 1871.39 | 1875.09 | 3.70 | 7.46 | 7.47 |
| 252 | 1876.65 | 1881.27 | 4.61 | 7.45 | 7.47 |
| 253 | 1881.90 | 1886.07 | 4.17 | 7.44 | 7.45 |
| 254 | 1887.13 | 1892.10 | 4.97 | 7.43 | 7.45 |
| 255 | 1892.34 | 1896.64 | 4.30 | 7.42 | 7.44 |
| 256 | 1897.53 | 1902.54 | 5.01 | 7.41 | 7.43 |
| 257 | 1902.70 | 1907.50 | 4.80 | 7.40 | 7.42 |
| 258 | 1907.86 | 1911.69 | 3.84 | 7.39 | 7.41 |
| 259 | 1912.99 | 1906.33 | -6.66 | 7.39 | 7.36 |
| 260 | 1918.11 | 1909.07 | -9.04 | 7.38 | 7.34 |
| 261 | 1923.20 | 1923.93 | 0.72 | 7.37 | 7.37 |
| 262 | 1928.28 | 1923.39 | -4.89 | 7.36 | 7.34 |
| 263 | 1933.34 | 1929.63 | -3.71 | 7.35 | 7.34 |
| 264 | 1938.38 | 1937.23 | -1.15 | 7.34 | 7.34 |
| 265 | 1943.41 | 1943.25 | -0.16 | 7.33 | 7.33 |
| 266 | 1948.41 | 1950.31 | 1.90 | 7.32 | 7.33 |
| 267 | 1953.40 | 1956.31 | 2.91 | 7.32 | 7.33 |
| 268 | 1958.36 | 1963.37 | 5.01 | 7.31 | 7.33 |
| 269 | 1963.31 | 1968.54 | 5.23 | 7.30 | 7.32 |
| 270 | 1968.24 | 1974.78 | 6.54 | 7.29 | 7.31 |
| 271 | 1973.15 | 1979.66 | 6.50 | 7.28 | 7.31 |
| 272 | 1978.04 | 1985.87 | 7.83 | 7.27 | 7.30 |
| 273 | 1982.92 | 1990.44 | 7.53 | 7.26 | 7.29 |
| 274 | 1987.77 | 1994.17 | 6.40 | 7.25 | 7.28 |
| 275 | 1992.61 | 2000.08 | 7.47 | 7.25 | 7.27 |
| 276 | 1997.42 | 2004.86 | 7.44 | 7.24 | 7.26 |
| 277 | 2002.22 | 2009.64 | 7.41 | 7.23 | 7.26 |
| 278 | 2007.00 | 2013.00 | 6.00 | 7.22 | 7.24 |
| 279 | 2011.76 | 2019.40 | 7.64 | 7.21 | 7.24 |
| 280 | 2016.50 | 2023.56 | 7.06 | 7.20 | 7.23 |
| 281 | 2021.23 | 2028.82 | 7.59 | 7.19 | 7.22 |
| 282 | 2025.93 | 2031.81 | 5.88 | 7.18 | 7.21 |
| 283 | 2030.62 | 2038.45 | 7.83 | 7.18 | 7.20 |
| 284 | 2035.29 | 2042.53 | 7.24 | 7.17 | 7.19 |
| 285 | 2039.94 | 2047.73 | 7.79 | 7.16 | 7.19 |
| 286 | 2044.57 | 2050.33 | 5.77 | 7.15 | 7.17 |
| 287 | 2049.18 | 2057.22 | 8.04 | 7.14 | 7.17 |
| 288 | 2053.77 | 2060.64 | 6.87 | 7.13 | 7.16 |
| 289 | 2058.34 | 2066.06 | 7.72 | 7.12 | 7.15 |
| 290 | 2062.90 | 2068.28 | 5.38 | 7.11 | 7.13 |
| 291 | 2067.44 | 2075.12 | 7.69 | 7.10 | 7.13 |
| 292 | 2071.95 | 2078.16 | 6.21 | 7.10 | 7.12 |
| 293 | 2076.45 | 2083.52 | 7.07 | 7.09 | 7.11 |
| 294 | 2080.93 | 2085.34 | 4.41 | 7.08 | 7.09 |
| 295 | 2085.39 | 7.07 | |||
| 296 | 2089.84 | 7.06 | |||
| 297 | 2094.26 | 7.05 | |||
| 298 | 2098.67 | 7.04 | |||
| 299 | 2103.05 | 7.03 | |||
| 300 | 2107.42 | 7.02 | |||
| 301 | 2111.77 | 7.02 | |||
| 302 | 2116.10 | 7.01 | |||
| 303 | 2120.41 | 7.00 | |||
| 304 | 2124.71 | 6.99 | |||
| 305 | 2128.98 | 6.98 | |||
| 306 | 2133.24 | 6.97 | |||
| 307 | 2137.48 | 6.96 | |||
| 308 | 2141.69 | 6.95 | |||
| 309 | 2145.89 | 6.94 | |||
| 310 | 2150.07 | 6.94 | |||
| 311 | 2154.24 | 6.93 | |||
| 312 | 2158.38 | 6.92 | |||
| 313 | 2162.50 | 6.91 | |||
| 314 | 2166.61 | 6.90 | |||
| 315 | 2170.70 | 6.89 | |||
| 316 | 2174.77 | 6.88 | |||
| 317 | 2178.82 | 6.87 | |||
| 318 | 2182.85 | 6.86 | |||
| 319 | 2186.86 | 6.86 | |||
| 320 | 2190.85 | 6.85 | |||
| 321 | 2194.83 | 6.84 | |||
| 322 | 2198.78 | 6.83 | |||
| 323 | 2202.72 | 6.82 | |||
| 324 | 2206.64 | 6.81 | |||
| 325 | 2210.54 | 6.80 | |||
| 326 | 2214.42 | 6.79 | |||
| 327 | 2218.28 | 6.78 | |||
| 328 | 2222.13 | 6.77 | |||
| 329 | 2225.95 | 6.77 | |||
| 330 | 2229.76 | 6.76 | |||
| 331 | 2233.54 | 6.75 | |||
| 332 | 2237.31 | 6.74 | |||
| 333 | 2241.06 | 6.73 | |||
| 334 | 2244.79 | 6.72 | |||
| 335 | 2248.51 | 6.71 | |||
| 336 | 2252.20 | 6.70 | |||
| 337 | 2255.88 | 6.69 | |||
| 338 | 2259.53 | 6.69 | |||
| 339 | 2263.17 | 6.68 | |||
| 340 | 2266.79 | 6.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





