Understanding the Role of Nuclear Elementary Charge and Its Potential in Estimating Nuclear Binding Energy and Strong Coupling Constant

1. Introduction

With reference to our 4G model of final unification, in our recent publications [1,2,3,4,5,6,7,8,9,10,11,12], we have developed a new formula for estimating nuclear binding energy [13,14,15,16,17,18,19,20,21,22,23,24] in terms of strong and electroweak interactions [25,26]. Our formula constitutes 4 simple terms and only one energy coefficient of magnitude 10.1 MeV. First term is a volume term, second term seems to be a representation of free nucleons associated with electroweak interaction, third term is a radial term and fourth one is an asymmetry term about the mean stable mass number. Considering this kind of approach, nuclear structure can be understood in terms of strong and weak interactions and complicated concepts like cold nuclear fusion can be understood in a theoretical approach positively.

In this short paper, we have presented a revised form of semi empirical mass formula (SEMF) with surface, coulomb and asymmetric energy coefficients as variables. This can be considered as a hybrid form of available SEMF. With a single set of energy coefficients, it seems to work for Z=1 to 137 and needs fine tuning for heavy isotopes of light proton numbers. In this context, we would like to emphasize the point that, strong coupling constant plays a vital role in fitting the nuclear binding energy coefficients. Clearly speaking, strong coupling can be inferred from nuclear binding energy coefficients. Considering our strong and electroweak mass formula and considering the proposed (revised) 6 term semi empirical mass formula, there is a chance to identify the strong coupling constant as a fundamental building block of atomic nuclei.

2. Three Assumptions of 4G Model of Final Unification

Following our 4G model of final unification [1,2,3,4,5,6,7,8,9,10,11,12]

1)

There exists a characteristic electroweak fermion of rest energy, $M_{wf}{c}^2\cong 584.725\mathrm{GeV}$. It can be considered as the zygote of all elementary particles.

2)

There exists a nuclear elementary charge in such a way that, ${\left({\displaystyle \frac{e}{e_n}}\right)}^2\cong {\alpha }_s\cong 0.1152$ = Strong coupling constant and $e_n\cong 2.9464e$.

3)

Each atomic interaction is associated with a characteristic large gravitational coupling constant. Their fitted magnitudes are,

$\begin{array}{l}{G}_e\cong \mathrm{Electromgnetic}\mathrm{gravitational}\mathrm{constant}\cong 2.374335\times {10}^{37}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\sec }^{-2}\\ G_n\cong \mathrm{Nuclear}\mathrm{gravitational}\mathrm{constant}\cong 3.329561\times {10}^{28}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\sec }^{-2}\\ G_w\cong \mathrm{Electroweak}\mathrm{gravitational}\mathrm{constant}\cong 2.909745\times {10}^{22}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\sec }^{-2}\end{array}$

It may be noted that,

1)

Weak interaction point of view [25,26], following our assumptions, Fermi’s weak coupling constant can be fitted with the following relations.

$$\left.\begin{array}{l}{G}_F\cong {\left({\displaystyle \frac{m_e}{m_p}}\right)}^2\hslash c{R}_0^2\cong G_w{M}_{wf}^2{R}_w^2\cong 1.44021\times {10}^{-62}\mathrm{J}{.\mathrm{m}}^3\\ \mathrm{where},\left\{\begin{array}{l}{R}_0\cong {\displaystyle \frac{2G_n{m}_p}{c^2}}\cong 1.24\times {10}^{-15}\mathrm{m}\\ R_w\cong {\displaystyle \frac{2G_w{M}_{wf}}{c^2}}\cong 6.75\times {10}^{-19}\mathrm{m}\end{array}\right.\end{array}\right\}$$

(1)

2)

In a unified approach, most important point to be noted is that [10],

$$\hslash c\equiv G_w{M}_{wf}^2$$

(2)

Clearly speaking, based on the electroweak interaction, the well believed quantum constant $\hslash c$ seems to have a deep inner meaning. Following this kind of relation, there is a possibility to understand the integral nature of quantum mechanics with a relation of the form, $n^2\hslash \equiv {\displaystyle \frac{G_w{\left(n{M}_{wf}\right)}^2}{c}}\mathrm{where}n=1,2,3,\mathrm{..}$ It needs further study with reference to EPR argument [27,28,29,30] and [1,31]. String theory [32,33,34,35,36] can be made practical with reference to the three atomic gravitational constants associated with weak, strong and electromagnetic interaction gravitational constants. See Table 1. and Table 2. for sample string tensions and energies without any coupling constants.

2.1. Understanding the Electroweak Coefficient and Nuclear Stability

Our basic idea is that, all the nucleons are not participating in the nuclear binding energy scheme and non-participating nucleons can be called as ‘Free nucleons’. These free nucleons revolve round the nuclear core. Each free nucleon reduces the nuclear binding energy by 10.1 MeV. Protons and neutrons jointly play a crucial role in fixing the number of free nucleons. Electroweak interaction is having a key role in understanding free nucleons and nuclear stability against beta decay. In this context, we noticed that,

$${\displaystyle \frac{m_p}{M_{wf}}}\cong \left({\displaystyle \frac{\sqrt{{\left(m_{\pi }{c}^2\right)}^0{\left(m_{\pi }{c}^2\right)}^{\pm }}}{\sqrt{{\left(m_z{c}^2\right)}^0{\left(m_w{c}^2\right)}^{\pm }}}}\right)\cong \left({\displaystyle \frac{\sqrt{134.98\times 139.57}\mathrm{MeV}}{\sqrt{91187.6\times 80379.0}\mathrm{MeV}}}\right)\cong 0.0016032$$

(3)

Here ratio of rest mass of proton to the assumed electroweak fermion is equal to the ratio of mean mass of pions to the mean mass of electroweak bosons. Based on this unique and concrete observation, we are very confident to say that, strong and weak interactions play a vital role exploring the secrets of nuclear structure. Based on this electroweak coefficient 0.0016, stability corresponding to nuclear beta decay can be understood with the following relation.

$$\left.\begin{array}{l}{A}_s\cong 2Z+0.0016{\left(2Z\right)}^2\cong 2Z+0.0064Z^2\\ \to {\displaystyle \frac{A_s-2Z}{4Z^2}}\cong 0.0016\end{array}\right\}$$

(4A)

One can find a similar relation in the literature [16]. This relation can be well tested for Z=21 to 92. For example,

$\begin{array}{l}{\displaystyle \frac{45-\left(2\times 21\right)}{4{\left(21\right)}^2}}\cong 0.00170;{\displaystyle \frac{63-\left(2\times 29\right)}{4{\left(29\right)}^2}}\cong 0.00149;{\displaystyle \frac{89-\left(2\times 39\right)}{4{\left(39\right)}^2}}\cong 0.00181;\\ {\displaystyle \frac{109-\left(2\times 47\right)}{4{\left(47\right)}^2}}\cong 0.0017;{\displaystyle \frac{169-\left(2\times 69\right)}{4{\left(69\right)}^2}}\cong 0.00163;{\displaystyle \frac{238-\left(2\times 92\right)}{4{\left(92\right)}^2}}\cong 0.001595;\end{array}$

This is one best practical and quantitative application of our proposed electroweak fermion and bosons. Following this relation and based on various semi empirical mass formulae [13,14,15,16,17,18,19,20,21], by knowing any stable mass number, its corresponding proton number can be estimated with,

$$Z\cong {\displaystyle \frac{A_s}{1+\sqrt{1+0.0064A_s}}}\cong {\displaystyle \frac{A_s}{2+0.0153A_s^{2/3}}}$$

(4B)

$\mathrm{where}{\displaystyle \frac{a_c}{2a_{asy}}}\cong {\displaystyle \frac{0.71\mathrm{MeV}}{2\times 23.21\mathrm{MeV}}}\cong {\displaystyle \frac{0.6615\mathrm{MeV}}{2\times 21.6091\mathrm{MeV}}}\cong 0.0153$Considering this relation, we are working on understanding stable super heavy elements.

2.2. Revised Strong and Electroweak Mass Formula

Baaed on the liquid drop model, we present our revised strong and electroweak mass formula [1]. It needs a review for accuracy and we are working in this new direction. For Z=6 to 125,

$$\begin{array}{l}BE\cong \left(A-A_{free}-A_{radial}-A_{asym}\right)\left(B_0\cong 10.1\mathrm{MeV}\right)\\ \cong \left\{\begin{array}{l}A-\left\{{\displaystyle \frac{1}{2}}+\left[{\Upsilon }_Z\left[{\left(Z+Z^{2/3}+Z^{1/3}\right)}^2+{\left(N+N^{2/3}+N^{1/3}\right)}^2+\left({\displaystyle \frac{Z}{N}}\left(Z^2\right)\right)\right]\right]\right\}\\ -A^{1/3}-\left(\beta \times {\displaystyle \frac{{\left(A_s-A\right)}^2}{A_s}}\right)\end{array}\right\}10.1\mathrm{MeV}\end{array}$$

(5)

where,$A\times 10.1\mathrm{MeV}\text{represents the volume term}$

$$A_{free}\times 10.1\mathrm{MeV}\text{represents the electroweak term}$$

$$A_{radial}\times 10.1\mathrm{MeV}\text{represents the radial term}$$

$$A_{asym}\times 10.1\mathrm{MeV}\text{represents the asymmetry term}$$

$$\beta =1-{\left({\displaystyle \frac{N-Z}{A}}\right)}^2$$

$$\begin{array}{l}{\Upsilon }_Z\cong {\Upsilon }_0\left[1+\left({\Upsilon }_{0}Z\right)\right]\cong 0.000935\left[1+0.000935Z\right]\\ \mathrm{where}{\Upsilon }_0\cong \sqrt{{\displaystyle \frac{e}{e_n}}}\left(0.001605\right)\cong 0.000935\end{array}$$

$$\begin{array}{l}{A}_s\cong 2Z+0.0064Z^2\\ \cong \mathrm{Light}\mathrm{house}\mathrm{like}\left(\mathrm{mean}\right)\mathrm{stable}\mathrm{mass}\mathrm{number}\mathrm{of}\mathrm{Z}.\end{array}$$

$$\begin{array}{l}{B}_0\cong -\left({\displaystyle \frac{1}{\sqrt{{\alpha }_s}}}\right){\displaystyle \frac{e^2}{8\pi {\epsilon }_0\left(\hslash /m_{p}c\right)}}\cong -{\displaystyle \frac{e_n^2}{8\pi {\epsilon }_0\left(G_n{m}_p/c^2\right)}}\cong -10.1\mathrm{MeV}\\ \mathrm{where}\left\{\begin{array}{l}{\alpha }_s=\mathrm{Strong}\mathrm{coupling}\mathrm{constant}\cong 0.115\mathrm{to}0.12\\ \hslash /m_{p}c=\mathrm{Reduced}\mathrm{Comption}\mathrm{wavelength}\mathrm{of}\mathrm{proton}\\ G_n{m}_p/c^2\cong 0.62\times {10}^{-15}\mathrm{m}\end{array}\right.\end{array}$$

For evaluating the effectiveness of relation (5), we consider the following advanced relation as a reference [19].

$$\left.\begin{array}{l}BE\cong \left\{\left[1+\left({\displaystyle \frac{4k_v}{A^2}}\right)\left|T_z\right|\left(\left|T_z\right|+1\right)\right]a_v*A\right\}+\left\{\left[1+\left({\displaystyle \frac{4k_s}{A^2}}\right)\left|T_z\right|\left(\left|T_z\right|+1\right)\right]a_s*A^{{\displaystyle \frac{2}{3}}}\right\}\\ +\left\{a_c*\left({\displaystyle \frac{Z^2}{A^{1/3}}}\right)\right\}+\left\{f_p*{\displaystyle \frac{Z^2}{A}}\right\}+E_p\end{array}\right\}$$

(6)

where, $T_z\cong 3\mathrm{rd}\mathrm{component}\mathrm{of}\mathrm{isospin}={\displaystyle \frac{1}{2}}\left(Z-N\right)$

$\left\{\left.\begin{array}{l}{a}_v=-15.4963\mathrm{MeV},a_s=17.7937\mathrm{MeV}\\ k_v=-1.8232,k_s=-2.2593\\ a_c=0.7093\mathrm{MeV},f_p=-1.2739\mathrm{MeV}\\ d_n=4.6919\mathrm{MeV},d_p=4.7230\mathrm{MeV}\\ d_{np}=-6.4920\mathrm{MeV}\end{array}\right\}\right.$ and $\left.\left\{\begin{array}{l}\mathrm{for}\left(Z,N\right)\mathrm{Odd},E_p\cong {\displaystyle \frac{d_n}{N^{1/3}}}+{\displaystyle \frac{d_p}{Z^{1/3}}}+{\displaystyle \frac{d_{np}}{A^{2/3}}}\\ \mathrm{for}\left(\mathrm{Odd}Z,\mathrm{Even}N\right),E_p\cong {\displaystyle \frac{d_p}{Z^{1/3}}}\\ \mathrm{for}\left(\mathrm{Even}Z,\mathrm{Odd}N\right),E_p\cong {\displaystyle \frac{d_n}{N^{1/3}}}\\ \mathrm{for}\left(\mathrm{Even}Z,\mathrm{Even}N\right),E_p\cong 0\end{array}\right.\right\}$

3. Revised Semi Empirical Mass Formula Having 6 Terms

With reference to relation (6) and considering surface, Coulomb and asymmetry energy coefficients as variables, we present our revised 6 term semi empirical mass formula.

Volume energy coefficient, $a_v\cong 16.0\mathrm{MeV}$

Surface energy coefficient, $a_s\cong \left[1-{\left({\displaystyle \frac{\mathrm{N}-\mathrm{Z}}{\mathrm{A}}}\right)}^2\right]19.4\mathrm{MeV}$

Coulombic energy coefficient, $a_c\cong {\left\{1-{\left({\displaystyle \frac{\mathrm{N}-\mathrm{Z}}{\mathrm{A}}}\right)}^2\right\}}^{-x}\times 0.71\mathrm{MeV}\mathrm{where}x\cong 0.75-{\displaystyle \frac{Z}{2A}}$

Asymmetry energy coefficient, $a_{asy}\cong \left[1-{\displaystyle \frac{1}{\mathrm{A}}}\right]\times 24.5\mathrm{MeV}$

Pairing energy coefficient, $a_p\cong 10.0\mathrm{MeV}$

Congruent energy coefficient, $a_{cg}\cong 10.0\mathrm{MeV}$

$$\left.\begin{array}{l}BE\cong \left[16.0\times A\right]-\left[\beta \times 19.4\times A^{2/3}\right]-\left[{\displaystyle \frac{0.71\times Z^2}{{\beta }^x{A}^{1/3}}}\right]\\ -\left\{\left[\left(1-{\displaystyle \frac{1}{A}}\right)24.5\right]{\displaystyle \frac{{\left(A-2Z\right)}^2}{A}}\right\}\pm \left[{\displaystyle \frac{10}{\sqrt{A}}}\right]+\left[10\times \exp \left(-4.2{\displaystyle \frac{\left|\mathrm{N}-\mathrm{Z}\right|}{\mathrm{A}}}\right)\right]\end{array}\right\}$$

(7)

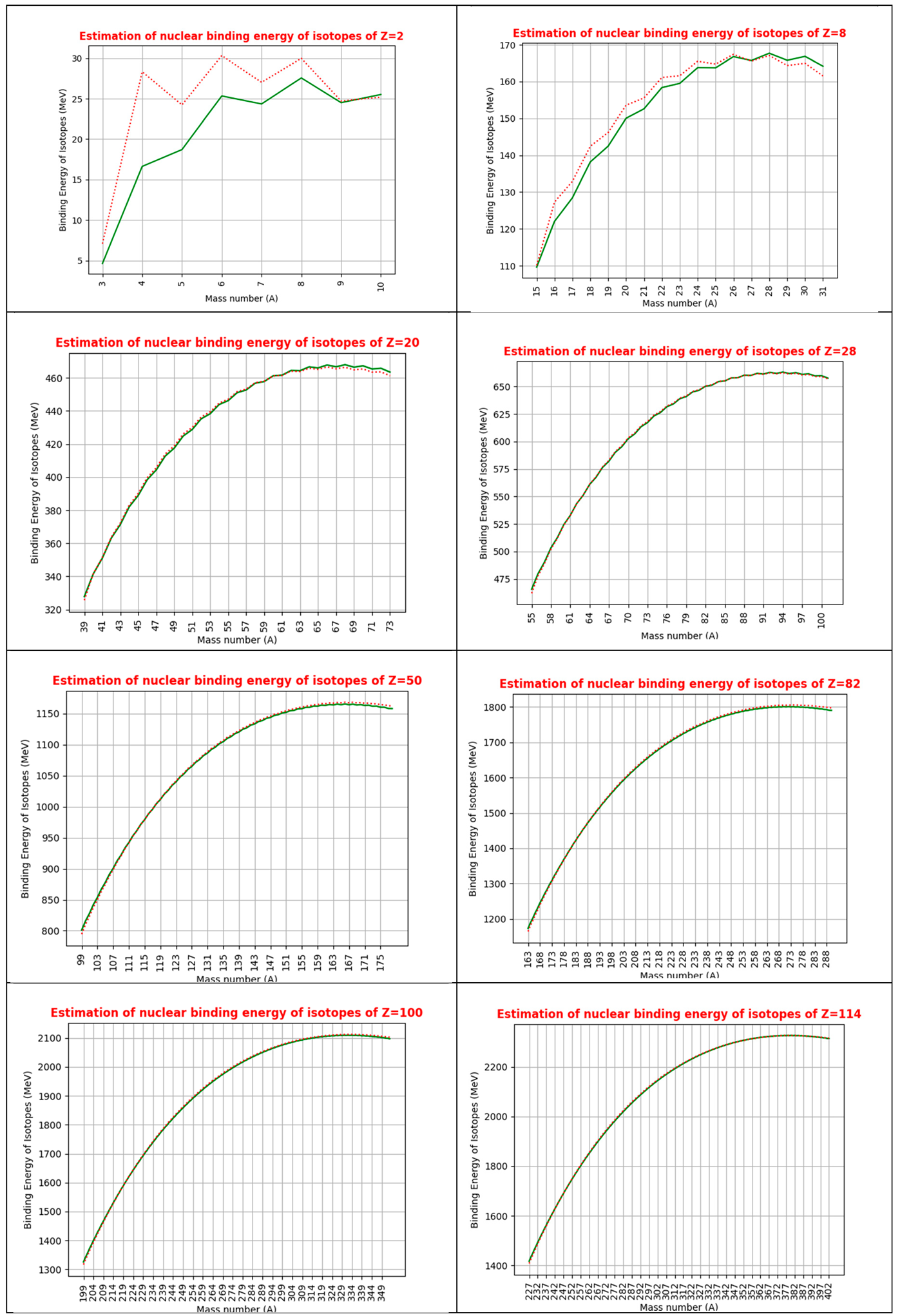
It seems to work from Z=1 to 137 without any difficulty and needs fine tuning for very heavy isotopes of very light proton numbers. See the following Table 3 for the binding energy curves prepared for magic numbers [37], Z=2,8,20,28,50,82,100 and 114. Red curve is our fit and green curve is the reference binding energy curve [19]. See the attached nuclear binding energy data table (supplementary material) starting from Z=1 to 137 where lower and upper mass numbers are (2Z)-1 and (3.5Z)+3 respectively. For our crude approximation, with reference to relation (6), for a wide range of protons and neutrons, relation (7) is having a root mean square deviation of 3.25 MeV.

4. Short Discussion on the Energy Coefficients of the Revised Semi Empirical Mass Formula

Let $e_n\equiv \mathrm{Nuclear}\mathrm{elementary}\mathrm{charge}\cong 2.9464e.$

$R_{pp}\cong {\displaystyle \frac{G_n{m}_p}{c^2}}\cong 0.61965\mathrm{fm}\cong \mathrm{Characteristic}\mathrm{physical}\mathrm{radius}\mathrm{of}\mathrm{proton}$

$\mathrm{where},\left\{\begin{array}{l}{G}_n\cong \mathrm{Nuclear}\mathrm{gravitational}\mathrm{constant}\\ m_p\cong \mathrm{Rest}\mathrm{mass}\mathrm{of}\mathrm{proton}\end{array}\right.$

Nuclear potential associated with $e_n$ and $R_{pp}$can be expressed as,

$$PE\cong -{\displaystyle \frac{e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong -20.174\mathrm{MeV}$$

(8)

$\mathrm{where},{\alpha }_{\mathrm{s}}\cong \mathrm{Strong}\mathrm{coupling}\mathrm{constant}$

With reference to both nucleons and considering a characteristic potential energy as,

$${\left(PE\right)}_{np}\equiv -{\displaystyle \frac{2e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{2e^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong -40.35\mathrm{MeV}$$

(9)

Based on this energy unit and beta decay, we consider the following relations for formulation of the energy coefficient. It needs further study.

Volume energy coefficient, $a_v\cong \left({\displaystyle \frac{m_e}{m_n-m_p}}\right)\left({\displaystyle \frac{2e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\right)\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right)\left({\displaystyle \frac{1}{2.531}}\right){\displaystyle \frac{2e^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong 15.94\mathrm{MeV}$

2) Asymmetry energy coefficient, $a_{asy}\cong \left(1-{\displaystyle \frac{1}{2.531}}\right)\left({\displaystyle \frac{2e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\right)\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right)\left(1-{\displaystyle \frac{1}{2.531}}\right){\displaystyle \frac{2e^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong 24.4\mathrm{MeV}$

3) Surface energy coefficient, $a_s\cong {\displaystyle \frac{2a_v{a}_{asy}}{a_v+a_{asy}}}\cong 19.3\mathrm{MeV}$

4) Pairing energy coefficient, $a_p\cong {\displaystyle \frac{e_n^2}{8\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{8\pi {\epsilon }_0{R}_{pp}}}\cong 10.1\mathrm{MeV}$

5) Congruence energy coefficient,$a_{cg}\cong {\displaystyle \frac{e_n^2}{8\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{8\pi {\epsilon }_0{R}_{pp}}}\cong 10.1\mathrm{MeV}$

6) Coulombic energy coefficient, $a_c\cong 0.7\mathrm{MeV}$

Based on these energy coefficients, to a very good approximation, starting from Z=1 to 137,

$$\left.\begin{array}{l}BE\cong a_{v}A-\beta a_s{A}^{2/3}-a_c{\displaystyle \frac{Z^2}{{\beta }^x{A}^{1/3}}}-a_{asy}{\displaystyle \frac{{\left(A-2Z\right)}^2}{A}}\pm {\displaystyle \frac{a_p}{\sqrt{A}}}+a_{cg}\exp \left(-4.2{\displaystyle \frac{\left|\mathrm{N}-\mathrm{Z}\right|}{\mathrm{A}}}\right)\\ \mathrm{where}\beta \cong 1-{\left({\displaystyle \frac{\mathrm{N}-\mathrm{Z}}{\mathrm{A}}}\right)}^2\mathrm{and}x\cong \left[0.75-\left({\displaystyle \frac{Z}{2A}}\right)\right]\cong \left(0.5\mathrm{to}0.6\right)\to \mathrm{Needs}\mathrm{further}\mathrm{study}.\end{array}\right\}$$

(10)

Points of interest are:

1) Characteristic nuclear radii linked with coulomb energy and nuclear binding energy [4,17] can be expressed as,

$$\begin{array}{l}{R}_{\left(Z,N\right)}\cong {\left[1-{\left({\displaystyle \frac{N-Z}{A}}\right)}^2\right]}^x{A}^{1/3}\times R_0\\ \mathrm{where}\left\{\begin{array}{l}{R}_0\cong \left(1.24\pm \mathrm{to}0.01\right)\mathrm{fermi}\\ x\cong 0.75-{\displaystyle \frac{Z}{2A}}\approx \left(0.5\mathrm{to}0.6\right)\end{array}\right.\end{array}$$

(11)

Considering $\left(A^{1/3}{R}_0\right)$, increasing neutron number, reduces the Coulomb repulsion between protons and thus helps in minimizing the radius by a factor ${\left[1-{\left({\displaystyle \frac{N-Z}{A}}\right)}^2\right]}^x\mathrm{where}x\cong 0.75-{\displaystyle \frac{Z}{2A}}.$

2) Considering the Fermi gas model of the nucleus [39,40],

a) Characteristic Fermi energy can be expressed as

$$E_F\cong \left({\displaystyle \frac{2e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\right)\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{2e^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{4}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}$$

(12)

b) Volume and asymmetry energy coefficients can be expressed as,

$$\left.\begin{array}{l}{a}_v\cong \left(1-{\displaystyle \frac{3}{5}}\right)E_F\cong \left(1-{\displaystyle \frac{3}{5}}\right)\left({\displaystyle \frac{2e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\right)\cong \left({\displaystyle \frac{4}{5{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_{pp}}}\\ \cong \left({\displaystyle \frac{8}{5{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\cong {\displaystyle \frac{\left(8\sqrt{3}\right)e^2}{4\pi {\epsilon }_0{R}_0}}\mathrm{where}\left({\displaystyle \frac{1}{5{\alpha }_s}}\right)\approx \sqrt{3}\end{array}\right\}$$

(13)

$$a_{asy}\cong {\displaystyle \frac{3}{5}}\left({\displaystyle \frac{2e_n^2}{4\pi {\epsilon }_0{R}_{pp}}}\right)\cong {\displaystyle \frac{3}{5}}{E}_F\cong \left({\displaystyle \frac{6}{5{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{12}{5{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\cong {\displaystyle \frac{12\sqrt{3}{e}^2}{4\pi {\epsilon }_0{R}_0}}$$

(14)

$$\left(a_{asy},a_v\right)\cong \left({\displaystyle \frac{10\pm 2}{5{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\cong {\displaystyle \frac{\left(10\pm 2\right)\sqrt{3}{e}^2}{4\pi {\epsilon }_0{R}_0}}$$

c) Surface energy coefficient can be expressed as,

$$a_s\cong {\displaystyle \frac{2a_v{a}_{asy}}{\left(a_v+a_{asy}\right)}}\cong \left({\displaystyle \frac{9.6}{5{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\cong {\displaystyle \frac{9.6\sqrt{3}{e}^2}{4\pi {\epsilon }_0{R}_0}}$$

(15)

d) Congruent and Pairing energy coefficients can be expressed as

$$a_{cg}\cong a_p\cong {\displaystyle \frac{E_F}{4}}\cong \left({\displaystyle \frac{e_n^2}{8\pi {\epsilon }_0{R}_{pp}}}\right)\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{8\pi {\epsilon }_0{R}_{pp}}}\cong \left({\displaystyle \frac{2}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{8\pi {\epsilon }_0{R}_0}}\cong \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}$$

(16)

See Table 4 for a rough estimation of our 6 term binding energy coefficients.

Proceeding further, binding energy point of view, considering a radius value close to the the root mean square radius of proton or neutron [41,42], for light, medium and heavy atomic nuclides, above nuclear radii can be can be approximated with the following relation. It needs further study.

$$R_{\left(Z,N\right)}\cong {\left[1-{\left({\displaystyle \frac{N-Z}{A}}\right)}^2\right]}^x{A}^{1/3}\times 1.25\mathrm{fm}\approx \left[\sqrt[3]{Z}+\sqrt[9]{Z^{2}N}\right]\times 0.79\mathrm{fm}$$

(17)

Clearly speaking, Coulomb energy term can be re-written as,

$$E_{cou}\cong -{\displaystyle \frac{3Z^2{e}^2}{20\pi {\epsilon }_0{R}_{\left(Z,N\right)}}}$$

(18)

Binding energy expression can be re-written as,

$$\left.\begin{array}{l}BE\cong 16A-19.4\beta A^{2/3}-{\displaystyle \frac{1.09365\times Z^2}{\left(\sqrt[3]{Z}+\sqrt[9]{Z^{2}N}\right)}}-\left[\left(1-{\displaystyle \frac{1}{A}}\right)\times 24.5{\displaystyle \frac{{\left(A-2Z\right)}^2}{A}}\right]\pm {\displaystyle \frac{10}{\sqrt{A}}}+10\times \exp \left(-4.2{\displaystyle \frac{\left|\mathrm{N}-\mathrm{Z}\right|}{\mathrm{A}}}\right)\\ \mathrm{where}\beta \cong 1-{\left({\displaystyle \frac{\mathrm{N}-\mathrm{Z}}{\mathrm{A}}}\right)}^2\mathrm{and}{\displaystyle \frac{3Z^2{e}^2}{20\pi {\epsilon }_0{R}_{\left(Z,N\right)}}}\cong {\displaystyle \frac{3Z^2{e}^2}{20\pi {\epsilon }_0}}{\left[\left(\sqrt[3]{Z}+\sqrt[9]{Z^{2}N}\right)\times 0.79\mathrm{fm}\right]}^{-1}\end{array}\right\}$$

(19A)

$$\left.\begin{array}{l}BE\cong 16A-19.4\beta A^{2/3}-{\displaystyle \frac{1.1\times Z^2}{\left(\sqrt[3]{Z}+\sqrt[9]{Z^{2}N}\right)}}-\left[\left(1-{\displaystyle \frac{1}{A}}\right)\times 24.5{\displaystyle \frac{{\left(A-2Z\right)}^2}{A}}\right]\pm {\displaystyle \frac{10}{\sqrt{A}}}+10\times \exp \left(-4.2{\displaystyle \frac{\left|\mathrm{N}-\mathrm{Z}\right|}{\mathrm{A}}}\right)\\ \mathrm{where}\beta \cong 1-{\left({\displaystyle \frac{\mathrm{N}-\mathrm{Z}}{\mathrm{A}}}\right)}^2\end{array}\right\}$$

(19B)

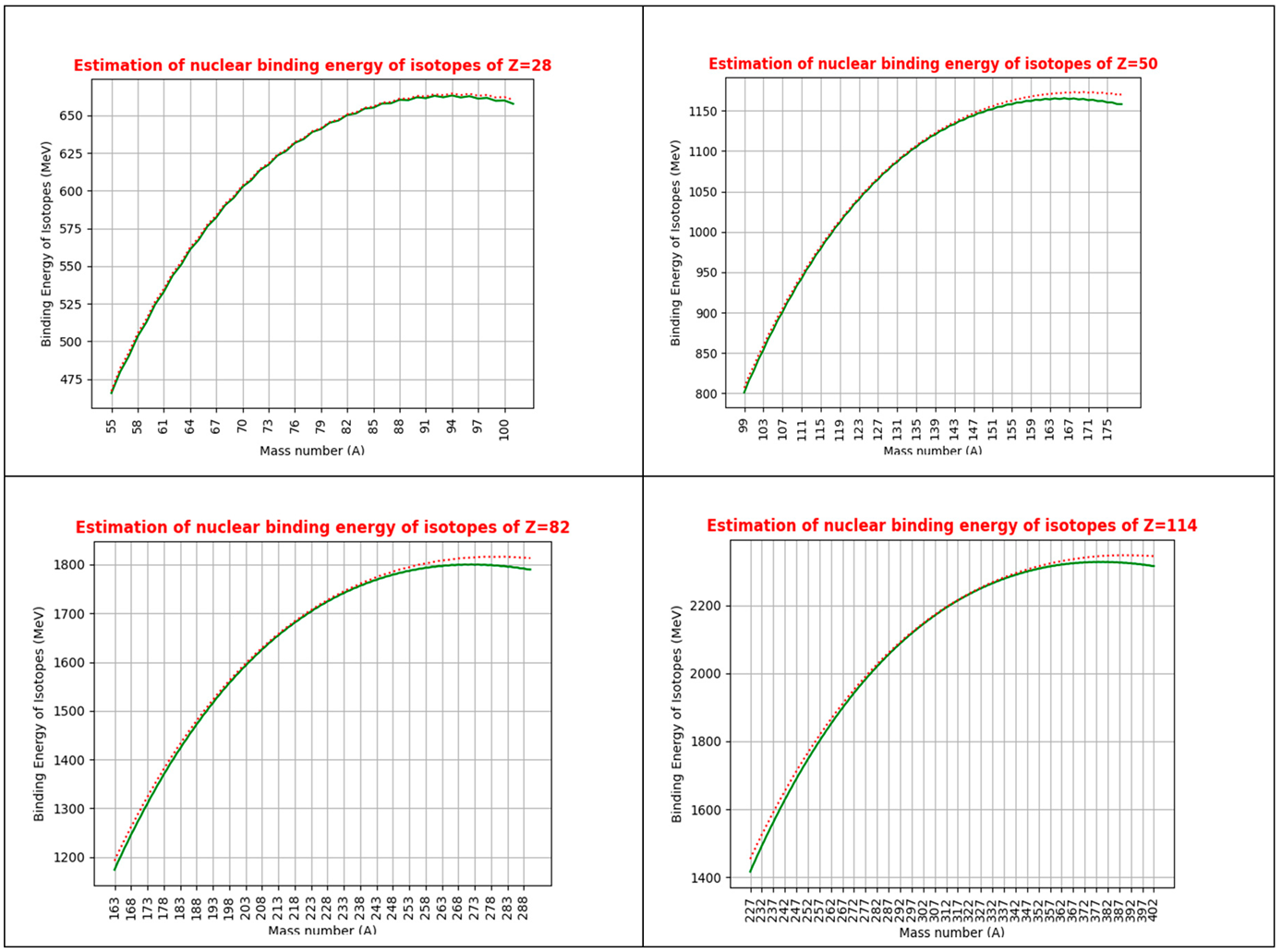
Following relations (6) and (19), it can be understood that, radii of higher isotopes of higher proton numbers, seem to have a lower radii than the expected radii. See the following Table 5 for the binding energy curves prepared for Z=28,50,82 and 114. Based on the energy coefficients proposed in relation (7), and if $R_0\cong 1.25\mathrm{fm},$ strong coupling constant [38] can be estimated as,

$$\begin{array}{l}{\alpha }_s\cong {\displaystyle \frac{8e^2}{20\pi {\epsilon }_0{R}_0{a}_v}}\cong 0.1151973\mathrm{where}{a}_v\cong 16.0\mathrm{MeV}\\ {\alpha }_s\cong {\displaystyle \frac{12e^2}{20\pi {\epsilon }_0{R}_0{a}_{asy}}}\cong 0.1128463\mathrm{where}{a}_{asy}\cong 24.5\mathrm{MeV}\\ {\alpha }_s\cong {\displaystyle \frac{9.6e^2}{20\pi {\epsilon }_0{R}_0{a}_s}}\cong 0.11401\mathrm{where}{a}_s\cong 19.4\mathrm{MeV}\\ {\alpha }_s\cong {\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0{a}_{cg}}}\cong {\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0{a}_p}}\cong 0.1151973\mathrm{where}{a}_{cg}\cong a_p\cong 10.0\mathrm{MeV}\\ {\alpha }_s\cong {\displaystyle \frac{1}{5\sqrt{3}}}\cong 0.11547\end{array}$$

In a simplified and unified approach, approximately, it is possible to infer that,

$$\left.\begin{array}{l}\left(a_v,a_{asy}\right)\approx \left({\displaystyle \frac{2\mp 0.4}{{\alpha }_s}}\right)\left({\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\right)\\ {\displaystyle \frac{2a_v{a}_{asy}}{\left(a_v+a_{asy}\right)}}\ge a_s\le \sqrt{a_v{a}_{asy}}\\ a_{cg}\approx a_p\approx \left({\displaystyle \frac{1}{{\alpha }_s}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\\ a_c\approx \left({\displaystyle \frac{3}{5}}\right){\displaystyle \frac{e^2}{4\pi {\epsilon }_0{R}_0}}\end{array}\right\}$$

(20)

Interesting point to be noted is that, the expression $\left({\displaystyle \frac{2\mp 0.40}{{\alpha }_s}}\right)$ represents the ratio of major nuclear binding energy coefficients to the basic nuclear potential.

5. Conclusion

Understanding nuclear binding energy with various physical terms and various coefficients is not a new point. With a single set of energy coefficients, our proposal helps in estimating the binding energy of all atomic nuclides starting from Z=1 to 137. Here, we would like to emphasize the point that, 4G model of the strong coupling constant $\left({\alpha }_s\right)$ plays a vital role in understanding the origin of the binding energy coefficients and further study certainly helps in connecting high and low energy branches of nuclear physics and particle physics. Interesting point to be noted is that, all the binding energy coefficients, can be expressed as, $k\left[{\left(2.95e\right)}^2/4\pi {\epsilon }_0\left(1.25\mathrm{fm}\right)\right]\cong \left(k/{\alpha }_s\right)\left[e^2/4\pi {\epsilon }_0\left(1.25\mathrm{fm}\right)\right]$ where $k=\left(1.0\mathrm{to}2.5\right).$