The Combination of Electro-Strong Interactions and Antiparticles

1. Introduction

It is well known that the Strong interaction is described by Quantum Chromodynamics(QCD)[1,2,3,4,5,6,7,8], a gauge theory with gauge group $\mathrm{SU}\left(3\right)$, which agrees with experiments very well. In QCD, the quark wave function is a color-$\mathrm{SU}\left(3\right)$ triplet

$$\Psi \left(x\right)=\left(\begin{array}{c}{\Psi }_{\mathrm{R}}\left(x\right)\\ {\Psi }_{\mathrm{B}}\left(x\right)\\ {\Psi }_{\mathrm{G}}\left(x\right)\end{array}\right).$$

(1)

Historically, colors were introduced to solve the wrong statistic problem[9,10]. The gauge group $\mathrm{SU}\left(3\right)$ has 8 generators, so there are 8 conservation charges according to Noether’s theorem. However the meaning of the 8-Noether charges is not clear enough, which does not correspond to the conservation of colors and/or anti-colors(three kinds as well).

Considering that the quark carries not only electric charge but also color charge, the interactions between quarks should be handled all together. Given that there are three kinds of degree of freedom, the unitary gauge group can be $\mathrm{SU}\left(2\right)$ too. However the triplet representation of $\mathrm{SU}\left(2\right)$ is real and hence the quarks are indistinct from anti-quarks in this representation without considering the electric charge, so $\mathrm{SU}\left(2\right)$ is abandoned. In order for the conservation of the three kinds of color charge to be the Noether charge, we reconsider the 3-dimensional unitary group $\mathrm{SU}\left(2\right)$ as the gauge group of the Strong interaction. The quantum theory of the Electro-magnetic interaction is a gauge theory(QED) with the gauge group $\mathrm{U}\left(1\right)$, which has 1 generator and the corresponding Noether charge is just the electric charge. So the combinatorial gauge group can be chosen as $\mathrm{U}\left(1\right)⨂\mathrm{SU}\left(2\right)\equiv \mathrm{U}\left(2\right)$, a direct product group, which is neither simple nor semi-simple. The transformation property of $\Psi \left(x\right)$ under the operation of the group element U of $\mathrm{U}\left(2\right)$ reads ${\Psi }^{\prime }\left(x\right)=U\Psi \left(x\right)$ and

$$\begin{array}{c}\hfill U=exp\left[-i{q}_f\theta \left(x\right)-i{Q}_f{T}^k{\theta }^k\left(x\right)\right],\end{array}$$

(2)

where $T^k$ or $T_k$($k=1,2,3$ or R,B,G) are basis elements of the Lie algebra $\mathfrak{su}\left(2\right)$, which can be expressed as

$$\begin{array}{ccc}\hfill T_1& =& {\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{ccc}0& -1& 0\\ -1& 0& 1\\ 0& 1& 0\end{array}\right),T_2={\displaystyle \frac{i}{\sqrt{2}}}\left(\begin{array}{ccc}0& 1& 0\\ -1& 0& -1\\ 0& 1& 0\end{array}\right),\hfill \\ \hfill T_3& =& \left(\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& -1\end{array}\right)\hfill \end{array}$$

(3)

in the adjoint representation of $\mathrm{SU}\left(2\right)$ group. $q_f$ is the electric charge carried by the f flavor quark in units of e (the electric charge of the electron) and $Q_f$ is the color charge carried by the f flavor quark in units of t, satisfying

$${\mathbf{T}}^2\Psi \left(x\right)=T(T+1)t^2\Psi \left(x\right),$$

(4)

where ${\mathbf{T}}^2$ is the Casimir operator of $\mathrm{SU}\left(2\right)$, t is the unit of the color charge carried by quarks. The covariant derivative is as

$$D_{\mu }={\partial }_{\mu }-i{q}_{f}e{A}_{\mu }-i{Q}_{f}t{T}^k{A}_{\mu }^k,$$

(5)

where the A with one Greek letter (Lorentz index) signifies the Electro-magnetic field, while the A with one Greek letter and one Latin letter signifies the gluon fields.

In the following two sections, first we will revisit the asymptotic freedom of Strong interactions based on the combination with Electro-magnetic interactions. Then the concept of antiparticle is reinvestigated. Some further discussions are given in the last section.

2. The Asymptotic Freedom of Strong Interactions Revisited

The coupled effective lagrangian can be expressed as[4]

$$\begin{array}{ccc}\hfill \mathcal{L}& =& i{Z}_2^f{\overline{\Psi }}_i^f{\gamma }^{\mu }{\partial }_{\mu }{\Psi }_i^f-Z_m^f{m}_f{\overline{\Psi }}_i^f{\Psi }_i^f-{\displaystyle \frac{1}{4}}{Z}_{3e}{F}_{\mu \nu }{F}^{\mu \nu }\hfill \\ & & +{\displaystyle \frac{1}{2}}{Z}_{3t}{A}^{k\mu }(g_{\mu \nu }{\partial }^2-{\partial }_{\mu }{\partial }_{\nu })A^{k\nu }\hfill \\ & & -Z_{3s}{Q}_{f}t{ϵ}^{ijk}{A}^{i\mu }{A}^{j\nu }{\partial }_{\mu }{A}_{\nu }^k\hfill \\ & & -{\displaystyle \frac{1}{4}}{Z}_{4s}{Q_f}^2{t}^2{ϵ}^{ijl}{ϵ}^{mnl}{A}^{i\mu }{A}^{j\nu }{A}_{\mu }^m{A}_{\nu }^n\hfill \\ & & +Z_{1e}^f{q}_{f}e{\overline{\Psi }}_i^f{\gamma }^{\mu }{A}_{\mu }{\Psi }_i^f+Z_{1t}^f{Q}_{f}t{\overline{\Psi }}_i^f{\gamma }^{\mu }{A}_{\mu }^k{T}_{ij}^k{\Psi }_i^f\hfill \\ & & -Z_{2FP}{\partial }^{\mu }{\overline{c}}^i{\partial }_{\mu }{c}^i+Z_{1FP}{Q}_{f}t{ϵ}^{ijk}{A}_{\mu }^k{\partial }^{\mu }{\overline{c}}^i{c}^i\hfill \\ & & +{\displaystyle \frac{1}{2{\xi }_e}}{A}^{\mu }{\partial }_{\mu }{\partial }_{\nu }{A}^{\nu }+{\displaystyle \frac{1}{2{\xi }_t}}{A}^{k\mu }{\partial }_{\mu }{\partial }_{\nu }{A}^{k\nu },\hfill \end{array}$$

(6)

where the superscript $f=1,2\dots N_f$ indicates the flavor of the quarks, the indices $i,j\dots =1,2,3$ denote the component of the adjoint representation of $\mathrm{SU}\left(2\right)$. The s and $FP$ in the subscript refers to self-coupled and Faddeev-Popov respectively.

The relation between the bare and renormalized couplings can be defined as[4]

$$\begin{array}{ccc}\hfill e_0& =& Z_3^{-1/2}{Z}_2^{-1}{Z}_1{\tilde{\mu }}^{\epsilon /2}e.\hfill \end{array}$$

(7)

$e_0$ is the bare electric charge, e is the renormalized electric charge and $\epsilon =4-d$ (where d is the number of space-time dimensions). Introducing the dimensionless fine-structure constant ${\alpha }_e=e^2/4\pi$ and its bare counterpart ${\alpha }_{e0}=e_0^2/4\pi$, then we have

$$\begin{array}{ccc}\hfill {\alpha }_{e0}& =& {Z_2^f}^{-2}{Z_{1e}^f}^2{Z}_{3e}^{-1}{\tilde{\mu }}^{\epsilon }{\alpha }_e.\hfill \end{array}$$

(8)

Similarly, for the Strong interactions, we have

$$\begin{array}{ccc}\hfill t_0& =& {Z_2^f}^{-1}{Z}_{1t}^f{Z}_{3t}^{-1/2}{\tilde{\mu }}^{\epsilon /2}t\hfill \end{array}$$

(9)

and

$$\begin{array}{ccc}\hfill {\alpha }_{t0}& =& {Z_2^f}^{-2}{Z_{1t}^f}^2{Z}_{3t}^{-1}{\tilde{\mu }}^{\epsilon }{\alpha }_t,\hfill \end{array}$$

(10)

where ${\alpha }_{t0}=t_0^2/4\pi$ and ${\alpha }_t=t^2/4\pi$.

We can calculate the $\beta$-function for e or ${\alpha }_e$ by computing $Z_2^f,Z_{1e}^f$ and $Z_{3e}$, in which $Z_{3e}$ can be computed through the photon propagator. Working in Feynman gauge and using the $\overline{\mathrm{MS}}$ scheme, at the 1-loop level the result is[4]

$$\begin{array}{c}\hfill Z_{3e}=1-\sum _{f=1}^{N_f}{q_f}^2{\displaystyle \frac{2{\alpha }_e}{3\pi \epsilon }}+O\left({{\alpha }_e}^2\right).\end{array}$$

(11)

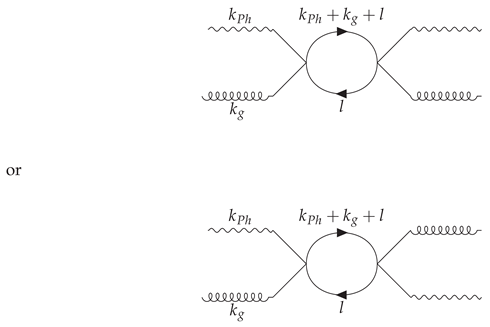
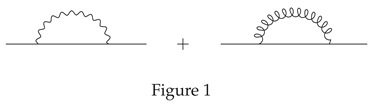
$Z_2^f$ can be computed through the quark propagator, and the Feynman diagram is shown in Figure 1(the corresponding 1-loop counter term is omitted),

the photon part and the gluon part have an interference. The result is[4]

$$\begin{array}{c}\hfill Z_2^f=1-{\displaystyle \frac{1}{2\pi \epsilon }}[C\left(A\right){Q_f}^2{\alpha }_t+{q_f}^2{\alpha }_e]+O\left({\alpha }^2\right).\end{array}$$

(12)

where $C\left(A\right)$ is defined by ${\left(T^k{T}^k\right)}_{ij}={\delta }_{ij}C\left(A\right)$ for the adjoint representation of $\mathrm{SU}\left(2\right)$.

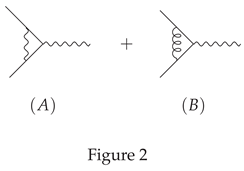
$Z_{1e}^f$ can be computed through the quark-quark-photon vertex. The Feynman diagram is shown in Figure 2.

Apart from the ordinary vertex diagram (A), there is also diagram (B) and they interfere. The result is[4]

$$\begin{array}{ccc}\hfill Z_{1e}^f& =& 1-{\displaystyle \frac{1}{2\pi \epsilon }}[C\left(A\right){Q_f}^2{\alpha }_t+{q_f}^2{\alpha }_e]+O\left({\alpha }^2\right)\hfill \\ & =& Z_2^f,\hfill \end{array}$$

(13)

which means that the Ward-Takahashi identity still holds at the 1-loop level.

Writing

$$\begin{array}{c}\hfill \ln \left[{Z_2^f}^{-2}{Z_{1e}^f}^2{Z}_{3e}^{-1}\right]=\sum _{n=1}^{\infty }{\displaystyle \frac{E_n({\alpha }_e,{\alpha }_t)}{{\epsilon }^n}},\end{array}$$

(14)

we can get the the $\beta$-function for ${\alpha }_e$

$$\begin{array}{ccc}\hfill \beta ({\alpha }_e,{\alpha }_t)& =& \beta \left({\alpha }_e\right)={{\alpha }_e}^2{E}_1^{\prime }\left({\alpha }_e\right)\hfill \\ & =& {\displaystyle \frac{2}{3\pi }}\sum _{f=1}^{N_f}{q_f}^2{{\alpha }_e}^2>0.\hfill \end{array}$$

(15)

To calculate the $\beta$-function for t or ${\alpha }_t$, we compute $Z_{1t}^f$ and $Z_{3t}$. The $Z_{3t}$ can be computed through the gluon propagator. At the 1-loop level the result is[4]

$$\begin{array}{c}\hfill Z_{3t}=1+\left[{\displaystyle \frac{5}{3}}T\left(A\right)-{\displaystyle \frac{4}{3}}{N}_{f}T\left(A\right)\right]{\displaystyle \frac{{Q_f}^2{\alpha }_t}{2\pi \epsilon }}+O\left({{\alpha }_t}^2\right),\end{array}$$

(16)

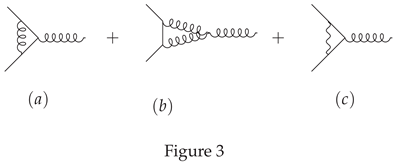
where $T\left(A\right)$ is defined by $Tr\left(T^a{T}^b\right)=T\left(R\right){\delta }^{ab}$(R can be an arbitrary representation of the gauge group) and $T\left(A\right)=2$ for the adjoint representation of $\mathrm{SU}\left(2\right)$. The $Z_{1t}^f$ can be computed through the quark-quark-gluon vertex, the Feynman diagram is shown in Figure 3.

Apart from the ordinary vertex diagram (a) and (b), there is also diagram (c) and they interfere. The result is[4]

$$\begin{array}{ccc}\hfill Z_{1t}^f& =& 1-{\displaystyle \frac{{\alpha }_t}{2\pi \epsilon }}[C\left(A\right)+T\left(A\right)]{Q_f}^2-{\displaystyle \frac{{\alpha }_e}{2\pi \epsilon }}{q_f}^2+O\left({\alpha }^2\right)\hfill \\ & \ne & Z_2^f,\hfill \end{array}$$

(17)

which is in accordance with the Slavnov-Taylor identities of pure Strong interactions,

$$\begin{array}{c}\hfill {\displaystyle \frac{Z_{1t}^f}{Z_2^f}}={\displaystyle \frac{Z_{3s}}{Z_{3t}}}=\dots \ne 1\end{array}$$

(18)

at the 1-loop level.

Writing

$$\begin{array}{c}\hfill \ln \left[{Z_2^f}^{-2}{Z_{1t}^f}^2{Z}_{3t}^{-1}\right]=\sum _{n=1}^{\infty }{\displaystyle \frac{G_n({\alpha }_e,{\alpha }_t)}{{\epsilon }^n}},\end{array}$$

(19)

we can get the the $\beta$-function for ${\alpha }_t$

$$\begin{array}{ccc}\hfill \beta ({\alpha }_e,{\alpha }_t)& =& \beta \left({\alpha }_t\right)={{\alpha }_t}^2{G}_1^{\prime }\left({\alpha }_t\right)\hfill \\ & =& -{\displaystyle \frac{T\left(A\right)}{\pi }}\left[{\displaystyle \frac{11}{6}}-{\displaystyle \frac{2}{3}}{N}_f\right]{Q_f}^2{{\alpha }_t}^2,\hfill \end{array}$$

(20)

decoupled with $\beta \left({\alpha }_e\right)$ at the 1-loop level.

In order that $\beta \left({\alpha }_t\right)<0$ we must have $N_f<{\displaystyle \frac{11}{4}}$, which apparently contradicts with the now fact $N_f=6$. What then is wrong? Noting that the creation and annihilation of quark-antiquark pair is not only a Strong interaction process but also an Electro-magnetic one, so the gluon and photon must be both involved. 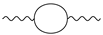Perhaps the problem lies in the closed quark-antiquark loop part of 1-loop corrections to the photon and gluon propagator, that is the diagram and respectively. The above diagram should probably be replaced by

equivalently, which means that the Strong interaction and the Electro-magnetic interaction couple together.

If the closed quark-antiquark loop part is removed from the 1-loop corrections to the photon and gluon propagator, then $\beta \left({\alpha }_e\right)=0$ and $\beta \left({\alpha }_t\right)$ is negative definite in 1-loop order. That is to say, asymptotic freedom holds for Strong interactions irrespective of $N_f$, neither should the dynamics of color charge or electric charge depend on the numbers of the kinds of the active carriers(fermions).

3. The Concept of Antiparticle Reinvestigated

Antiparticles were first predicted by Dirac from his equation. In 1932, C. D. Anderson discovered the anti-electron(positron) in cosmic rays and confirmed Dirac’s prediction. However, it may be just a coincidence. The complex Dirac fields belong to the direct sum representation $D({\displaystyle \frac{1}{2}},0)\oplus D(0,{\displaystyle \frac{1}{2}})$ of the Lorentz group and permit of some global or local $\mathrm{U}\left(1\right)$ symmetry. Thus there is an associated $\mathrm{U}\left(1\right)$ charge. The four-component solution of the Dirac fields tells us that there can exist two kinds of spin-1/2 Dirac particles with opposite $\mathrm{U}\left(1\right)$ charge, each with two possible spin orientations($S_Z=\pm 1/2$ or helicities $h=\pm 1$). In fact, they correspond to positively charged particle and negatively charged particle each with two possible spin states. It is much more clear by viewing the Dirac equation as a field equation and following the second quantization, the conserved charge associated with the Dirac field is given by

$$\begin{array}{ccc}\hfill Q& =& q\int {\displaystyle \frac{d^{3}p}{{\left(2\pi \right)}^{3}2E}}\sum _{h=\pm 1}[a^{†}(p,h)a(p,h)\hfill \\ & & -b^{†}(p,h)b(p,h)],\hfill \end{array}$$

(21)

from which we can see that the two kinds of operators $a^{†}(p,h)$ and $b^{†}(p,h)$ create two kinds of particles with opposite electric charge.

The concept of Casimir charge is introduced in Ref[11]. It is the characteristic quantity that discriminates particles. If the gauge group is the rank-1 $\mathrm{SU}\left(2\right)$ for Strong interactions, then the corresponding Casimir charge is characterized by the eigenvalue of ${\mathbf{T}}^2$(as the angular momentum ${\mathbf{J}}^2$) and the colored states can be expressed as

$$\begin{array}{c}\hfill |T,t_3\rangle ,\end{array}$$

(22)

where $T=1$ for quarks or “anti-quarks" and $t_3$ is the eigenvalue of $T_3$. That is to say the difference between quarks and “anti-quarks" is only in the electric charge. So the C transformation is just only a matter of electric charge conjugation and not concerned with color charge. Besides, charge conjugation seems not to be well-defined[11,12]. Hence, by Occam’s razor, perhaps there is no need to introduce the concept of antiparticle or antimatter, what exist in Nature are just various particles with different Casimir charges.

4. Discussion

If the gauge group of Strong interactions is indeed $\mathrm{SU}\left(2\right)$, then we will have the following expectations.

(1) If the four quark state($qqqq$) can be found experimentally, then it will offer a support of $\mathrm{SU}\left(2\right)$ and disfavor $\mathrm{SU}\left(3\right)$ with the assumption of color confinement.

(2) The electric charge and color charges can form a quaternion, or more precisely, the imaginary number i and the elements $\mathbf{i},\mathbf{j},\mathbf{k}$ of the quaternion(times a multiple of e or t) are the generators of Electro-strong interactions. the vector color charge is as monopole, so there might have a similar relation as $2eg/\hslash =n$[13] between e and t, which would agree with the quantization of electric charge, furthermore a unified theory might be obtained.

(3) For $\mathrm{U}\left(1\right)⨂\mathrm{SU}\left(2\right)$ is a subgroup of $\mathrm{SU}\left(3\right)$, so the $\mathrm{SU}\left(3\right)$ description of the Strong interaction might have redundancy.