An Attempt to Express the Critical Temperature of Elemental Superconductors Through the Atomic Numbers at Arbitrary Pressure and Radiation Dose

1. Introduction

Despite the great progress in describing superconductivity using the Bardeen-Cooper-Schrieffer (BCS) [1] and Ginzburg-Landau [2] theories and their derivatives [3,4], we still do not have a formula expressing T_c in terms of the atomic number Z of an elemental superconductor. Having this formula would mean a deeper understanding of the phenomenon of superconductivity. This will also allow us to predict new superconducting transuranic elements beyond americium. The possible existence of such a formula is determined by the presence of an experimental dependence of the critical temperature on the atomic number of the elements, represented in the Periodic Table of Superconductivity [5,6,7]. In this table we see 31 elements that superconduct at atmospheric pressure, four elements that superconductive under irradiation (Pd) or been grinded into fine powder (Np) or been in the nanotubes form (C) or been in the thin film form (Cr) and all of them at ambient pressure, and 22 – at high pressure. We have represented this table as a graph of a function (Figure 1) that we want to write in mathematical form.

The logarithmic scale on the ordinate of the T_c(Z) graph in Figure 1 is chosen for better perception, since T_c varies from 0.0004 K for lithium at normal pressure to 29 K for calcium at high pressure. The existing formulas describing the dependence of the critical temperature on the characteristics of the superconducting element contain physical quantities that are ambiguous in their derivation, such as the Hopfield parameter and the lattice spring constant [8]. These physical quantities determine or are determined by the electronic structure of the crystal, and the latter is determined not only by external conditions (temperature T, pressure p and indirectly by the radiation dose D), but also by the charge of the nucleus of the atom of the superconducting element. Since these dependences are too complex, we do not expect that the atomic number Z will be included in the desired formula T_c = T_c(Z) in an explicit form.

2. Finding a Mathematical Expression for the T_c(Z) Graph

First, we find the domain and range of the function T_c(Z), shown in Figure 1. The domain of this function is the set of natural numbers {Z ∈ N: 1 ≤ Z ≤ 95}, but this is at first glance. It is known that new transuranic superheavy elements continue to be discovered, and everyone hopes for the existence of an island of nuclear stability after Z = 164 [9], which, probably, in the distant future will make it possible to create at least microparticles of these elements to determine their physical properties. Therefore, we will extend the domain of T_c(Z) to infinity: {Z ∈ N: 1 ≤ Z < + ∞}. On the other hand, it is widely believed that the center of neutron stars contains nuclear matter consisting only of neutrons, and great efforts are being made to describe the properties of this matter [10]. Therefore, we will have to extend the domain of T_c(Z) to integers: {Z ∈ Z: 0 ≤ Z < + ∞}. But in 2011, 309 antihydrogen atoms were produced and trapped for 1000 seconds [11]. This means that we have the right to assume the possibility of obtaining in the distant future or detecting in space antimatter with an arbitrary negative Z. Therefore, the domain of T_c(Z) is the set of integers: {Z ∈ Z: – ∞ < Z < + ∞}. 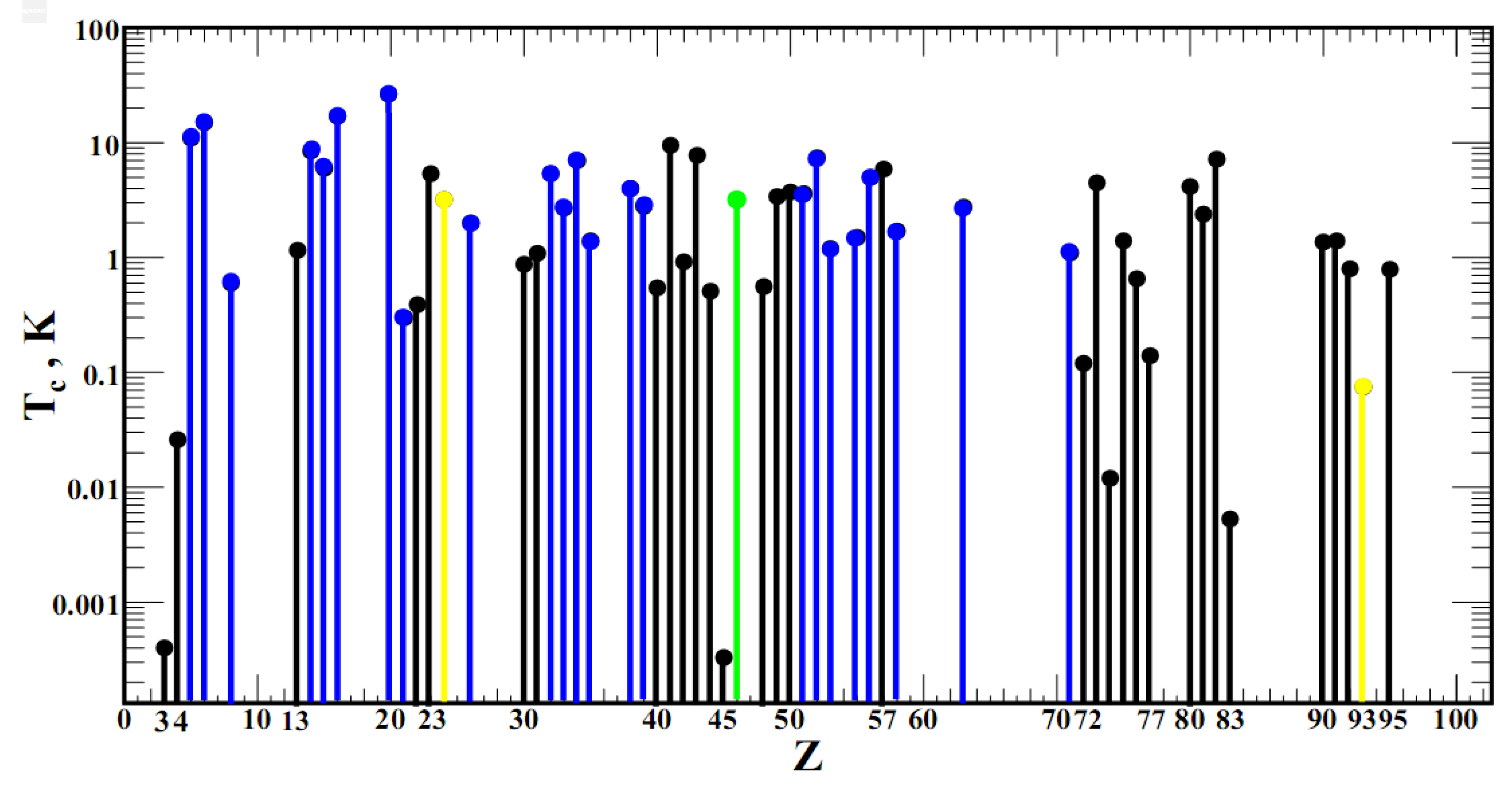Figure 1 shows what we have now, but how the graph T_c(Z) will expand along the Z axis over the next hundreds of years, no one knows. The range of T_c(Z) is the set of real numbers: {T_c ∈ R: 0 ≤ T_c ≤ 29}. But we must take into account the possibility of further increasing the critical temperature of elemental superconductors with the improvement of high-pressure technology. Taking into account the possible superconductivity of metallic hydrogen at 450 K and 3.5 TPa pressure [12], we will expand the range of T_c(Z) to 450 K: {T_c ∈ R: 0 ≤ T_c ≤ 450}.

Suppose we are trying to obtain T_c(Z) by solving the Schrödinger equation for electrons in a crystal with arbitrary Z of its atoms and arbitrary T, p, and D. Inevitably, we will obtain quantum selection rules for some quantum numbers that characterize our system of electrons in this crystal with the ability to form Cooper pairs. Let us denote these quantum numbers by the letter N, and let them run through integer values from 1 to 57 and further. Let us further assume that these selection rules determine those atomic numbers Z for which the existence of Cooper pairs is possible. This means that there is some function Z_sc = f (N) such that for N varying from N = 1 to 57, f (N) yields integers that coincide with the atomic numbers of superconducting elements: Z_sc = {3, 4, 5, 6, 8, 13, 14, 15, 16, 20, 21, 22, 23, 24, 26, 30, 31, 32, 33, 34, 35, 38, 39, 40, 41, 42, 43, 44, 45, 46, 48, 49, 50, 51, 52, 53, 55, 56, 57, 58, 63, 71, 72, 73, 74, 75, 76, 77, 80, 81, 82, 83, 90, 91, 92, 93, 95}. We assume that 57 values of N can be associated with 57 values from the set Z_sc in any order. We found a combination of integers that matches only 28 numbers from the set Z_sc. Since the range of this combination of integers coincides with the quantum rule (with a given Z_sc) not completely, but only by half, we designated it as f_1/2(N):

$$f_{1/2}(N)=rpi\left({\left[\left|{\displaystyle \frac{{(N+1)}^6\cdot (N+1)!+{(-1)}^{N+1}\cdot N^{N+1}}{95\cdot N^{N-1}/10}}+{(-1)}^N\cdot 2\cdot (30+N)\cdot (N+2)\right|\right]}^{1/2}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}(1)$$

(1)

where rpi(x) is a function that rounds x to the nearest integer of x [13], Table 1 contains the values of N and f_1/2 (N) without and with rounding. For some values of f_1/2(N) = Z we have different N (these values are highlighted in black in Table 1): if N=14 or 28, then Z = 58, etc.

Let us now return to the dependence of T_c on Z in Figure 1. It can be assumed that T_c should be expressed in terms of Dirac functions:

T_c(Z) ∝ δ (Z – Z₀)

(2)

where are integers: Z₀ ∈ Z_sc. The rule for elements of the set Z_sc is approximately expressed by formula (1). Among the physical characteristics of a superconducting crystal that affect T_c, we consider the lattice parameters a ≡ a(Z, T, p, D), b ≡ b(Z, T, p, D) and c ≡ c(Z, T, p, D) as functions of atomic number Z, temperature T, pressure p, and irradiation dose D. In this case the lattice parameters must be taken at T_c or near T_c, but as can be seen below, it is not easy to find from scientific data the lattice parameters of crystals of chemical elements at low temperatures.

In the next step, we take into account that most elemental superconductors have an inverse dependence of T_c on the lattice parameters with increasing pressure [6]. This dependence is valid only for the first gigapascals or the first tens of GPa. With further increase in pressure, the dependence becomes very complex. To simplify the reasoning, we will adopt a simple inversely proportional relationship between T_c and the lattice parameters and complicate the Dirac function, which will be responsible for the behavior of T_c at high pressure:

$$T_c(Z,p,D)\propto {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}\left(\frac{1}{a(Z,p,D)}+\frac{1}{b(Z,p,D)}+\frac{1}{c(Z,p,D)}\right)}\cdot {\delta }^{\prime }(Z-Z_0)\cdot dZ$$

(3)

where Z₀ ∈ Z_sc, and we plan to use the following property of the Dirac function: ${\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}f(x)}\cdot {\delta }^{\prime }(x-x_0)\cdot dx=-f^{\prime }(x_0)$. Applying this property to (3), we obtain:

$$T_c(Z,p,D)\propto {\left.{\displaystyle \frac{1}{a^2}}\cdot {\displaystyle \frac{\partial a}{\partial Z}}\right|}_{Z=Z_0}+{\left.{\displaystyle \frac{1}{b^2}}\cdot {\displaystyle \frac{\partial b}{\partial Z}}\right|}_{Z=Z_0}+{\left.{\displaystyle \frac{1}{c^2}}\cdot {\displaystyle \frac{\partial c}{\partial Z}}\right|}_{Z=Z_0}$$

(4)

These derivatives have a complex behavior with pressure, so we assume that they are responsible for the behavior of T_c at high pressure via lattice parameters since a ≡ a (Z, p, D), …. We must take into account that the left side is in Kelvin and to bring the right side to it we must multiply it by the coefficient$\hslash c/k_B$:

$$T_c(Z,p,D)=S_Z\cdot {\displaystyle \frac{\hslash c}{k_B}}\cdot \left\{{\left.{\displaystyle \frac{1}{a^2}}\cdot {\displaystyle \frac{\partial a}{\partial Z}}\right|}_{Z=Z_0}+{\left.{\displaystyle \frac{1}{b^2}}\cdot {\displaystyle \frac{\partial b}{\partial Z}}\right|}_{Z=Z_0}+{\left.{\displaystyle \frac{1}{c^2}}\cdot {\displaystyle \frac{\partial c}{\partial Z}}\right|}_{Z=Z_0}\right\}$$

(5)

where $\hslash$ is Planck constant, c is the speed of light, k_B is Boltzmann constant. We introduced a dimensionless quantity S_Z related to the symmetry of the crystal at given T_c, p and D.

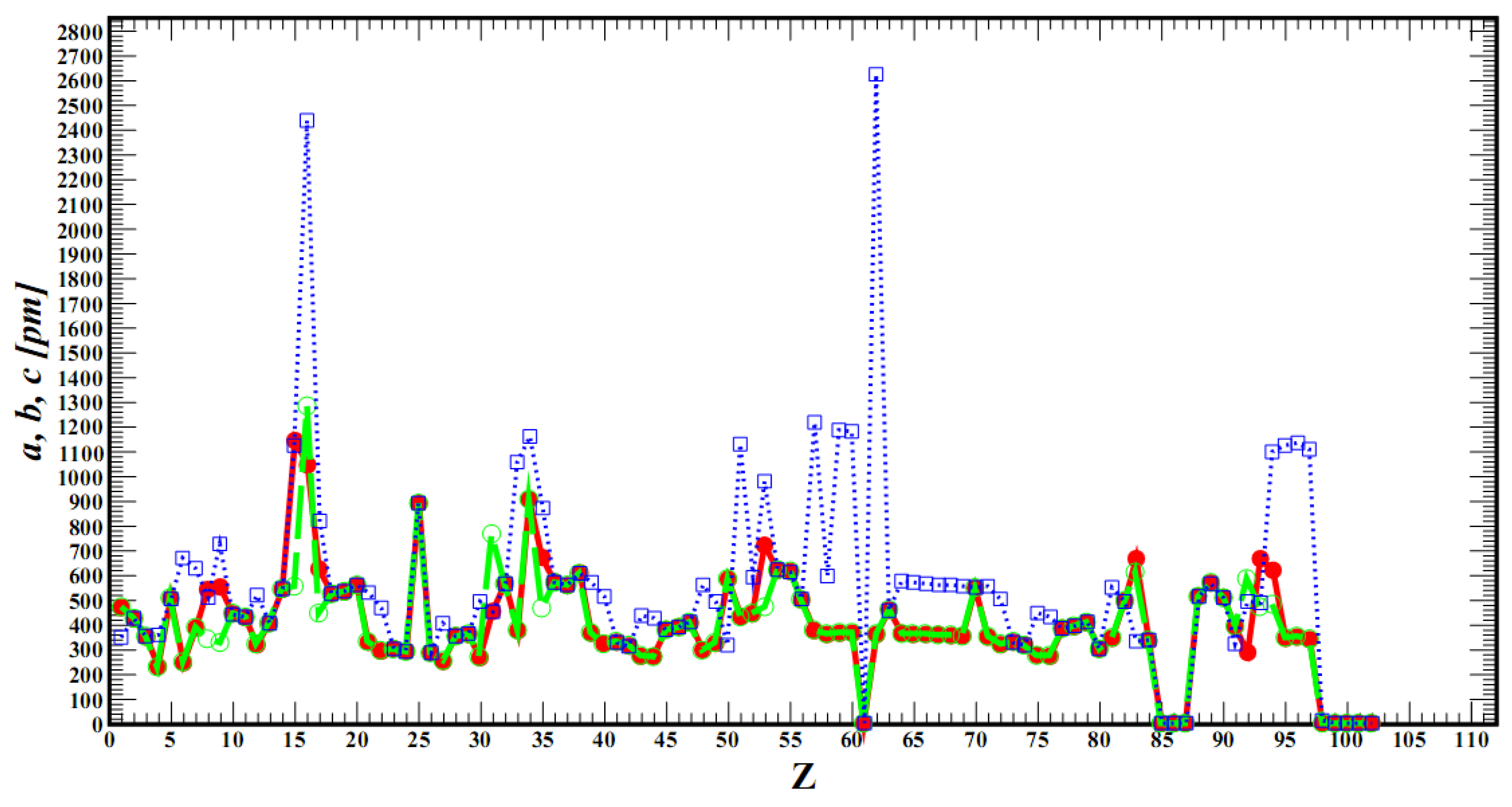
If we know T_c and the dependence of the lattice parameters on atomic numbers, we can substitute the derivatives into (5) and find S_Z for a particular elemental superconductor. If we find the law of change of S_Z, then we can substitute it into (5) and find the general law of dependence T_c(Z). We found that the law of change of lattice parameters from the atomic number of a chemical element does not exist in mathematical form. There are data on the lattice parameters of elements mainly at room temperatures and only for inert gases at low temperatures. In Figure 2 we have depicted this dependence. There are two ways to calculate the derivatives in (5). The first way is to find a mathematical relationship for a(Z), b(Z), and c(Z) (for fixed p = p′ and D = D′) using some phenomenology and take derivatives with respect to Z at Z₀ ∈ Z_sc. This is another scientific problem that distracts us from the problem posed in this article. The second way is to take into account that a(Z) (and of course b(Z), c(Z)) is a discrete function, the derivative of which is a simple change in the function when the argument changes by one. We calculate the derivative by averaging this change on the left and right sides of Z₀:

$${\left.{\displaystyle \frac{\partial a}{\partial Z}}\right|}_{Z=Z_0}=〈{\left.{\displaystyle \frac{\Delta a}{\Delta Z}}\right|}_{Z=Z_0}〉={\displaystyle \frac{1}{2}}\cdot \left({\displaystyle \frac{a_{Z_0}-a_{Z_0-1}}{Z_0-(Z_0-1)}}+{\displaystyle \frac{a_{Z_0+1}-a_{Z_0}}{Z_0+1-Z_0}}\right)={\displaystyle \frac{1}{2}}\cdot \left(a_{Z_0+1}-a_{Z_0-1}\right)$$

(6)

and for ${\left.{\displaystyle \frac{\partial b}{\partial Z}}\right|}_{Z=Z_0}$and ${\left.{\displaystyle \frac{\partial c}{\partial Z}}\right|}_{Z=Z_0}$we do the same.

Let us find the symmetry coefficients for lithium S ≡ S_Li at room and low temperatures. We will take the pressure equal to atmospheric p₀, and the ionizing radiation is zero (or natural) D₀. We do this to estimate errors in determining symmetry coefficients as majority of lattice parameters data in literature concerns only the room temperature. Lattice parameters of Li (Z₀ = 3) at room temperature: a = b = c = 351 pm [14]. Lattice parameters of He (Z = Z₀ – 1 = 2) at a temperature of 1 – 1.5 K and a pressure of 2.5 MPa (the solid state is absent at p < 2.5 MPa): a = b = c = 424.2 pm [15]. Lattice parameters of Be (Z = Z₀ + 1 = 4) at room temperature, ambient pressure and zero radiation: a = b = 228.58 pm, c = 358.43 pm [16]. As a result:

$〈{\left.{\displaystyle \frac{\Delta a}{\Delta Z}}\right|}_{Z=3}〉$ = (228.58 – 424.20)/2 = – 97.81 pm, $〈{\left.{\displaystyle \frac{\Delta b}{\Delta Z}}\right|}_{Z=3}〉$ = – 97.81 pm,

$〈{\left.{\displaystyle \frac{\Delta c}{\Delta Z}}\right|}_{Z=3}〉$ = (358.43 – 424.20)/2 = – 32.88 pm.

Now we substitute this result into (5) and find the symmetry coefficient for lithium S_Li:

T_c (Li, p₀, D₀) = – S_Li ⋅ ℏc/k_B ⋅10¹² ⋅ (97.81 + 97.81 + 32.88)/351² = – S_Li ⋅ 0.23 ⋅ 228.5/351² = – S_Li ⋅ 4.2658 ⋅ 10⁶, S_Li = – T_c (Li, p₀, D₀) / (4.2658 ⋅ 10⁶) = – 4 ⋅ 10 ^{– 4} / (4.2658 ⋅ 10⁶) = – 0.9377 ⋅ 10 ^{– 10}.

We have intentionally removed the brackets for the modulus to get the exact value of the symmetry coefficient. Let us repeat the above calculations, taking into account the lattice parameters of Li at T = 4.2 K: a = b = 311.1 pm, c = 509.3 pm [17]. We did not find data for beryllium at low temperatures, and we got:

$〈{\left.{\displaystyle \frac{\Delta a}{\Delta Z}}\right|}_{Z=3}〉$ = (228.58 – 424.20)/2 = – 97.81 pm, $〈{\left.{\displaystyle \frac{\Delta b}{\Delta Z}}\right|}_{Z=3}〉$ = – 97.81 pm,

$〈{\left.{\displaystyle \frac{\Delta c}{\Delta Z}}\right|}_{Z=3}〉$ = (358.43 – 424.20)/2 = – 32.88 pm,

T_c(Li,p₀,D₀)= – S_Li⋅$\hslash$⋅c/k_B⋅10¹²[m]⋅((2⋅97.81/311.1²) + 32.88/509.3²) = – S_Li⋅4.9403⋅10⁶,

S_Li = – T_c(Li, p₀, D₀) / (4.9403⋅10⁶) = – 4⋅10^–4 /(4.9403⋅10⁶) = – 0.8097⋅10^–10.

The relative deviation between S_Li at room temperature and low temperatures is about 14%. Let us keep in mind that the symmetry coefficients calculated for other superconducting elements with use of lattice parameters at room temperatures deviate from the symmetry coefficient at low temperatures to the same extent. We assume that, just as the derivatives of the lattice parameters of a superconducting element depend on the lattice parameters of neighboring elements with atomic numbers one unit higher and one unit lower, so the symmetry coefficient depends on the crystal structure of neighboring elements. The symmetry coefficients for superconducting bulk elements at ambient pressure p₀ and zero radiation D₀ are given in Table 2. We did not calculate the symmetry coefficients for superconductors at high pressure or at non-zero ionizing radiation due to the lack of data on the lattice parameters under these conditions. The space group numbers of superconducting elements and their neighbors are also shown in Table 2. For example, the space group of helium is 225, lithium is 194, and beryllium is also 194, and the transition between these symmetries is denoted as 225 – 194 – 194, where the space group of the superconductor is in the center.

To find a mathematical expression for S_Z, we first find in Table 2 those that have the same transition space groups, in the hope that they will be close in order of magnitude. And indeed, we have three associations: 1. The 194-194-229 transition for S_Ti, S_Zr and S_Hf is highlighted in red in Table 2, the S_Z for these three elements of Group 4 of the periodic table have similar negative values. 2. The 194-229-229 transition for S_V, S_Nb, and S_Ta, which are related to the elements in Group 5 of the periodic table, is highlighted in blue in Table 2. 3. The 229-194-194 transition for S_Tc, S_La and S_Re in Table 2 is highlighted in green and has the worst agreement. And three more associations with two elements in each, highlighted in bold black, light gray and yellow. Within pairs, their values have at least the same sign. We explain the discrepancy in each association by using incorrect crystal lattice parameters at room temperatures (they should be at low temperatures), which additionally affects the calculations of derivatives. Now we need to express the symmetry coefficient S_Z in terms of the symmetry properties of crystals of superconducting elements and their neighbors in the periodic table for all these associations.

Since S_Z depends on the symmetry of the superconductor crystal and its neighbors in the periodic table, we can write, for example, for the three transitions 194 – 194 – 229:

S_Hf ≈ S_Zr ≈ S_Ti = A₁₉₄ ± A₁₉₄ ± A₂₂₉

(7)

where A₁₉₄ characterizes the hcp crystal structure, since the space group number 194 corresponds to the hcp (hexagonal close-packed) crystal structure of the P6₃/mmc space group, A₂₂₉ characterizes the bcc (body-centered cubic) crystal structure. Similarly for the other two associations 194 – 229 – 229 and 229 – 194 – 194:

S_V ≈ S_Nb ≈ S_Ta = A₁₉₄ ± A₂₂₉ ± A₂₂₉

(8)

S_Tc ≈ S_La ≈ S_Re = A₂₂₉ ± A₁₉₄ ± A₁₉₄

(9)

Since the order of the space groups in their combination for S_Z matters, the signs in (7 – 9) can be different, despite the fact that we have only two coefficients: A₁₉₄ and A₂₂₉. Having struggled with these expressions, we came to the conclusion that when going from hexagonal to cubic symmetry there should be a sum, and when going from cubic to hexagonal symmetry there should be a subtraction:

S_Ti = 2⋅A₁₉₄ + A₂₂₉, S_V = A₁₉₄ + 2⋅A₂₂₉

(10)

S_Tc = A₂₂₉ – 2⋅A₁₉₄

(11)

A_{(space grope number)} ≡ A_sgn must be a function of integers representing the number of mirror planes, the order of the symmetry axes and their number, the presence of a center and axes of inversion, and so on. The best expressions we found satisfactory (10 – 11): A₁₉₄ = 1/(9!3!4) = 0.115⋅10^–6, A₂₂₉ = –1/(8!3!4) = – 1.033⋅10^–6. These values give an approximate S_Z of (10 – 11). Knowing A₁₉₄, we found A₂₂₅ from 194 – 194 – 225 for S_Ru and S_Os using rule (10): A₂₂₅ = – 1/(9!4!4) = – 3⋅10^–8. And we can write approximate formula for S_Z:

S_Z = A_sg(Z-1) ± A_sgZ ± A_sg(Z+1), A_{sg(atomic number)} ≈ (±1)/(n! ⋅ k! ⋅ m)

(12)

where A_{sg(atomic number)} is the symmetry factor for the element with atomic number Z with space group number sg, n is the number of symmetry axes, k is the number of mirror planes plus 1 for hexagonal or plus 2 for cubic symmetry, m = 4 at least for hexagonal and cubic symmetry. And we recall that S_Z is a function of external parameters: S_Z = S_Z (T, p, D), that is, the symmetry of the crystal changes under the influence of external parameters, which we must take into account in the calculations.

3. Conclusion

Trying to describe the experimental dependence of T_c through Z at an arbitrary pressure p and radiation dose D, we obtained the following formula:

$$\begin{array}{c}{T}_c(Z_0,p,D)\hspace{0.17em}=S_{Z_0}{\displaystyle \frac{\hslash c}{2k_B}}\left\{{\displaystyle \frac{a_{Z_0+1}(Z_0+1,p,D)–a_{Z_0-1}(Z_0-1,p,D)}{a_{Z_0}^2(Z_0,p,D)}}+{\displaystyle \frac{b_{Z_0+1}(Z_0+1,p,D)–b_{Z_0-1}(Z_0-1,p,D)}{b_{Z_0}^2(Z_0,p,D)}}+{\displaystyle \frac{c_{Z_0+1}(Z_0+1,p,D)–c_{Z_0-1}(Z_0-1,p,D)}{c_{Z_0}^2(Z_0,p,D)}}\right\} ,\\ Z_0\in Z_{sc}=f\left(N\right), N=1, \dots , 57, \dots ,\\ S_{Z_0}=A_{\hspace{0.17em}sg\hspace{0.17em}(Z_0-1)}\pm A_{sg\hspace{0.17em}{Z}_0}\pm A_{\hspace{0.17em}sg\hspace{0.17em}(Z_0+1)},\hspace{0.17em}\hspace{0.17em}{A}_{\hspace{0.17em}\hspace{0.17em}sg\hspace{0.17em}(atomic number)}=(\pm 1)/(n!k!m).\end{array}$$

(13)

From this formula it is clear that T_c depends on the lattice parameters of not only the superconducting element, but also neighboring elements with an atomic number one unit less and one unit greater. The lattice parameters of neighboring elements must be taken at the same temperature, pressure and radiation dose as those of the superconductor.

At the moment it is not clear whether the quantum selection rule Z_sc = f(N) should be written for all 57 elemental superconductors or whether there should be a different expression for selection by atomic numbers for high-pressure superconductors. An approximate expression for f(N) is shown in (1). The quantum rule on the atomic numbers of superconducting elements allows us to predict new elemental superconductors when the exact form of f(N) will be found. Of particular interest are transuranium elements with Z > 95. In (13) we put many dots for N after 57, which means that at N = 58 we should get Z for the new elemental superconductor.

The main problem we found was the lack of information about the lattice parameters of the elements at low temperatures. For correct use (13) it is also necessary to know the lattice parameters of the elements at high pressure from low to room temperature. It would be great if there was a database of such data, including information on the symmetry of crystals under pressure and at different temperatures. The data in [18] concern only room temperatures, except for hydrogen and inert gases, for which the lattice parameters are taken at low temperatures. There is no information at all about changes in the lattice parameters and symmetry of crystals of elemental superconductors under the influence of ionizing radiation, especially at low temperatures.