Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Superconducting Gaps in Pressurized Ruddlesden-Popper Nickelate La4Ni3O10-δ

Submitted:

04 March 2025

Posted:

05 March 2025

You are already at the latest version

Abstract
The experimental discovery of high-temperature superconductivity in Ruddlesden-Popper (RP) nickelates Lan+1NinO3n+1 (n = 2, 3, 4) under pressure, as well as the observation of a state with zero resistance at T ~10 K in thin films of (La,Pr)n+1NinO3n+1 (n = 2) at ambient pressure initiated a wide range of experimental and theoretical studies aimed at clarifying the nature of the occurrence of the superconducting state in RP nickelates. The upper critical field, Bc2(T), is one of two fundamental fields of any type II superconductor which can be used to extract some of the main parameters of a given superconductor. Recently, Peng et al (arXiv:2502.14410) reported in-plane, and out-of-plane temperature dependent upper critical field datasets measured at wide temperature ranges in La4Ni3O10-d single crystals pressurized at P = 48.6 GPa and P = 50.2 GPa. Here, the reported Bc2(T) data were analyzed, and it was found that the compressed nickelate La4Ni3O10-δ exhibits two-band s-wave superconductivity. Derived parameters showed that both gaps are almost isotropic. The larger gap has a moderate level of coupling strength (with a gap-to-transition temperature ratio 3.7 < 2ΔL/kBTc < 4.3). The smaller gap has the ratio of 1.0 < 2ΔS/kBTc < 1.1. Deduced ratios are in the same ballpark as those in ambient pressure MgB2.
Keywords: 
Ruddlesden-Popper nickelates
;  
compressed superconducting nickelates
;  
superconducting energy gap
;  
two-band superconductivity
;  
superconducting gap anisotropy
Subject: 
Physical Sciences  -   Condensed Matter Physics

I. Introduction

High-temperature superconductivity (HTS) in pressurized [1,2,3,4,5,6,7] and ambient pressure [8,9,10] Ruddlesden-Popper (RP) nickelates Lan+1NinO3n+1 (n = 2, …, 5) is a fascinating physical phenomenon whose nature remains unknown [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27].
One of the most recent achievements in the experimental studies of RP nickelates is the report by Peng et al. [28], who measured in-field temperature dependent resistance R T , P , B for two principal directions (along ab-plane and c-axis) in pressurized La4Ni3O10-δ over a wide temperature range and applying DC magnetic field. Peng et al. [28] defined the upper critical fields, B c 2 , a b T and B c 2 , c T , by utilizing 50% normal state resistance criterion for measured R T , P , B datasets. The derived B c 2 , a b T and B c 2 , c T datasets were analyzed [28] by the Werthamer- Helfand-Hohenberg (WHH) model [29,30].
Here, a different approach [31,32] has been applied to analyze temperature dependent upper critical field data, the following results were obtained:
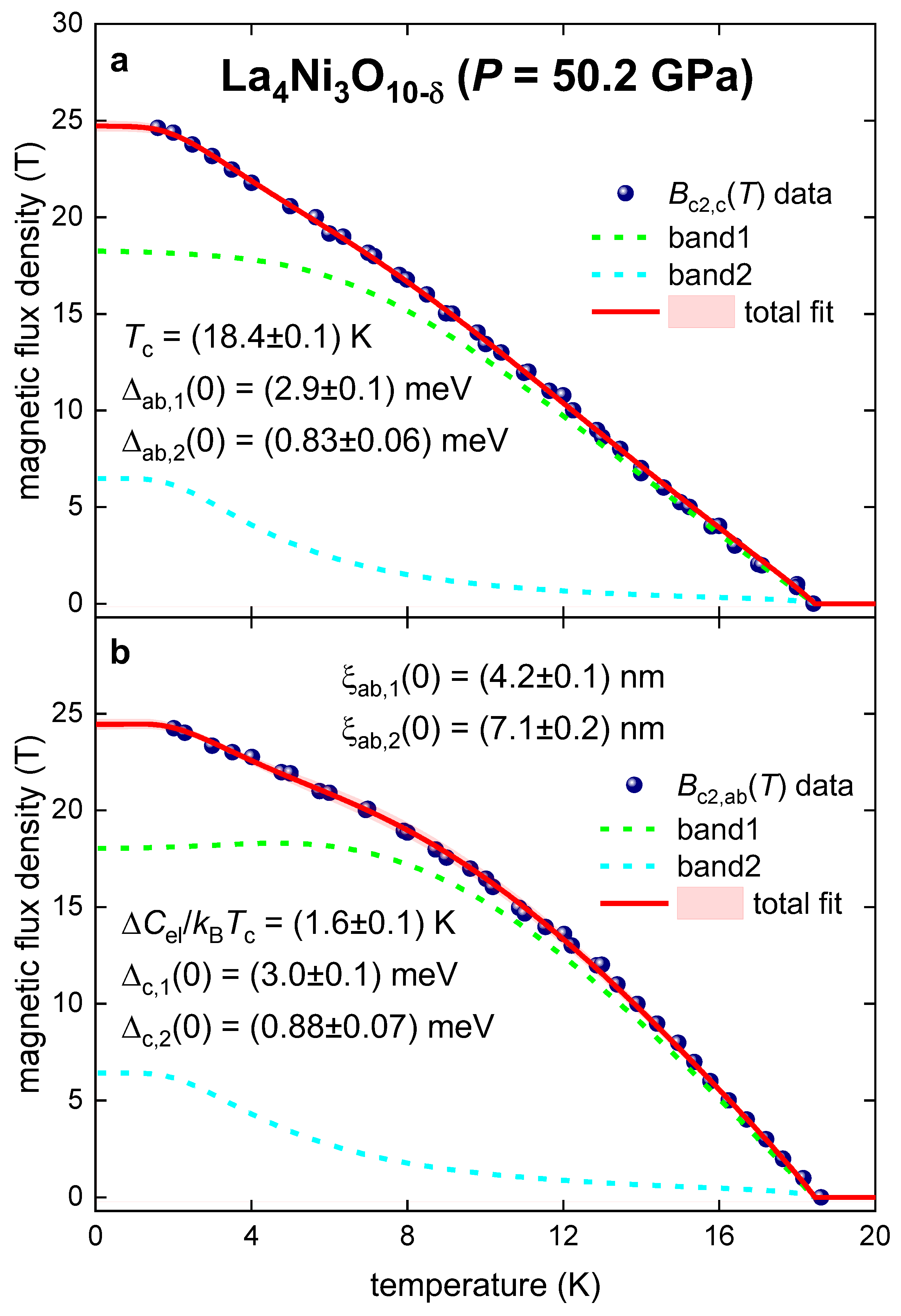
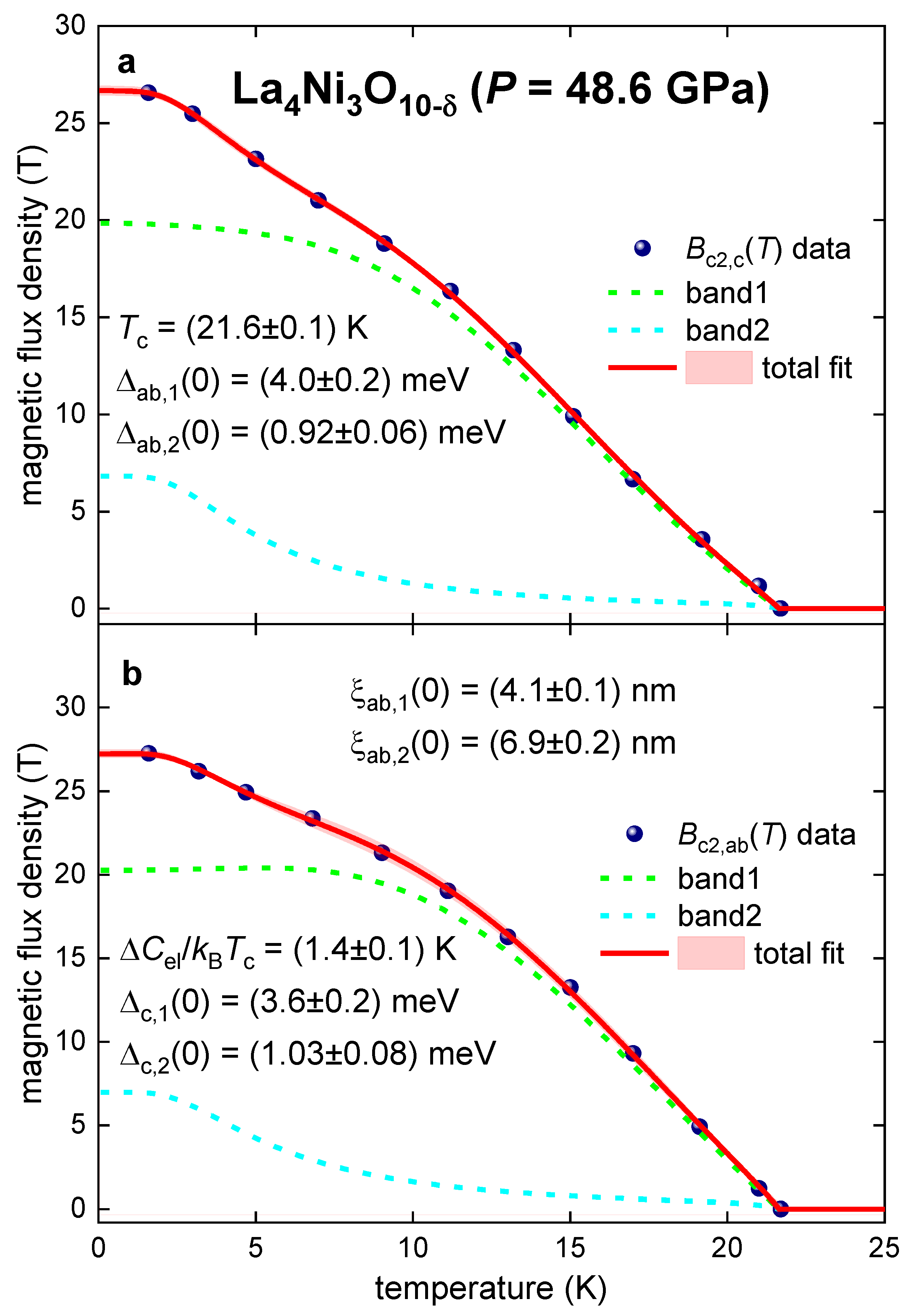
  • La4Ni3O10-δ is two-band s-wave superconductor;
  • Both superconducting gaps in La4Ni3O10-δ are practically isotropic;
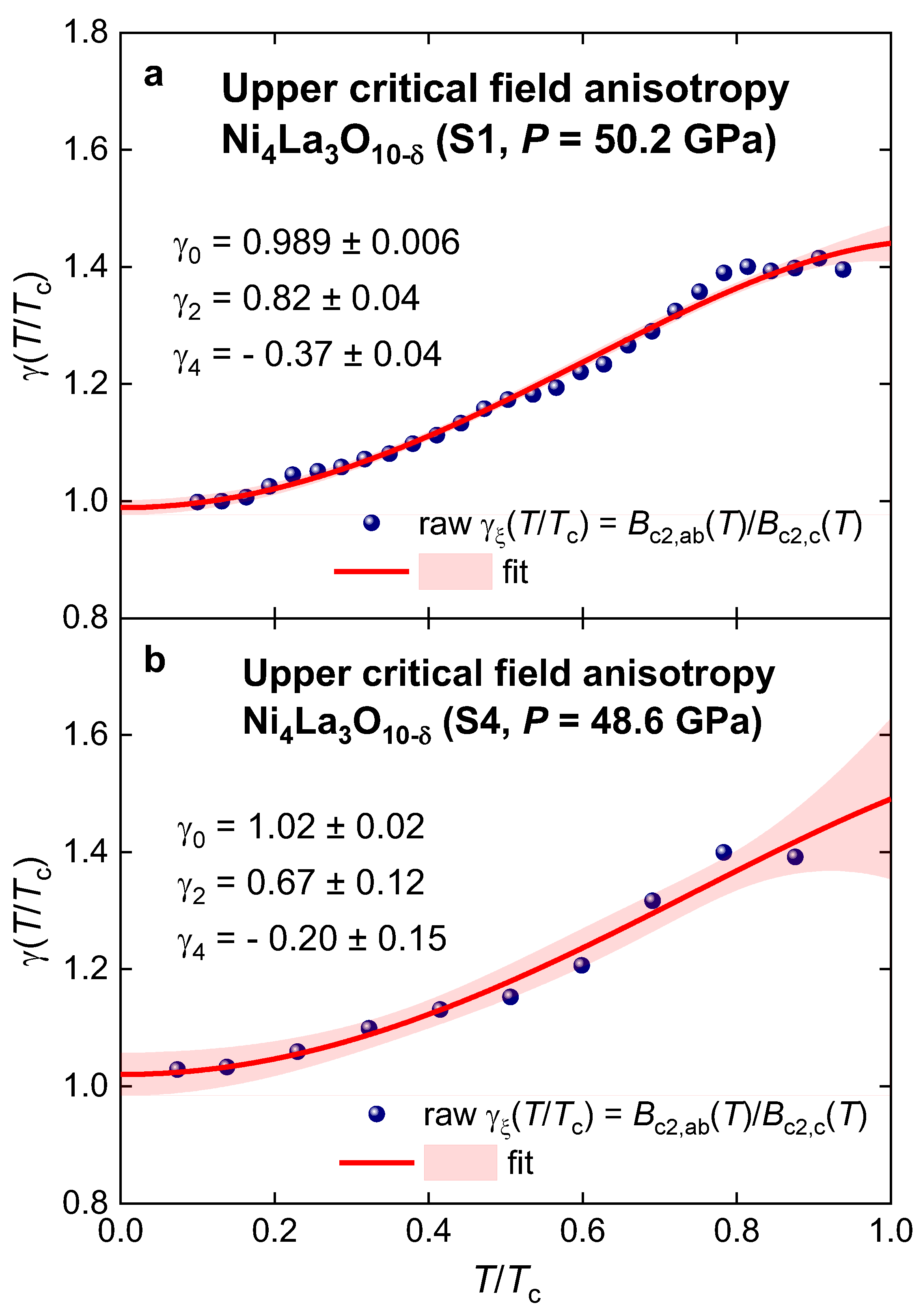
  • The largest anisotropy was revealed for the larger gap, for which the ratio of amplitudes is 0.90 ≤ Δ c , 1 0 Δ a b , 1 0 ≤ 1.03 );
  • Larger gap has 3.7 ≤ 2 Δ 1 0 k B T c ≤ 4.3 and smaller gap has 1.0 ≤ 2 Δ 2 0 k B T c ≤ 1.1 , which is similar to the 2 Δ 0 k B T c ratios in ambient pressure MgB2 [33].

II. Developed Model

The approach is based on the temperature-dependent parameter of the Ginzburg-Landau theory (GL):
κ T = λ T ξ T ，
where λ T is the London penetration depth, and ξ T is the coherence length. Eq. 1 can be used to rewrite the GL expression for the temperature-dependent upper critical field:
B c 2 T = ϕ 0 2 π ξ 2 T = ϕ 0 2 π × κ T λ T 2 ,
where ϕ 0 is the superconducting flux quantum. There is an exact analytical expression (within the framework of the Bardeen-Cooper-Schrieffer theory of superconductivity [34,35]) for the temperature-dependent London penetration depth in s-wave superconductors [34,35]:
λ T = λ 0 1 − 1 2 k B T ∫ 0 ∞ d ε c o s h 2 ε 2 + Δ 2 T 2 k B T ,
where k B is Boltzmann’s constant, and the amplitude of the temperature-dependent superconducting gap Δ T is given by [36,37]:
Δ T = Δ 0 × tan h π k B T c Δ 0 η Δ C e l γ T c T c T − 1 ,
where η = 2 / 3 for s-wave superconductors, γ is the Sommerfeld constant, and Δ C e l γ T c is the relative jump in the electronic heat at T c . There are several expressions [38,39,40,41] for the temperature dependent GL parameter κ T , from which in this study I used the expression given by Gor’kov [38] (which was explained by Jones et al. [39]):
T = k 0 × 1 − 0.2429 × T T c 2 + 0.0395 × T T c 4 .
Substituting Eqs. 3-5 into Eq. 2 yields the equation:
B c 2 T = ϕ 0 2 π ξ 2 0 1 − 0.2429 T T c 2 + 0.0395 T T c 4 2 1 − 1 2 k B T ∫ 0 ∞ d ε c o s h 2 ε 2 + Δ 2 T 2 k B T
which can be used to fit experimental B c 2 T datasets to deduce several fundamental parameters of the superconductor (for instance, T c , ξ 0 , Δ 0 , 2 Δ 0 k B T c and Δ C e l γ T c ) as free fitting parameters.
Eq. 6 was used to extract these parameters from the B c 2 T datasets in highly compressed H3S [31,42] (raw data reported by Drozdov et al. [43] and Mozaffari et al. [44]), magic-angle twisted bilayer graphene [45] (raw data reported by Cao et al. [46]), magic-angle twisted trilayer graphene [47] (raw data reported by Cao et al. [48]), and, by utilizing two-band model:
B c 2 , t o t a l T = B c 2 , b a n d 1 T + B c 2 , b a n d 2 T
in MgB2 single crystal [32] (raw data reported by Zehetmayer et al. [49]).
For anisotropic superconductors, the Eq. 6 is transformed in two equations:
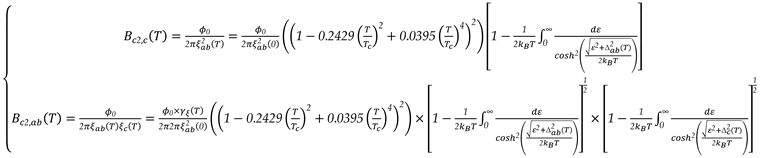
Preprints 151304 i001
where B c 2 , c T is out-of-plane upper critical field, and B c 2 , a b T is in-plane upper critical field, γ ξ T = ξ a b T ξ c T , and where the assumption of:
κ a b T κ a b 0 = κ c T κ c 0 = 1 − 0.2429 × T T c 2 + 0.0395 × T T c 4
has been made (this implies that the GL parameter κ T has the same temperature dependence for the in-plane and out-of-plane components, and which describe by Eq. 5).

III. Results and Discussion

It should be noted that Peng et al. [28] reported experimental values for the ratio:
γ ξ T = ξ a b T ξ c T = B c 2 , a b T B c 2 , c T ,
for both La4Ni3O10-δ samples (S1 and S4). In Figure 1, I have fitted the γ ξ T data reported [28] for two La4Ni3O10-δ single crystals to a simple function (having a form similar to Eq. 5):
γ T = γ 0 + γ 2 × T T c 2 + γ 4 × T T c 4 ,
where γ 0 , γ 2 , and γ 4 are free fitting parameters. The obtained functions γ T for Sample S1 and Sample S4 were substituted into Eq. 7.
The global fits of the data B c 2 , c T and B c 2 , a b T for Sample S1 and Sample S4 were performed to two-band model:
B c 2 , c , t o t a l T = B c 2 , c , b a n d 1 T + B c 2 , c , b a n d 2 T   B c 2 , a b , t o t a l T = B c 2 , a b , b a n d 1 T + B c 2 , a b , b a n d 2 T    
where the contribution of each band described by respectful equation in Eq. 7, and the global fits of the data B c 2 , c T and B c 2 , a b T to Eqs. 8,12 for Sample S1 and Sample S4 are shown in Figure 2 and Figure 3, respectively. Detailed information on performing global data fittings can be found elsewhere [47,50].
In global fits (to reduce the number of free-fitting parameters), I assumed that two bands have the same transition temperature (this is the same assumption that has been made for the fits to the WHH model by Peng et al. [28]):
T c , b a n d 1 = T c , b a n d 2 = T c
Also, I assumed that two bands have the same (averaged) jump in specific heat at the transition temperature:
Δ C e l γ T c b a n d 1 = Δ C e l γ T c b a n d 2 = Δ C e l γ T c .
The latter assumption (Eq. 14) was also implemented in other two-band models for superconductors [47,51,52,53], because, as a rule, raw datasets do not have enough measurement points to derive the Δ C e l γ T c values for each band from the fit to two-band models.
Derived parameters for two La4Ni3O10-δ single crystals are summarized in Table 1, from which one can see that larger gap (Band 1 in Table 1) has moderate level of coupling strength, while the coupling strength of the smaller gap (Band 2 in Table 1) has the ratio in the range of 2 Δ a b , 2 0 k B T c ≅ 2 Δ c , 2 0 k B T c ≅ 1.0 and these ratios are independent from pressure. The ratios for c-axis component of the gap are also remained unchanged vs pressure.

IV. Conclusions

In this study, recently reported B c 2 , c T and B c 2 , a b T data for La4Ni3O10-δ single crystals [28] have analyzed and showed that:
  • La4Ni3O10-δ is two-band s-wave superconductor;
  • Both superconducting gaps in La4Ni3O10-δ are practically isotropic, where the largest anisotropy was revealed for the larger gap, for which the ratio of amplitudes is 0.90 ≤ Δ c , 1 0 Δ a b , 1 0 ≤ 1.03 );
  • Larger gap has 3.7 ≤ 2 Δ 1 0 k B T c ≤ 4.3 and smaller gap has 1.0 ≤ 2 Δ 2 0 k B T c ≤ 1.1 , which is similar to the 2 Δ 0 k B T c ratios in ambient pressure MgB2 [33].

Acknowledgement

The work was carried out within the framework of the state assignment of the Ministry of Science and Higher Education of the Russian Federation for the IMP UB RAS.

Conflict of Interest

The author declared that he does not have any conflict of interest.

References

  1. H. Sun, M. H. Sun, M. Huo, X. Hu, J. Li, Z. Liu, Y. Han, L. Tang, Z. Mao, P. Yang, B. Wang, J. Cheng, D.-X. Yao, G.-M. Zhang, M. Wang, Signatures of superconductivity near 80 K in a nickelate under high pressure, Nature 621 (2023) 493–498. [CrossRef]
  2. E. Zhang, D. E. Zhang, D. Peng, Y. Zhu, L. Chen, B. Cui, X. Wang, W. Wang, Q. Zeng, J. Zhao, Bulk superconductivity in pressurized trilayer nickelate Pr4Ni3O10 single crystals, (2025). http://arxiv.org/abs/2501.17709.
  3. J. Li, D. J. Li, D. Peng, P. Ma, H. Zhang, Z. Xing, X. Huang, C. Huang, M. Huo, D. Hu, Z. Dong, X. Chen, T. Xie, H. Dong, H. Sun, Q. Zeng, H. Mao, M. Wang, Identification of the superconductivity in bilayer nickelate La$_3$Ni$_2$O$_7$ upon 100 GPa, (2024). http://arxiv.org/abs/2404.11369.
  4. Y. Zhu, D. Y. Zhu, D. Peng, E. Zhang, B. Pan, X. Chen, L. Chen, H. Ren, F. Liu, Y. Hao, N. Li, Z. Xing, F. Lan, J. Han, J. Wang, D. Jia, H. Wo, Y. Gu, Y. Gu, L. Ji, W. Wang, H. Gou, Y. Shen, T. Ying, X. Chen, W. Yang, H. Cao, C. Zheng, Q. Zeng, J. Guo, J. Zhao, Superconductivity in pressurized trilayer La4Ni3O10−δ single crystals, Nature 631 (2024) 531–536. [CrossRef]
  5. Y. Zhang, D. Y. Zhang, D. Su, Y. Huang, Z. Shan, H. Sun, M. Huo, K. Ye, J. Zhang, Z. Yang, Y. Xu, Y. Su, R. Li, M. Smidman, M. Wang, L. Jiao, H. Yuan, High-temperature superconductivity with zero resistance and strange-metal behaviour in La3Ni2O7−δ, Nat Phys (2024). [CrossRef]
  6. N. Wang, G. N. Wang, G. Wang, X. Shen, J. Hou, J. Luo, X. Ma, H. Yang, L. Shi, J. Dou, J. Feng, J. Yang, Y. Shi, Z. Ren, H. Ma, P. Yang, Z. Liu, Y. Liu, H. Zhang, X. Dong, Y. Wang, K. Jiang, J. Hu, S. Nagasaki, K. Kitagawa, S. Calder, J. Yan, J. Sun, B. Wang, R. Zhou, Y. Uwatoko, J. Cheng, Bulk high-temperature superconductivity in pressurized tetragonal La2PrNi2O7, Nature 634 (2024) 579–584. [CrossRef]
  7. Z. Dong, M. Z. Dong, M. Huo, J. Li, J. Li, P. Li, H. Sun, L. Gu, Y. Lu, M. Wang, Y. Wang, Z. Chen, Visualization of oxygen vacancies and self-doped ligand holes in La3Ni2O7−δ, Nature 630 (2024) 847–852. [CrossRef]
  8. E.K. Ko, Y. E.K. Ko, Y. Yu, Y. Liu, L. Bhatt, J. Li, V. Thampy, C.-T. Kuo, B.Y. Wang, Y. Lee, K. Lee, J.-S. Lee, B.H. Goodge, D.A. Muller, H.Y. Hwang, Signatures of ambient pressure superconductivity in thin film La3Ni2O7, Nature (2024). [CrossRef]
  9. G. Zhou, W. G. Zhou, W. Lv, H. Wang, Z. Nie, Y. Chen, Y. Li, H. Huang, W. Chen, Y. Sun, Q.-K. Xue, Z. Chen, Ambient-pressure superconductivity onset above 40 K in bilayer nickelate ultrathin films, (2024). http://arxiv.org/abs/2412.16622.
  10. Y. Liu, E.K. Y. Liu, E.K. Ko, Y. Tarn, L. Bhatt, B.H. Goodge, D.A. Muller, S. Raghu, Y. Yu, H.Y. Hwang, Superconductivity and normal-state transport in compressively strained La$_2$PrNi$_2$O$_7$ thin films, (2025). http://arxiv.org/abs/2501.08022.
  11. Q.N. Meier, J.B. Q.N. Meier, J.B. de Vaulx, F. Bernardini, A.S. Botana, X. Blase, V. Olevano, A. Cano, Preempted phonon-mediated superconductivity in the infinite-layer nickelates, ArXiv (2023). http://arxiv.org/abs/2309.05486.
  12. J. Zhan, Y. J. Zhan, Y. Gu, X. Wu, J. Hu, Cooperation between electron-phonon coupling and electronic interaction in bilayer nickelates La$_3$Ni$_2$O$_7$, (2024). http://arxiv.org/abs/2404.03638.
  13. D.K. Singh, G. D.K. Singh, G. Goyal, Y. Bang, Possible pairing states in the superconducting bilayer nickelate, (2024). http://arxiv.org/abs/2409.09321.
  14. H. Schlömer, U. H. Schlömer, U. Schollwöck, F. Grusdt, A. Bohrdt, Superconductivity in the pressurized nickelate La$_3$Ni$_2$O$_7$ in the vicinity of a BEC-BCS crossover, (2023). http://arxiv.org/abs/2311.03349.
  15. M. Kakoi, T. M. Kakoi, T. Kaneko, H. Sakakibara, M. Ochi, K. Kuroki, Pair correlations of the hybridized orbitals in a ladder model for the bilayer nickelate La$_3$Ni$_2$O$_7$, (2023). http://arxiv.org/abs/2312.04304.
  16. C. Xia, H. C. Xia, H. Liu, S. Zhou, H. Chen, Sensitive dependence of pairing symmetry on Ni-eg crystal field splitting in the nickelate superconductor La3Ni2O7, Nat Commun 16 (2025) 1054. [CrossRef]
  17. Y. Zhang, L.-F. Y. Zhang, L.-F. Lin, A. Moreo, T.A. Maier, E. Dagotto, Trends in electronic structures and s±-wave pairing for the rare-earth series in bilayer nickelate superconductor R3Ni2O7, Phys Rev B 108 (2023) 165141. [CrossRef]
  18. Q.-G. Yang, K.-Y. Q.-G. Yang, K.-Y. Jiang, D. Wang, H.-Y. Lu, Q.-H. Wang, Effective model and s± -wave superconductivity in trilayer nickelate a4Ni3O10, Phys Rev B 109 (2024) L220506. [CrossRef]
  19. Z. Ouyang, M. Z. Ouyang, M. Gao, Z.-Y. Lu, Absence of phonon-mediated superconductivity in La3Ni2O7 under pressure, ArXiv (2024). [CrossRef]
  20. C. Zhu, B. C. Zhu, B. Li, Y. Fan, C. Yin, J. Zhai, J. Cheng, S. Liu, Z. Shi, Magnetic phases and electron–phonon coupling in under pressure, Comput Mater Sci 250 (2025) 113676. [CrossRef]
  21. X. Zhou, W. X. Zhou, W. He, Z. Zhou, K. Ni, M. Huo, D. Hu, Y. Zhu, E. Zhang, Z. Jiang, S. Zhang, S. Su, J. Jiang, Y. Yan, Y. Wang, D. Shen, X. Liu, J. Zhao, M. Wang, M. Liu, Z. Du, D. Feng, Revealing nanoscale structural phase separation in La3Ni2O7 single crystal via scanning near-field optical microscopy, (2024). http://arxiv.org/abs/2410.06602.
  22. M. Shi, Y. M. Shi, Y. Li, Y. Wang, D. Peng, S. Yang, H. Li, K. Fan, K. Jiang, J. He, Q. Zeng, D. Song, B. Ge, Z. Xiang, Z. Wang, J. Ying, T. Wu, X. Chen, Absence of superconductivity and density-wave transition in ambient-pressure tetragonal La$_4$Ni$_3$O$_{10}$, (2025). http://arxiv.org/abs/2501.12647.
  23. L. Bhatt, A.Y. L. Bhatt, A.Y. Jiang, E.K. Ko, N. Schnitzer, G.A. Pan, D.F. Segedin, Y. Liu, Y. Yu, Y.-F. Zhao, E.A. Morales, C.M. Brooks, A.S. Botana, H.Y. Hwang, J.A. Mundy, D.A. Muller, B.H. Goodge, Resolving Structural Origins for Superconductivity in Strain-Engineered La$_3$Ni$_2$O$_7$ Thin Films, (2025). http://arxiv.org/abs/2501.08204.
  24. X. Yan, H. X. Yan, H. Zheng, Y. Li, H. Cao, D.P. Phelan, H. Zheng, Z. Zhang, H. Hong, G. Wang, Y. Liu, A. Bhattacharya, H. Zhou, D.D. Fong, Superconductivity in an ultrathin multilayer nickelate, Sci Adv 11 (2025). [CrossRef]
  25. M. Xu, S. M. Xu, S. Huyan, H. Wang, S.L. Bud’ko, X. Chen, X. Ke, J.F. Mitchell, P.C. Canfield, J. Li, W. Xie, Pressure-dependent “Insulator-Metal-Insulator” Behavior in Sr-doped La3Ni2O7, (2023). http://arxiv.org/abs/2312.14251.
  26. X. Chen, E.H.T. X. Chen, E.H.T. Poldi, S. Huyan, R. Chapai, H. Zheng, S.L. Budko, U. Welp, P.C. Canfield, R.J. Hemley, J.F. Mitchell, D. Phelan, Non-bulk Superconductivity in Pr4Ni3O10 Single Crystals Under Pressure, (2024). http://arxiv.org/abs/2410.10666.
  27. D.A. Shilenko, I. V. D.A. Shilenko, I. V. Leonov, Correlated electronic structure, orbital-selective behavior, and magnetic correlations in double-layer La3Ni2O7 under pressure, Phys Rev B 108 (2023) 125105. [CrossRef]
  28. D. Peng, Y. D. Peng, Y. Bian, Z. Xing, L. Chen, J. Cai, T. Luo, F. Lan, Y. Liu, Y. Zhu, E. Zhang, Z. Wang, Y. Sun, Y. Wang, X. Wang, C. Wang, Y. Yang, Y. Yang, H. Dong, H. Lou, Z. Zeng, Z. Zeng, M. Tian, J. Zhao, Q. Zeng, J. Zhang, H. Mao, Isotropic superconductivity in pressurized trilayer nickelate La4Ni3O10, (2025). http://arxiv.org/abs/2502.14410.
  29. E. Helfand, N.R. E. Helfand, N.R. Werthamer, Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. II, Physical Review 147 (1966) 288–294. [CrossRef]
  30. N.R. Werthamer, E. N.R. Werthamer, E. Helfand, P.C. Hohenberg, Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects, Physical Review 147 (1966) 295–302. [CrossRef]
  31. E.F. Talantsev, Classifying superconductivity in compressed H3S, Modern Physics Letters B 33 (2019) 1950195. [CrossRef]
  32. E.F. Talantsev, D-Wave Superconducting Gap Symmetry as a Model for Nb1−xMoxB2 (x = 0.25; 1.0) and WB2 Diborides, Symmetry (Basel) 15 (2023) 812. [CrossRef]
  33. C. Buzea, T. C. Buzea, T. Yamashita, Review of the superconducting properties of MgB 2, Supercond Sci Technol 14 (2001) R115–R146. [CrossRef]
  34. J. Bardeen, L.N. J. Bardeen, L.N. Cooper, J.R. Schrieffer, Theory of Superconductivity, Physical Review 108 (1957) 1175–1204. [CrossRef]
  35. C.P. Poole, H. C.P. Poole, H. Farach, R. Creswick, R. Prozorov, Superconductivity, 2nd ed., Academic Press, London, UK, 2007.
  36. F. Gross-Alltag, B.S. F. Gross-Alltag, B.S. Chandrasekhar, D. Einzel, P.J. Hirschfeld, K. Andres, London field penetration in heavy fermion superconductors, Zeitschrift Fr Physik B Condensed Matter 82 (1991) 243–255. [CrossRef]
  37. F. Gross, B.S. F. Gross, B.S. Chandrasekhar, D. Einzel, K. Andres, P.J. Hirschfeld, H.R. Ott, J. Beuers, Z. Fisk, J.L. Smith, Anomalous temperature dependence of the magnetic field penetration depth in superconducting UBe13, Zeitschrift Fr Physik B Condensed Matter 64 (1986) 175–188. [CrossRef]
  38. L. P. Gor’kov, The critical supercooling field in superconductivity theory., Sov Phys JETP 10 (1960) 593–599.
  39. Godeke, B. ten Haken, H.H.J. ten Kate, D.C. Larbalestier, A general scaling relation for the critical current density in Nb 3 Sn, Supercond Sci Technol 19 (2006) R100–R116. [CrossRef]
  40. L.T. Summers, M.W. L.T. Summers, M.W. Guinan, J.R. Miller, P.A. Hahn, A model for the prediction of Nb/sub 3/Sn critical current as a function of field, temperature, strain, and radiation damage, IEEE Trans Magn 27 (1991) 2041–2044. [CrossRef]
  41. C.K. JONES, J.K. C.K. JONES, J.K. HULM, B.S. CHANDRASEKHAR, Upper Critical Field of Solid Solution Alloys of the Transition Elements, Rev Mod Phys 36 (1964) 74–76. [CrossRef]
  42. E.F. Talantsev, Universal Fermi velocity in highly compressed hydride superconductors, Matter and Radiation at Extremes 7 (2022) 058403. [CrossRef]
  43. A.P. Drozdov, M.I. A.P. Drozdov, M.I. Eremets, I.A. Troyan, V. Ksenofontov, S.I. Shylin, Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system, Nature 525 (2015) 73–76. [CrossRef]
  44. S. Mozaffari, D. S. Mozaffari, D. Sun, V.S. Minkov, A.P. Drozdov, D. Knyazev, J.B. Betts, M. Einaga, K. Shimizu, M.I. Eremets, L. Balicas, F.F. Balakirev, Superconducting phase diagram of H3S under high magnetic fields, Nat Commun 10 (2019) 2522. [CrossRef]
  45. E.F. Talantsev, R.C. E.F. Talantsev, R.C. Mataira, W.P. Crump, Classifying superconductivity in Moiré graphene superlattices, Sci Rep 10 (2020) 212. [CrossRef]
  46. Y. Cao, V. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras, P. Jarillo-Herrero, Unconventional superconductivity in magic-angle graphene superlattices, Nature 556 (2018) 43–50. [CrossRef]
  47. E.F. Talantsev, Thermodynamic parameters of atomically thin superconductors derived from the upper critical field, Supercond Sci Technol 35 (2022) 084007. [CrossRef]
  48. Y. Cao, J.M. Y. Cao, J.M. Park, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero, Pauli-limit violation and re-entrant superconductivity in moiré graphene, Nature 595 (2021) 526–531. [CrossRef]
  49. M. Zehetmayer, M. M. Zehetmayer, M. Eisterer, J. Jun, S.M. Kazakov, J. Karpinski, A. Wisniewski, H.W. Weber, Mixed-state properties of superconducting MgB2 single crystals, Phys Rev B 66 (2002) 052505. [CrossRef]
  50. E.F. Talantsev, Quantifying interaction mechanism in infinite layer nickelate superconductors, J Appl Phys 134 (2023). [CrossRef]
  51. E. Talantsev, W.P. E. Talantsev, W.P. Crump, J.L. Tallon, Thermodynamic Parameters of Single- or Multi-Band Superconductors Derived from Self-Field Critical Currents, Ann Phys 529 (2017) 1–18. [CrossRef]
  52. E.F. Talantsev, W.P. E.F. Talantsev, W.P. Crump, J.L. Tallon, Two-band induced superconductivity in single-layer graphene and topological insulator bismuth selenide, Supercond Sci Technol 31 (2018). [CrossRef]
  53. E.F. Talantsev, W.P. E.F. Talantsev, W.P. Crump, J.O. Island, Y. Xing, Y. Sun, J. Wang, J.L. Tallon, On the origin of critical temperature enhancement in atomically thin superconductors, 2d Mater 4 (2017). [CrossRef]
Preprints 151304 g001
Figure 1. Experimental γ ξ T = B c 2 , a b T B c 2 , c T data for La4Ni3O10-δ single crystals reported by Peng et al. [28]. (a) Sample S1 compressed at P = 50.2   G P a and data fit to Eq. 10. (b) Sample S1 compressed at P = 48.6   G P a and data fit to Eq. 10. Fits quality (R-square COD) is (a) 0.990 and (b) 0.974. 95% confidence bands are shown by pink shadow areas.
Figure 1. Experimental γ ξ T = B c 2 , a b T B c 2 , c T data for La4Ni3O10-δ single crystals reported by Peng et al. [28]. (a) Sample S1 compressed at P = 50.2   G P a and data fit to Eq. 10. (b) Sample S1 compressed at P = 48.6   G P a and data fit to Eq. 10. Fits quality (R-square COD) is (a) 0.990 and (b) 0.974. 95% confidence bands are shown by pink shadow areas.
Preprints 151304 g001
Preprints 151304 g002
Figure 2. (a) B c 2 , c T and (b) B c 2 , a b T datasets and global fit to two-band anisotropic model (Eqs. 8-14) for the La4Ni3O10-δ single crystals compressed at P = 50.2   G P a (Sample S1). Raw B c 2 , c T and B c 2 , a b T data reported by Peng et al. [28]. Derived parameters are shown in panels (a) and (b). Deduced gap-to-transition temperature ratios are: 2 Δ a b , 1 0 k B T c = 3.7 ± 0.1 ; 2 Δ a b , 2 0 k B T c = 1.0 ± 0.1 ; 2 Δ c , 1 0 k B T c = 3.8 ± 0.1 ; 2 Δ a b , 2 0 k B T c = 1.1 ± 0.1 . Goodness of fit: (a) R = 0.9995 and (b) R = 0.9994. 95% confidence bands are shown by pink shadow areas.
Figure 2. (a) B c 2 , c T and (b) B c 2 , a b T datasets and global fit to two-band anisotropic model (Eqs. 8-14) for the La4Ni3O10-δ single crystals compressed at P = 50.2   G P a (Sample S1). Raw B c 2 , c T and B c 2 , a b T data reported by Peng et al. [28]. Derived parameters are shown in panels (a) and (b). Deduced gap-to-transition temperature ratios are: 2 Δ a b , 1 0 k B T c = 3.7 ± 0.1 ; 2 Δ a b , 2 0 k B T c = 1.0 ± 0.1 ; 2 Δ c , 1 0 k B T c = 3.8 ± 0.1 ; 2 Δ a b , 2 0 k B T c = 1.1 ± 0.1 . Goodness of fit: (a) R = 0.9995 and (b) R = 0.9994. 95% confidence bands are shown by pink shadow areas.
Preprints 151304 g002
Preprints 151304 g003
Figure 3. (a) B c 2 , c T and (b) B c 2 , a b T datasets and global fit to two-band anisotropic model (Eqs. 8-14) for the La4Ni3O10-δ single crystals compressed at P = 48.6   G P a (Sample S4). Raw B c 2 , c T and B c 2 , a b T data reported by Peng et al. [28]. Derived parameters are shown in panels (a) and (b). Deduced gap-to-transition temperature ratios are: 2 Δ a b , 1 0 k B T c = 4.3 ± 0.3 ; 2 Δ a b , 2 0 k B T c = 1.0 ± 0.1 ; 2 Δ c , 1 0 k B T c = 3.9 ± 0.2 ; 2 Δ a b , 2 0 k B T c = 1.1 ± 0.1 . Goodness of fit is R = 0.9998 for both panels. 95% confidence bands are shown by pink shadow areas.
Figure 3. (a) B c 2 , c T and (b) B c 2 , a b T datasets and global fit to two-band anisotropic model (Eqs. 8-14) for the La4Ni3O10-δ single crystals compressed at P = 48.6   G P a (Sample S4). Raw B c 2 , c T and B c 2 , a b T data reported by Peng et al. [28]. Derived parameters are shown in panels (a) and (b). Deduced gap-to-transition temperature ratios are: 2 Δ a b , 1 0 k B T c = 4.3 ± 0.3 ; 2 Δ a b , 2 0 k B T c = 1.0 ± 0.1 ; 2 Δ c , 1 0 k B T c = 3.9 ± 0.2 ; 2 Δ a b , 2 0 k B T c = 1.1 ± 0.1 . Goodness of fit is R = 0.9998 for both panels. 95% confidence bands are shown by pink shadow areas.
Preprints 151304 g003
Table 1. Derived parameters for two La4Ni3O10-δ single crystals (Figs. 2,3 and Eqs. 4,5,8-14) for raw B c 2 , c T and B c 2 , a b T data reported by Peng et al. [28].
Table 1. Derived parameters for two La4Ni3O10-δ single crystals (Figs. 2,3 and Eqs. 4,5,8-14) for raw B c 2 , c T and B c 2 , a b T data reported by Peng et al. [28].
T c   K Δ C e l γ T c ξ a b 0   n m 2 Δ a b 0 k B T c 2 Δ c 0 k B T c
La 4 Ni 3 O 10 − δ   S 1 P = 50.2   G P a 18.4 ± 0.1 1.6 ± 0.1 B a n d   1 4.2 ± 0.1 3.7 ± 0.1 3.8 ± 0.1
B a n d   2 7.1 ± 0.2 1.0 ± 0.1 1.1 ± 0.1
La 4 Ni 3 O 10 − δ   S 4 P = 48.6   G P a 21.6 ± 0.1 1.4 ± 0.1 B a n d   1 4.1 ± 0.1 4.3 ± 0.3 3.9 ± 0.2
B a n d   2 6.9 ± 0.2 1.0 ± 0.1 1.1 ± 0.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated