Submitted:
28 July 2025
Posted:
30 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Participants
| Characteristic | Mean ± SD |
|---|---|
| Age (years) | 37,27 ± 6,55 |
| ITRA (points) | 676 ± 101 |
| Weight (kg) | 70,89 ± 7,05 |
| Height (m) | 176,06 ± 5,96 |
| BMI (kg·m−2) | 22,85 ± 1,63 |
| vV̇O2max (m·s−1) | 4,85 ± 0,44 |
| 70% vV̇O2max (m·s−1) | 3,33 ± 0,31 |
| HRmax (bpm) | 171,47 ± 10,31 |
| V̇O2max (mL·min¯1) | 4314,87 ± 476,46 |
| V̇O2max (mL·kg¯1·min¯1) | 61,16 ± 6,89 |
| RPOmax (W) | 368,07 ± 38,04 |
| RPOmax (W·kg¯1) | 5,20 ± 0,32 |
2.2. Statistical Analysis
3. Results
3.1. Descriptive and Difference Analysis
3.2. Correlation Analysis
4. Discussion
4.1. Limitations
4.2. Practical Considerations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VO2 | Oxygen uptake |
| VCO2 | Carbon dioxide output |
| RQ | Respiratory quotient |
| HR | Heart rate |
| EE | Energy expenditure |
| EEmin | Energy expenditure per minute |
| RPO | Running power output |
| RPE | Rating of perceived exertion |
| BMI | Body mass index |
| vVO2max | Velocity at maximal oxygen uptake |
| VO2max | Maximal oxygen uptake |
| ITRA | International Trail Running Association |
References
- Scheer, V. Participation Trends of Ultra Endurance Events. Sports Med. Arthrosc. 2019, 27(1), 3–7. [Google Scholar] [CrossRef]
- Waal, Simon J. ; Gomez-Ezeiza, Josu ; Venter, R. Physiological Indicators of Trail Running Performance: A Systematic Review. Int. J. Sports Physiol. Perform. 2024, 16 (3), 325–332. [CrossRef]
- Vernillo, G.; Giandolini, M.; Edwards, W. B.; Morin, J. B.; Samozino, P.; Horvais, N.; Millet, G. Y. Biomechanics and Physiology of Uphill and Downhill Running. Sport. Med. 2017, 47(4), 615–629. [Google Scholar] [CrossRef]
- Boshielo, P. M.; Jansen van Rensburg, A.; Viljoen, C.; Botha, T.; de Villiers, C. E.; Ramagole, D.; Seyani, L.; Janse van Rensburg, D. C. Illness Is More Prevalent than Injury in Trail Runners Participating in a Mountainous Ultra Trail Race. Phys. Sportsmed. 2024, 00(00), 1–9. [Google Scholar] [CrossRef]
- Vernillo, G.; Savoldelli, A.; Zignoli, A.; Skafidas, S.; Fornasiero, A.; Torre, A. La; Bortolan, L.; Pellegrini, B.; Schena, F. Energy Cost and Kinematics of Level, Uphill and Downhill Running: Fatigue-Induced Changes after a Mountain Ultramarathon. J. Sports Sci. 2015, 33(19), 1998–2005. [Google Scholar] [CrossRef]
- Abbiss, C. R.; Laursen, P. Describing and Understanding Pacing Strategies. Sport. Med. 2008, 38(3), 239–252.
- Zimmermann, P.; Müller, N.; Schöffl, V.; Ehrlich, B.; Moser, O.; Schöffl, I. The Energetic Costs of Uphill Locomotion in Trail Running: Physiological Consequences Due to Uphill Locomotion Pattern—A Feasibility Study. Life 2022, 12(12), 3–6. [Google Scholar] [CrossRef] [PubMed]
- Burke, L. M.; Jones, A. M.; Jeukendrup, A. E.; Mooses, M. Contemporary Nutrition Strategies to Optimize Performance in Distance Runners and Race Walkers. Int. J. Sport Nutr. Exerc. Metab. 2019, 29(2), 117–129. [Google Scholar] [CrossRef]
- Clemente-Suárez, V. J. Psychophysiological Response and Energy Balance during a 14-h Ultraendurance Mountain Running Event. Appl. Physiol. Nutr. Metab. 2015, 40(3), 269–273. [Google Scholar] [CrossRef]
- Spurr, G. B.; Prentice, A. M.; Murgatroyd, P. R.; Goldberg, G. R.; Reina, J. C.; Christman, N. T. Energy Expenditure from Minute-by-Minute Heart-Rate Recording: Comparison with Indirect Calorimetry. Am. J. Clin. Nutr. 1988, 48(3), 552–559. [Google Scholar] [CrossRef]
- Booyens, J.; Hervey, G. R. The Pulse Rate As a Means of Measuring Metabolic Rate in Man. Can. J. Biochem. Physiol. 1960, 38(1), 1301–1309. [Google Scholar] [CrossRef]
- Achten, J.; Jeukendrup, A. E. Heart Rate Monitoring: Applications and Limitations. Sport. Med. 2003, 33(7), 517–538. [Google Scholar] [CrossRef]
- Leonard, W. R. Laboratory and Field Methods for Measuring Human Energy Expenditure. Am. J. Hum. Biol. 2012, 24(3), 372–384. [Google Scholar] [CrossRef]
- Nobuco, Hongu, Barron J. Orr, Denise J Roe, Rebecca G. Reed, S. B. G. Global Positioning System Watches for Estimating Energy Expenditure. J. strength Cond. Res. 2013, 1, 3216–3220.
- Mejer, G.; Westerterp, K. R.; Koper, H. Assessment of Energy Expenditure by Recording Heart Rate and Body Acceleration. Med. Sci. Sports Exerc. 1989, 21(3), 343–347. [Google Scholar] [CrossRef]
- Murakami, H.; Kawakami, R.; Nakae, S.; Nakata, Y.; Ishikawa-Takata, K.; Tanaka, S.; Miyachi, M. Accuracy of Wearable Devices for Estimating Total Energy Expenditure: Comparisonwith Metabolic Chamber and Doubly Labeledwater Method. JAMA Intern. Med. 2016, 176(5), 702–703. [Google Scholar] [CrossRef] [PubMed]
- García-Pinillos, F.; Roche-Seruendo, L. E.; Marcén-Cinca, N.; Marco-Contreras, L. A.; Latorre-Román, P. A. Absolute Reliability and Concurrent Validity of the Stryd System for the Assessment of Running Stride Kinematics at Different Velocities. J. Strength Cond. Res. 2018, No. May, 1. [Google Scholar] [CrossRef]
- Perrotin, N.; Gardan, N.; Lesprillier, A.; Le Goff, C.; Seigneur, J. M.; Abdi, E.; Sanudo, B.; Taiar, R. Biomechanics of Trail Running Performance: Quantification of Spatio-Temporal Parameters by Using Low Cost Sensors in Ecological Conditions. Appl. Sci. 2021, 11(5), 1–14. [Google Scholar] [CrossRef]
- Navalta, J. W.; Montes, J.; Bodell, N. G.; Aguilar, C. D.; Radzak, K.; Manning, J. W.; Debeliso, M. Reliability of Trail Walking and Running Tasks Using the Stryd Power Meter. Int. J. Sports Med. 2019, 40(8), 498–502. [Google Scholar] [CrossRef] [PubMed]
- Van Hooren, B.; Goudsmit, J.; Restrepo, J.; Vos, S. Real-Time Feedback by Wearables in Running: Current Approaches, Challenges and Suggestions for Improvements. J. Sports Sci. 2020, 38(2), 214–230. [Google Scholar] [CrossRef]
- Margaria, R.; Cerretelli, P.; Aghemo, P.; Sassi, G. Energy Cost of Running. J. Appl. Physiol. 1963, 18(2), 367–370. [Google Scholar] [CrossRef]
- Minetti, A. E.; Moia, C.; Roi, G. S.; Susta, D.; Ferretti, G. Energy Cost of Walking and Running at Extreme Uphill and Downhill Slopes. J. Appl. Physiol. 2002, 93(3), 1039–1046. [Google Scholar] [CrossRef] [PubMed]
- Cerezuela-Espejo, V.; Hernández-Belmonte, A.; Courel-Ibáñez, J.; Conesa-Ros, E.; Mora-Rodríguez, R.; Pallarés, J. G. Are We Ready to Measure Running Power? Eur. J. Sport Sci. 2021, 21(3), 341–350. [Google Scholar] [CrossRef] [PubMed]
- Barnes, K. R.; Kilding, A. E. Running Economy: Measurement, Norms, and Determining Factors. Sport. Med. - Open 2015, 1 (8), 1–15. [CrossRef]
- McKay, A. K. A.; Stellingwerff, T.; Smith, E. S.; Martin, D. T.; Mujika, I.; Goosey-Tolfrey, V. L.; Sheppard, J.; Burke, L. M. Defining Training and Performance Caliber: A Participant Classification Framework. Int. J. Sports Physiol. Perform. 2022, 17(2), 317–331. [Google Scholar] [CrossRef] [PubMed]
- Björklund, G.; Swarén, M.; Born, D. P.; Stöggl, T. Biomechanical Adaptations and Performance Indicators in Short Trail Running. Front. Physiol. 2019, 10(506), 1–10. [Google Scholar] [CrossRef]
- Imbach, F.; Candau, R.; Chailan, R.; Perrey, S. Validity of the Stryd Power Meter in Measuring Running Parameters at Submaximal Speeds. Sports 2020, 8(7), 1–19. [Google Scholar] [CrossRef] [PubMed]
- Noakes, T. D.; Myburgh, K. H.; Schall, R. Peak Treadmill Running Velocity during the Vo2 Max Test Predicts Running Performance. J. Sports Sci. 1990, 8(1), 35–45. [Google Scholar] [CrossRef]
- Padulo, J.; Powell, D.; Milia, R.; Ardigò, L. P. A Paradigm of Uphill Running. PLoS One 2013, 8(7), 1–9. [Google Scholar] [CrossRef]
- Billat, L. V; Koralsztein, J. P. Significance of the Velocity at VO2max and Time to Exhaustion at This Velocity. Sports Med. 1996, 22(2), 90–108. [Google Scholar] [CrossRef]
- Beaver, W. L.; Wasserman, K.; Whipp, B. J. A New Method for Detecting Anaerobic Threshold by Gas Exchange. J Appl Physiol 1986, 60(6), 2020–2027. [Google Scholar] [CrossRef]
- Weir, J. B. d. V. New Methods for Calculating Metabolic Rate with Special Reference to Protein Metabolism. J. Physiol. 1949, 109 (1–2), 1–9. [CrossRef]
- Foster, C.; Florhaug, J. A.; Franklin, J.; Gottschall, L.; Hrovatina, L. A.; Suzanne, P.; Doleshal, P.; Dodge, C. A New Approach to Monitoring Exercise Training. J. Strength Cond. Res. 2001, 15(1), 109–115. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates, P; 1988.
- Lalanne, C.; Mesbah, M. Measures of Association, Comparisons of Means and Proportions for Two Samples or More. In Biostatistics and Computer-based Analysis of Health Data using Stata; 2016; pp 25–57. [CrossRef]
- Padulo, J.; Annino, G.; Smith, L.; Migliaccio, G. M.; Camino, R.; Tihanyi, J.; Dottavio, S. Uphill Running at Iso-Efficiency Speed. Int. J. Sports Med. 2012, 33(10), 819–823. [Google Scholar] [CrossRef]
- Margaria, R. Positive and Negative Work Performances and Their Efficiencies in Human Locomotion. Int. Zeitschrift für Angew. Physiol. Einschließlich Arbeitsphysiologie 1968, 25 (4), 339–351. [CrossRef]
- Wall-Scheffler, C. M.; Chumanov, E.; Steudel-Numbers, K.; Heiderscheit, B. Electromyography Activity across Gait and Incline: The Impact of Muscular Activity on Human Morphology. Am. J. Phys. Anthropol. 2010, 143(4), 601–611. [Google Scholar] [CrossRef] [PubMed]
- Olesen, H. L. Accumulated Oxygen Deficit Increases with Inclination of Uphill Running. J. Appl. Physiol. 1992, 73(3), 1130–1134. [Google Scholar] [CrossRef]
- Saito, A.; Tomita, A.; Ando, R.; Watanabe, K.; Akima, H. Muscle Synergies Are Consistent across Level and Uphill Treadmill Running. Sci. Rep. 2018, 8(1), 1–10. [Google Scholar] [CrossRef] [PubMed]
- Breiner, T. J.; Ortiz, A. L. R.; Kram, R. Level, Uphill and Downhill Running Economy Values Are Strongly Inter-Correlated. Eur. J. Appl. Physiol. 2019, 119(1), 257–264. [Google Scholar] [CrossRef]
- Jaén-Carrillo, D.; Roche-Seruendo, L. E.; Cartón-Llorente, A.; Ramírez-Campillo, R.; García-Pinillos, F. Mechanical Power in Endurance Running: A Scoping Review on Sensors for Power Output Estimation during Running. Sensors (Switzerland) 2020, 20(22), 1–20. [Google Scholar] [CrossRef] [PubMed]
- Brooks, G. A.; Mercier, J. Balance of Carbohydrate and Lipid Utilization during Exercise: The “crossover” Concept. J. Appl. Physiol. 1994, 76(6), 2253–2261. [Google Scholar] [CrossRef]
- G. A. Cavagna, M. K. Mechanical Work and Efficiency in Level Walkink and Running. J.Physiol. 1977, 268, 467–481.
- Murphy, M. P. How Mitochondria Produce Reactive Oxygen Species. Biochem. J. 2009, 417(1), 1–13. [Google Scholar] [CrossRef]
- Plotkin, D. L.; Roberts, M. D.; Haun, C. T.; Schoenfeld, B. J. Muscle Fiber Type Transitions with Exercise Training: Shifting Perspectives. Sports 2021, 9(9), 1–11. [Google Scholar] [CrossRef]
- Bontemps, B.; Vercruyssen, F.; Gruet, M.; Louis, J. Downhill Running: What Are The Effects and How Can We Adapt? Sport. Med. 2020, 50(12), 2083–2110. [Google Scholar] [CrossRef]
- Snyder, K. L.; Kram, R.; Gottschall, J. S. The Role of Elastic Energy Storage and Recovery in Downhill and Uphill Running. J. Exp. Biol. 2012, 215(13), 2283–2287. [Google Scholar] [CrossRef]
- Chen, T. C.; Nosaka, K.; Tu, J. H. Changes in Running Economy Following Downhill Running. J. Sports Sci. 2007, 25(1), 55–63. [Google Scholar] [CrossRef] [PubMed]
- Halson, S. L. Monitoring Training Load to Understand Fatigue in Athletes. Sport. Med. 2014, 44, 139–147. [Google Scholar] [CrossRef]
- Hills, A. P.; Mokhtar, N.; Byrne, N. M. Assessment of Physical Activity and Energy Expenditure: An Overview of Objective Measures. Front. Nutr. 2014, 1 (June), 1–16. [Google Scholar] [CrossRef] [PubMed]
- Riddick, R. C.; Kuo, A. D. Mechanical Work Accounts for Most of the Energetic Cost in Human Running. Sci. Rep. 2022, 12(1), 1–11. [Google Scholar] [CrossRef] [PubMed]
- Wilson, R. P.; Börger, L.; Holton, M. D.; Scantlebury, D. M.; Gómez-Laich, A.; Quintana, F.; Rosell, F.; Graf, P. M.; Williams, H.; Gunner, R.; Hopkins, L.; Marks, N.; Geraldi, N. R.; Duarte, C. M.; Scott, R.; Strano, M. S.; Robotka, H.; Eizaguirre, C.; Fahlman, A.; Shepard, E. L. C. Estimates for Energy Expenditure in Free-Living Animals Using Acceleration Proxies: A Reappraisal. J. Anim. Ecol. 2020, 89(1), 161–172. [Google Scholar] [CrossRef]
- Sutton, G. J.; Botha, J. A.; Speakman, J. R.; Arnould, J. P. Y. Validating Accelerometry-Derived Proxies of Energy Expenditure Using the Doubly Labelled Water Method in the Smallest Penguin Species. Biol. Open 2021, 10(4), 1–10. [Google Scholar] [CrossRef]
- Berzosa, C.; Comeras-Chueca, C.; Bascuas, P. J.; Gutiérrez, H.; Bataller-Cervero, A. V. Assessing Trail Running Biomechanics: A Comparative Analysis of the Reliability of StrydTM and GARMINRP Wearable Devices. Sensors 2024, 24(11), 1–18. [Google Scholar] [CrossRef]
- García-Pinillos, F.; Roche-Seruendo, L. E.; Marcén-Cinca, N.; Marco-Contreras, L. A.; Latorre-Román, P. A. Absolute Reliability and Concurrent Validity of the Stryd System for the Assessment of Running Stride Kinematics at Different Velocities. J. Strength Cond. Res. 2018, No. May, 1. [Google Scholar] [CrossRef]
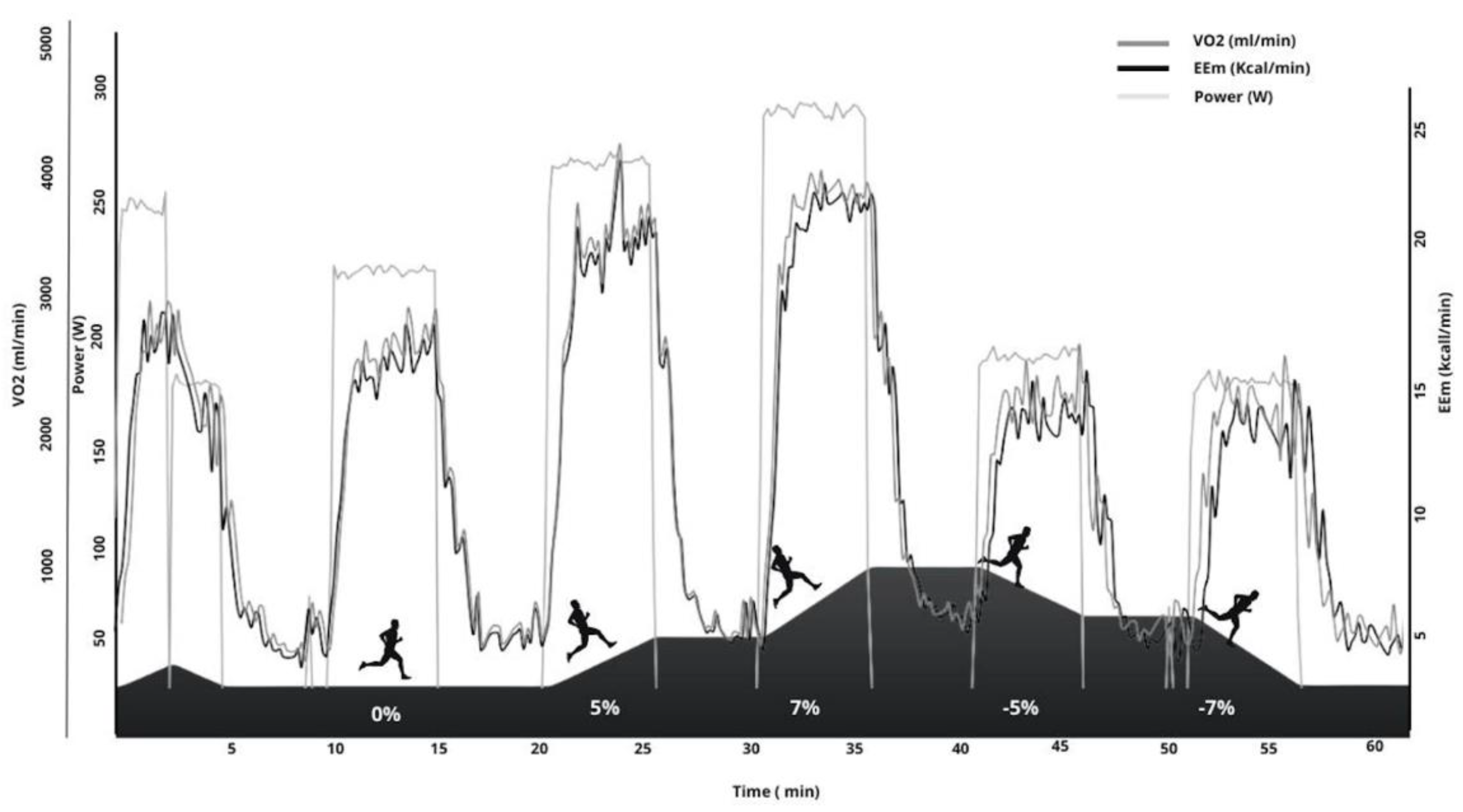
| Slope | |||||
|---|---|---|---|---|---|
| -7% | -5% | 0% | 5% | 7% | |
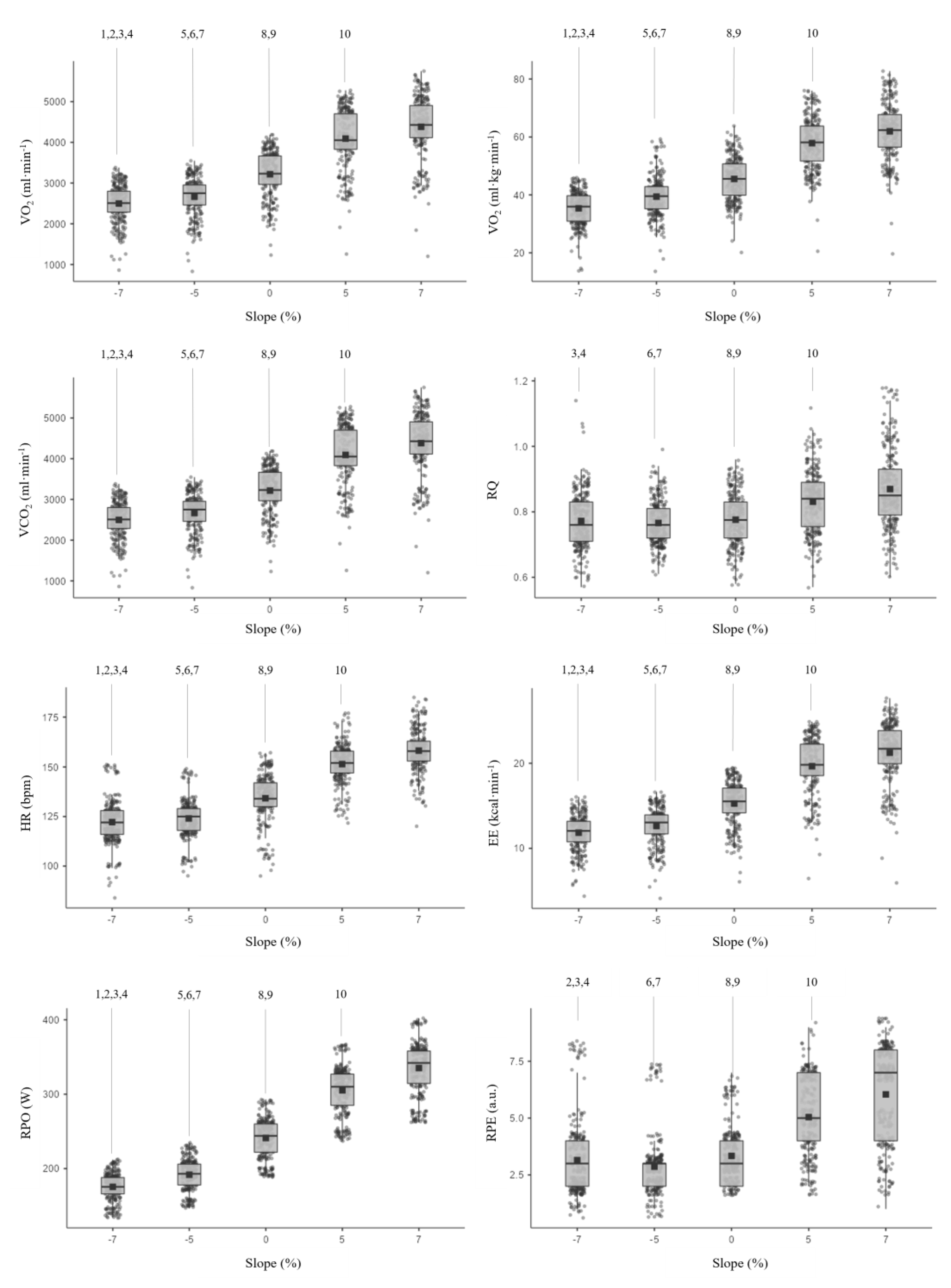
| VO2 (mL·min−1) | 2521,4 ± 397,3 | 2682,8 ± 425,4 | 3233,7 ± 525,4 | 4111,6 ± 662,4 | 4390,2 ± 694,2 |
| VO2 (mL·min−1·kg−1) | 35,66 ± 4,89 | 37,91 ± 5,15 | 45,75 ± 6,85 | 58,12 ± 8,15 | 62,09 ± 8,87 |
| VCO2 (mL·min−1) | 1919,1 ± 290,9 | 2031,9 ± 283,6 | 2478,0 ± 372,9 | 3360,6 ± 470,8 | 3772,2 ± 569,9 |
| RQ | 0,77 ± 0,08 | 0,76 ± 0,06 | 0,77 ± 0,08 | 0,82 ± 0,09 | 0,87 ± 0,11 |
| HR (bpm) | 122,5 ± 11,0 | 124,3 ± 9,7 | 134,3 ± 11,7 | 151,6 ± 8,8 | 158,5 ± 9,4 |
| EE (kcal·min−1) | 11,9 ± 1,8 | 12,7 ± 1,9 | 15,3 ± 2,4 | 19,7 ± 3,0 | 21,3 ± 3,1 |
| RPO (W) | 175,9 ± 18,9 | 192,0 ± 21,3 | 242,3 ± 26,9 | 305,7 ± 32,5 | 335,1 ± 35,7 |
| a.u.: arbitrary units; VO2 (mL·min−1): oxygen uptake; VO2 (mL·min−1·kg−1): relative oxygen uptake; VCO2 (mL·min−1): carbon dioxide; RQ: respiratory quotient; HR (bpm): heart rate; EE(kcal·min−1): energy expenditure minute; RPO (W): running power output; RPE: rate of perceived exertion. | |||||
| Data Analysis | VO2(ml/min) | VCO2 (ml/min) | PO (W) | EE (kcal/min) | |
|---|---|---|---|---|---|
| All data included | VO2 (mL·min−1) | - | |||
| VCO2 (mL·min−1) | 0.929*** | - | |||
| PO (W) | 0.904*** | 0.910*** | - | ||
| EE (kcal·min−1) | 0.997*** | 0.953*** | 0.916*** | - | |
| -7% slope | VO2 (mL·min−1) | - | |||
| VCO2 (mL·min−1) | 0.625*** | - | |||
| RPO (W) | 0.679*** | 0.598*** | - | ||
| EE (kcal·min−1) | 0.968*** | 0.774*** | 0.702*** | - | |
| -5% slope | VO2 (mL·min−1) | - | |||
| VCO2 (mL·min−1) | 0.659*** | - | |||
| RPO (W) | 0.758*** | 0.621*** | - | ||
| EE (kcal·min−1) | 0.985*** | 0.751*** | 0.776*** | - | |
| 0% slope | VO2 (mL·min−1) | - | |||
| VCO2 (mL·min−1) | 0.721*** | - | |||
| RPO (W) | 0.714*** | 0.614*** | - | ||
| EE (kcal·min−1) | 0.991*** | 0.788*** | 0.727*** | - | |
| 5% slope | VO2 (mL·min−1) | - | |||
| VCO2 (mL·min−1) | 0.778*** | - | |||
| RPO (W) | 0.719*** | 0.598*** | - | ||
| EE (kcal·min−1) | 0.994*** | 0.832*** | 0.715*** | - | |
| 7% slope | VO2 (mL·min−1) | - | |||
| VCO2 (mL·min−1) | 0.741*** | - | |||
| RPO (W) | 0.692*** | 0.538*** | - | ||
| EE (kcal·min−1) | 0.994*** | 0.795*** | 0.693*** | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





