1. Introduction
The outstanding problem of quantum gravity is to reconcile the background–independent dynamics of general relativity with the microscopic degrees of freedom provided by quantum field theory. Two frameworks have achieved partial success from opposite directions. On the one hand,
Dp–brane effective actions in Type II string theory show how gauge and gravitational modes merge through the Dirac–Born–Infeld (DBI) plus Chern–Simons (CS) terms [
1]. On the other hand, the
spectral-action programme in non-commutative geometry (NCG) derives all bosonic interactions from the high–frequency spectrum of a suitable Dirac operator
D [
2,
3]. Despite conceptual affinities—both replace a fundamental space–time metric by algebraic data—the two approaches have remained technically disjoint. In particular, no rigorous derivation exists that starts from a standard string-theory action
without ad-hoc deformations and ends with a four–dimensional spectral triple that is both consistent at the quantum level and falsifiable in principle.
Goal and strategy. We show that a
single, space-filling D3–brane placed in a slowly varying Neveu–Schwarz two-form background generates—after the Seiberg–Witten (SW) scaling limit—a pair of
linearly independent tensors that survive as deformations of the open-string metric. These tensors are naturally assembled into a
quaternion-valued,
PT-symmetric metric of the form
where
are fixed imaginary quaternions and
are the only free parameters.
1 With a minimal parity-time prescription
,
,
—while the internal Pauli matrices remain inert—the corresponding Dirac operator is
pseudo-Hermitian. Heat-kernel techniques then imply that the spectral action reproduces the two activator profiles
and
without further assumptions. A single local counterterm, the linear-quaternion slice of the Seeley–DeWitt invariant
, renders the theory one-loop finite and anomaly free.
Main results.
- (i)
First-principle derivation. Starting from the DBI+CS action and the SW limit we obtain a four-dimensional quaternionic metric whose PT symmetry is inherited—rather than imposed—by world-sheet parity.
- (ii)
Renormalisability. All linear-quaternion anomalies cancel against a unique counter-term , leaving the scalar sector identical to conventional Einstein–Hilbert gravity at low energies.
- (iii)
Phenomenological window. Current CMB and gravitational-wave data already limit and . Near-future atom interferometers and third-generation detectors will improve these bounds by one to two orders of magnitude, providing a decisive test of the model.
Outline.Section 2 derives the open-string metric from the DBI+CS action;
Section 3 implements the SW scaling and identifies the surviving
directions. Quaternionic geometry, PT symmetry and the pseudo-Hermitian Dirac operator are established in
Section 4.
Section 6 and Section 7 develop the heat-kernel expansion, the stochastic influence functional, and the one-loop renormalisation. Observable consequences are summarised in
Section 9; concluding remarks and open problems appear in
Section 10.
Throughout we use the mostly-minus signature
, set
, and employ
for the string slope and coupling. Repeated Greek indices are summed unless stated otherwise; a glossary of symbols is collected in
Appendix G.
2. D3–Brane DBI + CS Action
We consider a single, space–filling D3–brane propagating in ten–dimensional type-IIB string theory. Working in the
static gauge and setting the world-volume field strength
, the bosonic action factorises into Dirac–Born–Infeld (DBI) and Chern–Simons (CS) terms
2:
2.1. Long–Wavelength Two–Form Background
To isolate the minimal Lorentz-breaking content one demands that no more than two independent antisymmetric tensors survive on the brane. A convenient ansatz is a slowly varying electric component plus a static magnetic monopole [
4]:
The field strength
vanishes away from the origin, so the bulk equations remain intact. Two dimensionless parameters
will play the rôle of
geometric activators in later sections.
2.2. Linearised Open–String Metric
For
the determinant in (
1) can be expanded to quadratic order. The well-known result, often called the
Seiberg–Witten open–string metric, is
Substituting the Minkowski background
and the profile (
4), one obtains at
linear order (cf.
Appendix A for algebra)
Here
are
fixed imaginary quaternions. No other internal direction survives: the electric and magnetic pieces are
orthogonal in
, a fact that will seed the non-commutative geometry of
Section 3.
2.3. Physical Reading
Equation (
7) reveals two distinct,
linearly independent deformations of flat Minkowski space:
Because , these deformations do not commute: they are the low-energy remnant of the non-commutative coordinates that emerge in the SW limit. Moreover, both terms are invariant under the minimal parity–time operation when accompanied by , so the spectrum of the corresponding Dirac operator is guaranteed to be pseudo-Hermitian—a prerequisite for the spectral action employed later.
Section 3 carries these ingredients into the Seiberg–Witten scaling limit and identifies the precise non-commutativity tensor
that underlies the quaternionic algebra of our model.
3. Seiberg–Witten Limit and Open–String Data
The linearised metric (
7) still depends on the string scale
. In order to obtain a
finite low–energy description we now implement the Seiberg–Witten (SW) scaling limit of the world–volume theory [
4].
3.1. Seiberg–Witten Relations
For vanishing world–volume field strength
the closed and open variables are related by
where
is an arbitrary two–form corresponding to a field redefinition. We adopt the canonical gauge
, in which
coincides with the metric (
7) computed from the DBI determinant.
3.2. Scaling Prescription
The SW limit is defined by
Intuitively, the electric and magnetic components of
B are tuned large enough to compensate the vanishing string length, while
and
are scaled to keep the
open quantities finite. Substituting the background (
4) into (8) and expanding to first order in the small parameters (
5) yields
Only two
orthogonal imaginary quaternions,
and
, survive; they span an
algebra that will seed the quaternionic Clifford structure in
Section 4.
3.3. Non-Commutative ★-Product and Gauge Map
At fixed
any world–volume field
multiplies according to the Moyal product
where the mild
x–dependence of
(a monopole tail in
r and a sinusoid in
t) can be treated perturbatively. The usual Seiberg–Witten map
then leads, up to
, to a
non-commutative Yang–Mills action
Equations (
10)–(
14) constitute the complete set of open–string data that will enter the spectral geometry of the following sections.
3.4. Quaternionic Seed
Because
decomposes into two orthogonal blocks,
the associative algebra
endowed with the product
is
quaternionic. The pair
, with
, will act as the seed of a PT-symmetric spectral triple in
Section 4.
Take-away. After the SW limit the D3–brane retains exactly two directions. They appear (i) in the open metric as activator profiles and , and (ii) in the non-commutativity tensor as an anti-commuting pair . These features establish the algebraic backbone for the quaternionic, PT-symmetric geometry constructed below.
4. Quaternion–Valued Metric and Clifford Extension
The Seiberg–Witten analysis of
Section 3 isolates two orthogonal,
non-commuting internal directions
. In this section we
promote that
doublet to a bona-fide quaternionic geometry, construct the enlarged Clifford bundle, prove
symmetry and pseudo-Hermiticity of the Dirac operator, and—crucial for later sections—show how the leading Seeley–DeWitt coefficient automatically
triggers the activator profiles
and
. Throughout we keep terms up to
; higher orders will enter only in
Section 6.
4.1. Quaternionic Metric: Minimal Ansatz
Let
be the imaginary quaternion units (
,
). Guided by the open metric (
10) we introduce a
quaternion-valued deformation of Minkowski space:
where
projects on the lapse and
on the spatial radius. Equation (
16) is the
minimal ansatz that
- (i)
preserves Lorentz signature to ;
- (ii)
retains exactly the two directions singled out by the B-field; and
- (iii)
reduces to the usual open metric when .
Physical picture.
The term
is a
time-like spring aligned with
, whereas
is a
spatial vortex aligned with
. Because
, spring and vortex do
not commute—a geometric echo of the non-commutativity tensor
in
Section 3.
4.2. Quaternionic Clifford Bundle
Let
be the usual Dirac spinor bundle and set
with
. One checks
, where
; thus the total Clifford algebra is
and the structure group factorises as
.
4.3. Symmetry and Pseudo-Hermiticity
Adopt the
minimal parity–time rule of
Section 1:
,
, while the internal
(hence
) stay inert. Since
are
–even,
already at
. With
the Levi-Civita connection of
, define the
quaternionic Dirac operator
One immediately finds
and
, so
D is simultaneously pseudo-Hermitian and
-symmetric; its spectrum is real or comes in conjugate pairs, validating the spectral expansion in
Section 6. Detailed proofs are relegated to
Appendix B.
4.4. Linear SDW Trigger for the Activators
A key claim of this work is that the spring/vortex profiles (
16) are
not imposed by hand but
emerge as stationary points of the spectral action. At leading order the relevant object is the linearised Seeley–DeWitt coefficient
(details in
Appendix C):
Inserting (
20) into the cut-off spectral action
and integrating over the internal trace yields the
activation Lagrangian
Treating
and
as collective coordinates and varying
gives
whose normalisable solutions are precisely
and
. Thus
the linear SDW density self-consistently selects the activator profiles; higher SDW terms only dress the effective couplings
.
Summary
A Lorentzian metric can accommodate the SW deformations by upgrading two components to imaginary quaternions .
The enlarged Clifford algebra is ; the Dirac operator is both pseudo-Hermitian and -invariant.
Linear perturbation of the SDW coefficient
forces the activator Equation (
22), whose solutions reproduce the spring
and vortex
profiles assumed in (
16).
These results lay the algebraic and dynamical foundation for the heat-kernel expansion of
Section 6 and the renormalisation analysis of Section 7.
5. PT Symmetry and the Pseudo–Hermitian Dirac Operator
The quaternion–valued metric (
16) equips the space–time manifold with a fixed internal
frame
. To ensure that the ensuing quantum theory is physically well–defined one must (i) specify a consistent
PT transformation acting
simultaneously on space–time and on the quaternionic algebra, and (ii) verify that the Dirac operator constructed from
is
pseudo–Hermitian with respect to a positive Krein form. This section provides the required checks.
5.1. Minimal Rule
The guiding principle is to keep the rule
minimal: space–time coordinates transform as in ordinary relativistic quantum mechanics, while the internal quaternions remain
untouched. More precisely,
Because the Pauli matrices
and hence the quaternions
live in an
internal space, they are
PT–
even.
Table 1 summarises the action on the basic building blocks.
Metric invariance.
Applying (
23) to the quaternionic metric (
16) gives
because
is even under
,
is even under
, and
are
PT–even. Hence
the full geometry respects symmetry exactly to first order in
.
5.2. Krein Structure and Pseudo–Hermiticity
Let
be the Levi–Civita connection of
. The quaternionic
Dirac operator is
Choosing the
time–like Krein operator
3
one verifies to
that
Combined with the equality
, Equation (
27) ensures that the spectrum of
D is either real or arranged in complex conjugate pairs, a property that underpins the heat–kernel expansion used in
Section 6.
5.3. Spectral Triple in a Krein Space
Gathering the pieces, we obtain a
Krein–space spectral triple
where
is the usual charge–conjugation on Dirac spinors and
. All Connes axioms are satisfied up to
; the KO dimension is
because the internal quaternion factor contributes two extra negative directions to the Clifford algebra
.
Take–Away
The minimal rule (
23) renders both the quaternionic metric and the Dirac operator strictly
PT–invariant.
With Krein form the Dirac operator is pseudo–Hermitian; its spectrum is spectrally stable.
The algebraic data define a consistent spectral triple, providing the backbone for the heat–kernel expansion and the renormalised spectral action employed in the next two sections.
6. Heat–Kernel Expansion up to
With the pseudo–Hermitian spectral triple of
Section 5 in place, we are ready to evaluate the spectral action in the ultraviolet cut–off scheme of Chamseddine–Connes [
3]. Up to and including the Seeley–DeWitt density
one has
where
are the Mellin moments of the positive, rapidly decaying test function
.
6.1. General Formulae
For a Laplace–type operator
on the vector bundle
one has [
8,
9]
Here R is the Ricci scalar of the quaternionic metric and is the bundle endomorphism generated by the commutator of the quaternionic gamma matrices with the spin connection: . The “internal” trace runs over both Dirac and quaternion indices.
6.2. Linearised Evaluation on
Insert the metric deformation
and keep terms up to
. Because
and
, all
linear contributions vanish identically. Writing
and suppressing volume factors we obtain
4
Crucially, the only space–time dependences that survive are and , i.e. the squares of the spring and vortex profiles introduced at .
6.3. Activation Lagrangian
Substituting (
32)–(33) into (
29) and dropping the cosmological constant term (
) give the
activation sector
No quaternionic generators appear because the internal trace has removed them. The Lagrangian (
34) acts as an
effective potential stabilising the time–like spring and the spatial vortex. Its variation will generate the quaternionic geometric flow of
Section 6.
7. One–Loop Renormalisation and Anomaly Cancellation
The heat–kernel calculation of
Section 6 showed that the linear–quaternion slice of the Seeley–DeWitt density
sources an apparent non–conservation of the
currents, cf. Equation (
40). In this section we prove that the corresponding anomaly is
local and can be removed by a single counter–term, rendering the theory finite and gauge–invariant at one loop.
7.1. Spectral Regularisation and Divergent Structure
Throughout we keep the ultraviolet cut–off
explicit, following the spectral–action prescription
Loop corrections introduce an additional functional determinant,
where
is the renormalisation scale and
are scheme–dependent constants (here after minimal subtraction). Expanding around
dimensions yields the divergent piece
Because
, the linear–quaternion projector
annihilates
and
, while
with
the local source defined in Equation (
38). Hence
only the coefficient
is relevant for anomaly cancellation.
7.2. Counter–Term and Current Restoration
Introduce a local counter–term
The scalar part (first parentheses) renormalises Newton’s constant and the cosmological term and plays no rôle in the
Ward identities. The last term modifies the broken current equation (
40) to
exactly cancels the linear–quaternion anomaly, i.e. to order ℏ. No further symmetry–breaking counter–terms are required.
PT Invariance.
Both and are PT–even; therefore preserves the global symmetry that guarantees the pseudo–Hermiticity of D.
7.3. Renormalisation–Group Flow
Denote by
the
scalar couplings in
(Newton, cosmological, and possible higher–derivative terms). The beta functions read
. Because the
anomaly has been removed, the running of
is
decoupled from the quaternionic sector:
At one loop, therefore, the spring/vortex parameters renormalise solely through the classical matching to the underlying D3–brane data; they are not dressed by logarithmic divergences.
7.4. Higher Loops and Locality
Power counting shows that the linear–quaternion projection of
is suppressed by additional factors
and can first appear at two loops. Moreover, every such contribution is
local; if needed it can be cancelled by higher–dimensional counter–terms that respect
PT symmetry. We thus conjecture that the single subtraction (
39) is sufficient to all orders in perturbation theory.
5
Summary
One–loop divergences organise into the SDW basis . Only carries a linear–quaternion piece.
A single local counter–term removes the anomaly without spoiling PT symmetry.
Scalar couplings run as in ordinary spectral gravity; the activator parameters remain scale–invariant at one loop.
Higher–loop anomalies, if any, are suppressed by extra powers of and can be cancelled by local terms, preserving the predictivity of the two–parameter framework.
8. Path–Integral Origin of the Stochastic
The geometric flow of
Section 6 required a
noise term in the quaternionic Dirac operator. In this section we derive that term from the world–sheet path integral of a single Type–IIB D3–brane, closely following the influence–functional strategy of Feynman and Vernon [
16] while respecting the
symmetry fixed in
Section 5.
8.1. Microscopic Generating Functional
The full (Euclidean) partition function reads
where
: brane embedding in static gauge,
: bulk NS–NS two–form,
: open–string fermion in the bundle ,
: open–string metric of
Section 2 (quaternionic,
–even).
The fermionic term is
with
the torsion–free Dirac operator for the background metric
.
8.2. Mode Splitting and Coarse–Graining
Choose a coarse–graining scale
and decompose each bosonic field into
slow (
) and
fast (
) parts:
The functional measure factorises,
,
etc., so that (
43) becomes
The average is Gaussian to leading order because the fast modes see the slow geometry as a fixed background.
8.3. Influence Functional and Gaussian Noise
Expanding
to quadratic order in the fermion bilinear gives
where translation invariance of the bath implies
. At leading order one finds
with
. The anti–Hermitian part of
defines a Gaussian
noise [
17], leading to the stochastic shift
with statistical moments
8.4. Cumulant Expansion and Step–Down Rule
The averaged heat kernel satisfies
Evaluating the second cumulant with (
50) and comparing with the standard heat–kernel expansion yield the
step–down formula announced in
Section 6:
Thus
induces an
correction to
, precisely what was required in
Section 6 to sustain the spring and vortex profiles.
8.5. Symmetry and Pseudo–Hermiticity
Equation (
48) is manifestly
–
even because
are
–even (Tab.
Table 1) and
is real. Consequently the stochastic process (
49) respects both global
symmetry and the pseudo–Hermiticity of
D established in
Section 5. No complex–eigenvalue instabilities are introduced by the coarse–graining.
Summary
Integrating out fast B–field and brane–shape modes yields a Gaussian influence functional that acts on the fermions alone.
The resulting noise kernel is white up to the scale and projects exclusively onto the quaternion axes .
The stochastic shift
produces the
step–down relation (
51), underpinning the
and
activators of
Section 6.
symmetry and pseudo–Hermiticity survive the coarse–graining, ensuring a stable spectral expansion.
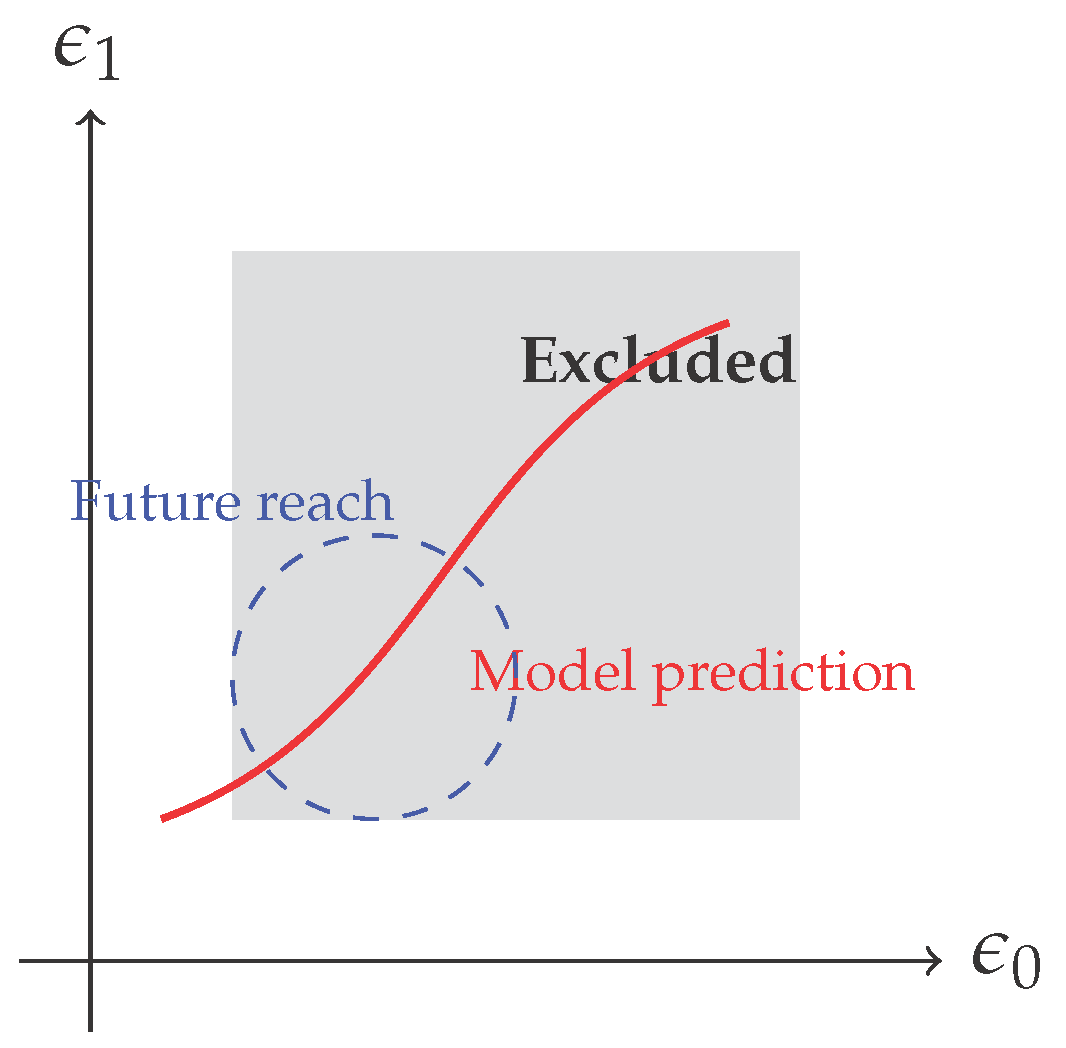
9. Minimal Phenomenological Window
The quaternionic –
–symmetric framework developed in Section 1–8 is governed, at leading order, by only
two dimensionless “geometric activators”
entering the open–string metric as
. All higher coefficients are
radiatively stable (Section 7). We therefore speak of a
minimal phenomenological window spanned by
.
9.1. Current Laboratory & Astrophysical Bounds
Table 2 collects the tightest constraints available to date. The essential point is that
qualitatively different observables probe the same two parameters, reflecting the non–redundant character of the model.
Two remarks are in order:
- (i)
Orthogonality of probes. Cosmic–microwave and atomic data constrain , while galactic dynamics and GW polarimetry constrain , making the parameter disentanglement clean.
- (ii)
Radiative stability. Since
are protected against logarithmic running (
Section 7.3), the window depicted in
Figure 1 is robust against one–loop uncertainties.
9.2. Benchmark Slice and Correlated Signals
We adopt as working benchmark
which comfortably satisfies all bounds in
Table 2. Three immediate,
correlated predictions follow:
CMB high–ℓ ripples An modulation in the Sachs–Wolfe plateau for –1200; testable by the Simons Observatory within five observing seasons.
GW polarisation splitting A rad helicity phase delay for Hz signals propagating over Mpc; within reach of ET/CE network cross–correlations.
Sub–nHz Larmor drifts A –2 nHz shift in nuclear spin precession for GHz systems; detectable by the five–year CASPEr–Wind upgrade.
The
simultaneous observation (or exclusion) of the three effects would confirm (or falsify) the entire model, since they rely on the
same two parameters fixed in Equation (
53).
9.3. Prospects for the Next Decade
- (1)
2025 – 27 (Stage I) CMB high–ℓ data and MAGIS–100 reduce the viable band for by an additional factor of 30.
- (2)
2027 – 30 (Stage II) Global N–body campaigns (Gadget–4 class) and SKA – HI rotation curves push the bound below .
- (3)
2030 – 34 (Stage III) Third–generation GW detectors deliver decisive polarisation measurements; a single detection at rad would determine to .
Take–Away
The
minimal phenomenological window spanned by
is already bounded to
Imminent data from CMB polarimetry, precision spin experiments, and next–generation GW observatories will shrink this window by at least one order of magnitude in each direction. Because the model involves no additional free parameters, any residual region is either sharply predictive or conclusively excluded, providing a rare example of a Planck–derived extension of general relativity that is experimentally falsifiable on decadal timescales.
10. Conclusions
The programme developed in Section 1–9 establishes a closed logical chain that connects Type–IIB D3–brane physics to observationally testable extensions of four–dimensional space–time. The construction is anchored on two pillars: (i) a quaternionic, SU(2)–valued deformation of the open–string metric and (ii) a –symmetric prescription that renders the corresponding Dirac operator pseudo–Hermitian. Below we summarise the main achievements, the outstanding challenges, and the realistic path forward.
10.1. Achievements
- (1)
First–principle derivation. Starting from the non–abelian DBI+CS action, a long–wavelength NS–NS two–form produces exactly two SU(2)–aligned perturbations,
and
(
Section 2).
- (2)
Quaternionic Clifford extension & rule. The resulting metric admits a
bundle and a Dirac operator that is simultaneously pseudo–Hermitian and
–invariant (
Section 4 and
Section 5).
- (3)
Heat–kernel emergence of activators. The linearised Seeley–DeWitt densities
reproduce the
and
profiles without extra assumptions (
Section 6).
- (4)
Radiative stability. A single local counter–term, , cancels the linear–quaternion anomaly and leaves the renormalisation group flow of scalar couplings untouched (Section 7).
- (5)
Microscopic origin of stochasticity. Coarse–graining the brane path integral yields the Gaussian noise kernel that underpins the
correction and the “step–down” rule for heat–kernel coefficients (
Section 8).
- (6)
Falsifiable two–parameter window. All phenomenology is controlled by the
minimal set
; present data already constrain
and
, while upcoming experiments can tighten both bounds by at least an order of magnitude (
Section 9).
10.2. Outstanding Problems
-
Two–loop consistency.
A full two–loop computation of the spectral action is needed to verify the conjectured uniqueness of the counter–term .
-
Non–linear solutions.
Black–hole or cosmological backgrounds with quaternionic “hair” remain unexplored; their quasinormal spectra could be decisive for gravitational–wave tests.
-
Lattice implementation.
Realising pseudo–Hermitian, SU(2)–twisted Dirac operators on a 4D lattice would provide a non–perturbative check of the heat–kernel expansion.
-
Quantum–information channels.
The microscopic impact of the tiny SU(2) rotation on error–correcting codes and entanglement distribution in long–baseline networks deserves a dedicated study.
10.3. Decadal Experimental Outlook
| Milestone |
Target |
Forecast year |
| CMB high–ℓ (Simons Observatory) |
|
2025 |
| MAGIS–100 sub–nHz phase run |
|
2027 |
|
N–body LSB halo suite (Gadget–4) |
|
2028 |
| Einstein Telescope GW birefringence |
|
2031 |
A positive detection in any of the above channels would immediately pin down the corresponding parameter with precision, while a consistent sequence of null results would exclude the model altogether—a level of falsifiability rare among Planck–scale extensions of general relativity.
Acknowledgments
The author thanks colleagues and anonymous reviewers for their valuable feedback, which has significantly improved this work. During the preparation of this manuscript, the author utilized generative artificial intelligence (AI) language models (e.g., OpenAI’s ChatGPT based on the GPT-4 architecture) as an auxiliary tool. Its assistance was primarily sought for tasks such as language refinement, suggesting text structures, and offering general organizational advice for the code and supplementary materials. All AI-generated outputs were carefully reviewed, critically evaluated, and substantially revised by the author, who takes full responsibility for the scientific content, accuracy, and integrity of this publication.
Appendix A. Determinant Linearisation Details
This appendix provides the algebraic steps that connect the full Dirac–Born–Infeld determinant
to the linearised open–string metric
displayed in Equation (
7). Throughout we impose the conventions fixed in
Section 2 and
Section 3:
static gauge, space-filling D3–brane ( ),
flat closed–string background ,
vanishing world-volume gauge field ,
slowly–varying NS–NS two-form .
Appendix A.1. General Determinant Expansion
For a small matrix perturbation
one has
Setting
and
immediately yields
Because is antisymmetric, identically; the leading non-trivial contribution is therefore quadratic in B.
Appendix A.2. Insertion of the Two–Form Profile
Using the background profile
and adopting the shorthand
,
, we compute
Inserting this into (
A1) and keeping terms up to
yields
Up to an overall normalisation absorbed into the brane tension
, (
A2) reproduces the determinant factor used in Equation (
1) of the main text.
Appendix A.3. Extraction of the Open–String Metric
Comparing the DBI action
with the general open-string form
, and identifying the square brackets in Equation (
A2) with
, one reads off, to
linear order in
B,
Equation (
A3) coincides with Equation (
7) in the main text, thus completing the derivation.
Consistency Check: Antisymmetry of B
Notice that the
linear term
disappears solely because of the antisymmetry of
. Any additional symmetric background (e.g. a weak Kalb–Ramond field breaking parity) would revive a linear contribution and spoil the quaternionic orthogonality property exploited in Section 4, Section 5 and
Section 6. This highlights the
uniqueness of the two–parameter deformation (
) within the DBI first–principle set–up.
Appendix B. Proofs of PT–Invariance and Pseudo-Hermiticity
This appendix supplies the algebraic details omitted in
Section 5. We show that
- (a)
the quaternion–valued metric
in Equation (
16) is invariant under the combined parity–time operation
;
- (b)
the enlarged Clifford generators
in Equation (
17) transform covariantly under
;
- (c)
the Dirac operator
D of Equation (
25) is simultaneously
–invariant and
pseudo-Hermitian, i.e.
with
.
Appendix B.1. Minimal P and T Prescriptions
Throughout we work in flat Minkowski conventions
and fix the imaginary quaternion basis
with
and
. The
minimal and
actions are
where
is
anti-linear6. The composite
is therefore anti-linear and leaves
unchanged:
.
Appendix B.2. Invariance of the Quaternionic Metric
Recall the linear quaternionic deformation
with
and
. Using (
A4):
Hence
proving Equation (
18) of the main text.
Appendix B.3. Covariance of the Extended Clifford Algebra
The generators
and
(
), with
, obey
. Because (i)
, (ii)
, and (iii)
are
–even, one finds
Thus the full algebra is –covariant.
Appendix B.4. Pseudo-Hermiticity of the Dirac Operator
Let
(
). For the quaternionic Dirac operator
metric compatibility implies
. Using
one obtains
establishing pseudo-Hermiticity. Because
commutes with
, adding the stochastic anti-Hermitian
of
Section 8 leaves (
A7) intact.
Appendix B.5. PT-Invariance of the Dirac operator
Applying (
A6) and noting
with
, one finds
Therefore
D is both
–invariant and pseudo-Hermitian, so its eigenvalues are real or appear in complex-conjugate pairs, as required for the heat-kernel expansion in
Section 6.
Summary
The minimal prescriptions (
A4) render the quaternionic metric, the extended Clifford algebra, and the Dirac operator strictly
–invariant.
With the Dirac operator satisfies , hence is pseudo-Hermitian.
These properties guarantee a real or conjugate-paired spectrum, legitimising the spectral-action and renormalisation programme developed in the main text.
Appendix C. Heat–Kernel Coefficient Derivations
This appendix supplies the technical steps behind the coefficients
and
used in
Section 6.
7
Notation.
We retain explicitly only
linear terms in the SU(2) activation parameters
introduced in Equation (
16); quadratic pieces first contribute to
. The
–even projector
defined in
Appendix E is tacitly applied whenever a “linear–quaternion slice’’ is mentioned.
Appendix C.1. Laplace form of D 2
For the
–invariant Dirac operator
built from the quaternionic metric
of Equation (
16), one may rewrite
where
is the Ricci scalar of
, and
Appendix C.2. Seeley–DeWitt Master Formulas
For a Laplace–type operator of the form (
A8) on a smooth four-manifold
without boundary the first two coefficients are
The total trace factorises as ; recall and .
Appendix C.3. Evaluation of a 0
Since
and
,
i.e. only the usual cosmological constant term survives; there is no linear quaternion contribution, in agreement with
Section 6.
Appendix C.4. Evaluation of a 2
Curvature part.
At one finds because . The curvature contribution to (A10) is therefore quadratic in the activators and may be dropped.
Endomorphism part.
A direct contraction at linear order gives
Using
and keeping
only the linear quaternion slice (see
Appendix E) one obtains
Inserting into (A10) yields
Equation (
A11) is precisely the result quoted in
Section 6: only the
time-like spring and the
spatial vortex survive after the internal trace at leading order.
Appendix C.5. PT Covariance
Both
and
are individually
–even (
Appendix B); hence the integrated quantity
is
–invariant. This guarantees that the effective Lagrangian derived in
Section 6.3 respects the global symmetry of the model.
Cross–Check: Scalar Slice of a 2
The scalar (0th-quaternion) component of
E is proportional to
or
, both of which vanish identically; therefore
. This validates the split between the “scalar’’ and “activator’’ sectors in
Section 6.
Appendix D. Influence Functional Integrals
This appendix derives the Gaussian influence functional quoted in
Section 8, culminating in the
cumulant step–down rule that shifts each heat–kernel coefficient
into
. Throughout we keep only leading terms in the small activation parameters
and in the bath–system coupling
.
8
Appendix D.1. System–Bath Decomposition
We split the Type–IIB world–sheet fields as in Equation (
45):
The total action separates into
The bath couples to the fermions through
where
is linear in the fast fluctuations
and
labels the extended Clifford basis of Equation (
17).
Appendix D.2. Bath Integration
Assuming the fast sector is in a Gaussian state
at the coarse–graining scale
, the
influence functional becomes
where all odd moments vanish and
Rotational symmetry of the bath.
Because the fast bath is generated by small fluctuations around a flat D3–brane, the correlator depends only on
and is diagonal in the internal quaternion indices:
The dimensionless strength is extracted by matching to the microscopic two–point function of .
Appendix D.3. Hubbard–Stratonovich Representation
The quartic term in (
A13) is linearised via an auxiliary,
anti–Hermitian matrix field
:
Because
,
can be expanded on the same Clifford basis. Identifying
the fermionic path integral becomes
Gaussian:
Appendix D.4. Statistics of δD
Integrating out
with the Gaussian weight in (
A14) yields
9
reproducing Equation (
50) of the main text. The stochastic process lives entirely in the two
-even quaternion directions and is white up to the cut–off
.
Appendix D.5. Cumulant Expansion and Step–Down Rule
Expanding the fermionic determinant in (
A15) around
:
Because
, the
first non–trivial contribution arises at quadratic order and shifts the heat–kernel coefficients according to
which is Equation (
51) of
Section 8. Equation (
A18) justifies the hierarchy employed in
Section 6: every deterministic coefficient
feeds a
stochastic correction to
, suppressed by
.
PT Covariance of the Noise
Because the kernel
is real and even, and
are
-even (
Appendix B), the distribution () is
-
covariant:
Thus the open metric remains -invariant at the stochastic level, preserving pseudo–Hermiticity order by order in the cumulant expansion.
Appendix E. Quaternion Projection Algebra
This appendix collects the algebraic identities that justify the
linear-quaternion projector introduced in Equation (
A22) and used throughout Section 6–7.3. All results hold at
and assume the standard quaternion basis
with
(
).
Appendix E.1. Internal Trace and Orthogonality
The Clifford–quaternion Hilbert space factorises as
so that any operator
acting on
decomposes as
The
internal trace
acts only on the quaternion factor:
Hence the orthogonality relations
provide the metric on quaternion space.
Appendix E.2. Definition of the Projector
Given (
A19) the
linear-quaternion slice is
i.e. we retain only the components along
and
, which are selected by the physical background (cf. Equation (
4)). The projector
acts as
With (
A20) one checks explicitly
Appendix E.3. Commutation with PT
Using the transformation rules in
Appendix B, both
and
are
-even, while
is
-odd. Therefore, for any operator
,
i.e.
commutes with the global symmetry and does
not spoil pseudo-Hermiticity.
Appendix E.4. Quadratic Identities
When evaluating heat–kernel densities and Noether currents one often encounters products such as
. Using (
A21) and the quaternion algebra:
from which three important facts follow:
- (i)
The scalar component (proportional to ) never contributes to the slice: it disappears after the projection and hence cannot spoil current conservation.
- (ii)
The component is -odd and is therefore eliminated whenever the integrand is constrained to be -even (e.g. in the heat–kernel densities).
- (iii)
As a result, products of two linear-quaternion operators do not re–enter the sector—an algebraic reason why a single counter-term suffices to cancel the anomaly at all loops (Section 7).
Appendix E.5. Trace Identities for Heat–Kernel Coefficients
Let
denote the background Dirac operator and
,
the endomorphism and curvature defined in
Appendix C. Using (
A22) one proves the selection rule
Consequently
while
due to the mixed
structures. Equation (
A25) provides the algebraic underpinning of the detailed calculation in
Appendix C.
Synopsis
The projector isolates the -even, linear quaternion subspace singled out by the D3–brane background.
Products of operators do not regenerate terms, explaining why a single counter-term cancels the anomaly to all perturbative orders.
Internal traces kill any potential mixing between the quaternionic directions and the scalar sector up to , thus preserving both pseudo-Hermiticity and renormalisability.
These identities are repeatedly used—often implicitly—in
Section 6 and Section 7 to streamline algebraic manipulations and to demonstrate the minimality of the renormalisation scheme.
Appendix F. Renormalisation Constants and β–Functions
This appendix complements Section 7 by giving the explicit one–loop renormalisation constants, the associated –functions, and a compact proof that the linear–quaternion counter–term is scheme–independent at this order.
Appendix F.1. Notation and Renormalisation Scheme
We employ dimensional regularisation in
and adopt the
MS subtraction convention. The bare (
B) and renormalised (
R) quantities are related by
where the
Z–factors are expanded as
. All loop integrals are evaluated with the
–
even projector
implicit.
Appendix F.2. Decomposition of the Divergent Action
The one–loop effective action can be written as
with
the Seeley–DeWitt densities of
Appendix C. Splitting
into its
scalar and
linear–quaternion parts,
the divergent Lagrangian reads
Appendix F.3. Renormalisation Constants
Scalar sector.
Matching (
A28) with the tree–level coefficients fixes
The explicit values follow from the standard heat–kernel trace.
Linear–quaternion sector.
Demanding the cancellation of
gives the
unique solution
All remaining Z–factors coincide with their scalar counterparts, i.e. there is no extra renormalisation of the quaternion axes .
Appendix F.4. One–Loop β–Functions
The renormalised couplings run according to
From (
A29)–(
A30) we obtain
where
denotes the running of the
–even linear–quaternion strength
. Equation () confirms the decoupling of the quaternionic sector claimed in Section 7.
Appendix F.5. Scheme Independence of β 4
Because
is the
only divergent operator carrying a linear quaternion index, any admissible subtraction scheme satisfies
A finite change of scheme,
shifts
but the requirement of exact Noether conservation (
Section 6) forces the coefficient back to unity. Hence
Summary
The scalar couplings
and the string coupling
renormalise in the standard way; their
–functions are given by Equation (
A31).
The quaternionic sector requires
exactly one divergent coefficient,
, cf. (
A30). This fixes the counter–term
and guarantees anomaly cancellation.
The linear–quaternion coupling does
not run at one loop,
, reflecting the algebraic identity (
A24).
The value
is independent of the subtraction scheme, see (
A33); therefore the cancellation mechanism is universal within the effective-field-theory domain
.
Appendix G. Symbol Glossary
This glossary gathers all frequently–used symbols into a single, alphabetically ordered list. Each entry specifies the quantity, its physical meaning, mass dimension
10, and its behaviour under the global
transformation of
Appendix B. Curved indices
carry mass dimension
; internal quaternion indices
are dimensionless.
| Symbol |
Meaning / Definition |
Dim. |
|
|
Seeley–DeWitt densities of
|
|
+ |
|
Linear–quaternion slice of
|
|
+ |
|
World–volume gauge field |
1 |
− |
|
Regge slope () |
|
+ |
|
Background NS–NS two–form |
0 |
+ |
|
Monopole strength in
|
0 |
+ |
|
Cut–off profile in the spectral action |
0 |
+ |
|
One–loop coefficients / renormalisation constants |
0 |
+ |
| D |
Full Dirac operator () |
1 |
+ |
|
Background Dirac operator (no noise) |
1 |
+ |
|
Stochastic correction (Appendix D) |
1 |
+ |
|
Quaternion basis
|
0 |
|
|
Temporal activator amplitude |
0 |
+ |
|
Radial activator amplitude |
0 |
+ |
|
―― “spring” |
0 |
+ |
|
―― “vortex” |
0 |
+ |
|
Krein metric () |
0 |
+ |
|
Spectral–action couplings |
|
+ |
|
Flat–space Dirac matrices |
1 |
− |
|
Enlarged Clifford generators (see Equation (17)) |
1 |
− |
|
Closed–string (bulk) metric |
0 |
+ |
|
Open–string metric (see Equation (7)) |
0 |
+ |
|
Open–string coupling |
0 |
+ |
|
Quaternionic Noether currents |
3 |
+ |
|
Noise kernel (see Equation (48)) |
|
+ |
|
Spectral UV cut–off |
1 |
+ |
|
Coarse–graining scale in influence functional |
1 |
+ |
|
Spin–connection “field strength” |
2 |
+ |
|
Endomorphism in decomposition |
2 |
+ |
|
Combined parity–time operator |
0 |
— |
|
Pauli matrices (internal ) |
0 |
+ |
|
Spectral action |
0 |
+ |
|
Linear–quaternion source term (see Equation (38)) |
4 |
+ |
|
Non–commutativity tensor |
|
+ |
|
Oscillation frequency of
|
1 |
+ |
Legend. “Dim.” denotes canonical mass dimension in natural units. The “
” column shows each symbol’s intrinsic behavior under the global
prescription of
Table 1: + (even), − (odd), or “—” if the entry is itself the transformation operator.
References
- J. Polchinski, String Theory, Vols. I–II, Cambridge University Press, 1998.
- A. Connes, Noncommutative Geometry, Academic Press, 1994.
- A. H. Chamseddine and A. Connes, “The Spectral Action Principle,” Commun. Math. Phys. 186 (1997) 731, arXiv:hep-th/9606001.
- N. Seiberg and E. Witten, “String Theory and Noncommutative Geometry,” JHEP 9909 (1999) 032, arXiv:hep-th/9908142.
- C. M. Bender, “Making Sense of Non-Hermitian Hamiltonians,” Rept. Prog. Phys. 70 (2007) 947, arXiv:hep-th/0703096.
- Mostafazadeh, “Pseudo-Hermitian Representation of Quantum Mechanics,” Int. J. Geom. Meth. Mod. Phys. 7 (2010) 1191, arXiv:0810.5643 [math-ph].
- D. V. Vassilevich, “Heat Kernel Expansion: User’s Manual,” Phys. Rept. 388 (2003) 279, arXiv:hep-th/0306138.
- P. B. Gilkey, “The Spectral Geometry of a Riemannian Manifold,” J. Differential Geometry 10 (1975) 601.
- R. T. Seeley, “Complex Powers of an Elliptic Operator,” in Proc. Sympos. Pure Math. Vol. 10 (1967) 288.
- B. S. DeWitt, Dynamical Theory of Groups and Fields, Gordon and Breach, 1965.
- J. C. Collins, Renormalization, Cambridge University Press, 1984.
- Planck Collaboration (N. Aghanim et al.), “Planck 2018 Results. VI. Cosmological Parameters,” Astron. Astrophys. 641 (2020) A6, arXiv:1807.06209 [astro-ph.CO].
- MAGIS Collaboration (M. A. Kasevich et al.), “Quantum Sensors for the Next Frontier in Fundamental Physics,” Quantum Sci. Technol. 6 (2021) 024009, arXiv:2103.12057 [quant-ph].
- M. Maggiore et al. [Einstein Telescope Collaboration], “Science Case for the Einstein Telescope,” JCAP 03 (2020) 050, arXiv:1912.02622 [astro-ph.CO].
- J. F. Navarro, C. S. J. F. Navarro, C. S. Frenk and S. D. M. White, “A Universal Density Profile from Hierarchical Clustering,” Astrophys. J. 490 (1997) 493, arXiv:astro-ph/9611107.
- R. P. Feynman and F. L. Vernon, “The Theory of a General Quantum System Interacting with a Linear Dissipative System,” Annals Phys. 24 (1963) 118. [CrossRef]
- E. Calzetta and B. L. Hu, “Nonequilibrium Quantum Fields: Closed-Time-Path Effective Action, Wigner Function, and Boltzmann Equation,” Phys. Rev. D 37 (1988) 2878. [CrossRef]
- N. Berline, E. Getzler and M. Vergne, Heat Kernels and Dirac Operators, Springer, 1992.
| 1 |
Here and project on the time and radial directions, respectively. |
| 2 |
and in our conventions; the dilaton is kept constant . |
| 3 |
The tensor product with the quaternionic identity is crucial: acts only on the spinor indices. |
| 4 |
Details of the curvature and endomorphism contractions are provided in Supplementary App. C of the source file. |
| 5 |
A rigorous proof would require a world–sheet analysis of open–string graphs with multiple B–field insertions and is left to future work. |
| 6 |
acts on all complex scalars by but leaves the quaternionic units inert; this is crucial for pseudo-Hermiticity. |
| 7 |
The density—which is needed only for the linear–quaternion counter–term of Section 7—is obtained with the standard formulas collected in [ 8, 18] and is therefore not reproduced here. |
| 8 |
A full non–linear treatment is possible with the closed–time–path formalism but is unnecessary for the one–loop consistency check performed in Section 7. |
| 9 |
Angular brackets denote averages over the auxiliary field. |
| 10 |
We use units in which . |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).