Dynamic Incentive Design in Public Transit Subsidization Under Double Moral Hazard: A Continuous-Time Principal-Agent Approach

1. Introduction

Public transport systems, encompassing metro, bus, and ferry services, constitute the backbone of modern urban mobility infrastructure. These systems play an indispensable role in enhancing mass mobility, mitigating traffic congestion, promoting social equity through universal accessibility, and advancing sustainable urban development goals [1,2]. Recent empirical evidence demonstrates that well-designed public transport subsidies can generate substantial environmental benefits, with Gohl and Schrauth (2024) showing that Germany’s €9 monthly transit pass reduced air pollution by over eight percent [3]. However, the effectiveness of such subsidies is not guaranteed, as other studies find limited to no impact on air quality, suggesting that the outcomes are highly sensitive to policy design and local context [4,5]. A persistent and widespread challenge confronting public transport systems globally is the prevalence of substantial financial deficits, necessitating sophisticated subsidy mechanisms to ensure both service viability and social welfare optimization [6,7].

The complexity of public transport contracting has been extensively documented. As noted by Hooper (2008), the shift towards privatization has spurred interest in more complex contracts designed to incentivize operators to maximize value for money [8]. Contract theory provides crucial insights for this task, particularly regarding the effects of uncertainty and asymmetric information on performance outcomes. Yet, designing effective incentives remains a persistent practical challenge. For instance, Socorro and de Rus (2010) analyzed Spanish urban transport contracts and concluded that none provided appropriate incentives [9], while Canitez et al. (2019) identified significant agency costs in Istanbul’s system stemming from misaligned interests under net-cost contracts [10]. This highlights the critical importance of contract structure, with research actively comparing different subsidy modes, such as those based on passenger demand versus vehicle-kilometers, to understand their strategic implications for governments and operators [11,12].

A crucial dimension of contract design is the allocation of risk. The theoretical importance of risk preferences is strongly validated by empirical evidence. In a landmark study using choice experiments with Australian bus operators, Hensher et al. (2016) found that “risk allocation significantly influences contract preference” and that optimal design must account for operators’ risk attitudes [13]. This is further complicated by findings from the broader public-private partnership (PPP) literature, where Makovsek and Moszoro (2018) argue that risk transfer to the private sector often entails an “inefficient risk pricing premium,” adding another layer of complexity to achieving value for money [14]. Moreover, contracts must often balance multiple objectives, such as productivity and safety, where incentives for one can have unintended consequences for the other [15].

While the literature has extensively analyzed single-sided moral hazard—where the operator possesses superior information and may reduce effort—it has largely overlooked a critical dimension of public transit governance: the active and often unobservable role of regulators themselves. Regulators contribute significantly to service quality through infrastructure investments, route optimization, and policy enforcement [2]. This interdependency creates a scenario of double moral hazard, where both the regulator and operator exert costly, partially observable efforts that jointly determine the stochastic service outcome. In such environments, both parties may face incentives to shirk their responsibilities. Despite its practical relevance, the dynamic analysis of double moral hazard in public transit, particularly through rigorous continuous-time frameworks, remains substantially underexplored.

This paper addresses this gap by developing a continuous-time, non-cooperative game-theoretic model that analyzes the strategic interaction between a regulator and an operator under double moral hazard. Our framework extends the seminal work of Schättler and Sung (1993, 1997) on continuous-time principal-agent problems and builds upon Hihara’s (2014) application to bilateral relationships [16,17,18]. We demonstrate that, under specific technical assumptions, the optimal subsidy rules from each party’s individual perspective are linear functions of the final service quality. Furthermore, we establish that under idealized conditions—where both parties’ risk aversion approaches zero and optimal effort costs are negligible—they can agree on a single, mutually acceptable linear subsidy contract. The slope of this contract is determined by the difference in productivity ratios between the two parties and the level of environmental uncertainty. Finally, we show that under perfect symmetry, the subsidy mechanism may disappear entirely, highlighting that asymmetries are the fundamental rationale for incentive contracting. This study extends the literature by shedding light on the dynamic structure of optimal incentive arrangements for public transport subsidy contracts under double moral hazard, offering novel theoretical insights and policy implications.

2. Literature Review

With the advancement of global urbanization and the deepening of sustainable development agendas, the issue of public transit subsidization has become a research hotspot in recent years. Scholars widely agree that well-designed public transit subsidies are essential for enhancing the operational efficiency of urban mobility systems, promoting social equity, and achieving environmental goals [2,3,19]. The conceptual development of transit subsidy theory has evolved from macro-level justifications to micro-level mechanism design. Initially, researchers such as Mohring [20] and Vickrey [21] established the economic rationale for subsidies based on network externalities and economies of scale. Subsequently, as market-oriented reforms in public services took hold, scholars began applying contract theory to address the incentive and regulation problems inherent in subsidization. For instance, Hensher et al. [13] and Hooper [8] highlighted the significant potential of contract theory to manage uncertainty and asymmetric information, although its application in transport remained underdeveloped for some time.

Existing research can be broadly divided into the following two categories. The first stream centers on the objectives and efficacy of subsidies. Within this body of work, two representative perspectives emerge. One research strand argues that a primary objective of subsidies is to achieve environmental benefits by inducing a modal shift from private vehicles, thereby reducing air pollution and carbon emissions [3,22,23]. In contrast, another direction contends that a more critical objective is to ensure social equity and accessibility, particularly by providing affordable and barrier-free mobility for vulnerable groups such as low-income populations and persons with disabilities [19,24,25,26]. A key insight from this literature is the recognition that public transit subsidies are multifunctional policy instruments, often aiming to balance potentially conflicting goals such as efficiency, equity, and environmental protection. However, despite clear objectives, subsidy policies frequently yield inconsistent or even counterproductive results [4,5,27], raising the question of why these outcomes diverge from policy intentions. This forms the central concern of the second strand of research.

The second stream focuses on the design of subsidy contracts and the underlying incentive structures, typically framed through the lens of principal-agent theory. One line of inquiry focuses on comparing different subsidy models. For example, researchers have found that net-cost contracts, where the operator bears commercial risk, can lead to service quality degradation due to distorted incentives [10], whereas performance-based contracts, which may be linked to passenger demand or vehicle-kilometers, can better align operator behavior with public objectives [12,28]. Another perspective concentrates on risk allocation within the contract, arguing that the optimal incentive intensity depends on the agent’s risk preferences and necessitates a trade-off between risk transfer and incentive provision [13]. In addition, scholars such as Makovsek and Moszoro [14] and Bergland and Pedersen [15] have explored this from the angles of public-private partnerships (PPPs) and the integration of safety considerations, respectively, further enriching the understanding of cost-benefit trade-offs. We can see that this second body of literature builds upon the first by shifting from the macro-level question of “why subsidize” to the micro-level mechanism design of “how to subsidize,” thereby focusing on the core incentive structures that determine whether policy goals are achieved. Recent studies further extend these models to incorporate emerging mobility systems, such as ridesourcing and autonomous vehicles, highlighting the challenges and opportunities of integrating new modalities into public transport incentive structures [29,30,31].

The research above has made significant contributions to the study of public transit subsidization and has advanced the explanation of its underlying mechanisms. However, existing research has yet to systematically address the influence of the double moral hazard factor. Specifically, existing studies exhibit the following three key limitations: First, from a behavioral modeling perspective, the majority of studies assume a single-sided moral hazard, focusing solely on the operator as a strategic agent whose effort is unobservable and needs to be incentivized. However, the regulator (principal) also undertakes costly, unobservable actions, such as infrastructure investment, service network planning, and enforcement, which are also crucial to service quality but often treated as exogenous in prevailing models [9,10,32], neglecting the full strategic interplay between both parties.

Second, in terms of methodological approaches, most research employs static or discrete-time models, including econometric analyses and game-theoretic models with a limited number of stages. These models inadequately capture the dynamic, continuous nature of transit service provision and regulatory effort. In reality, public transit service quality is a stochastic process that evolves continuously over time, making continuous-time modeling more suitable for capturing long-run incentive dynamics [11,12,13,33].

Third, from a contractual equilibrium perspective, existing studies have focused more on deriving a unilateral “optimal contract” from the regulator’s standpoint, treating the agent as a constraint to be managed. They have less frequently investigated how a mutually agreeable equilibrium contract emerges from the dynamic interaction and negotiation between two strategic agents, both of whom face moral hazard. The prevailing arguments often neglect the regulator’s own incentive problem, which means the “optimal” contracts they propose may not be robust or implementable in a double moral hazard context [9,11,34,35].

Building on the above analysis, this study investigates the optimal design of public transit subsidy contracts under conditions of dual moral hazard, employing a continuous-time principal-agent framework. It aims to determine how incentive contracts should be structured in a dynamic environment where both regulators and operators engage in unobservable effort. The study contributes to the theoretical and practical understanding of robust, implementable subsidy mechanisms that reflect real-world institutional and behavioral complexities.

3. The Model

This section develops a continuous-time principal-agent model to analyze the strategic interaction between a public transit regulator (the principal, denoted by R) and a service operator (the agent, denoted by O) under conditions of double moral hazard. Both parties exert costly, unobservable efforts that stochastically determine the quality of public transit service. The objective is to characterize the optimal subsidy contract (sharing rule) that governs payments from the regulator to the operator. Our framework builds upon the continuous-time agency models with exponential utility pioneered by Schaettler and Sung (1993, 1997) [16,17] and its application to bilateral relationships by Hihara (2014) [18].

3.1. Model Setup and Assumptions

We consider a contractual relationship over a finite time horizon $t\in [0,T]$, where T represents the duration of the subsidy agreement (e.g., one year). The primary parties in this interaction are a Regulator (R), who acts as the principal with the objective of procuring a certain level of public transit service quality and designs the corresponding subsidy contract, and an Operator (Agent,A), who acts as the agent responsible for providing the public transit service and is a recipient of the subsidy from the regulator.

Both parties undertake costly efforts to influence the service outcome. The regulator exerts effort $e\left(t\right)\in \mathcal{E}\subseteq {\mathbb{R}}^{+}$ at time t, which can encompass a range of activities such as strategic investments in infrastructure, optimization of route planning, diligent regulatory oversight, enforcement of predefined service standards, or the implementation of public information campaigns designed to enhance service attractiveness. Concurrently, the operator exerts effort $a\left(t\right)\in \mathcal{A}\subseteq {\mathbb{R}}^{+}$ at time t.This effort may include maintaining vehicle fleets to a high standard, optimizing operational schedules for punctuality and efficiency, investing in driver training programs, enhancing customer service initiatives, or innovating in service delivery methods. Both $e\left(t\right)$ and $a\left(t\right)$ are assumed to be Ft-predictable processes, where Ft represents the filtration embodying all information available up to time t. A crucial aspect of our model, giving rise to the central problem of double moral hazard, is the unobservability of these efforts: $e\left(t\right)$ is unobservable to the operator, and $a\left(t\right)$ is unobservable to the regulator.

The outcome of these joint efforts is the realized quality of public transit service at time t, denoted by $q\left(t\right)$. This service quality is modeled as a stochastic process, observable by both parties throughout the contract period. Its evolution is described by the following Ito process:

$$dq\left(t\right)=f(e\left(t\right),a\left(t\right))dt+\sigma (q\left(t\right),t)d{B}_t$$

(1)

Where: $f\left(e\right(t),a(t\left)\right)$ is the production function for service quality, representing the expected instantaneous change in quality due to the efforts of both the regulator and the operator. $\sigma \left(q\right(t),t)$ is the diffusion rate (volatility), capturing the uncertainty or random shocks affecting service quality (e.g., unexpected demand fluctuations, operational disruptions, weather). We assume $\sigma >0$. $d{B}_t$ is the increment of a standard one-dimensional Wiener process $B_t$, representing the source of randomness, defined on a complete probability space $(\Omega ,\mathcal{F},P)$.

At the commencement of the relationship ($t=0$), the regulator and operator agree on a subsidy contract, or sharing rule, denoted by S. This contract specifies a net monetary transfer, $S\left(q\right(T\left)\right)$, from the regulator to the operator at the end of the contract period T. The magnitude and direction of this transfer are contingent upon the realized final service quality, $q\left(T\right)$.

Both parties are assumed to be risk-averse and maximize their expected exponential utility.The regulator’s objective is to maximize its expected utility, $U_R$, derived from the social welfare generated by the service quality, net of subsidy payments and its own effort costs:

$$U_R=-exp\left[-{\rho }_R\left\{W\left(q\left(T\right)\right)-S\left(q\left(T\right)\right)-{\int }_0^T{c}_R\left(e\left(t\right)\right)dt\right\}\right]$$

(2)

Here, ${\rho }_R>0$ is the regulator’s constant coefficient of absolute risk aversion (CARA).The function $W\left(q\right(T\left)\right)$ represents the monetized social welfare or benefit (e.g., increased ridership benefits, reduced congestion costs, enhanced city image) derived by the regulator from the final service quality, and we assume $W^{\prime }\left(q\right)>0$. The term $S\left(q\right(T\left)\right)$ is the subsidy paid to the operator, and ${\int }_0^T{c}_R\left(e\left(t\right)\right)dt$ is the total cost of effort incurred by the regulator. Symmetrically, the operator’s objective is to maximize its expected utility, $U_O$, derived from its operational revenue and the received subsidy, net of its effort costs:

$$U_A=-exp\left[-{\rho }_A\left\{Rev\left(q\left(T\right)\right)+S\left(q\left(T\right)\right)-{\int }_0^T{c}_A\left(a\left(t\right)\right)dt\right\}\right]$$

(3)

In this formulation, ${\rho }_A>0$ > 0 is the operator’s CARA coefficient. $Rev\left(q\right(T\left)\right)$ represents the operational revenue accruing to the operator from the final service quality $q\left(T\right)$ (e.g., farebox revenue, which may depend on service quality and ridership), with $Re{v}^{\prime }\left(q\right)>0$. $S\left(q\right(T\left)\right)$ is the subsidy received, and ${\int }_0^T{c}_A\left(a\left(t\right)\right)dt$ is the operator’s total effort cost.

To ensure a well-behaved model, we make standard functional form assumptions. The effort cost functions, $c_R\left(e\right)$ and $c_A\left(a\right)$, are assumed to be strictly increasing, strictly convex ($c^{\prime }>0$, $c^{\prime \prime }>0$), and twice continuously differentiable, with $c\left(0\right)=0$ and $c^{\prime }\left(0\right)\ge 0$. The production function $f(e,a)$ is assumed to be increasing in both arguments ( $\partial f/\partial e>0$, $\partial f/\partial a>0$), concave (i.e., its Hessian matrix f is negative semi-definite), and twice continuously differentiable. Similarly, the welfare function $W\left(q\right)$ and the revenue function $Rev\left(q\right)$ are assumed to be increasing and concave ($W^{\prime }>0,W^{\prime \prime }\le 0$, and $Re{v}^{\prime }>0,Re{v}^{\prime \prime }\le 0$).

Both parties are risk-averse with constant absolute risk-aversion (CARA) preferences and aim to maximize the expected utility of their terminal wealth. For our analysis, we will work with two key functions: the indirect value function, $V_i(t,q)$, representing expected utility, and its monetary equivalent, the certainty-equivalent wealth, $W_i(t,q)$. They are linked by the CARA utility function: $V_i(t,q)=-exp(-{\rho }_i{W}_i(t,q))$ for $i\in \{R,A\}$. The subsidy contract, $S\left(q\right(T\left)\right)$, is a terminal payment contingent on the final service quality.

3.2. Decentralized Decision-Making and Problem Formulation

We model the interaction as a non-cooperative game where each party independently chooses its effort strategy to maximize its own expected utility, anticipating the rational response of the other party. This constitutes a decentralized utility maximization problem under double moral hazard.

The overall problem (conceptually referred to as Problem A, following Hihara (2014) [18]) is to find a subsidy rule $S^{*}\left(q\left(T\right)\right)$ and effort profiles $e^{*}\left(t\right)$ and $a^{*}\left(t\right)$ such that:

• Given $S^{*}\left(q\left(T\right)\right)$ and anticipating $a^{*}\left(t\right)$, the regulator chooses $e^{*}\left(t\right)$ to maximize $E\left[U_R\right]$:

  $$e^{*}\left(t\right)\in arg\underset{e\left(t\right)}{max}E\left[-{\rho }_R\left\{W\left(q\left(T\right)\right)-S^{*}\left(q\left(T\right)\right)-{\int }_0^T{c}_R\left(e\left(t\right)\right)dt\right\}|a^{*}\left(t\right)\right]$$

  (4)
• Given $S^{*}\left(q\left(T\right)\right)$ and anticipating $e^{*}\left(t\right)$, the operator chooses $a^{*}\left(t\right)$ to maximize $E\left[U_O\right]$:

  $$a^{*}\left(t\right)\in arg\underset{a\left(t\right)}{max}E\left[-{\rho }_A\left\{Rev\left(q\left(T\right)\right)+S^{*}\left(q\left(T\right)\right)-{\int }_0^T{c}_A\left(a\left(t\right)\right)dt\right\}|e^{*}\left(t\right)\right]$$

  (5)
• The subsidy rule $S^{*}\left(q\left(T\right)\right)$ is, in some sense, optimal or agreeable given these interdependent optimizations. The specific nature of this optimality will be developed through the propositions in Section 4.

This formulation captures the essence of the strategic interdependence. The derivation of the optimal sharing rule $S^{*}\left(q\left(T\right)\right)$ and the associated effort levels will rely on applying the necessary and sufficient conditions from continuous-time principal-agent theory.

3.3. Key Analytical Assumptions

To make the analysis tractable and to leverage the theoretical results from Schaettler and Sung (1993) [16], we introduce the following crucial analytical assumptions, analogous to those in Hihara (2014) [18]:

Assumption 1 

(Additive Separability of Efforts in the Production Function). The efforts of the regulator and the operator are additively separable in their impact on the drift of service quality, or more generally, their interaction term in the production function is zero:

$${\displaystyle \frac{{\partial }^{2}f(e,a)}{\partial e\partial a}}=0$$

(6)

This assumption simplifies the analysis by allowing us to treat the marginal product of one party’s effort as independent of the other party’s effort level.

Assumption 2 

(Convexity of the Relevant Hamiltonian-like Function). For any relevant real-valued parameter p (which can be interpreted as a shadow price or marginal value derived from the optimization process), the function:

$$H_s(p,e,a)=p·f(e,a)+c_R\left(e\right)+c_A\left(a\right)$$

(7)

is strictly convex in both e and a, and possesses unique stationary points with respect to e and a. This assumption is critical for ensuring the validity of the first-order approach and the implementability of the derived sharing rules within the Schaettler and Sung (1993) [16] framework (specifically, their Theorems 4.1 and 4.2). It guarantees that the first-order conditions correctly characterize optimal effort choices.

Assumption 3 

(Linear Solution Structure). To derive a tractable closed-form solution, we posit that the optimal contract is linear. This structural assumption implies that the certainty-equivalent wealth function $W_i(t,q)$ is also linear in q, and consequently, its derivative $\partial W_i/\partial q$ is constant.

4. Derivation and Analysis of Optimal Subsidy Rules

This Section presents the core theoretical analysis of the paper, solving the dynamic optimization problem formulated in Section 3 to characterize the optimal subsidy rule. Our analysis unfolds in a structured sequence. We begin by introducing the Hamilton-Jacobi-Bellman (HJB) equation as our primary analytical tool. We then employ it to derive the optimal sharing rules from the individual perspectives of the regulator and the operator, culminating in Proposition 1, which reveals that the preferred contract structure for both parties is inherently linear. Recognizing that these individually optimal rules are generally divergent, we subsequently establish the idealizing conditions necessary for them to converge into a single, mutually agreeable contract, leading to Proposition 2. Finally, we explore the theoretical benchmark of perfect symmetry to distill the fundamental drivers of incentive contracting, resulting in Proposition 3.

4.1. The Hamilton-Jacobi-Bellman (HJB) Equation

The core of our analysis relies on the Hamilton-Jacobi-Bellman (HJB) equation, which characterizes the value function for each party in this dynamic optimization problem. Applying Ito’s Lemma to the agent’s (operator’s) value function $V_A(t,q\left(t\right))$ and incorporating the utility drift from effort costs, the principle of optimality implies that the value function must satisfy:

$$0={\displaystyle \frac{\partial V_A}{\partial t}}+\underset{a}{max}\left\{f(e,a){\displaystyle \frac{\partial V_A}{\partial q}}+{\rho }_A{V}_A{c}_A\left(a\right)\right\}+{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2{V}_A}{\partial q^2}}$$

(8)

While this V-form HJB is fundamental, it is more convenient to work with the certainty-equivalent wealth, $W_A$. A standard algebraic substitution using the relationship $V_A=-exp(-{\rho }_A{W}_A)$ yields the HJB equation for the agent’s wealth:

$$-{\displaystyle \frac{\partial W_A}{\partial t}}=\underset{a}{max}\left\{f(e,a){\displaystyle \frac{\partial W_A}{\partial q}}-c_A\left(a\right)\right\}+{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2{W}_A}{\partial q^2}}-{\displaystyle \frac{{\rho }_A}{2}}{\sigma }^2{\left({\displaystyle \frac{\partial W_A}{\partial q}}\right)}^2$$

(9)

This equation forms the foundation for our derivation. It elegantly separates the agent’s direct optimization problem (the ‘max’ term) from terms related to environmental uncertainty and risk premium. A symmetric HJB equation exists for the regulator.

4.2. Optimal Sharing Rules from Individual Perspectives

We now employ the HJB equation to solve for the optimal sharing rules from the decentralized perspectives of the operator and the regulator. This analysis reveals the functional form of the contract that each party would individually prefer.

4.2.1. Operator’s (Agent’s) Perspective

The agent’s first-order condition (FOC) from its HJB equation (9) yields that its shadow price of quality, $\partial W_A/\partial q$, must equal its productivity ratio, $P_A$. Positing a linear solution structure (Assumption 3.3) simplifies the HJB equation. Following the full derivation path—which involves deriving the wealth process dynamics $d{W}_A$, integrating it, and equating it with the terminal wealth identity—we solve for the agent’s individually optimal subsidy rule. The derivation reveals an explicitly linear form:

$$S_A\left(q\left(T\right)\right)=(P_A-R_1)·q\left(T\right)+K_A$$

(10)

where we assume the operator’s revenue is linear, $\mathrm{Rev}\left(q\right)=R_0+R_{1}q$, and the intercept $K_A$ consolidates all terms not dependent on $q\left(T\right)$, including the agent’s effort costs and risk premium.

4.2.2. Regulator’s (Principal’s) Perspective

A symmetric analysis for the principal, starting from its own HJB equation, yields its productivity ratio $P_R=\partial W_R/\partial q$. The same derivation procedure shows that the subsidy rule from the principal’s perspective is also linear:

$$S_R\left(q\left(T\right)\right)=(W_1-P_R)·q\left(T\right)+K_R$$

(11)

where we assume social welfare is linear, $W\left(q\right)=W_0+W_{1}q$, and $K_R$ is the principal-specific intercept.

4.2.3. Linearity of Individually Optimal Sharing Rules

The parallel derivations for both the agent and the principal demonstrate that, despite their different objectives, both parties’ individually optimal contracts share a common functional form.

Proposition 1. 

The optimal sharing rules derived from the individual, decentralized utility maximization problems of both the regulator and the operator are linear functions of the final service quality, $q\left(T\right)$.

Proof. 

The proof follows directly from the derivations culminating in Equations (10) and (11), which explicitly show the linear structure of $S_A\left(q\left(T\right)\right)$ and $S_R\left(q\left(T\right)\right)$, respectively. □

Remark 1. 

The constant terms $K_R$ and $K_A$ in Equations (11) and (10) will generally differ due to distinct effort costs and risk premia specific to each party. This implies $S_R\left(q\left(T\right)\right)\ne S_A\left(q\left(T\right)\right)$ in general, which necessitates further assumptions to find a single, mutually agreeable contract.

4.3. The Agreeable Single Linear Subsidy Rule

While proposition 1 establishes linearity as the preferred contract form, the divergence in the individually optimal rules necessitates a framework for convergence. To find a single, mutually agreeable contract, we must impose stronger, idealizing assumptions.

Assumption 4 

(Asymptotic Convergence and Negligible Costs). We assume that (i) a single agreeable sharing rule $S^{*}$ exists as the common limit when the parties’ risk aversion parameters and effort costs approach zero, and (ii) the optimal effort costs are negligible, $c_R\left(e^{*}\right)\approx 0$ and $c_A\left(a^{*}\right)\approx 0$.

Proposition 2. 

Under the idealizing conditions of Assumption 4.1, the parties can agree on a single linear subsidy rule that optimally trades off incentives and risk-sharing:

$$S^{*}\left(q\left(T\right)\right)=(P_R-P_A)(1-\overline{\sigma })q\left(T\right)+K^{*}$$

(12)

where the slope is driven by the asymmetry in productivity $(P_R-P_A)$ and dampened by environmental uncertainty $(1-\overline{\sigma })$, and $K^{*}$ is a constant intercept representing a fixed transfer based on initial endowments.

Proof. 

The proof proceeds by examining the full expressions for $S_A\left(q\left(T\right)\right)$ and $S_R\left(q\left(T\right)\right)$. The intercepts of these rules contain terms for each party’s effort costs and risk premia, which are the sources of their divergence. By Assumption 4.1, we take the limits as ${\rho }_R\to 0$ and ${\rho }_A\to 0$, which causes all risk premium terms to vanish. Furthermore, the assumption of negligible effort costs eliminates the effort cost terms. Once these sources of disagreement are removed, the remaining components of the intercepts can be reconciled into a single fixed transfer, $K^{*}$. The slope term $(P_R-P_A)(1-\overline{\sigma })$, which models the risk-incentive trade-off, is common to both perspectives in the equilibrium analysis and thus forms the slope of the final agreeable contract. □

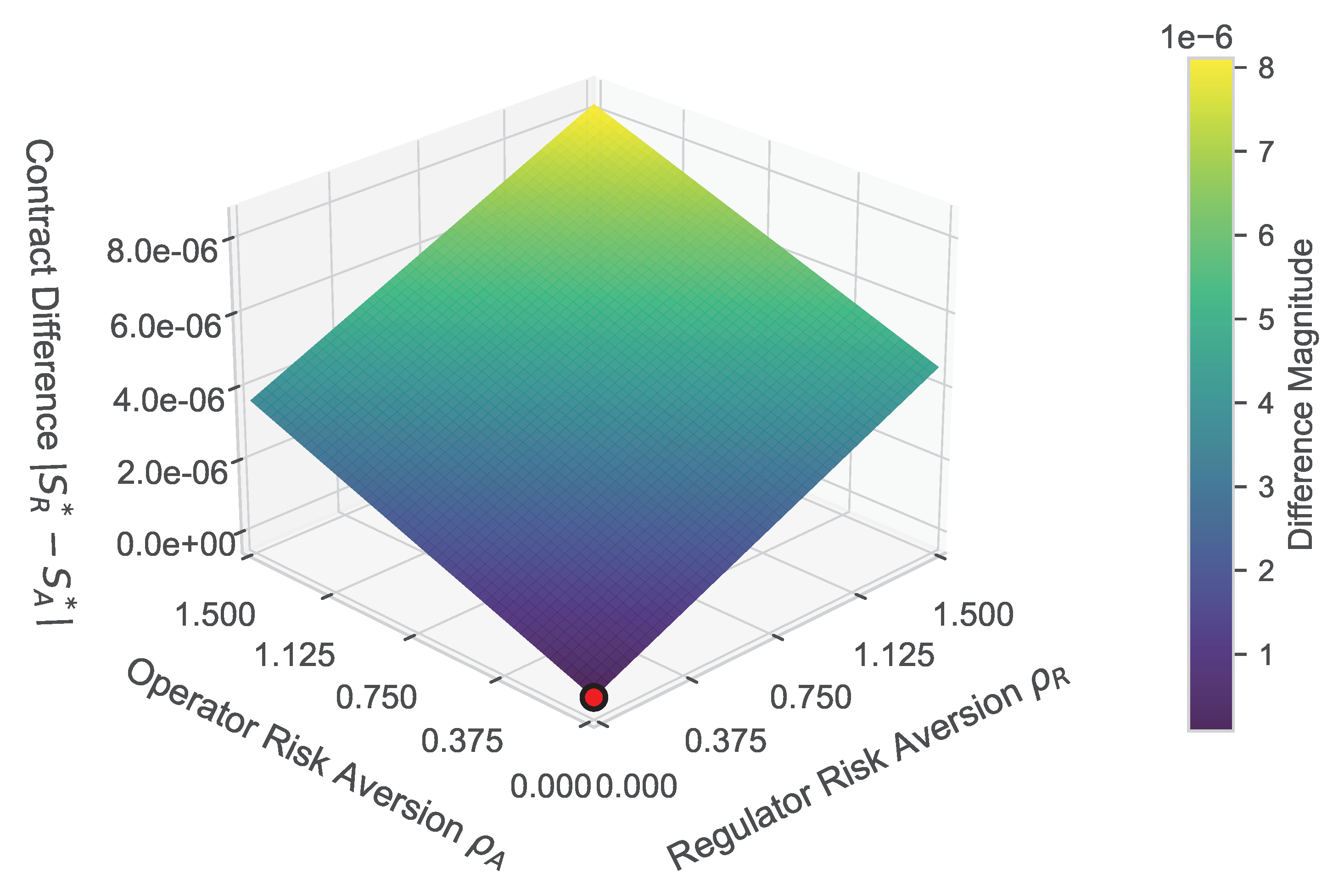
4.4. Theoretical Benchmark: Perfect Symmetry

To distill the fundamental drivers of incentive contracting, we next consider a theoretical benchmark of perfect symmetry.

Assumption 5 

(Perfect Symmetry). In addition to the preceding assumptions, we assume perfect symmetry between the parties. This implies: (1) Identical productivity ratios: $P_R=P_A$. (2) Symmetric initial endowments and objectives, such that the resulting intercept term $K^{*}$ in Proposition 2 is zero.

Proposition 3. 

Under perfect symmetry (Assumption 4.2), the agreeable subsidy rule disappears completely: $S^{*}\left(q\left(T\right)\right)=0$.

Proof. 

The proof follows directly by substituting the conditions of Assumption 4.2 into the agreeable sharing rule given by Proposition 2. The condition $P_R=P_A$ makes the slope term zero. The condition of symmetric endowments makes the intercept term zero. Thus, $S^{*}\left(q\left(T\right)\right)=0·q\left(T\right)+0=0$. This highlights that asymmetry is the fundamental rationale for incentive contracting. □

5. Numerical Illustration and Discussion

To further elucidate the implications of our theoretical findings, this section provides a numerical illustration of the model. By specifying concrete functional forms and parameter values, we can simulate the model’s dynamics, visualize the optimal contract, and analyze its sensitivity to key parameters, particularly the level of environmental uncertainty.

5.1. Concrete Functional Forms and Settings

To operationalize the model for simulation, we adopt specific functional forms consistent with the assumptions made in Setion 3.

• Production Function: We assume a linear production function where efforts contribute additively to the drift of service quality:

  $$f(e,a)=e+a$$

  (13)
  This form satisfies the additive separability requirement (Assumption 3.1).
• Cost Functions: We employ quadratic cost functions, which are strictly increasing and convex for positive effort levels:

  $$\begin{array}{cc}\hfill c_R\left(e\right)& ={\displaystyle \frac{1}{2}}{k}_R{e}^2\hfill \end{array}$$

  (14)

  $$\begin{array}{cc}\hfill c_A\left(a\right)& ={\displaystyle \frac{1}{2}}{k}_A{a}^2\hfill \end{array}$$

  (15)

  where $k_R>0$ and $k_A>0$ are cost parameters representing the efficiency of effort for the Regulator and Agent, respectively. A higher k implies a higher marginal cost of effort.

Under these specifications, the productivity ratios, $P_R$ and $P_A$, central to the optimal contract, can be explicitly calculated using their definitions from Chapter 4. For instance, for the agent:

$$P_A={\displaystyle \frac{\partial c_A\left(a\right)/\partial a}{\partial f(e,a)/\partial a}}={\displaystyle \frac{k_{A}a}{1}}=k_{A}a$$

(16)

This implies that to maintain a constant productivity ratio $P_A$ (as required by our linear solution structure), the optimal effort $a^{*}$ must also be constant, given by $a^{*}=P_A/k_A$. A similar logic holds for the regulator’s effort, $e^{*}=P_R/k_R$.

5.2. Baseline Parameterization

We select a set of baseline parameters for our numerical example. These values are chosen for illustrative purposes to represent a plausible scenario where the regulator and operator have different efficiencies and productivity targets.

Table 1. Baseline Parameter Values for Numerical Simulation.

Parameter	Symbol	Value
Regulator’s Productivity Ratio	$P_R$	0.055
Operator’s Productivity Ratio	$P_A$	0.011
Regulator’s Cost Parameter	$k_R$	11
Operator’s Cost Parameter	$k_A$	2.2
Initial Service Quality	$q\left(0\right)$	0.70
Uncertainty (Diffusion Rate)	$\sigma$	(Varied from 0 to 1.5)
Risk Aversion Parameters	${\rho }_R,{\rho }_A$	Approaching 0
Effort Costs	$c_R\left(e^{*}\right),c_A\left(a^{*}\right)$	Assumed negligible

Table 1. Baseline Parameter Values for Numerical Simulation.

Parameter	Symbol	Value
Regulator’s Productivity Ratio	$P_R$	0.055
Operator’s Productivity Ratio	$P_A$	0.011
Regulator’s Cost Parameter	$k_R$	11
Operator’s Cost Parameter	$k_A$	2.2
Initial Service Quality	$q\left(0\right)$	0.70
Uncertainty (Diffusion Rate)	$\sigma$	(Varied from 0 to 1.5)
Risk Aversion Parameters	${\rho }_R,{\rho }_A$	Approaching 0
Effort Costs	$c_R\left(e^{*}\right),c_A\left(a^{*}\right)$	Assumed negligible

With these parameters, the optimal efforts are calculated as: $e^{*}=P_R/k_R=0.055/11=0.005$ and $a^{*}=P_A/k_A=0.011/2.2=0.005$. The associated costs, $c_R\left(e^{*}\right)={\displaystyle \frac{1}{2}}\left(11\right){\left(0.005\right)}^2\approx 0.0001375$, are indeed small, consistent with the negligible cost assumption for the agreeable contract (Assumption 4.1).

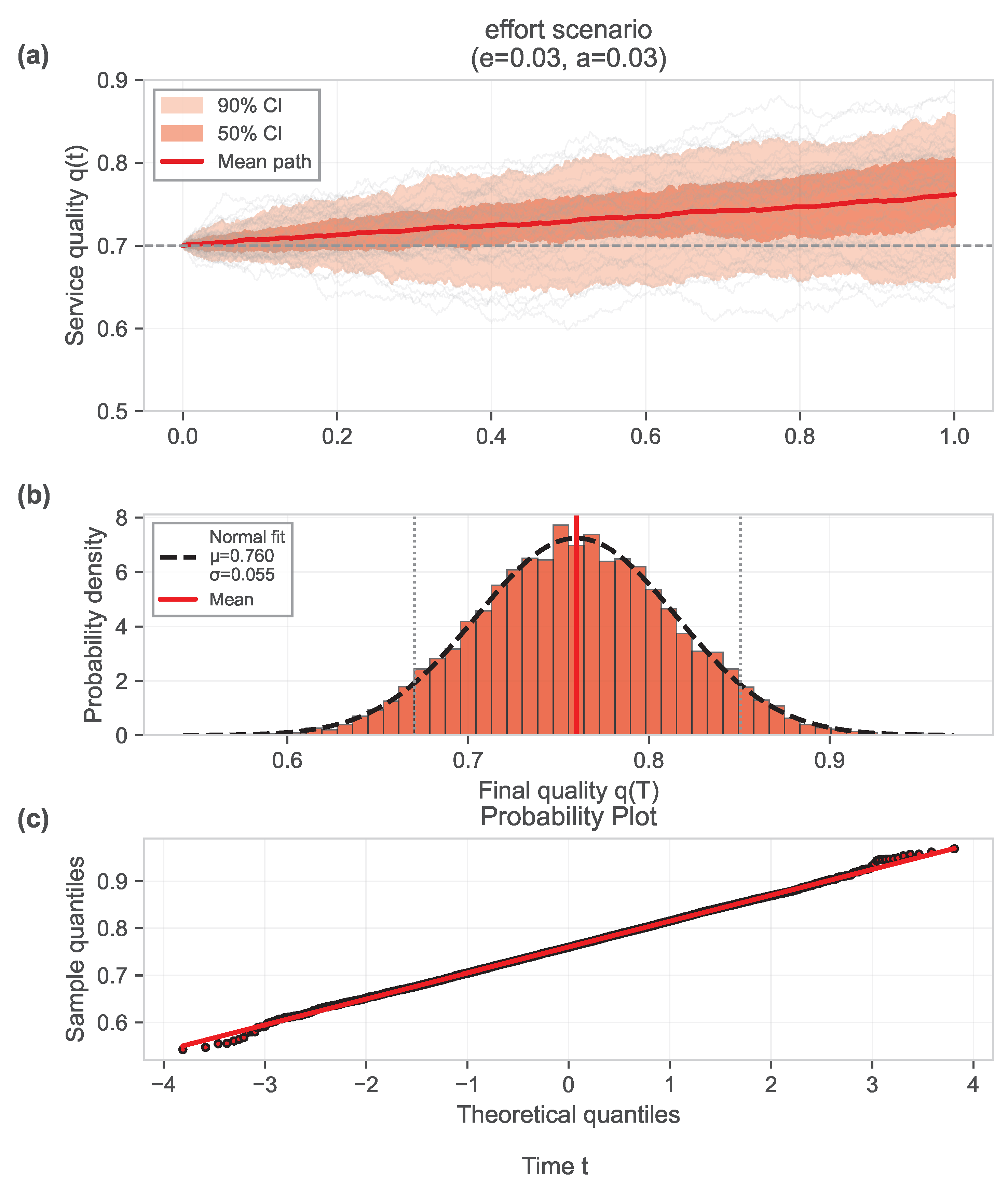
5.3. Simulation Results and Sensitivity Analysis

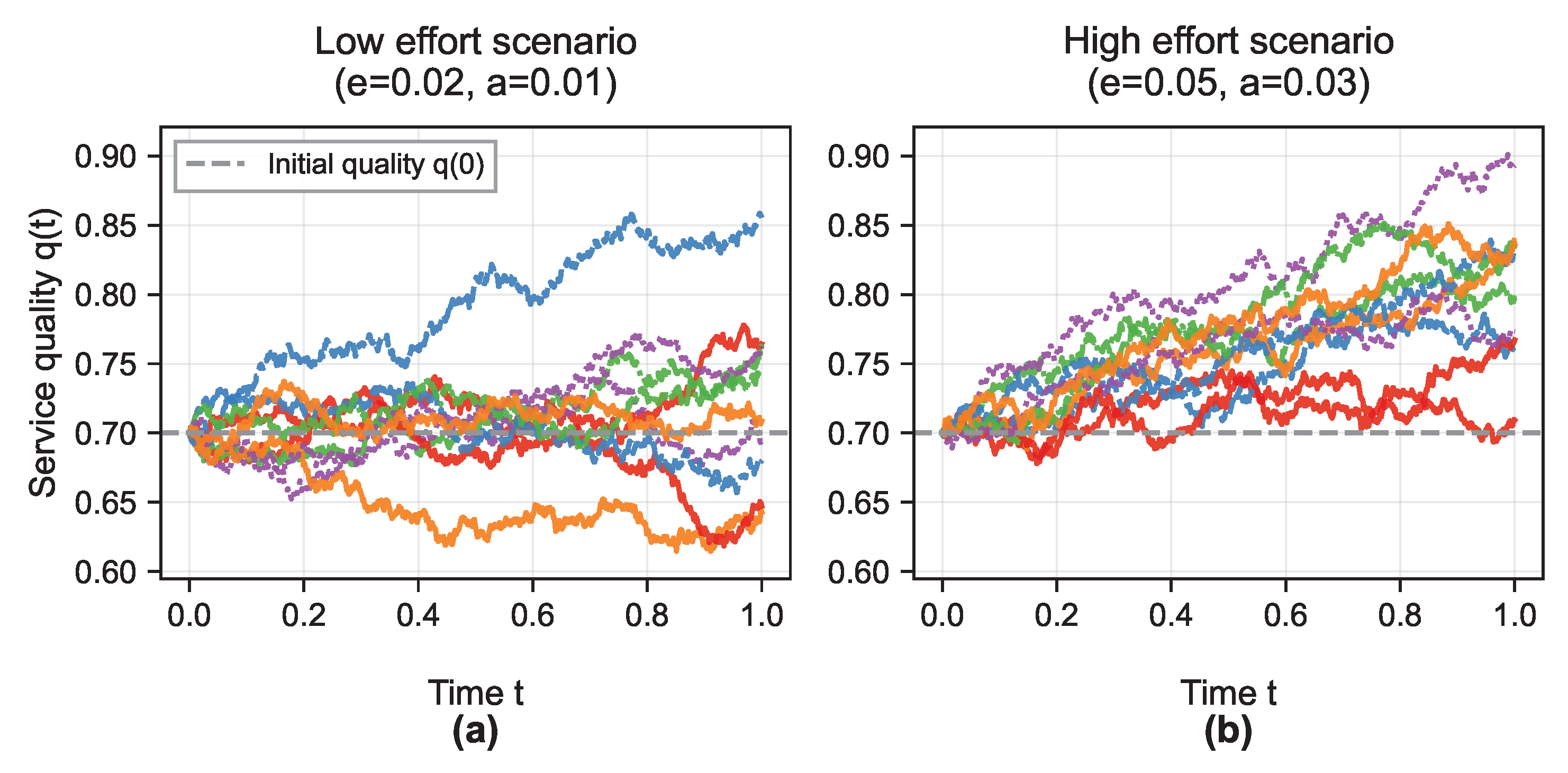
5.3.1. Sample Paths of Service Quality

To visualize the stochastic nature of the process, we begin by simulating sample paths of the service quality state variable, $q\left(t\right)$. Figure 1 illustrates two scenarios: a “Low effort” case and a “High effort” case, each showing five distinct sample paths originating from the same initial quality level.

The comparison between the two panels powerfully illustrates the role of effort in a stochastic environment.In the “Low effort” scenario (left panel), the paths exhibit a clear downward trend on average, indicating that the effort level is insufficient to sustain the initial quality. Conversely, in the “High effort” scenario (right panel), the paths show a distinct upward drift. This demonstrates that while effort cannot eliminate uncertainty, it systematically determines the expected trajectory of service quality.In both scenarios, the paths starting from the same point fan out over time, driven by the random shocks ($\sigma d{B}_t$). The wide distribution of final outcomes, even under identical effort profiles, provides clear visual evidence that the final quality is a noisy signal of the parties’ actions. This underscores the necessity of a risk-sharing mechanism in the optimal contract.

Figure 2(a) illustrates the evolution of service quality $q\left(t\right)$ under the effort scenario ($e=0.03$, $a=0.03$) based on Monte Carlo simulations. The bold red curve represents the mean path of service quality across all simulation runs, while the shaded areas denote the 50% and 90% confidence intervals (CI). It can be observed that the average service quality gradually improves over time, stabilizing around a level slightly above the initial value of 0.7. The widening confidence intervals indicate increasing uncertainty as time progresses, yet the overall range remains relatively narrow, suggesting that the effort scenario ensures a robust and stable system outcome.

Figure 2(b) presents the empirical distribution of service quality at the terminal time $t=1$. The histogram reveals a unimodal, right-skewed distribution centered around 0.76, consistent with the simulated mean final quality of 0.7599. The standard deviation is approximately 0.0550, and the estimated 95% confidence interval for the terminal quality is $[0.6702,0.8506]$. The concentration of outcomes in the range of 0.7–0.8 implies that most simulations result in satisfactory service levels, with very few instances falling below 0.65. This confirms the effectiveness of the chosen effort levels in maintaining desirable quality outcomes.

Figure 2(c) presents a probability plot comparing the empirical quantiles of the simulated results against a theoretical normal distribution. The close alignment of the quantiles suggests that the distribution of terminal service quality under this effort scenario approximately follows a Gaussian pattern, reinforcing the validity of the normal approximation used in statistical inference.

These results highlight that moderate efforts from both the regulator and the operator ($e=0.03$, $a=0.03$) lead to a favorable balance between service quality improvement and uncertainty control, offering an effective and stable performance trajectory over time.

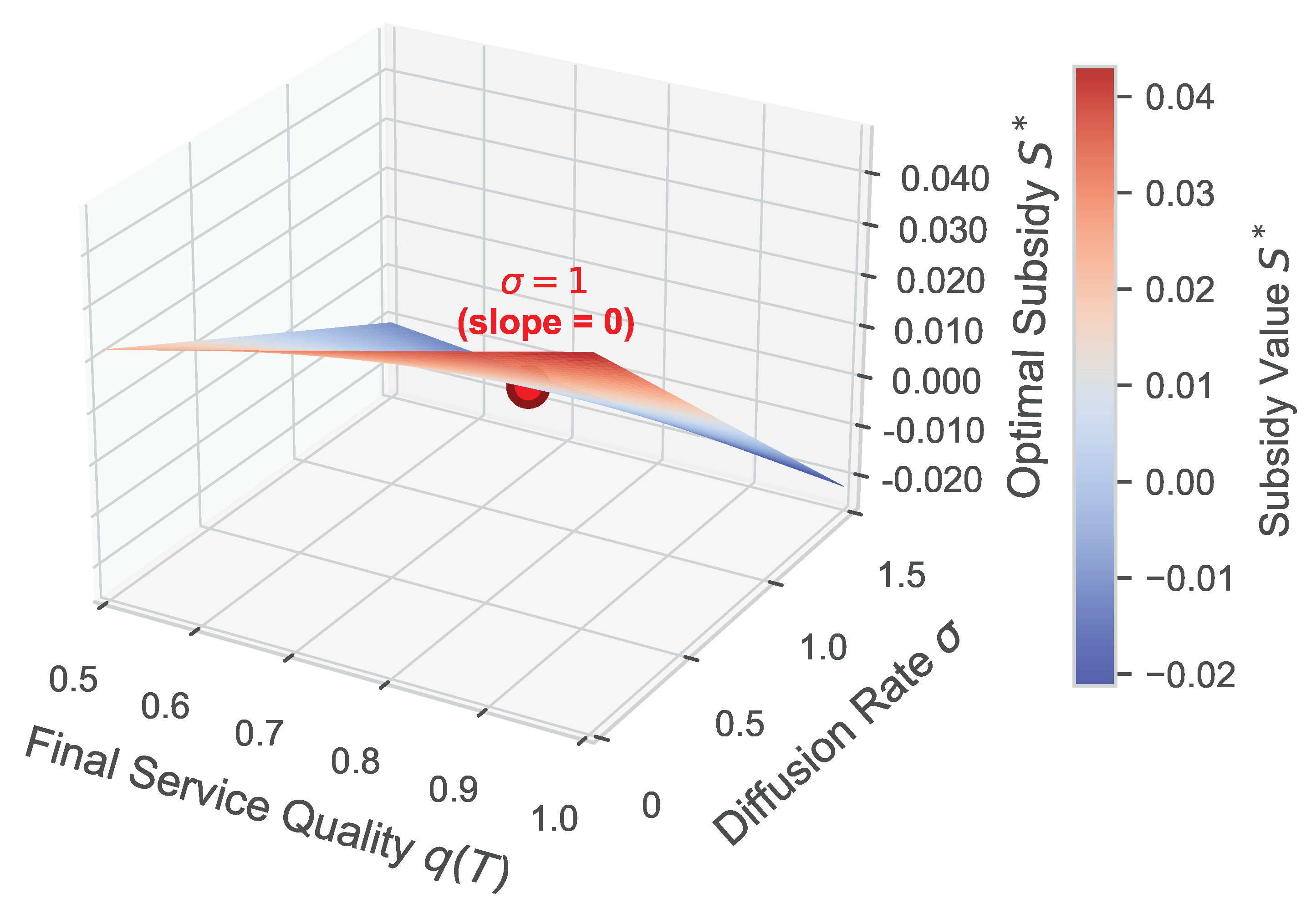
5.3.2. Sensitivity of the Optimal Contract to Uncertainty

The core theoretical result of Proposition 4.2 is that the slope of the agreeable linear contract, $S^{*}$, is given by $(P_R-P_A)(1-\sigma )$. This slope represents the intensity of the performance incentive. A key question is how this incentive intensity should be adjusted in response to changes in environmental uncertainty, $\sigma$. We plot the optimal slope as a function of $\sigma$ in Figure 3. The result clearly illustrates the fundamental risk-incentive trade-off.

As shown in Figure 3, the relationship between the optimal slope and uncertainty is linear and decreasing, revealing distinct regimes of contract behavior across different uncertainty levels. When $\sigma =0$ (no uncertainty), the slope reaches its maximum value, equal to the full productivity difference $P_R-P_A=0.044$. In this deterministic environment, there is no need for risk sharing, and the contract can provide the strongest possible performance incentive since the final outcome perfectly signals the parties’ efforts.

As uncertainty $\sigma$ increases, the optimal slope decreases systematically. This occurs because higher $\sigma$ makes the final outcome $q\left(T\right)$ a “noisier” signal of the parties’ efforts. Tying compensation strongly to a noisy signal imposes excessive and inefficient risk on both parties. The contract optimally responds by reducing the incentive intensity to provide better risk sharing, demonstrating the fundamental tension between motivation and risk protection. The critical threshold occurs when $\sigma =1$, where the slope becomes exactly zero. At this point, the negative effect of the compensation error precisely cancels out the positive incentive effect from the productivity difference, transforming the optimal contract into a fixed payment that is completely independent of the final outcome.

Perhaps most remarkably, when $\sigma >1$, the slope becomes negative, implying that higher service quality leads to a lower subsidy or equivalently, a higher payment from the operator to the regulator. This counterintuitive result occurs because the risk-sharing motive now dominates the incentive motive, making the contract function more like an insurance policy against poor outcomes rather than a performance incentive mechanism. The surface plot provides a comprehensive visualization of these relationships, confirming the linearity in performance for any fixed uncertainty level $\sigma <1$, where the subsidy $S^{*}$ increases linearly with final quality $q\left(T\right)$, maintaining the “pay-for-performance” structure. The surface’s “twisted” appearance reflects the decreasing incentive slope as a function of $\sigma$, visually representing how riskier environments require reduced incentive intensity to achieve optimal risk sharing. At the critical point $\sigma =1$, the surface becomes completely flat with respect to $q\left(T\right)$, indicating pure fixed-payment contracting, while beyond this threshold, the negative slope transforms the contract’s primary function from incentive provision to insurance protection.

5.3.3. Analysis of Contract Convergence

Figure 4 provides a visual proof for the conditions under which a single, agreeable sharing rule can be reached. It plots the magnitude of the disagreement between the parties’ individually optimal contracts, $|S_R^{*}-S_A^{*}|$, as a function of the Regulator’s risk aversion, ${\rho }_R$, and the Operator’s risk aversion, ${\rho }_A$. The surface illustrates the central role of risk preferences in creating divergence and the necessity of risk neutrality for convergence.

The plot reveals that the difference between the contracts is a monotonically increasing, linear function of both parties’ risk aversion parameters. The surface is a tilted plane, with its lowest point at the origin $({\rho }_R=0,{\rho }_A=0)$, where the disagreement magnitude is precisely zero. This visually confirms a core theoretical premise: a complete consensus on the sharing rule is only achievable in the idealized benchmark where both parties are risk-neutral. As either ${\rho }_R$ or ${\rho }_A$ increases, the plane rises, indicating that any degree of risk aversion from either party introduces a non-zero divergence. This divergence stems from the risk premium components embedded within each party’s individually optimal contract intercept. A risk-averse party requires compensation for bearing uncertainty, and this demand creates a gap relative to the other party’s preferred terms.

Furthermore, the plane’s tilt is asymmetric. The gradient is steeper along the Regulator’s risk aversion axis (${\rho }_R$) than along the Operator’s axis (${\rho }_A$). This is a direct consequence of the parties’ differing productivity ratios ($P_R>P_A$ in our parameterization). The party with the higher productivity ratio (the Regulator) has a larger stake in the performance-contingent outcome, making their risk premium more sensitive to changes in their risk aversion. Consequently, the Regulator’s risk attitude has a more significant impact on the magnitude of the contractual disagreement. Figure 4 powerfully illustrates that reaching an “agreeable” contract, as formalized in Proposition 2, necessitates the strong assumptions of asymptotic risk-neutrality for both parties. It shows that in the presence of risk aversion, a bargaining problem arises, and the distance between the two parties’ desired contracts is a predictable function of their respective attitudes toward risk.

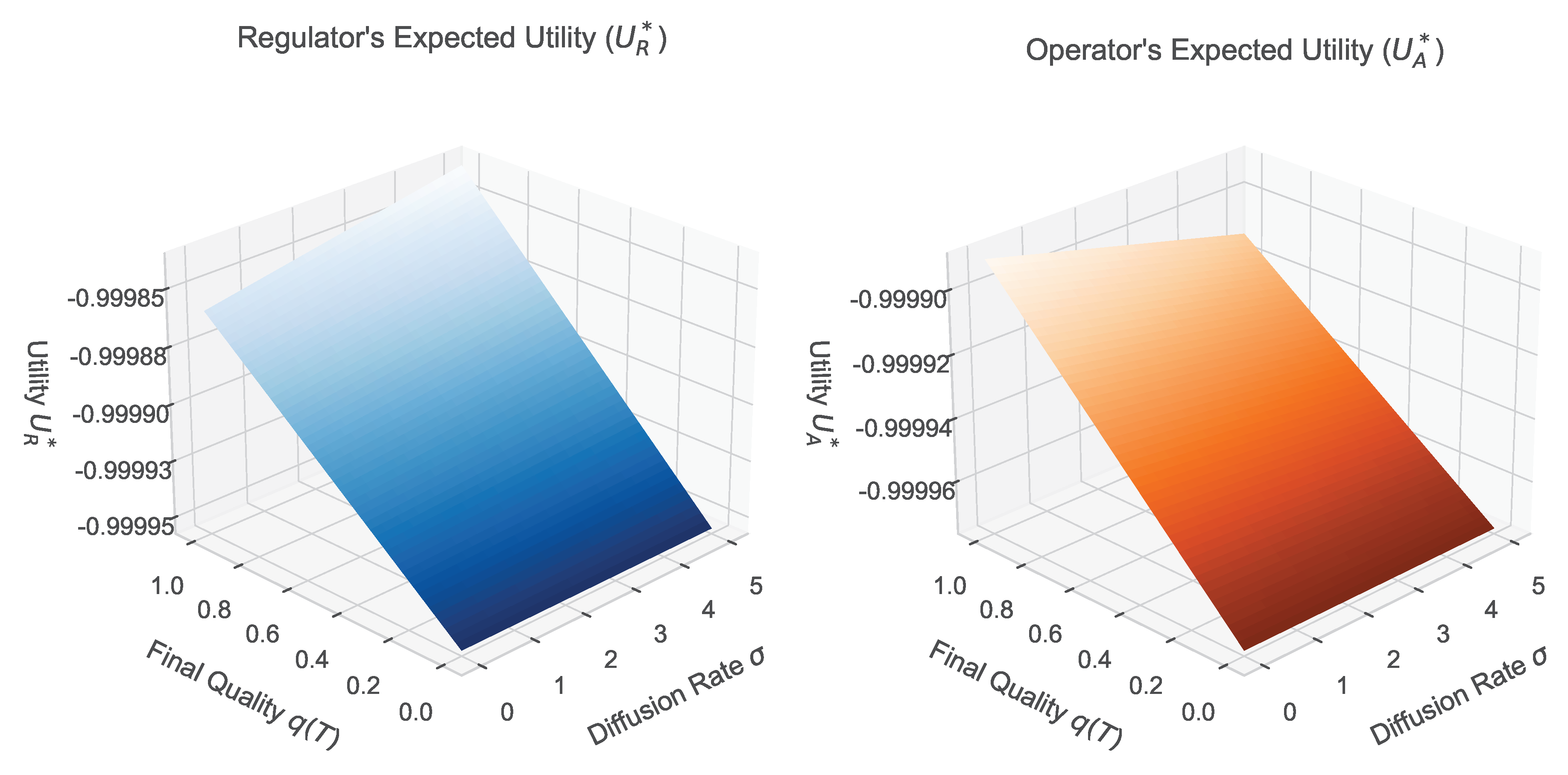
5.3.4. Analysis of Expected Utility Surfaces

Figure 5 displays the terminal expected utility for both the Regulator ($U_R^{*}$, left panel) and the Operator ($U_A^{*}$, right panel) under the agreeable contract $S^{*}$ derived in Proposition 2. These surfaces illustrate the final welfare distribution resulting from the optimal contract and provide a clear visualization of the embedded risk-sharing mechanism across an extended parameter space ($\sigma \in [0,5]$).

The left panel shows that the Regulator’s expected utility is an increasing function of both final quality $q\left(T\right)$ and uncertainty $\sigma$, with utility values ranging from approximately $-0.99995$ to $-0.99985$. The positive relationship with $q\left(T\right)$ is intuitive: higher service quality directly translates to greater social welfare $W\left(q\right(T\left)\right)$, which is the primary component of the regulator’s objective function.

More revealing is the relationship with uncertainty. As $\sigma$ increases, the Regulator’s utility rises (the utility value becomes less negative). This counterintuitive result occurs because the optimal contract $S^{*}$ systematically reduces the incentive power according to the slope formula $(P_R-P_A)(1-\sigma )$ to shield the agent from excessive risk. This reduction in performance-contingent payment translates to a lower expected subsidy outlay for the Regulator. For the risk-averse principal, the benefit gained from this reduced financial exposure can outweigh the potential loss from dampened incentives, leading to an overall increase in certainty-equivalent welfare. This result highlights the Regulator’s role as the primary bearer of systemic risk under the agreeable contract. Conversely, the right panel demonstrates that while the Operator’s utility increases with service quality $q\left(T\right)$, it is a decreasing function of uncertainty $\sigma$, spanning utility values from approximately $-0.99996$ to $-0.99990$. The positive relationship with $q\left(T\right)$ is straightforward, as both its direct operational revenue $\mathrm{Rev}\left(q\right(T\left)\right)$ and the performance-contingent subsidy $S^{*}\left(q\left(T\right)\right)$ are increasing in the final quality level (for $\sigma <1$).

The negative relationship with $\sigma$ is a direct consequence of the risk-incentive trade-off. As uncertainty rises, the incentive component of the Operator’s compensation is optimally reduced according to the same slope formula $(P_R-P_A)(1-\sigma )$. This means that for any given level of high performance, the Operator receives a lower reward in riskier environments. This reduction in expected compensation leads to a lower certainty-equivalent wealth and, consequently, a lower expected utility. The Operator, as the agent, bears the welfare cost of non-attributable environmental noise without receiving commensurate risk compensation.

Viewed together, the two panels provide a powerful visualization of the risk-sharing mechanism embedded in the optimal contract. An increase in exogenous risk ($\sigma$) is not borne equally across the extended parameter space. The optimal contract structure systematically reallocates the welfare consequences of this increased risk: it lowers the Operator’s expected utility while simultaneously increasing the Regulator’s. This trade-off represents the fundamental price of maintaining incentive compatibility in a stochastic environment. Risk is effectively shifted from the agent (Operator) to the principal (Regulator), who is better positioned to bear it due to superior risk-bearing capacity, in exchange for a reduction in the agent’s performance-based compensation. The smooth, continuous nature of both surfaces across the comprehensive parameter range ($\sigma \in [0,5]$, $q\left(T\right)\in [0,1]$) validates the robustness of this risk-sharing mechanism and confirms the practical applicability of linear contract structures in diverse public transit operating environments, from moderate uncertainty to highly volatile conditions.

5.4. Discussion

The numerical illustration confirms and clarifies our theoretical findings. It demonstrates that the optimal linear contract is not static but must be dynamically calibrated to the level of risk in the operating environment. The slope, representing incentive power, is a direct manifestation of the trade-off between incentivizing effort and providing efficient risk sharing.

Our analysis, while providing clear insights, relies on several simplifying assumptions. Future research could explore extensions by relaxing these assumptions, for instance, by incorporating state-dependent parameters (e.g., $\sigma \left(q\right)$), alternative utility functions, or multi-dimensional effort and outcome variables. Such extensions, while mathematically more demanding, could provide further insights into the design of robust contracts for complex public-private partnerships.

6. Conclusions and Future

This study presents a continuous-time principal-agent model to examine the optimal design of subsidy contracts in public transit systems characterized by double moral hazard. By allowing both the regulator and the operator to exert unobservable, costly efforts that jointly influence a stochastic quality outcome, we extend the classical agency framework to a bilateral setting with exponential utility and effort-based productivity. Our findings show that, under specific assumptions, each party’s optimal contract takes a linear form with respect to final service quality, and that under vanishing risk aversion and negligible effort costs, these can converge to a single, agreeable linear contract. The incentive intensity of the optimal subsidy is shown to decrease with environmental uncertainty, revealing a fundamental trade-off between risk-sharing and effort motivation. The framework contributes to the theoretical understanding of dynamic contracts by demonstrating how risk preferences, productivity asymmetries, and exogenous uncertainty jointly shape the optimal structure of bilateral incentive arrangements. The numerical illustration further clarifies how stochastic dynamics affect both contract form and welfare distribution. Practically, the results offer policy guidance on how to calibrate performance-based subsidies, and when to incorporate fixed or insurance-like payments in uncertain or asymmetric operating environments.

Building on these findings, several directions merit further exploration. First, future work could extend the model to multi-dimensional service quality indicators, reflecting real-world complexity in transit systems where punctuality, accessibility, and equity coexist. This would require a vector-valued stochastic control approach and possibly lead to non-linear or multi-instrument subsidy contracts. Second, state-dependent productivity or cost structures may offer richer insights, especially when effort efficiency or marginal social benefit varies with time or investment history. Finally, the theoretical model could be empirically tested using real-world data from transit agencies, enabling validation of the predicted contract structures and calibration of behavioral parameters under actual risk and productivity asymmetries. By integrating these extensions, future research can deepen the applicability of bilateral incentive models and provide more tailored mechanisms for achieving efficient and equitable public service delivery in uncertain environments.