Information, Geometry, and Chaos: Revealing Latent Cysteine Butterflies on Fractal Redox Shapes in the Proteomic Spectra

1. Introduction

Reversible cysteine residue oxidation redox-regulates biological processes by dynamically modifying protein structure and function [1]. These oxidative post-translational modifications (PTMs [2,3,4,5,6]) influence protein activity, stability, localization, interactions, and phase [7]—making cysteine oxidation a powerful and versatile mechanism of cellular control [8]. Viewed from a systems perspective, redox regulation operates like an electrical circuit: the sulfur atom in cysteine functions as a live node, continuously reshaped by the flux of oxidizing and reducing equivalents [9]. This nodal flux is modulated by a metabolically wired redox module comprising oxidants—reactive oxygen species (ROS) like hydrogen peroxide (H₂O₂)—and reductants, including the glutathione (GSH) and thioredoxin (Trx) systems [10,11,12].

As reviewed elsewhere [13,14,15,16,17], mass spectrometry-based redox proteomics enables a systems-level readout of this biochemical circuitry by quantifying the percentage oxidation of individual cysteine residues across the proteome [18,19,20,21,22,23,24,25]. These residue-resolved oxidation states provide a relative, condition-specific map of electron flux throughout the networked circuit [26]—offering a powerful lens through which to observe the dynamic output of the upstream redox module [27]. These redox proteomic approaches have yielded important insights into signaling pathways [28], stress responses [29], aging [18], immunity [30], and disease mechanisms [31]—each shaped by the underlying flux of oxidants and reductants [32].

Current redox proteomic frameworks largely treat the redox state of each residue as a vector with direction and magnitude. These residue-level vectors enable condition-specific changes to be analyzed using standard approaches, such as volcano plots. Excitingly, the power of such analyses can be amplified by considering the latent information encoded by the ensemble of vectors as a whole. This holistic perspective can reveal emergent structure, function, and circuit-level output—features of the redox system that may remain hidden when residues are considered in isolation. For example, high-dimensional analyses can provide transformative insights—like ordered and chaotic cysteine redox state patterns—that may already be latent features in extant datasets [27].

To reveal latent features, the present review focuses on the analysis and the reinterpretation of redox proteomic datasets using high-dimensional, information theory-grounded metrics like Shannon entropy [33]. Since the underlying redox biology and proteomic technologies have been comprehensively reviewed [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48], we begin by defining how redox proteomic data are currently analyzed and interpreted. We then introduce a set of information-theoretic tools for high-dimensional analysis and demonstrate how these concepts can uncover emergent features—including structure, symmetry, and chaos [49]. These emergent features enable peptide-centric proteomics to better describe cysteine proteoform defined bioelectrical circuits [50]. What follows is a new way of thinking and speaking about redox biology. It is a language grounded in the grammar of information theory, shaped by chaos, and expressed through dynamic nonlinear systems.

2. Methods

Consistent with our previous work [51], all of the python-scripted source codes are available on Github at https://github.com/JamesCobley/Redox_information inclusive of requirements, readme, and MIT license files. To enable interested readers to implement the analyses described, each script is configured for open-sourced google colab jupyter notebook run times. One simply needs to render the scripts compatible with the relevant source data.

For the information theory analysis, we demonstrated proof-of-principle using empirical priors. To compute several metrics on empirical priors, we computationally implemented the relevant equations on the OxiMouse dataset [18], downloaded from https://oximouse.hms.harvard.edu/. This dataset provided the cysteine redox state of residue level vectors in ten different tissues from young and old mice. For the purposes of brevity, the present analysis was restricted to analyzing the young and old brain data [52,53]. Since a full reanalysis of the raw instrument files was beyond the scope of the present work, we used the mean and standard error of the mean to bootstrap the statistical testing—as detailed in the legend of each figure.

For the chaos theory analysis, we demonstrated proof-of-principle using synthetic priors due to the limited time-resolved redox proteomic datasets that are presently available. Upon generation of the appropriate empirical priors, the equations can be implemented without changing their general form—the mathematics is invariant.

3. Results

3.1. The Flatland Problem: How Scalar Redox Values Conceal the High-Dimensional Structure of Peptide Data

Redox proteomic datasets usually comprise redox state vectors encoding the direction and magnitude of a given state in the percentage basis—from 0 to 100% oxidized—for thousands of cysteine residues across one or more conditions [18,54,55,56,57,58,59,60,61,62]. Typically, these vectors arise from the spectral measurement of peptide ensembles bearing light (reduced) and heavy (reversibly oxidized) labels—such as isotopically distinct maleimide probes [25,63,64]—at both the MS¹ (intact peptide) and MS² (fragment ion) levels [65,66,67,68,69,70]. Each spectral "read" is therefore an amalgam of binary 0 and 1 intensities—corresponding to light and heavy modified peptides and their fragments—that collectively encode the overall signal for a given peptide. These signals are usually converted into percentages following the processing of the raw files using appropriate software like MaxQuant or DIA-NN for data-dependent acquisition (DDA) and data-independent acquisition (DIA) schemes, respectively [71,72,73].

Most current frameworks treat the residue-level redox state as a scalar datapoint—a single numerical value encoding the degree of oxidation—to enable rigorous statistical comparisons between conditions. Each scalar is treated as a scale-bounded continuous variable, capable of assuming any real value within the closed interval [0, 100] [74,75]. These data are typically analyzed by comparing scalar values between conditions using appropriate statistical tests, such as independent t-tests for parametric datasets, with corrections applied to control for family-wise error rates. A common visualization method is the volcano plot, in which the mean oxidation difference (the delta change) between conditions is plotted as the log₂ fold-change against a significance metric, such as the –log₁₀ adjusted P-value. This approach captures both the magnitude and direction of redox shifts and is particularly useful for identifying cysteine residues with significant, condition-specific perturbations—for instance, in age-associated redox stress response [76,77,78,79,80].

To extract broader biological patterns from the scalar redox data, many studies apply dimensionality reduction techniques, such as Principal Component Analysis (PCA) [81]. PCA transforms the original high-dimensional dataset—where each residue is a variable—into a reduced set of orthogonal axes (principal components) that capture the greatest variance in the data. This enables the visualization of global structure, such as sample clustering by condition, tissue, or genotype, while preserving the most informative variation. In parallel, unsupervised clustering algorithms—such as hierarchical clustering or k-means—are often used to group residues or samples based on shared redox patterns [27]. These approaches can reveal context-specific clusters, like tissue-specific oxidation signatures [18,52], helping to identify coherent redox modules across biological systems [82,83]. Together, PCA and clustering extend scalar analysis beyond univariate comparisons by revealing coarse-grained structure in the data, forming a conceptual bridge between single-site analysis and more integrated, systems-level insights.

While scalar-based approaches enable powerful statistical analyses, they also impose a reductionist structure that can obscure biological meaning, which we term the “flatland problem”. By treating each cysteine residue as an independent variable, these methods flatten the system into a residue-centric view, fragmenting the natural continuity of protein-level redox behavior. This flat projection into low-dimensional space disrupts the coordinated structure of the underlying redox manifold. In this manifold, each residue belongs to a specific cysteine proteoform—a defined molecular configuration determined by the redox state of all cysteines in that protein molecule [50]. Hence, clusters or components derived from conventional analyses reflect statistical groupings of residues, not coherent proteoform dynamics. This disconnect matters: it is proteoforms—not their disembodied peptides—that enact biology [84,85,86,87,88]. Redox regulation is not merely a collection of residue shifts [89], but a coordinated molecular choreography that scalar analysis cannot fully resolve [90,91,92].

While peptide-level oxidation percentages appear continuous, they are ensemble averages over discrete molecular states [93,94,95,96,97]. For example, a protein molecule with three cysteines can exist only in one of four possible proteoform oxidation modes: 0%, 33%, 66%, or 100% [27,50,51,89,98]. However, what we measure is a peptide-level readout—an aggregate signal reflecting a distribution over these unseen modes [99]. Linear models treat this data as continuous, but the originating system is fundamentally discrete and combination constrained.

The tension—between continuous analysis and discrete biological configuration—reveals a core limitation of current frameworks. It invites new models that acknowledge the latent structure of cysteine proteoforms embedded in high-dimensional state space [51,100]While these proteoforms are not directly observed in bottom-up mass spectrometry [101,102,103], peptide measurements are projections of their redox state distributions. Hence, methods that recognize this structured embedding are better equipped to recover the coordinated, nonlinear behavior of redox systems [104,105,106].

Nonlinear models from information can chaos theory can be directly applied to peptide-level oxidation data [107]. Nonlinear models are sensitive to thresholds, feedback loops, bifurcations, and emergent behaviors [49,98,108]. For example, a small change in oxidation at one cysteine may lead to a disproportionate structural or functional shift in the protein, particularly if it triggers allosteric change or destabilizes a critical motif [109,110,111,112]. Even without measuring cysteine proteoforms [89], nonlinear models applied to peptide data can uncover signatures of non-additivity and non-monotonicity in redox behavior. These models can help to recover the logic of the system: a redox landscape not governed by smooth gradients but by discrete jumps, state transitions, and multi-stable basins of behavior [113].

3.2. Conceptual Foundations of Information and Chaos Theory

When seeking to quantify the uncertainty or structure within a signal, Claude Shannon’s 1948 masterpiece [33] introduced a new mathematical framework now known as information theory. Shannon's goal was to formalize the process of communication—how to transmit messages over noisy channels with maximal efficiency and minimal error. He defined informational entropy as the average uncertainty or surprise associated with a set of outcomes. The resulting entropy was not about the second law of thermodynamics, but about the number of choices available—the informational richness of a distribution of datapoints in the discrete binary basis [114].

In transcending telecommunications, information theory permeated virtually every branch of scientific study, including biology [115,116,117]. It now provides a general language for quantifying structure, uncertainty, redundancy, and complexity in diverse systems—from neural networks and genetic sequences to language, learning, and thermodynamics. Central concepts such as mutual information, Kullback–Leibler divergence, and algorithmic complexity enable precise descriptions of how patterns emerge, propagate, and are constrained by prior states. This naturally intersects with Bayesian inference [118], which formalizes how prior knowledge influences probabilistic updates in light of new data. In essence, information theory reveals how order and unpredictability are balanced within any probabilistic system, making it a natural partner to dynamical frameworks like chaos theory that explore how such systems evolve over time [119].

While modeling atmospheric convection in the early 1960’s, Edward Lorenz discovered that even deterministic systems could behave unpredictably [120]. His seemingly minor rounding error in initial conditions led to radically different weather simulations—an observation that inspired chaos theory [121]. Lorenz’s insight revealed that nonlinear dynamical systems, though governed by deterministic rules, could exhibit sensitive dependence on initial conditions—the “butterfly effect” [122]. This realization catalyzed the development of advanced mathematical frameworks—including strange attractors, Lyapunov exponents, and fractals—to characterize the intricate, self-similar, and often beautiful structures underlying complex dynamical behavior [123,124,125].

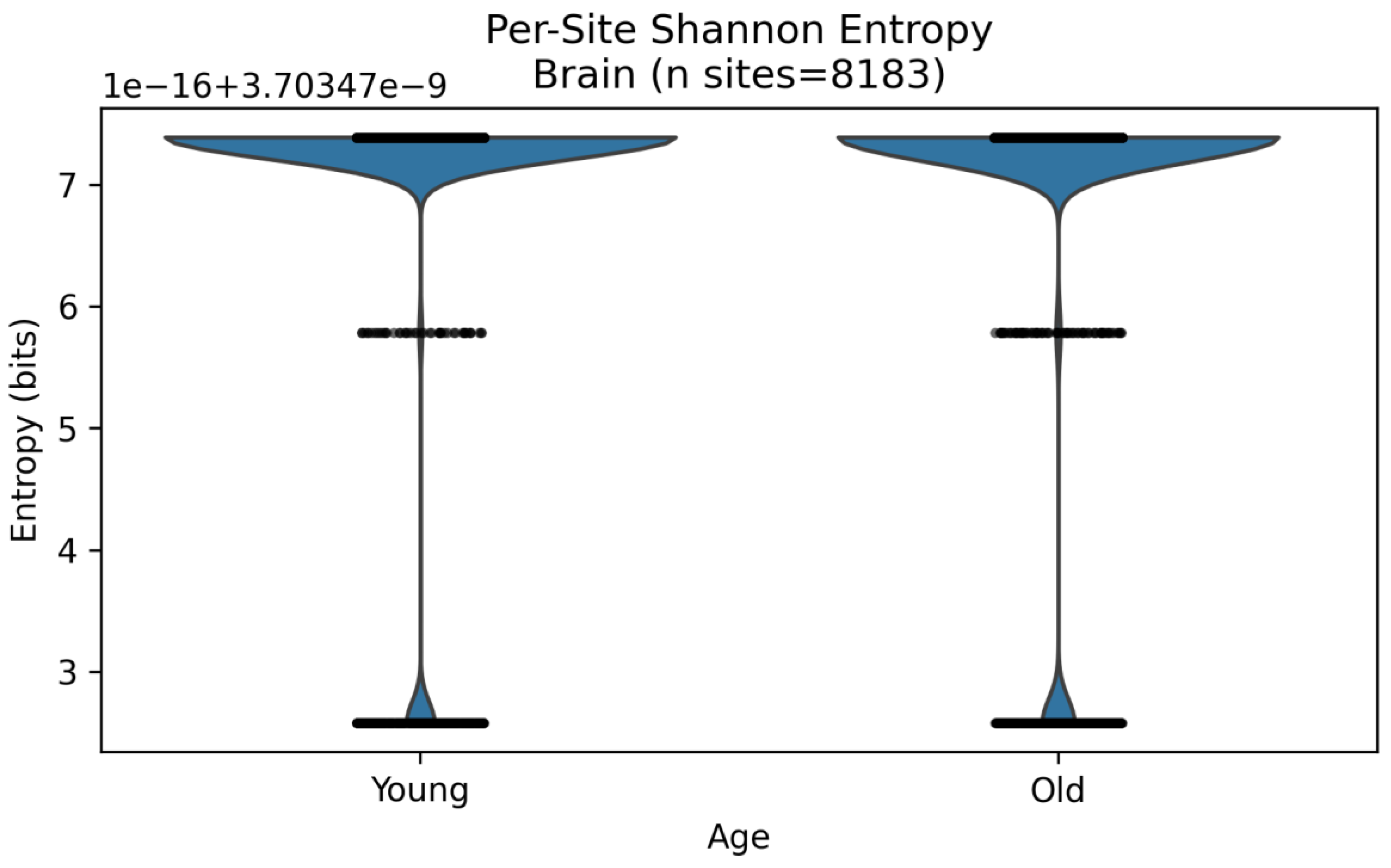
3.3. Shannon Entropy: Quantifying Uncertainty in Redox Distributions

Let the redox proteomic dataset be discretized into percentage oxidized bins, where each bin defines a given range of peptide oxidation values. For example, 50, 2%-oxidized bins over the [0,100] interval. Let p_i be the proportion of peptide datapoints falling within bin i, such that the sum of all bins equals 1. Then Shannon entropy (H) becomes:

$$H\mathrm{ }=\mathrm{ }-\sum _{i=1}^n{p}_i{log}_2{P}_i$$

By binning the redox state into discrete intervals, the continuous oxidation data are converted into a valid probability distribution which is mathematically justified because Shannon entropy is defined over discrete outcome spaces. Biologically, the bins correspond to semantically meaningful states (e.g., 100%-reduced [126,127,128]). The range of each bin can be adjusted depending on the nature of the experiment.

Shannon entropy quantifies the distribution of information—that is, how redox values are spread across discrete oxidation bins. A uniform distribution corresponds to maximal entropy, indicating maximal uncertainty or randomness in the oxidation state data. In contrast, a sharp peak localized to a single bin implies minimal entropy—high predictability and low diversity in cysteine redox states. Geometrically, entropy reflects the distribution shape: a flat plateau suggests maximal uncertainty, while a narrow spike reveals an ordered, constrained system.

To capture the information structure embedded within complex, high-dimensional redox proteomic landscape [129,130,131], we calculated the Shannon entropy across 5%-oxidation increments over the 0,100 interval from the 8,183 cysteine residue vectors in young and old mouse brains. Even though the oxidation of this subset of the proteome decreased by 0.8% from 8.9 in young to 8.1%-oxidized in old mouse brains, the Shannon entropy increased from 3.884 bits in young to 4.143 bits in old mouse brains. This ~0.26-bit increase means the distribution of oxidation levels across the ~8,000 cysteine sites are more dispersed—geometrically spread—in aging brains (Figure 1). Bootstrapping from the SEM revealed this was a significant and appreciable effect (Cohen’s d = 10.6).

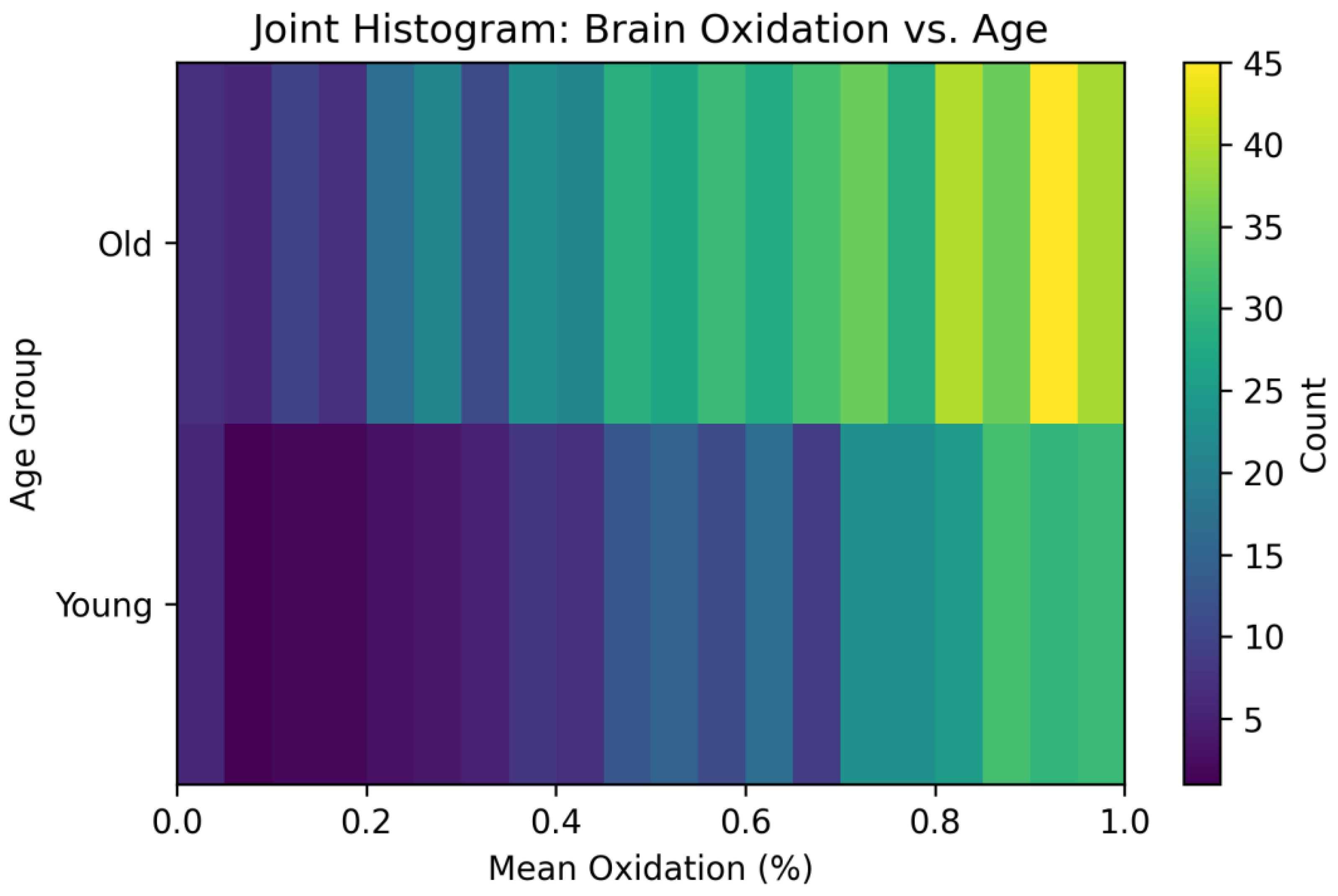
3.4. Mutual Information: Quantifying Shared Information Between Redox States

Let the same discretized redox state from section 3.3 define a random variable $X$ taking values $x=1,....n$ for each oxidation bin, and let $A$ be a binary variable, such as age were $A\in \{young,old\}$. Denote the joint probability

$$p_{x,a}=Pr(X=x,A=\mathrm{ }a),$$

and the marginals

$$P_{x\mathrm{ }}=\sum _{a}x,a,\mathrm{ }\mathrm{ }\mathrm{ }{P}_a=\sum _{z}Px,a,$$

so that ${\sum }_{x,a}{P}_{x,a}=1$. The mutual information $I(X;A)$ in bits is defined by

$$I(X;A)=\sum _{x=1}^n\sum _{a\in \{young,old\}}{p}_{x,a}{log}_2{\displaystyle \frac{P_{x,a}}{P_x{P}_a}}$$

By discretizing oxidation into bins, we obtain a valid discrete joint distribution $\left\{P_{x,a}\right\}$. Mutual information measures the reduction in uncertainty about A (e.g., age) gained by observing the oxidation bin X:

• $I\left(X;A\right)=0$ (the minimum) bits if X and A are statistically independent—knowing oxidation gives no clue to age.
• $I(X;A)=1$ (the maximum) bits if and only if oxidation perfectly predicts age (each bin occurs in only one age group).

A high $I\left(X;A\right)$ indicates that certain redox-state intervals are strongly age-specific, revealing cysteine sites whose oxidation patterns carry significant “age information.” Conversely, a low $I\left(X;A\right)$ implies that, despite any shifts in mean or variance, the oxidation distributions for young vs. old overlap so extensively that a single measurement scarcely informs on age. The latter is the case (0.001 bits) when mutual information is applied globally to the cysteine redox proteomic vectors in young and old mouse brains due to the statistical dependence of X and A in each oxidation bin (Figure 2).

Like the other metrics, mutual information can be computed per pathway or site. Hence, we performed a site-wise analysis using a script to identify 100 cystienes exhibiting the greatest delta change between young and old, pinpointing potential brain-specific aging biomarkers, which increased the mutual information bits by an order of magnitude (from 0.001 to 0.014 bits). The top ten sites yeilded an mutual infromation score of 0.693 bits. For example, the delta change for Cys59 in Acyl-coenzyme A thioesterase THEM4 was 98.8%. The resultant mutual information score of 0.693 bits renders the site highly predicitve of age.

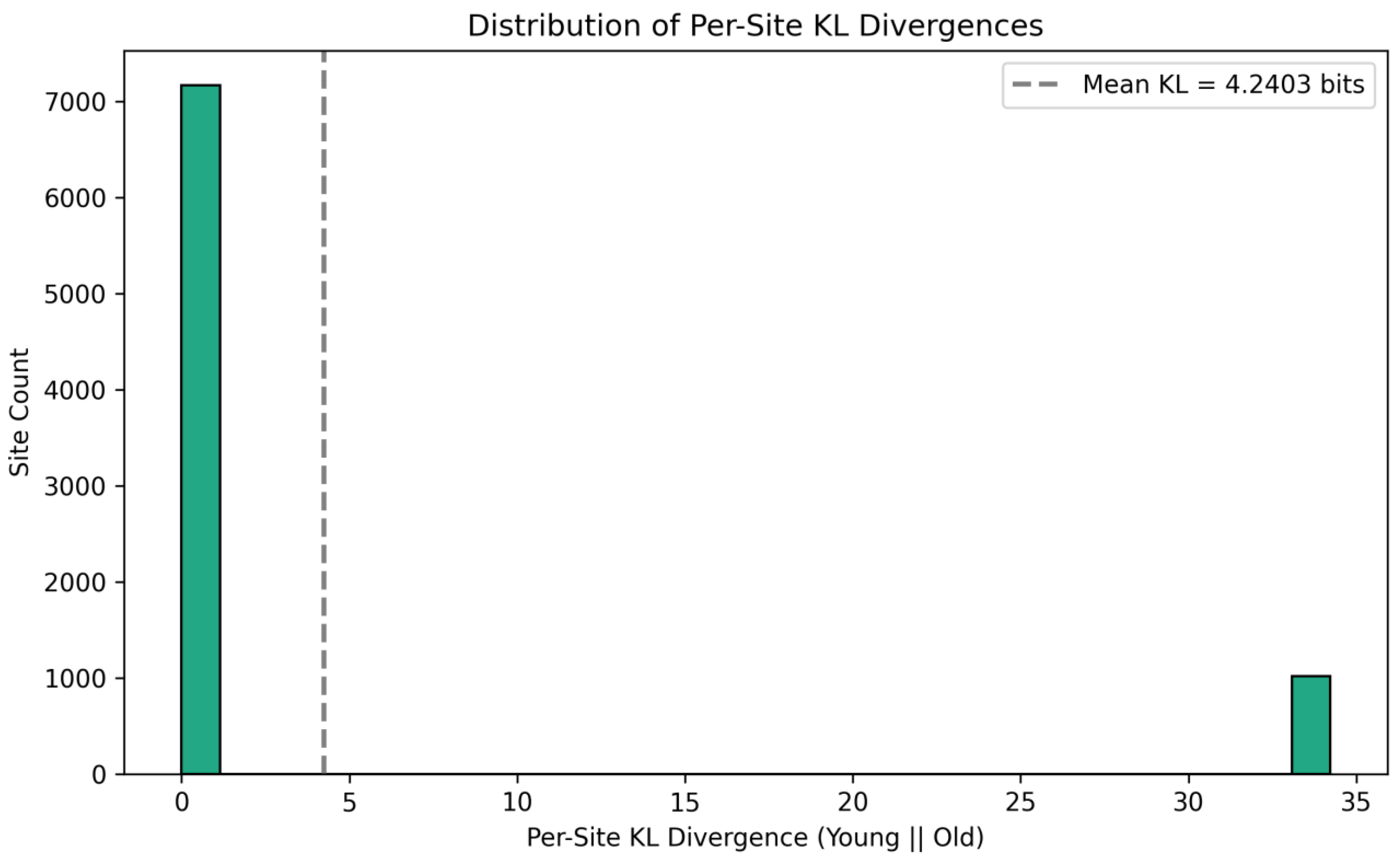
3.5. Kullback-Liebler Divergence: Quantifying the Geometric Difference Between Redox State Distributions in Information Space

Let redox proteomic data from two conditions like control and H₂O₂-treated [132] be discretized into the same percentage-oxidized bins, such that $P=\left\{P_i\right\}$ represents the baseline condition (e.g., control) and $Q=\left\{Q_i\right\}$ represents the perturbed state (e.g., H₂O₂). Each P_i and Q_i denotes the proportion of peptides falling into bin i, normalized such that $\sum P_i=\sum Q_i=1$. The Kullback-Leibler (KL) divergence from Q to P is defined as:

$$D_{KL}\left(P\mathrm{ }‖\mathrm{ }Q\right)=\sum _{i=\mathrm{ }1}^n{p}_i{log}_2\left({\displaystyle \frac{p_i}{q_i}}\right)$$

This equation formalizes the informational cost of assuming distribution Q compared to P. KL divergence captures how much the cysteine redox state has changed across the full distributional structure when the system is perturbed. Geometrically, KL divergence measures how one probability distribution shape differs from another in information space. Unlike Euclidean distance, it is asymmetric $D_{KL}\left(P‖Q\right)\ne D_{KL}\left(Q‖P\right)$, preserving the temporal or causal directionality of cysteine redox state changes.

Consistent with Figure 2, the site-wise KL score for most of the 8,183 peptide vectors was 0.000 bits, indicating that no information is gained or lost across the majority of sites in old compared to young mice (Figure 3). These zero scores suggest minimal redistribution of oxidized peptides. However, 1,014 (12.4%) of the cysteine vectors displayed a nonzero KL divergence, such that the data displayed a bimodal distribution with a large peak at 0 and a nontrivial peak at 30-35 bits.

For example, the KL divergence score for Cys59 in peptidyl-prolyl cis-trans isomerase NIMA-interacting 1 (PIN1) was 34.21 bits. This reflects complete non-overlap between its young and old oxidation distributions. In young brains, Cys59 averages 6.8 % ± 0.56 % oxidation, while in Old it shifts to 0.97 % ± 0.25 %, with the two tight SEM-derived replicate clouds each falling into distinct histogram bins. A KL of ~34 bits arises because $DQ\approx {10}^{-9}inthewrongbin,drivingp{log}_2(p/q)to~{log}_2\left({10}^9\right)$.

Biologically, this “all-or-nothing” change signals a re-parameterization of Cys59’s redox state with age: its oxidation profile in old mice carries maximal information relative to young (i.e., perfect separation), even though the absolute change in percent oxidation may seem modest.

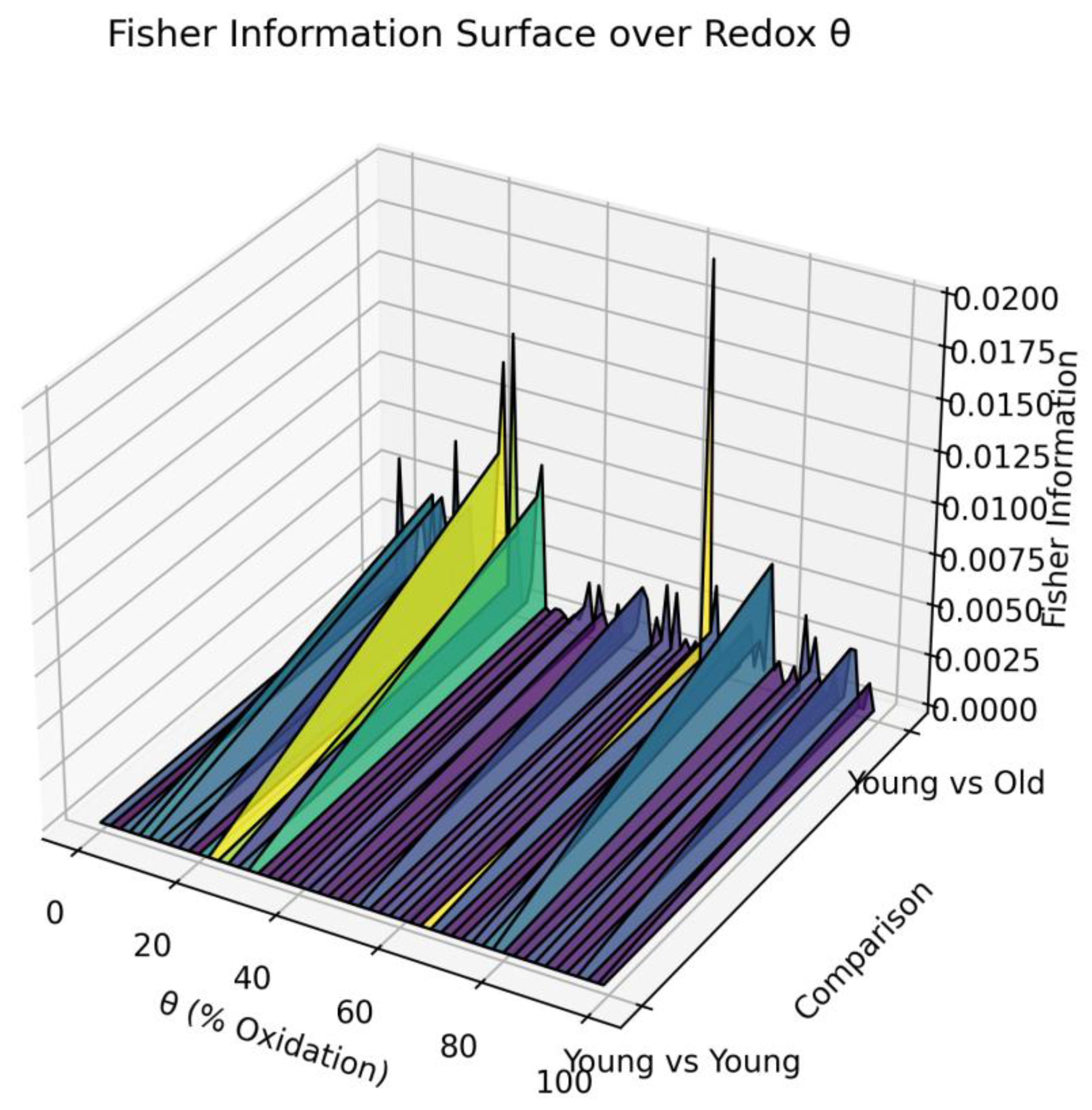
3.6. Fisher Information Metric: Quantifying the Geometry of Curved Redox State Manifolds

Let the redox peptide oxidation data be characterized by a probability distribution p(x;θ), where θ is a parameter (or vector of parameters) that defines the shape or structure of the distribution—such as a mean oxidation state across peptides. The Fisher Information metric (FIM, I(θ) quantifies how much information the data carries about this parameter, which can be formalized as:

$${\rm I}\left(\theta \right)=\mathbb{E}\left[\left({\displaystyle \frac{\delta }{\delta \theta }}\left.log,p(\mathrm{x};\theta \right)\right)2\right]$$

FIM describes how sharply a system responds to perturbations like exercise [133,134,135,136,137,138,139,140,141]. For instance, two distributions with the same mean oxidation might differ in how tightly they are concentrated around that mean [142]. Hence, the FIM captures this second-order structure—the local curvature of the data landscape. Geometrically, the FIM defines a Riemannian geometry on the space of probability distributions. It introduces curvature to the informational manifold: distributions that are more sensitive to parameter shifts lie on steeper, more curved regions, whereas robust or flat distributions lie in shallower area. These redox state data-derived manifolds can be described in terms of geometric distances and angles.

Interpretationally, high FIM values might correspond to tipping points, where small redox shifts drastically reconfigure the proteomic landscape (e.g., triggering signal response thresholds [143,144,145]). Conversely, flat regions with low Fisher Information may indicate robust zones [146,147,148], where cysteine redox state changes are dynamically buffered—“homeo-dynamics” [149].

The global FIM—dimensionless squared Hellinger distance (range 0-2)—was 0.1887, signifying that the overall surface between the cysteine redox state vectors in young compared to old mouse brains was mostly flat—small geodesic—across the oxidation bins (Figure 4). Interpretationally, this is consistent with the mutual information (0.001 bits) score and the substantial peak at 0 in the KL divergence distribution.

However, one can observe tall peaks in some binds, especially at intermediate oxidation states (30-60%-oxidized). At these vector points in the overall high dimensional manifold, the geodesic distance between the young and old is considerable, denoting a reconfiguration of the landscape. Specifically, the curvature is near maximal at θ60%, meaning this bin contributs substantially to the overall FIM score.

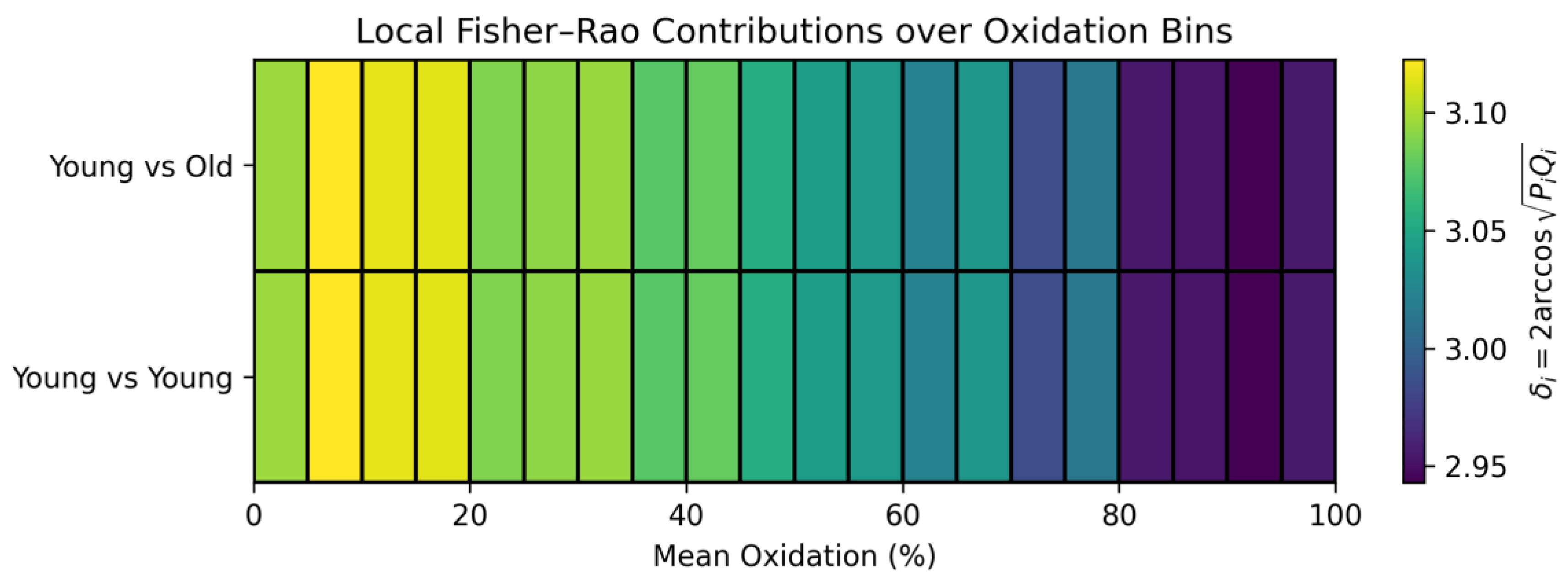
3.7. Fisher-Rao Distance: Quantifying the Distance Between Curved Redox Manifolds

Let the redox peptide oxidation data be characterized by a probability distribution p(x;θ), where θ parameterizes a family of redox states. While the FIM describes the local curvature around a single distribution, the Fisher–Rao distance (d_FR) measures the true path length between two such distributions on the curved statistical manifold. Formally, this geodesic—the shortest path length—distance is defined as:

$$d_{FR}\left({\theta }_1{,\theta }_2\right)\mathrm{ }=\mathrm{ }{\int }_{{\theta }_2}^{{\theta }_1}\sqrt{{\rm I}\left(\theta \right)\delta \theta }$$

(1)

Fisher–Rao distance defines the true informational displacement between redox states—accounting not just for the magnitude of redox change, but for how the statistical curvature of the system warps that change. Two distributions might appear close in Euclidean metrics, yet lie far apart on the information manifold if one lies in a steep, sensitive region and the other in a flat, buffered one.

Geometrically, the Fisher–Rao distance measures the shortest possible path between redox states while honoring the manifold’s internal curvature—akin to walking over a hill instead of cutting through it. This defines the “true” distance between redox states in terms of the system’s sensitivity to change—where a greater distance indicates the systems not only differ in their values but their geometry.

Interpretationally, large Fisher–Rao distances between conditions (e.g., healthy vs. diseased [150]) may signify deep structural shifts in the system. Small Fisher–Rao distances, by contrast, may reflect smooth adaptation—a curved, minimal transition within a robust regulatory space.

Computing the Fisher-Rao distances in young and old mouse brains revealed an overall distance of 0.4399 radians maps to 25 degrees between two cysteine oxidation distance, signifying moderate angular separation (Figure 5). A maximum distance of 3.14 radians would indicate maximal separation. Hence, the angular separation of the distributions is more convergent than divergent.

The nonzero score indicates a degree of separation concentrated around the intermediate oxidation bins, particularly 20-30%-oxidized. Hence, subsets of the cysteine proteome do undergo substantial reparameterization, effectively defining a local reshaping of the manifold at specific points.

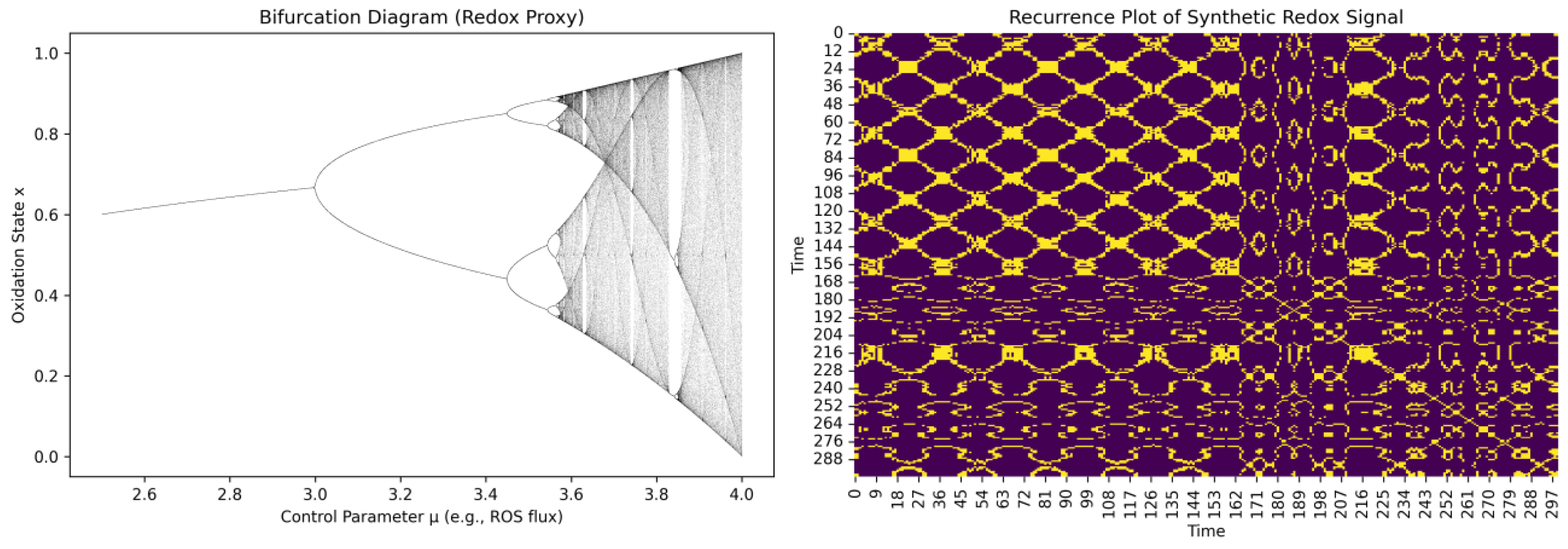
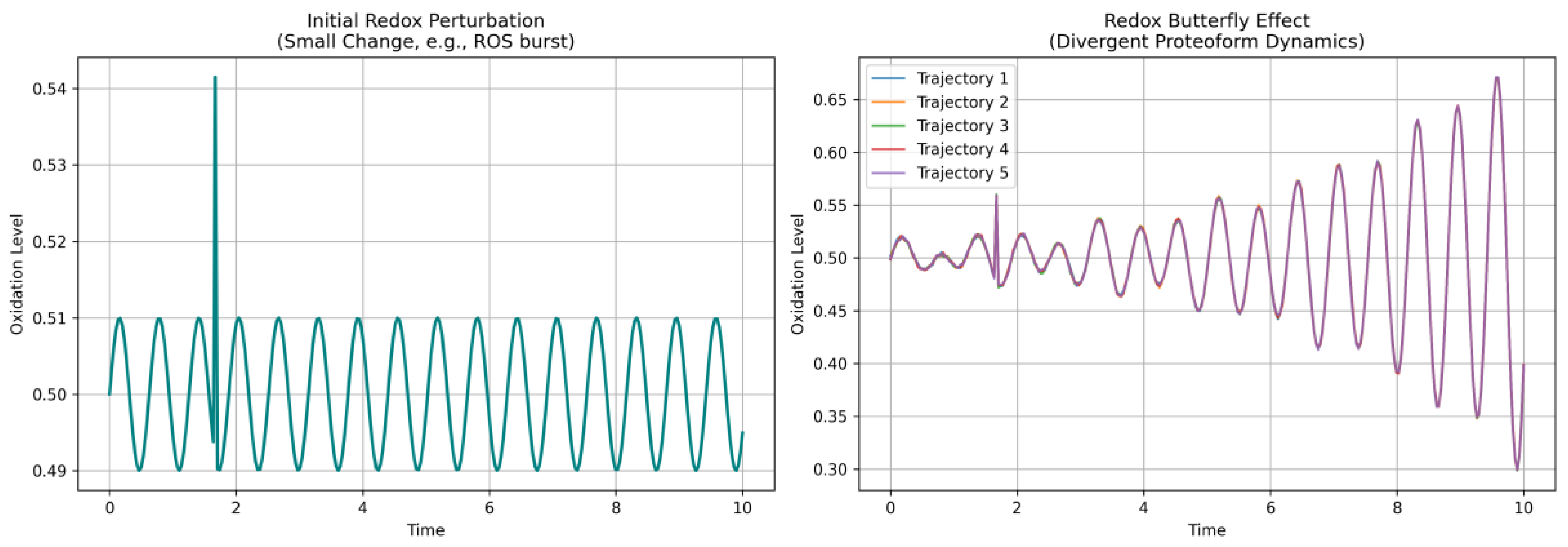
3.8. Distinguishing Order from Chaos in Time-Resolved Redox Dynamics

Let the redox proteome be measured across a time series—such as sequential timepoints under altered mitochondrial function, circadian cycles, or developmental transitions [151,152,153,154,155,156,157,158,159,160,161,162,163]. This temporally resolved data introduces a new analytic axis: how the system evolves, not just where it is. The temporal trajectory of the cysteine redox state may exhibit patterns that are:

• Ordered—following predictable or quasi-linear dynamics.
• Chaotic—diverging over time due to small differences in the initial conditions.
• Hybrid—a cysteine redox system where orderly and chaotic behaviors coexist either across different subsystems, within different time windows, or as structured chaos near low-dimensional attractors.

Chaos theory provides a mathematical framework to distinguish between these regimes by characterizing the underlying attractor structure of the dynamical system (Figure 6). Here, the redox trajectory is treated as an evolving signal in phase space, and we ask: Does it converge to a stable pattern, cycle through predictable states, or exhibit sensitive dependence on initial conditions?

To distinguish between these behavioral regimes, we draw from a set of mathematically grounded metrics in nonlinear dynamics. These tools quantify whether redox trajectories evolve stably, diverge chaotically, or settle into structured attractors. These tools capture distinct signatures of complexity: Lyapunov exponents quantify divergence of nearby trajectories, recurrence analysis detects hidden periodicities and long-range dependencies, correlation dimension characterizes the geometry of the underlying attractor, and bifurcation analysis reveals phase transitions triggered by small parametric shifts [164,165,166,167,168,169]. Table 1 summarizes each metric, its mathematical formulation, and its interpretation in the context of peptide-resolved proteomics, such as time-resolved cell cycle or signaling analyses [23,170,171,172].

At the peptide level, these tools allow us to treat nonlinear cysteine redox dynamics as an evolving informational signal trajectory in a high-dimensional state space [98]. These signal trajectories can fold and stretch like a shape being continually remodeled. The resulting shapes—patterns—can exhibit instability and a memory. These measures offer a generative map of how redox perturbations propagate, whether they resolve into ordered recovery or spiral into new basin attractors, which we term strange oxi-attractors.

Small differences in initial cysteine oxidation states can cascade into dramatically different outcomes. A minute shift in oxidation at a specific site—triggered by the upstream redox module [173,174,175]—may push the system across a bifurcation point or into a new attractor basin—a dissipative structure: the strange oxi-attractor [176].

We define this phenomenon as the cysteine redox butterfly effect. This effect captures the sensitive dependence to initial conditions in nonlinear systems, which while manifest at the proteoform level can be recorded in the redox states of peptides. The cysteine redox butterfly effect explains how noise can become a biological signal—how tiny molecular events can influence fate decisions, stress responses, or pathogenesis [177,178,179,180,181,182,183,184,185,186,187]. And critically, these changes are not arbitrary. Hence, cysteine oxidation encodes not only the current biochemical state—but the memory of its perturbation history, fractally embedded in time.

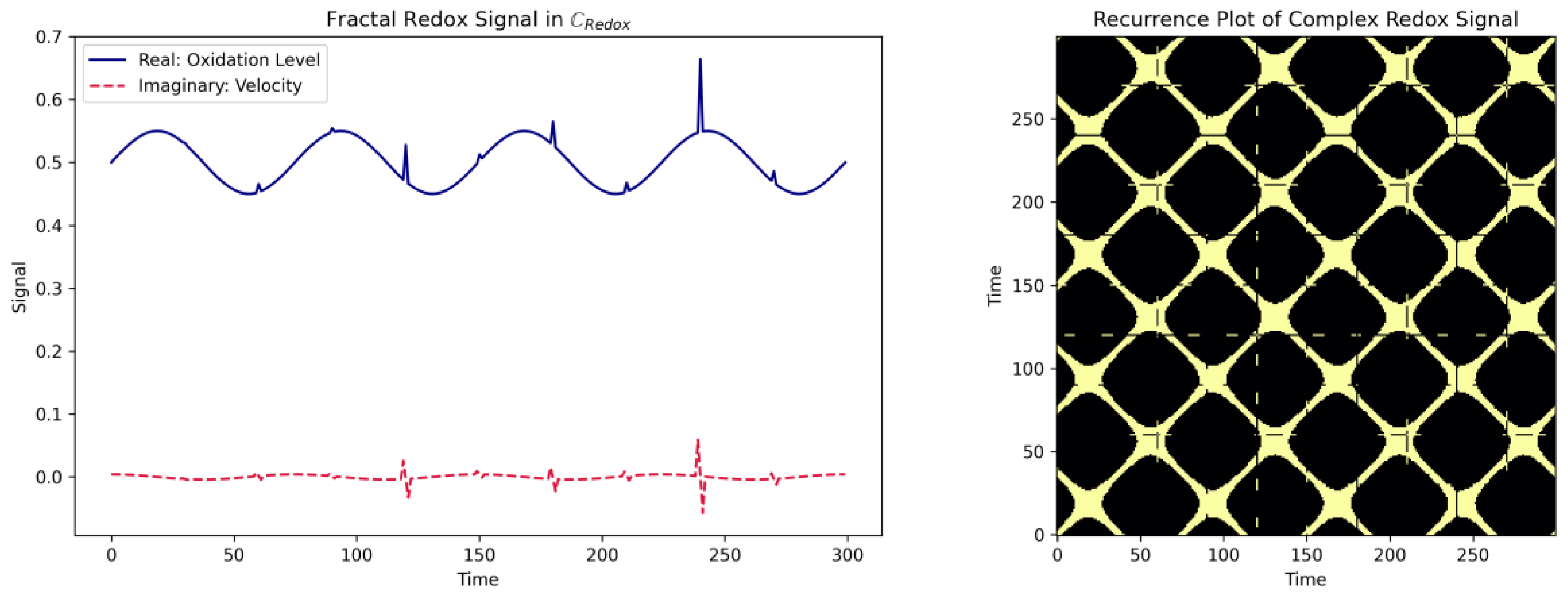
3.9. Fractal Geometry: Quantifying Scale-Invariant Self-Similar Cysteine Redox State Patterns

Let a peptide level cysteine redox trajectory be conceptualized as a curve evolving in complex space, where each peptide’s oxidation state is modeled not as a scalar value but as a complex number:

$$Z\left(t\right)=R\left(t\right)+iI\left(t\right)$$

In this formalism,$R\left(t\right)\in \mathbb{R}$is the real measured percentage oxidation of the peptide at time t, and$I\left(t\right)\in \mathbb{R}$is an imaginary component, capturing a latent structure, such as the velocity of the redox state change, the geometry (e.g., Fisher-Rao distance), or a measure of entropy (e.g., approximate entropy or Shannon entropy). This transformation lifts peptide-coded cysteine redox dynamics into the complex plane (${\mathbb{C}}_{Redox}$), where the trajectories—paths in phase space [0,100]—can generate fractals.

Pioneered by Benoit Mandelbrot [124,125,168,188,189], fractals are geometric structures that exhibit self-similarity across scales, often governed by recursive rules or nested feedback. Applied to redox proteomics, fractal analysis asks: Does the oxidation trajectory of a peptide encode recursive or scale-invariant patterns? Do certain biochemical systems evolve along a fractal manifold in redox space? To help answer these questions, Table 2 defines a set of mathematically grounded tools for extracting fractal structure from complex-valued peptide oxidation trajectories. Figure 7 illustrates a synthetic example of a complex-valued redox signal and its recurrence structure, visually revealing fractal and recursive motifs in ${\mathbb{C}}_{Redox}$​.

These metrics may be applied on a per-peptide basis or aggregated across peptides or pathways to infer system-wide fractal signatures. These analyses may also be constrained within specific time windows to isolate localized self-similarity.

Interpretationally, fractal geometry can reveal if and how cysteine oxidation patterns recur, nest, or stretch over time. A residue signal with a non-integer fractal dimensional value $D_B\in \left(\mathrm{1,2}\right)$, suggests scale-invariant, and recursive redox dynamics, like a recurrent oxidation-reduction control cycle gravitating around a basin attractor. The imaginary component in the ${\mathbb{C}}_{Redox}$ expression, provides analytical flexibility. It can encode temporal derivatives, conformational entropy, of redox flux sensitivity. As a result, fractal patterns that spiral inward or explode outward can be produced. Fractal geometry can reveal whether the system or aspects thereof exhibits chaotic behavior about strange oxi-attractors via the analysis of fractal redox manifolds.

We define a fractal redox manifold as a recursive geometric space where peptide oxidation states evolve nonlinearly in a conserved self-similar manner. These manifolds may embody a memory of redox history.

4. Discussion

Ironically, redox biology resists reduction. It defies simple arithmetic. As evidenced by the failure of the original linear rooted free radical theory of aging [190,191,192,193,194], adding or subtracting electrons doesn’t yield proportionate cysteine redox state changes. Instead, it can provoke silence or unleash a cascade. Without violating physics, outputs diverge from inputs. How? Because the cysteine redox network is not a passive register of electrons. Instead, it is a dynamic, living network. Actively wiring, perpetually rewiring itself by funneling, channeling, dispersing the electron flux across sulfur nodes. This sulfur nodal flux dynamically remodels cysteine proteoforms distributions [27,50,51,89,98,195].

The instantiated now carries a memory. The oxidation state of cysteine—measured via a peptide level read—holds a record of its past that can offer insights even when the proteoform level information is inaccessible. These redox states tell us how now can shape the future. The profound consequence is that divergence from a given state might not be easily reversed by an “antioxidant” [36,38,196,197,198,199]. Even if the antioxidant works as intended [37,40,200], simply curtailing further oxidation will not provide the electrons needed to reduce what is already oxidized [133,201].

A core operating logic emerges where the flow of electron dynamically shapes and reshapes the live sulfur nodes of the cysteine proteome. This incessant flow of energy continually generates entropy by reshaping proteoform matter, structuring their nonlinear dynamics. From the relatively simple redox reactions that determine these states change dynamics, emerges complex behavior—hysteresis, order, chaos, and fractals (Figure 8). But, how do we understand this complexity? How do we differentiate between order and chaos? If needed, can we restore order or provoke redox chaos?

To better understand the structured signals underpinning complex phenotypes like sleep-loss induced neurodegeneration [202,203,204,205,206], information and chaos theory become indispensable tools for advancing redox proteomic analyses—even when it is peptides not their proteoforms that are measured [207,208,209,210,211,212,213,214,215,216,217,218,219].

• Information theory enables the oxidation state of a peptide to be analyzed and interpreted as an encoded signal, compressible or not, with measurable entropy. The more irregular, the less compressible—and paradoxically, the more information it may carry. By quantifying these dynamics across timepoints and conditions, one can begin to see that redox states are not random variables—they are deterministic signals with memory, unfolding on a nonlinear manifold.
• Chaos theory offers the interpretive lens. Small redox changes can produce outsized shifts in oxidation of peptides. This sensitivity to initial conditions defines the redox butterfly effect. Peptide-level oxidation patterns form trajectories—not just in time, but across a complex redox phase space, where certain states act as strange oxi-attractor. With tools like approximate entropy, recurrence quantification, and fractal dimension analysis, these structures are now computationally accessible, even at the peptide level.

A single oxidation event, once viewed in isolation, can now be seen as part of a larger dynamic system—a ripple in a structured informational field space. Part of a wider cysteine state pattern capable of producing redox fractal manifolds. What began as a measurement of oxidation becomes something else entirely:

A window into the informational and energetic landscape of the cell, where peptide-level data carries echoes of phase transitions, stability basins, and bifurcation points.

The dual lens of information and chaos theory can make sense of many anomalies. Like how chaotic attractors in atrial fibrillation demand a shock—not a gentle nudge—to restore rhythm, redox chaos—or ordered dysregulation—may require a systemic reset. Any reset is unlikely to stem from the “oxidants bad, antioxidants good” dichotomy [138] as no diseases where “oxidative stress” is implicated have yet been cured along these lines [220]. These disappointing results evidence how much current thinking in redox biology breaks down in the face of nonlinear dynamical systems.

So far, virtually every pharmaceutical redox therapy has fallen short. Perhaps, what’s needed is not a molecule, but a mode—a system-wide coherence. These coherent system states may be better achieved not by a “blockbuster antioxidant”—however well-designed—but through basic lifestyle choices [221,222,223]. As Barry Halliwell remarked [38], they include sleep, diet, exercise. Each one remodels the energy flowing, matter cycling dynamical logic of the cysteine proteome. For example, exercise induces nuanced reductive and oxidative cysteine redox state changes [139,223,224,225,226,227,228,229,230,231,232,233] These physiology-first systems strategies may ultimately be able to cross boundary conditions from order to chaos or vice versa within subsets of the network.

5. Conclusion

Erwin Schrodinger, Albert Szent-Györgyi and others are widely credited with the idea that discoveries consist of seeing what everybody else has seen and thinking what nobody else has thought. In this tradition, we have articulated a novel idea built atop what everybody in the field has seen—cysteine redox proteomic datasets.

We propose that these datasets can be reinterpreted through the lens of information theory and chaos theory—not just as static outputs but as signals from dynamic systems, revealing geometry, structure, and unpredictability in redox biology. From this perspective, a single oxidative shift could ripple over time crossing the chaotic boundary to a strange oxi-attractor—the cysteine redox butterfly effect.

Deriving novel insights does not depend on generating new data, but on rethinking what we already have. Petabytes of existing redox proteomic data can now be interrogated for Shannon entropy, KL divergence, Fisher information, and chaos signatures, extracting hidden order and transitions within complex peptide distributions. Hence, we expect these approaches to unlock latent patterns, enabling not just new discoveries but a shift in how we frame, model, and predict dynamics in redox biology [234,235,236].

Information and chaos theory metrics can be applied to virtually every proteomic dataset from global label-free quantification [237] studies, targeted analyses [238,239,240,241], to advanced chemo-proteomic workflows [242], including reactive cysteine labelling [243,244,245,246] and PTMs like phosphorylation [247,248]. Other oxidative PTMs include methionine oxidation, tyrosine nitration, and carbonylation at several amino acids, such as lysine [249,250,251,252,253,254,255,256,257,258,259,260]. We fully expect similar insights to emerge from their reinterpretation. Hence, scientists across disparate fields can leverage information and chaos theory to derive novel proteomic insights from preexisting datasets [261].

In conclusion, we have reframed the analysis and interpretation of redox proteomic datasets, and potentially proteomic datasets at large, using mathematically grounded information and chaos theory derived metrics. The result is a new of thinking about redox biology—one that embraces the complexities and emergent properties of nonlinear dynamical systems.