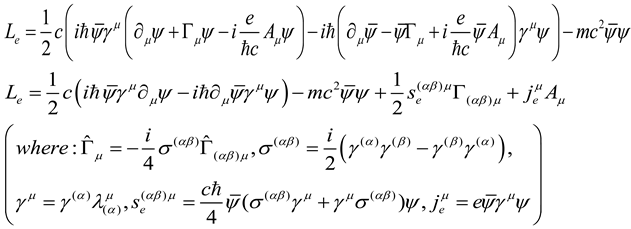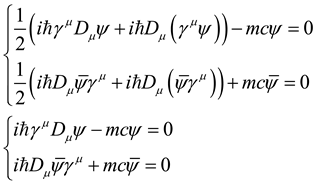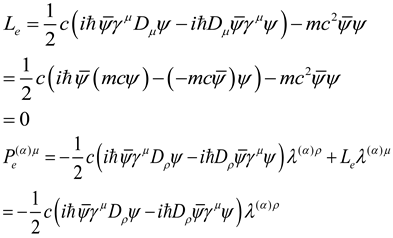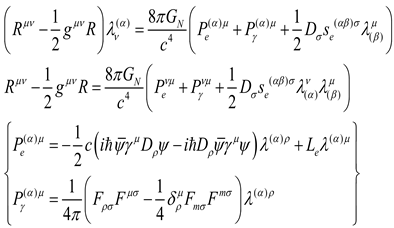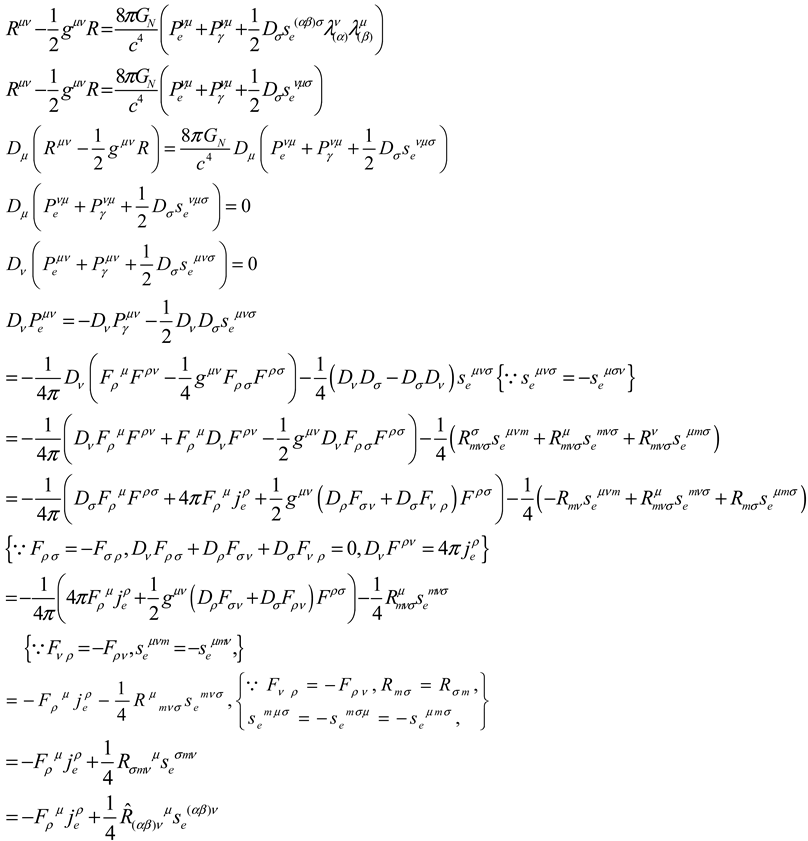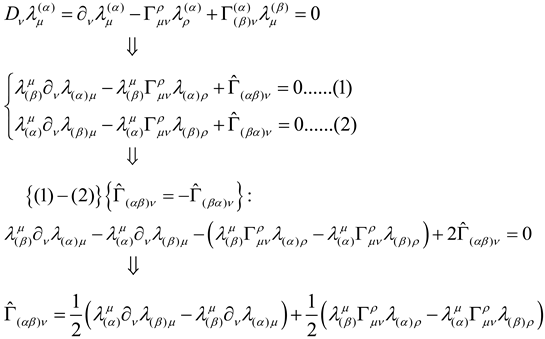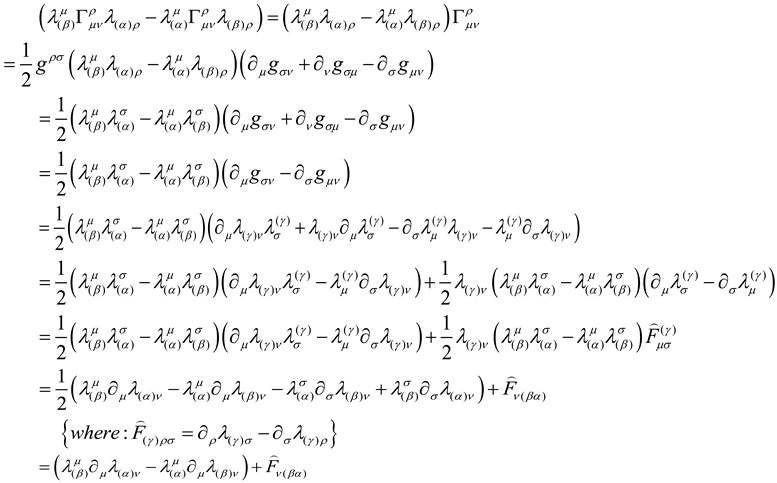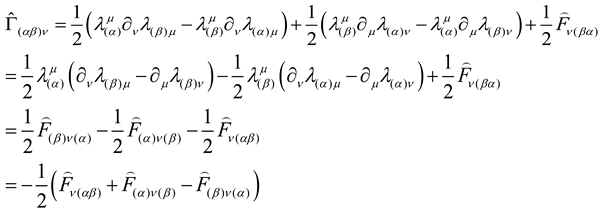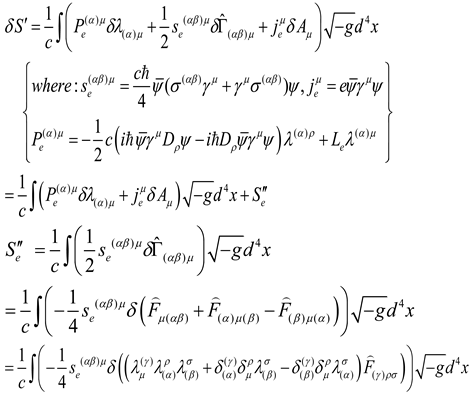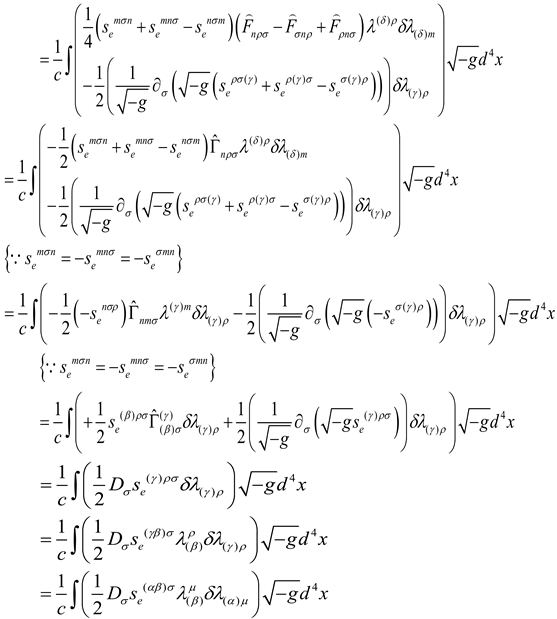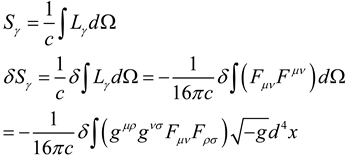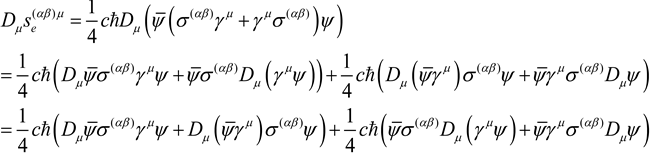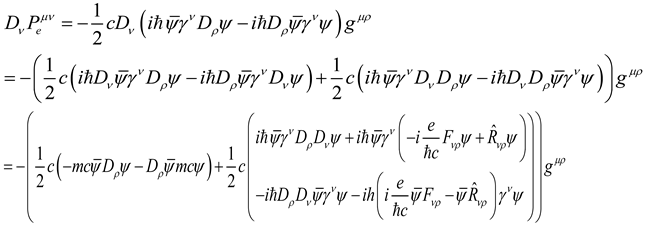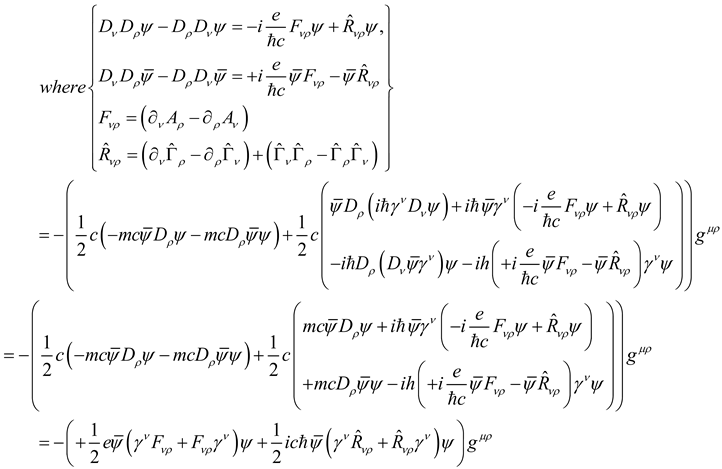1. Introduction
The following improvements have been made to the paper [
21]:
(1) Newtonian gravitational constant:
(2) Lagrange density of gravitational field:
(3) Basic covariant derivative of spinor:
(4) Metric of the vierbein(or tetrad) space:
Since Einstein established the curved space-time gravitational theory and has been a great success, people used a variety of secondary quantization methods, have failed to establish a accepted quantum gravity theory. Some scientists suspect: there is a profound contradiction between Einstein’s gravitational theory and quantum theory of material; only after resolved the contradiction, it is possible to establish a credible theory of quantum gravity. In this paper, through a joint analysis about Einstein’s gravitational theory and Dirac electron theory in Riemann curved space-time, and found that: there is a contradiction between the Einstein gravitational theory and the Dirac electron theory in Riemann space-time about the electron field energy-momentum motion. The contradiction showed that Einstein gravitational theory can not describe the gravitational field of particles with 1/2 spin. In order to eliminate this contradiction, we must modify the Einstein gravitational theory.
2. Theory Preparation
2.1. Basic Covariant Derivative
In order to extending Dirac electron theory to curved space-time, the Lorentz invariant intrinsic vierbein space-time was introduced at every point of coordinate space-time, due to the existence of equivalence principle, and further that: the local tangent space of virbein space-time is equivalent to the local tangent space of coordinate space-time. Let the element displacement of virbein space is and the element displacement of coordinate space is ,due to the existence of equivalence principle between virbein space-time and coordinate space-time, therefore the existence of . Let Therefore, the is a vector of coordinate space-time and a vector of virbein space-time.
Due to the local equivalence, therefore the existence of:
Where, is the infinitesimal space-time distance, is the constant metric tensor of vierbein space-time; is the metric tensor of coordinate space-time. Therefore, the existence of: ,where can be named vierbein field (half metric).
We can use
,
to rise and fall a vibein space-time indicator, and use
,
to rise and fall a coordinate space-time indicator. Therefore, the existence of:
And:
therefore, the existence of:
We can prove that it has the following variational properties:
We can define the basic covariant derivative in coordinate space-time [
1,
2]:
(2) For vector
:
where
is christoffel symbol:
Taking into account the local Lorentz invariance, the affine connection
can be introduced in vierbein space-time. Therefore, for the physical quantity in vierbein space-time, the following definition of basic covariant derivative in vierbein space-time can be made [
3,
4,
5]:
(2)For vector
:
(4)For Dirac Matric
:
Where
is Dirac matrix, content:
where
,
is electromagnetic potential.
2.2. Riemann Geometry
In Riemann space-time, The relationship between the affine connection
in vierbein space-time to the connection
in coordinate space-time is [
3,
4,
5,
6]:
Taking into account
, Therefore, the existence of:
the derivation is in [Appendix 1].
The following relationship can be proved:
where:
(1) The coordinate curvature tensor (Riemann curvature tensor):
(2)The tetrad curvature tensor:
(3)The Spinor curvature tensor:
(4)The electromagnetic Field tensor:
Because there are following relation:
So,the following relationship can be obtained:
3. The Lagrange density in Riemann Space-time
According to the Einstein Gravitational theory, the Lagrange density of gravitational field is[
1,
2]:
According to the Dirac electron theory in curved space-time, the Lagrange density of electron field is[
3,
4,
5]:
For electron, we can proved the relationship:
According to the Maxwell electromagnetic theory in curved space-time, the Lagrange density of electromagnetic field is [
1]:
4. The Equations of Field Motion in Riemann Space-time
(1)The action variation of Einstein gravitational field (the derivation is in [Appendix 2]):
(2)The action variation of Dirac electron field (the derivation is in [Appendix 3]):
The action variation of Maxwell electromagnetic field (the derivation is in [Appendix 4]):
At this time, in accordance with the principle of least action , equations of motion can be the following:
Dirac electron field equation of motion:
Maxwell electromagnetic field equation of motion:
Einstein gravitational field equation of motion:
5. The Contradiction Between Einstein Gravitational Theory and Dirac Electron Theory
5.1. The Equation of Electron Angular Momentum Motion
From equation of Dirac electron field motion (
Eq.4.1.4),we can get the following equation of electron angular momentum motion (the derivation is in [Appendix 5]):
But, from equation of Einstein gravitational field motion (
Eq.4.1.6),we can also get the following equation of electron angular momentum motion:
Eq.4.1.7 is the equation of Einstein gravitational field motion,
Eq.4.1.8 is the equation of angular momentum motion. From
Eq.4.1.8,we can obtain:
So:
There is not any contradiction between the equation of Dirac electron field motion and the equation of Einstein gravitational field motion about the electron angular momentum motion.
5.2. The Equation of Electron Energy-Momentum Motion
From equation of Dirac electron field motion (
Eq.4.1.4),we can get the following equation of electron energy-momentum motion (the derivation is in [Appendix 6]):
But, from equation of Einstein gravitational field motion (
Eq.4.1.6),we can also get the following equation of electron energy-momentum motion:
Considering eq.5.2.1 and eq.5.2.2,there must be:
This condition requires that: the electron spin direction is not independent of external gravitational field , the electron spin always orthogonal to the external gravitational field.For electron, this condition is not always set up. Because the electron spin direction is independent of the external gravitational field , when the spin is parallel to , there can be existed: .
For example:
In the external gravitational field
let a test electron’s spin is
we can get:
But, the above condition requires:
So:
There must be a contradiction between the Einstein gravitational theory and the Dirac electron theory in Riemann space-time about the electron field energy-momentum motion .
6. Conclusion
From the above analysis, we have the following two conclusions:
(1) When we comprehensive discuss the relationship between the Einstein Gravitational theory and the Dirac electron theory in Riemann curved space-time, it has been found that there is a contradiction between the Einstein gravitational theory and the Dirac electron theory about the electron field energy-momentum motion.
(2) The contradiction showed that Einstein gravitational theory can not describe the gravitational field of particles with half-number spin. If we assume that the Dirac electron theory in curved space-time is correct, the Einstein gravitational theory must be modified.
Appendix
Appendix1. The Derivation of the Connection in Vierbein(Tetrad) Space-Time
a.
therefore :
therefore :
According to the above derivation,we can get:
Appendix 2. The Derivation of the Variation of the Gravitational Field Action
The Lagrange density of Einstein gravitational field:
The Action of Einstein-Cartan gravitational field:
Let
,
is clear vector, let
is three-dimensional hypersurface Surrounded the four-dimensional region
.Because the variation of on three-dimensional hypersurface is equal to zero, so there is
on the three-dimensional hypersurface, therefore
Appendix 3. The Derivation of the Variation of the Electron Field Action
The Lagrange density of Diracelectron field:
The action of Dirac electron field:
where :
Appendix 4. The Derivation of the Variation of the Electromagnetic Field Action
The Lagrange density of Diracelectron field:
The action of Dirac electron field:
therefore, we get:
Appendix 5. The Equation of the Electron Angular-Momentum Motion
So, the equation of the electron angular momentum motion is:
Appendix 6. The Equation of the Electron Energy-Momentum Motion
So, the equation of the electron energy momentum motion is:
References
- L. D. Landau and E. M. Lifshitz, The Classical Theory of Fields (Pergamon Press,1987).
- P.A.M.Dirac, GENERAL THEORY OF RELATIVITY(Jobn Wiley,1975).
- Milutin Blagojevic, Gravitation and Gauge symmetries(INSTITUTE OF PHYSICS PUBLISHING BRISTOL AND PHILADELPHIA,2002,p.20-p.72).
- N. D. Birrell, P. Davies, Quantum fields in curved space, Cambridge University press,(1984).
- D. R. Brill, J. A. Wheeler, Rev. Mod. Phys., 29, 465 (1957).
- Cartan, ’E (1923), (1924) and (1925). Sur lesvari’et’es `a connexion affine et la th’eorie de la relativit’e g’en’eralis’ee. Part I: Ann. ’Ec. Norm.40: 325–412 and ibid. 41: 1–25; Part II: ibid.42: 17–88; English transl. by A Magnon and A Ashtekar, On manifolds with an affine connection and the theory of general relativity. Napoli: Bibliopolis (1986).
- R. Penrose, Structure of Space-time, in: Battelle Rencontres, 1967 Lectures in Mathematics and Physics eds. C. M. DeWitt and J. A. Wheeler(Benjamin, New York).
- R. Penrose and W. Rindler, Spinors and Space-Time, vol. 1, Two-Spinor Calculus and Relativistic Fields (Cambridge University Press, Cambridge, 1984).
- R. Penrose and W. Rindler, Spinors and Space-Time, vol. 2, Spinor and Twistor Methods in Space-Time Geometry (Cambridge University Press, Cambridge, 1986).
- C. W. Misner, K. S. Thorne and J. A. Wheeler, Gravitation (Freeman,1973).
- Y.N. Obukhov, Phys. Rev. Lett. 86 (2001) 192.
- Sergiu Vacaru, Panayiotis Stavrinos, Spinors and Space-Time Anisotropy,[arXiv:grqc/0112028].
- R. Aldrovandi, P. B. Barros and J. G. Pereira: “Spin and Anholonomy in General Relativity”, arXiv:gr-qc/0402022. [CrossRef]
- R. Aldrovandi, P. B. Barros, and J. G. Pereira, Found. Phys. 33, 545 (2003) [arXiv:gr-qc/0212034].
- Mayeul Arminjon, Frank Reifler, “ Quantum mechanics for three versions of the Dirac equation in a curved spacetime”, arXiv:gr-qc/0810.0671v1. [CrossRef]
- Arminjon, M., “Two alternative Dirac equations with gravitation”,arXiv:gr-qc/0702048 (2007).
- Reifler, F., Morris, R., “Hestenes’ tetrad and spin connections”, Int. J. Theor.Phys. 44, 1307–1324 (2005). [arXiv:0706.1258 (gr-qc)]. [CrossRef]
- Carlo Rovelli, Quantum Gravity (Cambridge Monographs on Mathematical Physics,2003,p.23-34).
- Watanabe, T , Hayashi, M J , “General Relativity with Torsion”, TOKAI-HEP-TH-2004-09. - 2004. – p.14 [arXiv:gr-qc/0409029].
- R. Miron, S. Watanabe and S. Ikeda, Some connections on Tangent bundle and their applications to the general relativity, Tensor N. S. 46(1987) 8–22.
- Feilin Tang, Contradiction Between Einstein Gravitational Theory and Dirac Electron Theory in Riemann Space-Time. Frontier Science 19(2011):56-68. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).