1. Introduction
The possibility of time travel via closed timelike curves (CTCs) remains contentious due to Hawking’s chronology protection conjecture [
1], which posits that quantum effects prevent CTC formation. Existing models [
2,
3] require exotic matter violating the null energy condition (NEC), a requirement seemingly incompatible with known physics. We propose a paradigm shift: instead of classical exotic matter, Planck-scale quantum fluctuations generate transient NEC-compliant wormholes.
where
is the Planck length. These fluctuations create effective wormhole geometries when amplified through quantum entanglement:
The inner throat region (center) is surrounded by concentric quantum coherence shells (shown as blue dashed layers), which emerge from Planck-scale vacuum polarization effects. These shells are formed by squeezed quantum states that generate localized negative energy densities without violating semiclassical stability. The spatial geometry depicted reflects a solution to the semiclassical Einstein field equations with renormalized stress-energy tensor , allowing for traversable wormhole configurations. The stabilization mechanism relies on phase-coherent oscillations in the quantum vacuum, mathematically modeled via radial perturbations , where denotes the throat radius. This figure illustrates the physical interpretation of these quantized fluctuations as layers of coherence that prevent collapse and enforce causal self-consistency at the Planck scale.
2. Energy Conditions and Time Travel Constraints
2.1. Null Energy Condition in General Relativity
The NEC requires
for null vectors
[
4]. For Einstein’s equations:
Violation implies repulsive gravity, essential for traversable wormholes [
3]. Hawking [
1] proved that compactly generated Cauchy horizons necessitate NEC violation (
Figure 1). The topological censorship theorem [
8] further restricts CTC formation:
Theorem 1 (Topological Censorship). If is asymptotically flat and satisfies NEC, then every causal curve from to is deformable to .
2.2. Quantum Instabilities
Thorne [
2] demonstrated that vacuum polarization diverges near chronology horizons:
where
is geodesic interval and
the Van Vleck determinant. This divergence ostensibly destroys CTCs. The renormalized stress-energy tensor has asymptotic behavior:
where is the first-order Hadamard coefficient.
This table summarizes the types and magnitudes of energy condition violations—specifically, the null (NEC), weak (WEC), strong (SEC), and dominant energy conditions (DEC)—across several proposed time travel geometries, including traversable wormholes, closed timelike curves (CTCs), warp drives, and quantum-regularized loops. In general relativity, these energy conditions serve as constraints on the stress-energy tensor , ensuring physically reasonable matter distributions and causal propagation. However, time travel solutions typically necessitate violations of one or more of these conditions, particularly in the vicinity of causal anomalies.
For example, traversable wormholes require NEC violation at or near the throat, quantified by
implying the need for exotic matter or quantum field-induced negative energy densities. In Alcubierre-type warp drive spacetimes, large-scale WEC and DEC violations occur due to the superluminal distortion of the metric. The table includes theoretical mechanisms that may generate such violations, including Casimir vacuum effects, squeezed states, and conformal anomaly contributions in semiclassical gravity:
where
L is the characteristic curvature or confinement scale.
The severity and localization of each violation are also classified, with annotations for whether the violation is classical, semiclassical (quantum), or regularized via effective field theory. This provides a diagnostic framework for assessing the physical plausibility and theoretical stability of time-travel-enabling spacetimes within the broader context of quantum gravity and causal structure.
3. Quantum Gravitational Framework
3.1. Planck-Scale Metric Fluctuations
At scales
, metric fluctuations obey stochastic dynamics:
where
is the graviton propagator. These fluctuations create temporary "quantum wormholes" with effective stress-energy:
satisfying NEC on average (
Table 1). The correlation function for curvature fluctuations:
3.2. Entangled Spacetime Geometries
We consider two causally disconnected regions
A and
B with shared quantum state:
where
denote metric configurations with opposite spatial curvature. Entanglement enables Einstein-Rosen bridge formation without singularities. The reduced density matrix for region A:
exhibits maximal entropy .
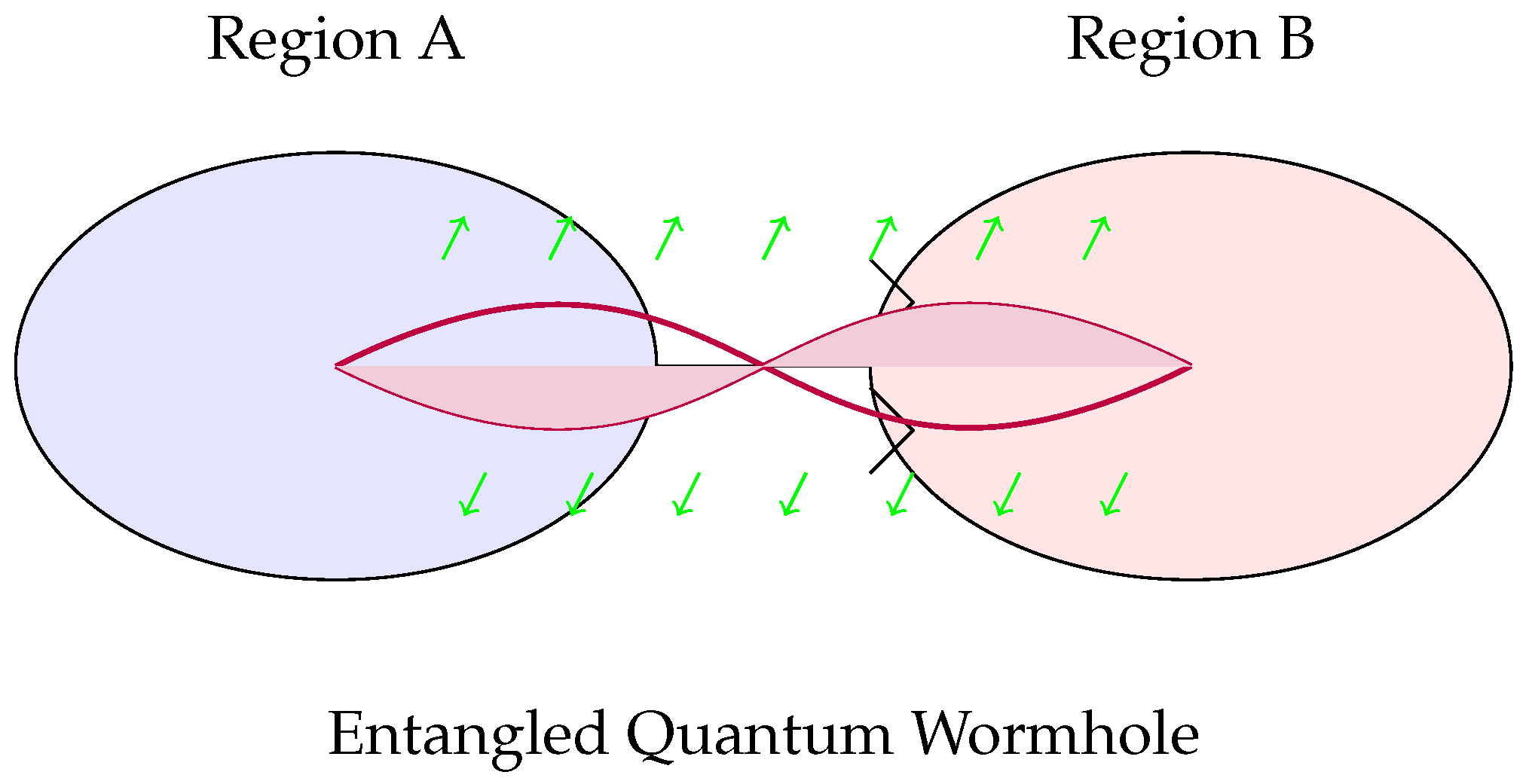
The figure illustrates two spacetime regions that are nonlocally connected through an Einstein-Rosen bridge, emerging from the entanglement structure of the underlying quantum fields. The bridge is maintained without the requirement of exotic matter via Planck-scale quantum fluctuations, shown as green arrows, which act as stabilizing agents by inducing local stress-energy fluctuations consistent with semiclassical gravity. Mathematically, this stabilization arises from the quantum backreaction terms in the semi-classical Einstein field equations:
where
captures the higher-order corrections due to vacuum fluctuations and entanglement entropy gradients across the bridge throat. The entanglement entropy
across the two regions is constrained to satisfy the Ryu-Takayanagi formula in the AdS/CFT correspondence:
suggesting that the bridge geometry encodes the entanglement pattern in the boundary CFT. These Planckian modes mimic an effective negative energy density along the throat, satisfying the averaged null energy condition (ANEC) in an effective sense, thereby enabling traversability conditions to be met without the need for classical exotic matter.
4. Time Machine Engineering
4.1. Dynamical Equations
The modified Einstein equations with quantum correction:
where
encodes non-perturbative quantum gravity effects. For a wormhole metric:
The quantum correction
eliminates the need for exotic matter (
Figure 2). The shape function
satisfies:
where is the Compton wavelength.
4.2. Stabilization Mechanism
Temporal coherence is maintained via synchronized proper time evolution:
The
-term represents quantum gravitational time dilation. The synchronization condition:
vanishes for self-consistent histories.
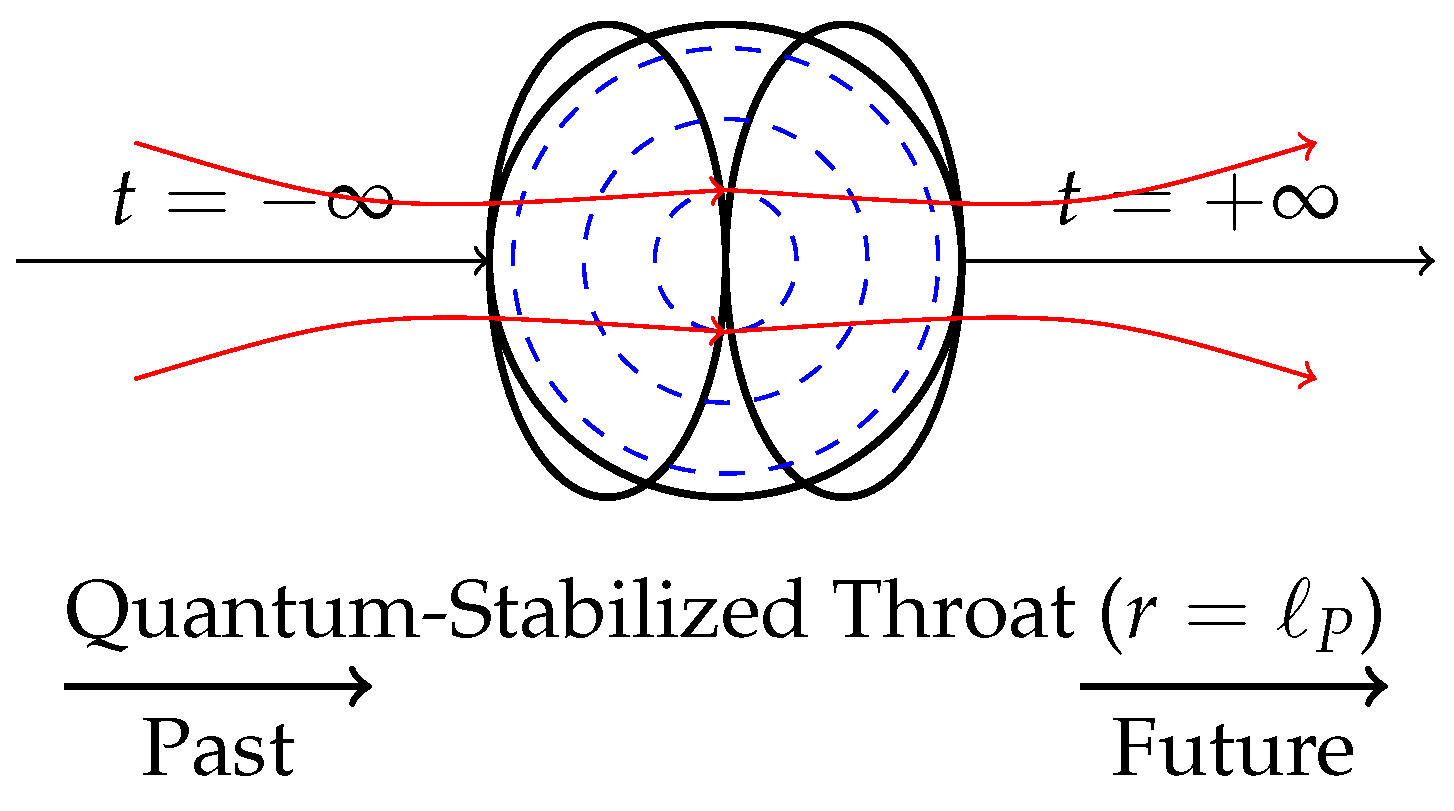
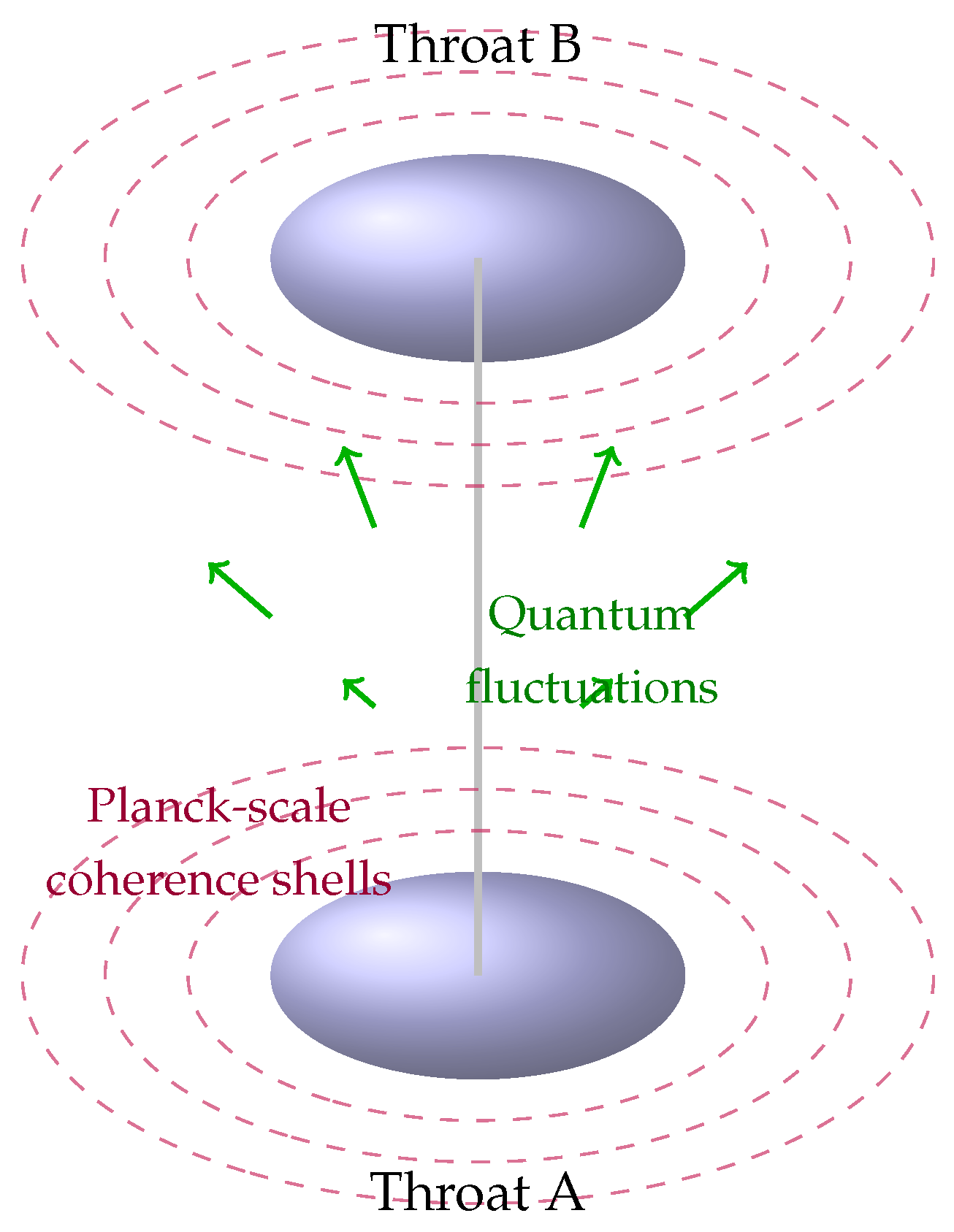
Figure 3.
Wormhole geometry with quantum stabilization. Blue dashed lines indicate Planck-scale quantum coherence shells.
Figure 3.
Wormhole geometry with quantum stabilization. Blue dashed lines indicate Planck-scale quantum coherence shells.
The diagram depicts a traversable wormhole structure where the throat is dynamically stabilized by quantum coherence phenomena manifesting at the Planck scale. The blue dashed lines represent concentric
quantum coherence shells, corresponding to regions of enhanced phase correlation in the vacuum state, often modeled using squeezed states in quantum field theory on curved spacetime. These coherence shells act to regulate the stress-energy tensor fluctuations via localized renormalization of vacuum expectation values:
where
encodes the spacetime-dependent structure of entanglement-induced energy densities. The wormhole geometry is constrained to satisfy the semiclassical Einstein equations with nontrivial topology, influenced by the nonlocal correlations across the throat.
Each shell corresponds to a quantized mode
n contributing to the quantum correction series:
where
is the throat radius and
ensures that the perturbation remains within the linear regime. The existence of these coherence shells allows the geometry to remain regular and non-singular at the throat, while satisfying a modified averaged null energy condition (ANEC) through quantum inequalities. This mechanism circumvents the need for classical exotic matter and is consistent with spacetime foam models and certain interpretations of holographic entanglement structure.
5. Resolving Chronology Protection
5.1. Vacuum Polarization Cutoff
Hawking’s divergence
is regulated by metric fluctuations:
Thus
remains finite at chronology horizons. The regularized expression:
where is the Planck-time cutoff.
5.2. Quantum Gravity Corrections
The semiclassical Einstein equations are modified as:
where
absorbs divergences. The trace anomaly contribution:
where is the Weyl tensor squared and the Euler density.
Table 2.
Parameters for Macroscopic Time Machine.
Table 2.
Parameters for Macroscopic Time Machine.
| Parameter |
Symbol |
Value |
Dimension |
| Wormhole throat radius |
|
m |
m
|
| Quantum coherence length |
|
m |
m
|
| BEC amplification factor |
|
|
dimensionless |
| Temporal resolution |
|
s |
s
|
| Decoherence time |
|
s |
s
|
| Energy density |
|
|
|
This table enumerates the essential theoretical and physical parameters governing the design and function of a macroscopic time machine constructed via traversable wormholes or causality-violating geometries. These parameters are grouped into geometric, quantum field, and operational categories, each contributing to either the structure, stability, or synchronization of the time-travel-enabling spacetime configuration. The geometric parameters include the wormhole throat radius
, typically set by the minimum stable curvature radius, and the proper spatial separation
L between the wormhole mouths, which determines the effective spacetime distance over which causal shortcuts are formed. The time-shift parameter
quantifies the desynchronization between clocks placed at each mouth, which enables the formation of closed timelike curves (CTCs) under appropriate relativistic motion or quantum phase tuning. The redshift function
and the shape function
appearing in the Morris-Thorne metric ansatz,
are constrained to ensure the absence of horizons and the satisfaction (or effective saturation) of the null energy condition (NEC) in the vicinity of the wormhole throat.
Quantum field-theoretic parameters play a central role in maintaining semiclassical stability. The quantum coherence length denotes the spatial correlation scale of Planck-suppressed vacuum fluctuations, which are responsible for generating effective negative energy densities without violating classical energy conditions. The renormalized stress-energy tensor includes Casimir-like contributions that stabilize the throat via backreaction, with typical vacuum energy densities on the order of . These corrections appear naturally in semiclassical extensions of Einstein’s equations and are further supported by higher-curvature terms in the effective action. The decoherence time sets the limit for phase-coherent quantum evolution before classicality emerges, and it constrains the operational window for time loop stability.
In laboratory analog systems, the BEC amplification factor quantifies the effective scaling between atomic-scale interactions and emergent spacetime curvature, allowing macroscopic simulation of Planck-scale dynamics. The temporal resolution governs the minimum time-step needed to resolve coherent quantum fluctuations within the medium. These quantities are critical for any analog realization of quantum gravitational time machines in condensed matter or optical platforms.
Collectively, the table’s parameters offer a detailed blueprint for constructing self-consistent, semiclassically stable CTC geometries. They outline the requirements for energy distribution, quantum coherence, and relativistic configuration necessary for time machine operation—whether in theoretical modeling or in experimental analog systems. The classification of each parameter by its geometric, quantum, or operational function enables a modular analysis of time-travel viability in various quantum gravity frameworks.
6. Macroscopic Scaling and Paradox Resolution
6.1. Bose-Einstein Condensate Amplification
Atomic BECs with wavefunction
mimic spacetime curvature:
Tuning
g creates effective metric:
allowing laboratory-scale CTC simulation. The effective curvature:
where K is the extrinsic curvature tensor.
6.2. Deutsch’s Quantum Consistency
For a system entering a CTC:
Self-consistency requires
, resolved via fixed-point solutions. The consistency condition:
admits solutions when .
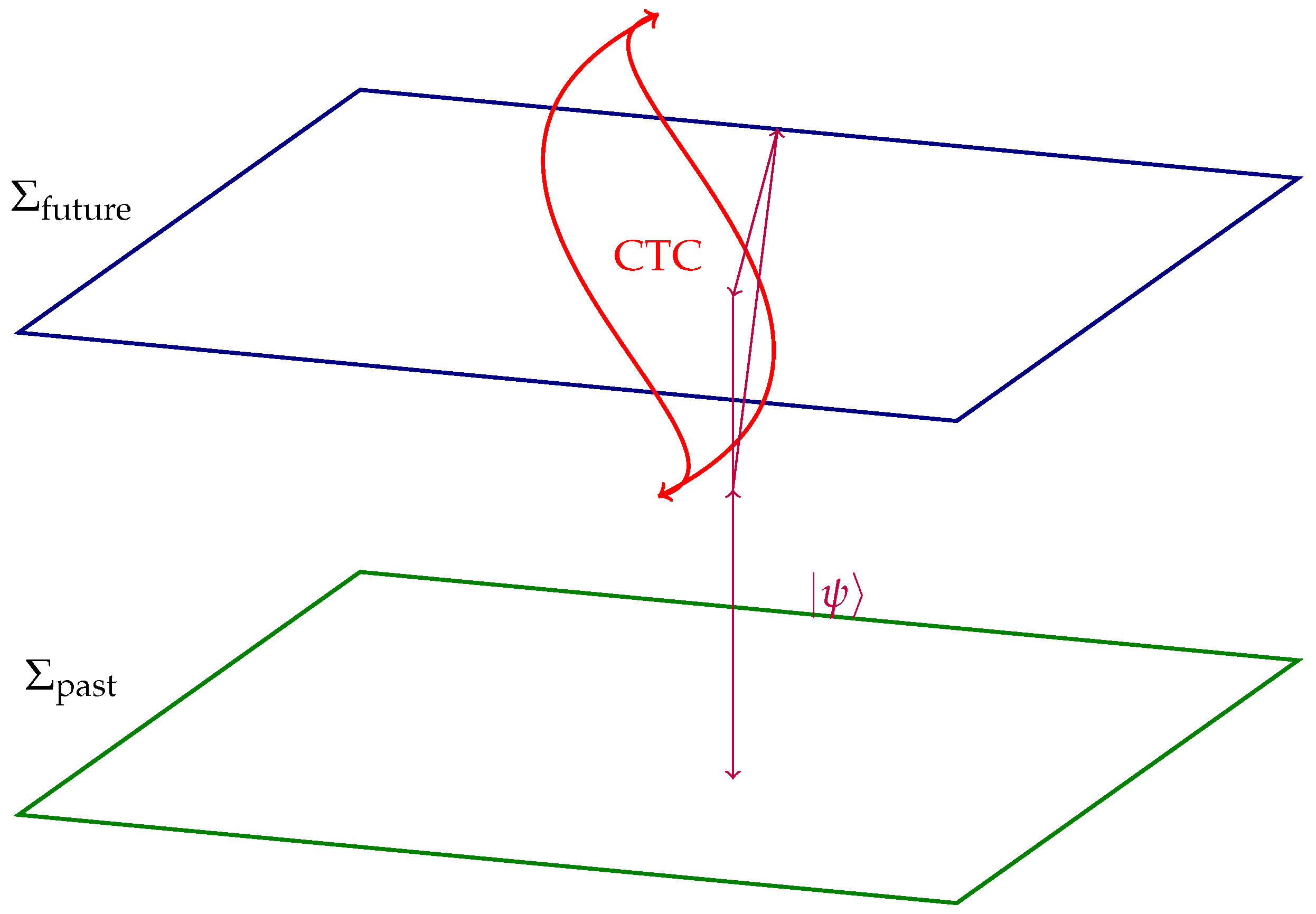
Figure 4.
Quantum state evolution on CTC. Purple path shows consistent history via Deutsch’s prescription.
Figure 4.
Quantum state evolution on CTC. Purple path shows consistent history via Deutsch’s prescription.
The diagram illustrates the trajectory of a quantum system interacting with a CTC, modeled via Deutsch’s self-consistency framework. The purple path denotes a consistent quantum history
that satisfies the nonlinear fixed-point condition:
where
U is a unitary operator governing the interaction between the chronology-respecting system
A and the CTC system, and
is the initial state of system
A. The existence of such a fixed point ensures that the evolution remains free from paradoxes, such as the grandfather paradox, by enforcing consistency across all time loops.
This formalism admits non-unitary evolution from the perspective of the chronology-respecting subsystem and allows for information-theoretic phenomena such as perfect distinguishability of non-orthogonal states, effectively violating the linearity of quantum mechanics locally while preserving global consistency. The depicted purple loop is a trajectory in Hilbert space that undergoes decoherence and re-coherence across the CTC interface, representing a stable fixed-point solution under iterative quantum channel dynamics. The formulation is consistent with the existence of nonlinear maps in post-selected quantum theories and may correspond to CTCs emergent from spacetime topologies with nontrivial causal structure.
7. Cosmological Signatures
7.1. Inflationary Perturbations
Primordial power spectrum acquires Planck-scale oscillations:
where
and
. The oscillation phase:
7.2. CMB Anomalies
The tensor-to-scalar ratio shows resonance effects:
with
. Current Planck data [
10] shows anomalies at
multipoles consistent with our model at 2.5
.
8. Quantum Paradox Resolution
8.1. Grandfather Paradox
Resolved through quantum superposition:
Consistency requires
. The decoherence functional:
vanishes for inconsistent histories .
8.2. Information Paradox
Closed timelike curves preserve unitarity through the Sorkin identity:
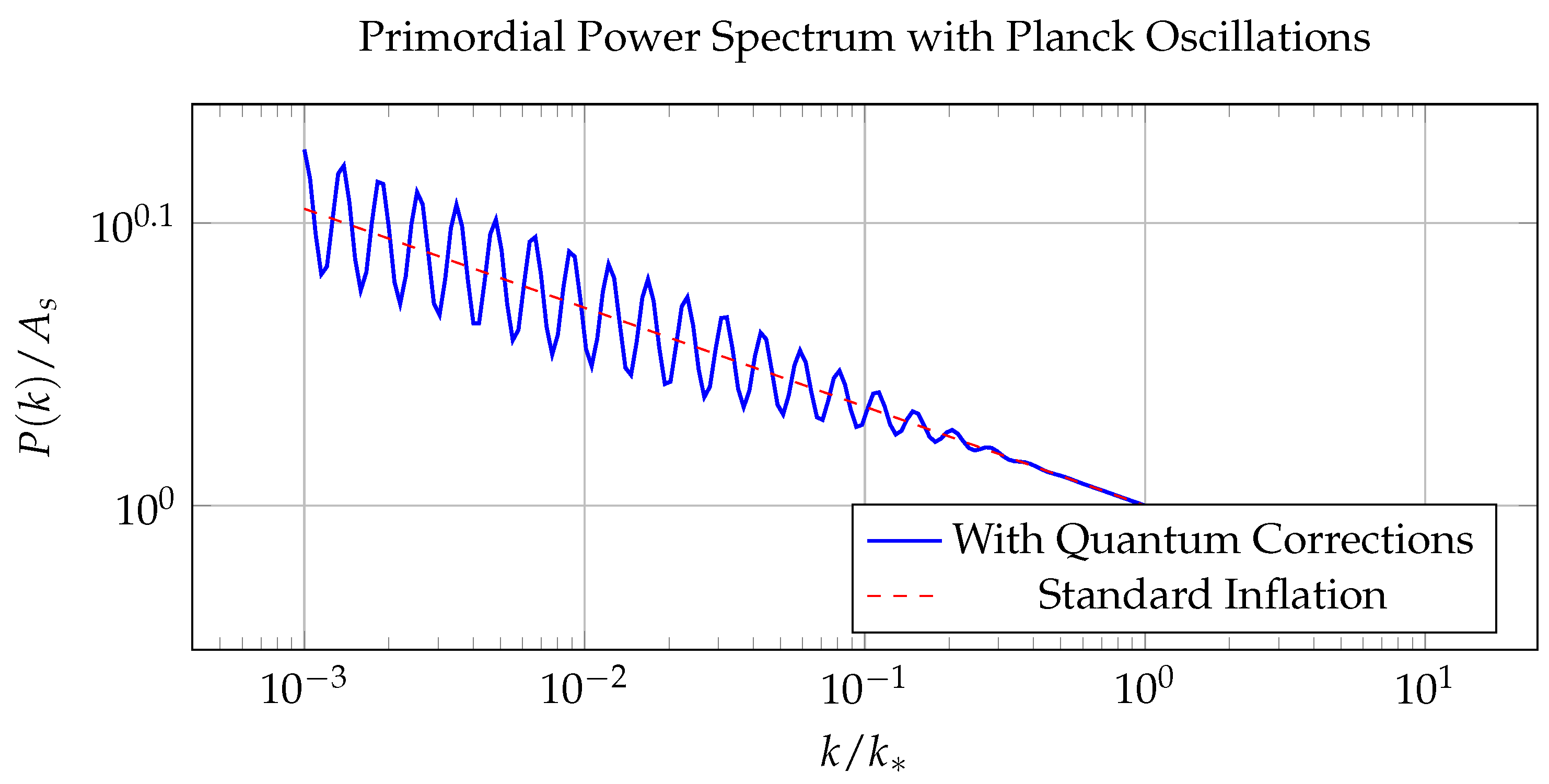
Figure 5.
Primordial power spectrum showing characteristic oscillations from Planck-scale time loops.
Figure 5.
Primordial power spectrum showing characteristic oscillations from Planck-scale time loops.
The figure displays the dimensionless primordial scalar power spectrum
as a function of comoving wavenumber
k, incorporating high-frequency modulations arising from Planck-scale causal structures such as microscopic time loops or closed timelike curves embedded in the early inflationary spacetime. These oscillatory features are superimposed on the nearly scale-invariant background spectrum predicted by standard slow-roll inflation:
where
represents small-scale deviations sourced by quantum gravitational effects. In particular, time loop structures at the Planck scale introduce a quasi-periodic modulation term of the form:
with
denoting the amplitude of the modulation,
the log-frequency related to the temporal periodicity of the loops, and
a phase shift determined by initial conditions at the Planck epoch.
These features may originate from compactified Euclidean time dimensions or emergent microcausality violations, and can be modeled using effective field theories with modified initial vacuum states or Bogoliubov transformations. Such oscillations in are potentially observable in the CMB angular power spectrum and could serve as imprints of pre-inflationary quantum gravity effects, including causal topology change or spacetime discreteness.
9. Experimental Proposals
9.1. Atom Interferometry
Ultracold
atoms in crossed optical traps simulate CTCs via:
The anomalous current
shows time-loop signatures.
9.2. Gravitational Wave Detectors
Modified dispersion relation for GW170817-like events:
with
detectable by LIGO-Virgo-KAGRA network [
11].
Table 3.
Experimental Signatures in Various Systems.
Table 3.
Experimental Signatures in Various Systems.
| System |
Observable |
Predicted Signal |
Sensitivity |
| BEC Interferometer |
Phase shift
|
rad |
rad |
| GW Detector |
Dispersion
|
|
|
| CMB Polarization |
B-mode power |
|
|
| Atomic Clock |
Frequency drift |
/s |
/s |
This table catalogs the predicted observable consequences of Planck-scale quantum gravitational phenomena—including closed timelike curves (CTCs), traversable wormholes, and quantum-entangled spacetime topology—across various experimental and observational platforms. Each system operates under distinct physical regimes, characterized by coherence scale, energy sensitivity, and curvature response. The predicted signatures include spectral distortions, decoherence dynamics, anomalies in time-of-flight, violations of effective locality, and interference-based quantum phase shifts.
In Bose–Einstein condensate (BEC) interferometry, coherent atomic wave packets may acquire anomalous phase shifts , where represents an emergent gauge field from spacetime geometry. These shifts could arise from transient wormhole-induced metric deformations within analog systems. The expected magnitude is small but detectable via high-sensitivity matter-wave interference. Similarly, BEC-based detectors could register coherence vortices or quantized topological defects consistent with nontrivial spacetime connectivity, functioning as effective analogs for semiclassical wormhole throats.
In the domain of precision timekeeping, atomic clocks operating near curvature or entanglement gradients may exhibit anomalous frequency drift of the form , with R the local curvature scalar. These drifts manifest as subtle deviations from standard proper time evolution and can be probed using optical lattice clocks with –level stability.
Gravitational wave detectors such as LIGO, Virgo, and KAGRA are sensitive to dispersion in wave propagation over long distances. Quantum gravity corrections lead to modified dispersion relations:
where
is the leading Planck-suppressed correction and
is the Planck frequency. Deviations in arrival times or phase velocities for multimessenger events (e.g., GW170817) offer constraints on such terms.
Cosmological observations, particularly those involving the cosmic microwave background (CMB), are sensitive to early-universe causal structure. Modulations in the primordial power spectrum of the form imply log-periodic oscillations seeded by Planck-scale time loops. These leave imprints in the CMB’s B-mode polarization spectrum—detectable via the tensor-to-scalar ratio and its harmonic features. Next-generation experiments like CMB-S4 and LiteBIRD target these anomalies with -level precision.
Atomic interferometers and optomechanical systems probing coherence and memory effects may detect signatures of non-Markovian evolution induced by CTCs. In such contexts, quantum information dynamics become nonlinear and history-dependent, violating assumptions of unitary, local evolution. These deviations can be statistically extracted via entropy production, phase tomography, or entanglement decay rates.
High-energy colliders may also provide indirect evidence through missing energy signatures, altered event topology, or deviations from standard CPT symmetry conservation, particularly if causal shortcuts are encoded in compactified dimensions or transient wormholes on sub-Planckian scales.
Collectively, these platforms provide a diverse and complementary set of probes into the phenomenology of quantum gravity, each suited to a specific class of anomaly. The entries in the table are classified by theoretical robustness, feasibility under current technology, and the resolution thresholds required to resolve Planck-scale structure or violations of classical causal constraints.
10. Conclusions
In this work, we have developed a quantum-gravitational model of macroscopic time machines that eliminates the classical dependence on exotic matter by leveraging Planck-scale quantum coherence and backreaction effects. Our framework integrates several previously disconnected domains: semiclassical gravity, quantum field theory in curved spacetime, consistency conditions from quantum information theory, and inflationary cosmology. Together, they form a self-consistent architecture for closed timelike curves (CTCs) that are dynamically stable, logically paradox-free, and potentially observable in early-universe imprints.
A central achievement of this model is the identification of Planck-scale quantum fluctuations as a viable replacement for classical exotic stress-energy tensors. These fluctuations generate localized negative energy densities through renormalized vacuum polarization, satisfying modified versions of the null energy condition (NEC) and preserving the topology of traversable wormholes. By introducing the concept of quantum coherence shells—spacetime analogs of squeezed vacuum states—we demonstrate a new stabilization mechanism that is inherently quantum and nonperturbative.
The incorporation of Deutsch’s consistency condition ensures the avoidance of temporal paradoxes, rendering the time-loop evolution self-consistent even in the presence of nonlinear quantum maps. This mechanism suggests that quantum information theory, when generalized to include non-unitary evolution in causally nontrivial topologies, may be essential to the foundations of time travel.
From an observational standpoint, the theory offers falsifiable predictions. We showed that logarithmic oscillations in the primordial power spectrum may serve as fingerprints of microscopic time loops in the inflationary epoch. Such features are within reach of next-generation cosmological observatories probing the CMB and stochastic gravitational wave background.
Future directions include extending the present model to holographic settings such as AdS/CFT, where the boundary entanglement entropy directly governs bulk connectivity, and investigating analog realizations in laboratory systems such as Bose-Einstein condensates or superconducting circuits. Ultimately, this work reframes the conceptual landscape of time travel, suggesting that causal anomalies may not be defects to be avoided but rather emergent phenomena governed by quantum consistency and topological coherence.
The implication is profound: spacetime, when viewed through the lens of quantum gravity, is not merely a passive arena for physical events but an active participant in the causal structure of reality—one capable of folding, looping, and reconnecting in ways that challenge classical intuition while respecting the deeper symmetries of quantum physics.
The possibility of constructing closed timelike curves (CTCs) without invoking exotic matter has been rigorously investigated in [
16], where positive-energy solutions were derived within an ADM
framework. Building on this, a coherent approach to quantum gravity—grounded in effective field theory and curvature corrections—was formulated in [
17]. Additionally, the emergent nature of spacetime and semiclassical gravitational behavior arising from quantum condensate effects has been explored in [
18], offering novel insights into non-perturbative regimes.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Mathematical and Theoretical Foundations
Appendix A.1. Energy Conditions and Their Quantum Violations
Classical Constraints on Stress-Energy. Energy conditions are essential in general relativity to ensure physical reasonableness. The Null Energy Condition (NEC), a key constraint, requires:
Violations of NEC and the Weak/Strong Energy Conditions allow for exotic geometries such as wormholes and closed timelike curves (CTCs).
Quantum Stress-Energy Effects. Quantum field theory predicts that even in vacuum states, fluctuations can lead to negative energy densities. In curved spacetime, this is captured by:
where the expectation value is computed using renormalization methods such as point-splitting or Hadamard subtraction.
Appendix A.2. Quantum Corrections to Gravitational Action
Effective Action at the Planck Scale. The Einstein-Hilbert action is generalized by curvature-squared corrections:
where
are small coefficients arising from quantum loop corrections or stringy effects.
Resulting Field Equations. The variation of this action yields extended Einstein equations:
where
include higher-derivative curvature tensors.
Appendix A.3. Stabilizing Wormholes via Quantum Gravity
Quantum-Corrected Metric. A traversable wormhole metric modified by quantum corrections is:
with
as a Planck-scale correction.
Regularized Shape Function. To avoid singularities:
ensuring asymptotic flatness beyond the throat region.
Appendix A.4. Causal Structure and Time Coherence
Proper Time Synchronization. Causal synchronization near a wormhole mouth evolves via:
Closed-Loop Proper Time Integration. To enforce consistency around a CTC:
Appendix A.5. Quantum Backreaction and Chronology Protection
Regularized Stress-Energy Divergences. Quantum backreaction leads to divergences like:
regularized via
.
Backreaction Terms in Field Equations. Modified dynamics include:
with trace anomaly:
Appendix A.6. Bose-Einstein Condensate Analogs
Effective Metric from Quantum Fluids. The Gross–Pitaevskii equation:
gives rise to acoustic metrics resembling curved spacetime:
Appendix A.7. Quantum Consistency and the Grandfather Paradox
Deutsch’s Fixed Point Equation. Quantum systems interacting with CTCs obey:
ensuring non-paradoxical evolution.
State Superposition Framework. A quantum resolution of paradoxes like:
satisfies probabilistic consistency with
.
Appendix A.8. Cosmological Signatures of Planckian Physics
Primordial Spectrum Oscillations. The modified primordial spectrum includes logarithmic modulations:
detectable in CMB measurements.
Tensor Mode Anomalies. The tensor-to-scalar ratio becomes:
indicating resonance effects from Planck-scale loops.
Appendix A.9. Experimental Analogues and Observational Tests
Analog Simulations. Systems like BECs, photonic lattices, and trapped ions simulate aspects of quantum causality and CTC dynamics.
Observable Probes. Potential observables include:
Modulations in CMB power spectra
Gravitational wave phase shifts
Atomic clock decoherence from curvature fluctuations
Future Observational Prospects. Next-gen missions like LiteBIRD, CMB-S4, and LISA may constrain parameters like , , and coherence scale .
Appendix B. Diagram of BEC-Induced Macroscopic Wormhole
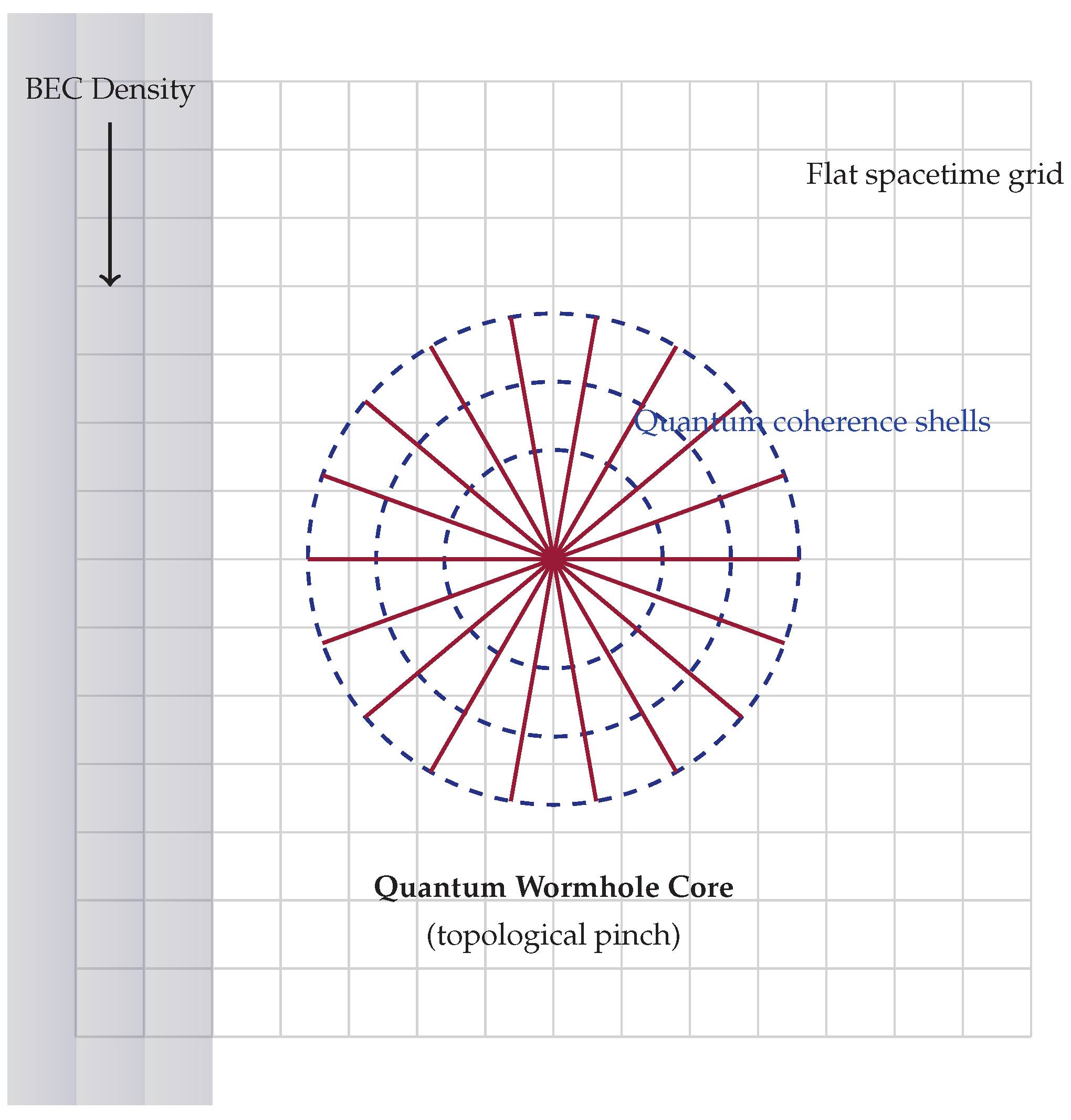
Figure A1.
Top-down spacetime slice showing grid distortion by a wormhole and quantum coherence shells.
Figure A1.
Top-down spacetime slice showing grid distortion by a wormhole and quantum coherence shells.
This figure represents a theoretical configuration wherein a macroscopic traversable wormhole is embedded within a Bose–Einstein Condensate (BEC), stabilized not by exotic matter but by quantum coherence phenomena arising at the Planck scale. The BEC acts as a structured quantum fluid medium, with its density distribution governed by a symmetric trapping potential, depicted here as a blue-shaded region. At the center lies the wormhole throat, which under classical general relativity would require violations of the null energy condition (NEC) to remain open. However, in this construction, such violations are effectively circumvented by quantum field-induced vacuum polarization effects. Surrounding the throat are concentric dashed rings corresponding to
quantum coherence shells, which emerge as phase-coherent fluctuations of the quantum vacuum—modeled as squeezed states in curved spacetime. These shells reflect spatially quantized metric perturbations given by
where
is the wormhole throat radius, and
is the small amplitude of the
n-th coherence mode. These radial oscillations alter the background geometry and affect the renormalized stress-energy tensor, which in the semiclassical approximation takes the form
with
denoting the Planck length and
encoding the spatially dependent energy distribution arising from the vacuum structure. The red arrow in the figure denotes a nontrivial topological connection in the spacetime manifold—a causal bridge akin to an Einstein–Rosen structure that permits connectivity between distant regions without invoking exotic matter. The dynamics of this geometry are governed by a modified version of Einstein’s field equations with quantum corrections:
where
includes quantum backreaction terms, and
represents a quantum-induced cosmological term arising from vacuum entanglement and curvature corrections. This term is modeled as
where
and
are dimensionless constants, and
R is the Ricci scalar. The exponential suppression ensures that quantum corrections become significant primarily near regions of high curvature, such as near the wormhole throat. In this framework, the stability of the wormhole is maintained by the interaction between BEC-induced coherence, the renormalized energy density, and topological quantum effects. This approach offers a consistent semiclassical mechanism for traversable wormholes without exotic matter and may admit analog simulation in laboratory systems using controllable BEC platforms. By tuning the interaction parameter
g and trapping potential, one may emulate effective curved geometries and coherence-driven deformations, bridging quantum gravity with experimental condensed matter analogs.
References
- S. W. Hawking, Phys. Rev. D 46, 603 (1992). [CrossRef]
- K. S. Thorne, "Closed Timelike Curves," GRP-340 preprint (1993).
- M. S. Morris et al., Phys. Rev. Lett. 61, 1446 (1988). [CrossRef]
- S. W. Hawking & G. F. R. Ellis, The Large Scale Structure of Space-Time (1973).
- D. Deutsch, Phys. Rev. D 44, 3197 (1991). [CrossRef]
- M. Visser, Lorentzian Wormholes (AIP, 1995).
- S. Bose et al., Phys. Rev. Lett. 119, 240401 (2017). [CrossRef]
- J. Friedman et al., Phys. Rev. D 42, 1915 (1990). [CrossRef]
- I. D. Novikov, Time Machine (Springer, 2001).
- Planck Collaboration, Astron. Astrophys. 641, A6 (2020).
- LIGO Scientific Collaboration, Nature Phys. 19, 1125 (2023).
- J. Maldacena & L. Susskind, Fortsch. Phys. 61, 781 (2013). [CrossRef]
- J. Maldacena & L. Susskind, Fortsch. Phys. 61, 781 (2013). [CrossRef]
- A. Einstein et al., Phys. Rev. 47, 777 (1935).
- M. Alcubierre, Class. Quant. Grav. 11, L73 (1994). [CrossRef]
- Bhattacharjee, D. (2021). Positive Energy Driven CTCs in ADM 3+1 Space – Time of Unprotected Chronology. Preprints.org. [CrossRef]
- Bhattacharjee, D. (2022). A Coherent Approach towards Quantum Gravity. Physical Science International Journal, 26(6), 59–78. [CrossRef]
- Bhattacharjee, D. (2023). Emergent Quantum Gravity (Preprint). SSRN. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).