Van der Waals Magnetic Tunnel Junctions Based on Two-Dimensional 1T-VSe₂ and Rotationally Aligned h-BN Monolayer

1. Introduction

Due to the functionality of magnetic tunnel junctions (MTJs) as spin-torque diodes [1], high-frequency oscillators[2], hard disk drive (HDD) read heads, and innovative spin-transfer torque magneto resistive random-access memory (STT-MRAM) devices[3], they have received substantial attention in the domain of spintronic devices. Alongside scientific advancements, new requirements for device integration have arisen, necessitating the development of novel materials and structures to miniaturize MTJ sizes while enhancing device performance. One approach is by constructing two-dimensional (2D) MTJs through van der Waals heterostructures stacking 2D ferromagnetic and non-ferromagnetic layered materials[4]. Despite their atomic thickness, these 2D ferromagnets maintain spin polarization in devices. The interlayer magnetic couplings in stacked ferromagnetic structures can be manipulated to control transport properties, enabling colossal magnetoresistance or TMR effects. Experimentally, magnetic materials that retain their magnetic properties after exfoliation from three-dimensional bulk materials include 1T-VSe₂[5], CrI₃[6], and Fe₃GeTe₂[7]. Further, monolayer 1T-VSe₂ demonstrating magnetism even at room temperature[5,8]. The discovery of these magnetic 2D materials has triggered extensive research on 2D MTJs and spin valve devices in spintronics.

The weak interlayer interactions in two-dimensional van der Waals heterostructures due to the vdW nature alleviate the experimental constraints of lattice matching between layers, thereby allowing various stable stacking configurations with diverse interlayer orientations. Experimentally accessible twist angles are more readily achievable in such stable rotation structures within the heterojunctions, where distinct rotation interfaces can be realized experimentally. These different interfaces exhibit unique transport characteristics. For example, twisted structures with angles of 0° and 60° have been synthesized in a two-dimensional system by growing monolayer MoS₂ onto an h-BN surface using CVD[6], and graphene has been rotationally aligned with an h-BN layer at 0° or 30° via thermally induced techniques[9]. Moreover, different helical fault types in WSe₂ bilayers can be tuned experimentally by adjusting the precursor ratios (powders of selenium and tungsten oxide) in CVD reactions[10]. Twist-induced moiré effects influence interfacial electromagnetic coupling, resulting in modulation of electrical, optical, and magnetic properties of the heterostructures through rotational manipulation.

Building upon the experimental advances outlined above, we employ DFT complemented by NEGF formalism to simulate and investigate the impact of rotation in an intermediate barrier layer on the performance and governing principles of a vertically stacked two-dimensional magnetically tunneling junction composed of graphene/1T-VSe₂/h-BN/1T-VSe₂/graphene, with a schematic representation schematically illustrated in Figure 1 (a). We systematically study how the transmission coefficients of the magnetic tunnel junction (MTJ) are influenced by rotating the h-BN layer, modeling 18 devices with inter-layer angular intervals of approximately 10°. Our results reveal that a rotation of the h-BN layer leads to substantial variations in the tunneling magnetoresistance (TMR) ratio, ranging from 2328% to 24608%. To probe the origin of this drastic change in TMR, we compute the projected density of states (PDOS) for graphene/h-BN/1T-VSe₂ heterostructures with the h-BN rotated by 62.5° and 83.7° relative to the 1T-VSe₂ heterojunction. Additionally, we obtain spin-resolved local density of states (LDOS) distributions and K_∥-space transmission coefficient maps for both spin paralleled and spin anti-paralleled configurations of the MTJs. By doing so, we gain detailed insights into the behavior difference induced by the h-BN rotation and uncover the underlying influential factors.

2. Materials and Methods

In this work, the structural optimization of the graphene/1T-VSe₂/h-BN heterostructure is performed using ATK[11,12], a computational package based on density functional theory (DFT). The electronic properties are calculated by applying the generalized gradient approximation GGA-PBE[13,14] alongside an adjusted effective on-site Hubbard parameter U. The value of U set for the 3d orbitals of vanadium V atoms is 1 eV[15], as referenced in. A planewave basis cutoff of 600 eV is used. A vacuum space of over 20 Å is maintained between supercells. We adopt a Monkhorst-Pack k-point mesh with a spacing of 0.01 Å^-1 across the Brillouin zone. Forces are considered converged when reaching values less than 0.01 eV/Å^-1.

Transport properties of MTJs are investigated using the combination of nonequilibrium Green’s function (NEGF) method[16] and DFT[17] in ATK, adopting a spin-polarized general gradient approximation with U corrections (SGGA+U)[18,19]. A double-zeta polarized (DZP) basis set[20] is employed with a real-space mesh cut-off at 100 Hartree. The device simulations are run under a temperature of 300 K with periodic boundary conditions in the x and y dimensions perpendicular to the transport direction, which is aligned along the z-axis.

Optimized structures stabilize once convergence thresholds are met, with the maximum residual forces kept below 0.01 eV/Å^-1 and energy convergence at 5 × 10^-6 eV per atom. For the electrode and device central regions, k-point grids densities are 0.01 Å^-1 along both a and b orientations, while the Monkhorst-Pack k-point grid for the transport direction is 100, corresponding to a range of h-BN rotation angles. Transmission coefficients, $T_{\mathsf{\sigma }}^{k_{//}}\left(E\right)$ representing the transmitted electrons through the MTJ, where $k_{//}$ designates in-plane reciprocal lattice vectors along the irreducible Brillouin zone boundary, and σ denotes the spin state, can be analyzed in line with approaches described in [21,22,23]. These coefficients help to unravel the transport behavior in various rotated h-BN heterostructures.

$$T_{\mathsf{\sigma }}^{k_{//}}\left(E\right)=\mathit{Tr}\left[{\mathsf{\Gamma }}_{l,\mathsf{\sigma }}^{k_{//}}\right(E\left)G_{\mathsf{\sigma }}^{k_{//}}\left(E\right){\mathsf{\Gamma }}_{r,\mathsf{\sigma }}^{k_{//}}\right(E\left)G_{\mathsf{\sigma }}^{k_{//}\text{†}}\left(E\right)\right]$$

(1)

The expressions $G_{\mathsf{\sigma }}^{k_{//}}\left(E\right)$ and$G_{\mathsf{\sigma }}^{k_{//}\text{†}}\left(E\right)$ denote the advanced and retarded Green’s functions, respectively. Given an energy E, the quantity T(E) is averaged over all distinct${\text{∑}}_{l/r,\mathsf{\sigma }}$ terms. ${\mathsf{\Gamma }}_{l/r,\mathsf{\sigma }}^{k_{//}}\left(E\right)=i\left({\text{∑}}_{l/r,\mathsf{\sigma }}{\text{∑}}_{l/r,\mathsf{\sigma }}^{\text{†}}\right)$. The spin-resolved drain current I_σ is computed using the Landauer-Büttiker formula[24,25]:

$$\mathit{I}\mathsf{\sigma }(V_b,V_g)={\displaystyle \frac{e}{h}}{\int }_{-\text{∞}}^{+\text{∞}}\left\{T_{\mathsf{\sigma }}\left(E,V_{\mathrm{b}},V_{\mathrm{g}}\right)\left[f_{\mathrm{S}}\left(E-{\mathsf{\mu }}_{\mathrm{S}}\right)-f_{\mathrm{D}}\left(E-{\mathsf{\mu }}_{\mathrm{D}}\right)\right]\right\}\mathit{dE}$$

(2)

Here, f_S and f_D denote the fermi-Dirac distribution functions of the source and drain, respectively, while μ_S and μ_D represent the fermi levels at the source and drain electrodes. T_σ signifies the transmission coefficient for spin component σ. All the transmission spectra computed in this work are based on the collinear spin configuration.

3. Results

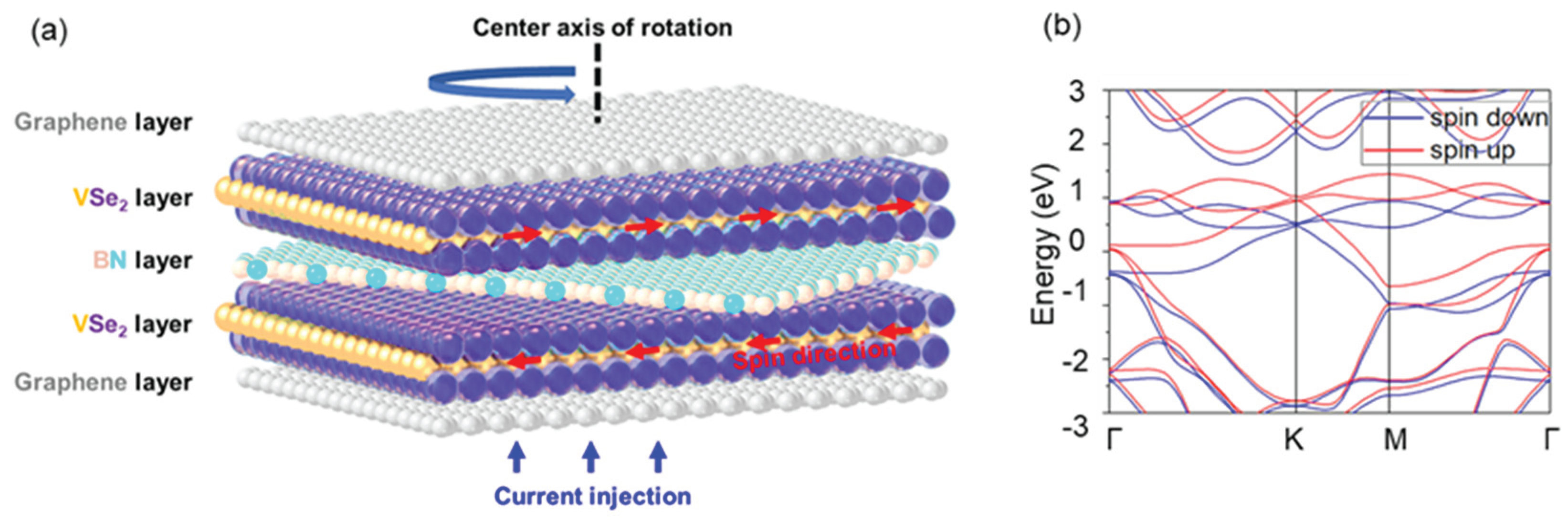
3.1. Device Structure of Van Der Waals Magnetic Tunnel Junction

Within the magnetic tunnel junction, graphene acts as both left and right metallic electrode layers, while 1T-VSe₂ serves as the ferromagnetic layer. By rotating the h-BN layer, we investigate the influence of barrier rotation on device performance. The 1T phase of VSe₂ is a magnetic transition metal dichalcogenide[5]; the band structure for a single-layer, displayed in the Figure 1 (b), corresponds with previous research [26]. Its lattice parameter is a=b=3.44 Å [2], while the h-BN barrier has a lattice constant of a=b=2.51 Å. Owing to the ability to grow monolayer 1T-VSe₂ on graphene or MoS₂ substrates via molecular beam epitaxy, we adopt single-layer graphene as the metal electrode layer adjacent to the VSe₂ layer. To avoid additional strain complications, only graphene’s lattice parameter is stretched to match that of VSe₂. The persistence of electronic states of graphene layers in the projected density of states diagrams of devices rotated 62.5° and 83.7° in Figure 5 and Figure 6, close to the fermi level, verifies that strained graphene still retains its metallic nature. In our work, we rotationally manipulate the h-BN layer while maintaining the same stacking configuration between VSe₂ and the strained graphene layers across all devices to minimize varying parameters. No pinning layers are included in our MTJs; all devices are configured with a basic MTJ structure.

We fabricate 18 magnetic tunnel junction devices, controlling the h-BN layer’s rotation relative to the 1T-VSe₂ layer over a range of approximately 0° to 180° in increments of 10°, ensuring a lattice mismatch of less than 3% for all heterostructures. The lattice parameters for all constructed structures are displayed in Table 1. For comparison purposes, we hold the 1T-VSe₂ and graphene layers at the same angles and positions while manipulating the orientation of the h-BN layer. Specifically, we highlight our rotation model with two examples, viz., graphene/1T-VSe₂/h-BN structures rotated at 62.5° and 83.7°.

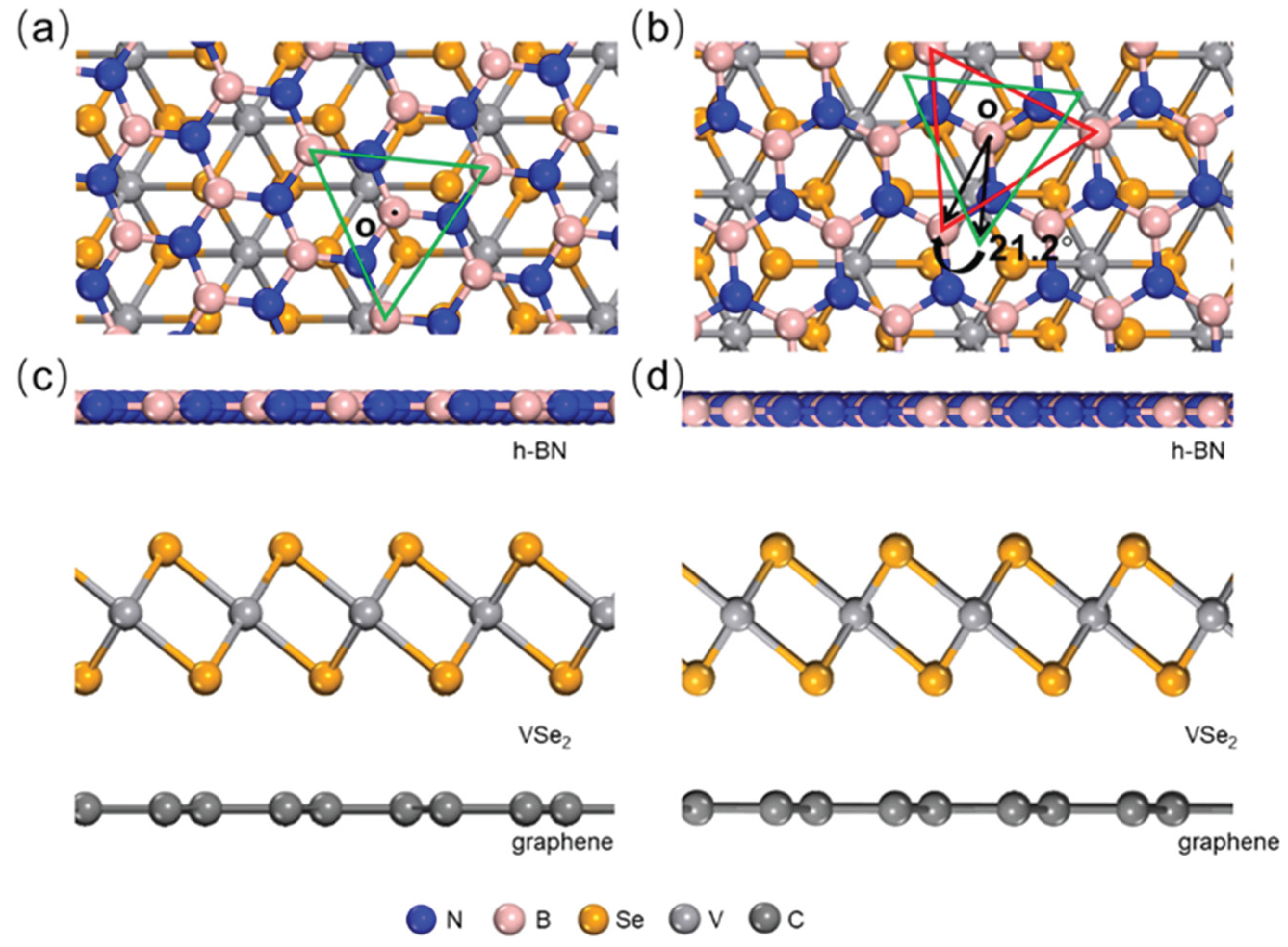
In the top-down view of the 62.5° heterojunction depicted in Figure 2 (a), equilateral green triangles identify a section of h-BN atoms. Equivalent h-BN atoms are framed by red equilateral triangles in the top-down view of the 83.7° stacking schematically illustrated in Figure 2 (b). To facilitate comparison, we duplicate the same-angle green triangle from (a) onto (b) and align their centroids O, illustrating that in the 83.7° heterojunction, the h-BN layer is rotated counterclockwise by 21.2° relative to that in the 62.5° structure. Additional evidence is provided by the side views in Figure 2 (c) and (d), revealing no relative rotation between the 1T-VSe₂ and graphene layers in either heterojunction, with the rotation confined solely to the h-BN layer.

Employing Atomistix ToolKit (ATK) software and DFT, we optimize the stable interlayer spacings within the devices, interlayer distances: 3.53 Å (graphene - graphene), 3.22 Å (graphene - VSe₂), and 3.48–3.54 Å (VSe₂ - h-BN, except 3.73 Å at 10.8°). These specific spacings can be found in Table 1.

3.2. Electrical Properties of Rotating h-BN Layer in the Magnetic Van Der Waals Tunnel Junctions

We construct a Graphene/1T-VSe₂/h-BN/1T-VSe₂/Graphene MTJ configuration and subject it to an external magnetic field to manipulate the magnetic moments of the two ferromagnetic layers into either parallel spin alignment or antiparallel alignment. In the parallel spin configuration, the tunneling resistance significantly drops compared to the resistance when they are in the antiparallel state. The normalized difference between these two resistances defines the tunnel magnetoresistance ratio (TMR). Assuming spin conservation during tunneling, we employ the most optimal definition to describe TMR:

$$\mathrm{TMR}={\displaystyle \frac{G_{\mathrm{PC}}-G_{\mathrm{APC}}}{G_{\mathrm{APC}}}}\times 100\%$$

(3)

The conductivity can be calculated using the following formula:

$$G_{\mathrm{PC}}={\displaystyle \frac{e^2}{h}}\left(T_{\uparrow }^{\mathrm{PC}}+T_{\downarrow }^{\mathrm{PC}}\right)$$

(4)

$$G_{\mathrm{APC}}={\displaystyle \frac{e^2}{h}}\left(T_{\uparrow }^{\mathrm{APC}}+T_{\downarrow }^{\mathrm{APC}}\right)$$

(5)

G_PC refers to the conductance of a MTJ with parallel spin orientation, while G_APC represents the conductance with antiparallel alignment. $T_{\text{↑}}^{\mathrm{PC}}$($T_{\text{↑}}^{\mathrm{APC}}$) and $T_{\text{↓}}^{\mathrm{PC}}$($T_{\text{↓}}^{\mathrm{APC}}$) denotes the parallel (antiparallel) transmission coefficients for spin-up and spin-down electrons, respectively. Similarly, the TMR effect can also be described in terms of the device’s resistance according to equation “(3)”, which expresses the TMR ratio as:

$$\mathrm{TMR}={\displaystyle \frac{R_{\mathrm{PC}}-R_{\mathrm{APC}}}{R_{\mathrm{APC}}}}$$

(6)

R_pc and R_apc represent the resistance in the spin-parallel and spin-antiparallel states, respectively. Based on the mentioned formula, to calculate the rotation effect of h-BN layers on the tunneling resistance and conductance of two-dimensional MTJs, we perform calculations of device transmission spectra at zero bias for MTJs with various h-BN layer rotational angles. A summary of parallel and antiparallel conductance values, along with their respective resistances and TMR, is compiled in Table 1 for devices with different rotation angles. 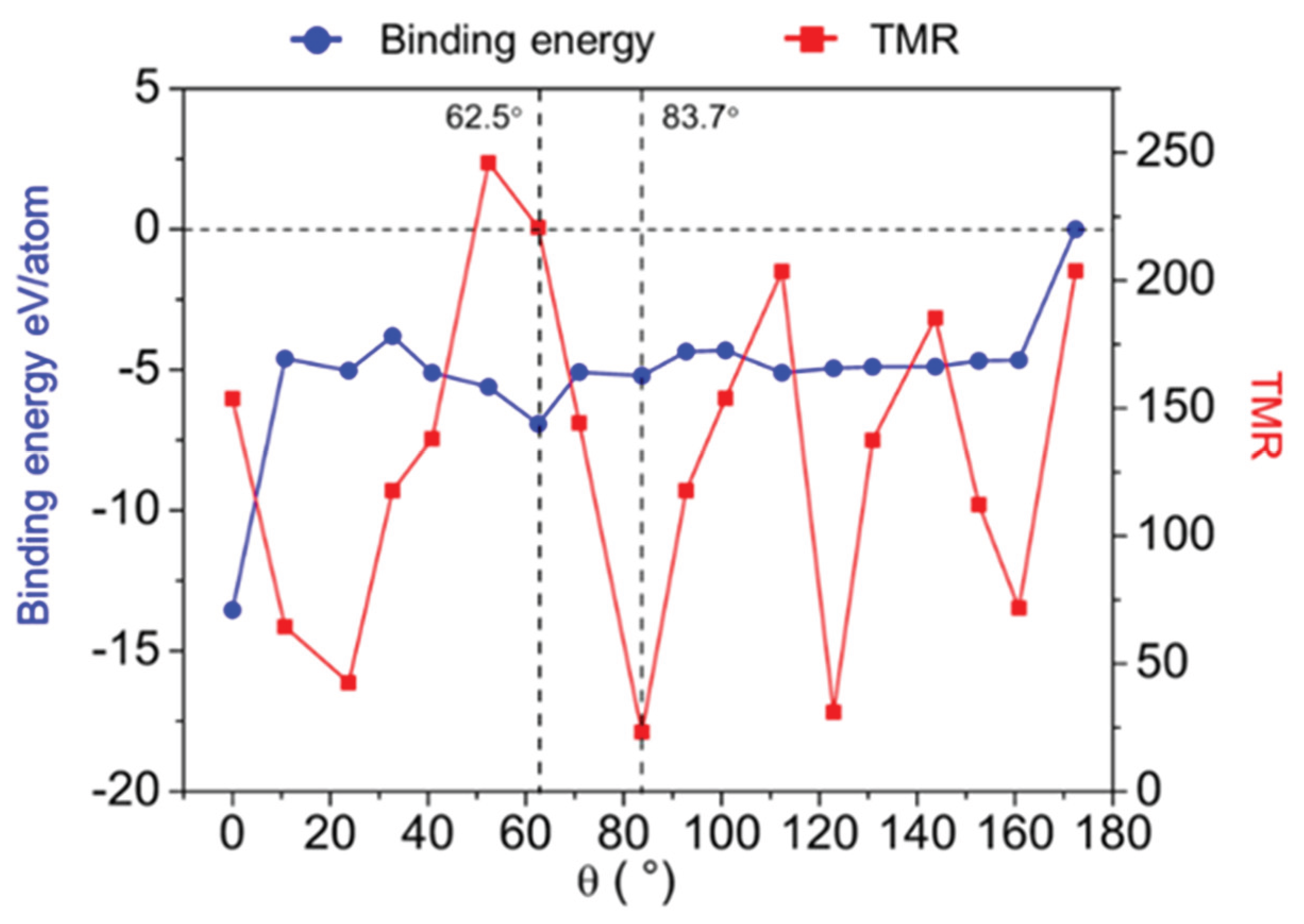The red curve in Figure 3 illustrates the variation of TMR with h-BN layer rotation, demonstrating a wide range from 2328% to 24680%. There is no evident pattern between the h-BN angular rotation within the devices and the distribution of TMR values. The device with the highest TMR performance corresponds to the one with a 52.4° rotation angle. Illustrated by the blue curve in Figure 3, it presents the binding energy of each atom within the 1T-VSe₂/h-BN heterostructure for differently rotated devices. The formation energy E_form within the interface of the heterojunction can be expressed as:

E_form = E(VSe₂/h-BN)-E(VSe₂)-E(h-BN)

(7)

E (VSe₂/h-BN) represents the total energy after stacking of the 1T-VSe₂/h-BN structure, while E (VSe₂) and E (h-BN) denote the energies of a single-layer 1T-VSe₂ and h-BN, respectively, in a vacuum environment. Higher binding energy signifies increased instability of the rotational configuration. We set the 1T-VSe₂/h-BN binding energy of the most stable structure, at 172.4°, to 0 meV/atom, against which we gauge the binding energies of other h-BN rotation structures.

Our calculated interface binding energies for the various rotation angles of the 1T-VSe₂/h-BN heterostructures showed in Figure 3, mainly cluster between -3.8 meV/atom and -6.9 meV/atom, suggesting that appreciable bonding interaction exists between 1T-VSe₂ and h-BN layers across these angles. Specifically, the 0° structure has the lowest interface binding energy of -13.5 meV/atom. While overcoming an interface binding energy difference of 8.9 meV/atom is required for h-BN to rotate from 0° to 10.8°, and a shift from 160.8° to 172.4° involves overcoming 4.7 meV/atom, the clockwise rotation of h-BN from 10.8° to 160.8° is relatively facile. Considering the experimentally observed 52.4° structure with the highest TMR is prone to slide to the 62.5° structure with lower local interface binding energy, indicated by a black dashed line in Figure 3, we highlight the interface binding energy and TMR characteristics of these two devices (62.5° with the second-highest TMR and 83.7° with the lowest TMR) for more profound investigations into the interplay between electric and magnetic properties due to h-BN layer rotations.

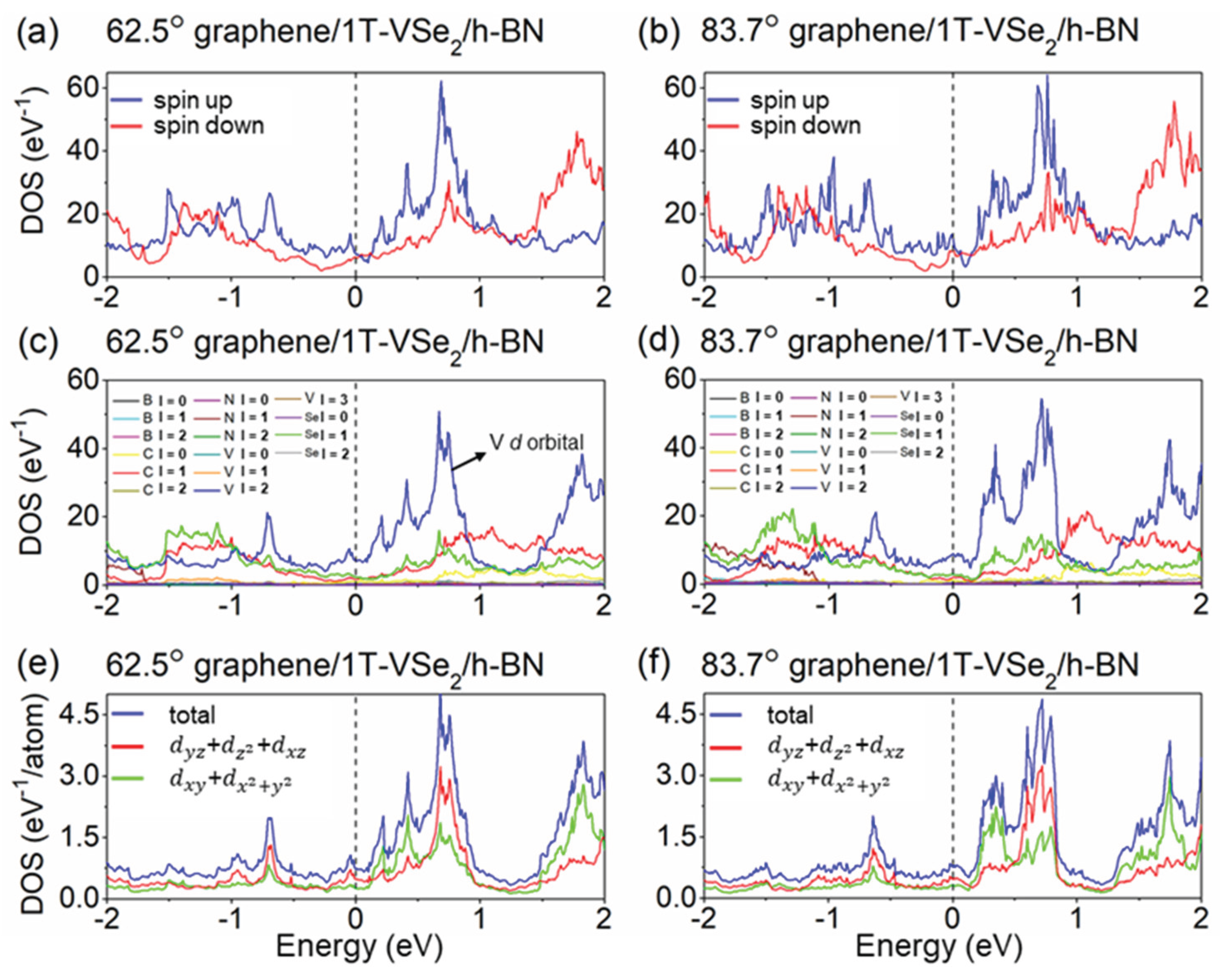
We proceed in Figure 4 (a) and (b) to investigate the PDOS for the spin-up and spin-down channels of graphene/1T-VSe_2/h-BN heterostructures at 62.5° and 83.7° after the rotation of h-BN. A distinct contrast in the electronic states near the fermi level and other peaks in PDOS profiles for both heterostructures’ spin-up and spin-down channels is observed. It is well-known that magnetic properties in the heterostructure are predominantly due to the presence of unpaired electrons in V atoms’ d orbitals. The differences in PDOS peak distributions between the spin-up and spin-down channels suggest that rotation of the h-BN layer influences the magnetization direction within the 1T-VSe₂ layer, thereby affecting electron states for the two spins. Moreover, the imbalance of spin-up and spin-down channel DOS in each heterostructure further indicates a spin polarization phenomenon within the 1T-VSe₂ layer that depends on the overall system.

Moving forward, in Figure 4 (c) and (d), we analyze the distribution of angular momentum quantum number l for distinct elements’ orbital in the two rotated heterostructures. The third atomic d-orbitals of the V atom in the 1T-VSe₂ layer contribute significantly to the PDOS compared to other elements or other V orbitals at the fermi level. Hence, we depict the projected DOS for individual V atom d-orbitals of the 62.5° and 83.7° heterostructures, as schematically illustrated in Figure 4 (e) and (f). Notably, both V atoms exhibit similar d-orbital DOS distributions, with two groups: the out-of-plane $d_{yz}$+$d_{z^2}$+$d_{xz}$orbitals and in-plane$d_{xy}$+$d_{x^2{+y}^2}$ orbitals [3]. Analyzing the fermi-level changes in V atom d-orbital states for the two angles, the DOS values for out-of-plane and in-plane d orbitals for the 62.5° structure are 0.47 eV^-1/atom and 0.25 eV^-1/atom, whereas for the 83.7° structure, they are 0.46 eV^-1/atom and 0.29 eV^-1/atom. Despite modest differences in these plane states at the fermi level, there is a noticeable peak difference (62.5°: 0.72 eV^-1/atom vs. 83.7°: 0.38 eV^-1/atom at E = -0.04 eV) in out-of-plane DOS just above the fermi level with much less variation in the in-plane orientation (within 0.09 eV^-1/atom). These contrasting features may account for the influence on TMR for the two devices with distinct rotations.

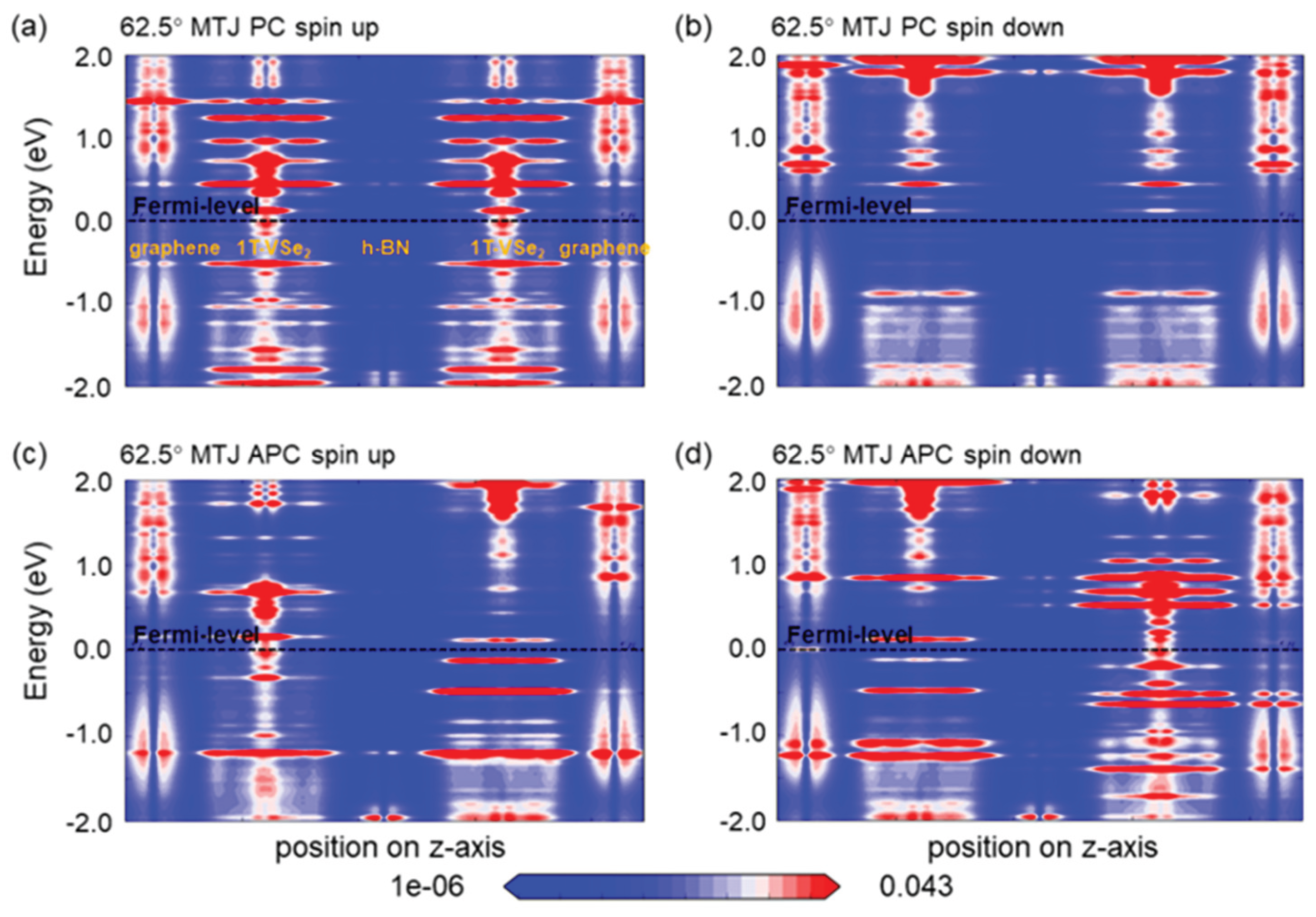
Further, we utilize spin-resolved local density of states (LDOS) maps for the 62.5° (Figure 5) and 83.7° (Figure 6) devices to scrutinize the change in energy bands within the devices. Focusing on the central region’s LDOS images (neglecting those from the graphene electrodes) and highlighting the location of different material layers in Figure 5(a), it is confirmed that graphene’s gap at the fermi level remains at 0 eV, preserving its metallic nature, while the h-BN layers retain insulating characteristics. Rotation of the h-BN layer alters the fermi-level spin-up and spin-down channels of 1T-VSe₂ and influences interface state distribution between the two, leading to dissimilar behavior between the devices.

Figure 5. The local density of states (LDOS) maps are illustrated for van der Waals magnetic tunnel junction devices under hexagonal boron nitride (h-BN) rotation. (a) shows the spin-up channel configuration for an h-BN rotation of 62.5°in a parallel spin geometry. (b) depicts the spin-down channel configuration under the same 62.5°h-BN rotation, also in a parallel spin geometry. (c) presents the spin-up channel configuration but in an antiparallel spin geometry with the 62.5°h-BN rotation. (d) represents the spin-down channel configuration within the antiparallel spin geometry at 62.5°h-BN rotation.

Figure 5. The local density of states (LDOS) maps are illustrated for van der Waals magnetic tunnel junction devices under hexagonal boron nitride (h-BN) rotation. (a) shows the spin-up channel configuration for an h-BN rotation of 62.5°in a parallel spin geometry. (b) depicts the spin-down channel configuration under the same 62.5°h-BN rotation, also in a parallel spin geometry. (c) presents the spin-up channel configuration but in an antiparallel spin geometry with the 62.5°h-BN rotation. (d) represents the spin-down channel configuration within the antiparallel spin geometry at 62.5°h-BN rotation.

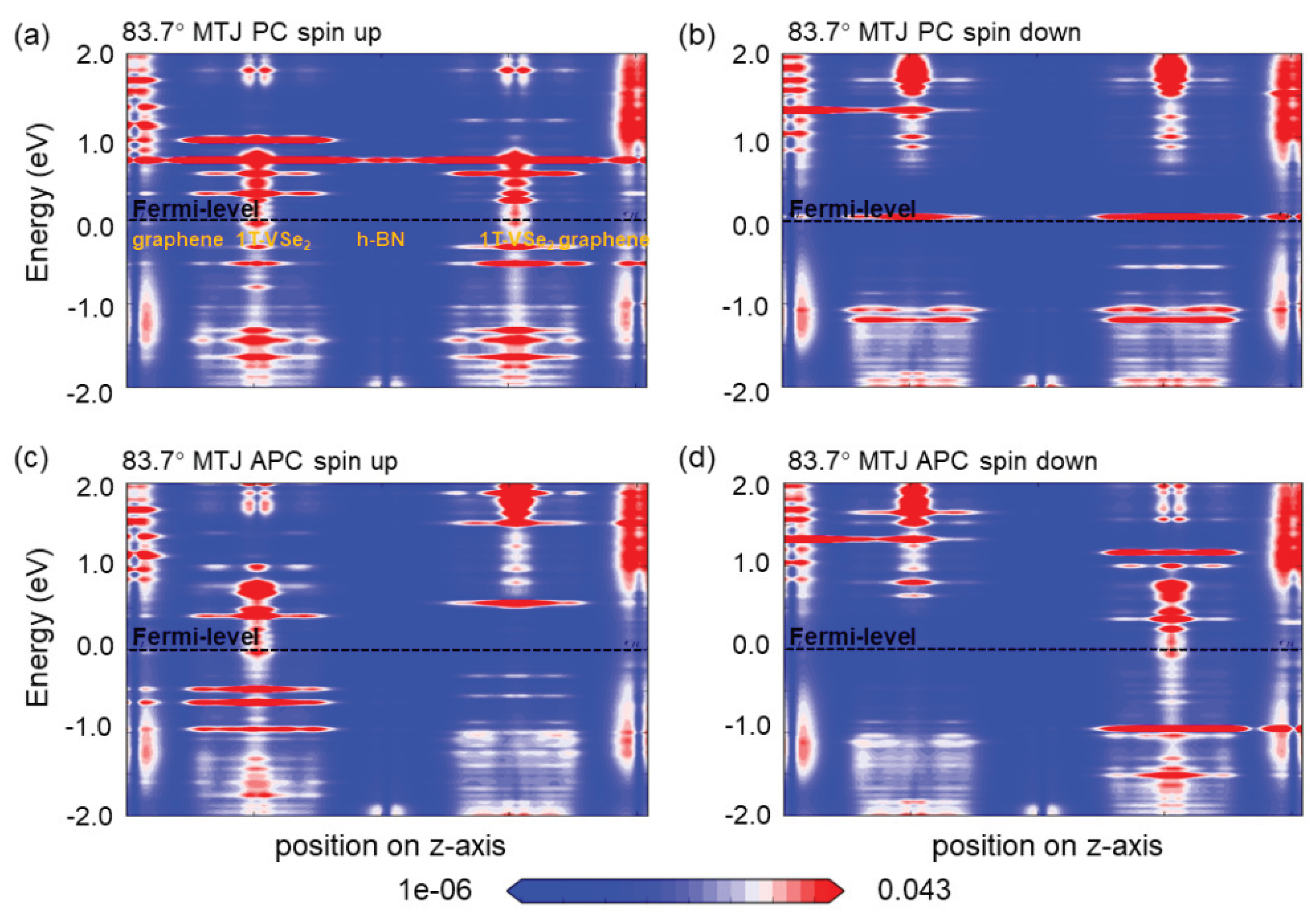
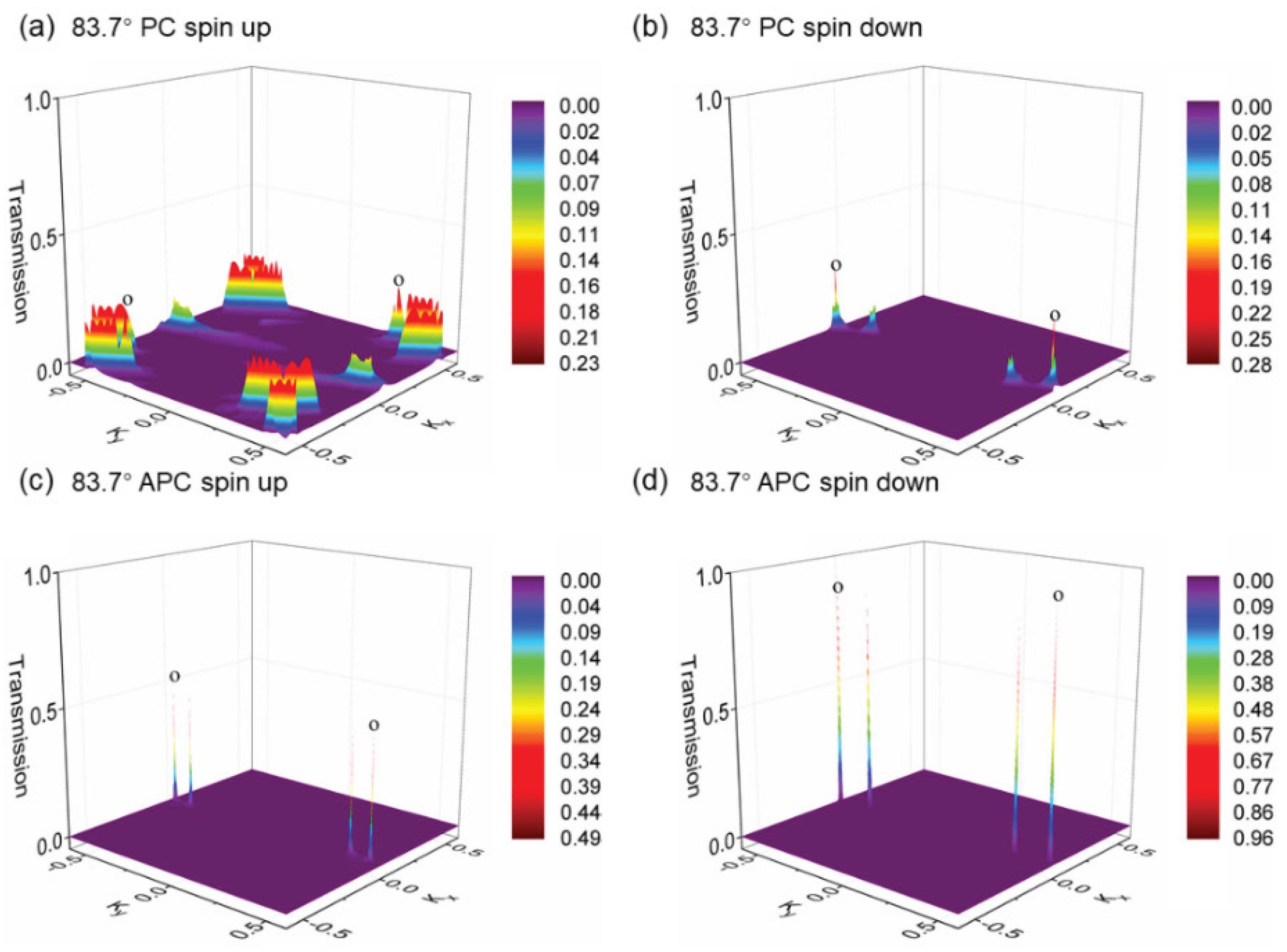
Figure 6. The local density of states (LDOS) maps for van der Waals magnetic tunnel junction devices under hexagonal boron nitride (h-BN) rotation are presented. (a) displays the spin-up channel configuration for an h-BN rotation of 83.7°in a parallel spin geometry. (b) illustrates the spin-down channel configuration under the same 83.7°h-BN rotation, also in a parallel spin geometry. (c) showcases the spin-up channel configuration but in an antiparallel spin geometry with the 83.7°h-BN rotation. (d) represents the spin-down channel configuration within the antiparallel spin geometry at 83.7°h-BN rotation.

Figure 6. The local density of states (LDOS) maps for van der Waals magnetic tunnel junction devices under hexagonal boron nitride (h-BN) rotation are presented. (a) displays the spin-up channel configuration for an h-BN rotation of 83.7°in a parallel spin geometry. (b) illustrates the spin-down channel configuration under the same 83.7°h-BN rotation, also in a parallel spin geometry. (c) showcases the spin-up channel configuration but in an antiparallel spin geometry with the 83.7°h-BN rotation. (d) represents the spin-down channel configuration within the antiparallel spin geometry at 83.7°h-BN rotation.

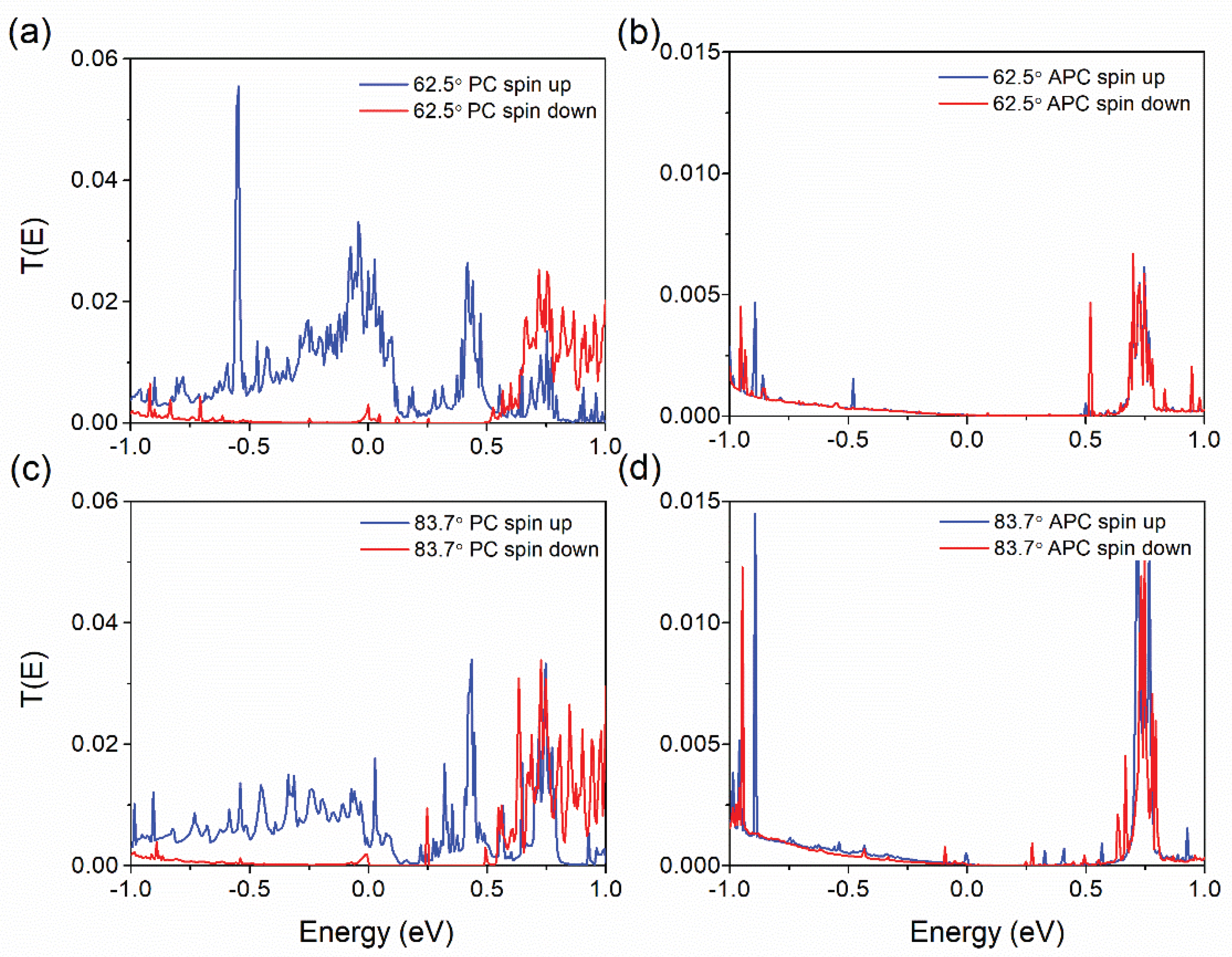
Figure 7 (a) and (b) present spin-resolved transmission spectra for MTJ with spin parallel and antiparallel configurations in h-BN devices with a rotation angle of 62.5°. SimilarlyFigure 7 (c) and (d) illustrate the spin-resolved transmission spectra for those with a rotation angle of 83.7° in both parallel and antiparallel arrangements. In the parallel configuration, a pronounced contrast in transmission coefficients near the fermi level is observed between the upward spin channel for 62.5° devices (0.025) and 83.7° devices (approximately 0.0033). Downward spin channel transmissions for these angles exhibit comparably low values, specifically 0.003 for 62.5° devices and 4.21E-04 for the 83.7° devices. Under antiparallel configurations, both angle-rotated devices exhibit negligible transmission coefficients for both upward and downward spins, ranging from 3.87×1E-05 to 4.21×1E-04. Calculating spin polarization using the formula η = (T_↑(E_f) - T_↓(E_f)) / (T_↑(E_f) + T_↓(E_f)), where T_↑(E_f) and T_↓(E_f) represent the transmission coefficients for the spin-up and spin-down channels at the fermi energy level, yields a spin polarization rate of 78.18% for the 62.5° device’s parallel configuration and 77.66% for the 83.7° device’s counterpart. These results indicate that the 62.5° rotated device facilitates effective spin injection in its parallel configuration, while spin injection of the Bloch states in the 83.7° device is relatively more challenging than in the 62.5° device. Conclusively, it can be inferred that the rotation of h-BN layers influences the device’s transmission characteristics, with variations also evident through the change in TMR values.

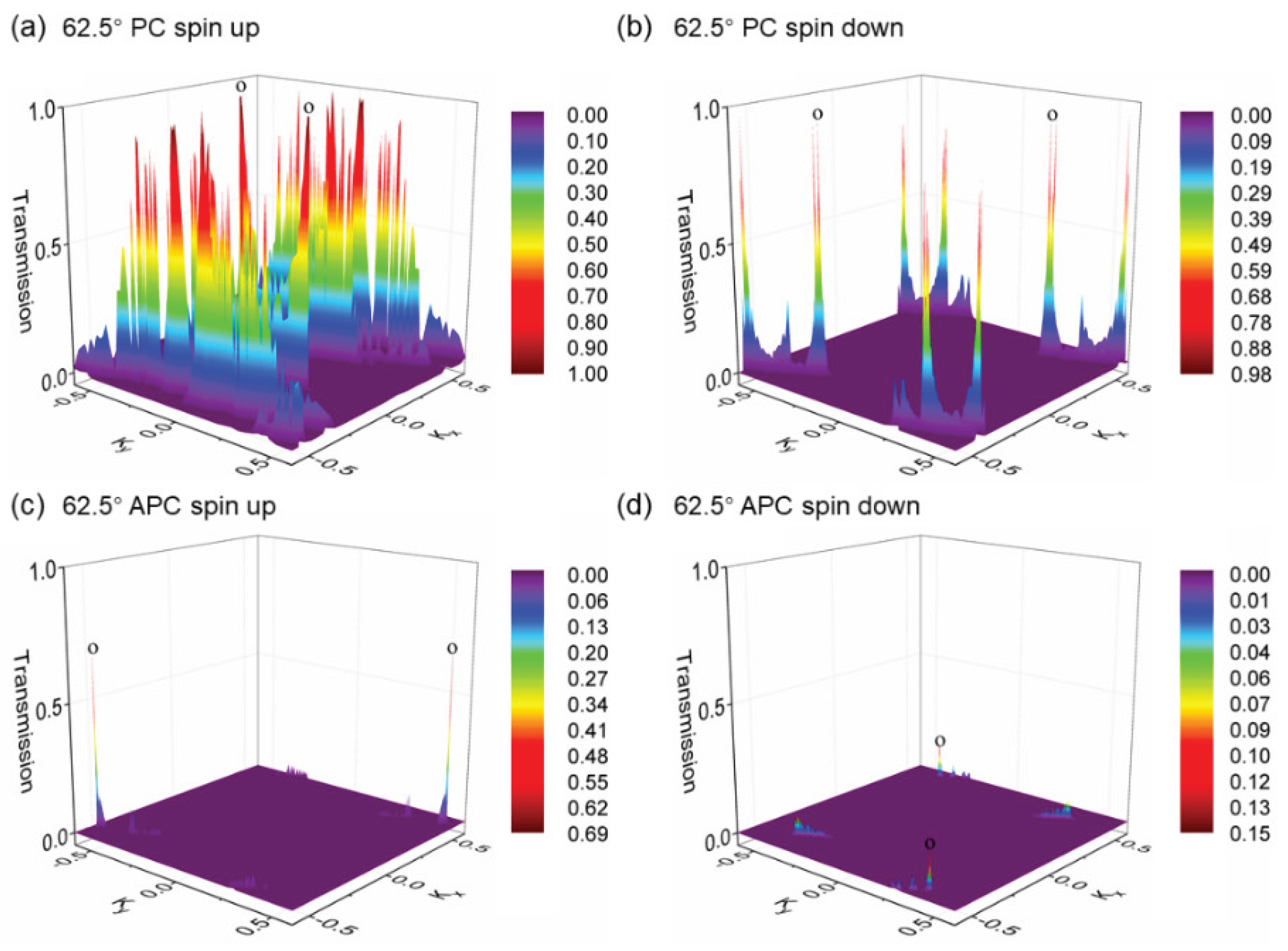
Next, for a more meticulous understanding of the magnetic tunnel junction’s fermi-level transmission spectrum, we present Figure 8 showing the k-resolved and spin-resolved transmission eigenvalue distribution in the vicinity of the fermi surface for the 62.5° device. In the parallel spin configuration for the 62.5° rotation device, the spin-up channel exhibits high transmission eigenvalues in regions distant from the center of the two-dimensional brillouin zone (BZ), indicating prominent interface states. Due to the larger distance from the Γ point, there is a higher decay coefficient, suggesting that increasing the number of h-BN layers would be disadvantageous to transmission. Conversely, for the spin-down channel, the interface state eigenvalues are significantly lower. In the anti-parallel spin configuration, the eigenvalue distributions for the spin-up and spin-down channels are comparable, predominantly located around and at the Γ point; however, their eigenvalues are substantially weaker compared to the hotspots of the spin-up channel in the parallel configuration at point o.

In Figure 9, we demonstrate the spin-resolved and k-resolved transmission eigenvalue distributions of the fermi level near the two-dimensional BZ for the 83.7° rotated h-BN device for both parallel and antiparallel alignments. The Figure 9 (a) reveals that the spin-up channel of the parallel spin configuration displays interface states significantly lower than those in the parallel spin-up channel of the 62.5° device, at an even greater distance from the Γ point, implying a higher attenuation factor. Furthermore, the interface states for the 83.7° device in both parallel spin-up and anti-parallel configurations appear particularly sparse.

We proceed by plotting the transmission spectrum eigenfunctions distribution at the hotspots o in the two-dimensional BZ for the 62.5° device with the parallel spin-up channel (a) and the spin-down channel (b), and for the 83.7° device with the parallel spin-up channel (c) and the spin-down channel (d), as depicted in Figure 10. Clearly, from Figure 10 (a), the Bloch states of the parallel spin-up channel in the 62.5° rotation device can penetrate the h-BN barrier to reach the 1T-VSe₂ layer on the right. On the other hand, it is evident in Figure 10 (b) that the bloch states of the parallel spin-up channel in the 83.7° device have great difficulty in traversing the h-BN barrier. As schematically illustrated in Figure 10 (c) and (d), for the parallel spin-down channels in both configurations, the eigenfunctions barely extend to the 1T-VSe₂ layer situated on the opposite side of the h-BN blocking layer. Regarding the antiparallel configurations with their lower eigenvalues, the Bloch states in the devices experience even greater difficulty in crossing the h-BN barrier, leading to comparably low fermi surface transmission rates. The contrasting distribution of the transmission eigenstates in the parallel spin-up channels between these two devices implies that the 62.5° device has a smaller attenuation coefficient and hence permits easier passage of the Bloch states through the h-BN layer, which results in the significant difference in TMR values owing to the distinct magnetic resistances in each device.

Considering the outcome of our computational process, it becomes apparent that the rotation of the h-BN layer leads to dramatic changes in TMR. We selected the 62.5° and 83.7° devices, with comparable stable h-BN/1T-VSe₂ binding energies and significant TMR disparities, for detailed analysis. First, we observe that the electronic state density of the valence d orbitals of V atoms in all the elements’ orbitals within the graphene/1T-VSe₂/h-BN heterostructure carries the highest weight. This is because the presence of unpaired electrons in the d orbital layer endows the 1T-VSe₂ monolayer with its magnetic property. As the h-BN layer rotates, a distinct peak emerges in the planar-state density of the $d_{yz}$+$d_{z^2}$+$d_{xz}$ orbitals at an energy of -0.04 eV for the 62.5° heterojunction compared to that of the 83.7° junction, potentially impacting transmission at the fermi level for the two devices. Furthermore, the local density of states (LDOS) for the spin-up and spin-down channels at the two different rotation angles of 1T-VSe₂ show distinct characteristics at the fermi energy.

4. Discussion

Combining these observations, it is clear that the rotation of the h-BN layer indeed affects the electron distribution within the 1T-VSe₂ layer, particularly influencing the electronic configuration of the outer d orbitals of the V atoms, hence altering the magnetization direction and magnetic resistance. Consequently, it comes as no surprise that the transmission coefficient for the spin-up channel in the 62.5° parallel configuration significantly exceeds that of the 83.7° configuration. To thoroughly investigate the underlying reasons behind the substantial TMR variation induced by the rotation of the h-BN layer, we compare the behaviors of these two devices representing differing angles.

5. Conclusions

To investigate the impact of the twist angle in the h-BN blocking layers on device performance, we construct a device model comprising 18 graphene/1T-VSe₂/h-BN/1T-VSe₂/graphene MTJ with the h-BN layer separated by roughly 10° rotations. Over an h-BN twist range from 0° to 172.4°, the TMR percentage distribution spans from 2328% to 24608%. We perform a thorough analysis of the transmission spectra for MTJ twisted at 62.5° and 83.7°. The spin polarization rate for parallel spin configuration in the device with a 62.5° rotation is 78.18%, compared to 77.66% for the one twisted at 83.7°. Our study reveals that rotation of the h-BN layer notably modifies the V atom’s d-orbital electronic state distribution within the 1T-VSe₂ layer, leading to substantial differences in TMR. The high TMR values suggest that 1T-VSe₂ combined with h-BN forms an excellent magnetic tunnel junction device, while the pronounced variation of TMR implies significant performance changes due to the twisted h-BN layers. Hence, guided by our findings, we demonstrate tunability of magnetic tunnel junction device characteristics through rotation of the h-BN layer. We propose an approach for engineering different TMR magnitudes by manipulating the rotation angle of the blocking layer in van der Waals MTJ, offering guidelines for experiments.