Energy Conservation in a Charged Retarded Field Engine

1. Introduction

Charged retarded systems represent a ground breaking approach to space propulsion, aimed at addressing the major limitations of traditional rocket fuel. Robertson et al. [1] reviewed the principal barriers slowing advancements in space propulsion technologies and highlights several theoretical ideas that, within the last twenty years, have evolved from speculative fiction into scientific theory. It is thus essential to explore various aspects of these systems, such as linear momentum and energy conservation, as all engines operate within the constraints of the laws of mechanics and the first law of thermodynamics: energy cannot be created or destroyed, only transformed.

This work discusses the retardation effects caused by the relativistic finite speed of signal propagation in a charged engine. As signals must propagate at a finite speed, it follows that an action and its corresponding reaction cannot occur simultaneously. Although retardation already exists in Maxwell’s equations relativity went even further to postulate that no object, message, signal (of any kind, including non-electromagnetic), or field can travel faster than the speed of light in a vacuum [2,3,4]. Griffiths and Heald [5] highlighted in their paper that Coulomb’s law and the Biot-Savart law are strictly valid only for determining electric and magnetic fields from static sources. To extend their applicability beyond the static domain, Jefimenko’s time-dependent generalizations [6] of these laws were formulated taking into account the retardation effect. In this case, momentum and energy are exchanged between the field and the material, enabling the relativistic engine effect. This result had already been observed and highlighted by several authors [7,8,9,10,11].

This process differs significantly from the transfer of momentum and energy between two material bodies which is the basis of standard transportation (a rocket ejects material to prorogate and a car must push the road to move forward). Relativistic effects indicate a novel type of motor, consisting not of two material components but of a combination of matter and an electromagnetic field. In [12] we provided a detailed analysis of the retardation effect and presents the conceptual framework and design principles underlying a charged relativistic motor. Recently, we [13] also investigated the interaction between charged bodies and magnetic currents generated by permanent magnetic materials, analyzing the potential implications for a charged relativistic engine utilizing a permanent magnet. Energy conservation has already been discussed in the case of uncharged relativistic engine [14], in which the energy transfer between the mechanical component of the relativistic engine and the electromagnetic field for a non charged engine. In this case the total electromagnetic energy utilized is six times the kinetic energy gained by the relativistic motor. Furthermore, previous research [15] has provided a mathematical proof that demonstrates that linear momentum is conserved in a retarded electric motor which is uncharged.

In the current work, we investigate a relativistic charged engine consisting of two subsystems of arbitrary geometry as in [12], with particular emphasis on the energy acquired by the system. We begin by analyzing the energy exchange between mechanical and electromagnetic components in the relativistic regime. Subsequently, we carry out a detailed examination of the engine’s energy dynamics by expanding the relevant field quantities as a power series in $1/c$, where c denotes the speed of light in vacuum. This expansion systematically incorporates the effects of retardation. The total energy comprising mechanical energy, electromagnetic field energy, and energy flux via the Poynting vector is analyzed to verify the energy balance equation at each order. Specifically, we evaluate the contributions to the energy equation for $n=0,1,2,3$ and 4, demonstrating how retardation influences energy exchange and confirming that the energy balance is satisfied at each order within the accuracy of the expansion. Finally we demonstrate that the kinetic energy acquired by the engine exactly equals the amount of electromagnetic energy lost.

2. Energy Conservation

The conservation of energy in the general electromagnetic system is expressed by the following equation:

$$\begin{array}{c}\hfill {\displaystyle \frac{d{E}_{mech}}{dt}}+{\displaystyle \frac{d{E}_{field}}{dt}}=-{\oint }_S{\overrightarrow{S}}_P·\widehat{n}da.\end{array}$$

(1)

This equation reflects that any decrease (or increase) in the total energy within the system is accounted for by the energy carried away (or supplied) by the electromagnetic field through the system’s boundary. Here S denotes a closed surface enclosing the volume of interest, $\widehat{n}$ is a unit vector normal to the surface, $da$ represents a surface element.

Poynting’s vector is defined as:

$$\begin{array}{c}\hfill {\overrightarrow{S}}_P={\displaystyle \frac{1}{{\mu }_0}}\overrightarrow{E}\times \overrightarrow{B}={\displaystyle \frac{{ϵ}_0}{{\mu }_0{ϵ}_0}}\overrightarrow{E}\times \overrightarrow{B}={ϵ}_0{c}^2\overrightarrow{E}\times \overrightarrow{B}.\end{array}$$

(2)

Here, ${ϵ}_0=8.85\times {10}^{-12}$ Fm⁻¹ is the vacuum permittivity, ${\mu }_0=4\pi \times {10}^{-7}$ (H/m) and $c\simeq 3\times {10}^8$ m/s is the velocity of light in vacuum. The term ${\oint }_S{\overrightarrow{S}}_P·\widehat{n}da$ represents the total electromagnetic power flux through the closed surface S. The field energy density is defined as:

$$\begin{array}{c}\hfill E_{field}={\displaystyle \frac{{ϵ}_0}{2}}\int \left({\overrightarrow{E}}^2+c^2{\overrightarrow{B}}^2\right)d^{3}x,\end{array}$$

(3)

and the derivative of the mechanical energy is the mechanical power given by:

$$\begin{array}{c}\hfill Power\equiv {\displaystyle \frac{d{E}_{mech}}{dt}}=\int d^{3}x\overrightarrow{J}·\overrightarrow{E},\end{array}$$

(4)

where $\overrightarrow{J}$ is the current density. Hence:

$$\begin{array}{c}\hfill \int d^{3}x\overrightarrow{J}·\overrightarrow{E}+{\displaystyle \frac{d{E}_{field}}{dt}}=-{\oint }_S{\overrightarrow{S}}_P·\widehat{n}da.\end{array}$$

(5)

Or:

$$\begin{array}{c}\hfill \int d^{3}x\overrightarrow{J}·\overrightarrow{E}=-{\displaystyle \frac{d{E}_{field}}{dt}}-{\oint }_S{\overrightarrow{S}}_P·\widehat{n}da.\end{array}$$

(6)

In what follows, we interpret equation (6) in terms of its role in governing energy conservation for a charged relativistic engine system.

2.1. Kinetic Energy

According to [12], the mechanical momentum associated with the time-dependent charged retarded field engine is expressed as:

$$\begin{array}{c}\hfill \overrightarrow{P}\left(t\right)={\displaystyle \frac{{\mu }_0}{4\pi }}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{2}}\left({\rho }_2{\partial }_t{\rho }_1-{\rho }_1{\partial }_t{\rho }_2\right)\widehat{R}-\left({\rho }_1\overrightarrow{J_2}+{\rho }_2\overrightarrow{J_1}\right)R^{-1}\right],\end{array}$$

(7)

or taking into account that: $c={\displaystyle \frac{1}{\sqrt{{\mu }_0{ϵ}_0}}}$ and defining as is customary that $k={\displaystyle \frac{1}{4\pi {ϵ}_0}}$:

$$\begin{array}{c}\hfill \overrightarrow{P}\left(t\right)={\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{2}}\left({\rho }_2{\partial }_t{\rho }_1-{\rho }_1{\partial }_t{\rho }_2\right)\widehat{R}-\left({\rho }_1\overrightarrow{J_2}+{\rho }_2\overrightarrow{J_1}\right)R^{-1}\right].\end{array}$$

(8)

It is clear from the expression that the mechanical momentum is of the order of ${\displaystyle \frac{1}{c^2}}$. The kinetic mechanical energy associated with this momentum is given by:

$$\begin{array}{c}\hfill E_k={\displaystyle \frac{{\overrightarrow{P}}^2}{2M}}={\displaystyle \frac{1}{2}}\overrightarrow{P}·{\overrightarrow{v}}_s.\end{array}$$

(9)

Where M is the mass of the relativistic engine and the engine velocity ${\overrightarrow{v}}_s$ is defined as:

$$\begin{array}{c}\hfill {\overrightarrow{v}}_s\equiv {\displaystyle \frac{\overrightarrow{P}}{M}}\propto {\displaystyle \frac{1}{c^2}}\end{array}$$

(10)

We notice that the expression for kinetic energy is of order ${\displaystyle \frac{1}{c^4}}$, lower order corrections do not exist and higher order corrections are neglected.

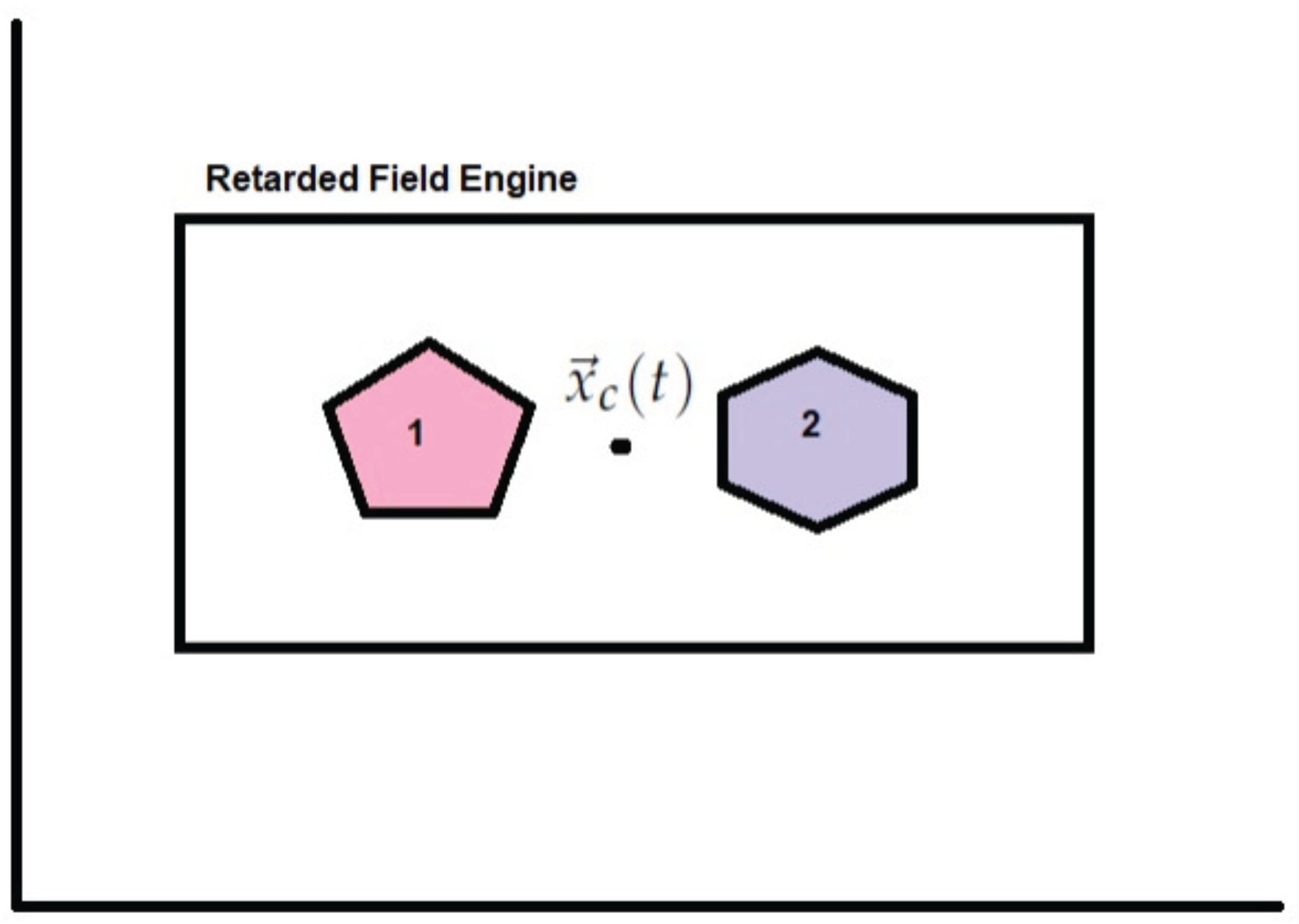
3. Field Energy for Two Charged Sub-Systems

Consider two arbitrary charged sub-systems denoted system 1 and system 2 which are far apart such that their interaction is negligible. In this case, equation (6) is correct for each sub-system separately, that is:

$$\begin{array}{c}\hfill \int d^{3}x\overrightarrow{J_1}·\overrightarrow{E_1}=-{\displaystyle \frac{d{E}_{field1}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P1}·\widehat{n}da.\end{array}$$

(11)

$$\begin{array}{c}\hfill \int d^{3}x\overrightarrow{J_2}·\overrightarrow{E_2}=-{\displaystyle \frac{d{E}_{field2}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P2}·\widehat{n}da.\end{array}$$

(12)

Next we will put them closer together such that they may interact but without modifying the charge and the current densities of each of the subsystems. The total fields of the combined system are:

$$\overrightarrow{E}={\overrightarrow{E}}_1+{\overrightarrow{E}}_2,\overrightarrow{B}={\overrightarrow{B}}_1+{\overrightarrow{B}}_2.$$

(13)

Since both the field energy equation (3) and Poynting’s vector equation (2) are quadratic in the fields, the following result is obtained:

$$\begin{array}{c}\hfill E_{field}\equiv {\displaystyle \frac{{ϵ}_0}{2}}\int \left({\overrightarrow{E}}^2+c^2{\overrightarrow{B}}^2\right)d^{3}x=E_{field1}+E_{field2}+E_{field12}.\end{array}$$

(14)

$$\begin{array}{c}\hfill E_{field1}\equiv E_{Efield1}+E_{Mfield1}\equiv {\displaystyle \frac{{ϵ}_0}{2}}\int \left(\overrightarrow{E_1^2}+c^2\overrightarrow{B_1^2}\right)d^{3}x,\end{array}$$

(15)

$$\begin{array}{c}\hfill E_{field2}\equiv E_{Efield2}+E_{Mfield2}\equiv {\displaystyle \frac{{ϵ}_0}{2}}\int \left(\overrightarrow{E_2^2}+c^2\overrightarrow{B_2^2}\right)d^{3}x,\end{array}$$

(16)

$$\begin{array}{c}\hfill E_{field12}\equiv E_{Efield12}+E_{Mfield12}\equiv {ϵ}_0\int \left(\overrightarrow{E_1}·\overrightarrow{E_2}+c^2\overrightarrow{B_1}·\overrightarrow{B_2}\right)d^{3}x.\end{array}$$

(17)

$$\begin{array}{c}\hfill {\overrightarrow{S}}_P\equiv {ϵ}_0{c}^2\overrightarrow{E}\times \overrightarrow{B}={\overrightarrow{S}}_{P1}+{\overrightarrow{S}}_{P2}+{\overrightarrow{S}}_{P12}.\end{array}$$

(18)

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P1}\equiv {ϵ}_0{c}^2\overrightarrow{E_1}\times \overrightarrow{B_1},\end{array}$$

(19)

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P2}\equiv {ϵ}_0{c}^2\overrightarrow{E_2}\times \overrightarrow{B_2},\end{array}$$

(20)

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}\equiv {ϵ}_0{c}^2\left(\overrightarrow{E_1}\times \overrightarrow{B_2}+\overrightarrow{E_2}\times \overrightarrow{B_1}\right).\end{array}$$

(21)

The power invested in the combined system in bilinear in the current density and the electric field according to equation (4). This will lead to the following expression:

$$\begin{array}{c}\hfill Power=\int d^{3}x\overrightarrow{J}·\overrightarrow{E}=Powe{r}_1+Powe{r}_2+Powe{r}_{12}.\end{array}$$

(22)

$$\begin{array}{c}\hfill Powe{r}_1=\int d^{3}x\overrightarrow{J_1}·\overrightarrow{E_1},\end{array}$$

(23)

$$\begin{array}{c}\hfill Powe{r}_2=\int d^{3}x\overrightarrow{J_2}·\overrightarrow{E_2},\end{array}$$

(24)

$$\begin{array}{c}\hfill Powe{r}_{12}=\int d^{3}x\left(\overrightarrow{J_1}·\overrightarrow{E_2}+\overrightarrow{J_2}·\overrightarrow{E_1}\right).\end{array}$$

(25)

Subtracting from equation (6) the expressions given in equation (11) and equation (12):

$$\begin{array}{c}\hfill Power-Powe{r}_1-Powe{r}_2=-{\displaystyle \frac{d\left(E_{field}-E_{field1}-E_{field2}\right)}{dt}}-{\oint }_S\left({\overrightarrow{S}}_P-{\overrightarrow{S}}_{P1}-{\overrightarrow{S}}_{P2}\right)·\widehat{n}da.\end{array}$$

(26)

taking into account equation (14)–equation (25) we arrive at:

$$\begin{array}{c}\hfill Powe{r}_{12}=-{\displaystyle \frac{d{E}_{field12}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}·\widehat{n}da.\end{array}$$

(27)

4. Power Expansion in ${\displaystyle \frac{1}{c}}$

Let us now expand equation (27) in power of ${\displaystyle \frac{1}{c}}$, we introduce the notation $G^{\left[n\right]}$ to designate a term of order ${\displaystyle \frac{1}{c}}$ of the quantity G. Thus any quantity G may be written as the sum:

$$G=\sum _{n=0}^{\infty }{G}^{\left[n\right]}.$$

(28)

Specifically:

$$Powe{r}_{12}^{\left[n\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[n\right]}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}^{\left[n\right]}·\widehat{n}da.$$

(29)

It follows from equation (25) that:

$$Powe{r}_{12}^{\left[n\right]}=\int d^{3}x\left(\overrightarrow{J_1}·{\overrightarrow{E}}_2^{\left[n\right]}+\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[n\right]}\right).$$

(30)

Also it follows from equation (17) that:

$$E_{field12}^{\left[n\right]}={ϵ}_0\int \left(\sum _{k=0}^n{\overrightarrow{E}}_1^{[n-k]}·{\overrightarrow{E}}_2^{\left[k\right]}+c^2\sum _{k=0}^{n+2}{\overrightarrow{B}}_1^{[n+2-k]}·{\overrightarrow{B}}_2^{\left[k\right]}\right)d^{3}x.$$

(31)

And finally from equation (21) it follows that:

$${\overrightarrow{S}}_{P12}^{\left[n\right]}={ϵ}_0{c}^2\sum _{k=0}^{n+2}\left({\overrightarrow{E}}_1^{[n+2-k]}\times {\overrightarrow{B}}_2^{\left[k\right]}+{\overrightarrow{E}}_2^{[n+2-k]}\times {\overrightarrow{B}}_1^{\left[k\right]}\right).$$

(32)

In the subsections below we discuss equation (29) for different values of n starting from 0 up to 4. The analysis of the field contributions can now be carried out, considering each order in turn.

4.1. n=0

Let us look at equation (27) and study it for the zeroth order in ${\displaystyle \frac{1}{c}}$:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[0\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[0\right]}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}^{\left[0\right]}·\widehat{n}da.\end{array}$$

(33)

4.1.1. Power

We shall start by calculating $Powe{r}_{12}^{\left[0\right]}$ according to equation (30):

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[0\right]}=\int d^{3}x\left(\overrightarrow{J_1}·{\overrightarrow{E}}_2^{\left[0\right]}+\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[0\right]}\right).\end{array}$$

(34)

Equations (51) and (54) of [12] give a detailed expressions for the zeroth order term in the electric field expansion which is just the Coulomb field:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[0\right]}=k\int d^3{x}_1{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right)}{R_1^2}}{\widehat{R}}_1,\end{array}$$

(35)

similarly:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_2^{\left[0\right]}=k\int d^3{x}_2{\displaystyle \frac{{\rho }_2\left(\overrightarrow{x_2}\right)}{R_2^2}}{\widehat{R}}_2,\end{array}$$

(36)

where $\overrightarrow{R_1}$ and $\overrightarrow{R_2}$ define the relative position vectors:

$$\overrightarrow{R_1}\equiv \overrightarrow{x}-\overrightarrow{x_1},\overrightarrow{R_2}\equiv \overrightarrow{x}-\overrightarrow{x_2},R_1\equiv |\overrightarrow{R_1}|,R_2\equiv \left|\overrightarrow{R_2}\right|,{\widehat{R}}_1\equiv {\displaystyle \frac{\overrightarrow{R_1}}{R_1}},{\widehat{R}}_2\equiv {\displaystyle \frac{\overrightarrow{R_2}}{R_2}}.$$

(37)

By substituting equation (35) and equation (36) into equation equation (34), we obtain:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[0\right]}=k\int d^{3}x\left[\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\left(\int d^3{x}_2{\displaystyle \frac{{\rho }_2\left(\overrightarrow{x_2}\right)}{R_2^2}}{\widehat{R}}_2\right)+\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\left(\int d^3{x}_1{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right)}{R_1^2}}{\widehat{R}}_1\right)\right].\end{array}$$

(38)

Applying the identities:

$${\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}=-\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_1}}\right),{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}=-\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_2}}\right),$$

(39)

the expression in equation (38) can be simplified:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[0\right]}=-k\int d^{3}x\left[\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\int d^3{x}_2\left({\rho }_2\left(\overrightarrow{x_2}\right)\left(\overrightarrow{\nabla }{R}_2^{-1}\right)\right)+\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\int d^3{x}_1\left({\rho }_1\left(\overrightarrow{x_1}\right)(\overrightarrow{\nabla }{R}_1^{-1}\right)\right].\end{array}$$

(40)

Or by changing the order of integration, in the form:

$$\begin{array}{ccc}\hfill Powe{r}_{12}^{\left[0\right]}& =& -k\left[\int d^3{x}_2{\rho }_2\left(\overrightarrow{x_2}\right)\int d^{3}x\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_2}}\right)\right.\hfill \\ & +& \left.\int d^3{x}_1{\rho }_1\left(\overrightarrow{x_1}\right)\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_1}}\right)\right].\hfill \end{array}$$

(41)

We next compute the individual integral terms to simplify the above equation:

$$\int d^{3}x\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_2}}\right)=\int d^{3}x\left[\overrightarrow{\nabla }·\left({\displaystyle \frac{\overrightarrow{J_1}\left(\overrightarrow{x}\right)}{R_2}}\right)-{\displaystyle \frac{1}{R_2}}\overrightarrow{\nabla }·\overrightarrow{J_1}\left(\overrightarrow{x}\right)\right]$$

(42)

Using Gauss theorem and continuity equation:

$${\partial }_t\rho +\overrightarrow{\nabla }·\overrightarrow{J}=0$$

(43)

we obtain the following result:

$$\int d^{3}x\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_2}}\right)=\oint dS·\left({\displaystyle \frac{\overrightarrow{J_1}\left(\overrightarrow{x}\right)}{R_2}}\right)+\int d^{3}x{\displaystyle \frac{1}{R_2}}{\partial }_t{\rho }_1\left(\overrightarrow{x}\right).$$

(44)

The surface integral is performed over a surface encapsulating the volume of the volume integral. If the volume integral is performed over all space, the surface is at infinity. Provided that there are no currents at infinity i.e., $\overrightarrow{J_1}(\infty )=0$,

$$\int d^{3}x\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_2}}\right)=\int d^{3}x{\displaystyle \frac{1}{R_2}}{\partial }_t{\rho }_1\left(\overrightarrow{x}\right).$$

(45)

Similarly:

$$\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\overrightarrow{\nabla }\left({\displaystyle \frac{1}{R_1}}\right)=\int d^{3}x{\displaystyle \frac{1}{R_1}}{\partial }_t{\rho }_2\left(\overrightarrow{x}\right).$$

(46)

Substituting these identities in equation (41), we obtain:

$$\begin{array}{ccc}\hfill Powe{r}_{12}^{\left[0\right]}& =\hfill & \hfill -k\left[\int d^3{x}_2{\rho }_2\left(\overrightarrow{x_2}\right)\int d^{3}x{\displaystyle \frac{1}{R_2}}{\partial }_t{\rho }_1\left(\overrightarrow{x}\right)+\int d^3{x}_1{\rho }_1\left(\overrightarrow{x_1}\right)\int d^{3}x{\displaystyle \frac{1}{R_1}}{\partial }_t{\rho }_2\left(\overrightarrow{x}\right)\right]\\ \hfill & =\hfill & \hfill -k\int d^3{x}_2{\rho }_2\left(\overrightarrow{x_2}\right)\int d^{3}x{\displaystyle \frac{1}{R_2}}{\partial }_t{\rho }_1\left(\overrightarrow{x}\right)+k\int d^3{x}_1{\rho }_1\left(\overrightarrow{x_1}\right)\int d^{3}x{\displaystyle \frac{1}{R_1}}{\partial }_t{\rho }_2\left(\overrightarrow{x}\right)\end{array}$$

(47)

Thus the power contains two contributions:

$$\begin{array}{c}\hfill Powe{r}_{{12}_1}^{\left[0\right]}=-k\int d^3{x}_2{\rho }_2\left(\overrightarrow{x_2}\right)\int d^{3}x{\displaystyle \frac{1}{R_2}}{\partial }_t{\rho }_1\left(\overrightarrow{x}\right)\end{array}$$

(48)

and

$$\begin{array}{c}\hfill Powe{r}_{{12}_2}^{\left[0\right]}=-k\int d^3{x}_1{\rho }_1\left(\overrightarrow{x_1}\right)\int d^{3}x{\displaystyle \frac{1}{R_1}}{\partial }_t{\rho }_2\left(\overrightarrow{x}\right)\end{array}$$

(49)

We now make a change of the integration variable $\overrightarrow{x}\to {\overrightarrow{x}}_1$ in $Powe{r}_{{12}_1}^{\left[0\right]}$, thus $\overrightarrow{R_2}=\overrightarrow{x}-{\overrightarrow{x}}_2\to {\overrightarrow{x}}_1-{\overrightarrow{x}}_2=\overrightarrow{R}$ and we obtain:

$$\begin{array}{cc}\hfill Powe{r}_{{12}_1}^{\left[0\right]}& =-k\int d^3{x}_2{\rho }_2\left(\overrightarrow{x_2}\right)\int d^3{x}_1{\displaystyle \frac{1}{R}}{\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right)\hfill \\ \hfill & =-k\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\rho }_2\left(\overrightarrow{x_2}\right){\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right)}{R}}.\hfill \end{array}$$

(50)

Similarly,

$$\begin{array}{c}\hfill Powe{r}_{{12}_2}^{\left[0\right]}=-k\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right){\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)}{R}}.\end{array}$$

(51)

We now present the complete expression for the power:

$$\begin{array}{cc}\hfill Powe{r}_{12}^{\left[0\right]}& =Powe{r}_{{12}_1}^{\left[0\right]}+Powe{r}_{{12}_2}^{\left[0\right]}\hfill \\ \hfill & =-k\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{R}}\left[{\rho }_1\left(\overrightarrow{x_1}\right){\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)+{\rho }_2\left(\overrightarrow{x_2}\right){\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right)\right]\hfill \\ \hfill & =-k\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\partial }_t\left({\rho }_1{\rho }_2\right)}{R}}.\hfill \end{array}$$

(52)

Or equivalently:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[0\right]}=-{\displaystyle \frac{d}{dt}}\left[k\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\rho }_1{\rho }_2}{R}}\right].\end{array}$$

(53)

4.1.2. Field Energy

Next we calculate field energy according to equation (31)

$$\begin{array}{c}\hfill E_{field12}^{\left[0\right]}={ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[0\right]}+c^2\left[{\overrightarrow{B}}_1^{\left[2\right]}·{\overrightarrow{B}}_2^{\left[0\right]}+{\overrightarrow{B}}_1^{\left[1\right]}·{\overrightarrow{B}}_2^{\left[1\right]}+{\overrightarrow{B}}_1^{\left[0\right]}·{\overrightarrow{B}}_2^{\left[2\right]}\right]\right)d^{3}x\end{array}$$

(54)

The magnetic field does not have terms which are lower than second order, we will use the null magnetic field expressions from Equation (58) of [12]:

$$\begin{array}{c}\hfill {\overrightarrow{B}}_1^{\left[0\right]}={\overrightarrow{B}}_2^{\left[0\right]}={\overrightarrow{B}}_1^{\left[1\right]}={\overrightarrow{B}}_2^{\left[1\right]}=0.\end{array}$$

(55)

Accordingly, the field energy takes the form:

$$\begin{array}{c}\hfill E_{field12}^{\left[0\right]}={ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[0\right]}\right)d^{3}x={ϵ}_0{k}^2\int \left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right){\rho }_2\left(\overrightarrow{x_2}\right)}{R_1^2{R}_2^2}}{\widehat{R}}_1·{\widehat{R}}_2\right]d^{3}x.\end{array}$$

(56)

Now solving separately the given integral:

$$II=\int \left({\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)d^{3}x=\int \left(\overrightarrow{\nabla }{\displaystyle \frac{1}{R_1}}·\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}\right)d^{3}x.$$

(57)

Using the identity:

$$\overrightarrow{\nabla }{\displaystyle \frac{1}{R_1}}·\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}=\overrightarrow{\nabla }·\left({\displaystyle \frac{1}{R_1}}\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}\right)-{\displaystyle \frac{1}{R_1}}\overrightarrow{{\nabla }^2}{\displaystyle \frac{1}{R_2}},$$

(58)

and taking into account that [3]:

$$\overrightarrow{{\nabla }^2}{\displaystyle \frac{1}{R_2}}=-4\pi \delta \left(\overrightarrow{R_2}\right),$$

(59)

in which $\delta \left(\overrightarrow{R_2}\right)$ is a three dimensional delta function. We obtain:

$$\overrightarrow{\nabla }{\displaystyle \frac{1}{R_1}}·\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}=\overrightarrow{\nabla }·\left({\displaystyle \frac{1}{R_1}}\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}\right)+{\displaystyle \frac{4\pi }{R_1}}\delta \left(\overrightarrow{R_2}\right).$$

(60)

The first term on the right is a divergence. Thus, using Gauss theorem, its volume integral will become a surface integral, the second term contains a delta function. This means that there is no contribution to the volume integral from the delta term unless $\overrightarrow{x}=\overrightarrow{x_2}$. Thus, equation (57) simplifies to:

$$II=\int \left({\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)d^{3}x=\int d\overrightarrow{S}·\left({\displaystyle \frac{1}{R_1}}\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}\right)+{\displaystyle \frac{4\pi }{R}}$$

(61)

Let us look at the surface integral and assume that the system is contained inside an infinite sphere, such that the surface integral is taken over a spherical surface of radius $r=|\overrightarrow{x}|\to \infty$:

$$\underset{r\to \infty }{lim}\int d\overrightarrow{S}·{\displaystyle \frac{1}{R_1}}\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}=\underset{r\to \infty }{lim}\int d\overrightarrow{S}·{\displaystyle \frac{1}{R_1}}{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}.$$

(62)

Here $d\overrightarrow{S}=r^{2}d\mathrm{\Omega }\widehat{r}$, in which $\mathrm{\Omega }$ is the solid angle. Also both $R_1\to r\to \infty$, $R_2\to r\to \infty$ and ${\widehat{R}}_2\to \widehat{r}$. It follows that:

$$\underset{r\to \infty }{lim}\int d\overrightarrow{S}·{\displaystyle \frac{1}{R_1}}\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}=\underset{r\to \infty }{lim}\int r^{2}d\mathrm{\Omega }{\displaystyle \frac{1}{r^3}}=\underset{r\to \infty }{lim}\int d\mathrm{\Omega }{\displaystyle \frac{1}{r}}=0.$$

(63)

(see also Appendix $A.1.2.$ of [14] for complete explanation of equation (62)). We conclude that simply:

$$II={\displaystyle \frac{4\pi }{R}}$$

(64)

Hence, the expression for the field energy becomes:

$$\begin{array}{c}\hfill E_{field12}^{\left[0\right]}={ϵ}_0{k}^2\left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right){\rho }_2\left(\overrightarrow{x_2}\right)}{R}}4\pi \right]\end{array}$$

(65)

as $k={\displaystyle \frac{1}{4\pi {ϵ}_0}}$,

$$\begin{array}{c}\hfill E_{field12}^{\left[0\right]}=k\left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{{\rho }_1{\rho }_2}{R}}\right]\end{array}$$

(66)

From equation (53) and equation (66), it is now clear that:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[0\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[0\right]}}{dt}}.\end{array}$$

(67)

It follows that the power related to mechanical work equals minus the temporal rate of change of the field energy.

4.1.3. Poynting Vector

Finally we shall study the Poynting vector according to equation (32):

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}^{\left[0\right]}={ϵ}_0{c}^2\left({\overrightarrow{E}}_1^{\left[2\right]}\times {\overrightarrow{B}}_2^{\left[0\right]}+{\overrightarrow{E}}_1^{\left[1\right]}\times {\overrightarrow{B}}_2^{\left[1\right]}+{\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{E}}_2^{\left[2\right]}\times {\overrightarrow{B}}_1^{\left[0\right]}+{\overrightarrow{E}}_2^{\left[1\right]}\times {\overrightarrow{B}}_1^{\left[1\right]}+{\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}\right).\end{array}$$

(68)

It is clear from equation (55), that:

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}^{\left[0\right]}={ϵ}_0{c}^2\left({\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}\right)\end{array}$$

(69)

as both ${\overrightarrow{E}}^{\left[0\right]}$ and ${\overrightarrow{B}}^{\left[2\right]}$ decrease as ${\displaystyle \frac{1}{r^2}}$ at infinity, it follows that their cross product decreases as ${\displaystyle \frac{1}{r^4}}$, thus a surface integral over an infinite sphere will also vanish, which is what should be expected from equation (67) that balances the changes in the electromagnetic energy and mechanical power without any Poynting contribution. For $n=0$, we conclude that the energy equation of order zero is indeed balanced as is expected.

4.2. n=1

Let us look at equation (27) and study it for the first order in ${\displaystyle \frac{1}{c}}$:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[1\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[1\right]}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}^{\left[1\right]}·\widehat{n}da.\end{array}$$

(70)

4.2.1. Power

The first order expression for the power invested in mechanical work is given below:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[1\right]}=\int d^{3}x\left(\overrightarrow{J_1}·{\overrightarrow{E}}_2^{\left[1\right]}+\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[1\right]}\right).\end{array}$$

(71)

According to equations (51) and (54) of [12], the first order term in the electric field expansion is:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[1\right]}={\overrightarrow{E}}_2^{\left[1\right]}=0.\end{array}$$

(72)

Therefore,

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[1\right]}=0.\end{array}$$

(73)

4.2.2. Field Energy

Now we shall calculate the field energy according to equation (31) for $n=1$

$$\begin{array}{c}\hfill E_{field12}^{\left[1\right]}={ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[1\right]}+{\overrightarrow{E}}_1^{\left[1\right]}·{\overrightarrow{E}}_2^{\left[0\right]}+c^2\sum _{k=0}^3{\overrightarrow{B}}_1^{[3-k]}·{\overrightarrow{B}}_2^{\left[k\right]}\right)d^{3}x.\end{array}$$

(74)

From equation (55) and equation (72), we obtain:

$$\begin{array}{c}\hfill E_{field12}^{\left[1\right]}=0.\end{array}$$

(75)

4.2.3. Poynting Vector

Taking into account equation (55) and equation (72), the first-order expression for the Poynting vector is given by:

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}^{\left[1\right]}={ϵ}_0{c}^2\left({\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[3\right]}+{\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[3\right]}\right),\end{array}$$

(76)

According to Equation (61) of [12], it follows that:

$${\overrightarrow{B}}^{\left[3\right]}=0.$$

(77)

Hence:

$${\overrightarrow{S}}_{P12}^{\left[1\right]}=0.$$

(78)

Thus, for $n=1$, we conclude that the energy equation of order one is indeed balanced in a trivial way. Equation (27) is satisfied in the sense that 0 = 0.

4.3. n=2

Let us look at equation (27) and study it for the second order in ${\displaystyle \frac{1}{c}}$:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[2\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[2\right]}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}^{\left[2\right]}·\widehat{n}da.\end{array}$$

(79)

4.3.1. Power

The second-order expression for the power invested in mechanical work is given below:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[2\right]}=\int d^{3}x\left(\overrightarrow{J_1}·{\overrightarrow{E}}_2^{\left[2\right]}+\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[2\right]}\right).\end{array}$$

(80)

We start by addressing the first integral in the above equation:

$$I_1=\int d^{3}x\overrightarrow{J_1}\left(\overrightarrow{x}\right)·{\overrightarrow{E}}_2^{\left[2\right]}\left(\overrightarrow{x}\right).$$

(81)

According to equations (51) and (54) of [12] the second-order term in the electric field expansion is:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_2^{\left[2\right]}\left(\overrightarrow{x}\right)={\displaystyle \frac{k}{c^2}}\int d^3{x}_2\left[-{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right){\widehat{R}}_2-{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R_2^{-1}\right].\end{array}$$

(82)

Inserting this in the $I_1$ expression will result in:

$$\begin{array}{cc}\hfill I_1=& {\displaystyle \frac{k}{c^2}}\int d^{3}x\left[\overrightarrow{J_1}\left(\overrightarrow{x}\right)·\int d^3{x}_2\left[-{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right){\widehat{R}}_2-{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R_2^{-1}\right]\right].\hfill \end{array}$$

(83)

We shall now change the integration variable $\overrightarrow{x}\to {\overrightarrow{x}}_1$ as before, such that:

$$\begin{array}{cc}\hfill I_1& =k\left({\displaystyle \frac{1}{c^2}}\right)\int d^3{x}_1\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\int d^3{x}_2\left[-{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)\widehat{R}-{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R^{-1}\right]\hfill \\ \hfill & =k\left({\displaystyle \frac{1}{c^2}}\right)\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{2}}\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\widehat{R}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)-\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R^{-1}\right].\hfill \end{array}$$

(84)

Let us look at the expression:

$$\begin{array}{c}\hfill \int \int d^3{x}_1{d}^3{x}_2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\widehat{R}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)=\int d^3{x}_2{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)\int d^3{x}_1\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\widehat{R},\end{array}$$

(85)

notice that:

$${\overrightarrow{\nabla }}_{{\overrightarrow{x}}_2}R=-\widehat{R},{\overrightarrow{\nabla }}_{{\overrightarrow{x}}_1}R=\widehat{R}.$$

(86)

From the continuity equation (43), and taking into account Gauss theorem and the vanishing of current densities on a far away encapsulating surface it follows that:

$$\int d^3{x}_1\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\overrightarrow{\nabla }}_{{\overrightarrow{x}}_1}R=\int d^3{x}_{1}R{\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right),\int d^3{x}_2\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·{\overrightarrow{\nabla }}_{{\overrightarrow{x}}_2}R=\int d^3{x}_{2}R{\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right).$$

(87)

Thus, equation (85) takes the following form:

$$\begin{array}{c}\hfill \int \int d^3{x}_1{d}^3{x}_2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\widehat{R}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)=\int \int d^3{x}_1{d}^3{x}_{2}R{\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right){\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right).\end{array}$$

(88)

Upon substitution of equation (88) into equation (84), the resulting expression is:

$$\begin{array}{c}\hfill I_1=k\left({\displaystyle \frac{1}{c^2}}\right)\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{2}}R{\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right){\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)-\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R^{-1}\right].\end{array}$$

(89)

Exchanging the indices 1 and 2, we obtain the second integral of equation (80):

$$\begin{array}{c}\hfill I_2=k\left({\displaystyle \frac{1}{c^2}}\right)\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{2}}R{\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right){\partial }_t^2{\rho }_1\left({\overrightarrow{x}}_1\right)-\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·{\partial }_t\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)R^{-1}\right].\end{array}$$

(90)

Combining equation (89) and equation (90), we obtain the complete expression for the power:

$$\begin{array}{cc}\hfill Powe{r}_{12}^{\left[2\right]}& =k\left({\displaystyle \frac{1}{c^2}}\right)\left[-\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{R}{2}}\left({\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right){\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right)+{\partial }_t^2{\rho }_1\left({\overrightarrow{x}}_1\right){\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)\right)\right.\hfill \\ \hfill & -\left.\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{R}}\left(\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)+\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·{\partial }_t\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right)\right].\hfill \end{array}$$

(91)

Applying the product rule of derivatives we obtain:

$$\begin{array}{cc}\hfill Powe{r}_{12}^{\left[2\right]}& =k\left({\displaystyle \frac{1}{c^2}}\right)\left[-\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{R}{2}}{\partial }_t\left({\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right){\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)\right)\right.\hfill \\ \hfill & -\left.\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{R}}{\partial }_t\left(\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)\right)\right].\hfill \end{array}$$

(92)

Or:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[2\right]}=-{\displaystyle \frac{k}{c^2}}{\displaystyle \frac{d}{dt}}\left[\int \int d^3{x}_1{d}^3{x}_2\left({\displaystyle \frac{R\left({\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right){\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)\right)}{2}}+{\displaystyle \frac{\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)}{R}}\right)\right].\end{array}$$

(93)

Thus we obtained a power expression accurate to second-order.

4.3.2. Field Energy

We now proceed to calculate the field energy using equation (31) for $n=2$:

$$E_{field12}^{\left[2\right]}={ϵ}_0\int \left(\sum _{k=0}^2{\overrightarrow{E}}_1^{[2-k]}·{\overrightarrow{E}}_2^{\left[k\right]}+c^2\sum _{k=0}^4{\overrightarrow{B}}_1^{[4-k]}·{\overrightarrow{B}}_2^{\left[k\right]}\right)d^{3}x$$

(94)

As we already know that:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[1\right]}={\overrightarrow{E}}_2^{\left[1\right]}=0,{\overrightarrow{B}}_1^{\left[0\right]}={\overrightarrow{B}}_2^{\left[0\right]}=0,{\overrightarrow{B}}_1^{\left[1\right]}={\overrightarrow{B}}_2^{\left[1\right]}=0.\end{array}$$

(95)

It follows that the field energy takes the simplified form:

$$\begin{array}{c}\hfill E_{field12}^{\left[2\right]}={ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[2\right]}+{\overrightarrow{E}}_1^{\left[2\right]}·{\overrightarrow{E}}_2^{\left[0\right]}+c^2{\overrightarrow{B}}_1^{\left[2\right]}·{\overrightarrow{B}}_2^{\left[2\right]}\right)d^{3}x.\end{array}$$

(96)

This can be expressed as the sum of the following terms:

$$\begin{array}{c}\hfill E_{field12}^{\left[2\right]}=i_1+i_2+i_3,\end{array}$$

(97)

where

$$i_1={ϵ}_0\left(\int {\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[2\right]}{d}^{3}x\right),$$

(98)

$$i_2={ϵ}_0\left(\int {\overrightarrow{E}}_1^{\left[2\right]}·{\overrightarrow{E}}_2^{\left[0\right]}{d}^{3}x\right),$$

(99)

and,

$$i_3={ϵ}_0{c}^2\left(\int {\overrightarrow{B}}_1^{\left[2\right]}·{\overrightarrow{B}}_2^{\left[2\right]}{d}^{3}x\right).$$

(100)

We now compute the integral of each term separately:

$$i_1={ϵ}_0\left(\int {\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[2\right]}{d}^{3}x\right)$$

(101)

The relevant field expressions are provided in [12] (and are previously mentioned in the current paper):

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[0\right]}\left(\overrightarrow{x}\right)=k\int d^3{x}_1{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right)}{R_1^2}}{\widehat{R}}_1,\end{array}$$

(102)

and

$$\begin{array}{c}\hfill {\overrightarrow{E}}_2^{\left[2\right]}\left(\overrightarrow{x}\right)=k\left({\displaystyle \frac{1}{c^2}}\right)\int d^3{x}_2\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)(-{\widehat{R}}_2)-{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R_2^{-1}\right].\end{array}$$

(103)

Substituting these field expressions into equation (101), we obtain:

$$\begin{array}{cc}\hfill i_1& ={ϵ}_{0}k{\displaystyle \frac{k}{c^2}}\int d^{3}x\left[\left(\int d^3{x}_1{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right)}{R_1^2}}{\widehat{R}}_1\right)·\left(\int d^3{x}_2\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right)(-{\widehat{R}}_2)-{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)R_2^{-1}\right]\right)\right].\hfill \end{array}$$

(104)

Or in the form:

$$\begin{array}{ccc}\hfill i_1& =& -{\displaystyle \frac{k}{4\pi c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right){\rho }_1\left(\overrightarrow{x_1}\right)\left(\int d^{3}x{\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}·{\widehat{R}}_2\right)\right.\hfill \\ & +& \left.{\rho }_1\left(\overrightarrow{x_1}\right){\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·\left(\int d^{3}x{\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}{\displaystyle \frac{1}{R_2}}\right)\right].\hfill \end{array}$$

(105)

Let us look at the expression:

$$i_{11}=\int \left({\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}·{\widehat{R}}_2\right)d^{3}x.$$

(106)

Taking into account equation (A.9):

$$i_{11}=2\pi R{\int }_0^{y_{max}}dy{\int }_{-1}^{1}ds{\displaystyle \frac{y+s}{\sqrt{1+y^2+2ys}}}.$$

(107)

Notice that:

$$\begin{array}{c}\hfill {\int }_{-1}^{1}ds{\displaystyle \frac{s}{\sqrt{1+y^2+2ys}}}=-{\displaystyle \frac{2}{3}}\left\{\begin{array}{cc}\hfill & {\displaystyle \frac{1}{y^2}}y\ge 1.\hfill \\ \hfill & yy<1.\hfill \end{array}\right.\end{array}$$

(108)

And

$$\begin{array}{c}\hfill y{\int }_{-1}^{1}ds{\displaystyle \frac{1}{\sqrt{1+y^2+2ys}}}=\left\{\begin{array}{cc}\hfill & 2y\ge 1.\hfill \\ \hfill & 2yy<1.\hfill \end{array}\right.\end{array}$$

(109)

Substituting these integral forms into equation (107), we obtain:

$$i_{11}=4\pi R\left[y_{max}-1+{\displaystyle \frac{1}{3y_{max}}}\right]\simeq 4\pi (R_{max}-R)$$

(110)

Next, we simplify the second integral appearing in equation (105):

$${\overrightarrow{i}}_{12}=\int d^{3}x{\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}{\displaystyle \frac{1}{R_2}}=-\int d^{3}x\left(\overrightarrow{\nabla }{\displaystyle \frac{1}{R_1}}\right){\displaystyle \frac{1}{R_2}}.$$

(111)

As is known from [15]:

$$\int d^{3}x{\displaystyle \frac{1}{R_1}}\left(\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}\right)=-2\pi \widehat{R}.$$

(112)

Subsequently, the required integral follows by a straightforward exchange of indices.

$$\int d^{3}x{\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}{\displaystyle \frac{1}{R_2}}=2\pi \widehat{R}.$$

(113)

Thus:

$$\begin{array}{c}\hfill {\overrightarrow{i}}_{12}=-2\pi \widehat{R}.\end{array}$$

(114)

Inserting the evaluated integrals into equation (105) yields:

$$\begin{array}{cc}\hfill i_1& =-{\displaystyle \frac{k}{4\pi c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right){\rho }_1\left(\overrightarrow{x_1}\right)\left(4\pi (R_{max}-R)\right)\right.\hfill \\ \hfill & \left.+{\rho }_1\left(\overrightarrow{x_1}\right){\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·\left(-2\pi \widehat{R}\right)\right].\hfill \end{array}$$

(115)

Or:

$$\begin{array}{c}\hfill i_1=-{\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\rho }_1(R_{max}-R)-{\displaystyle \frac{1}{2}}{\rho }_1{\partial }_t\overrightarrow{J_2}·\widehat{R}\right].\end{array}$$

(116)

We now focus on the second term to enable further simplification:

$$\begin{array}{cc}\hfill \int d^3{x}_2{\partial }_t\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·\widehat{R}& =-{\partial }_t\left(\int d^3{x}_2\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·{\overrightarrow{\nabla }}_{{\overrightarrow{x}}_2}R\right)=-{\partial }_t\left(\int d^3{x}_{2}R{\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)\right)\hfill \\ \hfill & =-\int d^3{x}_{2}R{\partial }_t^2{\rho }_2\left({\overrightarrow{x}}_2\right),\hfill \end{array}$$

(117)

in the above we used equation (86) and equation (87). By substituting this result into equation (116), we arrive at:

$$\begin{array}{ccc}\hfill i_1& =& -{\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{2}}{\rho }_1{\partial }_t^2{\rho }_2(R_{max}-R)+{\displaystyle \frac{1}{2}}{\rho }_1{\partial }_t^2{\rho }_{2}R\right]\hfill \\ & =& -{\displaystyle \frac{k{R}_{max}}{2c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\rho }_1{\partial }_t^2{\rho }_2\right].\hfill \end{array}$$

(118)

Notice that the following terms would be zero considering equation (43), Gauss theorem, and the null current densities at the convergence radius $R_{max}$:

$$\begin{array}{c}\hfill \int \left({\partial }_t^n\rho \right)d^{3}x=-{\partial }_t^{n-1}\left(\int \overrightarrow{\nabla }·\overrightarrow{J}{d}^{3}x\right)=-{\partial }_t^{n-1}\left(\oint \overrightarrow{J}·d\overrightarrow{S}\right)=0,n\ge 1.\end{array}$$

(119)

Hence as the double integral in equation (118) decouples, it follows that:

$$i_1=0.$$

(120)

Analogously, the second integral in the field energy expression also nullifies:

$$i_2=0.$$

(121)

Next, we calculate the third integral to finalize the field energy equation, employing Equation (61) of [12]:

$${\overrightarrow{B}}_1^{\left[2\right]}\left(\overrightarrow{x}\right)={\displaystyle \frac{k}{c^2}}\int d^3{x}_1{\displaystyle \frac{-{\widehat{R}}_1}{R_1^2}}\times \overrightarrow{J_1}\left(\overrightarrow{x_1}\right)=-{\displaystyle \frac{k}{c^2}}\int d^3{x}_1{\displaystyle \frac{{\widehat{R}}_1}{R_1^2}}\times \overrightarrow{J_1}\left(\overrightarrow{x_1}\right).$$

(122)

Similarly:

$$\begin{array}{c}\hfill {\overrightarrow{B}}_2^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2}}\int d^3{x}_2{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\times \overrightarrow{J_2}\left(\overrightarrow{x_2}\right).\end{array}$$

(123)

Hence,

$$\begin{array}{cc}\hfill i_3& ={ϵ}_0{c}^2\left(\int {\overrightarrow{B}}_1^{\left[2\right]}·{\overrightarrow{B}}_2^{\left[2\right]}{d}^{3}x\right)\hfill \\ \hfill & ={\displaystyle \frac{k}{4\pi c^2}}\int \left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{({\widehat{R}}_1\times \overrightarrow{J_1})·({\widehat{R}}_2\times \overrightarrow{J_2})}{R_1^2{R}_2^2}}\right]d^{3}x\hfill \end{array}$$

(124)

Applying the following vector identity:

$$({\widehat{R}}_1\times \overrightarrow{J_1})·({\widehat{R}}_2\times \overrightarrow{J_2})=({\widehat{R}}_1·{\widehat{R}}_2)(\overrightarrow{J_1}·\overrightarrow{J_2})-({\widehat{R}}_1·\overrightarrow{J_2})({\widehat{R}}_2·\overrightarrow{J_1}),$$

(125)

equation (124) can be rewritten as:

$$\begin{array}{ccc}\hfill i_3& =& {\displaystyle \frac{k}{4\pi c^2}}\left[\int \int d^3{x}_1{d}^3{x}_2(\overrightarrow{J_1}·\overrightarrow{J_2})\left(\int {\displaystyle \frac{{\widehat{R}}_1·{\widehat{R}}_2}{R_1^2{R}_2^2}}{d}^{3}x\right)\right.\hfill \\ & -& \left.\int d^{3}x\left(\int d^3{x}_1{\displaystyle \frac{\overrightarrow{J_1}·{\widehat{R}}_1}{R_1^2}}\right)\left(\int d^3{x}_2{\displaystyle \frac{\overrightarrow{J_2}·{\widehat{R}}_2}{R_2^2}}\right)\right].\hfill \end{array}$$

(126)

Similar to equation (45) it can be shown that:

$$\begin{array}{c}\hfill \int d^3{x}_1{\displaystyle \frac{\overrightarrow{J_1}·{\widehat{R}}_1}{R_1^2}}=\int d^3{x}_1{\displaystyle \frac{1}{R_1}}{\partial }_t{\rho }_1.\end{array}$$

(127)

Taking into account equation (64) and equation (127) it follows that:

$$\begin{array}{c}\hfill i_3={\displaystyle \frac{k}{4\pi c^2}}\left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{4\pi }{R}}\overrightarrow{J_1}·\overrightarrow{J_2}-\int \int d^3{x}_1{d}^3{x}_2{\partial }_t{\rho }_1{\partial }_t{\rho }_2\left(\int d^{3}x{\displaystyle \frac{1}{R_1{R}_2}}\right)\right].\end{array}$$

(128)

Taking into account equation (B.4) we obtain:

$$\begin{array}{ccc}\hfill i_3& =& {\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{\overrightarrow{J_1}·\overrightarrow{J_2}}{R}}+{\displaystyle \frac{1}{2}}(1-2y_{max}){\partial }_t{\rho }_1{\partial }_t{\rho }_{2}R\right]\hfill \\ & =& {\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{\overrightarrow{J_1}·\overrightarrow{J_2}}{R}}+{\displaystyle \frac{R}{2}}{\partial }_t{\rho }_1{\partial }_t{\rho }_2-R_{max}{\partial }_t{\rho }_1{\partial }_t{\rho }_2\right]\hfill \\ & =& {\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{\overrightarrow{J_1}·\overrightarrow{J_2}}{R}}+{\displaystyle \frac{R}{2}}{\partial }_t{\rho }_1{\partial }_t{\rho }_2\right],\hfill \end{array}$$

(129)

the last equation sign is due to the fact that in the term containing $R_{max}$ the volume integrals decouple, and thus by equation (119) this term is null. Combining equation (129), equation (120) and equation (121), we obtain an expression for the second-order field energy:

$$\begin{array}{c}\hfill E_{field12}^{\left[2\right]}={\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{\overrightarrow{J_1}·\overrightarrow{J_2}}{R}}+{\displaystyle \frac{R}{2}}{\partial }_t{\rho }_1{\partial }_t{\rho }_2\right].\end{array}$$

(130)

4.3.3. Poynting Vector

Next, we shall study the Poynting vector according to equation (32) for $n=2$:

$${\overrightarrow{S}}_{P12}^{\left[2\right]}={ϵ}_0{c}^2\sum _{k=0}^4\left({\overrightarrow{E}}_1^{[4-k]}\times {\overrightarrow{B}}_2^{\left[k\right]}+{\overrightarrow{E}}_2^{[4-k]}\times {\overrightarrow{B}}_1^{\left[k\right]}\right),$$

(131)

by equation (95) we obtain the following resulting form of the Poynting vector:

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}^{\left[2\right]}={ϵ}_0{c}^2\left({\overrightarrow{E}}_1^{\left[2\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[4\right]}+{\overrightarrow{E}}_2^{\left[2\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}+{\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[4\right]}\right).\end{array}$$

(132)

The Poynting vector term, typically associated with radiation, contributes to the energy balance only through the surface integral over a closed surface enclosing the system. When this surface is taken to be spherical and located at a far distance $R_{max}$, only the asymptotic forms of the electric and magnetic fields are relevant for evaluating the Poynting vector contribution. Accordingly, the expression for the Poynting flux on a far away sphere of radius $R_{max}$ is given by:

$$\begin{array}{c}\hfill P{F}^{\left[2\right]}=\oint {\overrightarrow{S}}_{P12}^{\left[2\right]}·\widehat{n}da=R_{max}^2{\oint }_{R_{max}}{\overrightarrow{S}}_{P12}^{\left[2\right]}·\widehat{r}d\mathrm{\Omega }.\end{array}$$

(133)

Following the approach used in the field energy analysis, the Poynting flux may likewise be represented as a sum of distinct terms, enabling the successive calculation of the corresponding integrals:

$$\begin{array}{c}\hfill P{F}^{\left[2\right]}=P{F}_1^{\left[2\right]}+P{F}_2^{\left[2\right]}+P{F}_3^{\left[2\right]}+P{F}_4^{\left[2\right]}.\end{array}$$

(134)

Such that:

$$\begin{array}{c}\hfill P{F}_1^{\left[2\right]}\equiv R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[2\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}\right)·\widehat{r}d\mathrm{\Omega },\end{array}$$

(135)

$$\begin{array}{c}\hfill P{F}_2^{\left[2\right]}\equiv R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_2^{\left[2\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}\right)·\widehat{r}d\mathrm{\Omega },\end{array}$$

(136)

$$\begin{array}{c}\hfill P{F}_3^{\left[2\right]}\equiv R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[4\right]}\right)·\widehat{r}d\mathrm{\Omega },\end{array}$$

(137)

and

$$\begin{array}{c}\hfill P{F}_4^{\left[2\right]}\equiv R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[4\right]}\right)·\widehat{r}d\mathrm{\Omega }.\end{array}$$

(138)

According to Equation (57) of [12]:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2}}\int d^3{x}_1\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1\left({\overrightarrow{x}}_1\right){\widehat{R}}_1+{\partial }_t\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)R_1^{-1}\right].\end{array}$$

(139)

Let us now write an asymptotic expression for the second order electric field:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2}}\left[{\displaystyle \frac{1}{2}}\int d^3{x}_1{\partial }_t^2{\rho }_1\left(\widehat{r}-{\displaystyle \frac{{\overrightarrow{x}}_1}{R_{max}}}+\widehat{r}\left({\displaystyle \frac{{\overrightarrow{x}}_1·\widehat{r}}{R_{max}}}\right)\right)+\int d^3{x}_1{\partial }_t\overrightarrow{J_1}{\displaystyle \frac{1}{R_{max}}}\right].$$

(140)

By equation (119) we have:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2{R}_{max}}}\left[{\displaystyle \frac{1}{2}}\int d^3{x}_1{\partial }_t^2{\rho }_1\left(-{\overrightarrow{x}}_1+\widehat{r}({\overrightarrow{x}}_1·\widehat{r})\right)+\int d^3{x}_1{\partial }_t\overrightarrow{J_1}\right].$$

(141)

Taking into account equation (D.5) we obtain:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{2c^2{R}_{max}}}\int d^3{x}_1\left[{\partial }_t{\overrightarrow{J}}_1+\widehat{r}({\partial }_t{\overrightarrow{J}}_1·\widehat{r})\right],$$

(142)

the above expression decreases as ${\displaystyle \frac{1}{R_{max}}}$. According to Equation (62) of [12]:

$$\begin{array}{c}\hfill {\overrightarrow{B}}_2^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2}}\int d^3{x}_2{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\times \overrightarrow{J_2}\left({\overrightarrow{x}}_2\right).\end{array}$$

(143)

Let us now write an asymptotic expression for the second order magnetic field:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{B}}_2^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2}}\widehat{r}\times {\displaystyle \frac{\int d^3{x}_2\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)}{R_{max}^2}},$$

(144)

the above expression decreases as ${\displaystyle \frac{1}{R_{max}^2}}$. From equation (142) and equation (144) it follows that the Poynting vector decays as $1/R_{max}^3$, the associated surface integral over a large sphere with radius $R_{max}$ whose surface area grows as $R_{max}^2$ will decrease as $1/R_{max}$, thus provided $R_{max}$ is large enough we consider this contribution to be negligible, that is:

$$P{F}_1^{\left[2\right]}\simeq 0$$

(145)

Similarly:

$$P{F}_2^{\left[2\right]}\simeq 0$$

(146)

Next, we compute the third integral:

$$\begin{array}{c}\hfill P{F}_3^{\left[2\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[4\right]}\right)·\widehat{r}d\mathrm{\Omega }.\end{array}$$

(147)

According to Equation (55) of [12]:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[0\right]}\left(\overrightarrow{x}\right)=k\int d^3{x}_1{\displaystyle \frac{{\rho }_1\left(\overrightarrow{x_1}\right)}{R_1^2}}{\widehat{R}}_1\end{array}$$

(148)

Let us now write an asymptotic expression for the zeroth-order electric field:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[0\right]}\left(\overrightarrow{x}\right)=k{\displaystyle \frac{\int d^3{x}_1{\rho }_1\left(\overrightarrow{x_1}\right)}{R_{max}^2}}\widehat{r}.$$

(149)

As this vector is radially oriented and cross product of the above with any other vector must be perpendicular to the radial direction. It follows that the said cross product will have a zero scalar product with a radially oriented surface vector and thus:

$$P{F}_3^{\left[2\right]}\simeq 0,$$

(150)

similarly:

$$P{F}_4^{\left[2\right]}\simeq 0$$

(151)

Thus by plugging equations (145, 146,150,151) into equation (134).

$$\begin{array}{c}\hfill P{F}^{\left[2\right]}=0,\end{array}$$

(152)

in which the equality sign is only correct to the current approximation. Hence there is no Poynting vector contribution to the energy balance. This is expected as the mechanical work equation (93) is balanced by the field energy loss equation (130) in second order terms of ${\displaystyle \frac{1}{c}}$:

$$Powe{r}_{12}^{\left[2\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[2\right]}}{dt}}.$$

(153)

It is remarkable that no radiation losses need to be considered up to the second order approximation, this will have implication for the retarded field motor that we discuss in later sections of this paper.

4.4. n=3

Let us look at equation (27) and study it for the third order in ${\displaystyle \frac{1}{c}}$:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[3\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[3\right]}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}^{\left[3\right]}·\widehat{n}da.\end{array}$$

(154)

4.4.1. Power

The third-order expression for the power invested in mechanical work is given below:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[3\right]}=\int d^{3}x\left(\overrightarrow{J_1}·{\overrightarrow{E}}_2^{\left[3\right]}+\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[3\right]}\right)\end{array}$$

(155)

Equations (51) and (54) of [12] combine to yield the third-order terms in the electric field expansions:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[3\right]}\left(\overrightarrow{x}\right)={\displaystyle \frac{k}{c^3}}\int d^3{x}_1\left[{\displaystyle \frac{1}{3}}{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right)R_1{\widehat{R}}_1+{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right]\end{array}$$

(156)

We proceed to evaluate each integral individually.

$$\begin{array}{ccc}\hfill I_1& \equiv & \int d^{3}x\left(\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[3\right]}\right)\hfill \\ & =& {\displaystyle \frac{k}{c^3}}\int d^{3}x\left[\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\left(\int d^3{x}_1\left({\displaystyle \frac{1}{3}}{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right)R_1{\widehat{R}}_1+{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right)\right)\right].\hfill \end{array}$$

(157)

Changing the order on integration we obtain:

$$\begin{array}{cc}\hfill I_1=& {\displaystyle \frac{k}{c^3}}\left[\int d^3{x}_1{\displaystyle \frac{1}{3}}{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right)\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\overrightarrow{R_1}+\int d^3{x}_1\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right].\hfill \end{array}$$

(158)

Let us look at the expression:

$$I_{1f}\equiv \int d^3{x}_1{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right)\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\overrightarrow{R_1}=\int d^{3}x{J}_2^k\left(\overrightarrow{x}\right)\int d^3{x}_1{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right)R_1^k,$$

(159)

in which we have changed the order of integrals and used the Einstein summation convention. Now by continuity:

$${\partial }_t{\rho }_1=-{\overrightarrow{\nabla }}_1·{\overrightarrow{J}}_1,$$

(160)

hence:

$$I_{1f}=-\int d^{3}x{J}_2^k\left(\overrightarrow{x}\right)\int d^3{x}_1{\partial }_t^2{\overrightarrow{\nabla }}_1·{\overrightarrow{J}}_1{R}_1^k=-\int d^{3}x{J}_2^k\left(\overrightarrow{x}\right)\int d^3{x}_1{\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1\right)R_1^k.$$

(161)

Now:

$${\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1\right)R_1^k={\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1{R}_1^k\right)-{\partial }_t^2{\overrightarrow{J}}_1·{\overrightarrow{\nabla }}_1{R}_1^k.$$

(162)

However:

$${\overrightarrow{\nabla }}_1{R}_1^k={\overrightarrow{\nabla }}_1(x^k-x_1^k)=-{\overrightarrow{\nabla }}_1{x}_1^k=-{\widehat{x}}^k.$$

(163)

Thus:

$${\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1\right)R_1^k={\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1{R}_1^k\right)+{\partial }_t^2{\overrightarrow{J}}_1·{\widehat{x}}^k={\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1{R}_1^k\right)+{\partial }_t^2{J}_1^k.$$

(164)

Inserting equation (164) into equation (161) and using Gauss theorem we obtain:

$$\begin{array}{ccc}\hfill I_{1f}& =& -\int d^{3}x{J}_2^k\left(\overrightarrow{x}\right)\int d^3{x}_1\left[{\overrightarrow{\nabla }}_1·\left({\partial }_t^2{\overrightarrow{J}}_1{R}_1^k\right)+{\partial }_t^2{J}_1^k\right]\hfill \\ & =& -\int d^{3}x{\overrightarrow{J}}_2\left(\overrightarrow{x}\right)·\int d^3{x}_1{\partial }_t^2{\overrightarrow{J}}_1-\int d^{3}x{J}_2^k\left(\overrightarrow{x}\right)\oint d{\overrightarrow{S}}_1·\left({\partial }_t^2{\overrightarrow{J}}_1{R}_1^k\right).\hfill \end{array}$$

(165)

Assuming lack of currents on a far away encapsulating surface, the above expression simplifies into:

$$I_{1f}=-\int d^{3}x{\overrightarrow{J}}_2\left(\overrightarrow{x}\right)·\int d^3{x}_1{\partial }_t^2{\overrightarrow{J}}_1.$$

(166)

Inserting equation (166) into equation (158), we obtain the form:

$$I_1={\displaystyle \frac{k}{c^3}}\int d^3{x}_1\int d^{3}x(1-{\displaystyle \frac{1}{3}})\overrightarrow{J_2}\left(\overrightarrow{x}\right)·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)={\displaystyle \frac{2k}{3c^3}}\int d^3{x}_1\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right).$$

(167)

We now change the integration variable $\overrightarrow{x}\to {\overrightarrow{x}}_2$. Thus: ${\overrightarrow{J}}_2\left(\overrightarrow{x}\right)\to {\overrightarrow{J}}_2\left({\overrightarrow{x}}_2\right)$, and also:

$$\begin{array}{c}\hfill I_1=\left({\displaystyle \frac{2k}{3c^3}}\right)\int d^3{x}_1{d}^3{x}_2\left[\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right].\end{array}$$

(168)

By switching the indices, we obtain the second integral:

$$\begin{array}{c}\hfill I_2=\left({\displaystyle \frac{2k}{3c^3}}\right)\int d^3{x}_1{d}^3{x}_2\left[\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\partial }_t^2\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)\right].\end{array}$$

(169)

Combining equation (168) and equation (169), we obtain:

$$Powe{r}_{12}^{\left[3\right]}=\left({\displaystyle \frac{2k}{3c^3}}\right)\int \int d^3{x}_1{d}^3{x}_2\left(\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\partial }_t^2\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)+\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right).$$

(170)

The expression obtained thus represents the third-order mechanical power.

4.4.2. Field Energy

We now proceed to calculate the field energy using equation (31) for $n=3$:

$$E_{field12}^{\left[3\right]}={ϵ}_0\int \left(\sum _{k=0}^3{\overrightarrow{E}}_1^{[3-k]}·{\overrightarrow{E}}_2^{\left[k\right]}+c^2\sum _{k=0}^5{\overrightarrow{B}}_1^{[5-k]}·{\overrightarrow{B}}_2^{\left[k\right]}\right)d^{3}x.$$

(171)

It is known from [12] (see also equation (95)) that:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[1\right]}={\overrightarrow{E}}_2^{\left[1\right]}=0,{\overrightarrow{B}}_1^{\left[0\right]}={\overrightarrow{B}}_2^{\left[0\right]}=0,{\overrightarrow{B}}_1^{\left[1\right]}={\overrightarrow{B}}_2^{\left[1\right]}=0,{\overrightarrow{B}}_1^{\left[3\right]}={\overrightarrow{B}}_2^{\left[3\right]}=0.\end{array}$$

(172)

Therefore, the field energy can be written as:

$$\begin{array}{c}\hfill E_{field12}^{\left[3\right]}={ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[3\right]}·{\overrightarrow{E}}_2^{\left[0\right]}+{\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[3\right]}\right)d^{3}x.\end{array}$$

(173)

As the first and third-order electric field expression is given in equation (156), we shall now focus on the first integral in the above expression:

$$\begin{array}{cc}\hfill i_1& \equiv {ϵ}_0\int \left[\left(k\left({\displaystyle \frac{1}{c^3}}\right)\int d^3{x}_1\left[{\displaystyle \frac{1}{3}}{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right)R_1{\widehat{R}}_1+{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)\right]\right)·\left(k\int d^3{x}_2{\displaystyle \frac{{\rho }_2\left(\overrightarrow{x_2}\right)}{R_2^2}}{\widehat{R}}_2\right)\right]d^{3}x.\hfill \end{array}$$

(174)

By separating the terms we obtain:

$$\begin{array}{ccc}\hfill i_1& =& {\displaystyle \frac{{ϵ}_0{k}^2}{c^3}}\int \left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{3}}{\partial }_t^3{\rho }_1\left({\overrightarrow{x}}_1\right){\rho }_2\left(\overrightarrow{x_2}\right)\left(R_1{\widehat{R}}_1·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)\right.\hfill \\ & +& \left.\int \int d^3{x}_1{d}^3{x}_2{\rho }_2\left(\overrightarrow{x_2}\right)\left({\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)\right]d^{3}x.\hfill \end{array}$$

(175)

Using equation (39) we obtain:

$$\begin{array}{ccc}& & \int \left({\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)d^{3}x=-\int \left({\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}\right)d^{3}x\hfill \\ & =& -\int \left(\overrightarrow{\nabla }·\left({\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right){\displaystyle \frac{1}{R_2}}\right)-\overrightarrow{\nabla }·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right){\displaystyle \frac{1}{R_2}}\right)d^{3}x,\hfill \end{array}$$

(176)

since:

$$\overrightarrow{\nabla }·{\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)={\partial }_t^2\overrightarrow{\nabla }·\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)=0,$$

(177)

as $\overrightarrow{J_1}$ is a function of ${\overrightarrow{x}}_1$ and does not depend on $\overrightarrow{x}$, it follows that :

$$\int \left({\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)d^{3}x=-\oint d\overrightarrow{S}·\left({\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right){\displaystyle \frac{1}{R_2}}\right)=0.$$

(178)

in which we used Gauss theorem and assumed as usual that there are no currents on the far away encapsulating surface. Thus it follows from equation (175) that:

$$i_1={\displaystyle \frac{k}{4\pi c^3}}\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{3}}{\partial }_t^3{\rho }_1{\rho }_2\left(\int d^{3}x\left(R_1{\widehat{R}}_1·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)\right).$$

(179)

We now evaluate the following integral independently:

$$i_{1f}\equiv \int d^{3}x\left(R_1{\widehat{R}}_1·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)=-\int {\overrightarrow{R}}_1·\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}{d}^{3}x,$$

(180)

this can also be written in the form:

$$i_{1f}=-\int \left[\overrightarrow{\nabla }·\left({\displaystyle \frac{{\overrightarrow{R}}_1}{R_2}}\right)-{\displaystyle \frac{1}{R_2}}\overrightarrow{\nabla }·{\overrightarrow{R}}_1\right]d^{3}x=-\int \overrightarrow{\nabla }·\left({\displaystyle \frac{{\overrightarrow{R}}_1}{R_2}}\right)d^{3}x+3\int {\displaystyle \frac{1}{R_2}}{d}^{3}x.$$

(181)

Using Gauss theorem we can recast $i_{1f}$ in the form:

$$i_{1f}=-\oint d\overrightarrow{S}·\left({\displaystyle \frac{{\overrightarrow{R}}_1}{R_2}}\right)+3\int {\displaystyle \frac{1}{R_2}}{d}^{3}x.$$

(182)

Calculating the surface integral on a far away spherical surface of radius $R_{max}$ and assuming that all currents and charges are close to the origin of axis with distances much smaller than $R_{max}$ such that $R_2\simeq R_{max}$ and ${\overrightarrow{R}}_1\simeq R_{max}\widehat{r}$, it follows that:

$$\oint d\overrightarrow{S}·\left({\displaystyle \frac{{\overrightarrow{R}}_1}{R_2}}\right)=\oint R_{max}^{2}d\mathrm{\Omega }\widehat{r}·\left({\displaystyle \frac{{\overrightarrow{R}}_1}{R_2}}\right)\simeq \oint R_{max}^{2}d\mathrm{\Omega }\widehat{r}·\widehat{r}=4\pi R_{max}^2.$$

(183)

Thus equation (182) takes the form:

$$i_{1f}\simeq -4\pi R_{max}^2+3\int {\displaystyle \frac{1}{R_2}}{d}^{3}x.$$

(184)

At this point we notice that up to rather small terms $i_{1f}$ depends only on ${\overrightarrow{x}}_2$ and not on ${\overrightarrow{x}}_1$, thus we may partition the double integral given in equation (179) in the form:

$$i_1={\displaystyle \frac{k}{12\pi c^3}}\int d^3{x}_1{\partial }_t^3{\rho }_1\int d^3{x}_2{\rho }_2{i}_{1f}=0,$$

(185)

because $\int d^3{x}_1{\partial }_t^3{\rho }_1=0$ (see equation (119)). Similarly:

$${ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[3\right]}\right)d^{3}x=0.$$

(186)

By inserting the results of equation (185) and equation (186) into equation (173) we obtain a null result:

$$\begin{array}{c}\hfill E_{field12}^{\left[3\right]}=0.\end{array}$$

(187)

It follows remarkably that no electromagnetic energy can be stored at the third order of ${\displaystyle \frac{1}{c}}$.

4.4.3. Poynting Vector

Next, we shall study the Poynting vector according to equation (32) for $n=3$

$${\overrightarrow{S}}_{P12}^{\left[3\right]}={ϵ}_0{c}^2\sum _{k=0}^5\left({\overrightarrow{E}}_1^{[5-k]}\times {\overrightarrow{B}}_2^{\left[k\right]}+{\overrightarrow{E}}_2^{[5-k]}\times {\overrightarrow{B}}_1^{\left[k\right]}\right),$$

(188)

by equation (172) the Poynting vector takes the form:

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}^{\left[3\right]}={ϵ}_0{c}^2\left({\overrightarrow{E}}_1^{\left[3\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[5\right]}+{\overrightarrow{E}}_2^{\left[3\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}+{\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[5\right]}\right).\end{array}$$

(189)

The Poynting flux on a far away sphere of radius $R_{max}$ is given by:

$$\begin{array}{c}\hfill P{F}^{\left[3\right]}=\oint {\overrightarrow{S}}_{P12}^{\left[3\right]}·\widehat{n}da=R_{max}^2{\oint }_{R_{max}}{\overrightarrow{S}}_{P12}^{\left[3\right]}·\widehat{r}d\mathrm{\Omega }.\end{array}$$

(190)

For ease of computation, we divide the Poynting flux expression into four independent integrals:

$$P{F}^{\left[3\right]}=P{F}_1^{\left[3\right]}+P{F}_2^{\left[3\right]}+P{F}_3^{\left[3\right]}+P{F}_4^{\left[3\right]}$$

(191)

We begin by evaluating the first integral:

$$\begin{array}{c}\hfill P{F}_1^{\left[3\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[3\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}\right)·\widehat{r}d\mathrm{\Omega }\end{array}$$

(192)

Let us now write an asymptotic expression for the third-order electric field given in equation (156):

$$\begin{array}{c}\hfill \underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[3\right]}=k\left({\displaystyle \frac{1}{c^3}}\right)\left[{\displaystyle \frac{R_{max}}{3}}\left(\int d^3{x}_1{\partial }_t^3{\rho }_1\right)\widehat{r}+\int d^3{x}_1{\partial }_t^2\overrightarrow{J_1}\right]\end{array}$$

(193)

Using equation (119), we obtain:

$$\begin{array}{c}\hfill \underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[3\right]}=k\left({\displaystyle \frac{1}{c^3}}\right)\left[\int d^3{x}_1{\partial }_t^2\overrightarrow{J_1}\right],\end{array}$$

(194)

and an asymptotic expression for the second-order magnetic field:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{B}}_2^{\left[2\right]}=-{\displaystyle \frac{k}{c^2}}\widehat{r}\times {\displaystyle \frac{\int d^3{x}_2\overrightarrow{J_2}}{R_{max}^2}}$$

(195)

Thus,

$$\begin{array}{cc}\hfill P{F}_1^{\left[3\right]}& =-{\displaystyle \frac{k}{4\pi c^3}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t^2\overrightarrow{J_1}\times \left(\widehat{r}\times \overrightarrow{J_2}\right)\right)\right]·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{k}{4\pi c^3}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left(\widehat{r}\left({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2}\right)-\left({\partial }_t^2\overrightarrow{J_1}·\widehat{r}\right)\overrightarrow{J_2}\right)\right]·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{k}{4\pi c^3}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left(\left({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2}\right)-\left({\partial }_t^2\overrightarrow{J_1}·\widehat{r}\right)\left(\overrightarrow{J_2}·\widehat{r}\right)\right)\right]d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{k}{4\pi c^3}}\int \int d^3{x}_1{d}^3{x}_2\left[4\pi \left({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2}\right)-\left({\partial }_t^2{\overrightarrow{J_1}}^k\left(\oint {\widehat{r}}_k{\widehat{r}}_{l}d\mathrm{\Omega }\right){\overrightarrow{J_2}}^l\right)\right]\hfill \end{array}$$

(196)

In the above we use the Einstein summation convention. Now the radial unit vector can be written in the cartesian coordinates in the form:

$$\widehat{r}=sin\theta cos\varphi \widehat{x}+sin\theta sin\varphi \widehat{y}+cos\theta \widehat{z}$$

(197)

in which $\varphi$ is the azimuthal angle, $\theta$ is the angle of latitude and $\widehat{x},\widehat{y},\widehat{z}$ are unit vector pointing in the direction of the Cartesian axes. Now:

$$I_{kl}\equiv \oint {\widehat{r}}_k{\widehat{r}}_{l}d\mathrm{\Omega }={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta sin\theta {\widehat{r}}_k{\widehat{r}}_l$$

(198)

As every non diagonal element of $I_{kl}$ is calculated by integrating over a complete period, a term containing either $sin\varphi$ or $cos\varphi$ it follows that the non diagonal elements of this matrix vanish. It remains to calculate the diagonal elements:

$$I_{11}={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta sin\theta {\widehat{r}}_1{\widehat{r}}_1={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta {sin}^3\theta {cos}^2\varphi ={\displaystyle \frac{4\pi }{3}},$$

(199)

$$I_{22}={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta sin\theta {\widehat{r}}_2{\widehat{r}}_2={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta {sin}^3\theta {sin}^2\varphi ={\displaystyle \frac{4\pi }{3}},$$

(200)

$$I_{33}={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta sin\theta {\widehat{r}}_3{\widehat{r}}_3={\int }_0^{2\pi }d\varphi {\int }_0^{\pi }d\theta sin\theta {cos}^2\theta ={\displaystyle \frac{4\pi }{3}},$$

(201)

Thus:

$$I_{kl}={\displaystyle \frac{4\pi }{3}}{\delta }_{kl}.$$

(202)

In which ${\delta }_{kl}$ is Kronecker’s delta. Inserting equation (202) into equation (196) it follows that:

$$P{F}_1^{\left[3\right]}=-{\displaystyle \frac{k}{c^3}}\int \int d^3{x}_1{d}^3{x}_2\left[\left({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2}\right)-{\displaystyle \frac{1}{3}}\left({\partial }_t^2{\overrightarrow{J_1}}^k{\delta }_{kl}{\overrightarrow{J_2}}^l\right)\right]=-{\displaystyle \frac{2k}{3c^3}}\int d^3{x}_1{\partial }_t^2\overrightarrow{J_1}·\int d^3{x}_2\overrightarrow{J_2}$$

(203)

Analogously, the second integral of the Poynting flux takes the form:

$$\begin{array}{cc}\hfill P{F}_2^{\left[3\right]}& =R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_2^{\left[3\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}\right)·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{2k}{3c^3}}\int d^3{x}_2{\partial }_t^2\overrightarrow{J_2}·\int d^3{x}_1\overrightarrow{J_1}\hfill \end{array}$$

(204)

We now proceed to evaluate the third integral:

$$\begin{array}{c}\hfill P{F}_3^{\left[3\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[5\right]}\right)·\widehat{r}d\mathrm{\Omega }.\end{array}$$

(205)

As referenced earlier, we adopt the electric and magnetic field expressions provided by [12]:

$$\begin{array}{c}\hfill \underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[0\right]}=k{\displaystyle \frac{\int d^3{x}_1{\rho }_1}{R_{max}^2}}\widehat{r}.\end{array}$$

(206)

and

$$\begin{array}{c}\hfill \underset{r\to R_{max}}{lim}{\overrightarrow{B}}_2^{\left[5\right]}=-{\displaystyle \frac{k}{3c^5}}\int d^3{x}_2{R}_{max}\widehat{r}\times {\partial }_t^3{\overrightarrow{J}}_2.\end{array}$$

(207)

Therefore:

$$\begin{array}{c}\hfill P{F}_3^{\left[3\right]}=-{\displaystyle \frac{k}{3c^3}}\left(\int \int d^3{x}_1{d}^3{x}_2{\rho }_1{R}_{max}\left(\widehat{r}\times \left(\widehat{r}\times {\partial }_t^3{\overrightarrow{J}}_2\right)\right)\right)·\widehat{r}=0.\end{array}$$

(208)

In a similar manner:

$$\begin{array}{c}\hfill P{F}_4^{\left[3\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[5\right]}\right)·\widehat{r}d\mathrm{\Omega }=0.\end{array}$$

(209)

Thus by inserting equation (203), equation (204), equation (208) and equation (209) into equation (191), we obtain the total Poynting flux contribution of the third order in ${\displaystyle \frac{1}{c}}$:

$$P{F}^{\left[3\right]}=-{\displaystyle \frac{2k}{3c^3}}\int \int d^3{x}_1{d}^3{x}_2\left({\overrightarrow{J}}_1·{\partial }_t^2{\overrightarrow{J}}_2+{\partial }_t^2{\overrightarrow{J}}_1·{\overrightarrow{J}}_2\right).$$

(210)

This term is minus equation (170), that is minus the power invested by the electromagnetic field to do mechanical work to the third order in ${\displaystyle \frac{1}{c}}$. It follows that in the third order no energy can be stored in the electromagnetic field and the energy equation is balanced between radiation and work. That is incoming radiation can cause charges to do work, or charges can radiate at the expense of their mechanical energy. However, if the currents in the two subsystems are orthogonal no radiation is radiated and no work is done.

4.5. n=4

Let us look at equation (27) and study it for the fourth order in ${\displaystyle \frac{1}{c}}$:

$$\begin{array}{c}\hfill Powe{r}_{12}^{\left[4\right]}=-{\displaystyle \frac{d{E}_{field12}^{\left[4\right]}}{dt}}-{\oint }_S{\overrightarrow{S}}_{P12}^{\left[4\right]}·\widehat{n}da.\end{array}$$

(211)

4.5.1. Power

The fourth order expression for the power invested in mechanical work is given below:

$$Powe{r}_{12}^{\left[4\right]}=\int d^{3}x\left(\overrightarrow{J_1}·{\overrightarrow{E}}_2^{\left[4\right]}+\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[4\right]}\right).$$

(212)

According to equations (51) and (54) of [12], the fourth order term in the electric field expansion is:

$$\begin{array}{c}\hfill {\overrightarrow{E}}_1^{\left[4\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{2c^4}}\int d^3{x}_1\left[{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_1{R}_1^2{\widehat{R}}_1+{\partial }_t^3\overrightarrow{J_1}{R}_1\right].\end{array}$$

(213)

Let us calculate both integrals of equation (212) one by one:

$$I_1=\int d^{3}x\overrightarrow{J_2}·{\overrightarrow{E}}_1^{\left[4\right]}=-{\displaystyle \frac{k}{2c^4}}\int d^{3}x\overrightarrow{J_2}\left(\overrightarrow{x}\right)·\int d^3{x}_1\left[{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_1\left({\overrightarrow{x}}_1\right)R_1^2{\widehat{R}}_1+{\partial }_t^3\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)R_1\right].$$

(214)

Changing the integration symbol from $\overrightarrow{x}$ to ${\overrightarrow{x}}_2$, this takes the form of:

$$I_1={\displaystyle \frac{k}{2c^4}}\int d^3{x}_1{d}^3{x}_{2}R\left[{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_1\left({\overrightarrow{x}}_1\right)\left(\overrightarrow{J_2}\left(\overrightarrow{x_2}\right)·\overrightarrow{R}\right)-{\partial }_t^3\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\overrightarrow{J_2}\left(\overrightarrow{x_2}\right)\right].$$

(215)

Exchanging the indices 1 and 2, we obtain the second integral of equation (212):

$$I_2={\displaystyle \frac{k}{2c^4}}\int d^3{x}_1{d}^3{x}_{2}R\left[-{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_2\left({\overrightarrow{x}}_2\right)\left(\overrightarrow{J_1}\left(\overrightarrow{x_1}\right)·\overrightarrow{R}\right)-{\partial }_t^3\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·\overrightarrow{J_1}\left(\overrightarrow{x_1}\right)\right].$$

(216)

Adding the contributions, we finally obtain the fourth order power expression:

$$\begin{array}{ccc}\hfill Powe{r}_{12}^{\left[4\right]}& =& {\displaystyle \frac{k}{2c^4}}\int d^3{x}_1{d}^3{x}_{2}R\left[{\displaystyle \frac{1}{4}}\left({\partial }_t^4{\rho }_1\left({\overrightarrow{x}}_1\right)\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)-{\partial }_t^4{\rho }_2\left({\overrightarrow{x}}_2\right)\overrightarrow{J_1}\left(\overrightarrow{x_1}\right)\right)·\overrightarrow{R}\right.\hfill \\ & -& \left.\left({\partial }_t^3\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\overrightarrow{J_2}\left(\overrightarrow{x_2}\right)+{\partial }_t^3\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)·\overrightarrow{J_1}\left(\overrightarrow{x_1}\right)\right).\right]\hfill \end{array}$$

(217)

4.5.2. Poynting Vector

Next, we analyze the Poynting vector for $n=4$ using equation (32):

$${\overrightarrow{S}}_{P12}^{\left[4\right]}={ϵ}_0{c}^2\sum _{k=0}^6\left({\overrightarrow{E}}_1^{[6-k]}\times {\overrightarrow{B}}_2^{\left[k\right]}+{\overrightarrow{E}}_2^{[6-k]}\times {\overrightarrow{B}}_1^{\left[k\right]}\right)$$

(218)

according to equation (172) the Poynting vector takes the following fourth order form:

$$\begin{array}{c}\hfill {\overrightarrow{S}}_{P12}^{\left[4\right]}={ϵ}_0{c}^2\left({\overrightarrow{E}}_1^{\left[4\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{E}}_2^{\left[4\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}+{\overrightarrow{E}}_1^{\left[2\right]}\times {\overrightarrow{B}}_2^{\left[4\right]}+{\overrightarrow{E}}_2^{\left[2\right]}\times {\overrightarrow{B}}_1^{\left[4\right]}+{\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[6\right]}+{\overrightarrow{E}}_2^{\left[0\right]}\times {\overrightarrow{B}}_1^{\left[6\right]}\right).\end{array}$$

(219)

Poynting flux on a far away sphere of radius $R_{max}$ is given by:

$$P{F}^{\left[4\right]}=\oint {\overrightarrow{S}}_{P12}^{\left[4\right]}·\widehat{n}da=R_{max}^2{\oint }_{R_{max}}{\overrightarrow{S}}_{P12}^{\left[4\right]}·\widehat{r}d\mathrm{\Omega }.$$

(220)

For each of the terms appearing in equation (219) we may write a Poynting flux, thus we obtain:

$$P{F}^{\left[4\right]}=P{F}_1^{\left[4\right]}+P{F}_2^{\left[4\right]}+P{F}_3^{\left[4\right]}+P{F}_4^{\left[4\right]}+P{F}_5^{\left[4\right]}+P{F}_6^{\left[4\right]}.$$

(221)

Let us now calculate the first term $P{F}_1^{\left[4\right]}$:

$$\begin{array}{c}\hfill P{F}_1^{\left[4\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[4\right]}\times {\overrightarrow{B}}_2^{\left[2\right]}\right)·\widehat{r}d\mathrm{\Omega }.\end{array}$$

(222)

Calculating the electric field on a far away sphere, we may write equation (213) in the asymptotic form:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[4\right]}=-{\displaystyle \frac{k}{2c^4}}\left[{\displaystyle \frac{1}{4}}\int d^3{x}_1\left({\partial }_t^4{\rho }_1\left((R_{max}^2\widehat{r}-R_{max}\left(({\overrightarrow{x}}_1·\widehat{r})\widehat{r}+{\overrightarrow{x}}_1\right)\right)\right)+R_{max}\int d^3{x}_1{\partial }_t^3\overrightarrow{J_1}\right].$$

(223)

Taking into account equation (119), we obtain:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[4\right]}={\displaystyle \frac{k{R}_{max}}{2c^4}}\left[{\displaystyle \frac{1}{4}}\int d^3{x}_1\left({\partial }_t^4{\rho }_1\left(({\overrightarrow{x}}_1·\widehat{r})\widehat{r}+{\overrightarrow{x}}_1\right)\right)-\int d^3{x}_1{\partial }_t^3\overrightarrow{J_1}\right].$$

(224)

As current density integrals are related to charge density integrals through equation (D.5), it follows that:

$$\begin{array}{ccc}\hfill \underset{r\to R_{max}}{lim}{\overrightarrow{E}}_1^{\left[4\right]}& =& {\displaystyle \frac{k{R}_{max}}{2c^4}}\left[{\displaystyle \frac{1}{4}}\left((\int d^3{x}_1{\partial }_t^3{\overrightarrow{J}}_1·\widehat{r})\widehat{r}+\int d^3{x}_1{\partial }_t^3{\overrightarrow{J}}_1\right)-\int d^3{x}_1{\partial }_t^3\overrightarrow{J_1}\right]\hfill \\ & =& {\displaystyle \frac{k{R}_{max}}{2c^4}}\left[{\displaystyle \frac{1}{4}}(\int d^3{x}_1{\partial }_t^3{\overrightarrow{J}}_1·\widehat{r})\widehat{r}-{\displaystyle \frac{3}{4}}\int d^3{x}_1{\partial }_t^3\overrightarrow{J_1}\right].\hfill \end{array}$$

(225)

The asymptotic expression for $B_2^{\left[2\right]}$ is given in equation (144). Using the asymptotic expressions, we are now in a position to calculate $P{F}_1^{\left[4\right]}$. Taking into account that radial components of either the electric or magnetic field do not contribute to the Poynting flux we obtain the following expression:

$$\begin{array}{cc}\hfill P{F}_1^{\left[4\right]}& ={\displaystyle \frac{3k{R}_{max}}{32\pi c^4}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t^3\overrightarrow{J_1}\times \left(\widehat{r}\times \overrightarrow{J_2}\right)\right)\right]·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & ={\displaystyle \frac{3k{R}_{max}}{32\pi c^4}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\widehat{r}\left({\partial }_t^3\overrightarrow{J_1}·\overrightarrow{J_2}\right)-\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t^3\overrightarrow{J_1}·\widehat{r}\right)\overrightarrow{J_2}\right]·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & ={\displaystyle \frac{3k{R}_{max}}{32\pi c^4}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t^3\overrightarrow{J_1}·\overrightarrow{J_2}\right)-\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t^3\overrightarrow{J_1}·\widehat{r}\right)\left(\overrightarrow{J_2}·\widehat{r}\right)\right]d\mathrm{\Omega }\hfill \\ \hfill & ={\displaystyle \frac{3k{R}_{max}}{32\pi c^4}}\left[\int \int d^3{x}_1{d}^3{x}_{2}4\pi \left({\partial }_t^3\overrightarrow{J_1}·\overrightarrow{J_2}\right)-\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t^3{\overrightarrow{J_1}}^k\left(\oint {\widehat{r}}_k{\widehat{r}}_{l}d\mathrm{\Omega }\right){\overrightarrow{J_2}}^l\right)\right].\hfill \end{array}$$

(226)

Inserting equation (202) into equation (226), it follows that:

$$\begin{array}{cc}\hfill P{F}_1^{\left[4\right]}& ={\displaystyle \frac{3k{R}_{max}}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[\left({\partial }_t^3\overrightarrow{J_1}·\overrightarrow{J_2}\right)-{\displaystyle \frac{1}{3}}\left({\partial }_t^3{\overrightarrow{J_1}}^k{\delta }_{kl}{\overrightarrow{J_2}}^l\right)\right].\hfill \end{array}$$

(227)

$$\begin{array}{cc}\hfill P{F}_1^{\left[4\right]}& ={\displaystyle \frac{k{R}_{max}}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2{\partial }_t^3\overrightarrow{J_1}·\overrightarrow{J_2}.\hfill \end{array}$$

(228)

Similarly, the second integral of the Poynting flux takes the form:

$$\begin{array}{c}\hfill P{F}_2^{\left[4\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_2^{\left[4\right]}\times {\overrightarrow{B}}_1^{\left[2\right]}\right)·\widehat{r}d\mathrm{\Omega }={\displaystyle \frac{k{R}_{max}}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2{\partial }_t^3\overrightarrow{J_2}·\overrightarrow{J_1}.\end{array}$$

(229)

We now proceed to calculate:

$$P{F}_3^{\left[4\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[2\right]}\times {\overrightarrow{B}}_2^{\left[4\right]}\right)·\widehat{r}d\mathrm{\Omega }.$$

(230)

The fourth order term of the magnetic field can be calculated using the asymptotic limit of Equation (61) of [12]:

$$\underset{r\to R_{max}}{lim}{\overrightarrow{B}}_2^{\left[4\right]}\left(\overrightarrow{x}\right)={\displaystyle \frac{k}{2c^4}}\widehat{r}\times \int d^3{x}_2{\partial }_t^2\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right).$$

(231)

Using the asymptotic form of the second order electric field given in equation (142), and recalling that the radial part of any field does not contribute to the Poynting flux we now obtain:

$$\begin{array}{cc}\hfill P{F}_3^{\left[4\right]}& =-{\displaystyle \frac{k{R}_{max}}{16\pi c^4}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left({\partial }_t\overrightarrow{J_1}\times \left(\widehat{r}\times {\partial }_t^2\overrightarrow{J_2}\right)\right)\right]·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{k{R}_{max}}{16\pi c^4}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left(\widehat{r}({\partial }_t\overrightarrow{J_1}·{\partial }_t^2\overrightarrow{J_2})-({\partial }_t\overrightarrow{J_1}·\widehat{r}){\partial }_t^2\overrightarrow{J_2}\right)\right]·\widehat{r}d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{k{R}_{max}}{16\pi c^4}}\oint \left[\int \int d^3{x}_1{d}^3{x}_2\left(({\partial }_t\overrightarrow{J_1}·{\partial }_t^2\overrightarrow{J_2})-({\partial }_t\overrightarrow{J_1}·\widehat{r})({\partial }_t^2\overrightarrow{J_2}·\widehat{r}\right)\right]d\mathrm{\Omega }\hfill \\ \hfill & =-{\displaystyle \frac{k{R}_{max}}{16\pi c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[4\pi ({\partial }_t\overrightarrow{J_1}·{\partial }_t^2\overrightarrow{J_2})-\left({\partial }_t{\overrightarrow{J_1}}^k\left(\oint {\widehat{r}}_k{\widehat{r}}_{l}d\mathrm{\Omega }\right){\partial }_t^2{\overrightarrow{J_2}}^l\right)\right].\hfill \end{array}$$

(232)

Using equation (202), we obtain:

$$\begin{array}{ccc}\hfill P{F}_3^{\left[4\right]}& =& -{\displaystyle \frac{k{R}_{max}}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\partial }_t\overrightarrow{J_1}·{\partial }_t^2\overrightarrow{J_2}-{\displaystyle \frac{1}{3}}{\partial }_t{\overrightarrow{J_1}}^k{\delta }_{kl}{\partial }_t^2{\overrightarrow{J_2}}^l\right]\hfill \\ & =& -{\displaystyle \frac{k{R}_{max}}{6c^4}}\int \int d^3{x}_1{d}^3{x}_2{\partial }_t\overrightarrow{J_1}·{\partial }_t^2\overrightarrow{J_2}.\hfill \end{array}$$

(233)

In a Similar manner:

$$P{F}_4^{\left[4\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_2^{\left[2\right]}\times {\overrightarrow{B}}_1^{\left[4\right]}\right)·\widehat{r}d\mathrm{\Omega }=-{\displaystyle \frac{k{R}_{max}}{6c^4}}\int \int d^3{x}_1{d}^3{x}_2{\partial }_t\overrightarrow{J_2}·{\partial }_t^2\overrightarrow{J_1}.$$

(234)

Subsequently, we calculate the fifth and sixth contributions appearing in equation (221):

$$P{F}_5^{\left[4\right]}=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}\left({\overrightarrow{E}}_1^{\left[0\right]}\times {\overrightarrow{B}}_2^{\left[6\right]}\right)·\widehat{r}d\mathrm{\Omega }=R_{max}^2{ϵ}_0{c}^2{\oint }_{R_{max}}{\overrightarrow{B}}_2^{\left[6\right]}·\left(\widehat{r}\times {\overrightarrow{E}}_1^{\left[0\right]}\right)d\mathrm{\Omega }.$$

(235)

The asymptotic form of the zeroth order electric field is given in equation (149) and has only a radial component hence it follows that:

$$P{F}_5^{\left[4\right]}=P{F}_6^{\left[4\right]}=0.$$

(236)

Thus by inserting equation (228), equation (229), equation (233), equation (234), and equation (236) into equation (221), we obtain the total Poynting flux contribution of the fourth order in ${\displaystyle \frac{1}{c}}$:

$$P{F}^{\left[4\right]}={\displaystyle \frac{k{R}_{max}}{2c^4}}\int \int d^3{x}_1{d}^3{x}_2\left({\displaystyle \frac{1}{2}}\left({\partial }_t^3\overrightarrow{J_1}·\overrightarrow{J_2}+{\partial }_t^3\overrightarrow{J_2}·\overrightarrow{J_1}\right)-{\displaystyle \frac{1}{3}}\left({\partial }_t\overrightarrow{J_1}·{\partial }_t^2\overrightarrow{J_2}+{\partial }_t\overrightarrow{J_2}·{\partial }_t^2\overrightarrow{J_1}\right)\right).$$

(237)

4.5.3. Field Energy

Now, the contribution of the field energy to the energy balance at fourth order is evaluated as follows:

$$E_{field12}^{\left[4\right]}={ϵ}_0\int \left(\sum _{k=0}^4{\overrightarrow{E}}_1^{[4-k]}·{\overrightarrow{E}}_2^{\left[k\right]}+c^2\sum _{k=0}^6{\overrightarrow{B}}_1^{[6-k]}·{\overrightarrow{B}}_2^{\left[k\right]}\right)d^{3}x.$$

(238)

Taking into account equation (172) the field energy simplifies as follows:

$$\begin{array}{c}\hfill E_{field12}^{\left[4\right]}={ϵ}_0\int \left[{\overrightarrow{E}}_1^{\left[4\right]}·{\overrightarrow{E}}_2^{\left[0\right]}+{\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[4\right]}+{\overrightarrow{E}}_1^{\left[2\right]}·{\overrightarrow{E}}_2^{\left[2\right]}+c^2\left({\overrightarrow{B}}_1^{\left[4\right]}·{\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{B}}_1^{\left[2\right]}·{\overrightarrow{B}}_2^{\left[4\right]}\right)\right]d^{3}x.\end{array}$$

(239)

This can be separated into a sum of terms, such that for each term the integral is calculated separately:

$$\begin{array}{cc}\hfill i_1& ={ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[4\right]}·{\overrightarrow{E}}_2^{\left[0\right]}\right)d^{3}x\hfill \\ \hfill & ={ϵ}_0\int \left[\left(-\left({\displaystyle \frac{k}{2c^4}}\right)\int d^3{x}_1\left[{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_1{R}_1^2{\widehat{R}}_1+{\partial }_t^3\overrightarrow{J_1}{R}_1\right]\right)·\left(k\int d^3{x}_2{\displaystyle \frac{{\rho }_2}{R_2^2}}{\widehat{R}}_2\right)\right]d^{3}x.\hfill \end{array}$$

(240)

Or in the form:

$$\begin{array}{ccc}\hfill i_1& =& -{\displaystyle \frac{k}{8\pi c^4}}\int \left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_1{\rho }_2\left(R_1^2{\widehat{R}}_1·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)\right.\hfill \\ & +& \left.\int \int d^3{x}_1{d}^3{x}_2{\rho }_2{\partial }_t^3\overrightarrow{J_1}·\left(R_1{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)\right]d^{3}x\hfill \end{array}$$

(241)

The following expression simplifies with the aid of equation (C.3) as follows:

$$\int {\displaystyle \frac{R_1{\widehat{R}}_2}{R_2^2}}{d}^{3}x=\int R_1{\overrightarrow{\nabla }}_2{\displaystyle \frac{1}{R_2}}{d}^{3}x={\overrightarrow{\nabla }}_2\int {\displaystyle \frac{R_1}{R_2}}{d}^{3}x=\pi R^2\widehat{R}.$$

(242)

Now let us evaluate the term:

$$i_{2f}\equiv \int d^{3}x\left(R_1^2{\widehat{R}}_1·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\right)=-\int R_1{\overrightarrow{R}}_1·\overrightarrow{\nabla }{\displaystyle \frac{1}{R_2}}{d}^{3}x,$$

(243)

this can also be written in the form:

$$i_{2f}=-\int \left[\overrightarrow{\nabla }·\left({\displaystyle \frac{R_1{\overrightarrow{R}}_1}{R_2}}\right)-{\displaystyle \frac{1}{R_2}}\overrightarrow{\nabla }·\left(R_1{\overrightarrow{R}}_1\right)\right]d^{3}x=-\int \overrightarrow{\nabla }·\left({\displaystyle \frac{R_1{\overrightarrow{R}}_1}{R_2}}\right)d^{3}x+4\int {\displaystyle \frac{R_1}{R_2}}{d}^{3}x.$$

(244)

Using Gauss theorem we can recast $i_{2f}$ in the form:

$$i_{2f}=-\oint d\overrightarrow{S}·\left({\displaystyle \frac{R_1{\overrightarrow{R}}_1}{R_2}}\right)+4\int {\displaystyle \frac{R_1}{R_2}}{d}^{3}x.$$

(245)

Calculating the surface integral on a far away spherical surface of radius $R_{max}$ and assuming that all currents and charges are close to the origin of axis with distances much smaller than $R_{max}$ such that: $R_1\simeq R_2\simeq R_{max}$ and ${\overrightarrow{R}}_1\simeq R_{max}\widehat{r}$, we thus obtain:

$$\oint d\overrightarrow{S}·\left({\displaystyle \frac{R_1{\overrightarrow{R}}_1}{R_2}}\right)=\oint R_{max}^{2}d\mathrm{\Omega }\widehat{r}·\left({\displaystyle \frac{R_1{\overrightarrow{R}}_1}{R_2}}\right)\simeq \oint R_{max}^{2}d\mathrm{\Omega }{R}_{max}\widehat{r}·\widehat{r}=4\pi R_{max}^3.$$

(246)

Hence using equation (C.3) it follows that:

$$i_{2f}=-4\pi R_{max}^3+4\int {\displaystyle \frac{R_1}{R_2}}{d}^{3}x=-4\pi R_{max}^3+{\displaystyle \frac{4\pi }{3}}\left(4R_{max}^3-R^3\right)={\displaystyle \frac{4\pi }{3}}\left(R_{max}^3-R^3\right).$$

(247)

We now can write the triple volume integral given in equation (241) as a double volume integral:

$$\begin{array}{ccc}\hfill i_1& =& -{\displaystyle \frac{k}{8\pi c^4}}\left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{1}{4}}{\partial }_t^4{\rho }_1{\rho }_2\left({\displaystyle \frac{4\pi }{3}}\left(R_{max}^3-R^3\right)\right)\right.\hfill \\ & +& \left.\int \int d^3{x}_1{d}^3{x}_2{\rho }_2{\partial }_t^3\overrightarrow{J_1}·\left(\pi R^2\widehat{R}\right)\right].\hfill \end{array}$$

(248)

Or more simply as:

$$i_1=-{\displaystyle \frac{k}{8c^4}}\left[\int \int d^3{x}_1{d}^3{x}_2{\partial }_t^4{\rho }_1{\rho }_2\left({\displaystyle \frac{1}{3}}\left(R_{max}^3-R^3\right)\right)+\int \int d^3{x}_1{d}^3{x}_2{\rho }_2{\partial }_t^3\overrightarrow{J_1}·\left(R^2\widehat{R}\right)\right].$$

(249)

Now for the $R_{max}^3$ term, the double volume integrals decouple, and following equation (119), we obtain:

$$i_1={\displaystyle \frac{k}{8c^4}}\left[\int \int d^3{x}_1{d}^3{x}_2{\partial }_t^4{\rho }_1{\rho }_2\left({\displaystyle \frac{1}{3}}{R}^3\right)-\int \int d^3{x}_1{d}^3{x}_2{\rho }_2{\partial }_t^3\overrightarrow{J_1}·\left(R^2\widehat{R}\right)\right].$$

(250)

Let us look at the term:

$$i_{1a}=\int d^3{x}_1{\partial }_t^3\overrightarrow{J_1}·\left(R^2\widehat{R}\right)={\displaystyle \frac{1}{3}}\int d^3{x}_1{\partial }_t^3{\overrightarrow{J}}_1·{\overrightarrow{\nabla }}_1{R}^3.$$

(251)

This can be written in the form:

$$i_{1a}={\displaystyle \frac{1}{3}}\int d^3{x}_1\left[{\overrightarrow{\nabla }}_1·\left({\partial }_t^3\overrightarrow{J_1}{R}^3\right)-R^3{\partial }_t^3{\overrightarrow{\nabla }}_1·{\overrightarrow{J}}_1\right].$$

(252)

Using Gauss theorem and the continuity equation (43) this can be written as:

$$i_{1a}={\displaystyle \frac{1}{3}}\left[\oint d{\overrightarrow{S}}_1·\left({\partial }_t^3\overrightarrow{J_1}{R}^3\right)+\int d^3{x}_1{R}^3{\partial }_t^4{\rho }_1\right].$$

(253)

Assuming no currents at far away surfaces this reduces to:

$$i_{1a}={\displaystyle \frac{1}{3}}\int d^3{x}_1{R}^3{\partial }_t^4{\rho }_1.$$

(254)

Plugging $i_{1a}$ back into equation (250), we obtain:

$${ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[4\right]}·{\overrightarrow{E}}_2^{\left[0\right]}\right)d^{3}x=i_1=0.$$

(255)

In a similar fashion, the second integral of equation (239) is obtained by interchanging the indices:

$$i_2={ϵ}_0\int \left({\overrightarrow{E}}_2^{\left[4\right]}·{\overrightarrow{E}}_1^{\left[0\right]}\right)d^{3}x=0.$$

(256)

Next we calculate using equation (82):

$$\begin{array}{ccc}\hfill i_3& =& {ϵ}_0\int \left({\overrightarrow{E}}_1^{\left[2\right]}·{\overrightarrow{E}}_2^{\left[2\right]}\right)d^{3}x={ϵ}_0\int \left(-{\displaystyle \frac{k}{c^2}}\int d^3{x}_1\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1{\widehat{R}}_1+{\partial }_t\overrightarrow{J_1}{R}_1^{-1}\right]\right)\hfill \\ & ·& \left(-{\displaystyle \frac{k}{c^2}}\int d^3{x}_2\left[{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\widehat{R}}_2+{\partial }_t\overrightarrow{J_2}{R}_2^{-1}\right]\right)d^{3}x.\hfill \end{array}$$

(257)

Which can be cast in the form:

$$\begin{array}{cc}\hfill i_3& ={\displaystyle \frac{k}{4\pi c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{4}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left(\int d^{3}x{\widehat{R}}_1·{\widehat{R}}_2\right)+{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1{\partial }_t\overrightarrow{J_2}·\left(\int {\displaystyle \frac{{\widehat{R}}_1}{R_2}}{d}^{3}x\right)\right.\hfill \\ \hfill & \left.+{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\partial }_t\overrightarrow{J_1}·\left(\int {\displaystyle \frac{{\widehat{R}}_2}{R_1}}{d}^{3}x\right)+{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(\int {\displaystyle \frac{1}{R_1{R}_2}}{d}^{3}x\right)\right].\hfill \end{array}$$

(258)

To reduce the above triple volume integral into a double volume integral we notice that by using equation (C.3) it follows that:

$$\int {\displaystyle \frac{{\widehat{R}}_1}{R_2}}{d}^{3}x=-\int {\displaystyle \frac{{\overrightarrow{\nabla }}_1{R}_1}{R_2}}{d}^{3}x=-{\overrightarrow{\nabla }}_1\int {\displaystyle \frac{R_1}{R_2}}{d}^{3}x=-{\overrightarrow{\nabla }}_1\left({\displaystyle \frac{\pi }{3}}\left(4R_{max}^3-R^3\right)\right)=\pi R^2\widehat{R}.$$

(259)

Exchanging the 1 and 2 indices, we obtain:

$$\int {\displaystyle \frac{{\widehat{R}}_2}{R_1}}{d}^{3}x=-\pi R^2\widehat{R}.$$

(260)

Taking into account equation (B.6), it follows that:

$$\int \left({\displaystyle \frac{1}{R_1{R}_2}}\right)d^{3}x=2\pi \left(2R_{max}-R\right).$$

(261)

The following integral can be computed using methods similar to those used in Appendix A such that:

$$\int d^{3}x{\widehat{R}}_1·{\widehat{R}}_2=2\pi R^3{\int }_0^{y_{max}}{y}^{2}dy{\int }_{-1}^1{\displaystyle \frac{y+s}{\sqrt{1+y^2+2ys}}}ds.$$

(262)

Using equation (108) and equation (109), we obtain:

$$\int d^{3}x{\widehat{R}}_1·{\widehat{R}}_2=2\pi R^3\left[{\displaystyle \frac{1}{3}}+{\displaystyle \frac{2}{3}}\left(y_{max}^3-y_{max}\right)\right]={\displaystyle \frac{2}{3}}\pi \left(2R_{max}^3-2R^2{R}_{max}+R^3\right).$$

(263)

Thus:

$$\begin{array}{ccc}\hfill & i_3& ={\displaystyle \frac{k}{4\pi c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{4}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left({\displaystyle \frac{2}{3}}\pi \left(2R_{max}^3-2R^2{R}_{max}+R^3\right)\right)\right.\hfill \\ \hfill & +& {\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1{\partial }_t\overrightarrow{J_2}·\left(\pi R^2\widehat{R}\right)+\left.{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\partial }_t\overrightarrow{J_1}·\left(-\pi R^2\widehat{R}\right)+{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2\pi \left(2R_{max}-R\right)\right)\right].\hfill \end{array}$$

(264)

Which can be slightly simplified:

$$\begin{array}{ccc}\hfill & i_3& ={\displaystyle \frac{k}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{4}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left({\displaystyle \frac{2}{3}}\left(2R_{max}^3-2R^2{R}_{max}+R^3\right)\right)\right.\hfill \\ \hfill & +& {\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1{\partial }_t\overrightarrow{J_2}·\left(R^2\widehat{R}\right)-\left.{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\partial }_t\overrightarrow{J_1}·\left(R^2\widehat{R}\right)+{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2\left(2R_{max}-R\right)\right)\right].\hfill \end{array}$$

(265)

The $R_{max}^3$ term decouples into a multiplication of two volume integrals and thus by equation (119) vanishes, thus we obtain:

$$\begin{array}{ccc}& i_3& ={\displaystyle \frac{k}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{4}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left({\displaystyle \frac{2}{3}}\left(R^3-2R^2{R}_{max}\right)\right)\right.\hfill \\ & +& {\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1{\partial }_t\overrightarrow{J_2}·\left(R^2\widehat{R}\right)-\left.{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\partial }_t\overrightarrow{J_1}·\left(R^2\widehat{R}\right)+{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2\left(2R_{max}-R\right)\right)\right].\hfill \end{array}$$

(266)

The above can also be written in the following form:

$$\begin{array}{ccc}& i_3& ={\displaystyle \frac{k}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{6}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left(R^3-2R^2{R}_{max}\right)\right.-{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_1{\partial }_t\overrightarrow{J_2}·\left({\displaystyle \frac{1}{3}}{\overrightarrow{\nabla }}_2{R}^3\right)\hfill \\ & -& \left.{\displaystyle \frac{1}{2}}{\partial }_t^2{\rho }_2{\partial }_t\overrightarrow{J_1}·\left({\displaystyle \frac{1}{3}}{\overrightarrow{\nabla }}_1{R}^3\right)+2{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2R_{max}-R\right)\right].\hfill \end{array}$$

(267)

Now:

$$\int d^3{x}_1{\partial }_t\overrightarrow{J_1}·{\overrightarrow{\nabla }}_1{R}^3=\int d^3{x}_1\left[{\overrightarrow{\nabla }}_1\left(·{\partial }_t\overrightarrow{J_1}{R}^3\right)-R^3{\partial }_t{\overrightarrow{\nabla }}_1·{\overrightarrow{J}}_1\right].=\oint d{\overrightarrow{S}}_1·\overrightarrow{J_1}{R}^3+\int d^3{x}_1{R}^3{\partial }_t^2{\rho }_1.$$

(268)

In which we have used Gauss theorem and the continuity equation (43). Taking a far away encapsulating surface in which no currents are to be found, it follows that:

$$\int d^3{x}_1{\partial }_t\overrightarrow{J_1}·{\overrightarrow{\nabla }}_1{R}^3=\int d^3{x}_1{R}^3{\partial }_t^2{\rho }_1.$$

(269)

Similarly:

$$\int d^3{x}_2{\partial }_t\overrightarrow{J_2}·{\overrightarrow{\nabla }}_2{R}^3=\int d^3{x}_2{R}^3{\partial }_t^2{\rho }_2.$$

(270)

Plugging equation (269) and equation (270) into equation (268) we obtain the simplified expression:

$$i_3={\displaystyle \frac{k}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{6}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left(R^3+2R^2{R}_{max}\right)+2{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2R_{max}-R\right)\right].$$

(271)

To summarize the electric part of the fourth order electromagnetic energy can be written in terms of the temporal derivatives of charge and current densities in the form:

$$\begin{array}{ccc}\hfill & & E_{field12electric}^{\left[4\right]}={ϵ}_0\int \left[{\overrightarrow{E}}_1^{\left[4\right]}·{\overrightarrow{E}}_2^{\left[0\right]}+{\overrightarrow{E}}_1^{\left[0\right]}·{\overrightarrow{E}}_2^{\left[4\right]}+{\overrightarrow{E}}_1^{\left[2\right]}·{\overrightarrow{E}}_2^{\left[2\right]}\right]d^{3}x\hfill \\ \hfill & =& {\displaystyle \frac{k}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{6}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left(R^3+2R^2{R}_{max}\right)+2{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2R_{max}-R\right)\right].\hfill \end{array}$$

(272)

We remind the reader that $R_{max}$ is the maximal radius for which the Taylor series expansion is applicable. Ir remains to calculate the magnetic terms contributions, a task which we shall now attend to. Set:

$$i_4={ϵ}_0{c}^2\int \left({\overrightarrow{B}}_1^{\left[4\right]}·{\overrightarrow{B}}_2^{\left[2\right]}\right)d^{3}x$$

(273)

Now by Equation (61) of [12]:

$${\overrightarrow{B}}_1^{\left[4\right]}\left(\overrightarrow{x}\right)={\displaystyle \frac{k}{2c^4}}\int d^3{x}_1{\widehat{R}}_1\times {\partial }_t^2\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right),$$

(274)

$${\overrightarrow{B}}_2^{\left[2\right]}\left(\overrightarrow{x}\right)=-{\displaystyle \frac{k}{c^2}}\int d^3{x}_2{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}\times \overrightarrow{J_2}\left({\overrightarrow{x}}_2\right).$$

(275)

Plugging equation (274) and equation (275) into equation (273) it follows that:

$$i_4=-{\displaystyle \frac{k}{8\pi c^4}}\int \left[\int \int d^3{x}_1{d}^3{x}_2{\displaystyle \frac{\left({\widehat{R}}_1\times {\partial }_t^2\overrightarrow{J_1}\right)·\left({\widehat{R}}_2\times \overrightarrow{J_2}\right)}{R_2^2}}\right]d^{3}x.$$

(276)

By a well known vector identity:

$$({\widehat{R}}_1\times {\partial }_t^2\overrightarrow{J_1})·({\widehat{R}}_2\times \overrightarrow{J_2})=({\widehat{R}}_1·{\widehat{R}}_2)({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})-({\widehat{R}}_1·\overrightarrow{J_2})({\widehat{R}}_2·{\partial }_t^2\overrightarrow{J_1}),$$

(277)

we may write equation (276) in the form:

$$\begin{array}{cc}\hfill i_4=& -{\displaystyle \frac{k}{8\pi c^4}}\left[\int \int d^3{x}_1{d}^3{x}_2({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})\left(\int {\displaystyle \frac{{\widehat{R}}_1·{\widehat{R}}_2}{R_2^2}}{d}^{3}x\right)\right.\hfill \\ \hfill & \left.-\int d^{3}x\left(\int d^3{x}_1{\partial }_t^2\overrightarrow{J_1}·{\widehat{R}}_1\right)\left(\int d^3{x}_2{\displaystyle \frac{\overrightarrow{J_2}·{\widehat{R}}_2}{R_2^2}}\right)\right].\hfill \end{array}$$

(278)

Notice that:

$$\begin{array}{ccc}\hfill \int d^3{x}_1{\partial }_t^2\overrightarrow{J_1}·{\widehat{R}}_1& =& -\int d^3{x}_1{\partial }_t^2\overrightarrow{J_1}·{\overrightarrow{\nabla }}_1{R}_1=-\int d^3{x}_1\left[{\overrightarrow{\nabla }}_1·\left({\partial }_t^2\overrightarrow{J_1}{R}_1\right)-R_1{\partial }_t^2{\nabla }_1·\overrightarrow{J_1}\right]\hfill \\ & =& -\oint d{\overrightarrow{S}}_1·\left({\partial }_t^2\overrightarrow{J_1}{R}_1\right)-\int d^3{x}_1{R}_1{\partial }_t^3{\rho }_1=-\int d^3{x}_1{R}_1{\partial }_t^3{\rho }_1.\hfill \end{array}$$

(279)

In the above, we have used the Gauss theorem, assumed that there is no current density on far away surfaces, and used the continuity equation (43). Similarly:

$$\begin{array}{ccc}\hfill \int d^3{x}_2\overrightarrow{J_2}·{\displaystyle \frac{{\widehat{R}}_2}{R_2^2}}& =& \int d^3{x}_2\overrightarrow{J_2}·{\overrightarrow{\nabla }}_2{\displaystyle \frac{1}{R_2}}=\int d^3{x}_2\left[{\overrightarrow{\nabla }}_2·\left({\displaystyle \frac{\overrightarrow{J_2}}{R_2}}\right)-{\displaystyle \frac{1}{R_2}}{\overrightarrow{\nabla }}_2·{\overrightarrow{J}}_2\right]\hfill \\ & =& \oint d{\overrightarrow{S}}_2·{\displaystyle \frac{\overrightarrow{J_2}}{R_2}}+\int d^3{x}_2{\displaystyle \frac{{\partial }_t{\rho }_2}{R_2}}=\int d^3{x}_2{\displaystyle \frac{{\partial }_t{\rho }_2}{R_2}}.\hfill \end{array}$$

(280)

Plugging equation (110), equation (279) and equation (280) into equation (278), we arrive at the expression:

$$\begin{array}{ccc}\hfill i_4& =& -{\displaystyle \frac{k}{8\pi c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})\left(4\pi \left(R_{max}-R\right)\right)-\int d^{3}x\left(-R_1{\partial }_t^3{\rho }_1\right)\left({\displaystyle \frac{1}{R_2}}{\partial }_t{\rho }_2\right)\right]\hfill \\ & =& -{\displaystyle \frac{k}{8\pi c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})\left(4\pi \left(R_{max}-R\right)\right)+\left({\partial }_t^3{\rho }_1{\partial }_t{\rho }_2\right)\int d^{3}x{\displaystyle \frac{R_1}{R_2}}\right].\hfill \end{array}$$

(281)

Taking into account equation (C.3), the above expression reduces to:

$$\begin{array}{ccc}\hfill i_4& =& -{\displaystyle \frac{k}{8\pi c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})\left(4\pi \left(R_{max}-R\right)\right)+\left({\partial }_t^3{\rho }_1{\partial }_t{\rho }_2\right){\displaystyle \frac{\pi }{3}}\left(4R_{max}^3-R^3\right)\right]\hfill \\ & =& -{\displaystyle \frac{k}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[4({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})\left(R_{max}-R\right)+{\displaystyle \frac{1}{3}}\left({\partial }_t^3{\rho }_1{\partial }_t{\rho }_2\right)\left(4R_{max}^3-R^3\right)\right].\hfill \end{array}$$

(282)

The term containing $R_{max}^3$ decouple into a multiplication of two volume integrals. However, by equation (119) and due to the fact that we assume no current density on the far away encapsulating surface it follows that: $\int d^3{x}_1{\partial }_t^3{\rho }_1=0$ and $\int d^3{x}_2{\partial }_t{\rho }_2=0$. We thus obtain a simplified form of equation (282):

$$i_4={\displaystyle \frac{k}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[4\left(R-R_{max}\right)({\partial }_t^2\overrightarrow{J_1}·\overrightarrow{J_2})+{\displaystyle \frac{1}{3}}{R}^3\left({\partial }_t^3{\rho }_1{\partial }_t{\rho }_2\right)\right].$$

(283)

By analogy:

$${ϵ}_0{c}^2\int \left({\overrightarrow{B}}_2^{\left[4\right]}·{\overrightarrow{B}}_1^{\left[2\right]}\right)d^{3}x={\displaystyle \frac{k}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[4\left(R-R_{max}\right)({\partial }_t^2\overrightarrow{J_2}·\overrightarrow{J_1})+{\displaystyle \frac{1}{3}}{R}^3\left({\partial }_t^3{\rho }_2{\partial }_t{\rho }_1\right)\right].$$

(284)

Summing up equation (283) and equation (284) we arrive at the fourth order contribution to the magnetic field energy in terms of a double volume integral:

$$\begin{array}{ccc}\hfill & & E_{field12magnetic}^{\left[4\right]}={ϵ}_0{c}^2\int \left[{\overrightarrow{B}}_1^{\left[4\right]}·{\overrightarrow{B}}_2^{\left[2\right]}+{\overrightarrow{B}}_1^{\left[2\right]}·{\overrightarrow{B}}_2^{\left[4\right]}\right]d^{3}x=\hfill \\ \hfill & & {\displaystyle \frac{k}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[4(R-R_{max})({\partial }_t^2{\overrightarrow{J}}_2·{\overrightarrow{J}}_1+{\partial }_t^2{\overrightarrow{J}}_1·{\overrightarrow{J}}_2)+{\displaystyle \frac{1}{3}}{R}^3({\partial }_t^3{\rho }_2{\partial }_t{\rho }_1+{\partial }_t^3{\rho }_1{\partial }_t{\rho }_2)\right].\hfill \end{array}$$

(285)

Hence, adding the fourth order electric field energy given in equation (272) with the fourth order magnetic field energy contribution given in equation (285) we arrive at the total field fourth order energy:

$$\begin{array}{ccc}\hfill & & E_{field12}^{\left[4\right]}=E_{field12electric}^{\left[4\right]}+E_{field12magnetic}^{\left[4\right]}=\hfill \\ \hfill & & {\displaystyle \frac{k}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{3}}{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\left(R^3+2R^2{R}_{max}\right)+{\displaystyle \frac{1}{3}}{R}^3({\partial }_t^3{\rho }_2{\partial }_t{\rho }_1+{\partial }_t^3{\rho }_1{\partial }_t{\rho }_2)+\right.\hfill \\ & & \left.4{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\left(2R_{max}-R\right)+4(R-R_{max})({\partial }_t^2{\overrightarrow{J}}_2·{\overrightarrow{J}}_1+{\partial }_t^2{\overrightarrow{J}}_1·{\overrightarrow{J}}_2)\right].\hfill \end{array}$$

(286)

This expression can be partitioned into volume contribution and surface contribution, in which the later type of contributions involves $R_{max}$ designating the maximal distance to which our expansion is applicable and thus also the radius of the sphere in which our energy calculations are performed. Thus:

$$\begin{array}{ccc}& & E_{field12}^{\left[4\right]}=E_{field12volume}^{\left[4\right]}+E_{field12surface}^{\left[4\right]}\hfill \\ & & E_{field12volume}^{\left[4\right]}\equiv {\displaystyle \frac{k}{8c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[{\displaystyle \frac{1}{3}}{R}^3\left({\partial }_t^3{\rho }_2{\partial }_t{\rho }_1+{\partial }_t^3{\rho }_1{\partial }_t{\rho }_2-{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2\right)+\right.\hfill \\ & & \left.4R\left({\partial }_t^2{\overrightarrow{J}}_2·{\overrightarrow{J}}_1+{\partial }_t^2{\overrightarrow{J}}_1·{\overrightarrow{J}}_2-{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\right)\right].\hfill \\ & & E_{field12surface}^{\left[4\right]}\equiv {\displaystyle \frac{k{R}_{max}}{4c^4}}\int \int d^3{x}_1{d}^3{x}_2\left[-{\displaystyle \frac{1}{3}}{R}^2{\partial }_t^2{\rho }_1{\partial }_t^2{\rho }_2-2\left({\partial }_t^2{\overrightarrow{J}}_2·{\overrightarrow{J}}_1+{\partial }_t^2{\overrightarrow{J}}_1·{\overrightarrow{J}}_2-\right.\right.\hfill \\ & & \left.\left.2{\partial }_t\overrightarrow{J_1}·{\partial }_t\overrightarrow{J_2}\right)\right].\hfill \end{array}$$

(287)

It can be shown after a few lines of calculations that:

$${\displaystyle \frac{d{E}_{field12volume}^{\left[4\right]}}{dt}}=-Powe{r}_{12}^{\left[4\right]},$$

(288)

in which $Powe{r}_{12}^{\left[4\right]}$ is the mechanical work done by the system and is given in equation (217). For the surface term we may only write:

$${\displaystyle \frac{d{E}_{field12surface}^{\left[4\right]}}{dt}}\approx -P{F}^{\left[4\right]},$$

(289)

in which $P{F}^{\left[4\right]}$ is the Poynting Flux given in equation (237). Although both sides of equation (289) contain the same type of expressions the numerical factor are only of the same order of magnitude not identical, this is probably due to the crude approximations used in Section 4.5.2 and in the appendices. Notice, however, that this will not change the final results of the current paper.

5. Discussion

In order to verify the validity of the energy balance equation at various orders of approximation, we systematically evaluate the mechanical work, field energy, and Poynting vector contributions corresponding to successive terms in the Taylor expansion of the electromagnetic fields. Each term, labeled by the index n, represents a distinct order in the $1/c$ expansion and contributes differently to the total energy dynamics of the system. Below, we summarize the outcome of this analysis for $n=0$ through $n=4$, highlighting the nature of energy exchange and the role of radiation at each order. For $n=0$, the zeroth order energy equation is found to be satisfied. Mechanical work performed on or by the system leads to a corresponding increase or decrease in the field energy, as expected in the absence of any contribution from the Poynting vector. For $n=1$, we find that the first-order energy equation is trivially satisfied, that is, it reduces to the identity $0=0$ under the condition that the mechanical work, field energy, and Poynting contribution all vanish individually. A vanishing mechanical work implies that, to first order in $1/c$, no mechanical energy is either supplied to or extracted from the relativistic engine. Furthermore, the first-order terms in the $1/c$ expansion do not contribute to either the field energy or the Poynting vector associated with the engine. In other words, at first order, the electromagnetic fields neither store energy nor transport it through radiation or absorption, indicating the absence of any real energy exchange. For $n=2$, We conclude that the second-order energy equation is indeed balanced: the power associated with mechanical work equals the negative time derivative of the field energy, as expected in the absence of any Poynting contribution. In the case $n=3$, the absence of field energy implies that the electromagnetic field cannot store energy, leading to an energy balance strictly between radiation and mechanical work. Thus, incident radiation has the potential to drive charged particles to perform work. However, when the currents in the two subsystems are orthogonal, radiation is not emitted, and consequently, no work is done. It is also important to note that, if not properly configured, a relativistic motor may emit radiation. This behavior has been demonstrated in earlier studies involving uncharged relativistic motors [16]. For $n=4$, We conclude that the fourth-order energy balance holds. At this order, both the electric and magnetic field energies are influenced by the mechanical work. At the order of $1/c^4$, the structure of our series expansion limits our ability to evaluate the radiation flux at infinity. Instead, we must restrict our analysis to the radiation flux through a spherical surface of radius $R_{max}$, beyond which the validity of our approximation breaks down. We also notice that for terms dependent on $R_{max}$ the approximation we use here is not sufficient to exactly balance the terms of the energy change and the Poynting flux, for which a better approximation is required.

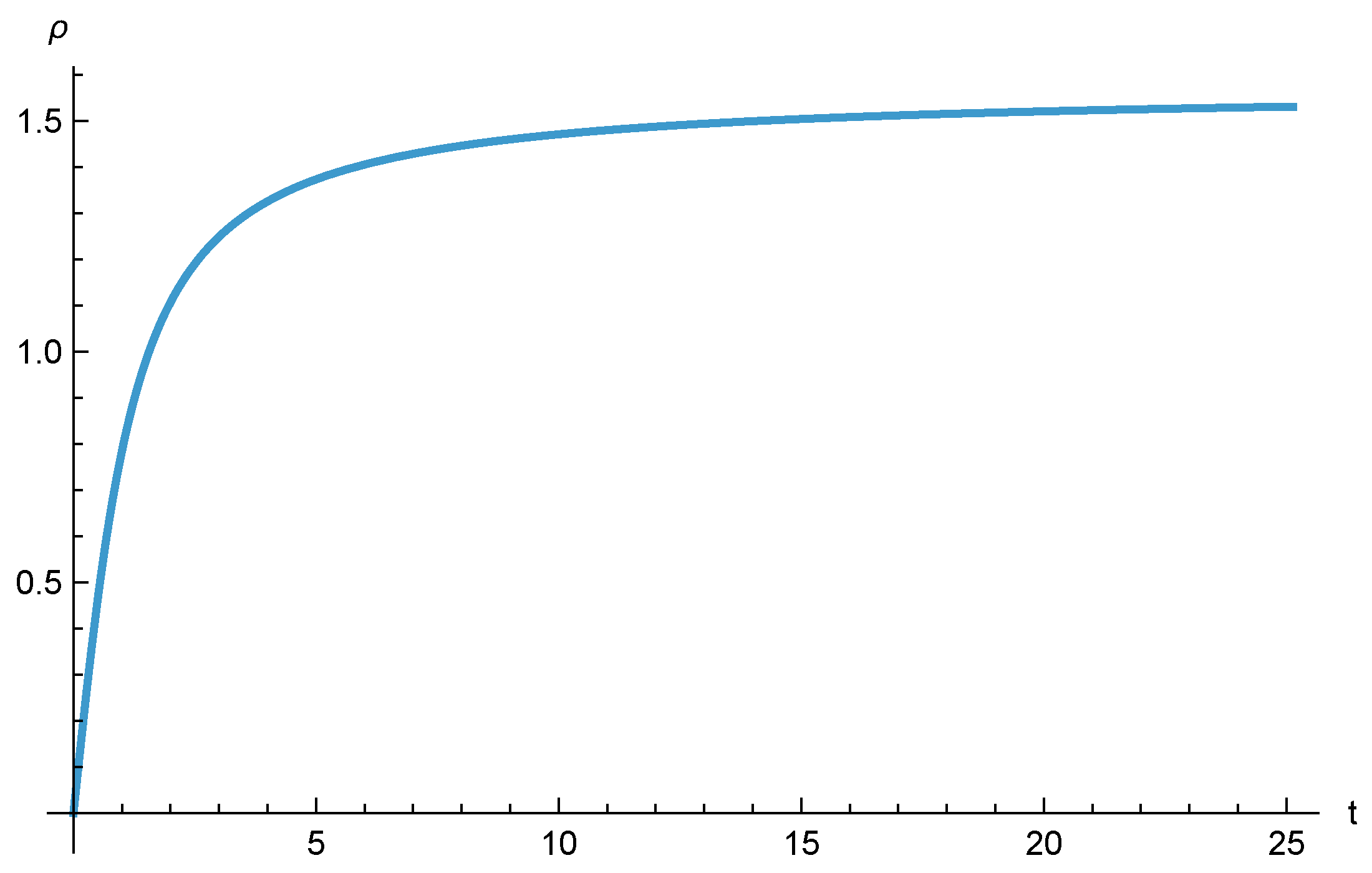
Our motivation for this study is to understand the energy exchange in a relativistic motor, however, for this motor one needs to consider only first order derivative of the charge density. On the other hand $n\ge 3$ terms in the energy equation depend on higher derivatives, this problem will be resolved in the next section.

6. The source of the Charged Retarded Field Engine Energy

So far our discussion was quite general, we have calculated the energy balance terms for various orders of $1/c^n$ up to $n=4$. We did not pay specific attention to the characteristics of the relativistic engine which we shall consider now. Suppose we have two static charge distributions consisting of a retarded field engine, and suppose one induces a time dependent change in one of the charge distributions generating momentum according to equation (8) after which the charge distribution becomes static again as in Figure 1.

Notice, that at this point we have two static charge distributions in the engine’s frame but not in the laboratory frame. In the laboratory frame the two subsystems connected with the engine are now moving with velocity ${\overrightarrow{v}}_s$ (see equation (10)) which is the velocity of the engine. The engine has gained a kinetic energy given by equation (9), we shall now inquire regarding the source of this energy.

Let $\overrightarrow{x}$ be the location vector of a point in the laboratory (inertial) frame, and let ${\overrightarrow{x}}_c\left(t\right)$ be the location of the engine in that frame as in Figure 2.

It follows that the location of the same point with respect to the engine is:

$${\overrightarrow{x}}^{\prime }=\overrightarrow{x}-{\overrightarrow{x}}_c\left(t\right),\Rightarrow \overrightarrow{x}={\overrightarrow{x}}^{\prime }+{\overrightarrow{x}}_c\left(t\right).$$

(290)

And also that:

$${\overrightarrow{v}}_s={\displaystyle \frac{d{\overrightarrow{x}}_c\left(t\right)}{dt}}.$$

(291)

The charge density can be expressed in either the laboratory (inertial) frame or in the engine frame. In the first case it is designated by $\rho$ and in the second by ${\rho }_m$, those two functions are related as follows:

$$\rho (\overrightarrow{x},t)={\rho }_m({\overrightarrow{x}}^{\prime },t)={\rho }_m(\overrightarrow{x}-{\overrightarrow{x}}_c\left(t\right),t).$$

(292)

In the case that the charge distribution is "static" in the engine frame this reduces to:

$$\rho (\overrightarrow{x},t)={\rho }_m(\overrightarrow{x}-{\overrightarrow{x}}_c\left(t\right)).$$

(293)

Similarly the partial temporal derivative can be calculated as follows:

$${\partial }_t\rho (\overrightarrow{x},t){|}_{\overrightarrow{x}}={\partial }_t{\rho }_m(\overrightarrow{x}-{\overrightarrow{x}}_c\left(t\right),t){{|}_{\overrightarrow{x}}=-{\overrightarrow{v}}_s·\overrightarrow{\nabla }{\rho }_m+{\partial }_t{\rho }_m|}_{{\overrightarrow{x}}^{\prime }}.$$

(294)

And for the case the charge density is "static" in the engine frame this reduces to:

$${\partial }_t\rho (\overrightarrow{x},t){|}_{\overrightarrow{x}}=-{\overrightarrow{v}}_s·\overrightarrow{\nabla }{\rho }_m=-\overrightarrow{\nabla }·\left(\rho {\overrightarrow{v}}_s\right).$$

(295)

Taking into account the continuity equation (43) we notice that although no current densities were initially assumed in the system, it now follows that from the laboratory point of view the engine now carries current density of the form:

$$\overrightarrow{J}=\rho {\overrightarrow{v}}_s$$

(296)

We are now at a position to calculate the work done by the internal electric field in such a system. This is done by using equation (93) which describes the time derivative of this work. We remind the reader that we have shown this work to be exactly equal to the amount of energy change in the electromagnetic field (see equation (130)). Thus:

$$E_{mech}=-{\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left({\displaystyle \frac{R\left({\partial }_t{\rho }_1\left({\overrightarrow{x}}_1\right){\partial }_t{\rho }_2\left({\overrightarrow{x}}_2\right)\right)}{2}}+{\displaystyle \frac{\overrightarrow{J_1}\left({\overrightarrow{x}}_1\right)·\overrightarrow{J_2}\left({\overrightarrow{x}}_2\right)}{R}}\right).$$

(297)

This can be written in the form:

$$E_{mech}=-{\displaystyle \frac{k}{2c^2}}\int \int d^3{x}_1{d}^3{x}_2\left({\displaystyle \frac{R}{2}}\left({\partial }_t{\rho }_1{\partial }_t{\rho }_2+{\partial }_t{\rho }_1{\partial }_t{\rho }_2\right)+{\displaystyle \frac{\overrightarrow{J_1}·\overrightarrow{J_2}+\overrightarrow{J_1}·\overrightarrow{J_2}}{R}}\right).$$

(298)

Taking into account equation (295) and equation (296) it follows that:

$$E_{mech}={\displaystyle \frac{k}{2c^2}}\int \int d^3{x}_1{d}^3{x}_2\left({\displaystyle \frac{R}{2}}\left({\partial }_t{\rho }_1{\overrightarrow{v}}_s·\overrightarrow{\nabla }{\rho }_2+{\overrightarrow{v}}_s·\overrightarrow{\nabla }{\rho }_1{\partial }_t{\rho }_2\right)-{\displaystyle \frac{\overrightarrow{J_1}·{\overrightarrow{v}}_s{\rho }_2+{\rho }_1{\overrightarrow{v}}_s·\overrightarrow{J_2}}{R}}\right).$$

(299)

Notice that:

$$\int d^3{x}_{2}R{\overrightarrow{v}}_s·{\overrightarrow{\nabla }}_2{\rho }_2=\int d^3{x}_2\left[{\overrightarrow{\nabla }}_2·\left(R{\rho }_2{\overrightarrow{v}}_s\right)-{\rho }_2{\overrightarrow{v}}_s·{\overrightarrow{\nabla }}_{2}R\right].$$

(300)

Using Gauss theorem and equation (86) this can be written in the form:

$$\int d^3{x}_{2}R{\overrightarrow{v}}_s·{\overrightarrow{\nabla }}_2{\rho }_2=\oint d{\overrightarrow{S}}_2·\left(R{\rho }_2{\overrightarrow{v}}_s\right)+\int d^3{x}_2{\rho }_2{\overrightarrow{v}}_s·\widehat{R}=\int d^3{x}_2{\rho }_2{\overrightarrow{v}}_s·\widehat{R},$$

(301)

in which we assume as usual that there is no charge on a far encapsulating surface. Similarly:

$$\int d^3{x}_{1}R{\overrightarrow{v}}_s·{\overrightarrow{\nabla }}_1{\rho }_1=-\int d^3{x}_1{\rho }_1{\overrightarrow{v}}_s·\widehat{R},$$

(302)

Plugging equation (301) and equation (302) into equation (299) it follows that:

$$E_{mech}={\displaystyle \frac{1}{2}}{\overrightarrow{v}}_s·{\displaystyle \frac{k}{c^2}}\int \int d^3{x}_1{d}^3{x}_2\left({\displaystyle \frac{\widehat{R}}{2}}\left({\partial }_t{\rho }_1{\rho }_2-{\rho }_1{\partial }_t{\rho }_2\right)-{\displaystyle \frac{\overrightarrow{J_1}{\rho }_2+{\rho }_1\overrightarrow{J_2}}{R}}\right)={\displaystyle \frac{1}{2}}{\overrightarrow{v}}_s·\overrightarrow{P}=E_k.$$

(303)

The linear momentum is given by equation (8) and the kinetic energy was defined in equation (9). Hence the work done by the retarded electromagnetic field is converted into the kinetic energy of the retarded field engine. We have used a $n=2$ expression for the work but since ${\overrightarrow{v}}_s$ is proportional to ${\displaystyle \frac{1}{c^2}}$ it turns to be proportional to ${\displaystyle \frac{1}{c^4}}$ as previously discussed thus resolving the dilemma stated in the end of the previous section.

7. Conclusions

A relativistic engine is not a self-sustaining device nor is a perpetuum mobile, it requires an input of energy to function. This energy is drawn from the electromagnetic field, reducing its energy in the process. In this study, we explore the validity of energy conservation in relation to a charged retarded engine. This research focuses on how energy is conserved in charged retarded systems, proposing an exciting new way to power spacecraft. By using electromagnetic fields instead of traditional rocket fuel, this technology could help spaceships travel faster and farther while using much less energy.