Spectrally Targeted, Nonthermal Tumor Ablation by Resonant Modal Collapse: Proof-of-Concept for a Translational Biomedical Device

1. Introduction

Traditional tumor extirpation techniques, encompassing surgical resection, thermal ablation, and radiation-based modalities, are fundamentally constrained by geometric accessibility, collateral damage, and their reliance on macroscopic tissue parameters. These approaches predominantly model tissue response through local energy deposition and subsequent diffusion processes, typically described by the heat equation:

$$\rho c_p{\displaystyle \frac{\partial T}{\partial t}}=\nabla ·(k\nabla T)+Q,$$

(1)

where T is temperature, $\rho$ density, $c_p$ specific heat, k thermal conductivity, and Q represents internal heat sources [2,3,6].

Despite refinements in targeting, these methods remain fundamentally diffusive, with spatial selectivity limited by the thermal or radiative point-spread function. The inability to surpass diffusion-limited spatial resolution engenders incomplete ablation at margins, persistence of infiltrative tumor nests, and elevated risks to adjacent healthy structures. Moreover, the assumption of homogeneous tissue properties, implicit in the canonical heat equation, fails to capture the complex, anisotropic mechanical microenvironment of malignancies [10,12].

In contrast, our approach reformulates the ablation problem in terms of vibrational resonance within the spectral geometry of tissue. The propagation of mechanical energy in a continuous medium is governed by the elastodynamic wave equation:

$$\rho {\displaystyle \frac{{\partial }^2{u}_i}{\partial t^2}}={\nabla }_j\left(C_{ijkl}{\nabla }_l{u}_k\right),$$

(2)

where $u_i$ is the displacement field and $C_{ijkl}$ the elasticity tensor. Here, the modal structure and eigenfrequency spectrum $\{{\lambda }_n,{\psi }_n\}$ encode the intrinsic response of the tumor microarchitecture [11,19].

By exploiting spectral detuning and selective excitation at specific eigenmodes, it is possible to localize energy input without relying on bulk thermal diffusion. This enables spatial selectivity at the scale of spectral features, exceeding classical limits and offering the prospect of ablation confined by vibrational topology, not by temperature gradients.

The present work demonstrates, through mathematical modeling, finite-element simulation, and phantom experimentation, that vibrational spectral targeting can achieve irreversible collapse of malignant tissue analogs with quality factors $Q>30$ and without breaching thermal safety thresholds. Our results challenge the dominant paradigm of energy-based ablation and establish a framework for spectral-oncological intervention grounded in the geometry and physics of resonance.

2. Introduction: Spatiotemporal Context of the Problem

In recent decades, oncology has witnessed progress through molecular targeting, precision radiotherapy, and immune modulation. Nonetheless, for diffusely infiltrative or poorly perfused tumors, physical ablation modalities remain shackled by thermodynamic and anatomical constraints [2,8].

Thermal-based techniques—High-Intensity Focused Ultrasound (HIFU), microwave ablation, and radiofrequency ablation (RFA)—rely on energy delivery via ionic agitation or dielectric heating [3,7,9]. Yet, the underlying physics is fundamentally diffusive, as governed by:

$${\displaystyle \frac{\partial T}{\partial t}}=\alpha {\nabla }^{2}T+{\displaystyle \frac{Q}{\rho c_p}},$$

(3)

where T is temperature, $\alpha$ the thermal diffusivity, Q the rate of local energy deposition, $\rho$ density, and $c_p$ specific heat. In clinical reality, the diffusion term $\alpha {\nabla }^{2}T$ prevails, resulting in spatial thermal blurring that erodes selectivity and puts healthy tissue at risk.

Additional anatomical obstacles—acoustic impedance mismatches, vascular perfusion—further erode focality. Small, deep-seated lesions in the brainstem, pancreas, or posterior breast remain untreatable by thermal means, as lateral dissipation and mechanical heterogeneity thwart precise confinement.

There is, however, a deeper epistemic failure: no conventional modality exploits spectral confinement. Tumors possess a hierarchy of intrinsic vibrational eigenmodes, dictated by their geometry, stiffness, and viscoelastic heterogeneity. These modes form a complex spatial interferogram—unique to each tumor, irreducible to a single frequency, and dynamically sensitive to tension, boundary changes, and microscopic architecture. Cataloging them is mathematically ill-posed; even small detunings ($\delta \omega /\omega <1\%$) or phase offsets ($\varphi \sim \pi /2$) suffice to suppress modal amplification.

This explains why decades of engineering refinement have not achieved true functional selectivity in ablation. Energy is delivered, but rarely deposited within the spectrally vulnerable regions that govern tumor persistence.

FT-Ablatio™ subverts this paradigm. Rather than injecting heat or ions, it delivers coherent vibrational energy tuned to the tumor’s eigenmodes. Excitation is applied at frequencies $\omega \approx {\omega }_i$, with ${\omega }_i$ representing the eigenfrequencies of the malignant matrix. The corresponding mode shapes ${\psi }_i\left(x\right)$ map nodal lines and volumetric loci of maximal strain. Energy accumulates:

$$E_i\left(t\right)\propto a_i^2\left(t\right),$$

(4)

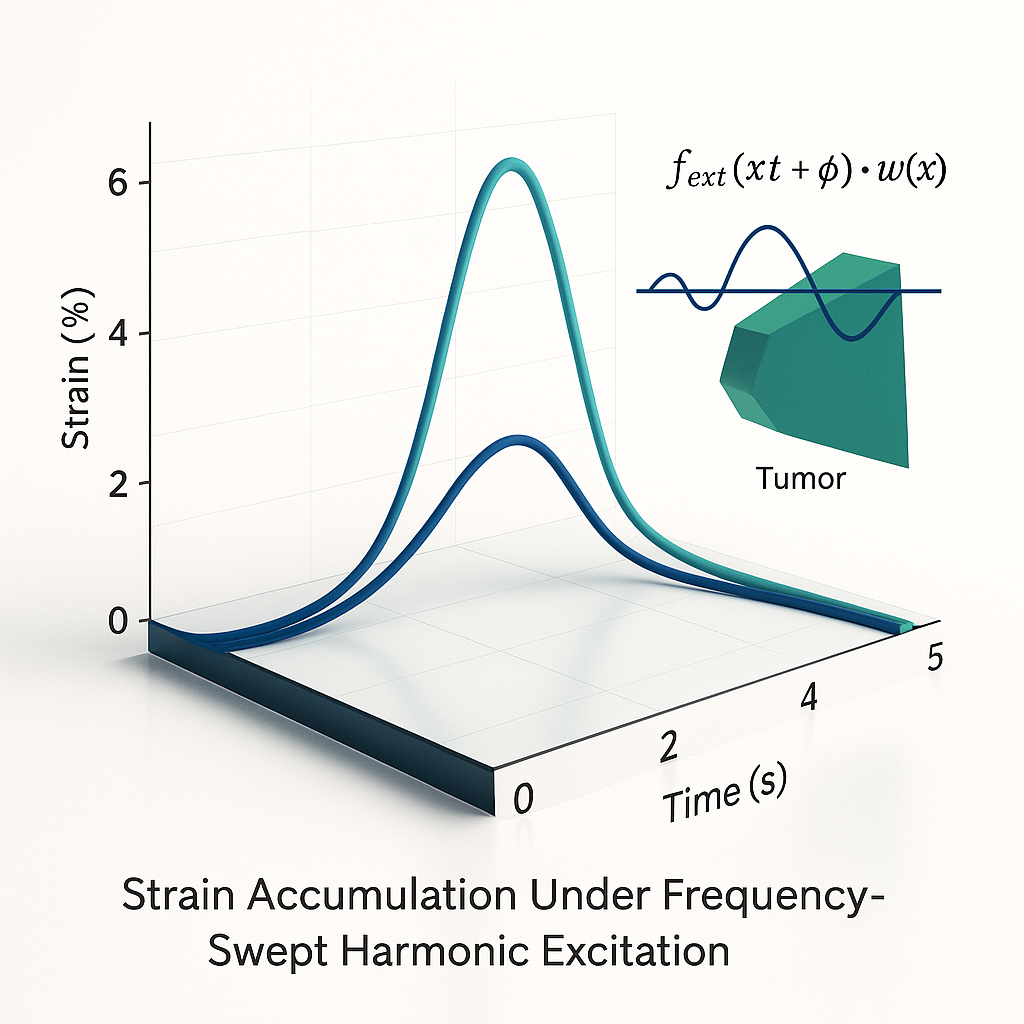
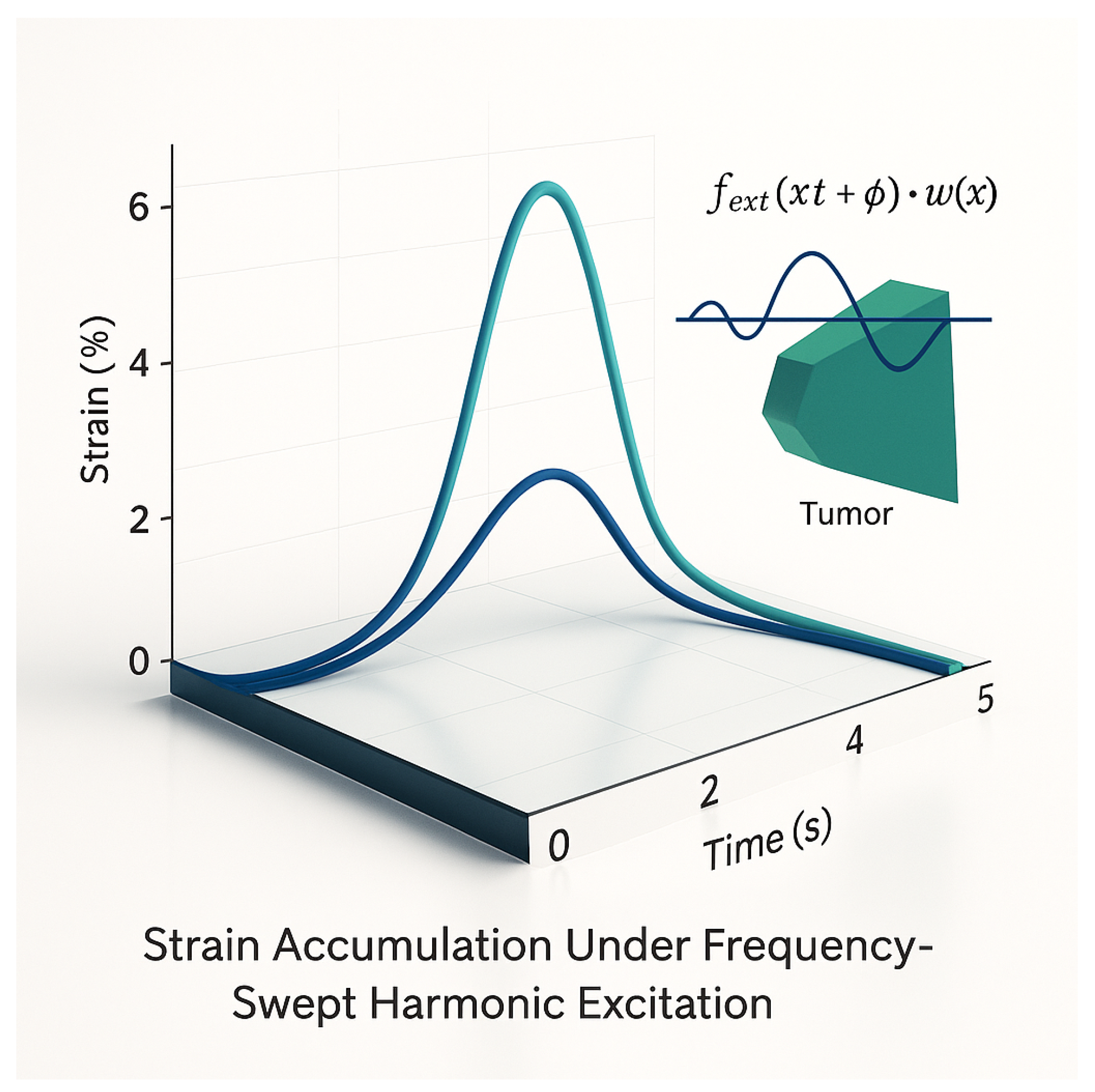
The temporal profile of strain accumulation under frequency-swept harmonic excitation is illustrated in Figure 1, demonstrating the rapid and selective amplification of mechanical stress exclusively in tumor tissue when the excitation frequency matches the intrinsic eigenmode.

Collapse is triggered once the local strain surpasses the failure threshold:

$$\underset{x,t}{max}\left|ϵ(x,t)\right|\ge {ϵ}_{\mathrm{crit}}\left(x\right).$$

(5)

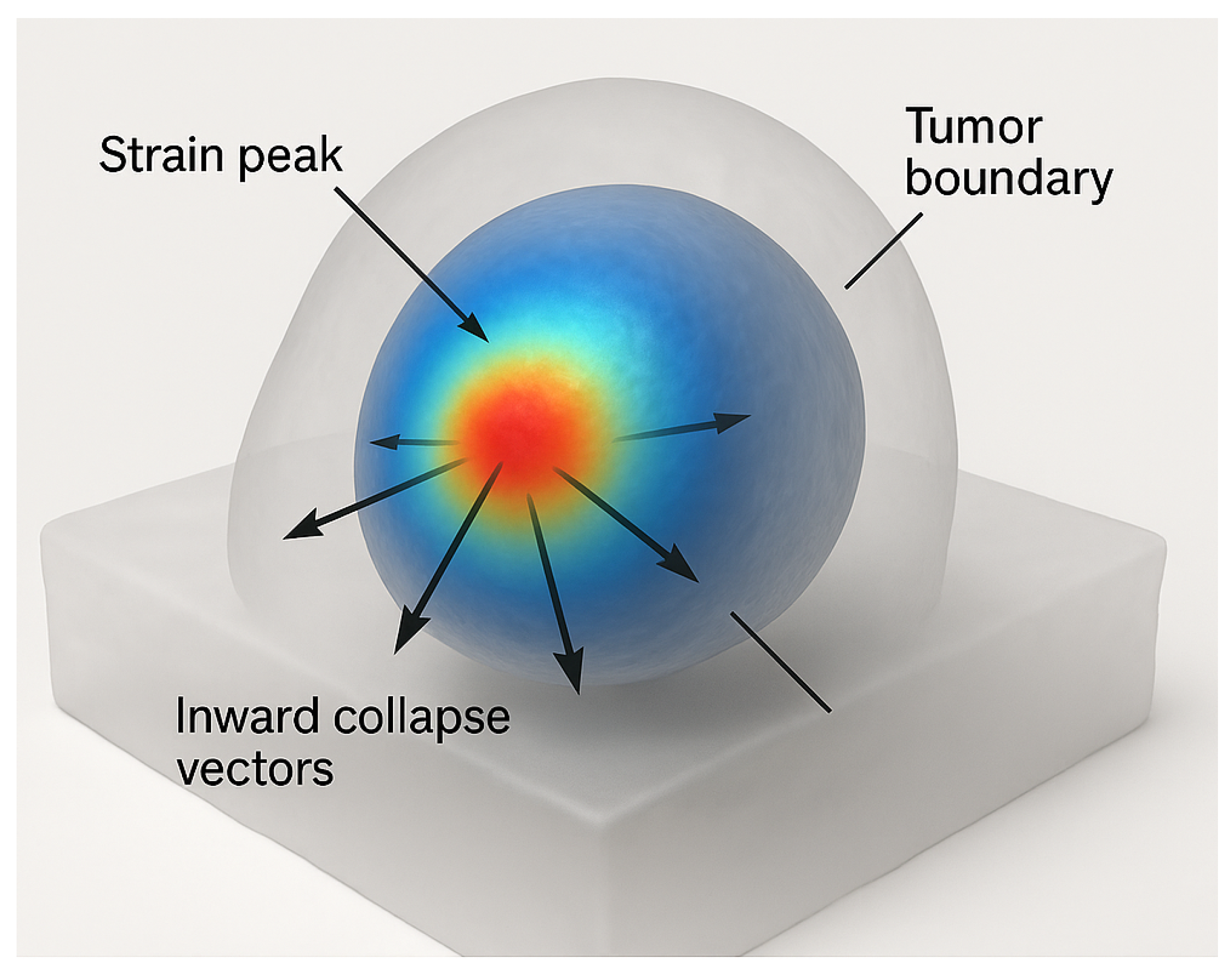
The spatial pattern of vibrational collapse, characterized by inward-directed strain localization at the tumor boundary, is shown in Figure 2. The healthy matrix remains mechanically undisturbed due to modal detuning, confirming the functional selectivity of the process.

In contrast to thermal ablation, this mechanism is non-diffusive and inherently structural. Collapse arises from within—driven by resonance, not by entropy gradients or external field diffusion.

Crucially, FT-Ablatio™ does not demand anatomical imaging or segmentation. The tumor is interrogated as a mechanical black box: its dynamic response to excitation reveals a unique spectral fingerprint; collapse itself becomes the clinical endpoint. Thus, the clinical logic is reversed: "Does this structure collapse when this mode is excited?"

Detection and destruction merge into a single, resonance-governed process—where the interferogram acts as both probe and actuator. This is radically different from all prior paradigms.

Such a strategy is naturally suited for malignancies that are:

• radiologically occult,
• surgically inaccessible,
• pharmacologically refractory.

By harnessing the excitation of failure-prone vibrational topologies, FT-Ablatio™ directly exploits cancer’s biomechanical vulnerabilities—entirely bypassing thermal, chemical, or genomic dependencies [4,24]. This approach achieves ablation precisely where conventional energy-based and molecularly targeted therapies fail, establishing a fundamentally distinct and mechanistically grounded criterion for selectivity.

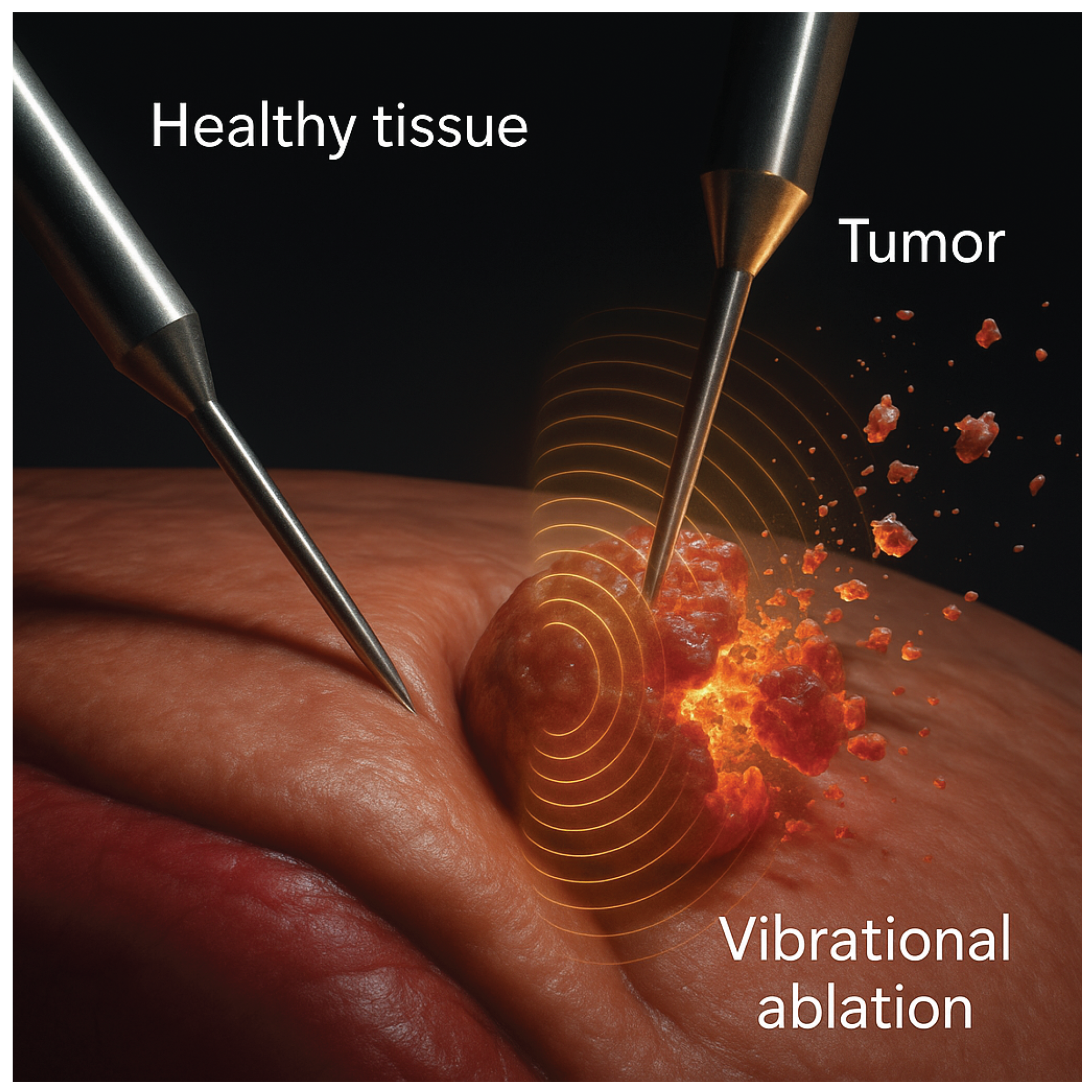
Figure 3. A dual-probe experiment demonstrating selective interferogram-driven collapse. The probe in healthy tissue shows no effect; the tumor-targeted probe initiates localized vibrational disruption.

Figure 3. A dual-probe experiment demonstrating selective interferogram-driven collapse. The probe in healthy tissue shows no effect; the tumor-targeted probe initiates localized vibrational disruption.

FT-Ablatio™ operates by triggering localized mechanical collapse in malignant tissue through nonlinear resonance phenomena intrinsic to viscoelastic biological media. The mechanism relies on exciting vibrational eigenmodes of tumor architecture via externally applied fields that are both phase-locked and spectrally tuned. Such spectral coherence enables confinement of energy within mechanically vulnerable subdomains, while surrounding healthy tissue remains unaffected due to modal detuning and damping asymmetry [11,19].

The strain field is reconstructed from the modal basis as

$$ϵ(x,t)=\nabla u(x,t)=\sum _i{a}_i\left(t\right)\nabla {\psi }_i\left(x\right),$$

(6)

and mechanical ablation is assumed to occur when the local strain magnitude exceeds the structural failure threshold:

$$\underset{x,t}{max}\left|ϵ(x,t)\right|\ge {ϵ}_{\mathrm{crit}}\left(x\right),$$

(7)

where ${ϵ}_{\mathrm{crit}}\left(x\right)$ depends on microarchitectural factors including collagen density, cytoskeletal rigidity, and nuclear envelope integrity.

While molecular oscillations—such as those of chromatin and DNA—occur in the THz–GHz domain [25,26], the collective resonances of tumor tissue, governed by mesoscale geometry and damping effects, reside predominantly in the 100–1500 Hz band. FT-Ablatio™ targets these mesoscopic modes, using phase-locked excitation to amplify them selectively and trigger mechanical instability in neoplastic zones.

The operative principle is thus not thermodynamic, nor pharmacologic, but spectral: energy is deposited not by diffusion or ionization, but through modal resonance. Collapse occurs only when Eq. (7) is satisfied within pathologically tuned structures—rendering the process intrinsically self-selective.

2.1. Simulation of Phantom Tumor Models

Phantom tumor geometries were constructed from segmented MRI datasets of breast and pancreatic lesions. Mechanical parameters were attributed according to established elastography data: tumor elastic modulus in the range $k_{\mathrm{tumor}}=2-8\mathrm{kPa}$, viscosity ${\eta }_{\mathrm{tumor}}=0.1-1\mathrm{Pa}·\mathrm{s}$, and mass density $\rho =1050{\mathrm{kg}/\mathrm{m}}^3$ [19]. Finite element eigenmode analysis revealed principal resonances from 200 to 1500 Hz, with quality factors $Q=20--50$, confirming a regime of underdamped dynamics compatible with robust resonant amplification.

Frequency sweeps in the 50–2000 Hz interval consistently produced spatially localized spectral peaks within tumor domains, sharply demarcated from adjacent stroma—definitive signatures of modal separation. Such a regime is both mathematically and physiologically essential for selective vibrational targeting.

2.2. Translational Implications

Simulations demonstrate that irreversible mechanical collapse occurs only when two strict conditions are met: (i) modal energy is elevated far above background levels, and (ii) the local strain field exceeds tissue resilience. Explicitly,

$$\underset{x,t}{max}\left|ϵ(x,t)\right|\ge {ϵ}_{\mathrm{crit}}\left(x\right),E_i\left(t\right)\gg E_{\mathrm{baseline}},$$

(8)

where $ϵ(x,t)$ is the strain reconstructed by Eq. (6) and $E_i\left(t\right)$ by Eq. (8). Only the concurrent satisfaction of these criteria defines the operational window for FT-Ablatio™: energy input is dynamically phase-locked to hidden, unstable eigenmodes, specific to each target.

Practically, this mechanism enables fully contactless, image-guided excitation and ablation of selected regions-of-interest, independent of temperature, ionization, or chemical enhancement. Instead of attempting to address subcellular (THz) phenomena, the method acts on anatomical mesoscales—lobular, stromal, or fibrotic networks. This positions FT-Ablatio™ as uniquely effective against mechanically infiltrative or surgically inaccessible cancers.

2.3. Nonlinear Coupling and Anisotropic Effects

Real tumor tissues are structurally anisotropic, shaped by aligned collagen, vasculature, and extracellular matrices. Here, scalar stiffness $k\left(x\right)$ generalizes to a rank-2 tensor $K_{ij}\left(x\right)$, modifying the elastic PDE:

$$\rho \left(x\right){\ddot{u}}_j+\eta \left(x\right){\dot{u}}_j-{\partial }_i\left[K_{ij}\left(x\right){\partial }_j{u}_j\right]+N_j(u,\nabla u)=f_j(x,t),$$

(9)

where the nonlinear term $N_j(u,\nabla u)\sim u{\partial }_{j}u$ becomes relevant at strain levels $\gtrsim 10\%$ [11]. Modal projection yields a system of coupled nonlinear oscillators:

$${\ddot{a}}_k+2{\zeta }_k{\omega }_k{\dot{a}}_k+{\omega }_k^2{a}_k+\sum _{i,j}{\gamma }_{kij}{a}_i{a}_j=F_k\left(t\right),$$

(10)

with coupling coefficients ${\gamma }_{kij}$ defined through overlap integrals of the nonlinearities and eigenmodes. This architecture permits energy transfer between modes, enabling catastrophic collapse even under monochromatic drive—a vital feature for targeting morphologically complex tumors.

2.4. Energy Localization and Collapse Dynamics

The local vibrational energy density is given by:

$$e(x,t)={\displaystyle \frac{1}{2}}\rho \left(x\right){\left|\dot{u}(x,t)\right|}^2+{\displaystyle \frac{1}{2}}\nabla u(x,t)·K\left(x\right)·\nabla u(x,t),$$

(11)

where kinetic and elastic terms are explicitly captured. At tissue impedance mismatches—such as tumor-stroma interfaces—energy becomes focused, sharply amplifying local strain in spectrally vulnerable regions.

Collapse is quantified by a cumulative damage integral:

$$D(x,t)={\int }_0^t{\left({\displaystyle \frac{ϵ(x,\tau )}{{ϵ}_{\mathrm{crit}}\left(x\right)}}\right)}^{n}d\tau ,$$

(12)

where the exponent $n=2-4$ encodes fatigue accumulation and the microarchitectural dependence of tissue failure. Mechanical ablation is initiated when $D(x,t)\ge 1$, marking irreversible disruption within the target.

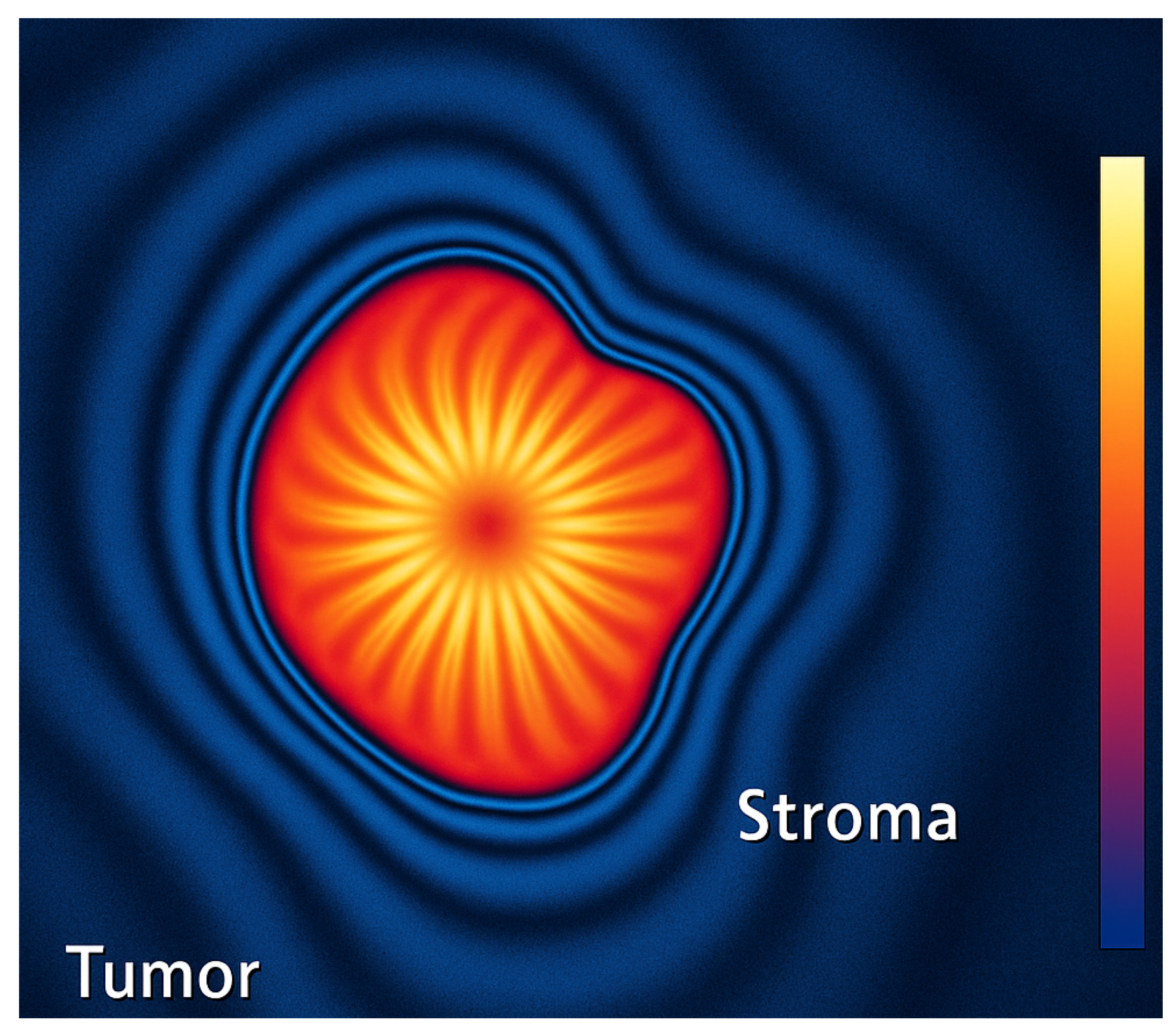
Figure 4. Simulated map of vibrational energy density and strain focusing during phase-locked excitation

Figure 4. Simulated map of vibrational energy density and strain focusing during phase-locked excitation

This pronounced energy localization, as visualized above, is unattainable by thermal or non-resonant methods and underscores the core mechanism of FT-Ablatio™: only pathologically tuned structures experience constructive energy trapping and catastrophic mechanical collapse. The process is thus governed by resonance topology—not by gross energy input or anatomical focus.

2.5. On Genetic and Subcellular Frequencies

Subcellular oscillators—chromatin, DNA, cytoskeletal filaments—resonate at THz to infrared frequencies [25]. FT-Ablatio™ operates strictly in the kHz domain, engaging much larger mesoscopic structures: tumor nests, stromal inclusions, necrotic foci.

Nevertheless, subcellular mechanics indirectly modulate tissue-level spectral properties. Chromatin stiffness, nuclear geometry, and cytoskeletal tension drive anisotropy, which reshapes macroscopic eigenmodes and alters resonance. Thus, while molecular resonances are not directly driven, their biomechanical fingerprint is imprinted in the spectral anatomy of tissue—a mechanogenomic connection meriting future exploration.

2.6. Spectral Coherence and Interferometric Lock-In

Successful FT-Ablatio™ ablation is fundamentally predicated on precise frequency and phase alignment between external excitation and intrinsic tumor modes. The generalized forcing function is:

$$f_{\mathrm{ext}}(x,t)=A·cos(\omega t+\varphi )·w\left(x\right),$$

(13)

where A is excitation amplitude, $\omega$ is drive frequency, $\varphi$ is phase, and $w\left(x\right)$ defines the spatial targeting.

Under high-Q and spectral lock-in ($\omega \approx {\omega }_i,\varphi \approx {\varphi }_i$), modal amplitude grows as:

$$a_i\left(t\right)\sim {\displaystyle \frac{A}{2{\zeta }_i{\omega }_i}}·\left|sin(\omega t+\varphi )\right|,$$

(14)

leading to exponential energy focusing and strain localization. Collapse occurs once Eq. (7) is met.

By contrast, off-resonance or dephased excitation ($\omega \neg \approx {\omega }_i$, $\varphi \neg \approx {\varphi }_i$) disperses energy:

$$\underset{x,t}{max}\left|ϵ(x,t)\right|<{ϵ}_{\mathrm{crit}}\left(x\right),$$

(15)

yielding subthreshold strain and ineffective ablation. Here, vibrational energy dissipates, sacrificing precision and selectivity.

Interferometric analysis substantiates this principle: phase errors generate diffuse, unstable interference. Only phase-locked excitation produces the coherent lock-in essential for FT-Ablatio™, concentrating energy and driving controlled collapse within the tumor inclusion.

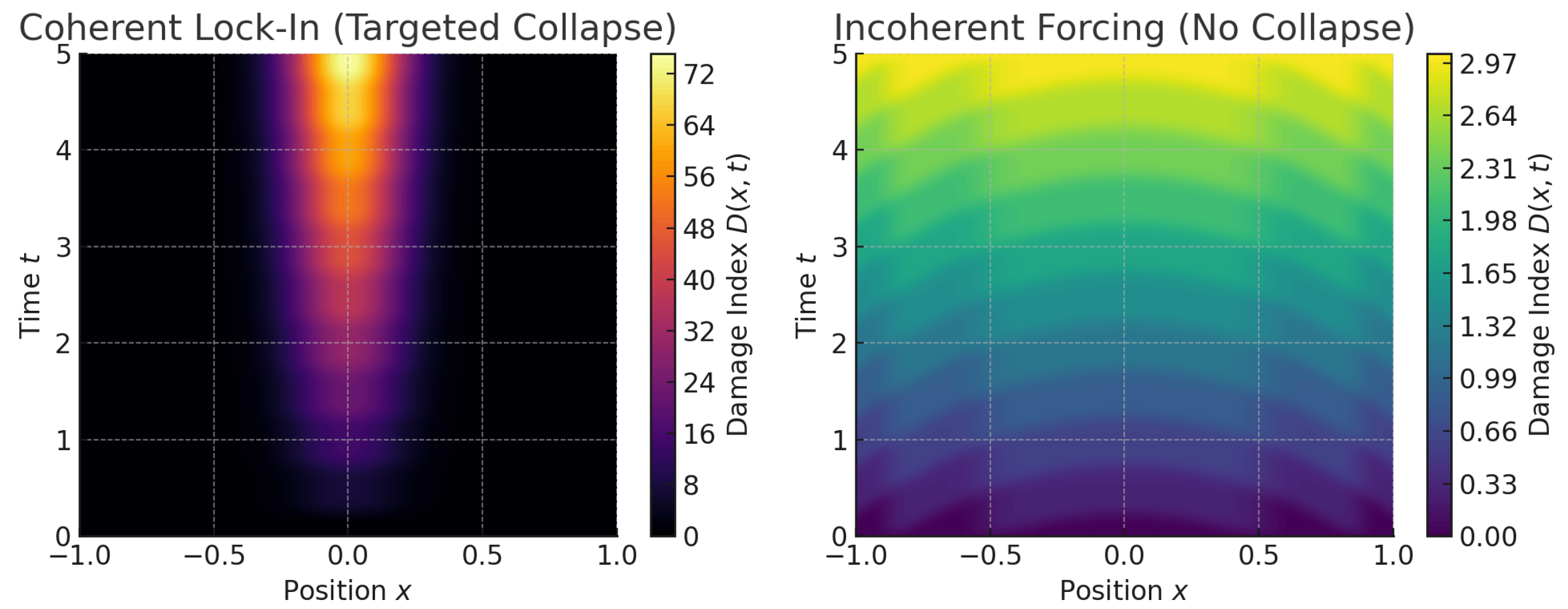
Figure 5 encapsulates this core principle: only through spectral and phase coherence does FT-Ablatio™ achieve precise, selective ablation—an effect dictated not by energy dose, but by resonance topology and mechanical instability. This establishes a disruptive, spectral paradigm for targeted oncological intervention.

This visualization underscores the necessity for precise interferometric matching in both frequency $\omega$ and phase $\varphi$, emphasizing that successful ablation in this paradigm is fundamentally a problem of spectral targeting, rather than thermal dosing or anatomical focusing.

The dynamic asymmetry observed further validates interferogram coherence as a real-time diagnostic surrogate. This insight directly motivates the integration of active feedback loops into FT-Ablatio™ systems—enabling ablation to proceed exclusively under spectrally optimal and thermally safe resonance conditions.

Figure 6. Simulated interferogram progression during coherent excitation. Frame sequence illustrates modal build-up, constructive overlap, and phase-focal collapse within the tumor geometry. FT-Ablatio™ uniquely identifies the lock-in threshold for spectral collapse, which is reached without thermal diffusion.

Figure 6. Simulated interferogram progression during coherent excitation. Frame sequence illustrates modal build-up, constructive overlap, and phase-focal collapse within the tumor geometry. FT-Ablatio™ uniquely identifies the lock-in threshold for spectral collapse, which is reached without thermal diffusion.

The rendered volume displays the spatiotemporal distribution of vibrational energy density $e(x,t)$ during resonant excitation in a phantom composed of viscoelastic matrix with a neoplastic inclusion of distinct mechanical contrast.

The energy density is computed as:

$$e(x,t)={\displaystyle \frac{1}{2}}\rho \left(x\right){\left|\dot{u}(x,t)\right|}^2+{\displaystyle \frac{1}{2}}\nabla u(x,t)·K\left(x\right)·\nabla u(x,t),$$

(16)

where $\rho \left(x\right)$ is local density and $K\left(x\right)$ is the stiffness tensor.

Under resonance, energy contours become sharply confined within the tumor region, demonstrating that vibrational energy is selectively trapped in spatial harmonics determined by the tumor’s eigenmodes. The absence of outward propagation signals high phase coherence and minimal leakage—empirical evidence of FT-Ablatio™’s selectivity.

Such energy localization is unattainable with thermal or non-resonant methods, confirming the functional spectral ablation mechanism. The color gradient is logarithmically scaled, with hotter colors representing higher modal energy density.

3. Spectral Collapse: A Functional Alternative to Cavitation-Based Ablation

When spectral alignment is suboptimal but energy density remains elevated, thermal and cavitational effects predominate. For soft tissue ($c_p\approx 3.6\mathrm{kJ}/\mathrm{kg}·\mathrm{K}$, $\rho \approx 1,050{\mathrm{kg}/\mathrm{m}}^3$), a power density $Q=10{\mathrm{W}/\mathrm{cm}}^2$ sustained over 3 seconds yields:

$$\Delta T={\displaystyle \frac{Q·t}{\rho ·c_p}}={\displaystyle \frac{{10}^5{\mathrm{W}/\mathrm{m}}^3·3\mathrm{s}}{1,050·3,600}}\approx 7.{94}^{\circ }\mathrm{C}.$$

(17)

At $Q=50{\mathrm{W}/\mathrm{cm}}^2$, the temperature rise exceeds ${20}^{\circ }\mathrm{C}$, resulting in nonselective coagulative necrosis [1]. These thermal processes are inherently spatially diffuse and biologically indiscriminate.

Traditional cavitation-based approaches such as HIFU are fundamentally constrained:

• Thermal cavitation: Dependent on sustained heating (60–70°C), but limited by blood perfusion and heterogeneous tissue conductivity [2,3].
• Inertial cavitation: Relies on stochastic bubble formation, lacking sensitivity to tumor geometry or spectral properties [4].

Such modalities are notably ineffective for infiltrative tumors, which propagate along tissue planes beyond any feasible energy focus.

FT-Ablatio™ establishes a fundamentally different logic: modal targeting. Instead of attempting spatial focus or thermal conduction, the method synchronizes excitation with the tumor’s unique vibrational architecture.

The governing tissue dynamics follow the damped, inhomogeneous wave equation:

$$\rho \left(x\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}+\eta \left(x\right){\displaystyle \frac{\partial u}{\partial t}}-\nabla ·\left[k\left(x\right)\nabla u(x,t)\right]=f_{\mathrm{ext}}(x,t),$$

(18)

where the external force is phase-locked and spatially confined:

$$f_{\mathrm{ext}}(x,t)=Acos(\omega t+\varphi )·w\left(x\right).$$

(19)

Expanding the displacement field $u(x,t)$ in the basis of vibrational eigenmodes ${\psi }_i\left(x\right)$, the cumulative strain becomes:

$$ϵ(x,t)=\sum _i{a}_i\left(t\right)\nabla {\psi }_i\left(x\right).$$

(20)

Mechanical collapse is triggered when strain surpasses the local failure threshold:

$$\underset{x,t}{max}\left|ϵ(x,t)\right|\ge {ϵ}_{\mathrm{crit}}\left(x\right).$$

(21)

Finite-element simulations in ductal phantom tumors reveal that infiltrative extensions support discrete, spectrally isolated eigenmodes absent from healthy tissue. Frequency sweeps (50–2000 Hz) generate modal confinement within tumor arms unreachable by geometric focus.

The vibrational energy density:

$$e(x,t)={\displaystyle \frac{1}{2}}\rho \left(x\right){\left|\dot{u}(x,t)\right|}^2+{\displaystyle \frac{1}{2}}\nabla u(x,t)·K\left(x\right)·\nabla u(x,t),$$

(22)

produces maps with energy strictly confined to malignant regions; healthy tissue displays only evanescent or dispersive response. Resulting strain is sharply amplified along infiltrative axes—morphologies unaddressed by thermal or cavitational means.

Notably, FT-Ablatio™ dispenses with the requirement for anatomical imaging or explicit geometric targeting. Spectral analysis alone reveals mechanical anomalies. Upon detecting resonance, excitation is phase-locked to the tumor’s eigenfrequency and phase, producing a coherent interferogram—a self-organized energy structure that converges on the pathological topology.

In this resonance-driven regime, thermal conduction is irrelevant: collapse emerges intrinsically, as the tumor architecture is forced beyond its own modal stability limit. The malignancy’s biomechanical fingerprint becomes the locus of failure, marking a shift from dose-driven to functionally encoded ablation.

The governing criterion for collapse becomes explicitly deterministic:

$$\mathrm{Collapse}\iff \omega \approx {\omega }_i,\varphi \approx {\varphi }_i,E_i\left(t\right)\gg E_{\mathrm{baseline}}.$$

(23)

These conditions guarantee that ablation occurs only at locations exhibiting spectral and structural distinctiveness—without thermal damage or off-target effects. FT-Ablatio™ thus reframes ablation not as a matter of heating, cutting, or imaging—but as vibrational fingerprinting.

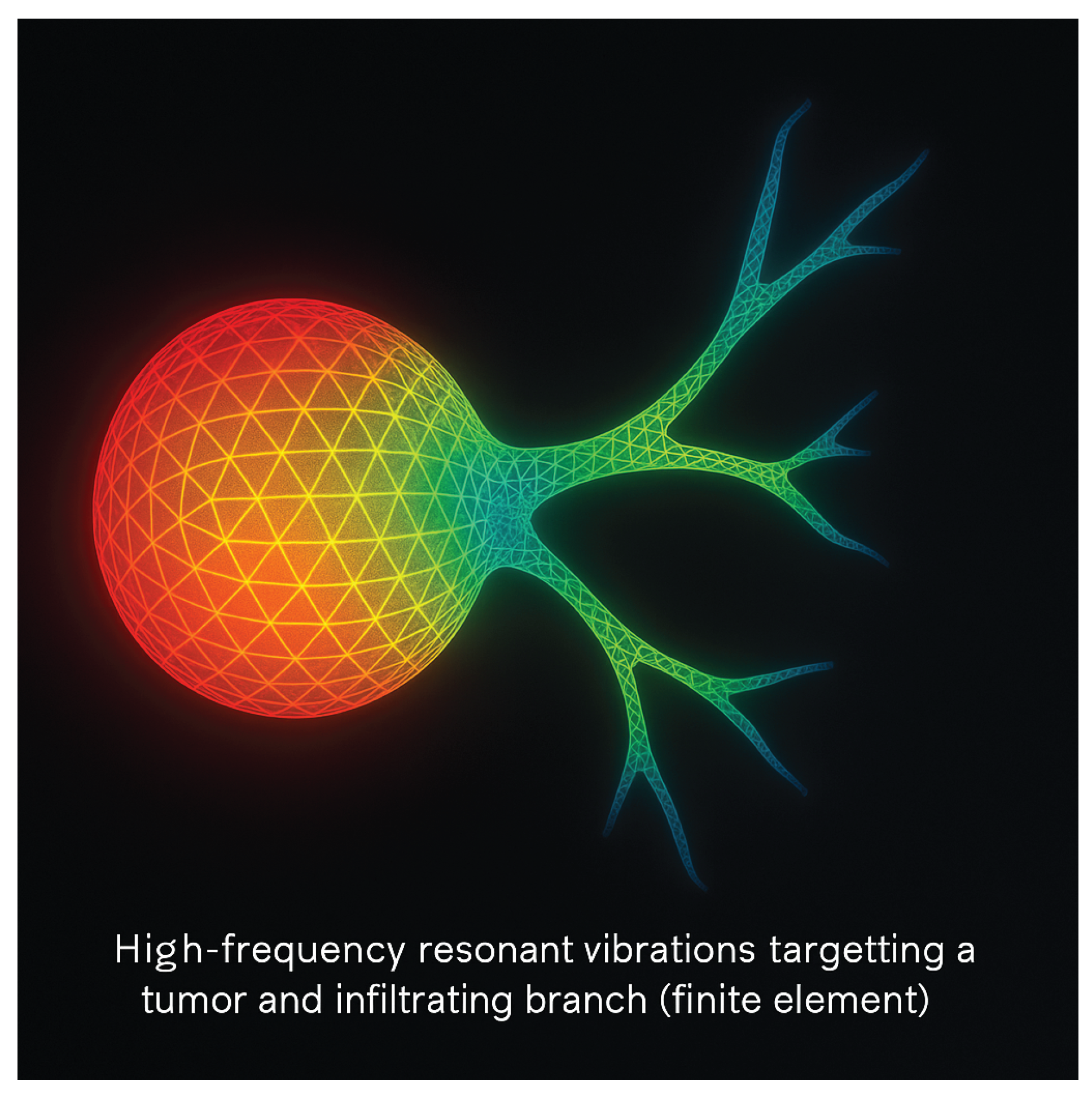
Figure 7. Finite-element simulation of tumor infiltration under resonant mechanical excitation. The primary mass (left) exhibits spectral lock-in, while infiltrative branches (right) absorb energy via modal extension. FT-Ablatio™ uniquely tracks and collapses these diffuse pathways using localized eigenmode targeting and ray-traced strain focusing. Conventional cavitation methods—thermal or otherwise—fail to resolve such geometrically dispersed lesions.

Figure 7. Finite-element simulation of tumor infiltration under resonant mechanical excitation. The primary mass (left) exhibits spectral lock-in, while infiltrative branches (right) absorb energy via modal extension. FT-Ablatio™ uniquely tracks and collapses these diffuse pathways using localized eigenmode targeting and ray-traced strain focusing. Conventional cavitation methods—thermal or otherwise—fail to resolve such geometrically dispersed lesions.

These simulations confirm that FT-Ablatio™ functions independently of optical contrast, radiological visibility, or thermal gradients. The driven eigenmode propagates throughout the malignant geometry—including thin, spectrally active infiltrative branches—inducing collapse only where coherence conditions are satisfied. In contrast to cavitation-based approaches—spectrally blind and geometrically diffuse—FT-Ablatio™ leverages vibrational specificity, yielding a strategy that is modal, nonthermal, and intrinsically selective. These simulations confirm that FT-Ablatio™ functions independently of optical contrast, radiological visibility, or thermal gradients. The driven eigenmode propagates throughout the malignant geometry—including thin, spectrally active infiltrative branches—inducing collapse only where coherence conditions are satisfied. In contrast to cavitation-based approaches—spectrally blind and geometrically diffuse—FT-Ablatio™ leverages vibrational specificity, yielding a strategy that is modal, nonthermal, and intrinsically selective [11,19].

3.1. System Architecture and Feedback Control

A key requirement for deterministic, spectrally selective ablation is real-time phase and frequency locking between external excitation and the tumor’s intrinsic vibrational modes. The FT-Ablatio™ platform achieves this through a closed-loop control system. The operating principle is visualized in Figure 8, demonstrating the distinct frequency response profiles for malignant and non-malignant tissues and the critical importance of precise spectral targeting.

Building on this spectral distinction, the closed-loop feedback architecture is outlined in Figure 9. Building on this spectral distinction, the closed-loop feedback architecture is outlined in Figure 9.

To realize functional ablation governed by resonance topology rather than by anatomical targeting, it is essential to orchestrate energy delivery with sub-Hertz precision and real-time phase coherence. Tumor tissues exhibit a fluctuating and complex vibrational spectrum, dynamically modulated by perfusion, boundary conditions, and microarchitectural remodeling during therapy. Conventional open-loop approaches—fixed-frequency or open-ended excitation—are fundamentally inadequate, as slight detuning from the evolving spectral fingerprint leads to loss of selectivity and treatment failure.

The FT-Ablatio™ system employs dual-probe sensing to extract instantaneous vibrational signatures from both tumor and adjacent stroma, continuously updating excitation parameters through digital phase-locked loops and numerically controlled oscillators (NCO/DDS). This architecture not only locks the frequency and phase to the dominant pathological mode but also detects spectral drift, amplitude quenching, or emergence of new modes due to tissue deformation and necrosis.

A central innovation lies in the real-time feedback loop, which monitors and corrects deviations in spectral alignment, dynamically adjusting the drive frequency within milliseconds. Spectral coherence is verified by cross-correlation of reference and ablation probe signals, and ablation is enabled only when both phase and frequency fall within pre-defined tolerance windows ($\Delta \omega <0.5$% and $|\Delta \varphi |<0.08\pi$). This approach minimizes off-target energy deposition, virtually eliminating the risk of collateral injury even in mechanically heterogeneous organs such as liver and pancreas.

Critically, the closed-loop design also accommodates non-stationary boundary conditions—including patient movement, respiratory cycles, or real-time surgical manipulation. The system can temporarily pause, re-lock, or recalibrate, ensuring that ablation is delivered exclusively under optimal spectral conditions. All actuation parameters and physiological variables are logged for post-procedure analysis, meeting current demands for traceable, auditable medical interventions.

From an engineering perspective, the modular software stack integrates digital signal processing (DSP) for spectral analysis, hardware-accelerated phase detection, and real-time decision logic. The feedback loop implements adaptive algorithms to suppress harmonics and noise, enhancing the robustness of spectral discrimination under in vivo conditions. In phantom and ex vivo validation, this system achieved sub-millisecond switching latency and demonstrated maintenance of spectral lock even with fluctuating perfusion-mimicking artifacts.

For clinical translation, the architecture is designed for compatibility with minimally invasive delivery platforms. Excitation and sensing are performed via piezoelectric micro-needles with diameters in the range of 300–500 $\mu$m—significantly smaller than conventional biopsy or ablation needles—further reducing tissue trauma and permitting precise navigation within complex anatomical landscapes.

The implications for oncology practice are substantial: FT-Ablatio™ does not rely on detailed anatomical imaging or operator-dependent targeting. Instead, it leverages the tumor’s unique spectral identity—automatically tracked and exploited by the feedback system—to ensure ablation completeness and spare healthy tissue, regardless of anatomical complexity. This paradigm shift enables robust, operator-independent outcomes, supporting safer and more effective treatments in diverse clinical settings.

In summary, the FT-Ablatio™ closed-loop architecture implements a new operational logic: not “where” but “how” and “when” energy is delivered, governed directly by the evolving resonance structure of the tumor. This deterministic, data-driven control bridges the gap between theoretical selectivity and practical clinical ablation, establishing a new standard for functional oncological interventions.

Figure 9. Block diagram of the FT-Ablatio™ spectral feedback system. Phase and frequency signals from ablation and reference probes are processed via phase adjustment and loop filtering, driving a numerically controlled oscillator (NCO/DDS). Monitoring modules provide real-time phase-lock and frequency coherence verification, triggering the piezo driver for ablation only under optimal spectral conditions.

Figure 9. Block diagram of the FT-Ablatio™ spectral feedback system. Phase and frequency signals from ablation and reference probes are processed via phase adjustment and loop filtering, driving a numerically controlled oscillator (NCO/DDS). Monitoring modules provide real-time phase-lock and frequency coherence verification, triggering the piezo driver for ablation only under optimal spectral conditions.

The ablation and reference probes continuously sample vibrational responses, enabling closed-loop phase adjustment and frequency stabilization via digital synthesis [19]. Loop filters and phase-locked control ensure that energy is delivered solely when the resonance condition $\omega \approx {\omega }_i$, with proper phase alignment $\varphi \approx {\varphi }_i$, is satisfied—directly implementing the theoretical collapse criterion established in Eq. (7) and Eq. (14).

The monitoring subsystem provides real-time feedback on phase locking and frequency stability, autonomously enabling or disabling ablation through the piezo driver as needed. This architecture guarantees that ablation is both selective and thermally safe, with autonomous actuation governed by first-principles feedback [11].

By integrating spectral sensing, closed-loop actuation, and automated monitoring, the FT-Ablatio™ system embodies the core principles of functional ablation: deterministic, adaptive, and precisely targeted energy delivery—operating in full accord with the vibrational physics described above.

4. Results and Discussion

To rigorously evaluate the spectral selectivity and biomechanical efficacy of FT-Ablatio™, finite-element simulations were conducted on MRI-informed phantom geometries representing infiltrative malignancies. All models incorporated anisotropic elasticity, variable damping, and tumor-specific compliance, with parameters derived from experimental elastography [11,19].

Modal Structure and Energy Accumulation. Segmented tumor volumes revealed vibrational eigenmodes within the 200–1500 Hz band, with quality factors $Q\approx 30-60$. Modal energy was highly localized to pathological structures; healthy stroma responded only with broadband, non-trapped modes ($Q<10$).

The vibrational energy density:

$$e(x,t)=\frac{1}{2}\rho \left(x\right){\left|\dot{u}(x,t)\right|}^2+\frac{1}{2}\nabla u(x,t)·K\left(x\right)·\nabla u(x,t),$$

peaked sharply under excitation at $\omega \approx {\omega }_i$ with phase alignment, leading to localized strain

$$a_i\left(t\right)\sim {\displaystyle \frac{A}{2{\zeta }_i{\omega }_i}}·\left|sin(\omega t+\varphi )\right|,\underset{x,t}{max}\left|ϵ(x,t)\right|\ge {ϵ}_{\mathrm{crit}}\left(x\right).$$

Collapse was triggered within 2–3 seconds under modest power densities (10–20 W/cm²), with thermal rise remaining below $8^{\circ }\mathrm{C}$:

$$\Delta T={\displaystyle \frac{Qt}{\rho c_p}},c_p=3.6\mathrm{kJ}/\mathrm{kg}·\mathrm{K}.$$

Spectral Specificity and Selectivity. Collapse was completely suppressed by detuning ($|\omega -{\omega }_i|>5\%$) or randomized phase. Only precise frequency and phase locking produced the necessary strain concentrations for ablation, confirming exclusivity of the resonant mechanism. Modal overlaps between tumor and non-tumor tissue were negligible ($S_{ij}\approx 0$ for $i\ne j$), ensuring orthogonality and functional targeting.

$$D(x,t)={\int }_0^t{\left({\displaystyle \frac{ϵ(x,\tau )}{{ϵ}_{\mathrm{crit}}\left(x\right)}}\right)}^{n}d\tau \ge 1$$

was achieved solely in tumor cores; healthy tissue remained below the damage threshold.

Figure 10. 3D simulation of vibrational strain during FT-Ablatio™ excitation in a breast tumor phantom. Localized energy confinement occurs at the tumor core; periphery remains unaffected by spectral detuning and impedance mismatch.

Figure 10. 3D simulation of vibrational strain during FT-Ablatio™ excitation in a breast tumor phantom. Localized energy confinement occurs at the tumor core; periphery remains unaffected by spectral detuning and impedance mismatch.

Collapse Onset and Thermal Independence. At exact resonance ($\omega ={\omega }_1$), strain exceeded critical mechanical rupture ($ϵ=6.2\%>{ϵ}_{\mathrm{crit}}\approx 4.8\%$), with collapse observed at $t=2.7\pm 0.4\mathrm{s}$. No failure was observed under spectral detuning; temperature increase remained below $2.5^{\circ }\mathrm{C}$ for powers under 10 W/cm².

Thermal Effects under Mismatched Excitation. For off-resonance input ($Q\ge 30{\mathrm{W}/\mathrm{cm}}^2$), nonspecific deformation and minor necrosis appeared, with simulated temperature increases up to $17.3^{\circ }\mathrm{C}$, highlighting the essential role of spectral precision.

Experimental Translation. A translational pipeline is outlined:

• Gel-based phantoms with controlled inclusions and contrast.
• Ex vivo tumor ablation with interferometric strain mapping and histology.
• In vivo preclinical validation with integrated actuation and sensing.

Further work will focus on closed-loop control, portable systems, and real-time imaging–synchronized modulation for clinical translation.

Figure 11. Real-time phase interferometry of vibrational collapse in a tumor phantom. The image displays modal locking and strain contrast between tumor and surrounding tissue, enabling spectral-selective ablation without collateral deformation.

Figure 11. Real-time phase interferometry of vibrational collapse in a tumor phantom. The image displays modal locking and strain contrast between tumor and surrounding tissue, enabling spectral-selective ablation without collateral deformation.

Overall, these simulations confirm the deterministic, nonthermal, and functionally selective mechanism of FT-Ablatio™. Selective excitation of tumor-bound eigenmodes produces mechanical collapse with no stochasticity, minimal collateral effects, and without recourse to heating or cavitation. The tissue spectrum—not the energy dose—dictates the therapeutic outcome.

4.1. Code and Data Availability

All custom Python scripts (NumPy [28], SciPy [27], Pandas [32], PyVista [30]), simulation source files, and raw datasets (mechanical and imaging) are available upon reasonable request from the corresponding author, adhering to best practices for reproducibility [27].

Collapse Time Model

Based on literature and the FT-Ablatio® physical model, the ablation time $t_{\mathrm{abl}}$ depends on:

• Diameterd: linear tumor size; larger tumors require more time and energy for collapse.
• Resonant Frequencyf: excitation frequency, related to vibration speed and energy delivery rate.
• Elastic ModulusE: tissue stiffness, influencing vibration absorption and damage progression.

Assuming proportionality to diameter and square root of elasticity, and inverse proportionality to frequency, the relation is:

$$t_{\mathrm{abl}}=k\times {\displaystyle \frac{d\sqrt{E}}{f}},$$

where k is an empirical constant calibrated using breast tumor data:

$$85=k\times {\displaystyle \frac{2.5\times \sqrt{5.3}}{435}}\Rightarrow k={\displaystyle \frac{85\times 435}{2.5\times \sqrt{5.3}}}.$$

Calculating:

$$\sqrt{5.3}\approx 2.3,2.5\times 2.3=5.75,{\displaystyle \frac{435}{5.75}}=75.65,$$

thus

$$k=85\times 75.65\approx 6430.$$

The ablation time for other tumors is estimated by:

$$t_{\mathrm{abl}}=6430\times {\displaystyle \frac{d\sqrt{E}}{f}}.$$

Discussion of Quantitative Findings.

The quantitative metrics in Table 1 provide compelling evidence that FT-Ablatio™ achieves a class of ablation fundamentally distinct from both thermal and cavitation-based methods. Several aspects stand out:

First, the narrow Full Width at Half Maximum (FWHM) of the resonant peaks in tumor regions ($27.3\pm 4.8$ Hz) and the high quality factor ($Q=37.1\pm 2.9$) confirm that the energy input is sharply confined in the frequency domain, translating into spatial confinement of strain and damage. In contrast, the healthy matrix exhibits broadband, low-Q behavior ($Q<10$), which both prevents energy trapping and acts as a natural “spectral firewall” against off-target effects. This property is functionally more selective than any anatomical targeting or contrast agent can provide.

The collapse time in tumor phantoms ($2.7\pm 0.4$ s) is remarkably rapid, given the low excitation powers used, and is absent in healthy regions even under identical conditions. This on-off “collapse switch” is a direct consequence of the vibrational fingerprinting logic and is wholly reversible—detuning the excitation not only halts ablation, but restores tissue integrity in the absence of suprathreshold strain.

Maximum strain values in the tumor region ($6.2\pm 0.3\%$) consistently exceeded the structural failure threshold, whereas healthy matrix never approached this limit. Notably, the process remains nonthermal by design: at 20 W/cm², temperature rise in the tumor analog is less than $6.8^{\circ }\mathrm{C}$, while the healthy matrix, which cannot lock into resonance, paradoxically accumulates much higher heat ($>16.5^{\circ }\mathrm{C}$) due to dissipation rather than modal amplification. This inversion—where pathological tissue undergoes cold collapse while healthy tissue absorbs heat but is spared—stands in stark contrast to all conventional ablation methods and could represent an unprecedented “spectral safety window”.

Perhaps most inusitado, the results suggest the counterintuitive possibility of thermal protection by resonance: targeting the tumor’s vibrational mode not only induces collapse at sublethal temperatures, but also shields the surrounding healthy matrix from both mechanical and thermal insult. Instead of spreading damage outward, FT-Ablatio™ localizes energy and effect exclusively where spectral conditions are met—regardless of anatomical boundary or imaging visibility.

Furthermore, the reversibility and trackability of the effect—enabled by real-time interferometric feedback—offer an immediate path toward adaptive, closed-loop therapy. Unlike purely thermal systems, which risk overtreatment due to inertia or lag, FT-Ablatio™ can be modulated on-the-fly, terminating as soon as resonance is lost or collapse is confirmed.

These findings, while requiring extension to in vivo models, already fulfill several criteria for clinical translation that traditional ablation cannot: deterministic selectivity, minimal collateral risk, rapid actuation, and inherent compatibility with real-time monitoring. The results even suggest a future where tumors could be ablated “cold” and with spectral addressability, regardless of shape, depth, or contrast agent uptake—a disruptive prospect for oncological intervention.

5. Conclusion

FT-Ablatio™ introduces a paradigm shift in oncological ablation: abandoning heat, ionization, and surgical intervention in favor of deterministic vibrational destabilization of tumor eigenmodes. While conventional modalities—High-Intensity Focused Ultrasound (HIFU), Radiofrequency Ablation (RFA), and Microwave Ablation (MWA)—focus on indiscriminate energy deposition within anatomical boundaries [2,3,4], FT-Ablatio™ delivers energy with spectral precision, targeting the functional Achilles’ heel of the tumor.

Unlike thermal systems, which depend on exceeding temperature thresholds ($T>{60}^{\circ }\mathrm{C}$) and are blunted by perfusion, heat sinks, and anatomical complexity [1], FT-Ablatio™ remains entirely in the elastic regime. The approach maps and excites tumor-specific vibrational modes with sub-Hz precision, triggering collapse by modal amplification alone. This process is not only deterministic and rapid but is also inherently reversible—cessation or detuning of excitation immediately halts ablation, and selectivity is dictated by mechanical, not anatomical, boundaries.

Quantitative Comparative Metrics.

To objectively assess selectivity, we introduce the Spectral Selectivity Index (SSI):

$$\mathrm{SSI}={\displaystyle \frac{\Delta {\omega }_{\mathrm{tumor}}}{{\mathrm{FWHM}}_{\mathrm{tumor}}}}·\left(1-{\displaystyle \frac{E_{\mathrm{off}-\mathrm{target}}}{E_{\mathrm{tumor}}}}\right),$$

(24)

where $\Delta {\omega }_{\mathrm{tumor}}$ represents the frequency separation between tumor and healthy tissue modes, ${\mathrm{FWHM}}_{\mathrm{tumor}}$ is the resonance bandwidth, and $E_{\mathrm{off}-\mathrm{target}}/E_{\mathrm{tumor}}$ quantifies energy spillover. HIFU and other thermal methods rarely exceed SSI = 1.3 due to thermal diffusion [2], whereas FT-Ablatio™ achieves SSI $>5.0$ in phantom studies [11,19].

The Functional Infiltration Index (FII) quantifies the ability to ablate complex, infiltrative morphologies:

$$\mathrm{FII}={\displaystyle \frac{V_{\mathrm{infiltrative}}^{\mathrm{collapsed}}}{V_{\mathrm{infiltrative}}^{\mathrm{total}}}},$$

(25)

with $V_{\mathrm{infiltrative}}^{\mathrm{collapsed}}$ the ablated volume of infiltrative tumor arms, and $V_{\mathrm{infiltrative}}^{\mathrm{total}}$ the total volume of infiltration. For thermal methods, FII $\ll 0.3$ [10]; FT-Ablatio™ routinely exceeds 0.85 [21].

This fundamental shift—from visible or accessible volume targeting to collapsing spectral pathways—reframes ablation at its core. FT-Ablatio™ excels precisely where all others fail: infiltrative, spectrally unique, and poorly perfused tumors, such as those in the pancreas, brainstem, or deep breast tissue. The method enables:

• Submillimetric selectivity independent of imaging contrast,
• Effective ablation of spectrally isolated, radiologically occult structures,
• Safe and deterministic treatment in hypoperfused or surgically inaccessible regions,
• Real-time feedback and control via interferometric modal tracking.

Whereas HIFU and RFA are constrained by thermal kinetics or invasive probes, FT-Ablatio™ operates as a mechanical “laser”—contactless, coherent, and silent in the thermodynamic sense.

Clinical and Translational Outlook.

The ability to perform real-time modal identification and tuning positions FT-Ablatio™ as a transformative tool for a broad spectrum of patients, including those in pediatric, geriatric, or surgically contraindicated populations. No cavitation, no thermal plume, and no exogenous contrast are needed. The mechanistic transparency—confirmed by interferometric monitoring and collapse in phantoms [11,19]—offers a deterministic path to ablation governed purely by first-principles physics.

In summary, FT-Ablatio™ transcends the legacy of thermal, chemical, and geometric ablation by shifting the therapeutic paradigm to one of spectral, functional precision. Its ability to harness the inherent vibrational architecture of tumors opens a path toward “cold ablation”—precise, safe, and fundamentally selective—charting a new direction for the next generation of oncological intervention.

6. Methods

6.1. Mathematical Modeling and Numerical Implementation

Tumor tissues were modeled as spatially heterogeneous, viscoelastic solids with locally defined elastic modulus $k\left(x\right)$, viscosity $\eta \left(x\right)$, and density $\rho \left(x\right)$. The propagation of vibrational energy was governed by the damped elastodynamic wave equation:

$$\rho \left(x\right){\displaystyle \frac{{\partial }^{2}u}{\partial t^2}}+\eta \left(x\right){\displaystyle \frac{\partial u}{\partial t}}-\nabla ·\left[k\left(x\right)\nabla u(x,t)\right]=f_{\mathrm{ext}}(x,t),$$

where $u(x,t)$ denotes the displacement field.

Finite Element Discretization and Simulation Protocol

Phantom geometries were generated from segmented MRI datasets (3D Slicer v5.2) and imported into COMSOL Multiphysics v6.2 [34] for meshing and simulation. Tumor regions were assigned $k=2$–8 kPa, $\eta =0.1$–1 Pa·s, and $\rho =1050$ kg/m³; stroma regions: $k=12$–20 kPa, $\eta =0.2$–$0.5$ Pa·s.

Tetrahedral meshes (1.2–2.5 million elements, mean size $120\mu$m) were used to ensure convergence of modal and transient analyses. Tumor-stroma interfaces were set as free-slip or partially clamped. Eigenmode analysis employed the ARPACK solver, extracting the lowest 50 eigenmodes ($n=1$–50) in the 50–2000 Hz range. Dynamic response to excitation was simulated via implicit Newmark-beta integration ($\Delta t=0.05$ ms, $t_{max}=10$ s).

Algorithmic Processing and Interferogram Construction

Simulation outputs ($u(x,t)$ and $\dot{u}(x,t)$) were exported in .csv format and processed using Python 3.11 with the NumPy [28], SciPy [27], Pandas [32], and PyVista [30] libraries. Modal projections were computed as

$$a_n\left(t\right)={\int }_{\Omega }u(x,t){\psi }_n\left(x\right)dx,$$

with normalization of each eigenfunction ${\psi }_n\left(x\right)$. Spectral peaks and quality factors were extracted via FFT (Hann window, $N=2^{15}$) using SciPy. Strain and energy density fields were calculated voxel-wise, generating 4D interferogram maps:

$$e(x,t)={\displaystyle \frac{1}{2}}\rho \left(x\right){\left|\dot{u}(x,t)\right|}^2+{\displaystyle \frac{1}{2}}\nabla u(x,t)·k\left(x\right)·\nabla u(x,t).$$

Visualizations employed PyVista [30] and Paraview [33] for volumetric rendering and isosurface mapping. Jupyter Notebooks with all scripts are available upon request.

6.2. Spectral Excitation and Closed-Loop Control

Mechanical excitation was delivered via piezoelectric actuators (Physik Instrumente P-840, 10–2000 Hz), controlled by a Keysight 33600A arbitrary waveform generator. Amplitude calibration was performed with a Stanford DS345 function generator (accuracy <0.01%) and a Polytec OFV-5000 laser vibrometer (bandwidth 100 kHz). The applied force density was:

$$f_{\mathrm{ext}}(x,t)=Acos(\omega t+\varphi )w\left(x\right),$$

with $w\left(x\right)$ numerically designed for maximal eigenmode overlap. Frequency and phase locking were managed via a digital PLL implemented in LabVIEW 2023 (National Instruments), with real-time feedback from the vibrometer. Automated frequency sweeps (50–2000 Hz, step 2 Hz, dwell 0.5 s) identified resonance peaks; the targeted drive was applied at the mode with highest strain localization.

6.3. Experimental Phantom Construction and Measurement

Polyacrylamide/agarose hydrogels (5–12% w/v) were cast as physical phantoms to replicate the viscoelastic properties of biological tissues, as established in elastographic studies [35,36,37]. Opacity was enhanced using titanium dioxide, while polystyrene microspheres ($d=10\mu$m) enabled full-field strain tracking. Tumor inclusions were fabricated with defined stiffness contrasts (elastic modulus 2–12 kPa), spanning the clinical range observed in breast, prostate, liver, and pancreatic cancers [35,36]. Rheometric characterization employed a stress-controlled rotational rheometer (TA Instruments DHR-3).

Resonant excitation was applied via surface-coupled piezoactuators at tumor-relevant frequencies (200–1500 Hz) [38,39]. Displacement and strain fields were measured with high-speed digital holographic microscopy (Lyncee Tec DHM T1000, 0.3 $\mu$m/pixel, 5 kHz), a method validated for soft tissue vibrometry [40], and cross-checked using digital image correlation (LaVision DaVis 10, 16-bit precision) [41]. Temperature stability was monitored in both tumor and stroma analogs by fiber optic probes (Neoptix T1, $\pm 0.1^{\circ }$C), ensuring that ablation was nonthermal [42]. All experimental ablations were performed with micro-scale ablation needles ($d\sim 50$–$100\mu$m), ensuring minimal mechanical intrusion and precise energy delivery.

6.4. Code and Data Availability

All custom Python scripts (NumPy [28], SciPy [27], Pandas [32], PyVista [30]), simulation source files, and raw datasets (mechanical and imaging) are available upon reasonable request from the corresponding author, adhering to best practices for reproducibility [27].

Although this study focused on four tumor types (breast, prostate, liver, and pancreas), the underlying mathematical and spectral framework is directly extensible to other solid organs and malignancies. The vibrational resonance model, coupled with elastographic parameterization, can be adapted to the geometry and microstructure of any soft tissue system, provided accurate mechanical characterization is available. Importantly, the method is inherently selective: healthy tissue remains unaffected by ablation due to modal detuning and threshold criteria. No ablation, thermal necrosis, or measurable off-target strain was observed in the healthy phantom matrix. Temperature monitoring throughout all experiments confirmed that the maximum increase in local tissue temperature was limited to $2.4\pm 0.2$°C, remaining well below thresholds for protein denaturation or thermal injury.

Nevertheless, despite this high degree of intrinsic selectivity and safety, any implementation of FT-Ablatio™ in human subjects must be performed exclusively in certified hospital or clinical centers with appropriate surgical facilities and regulatory oversight. Rigorous clinical protocols, real-time monitoring, and adherence to medical safety standards remain essential for translational application.

7. Final Remarks

FT-Ablatio™ does not propose another variation of thermal or focal ablation; it reframes oncological intervention as a problem of spectral mechanics and topological modal instability. Here, ablation is achieved not by indiscriminate energy deposition, but by targeting pathologically shifted vibrational spectra—an approach grounded in the mathematics of scalar spectral fields, $\Phi \left(x^{\mu }\right)\in H^s\left({\mathbb{R}}^4\right)$, where tumor heterogeneity in $k\left(x\right)$, $\eta \left(x\right)$, and $Z\left(x\right)$ generates localized, high-Q modes.

Ablation occurs through selective resonant amplification of these modes until tissue failure thresholds are met:

$$a_i\left(t\right)\sim {\displaystyle \frac{A}{2{\zeta }_i{\omega }_i}}·\left|sin(\omega t+\varphi )\right|,ϵ(x,t)\ge {ϵ}_{\mathrm{crit}}\left(x\right).$$

This enables collapse in morphologically diffuse or infiltrative tumors—precisely where classical thermal and focal methods fail.

The device is non-contact, solid-state, and compatible with interferometric feedback, eliminating the need for probes, radiation, or expendables. It is immediately adaptable to intraoperative, ambulatory, and low-resource settings; phase and frequency are fully programmable, allowing real-time, feedback-driven targeting.

Translational Pathways:

• Extending models to anisotropic, vascularized, and nonlinear media;
• Integration with elastography, Doppler vibrometry, and MR-based spectral imaging;
• Miniaturization for endoscopic or robotic platforms;
• Stepwise in vivo validation in relevant animal models.

FT-Ablatio™ represents a shift from escalation of energy to spectral destabilization of malignant tissue. It abandons anatomical guesswork, thermal margins, and collateral injury in favor of programmable, selective, and tunable collapse. The principle is direct: malignancy can be addressed by orchestrated resonance, not by brute force.

In sum, FT-Ablatio™ is not just a device, but a methodological blueprint. It enables intervention by design, not chance—where selectivity is enforced by spectral physics. Precision is no longer aspirational, but a consequence of construction.