Study on Deformation Characteristics of Gate Dam and Earth–Rock Dam Systems with Deep Overburden

1. Introduction

As China’s western hydropower development strategy continues to progress, the requirement for deep overburden foundations at dam sites become unavoidable [1]; in addition, river areas typically feature low-head and high-flow characteristics. Gate dam and earth–rock dam systems offer advantages such as minimal ecological impact, short construction periods, and good terrain adaptability, making them the preferred dam type for such sites. Several key regional projects, including Duobu, Futang, Shawan, and Yingliangbao, have been carried out, playing an important and positive role in regional power generation, irrigation, ecological protection, and navigation. However, there is limited research on the three-dimensional deformation characteristics of an entire gate dam and earth–rock dam system, making it difficult to accurately assess and quantitatively evaluate the safety status of these structures during construction and operation. Therefore, studying the deformation characteristics of the hybrid dam system and exploring the mechanisms of deformation interaction between structures is of great significance for dam management decision-making.

To this end, relevant scholars have conducted a series of studies targeting different engineering issues. For example, Wei Kuangmin et al. [2] introduced the settlement control method of gate dam foundation on the complex thick overburden, and a simplified method for simulating large-scale pile groups were proposed. Kong Ke et al. [3] used the Tongzilin Hydropower Station as a case study to investigate the influence of the joint form at the end of the frame-type underground continuous wall on its stress deformation. Jiang Yunlong et al. [4] investigated the stress–strain characteristics of the dam section at Dagu Tan. Wang Dengyin et al. [5] used a three-dimensional finite element model to analyze the static stress–strain characteristics of the dam at Danba. Wu Mengxi et al. [6] successfully simulated the seepage and deformation of spillway dams throughout their entire construction and operational lifecycle. Ren Wei et al. [7] addressed the key issues in settlement control for the Duobu Dam, proposing reasonable standards for uneven settlement, settlement control, and differentiated foundation treatment technologies. Overall, the aforementioned research findings provide important reference value for accurately understanding the deformation characteristics of weir dams. However, due to the limitations of conventional modeling and analysis methods in precision analysis [8], it is challenging to simultaneously consider important components such as earth–rock dams, gravity-retaining walls, spillway weir dams, cutoff walls, underground continuous walls, and unevenly distributed overburden layers within a hydropower plant hub. Therefore, the aforementioned studies primarily focused on local structural analysis and simplified models, specifically on the mechanical response of isolated components, which makes it difficult to reasonably identify the deformation interactions between components within the system.

Given this, this research uses an ongoing mixed dam project as its basis and employs self-developed refined modeling and analysis methods to conduct a three-dimensional deformation characteristic study of a gate dam and earth–rock dam system, exploring the deformation patterns and distribution characteristics of different components, which could act as a reference for improving and optimizing future dam design schemes.

2. Cross-Scale Refinement Analysis Method

2.1. Octree Grid Discretization Algorithm

An octree is a hierarchical tree-like data structure used for dividing three-dimensional space, suitable for mesh partitioning [9]. The basic principle of octree grid partitioning is to recursively divide the root cell into eight interconnected subcells according to a 2:1 balanced division principle, continuing until all grid cells meet the size criteria and the division stops. The advantages of the octree grid discretization algorithm include the ability to perform cross-scale grid partitioning, rapid unit size scaling, good mechanical matrix properties of the grid, high grid quality, and simple algorithm construction [10,11]. 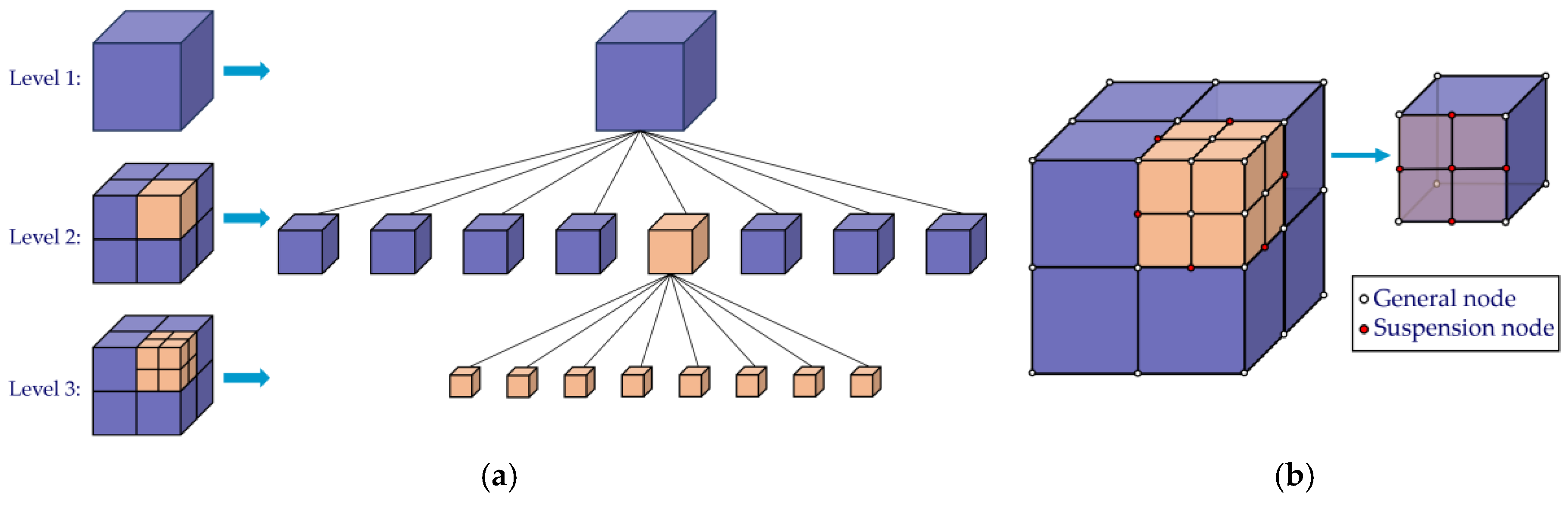Figure 1a shows the schematic structure of an octree grid discretization with a partitioning level of 3.

2.2. SBFEM Analysis Method

The octree discretization algorithm specifies that the size of adjacent cells varies by a factor of $2^n$, resulting in cubic cells and polyhedral cells with hanging edge nodes after discretization (with a total number of cell nodes greater than 8 and a number of faces greater than 6), as shown in Figure 1b. Cubic cells can be solved using FEM, but the number of nodes in polyhedral cells is not fixed, making it difficult to calculate using conventional FEM.

Wolf and Song [12] proposed the scale-boundary finite element method (SBFEM) based on a semi-analytical numerical solution method. This method combines the advantages of the finite element method and the boundary element method, offering a simple data structure, ease of constructing polyhedra, and convenient program implementation. This has been proven by multiple authors [8,13,14,15] to be an effective method for solving cross-scale grid computations. SBFEM has been applied in various fields, including elastic–plastic analysis [12,13], crack analysis [16,17], free vibration analysis [18], and soil–structure interactions [19,20]. For readers’ convenience and to better understand the work presented in this paper, detailed information concerning the SBFEM method can be found in [14,21].

3. Numerical Model of the Gate Dam and Earth–Rock Dam System

3.1. Geometric Model

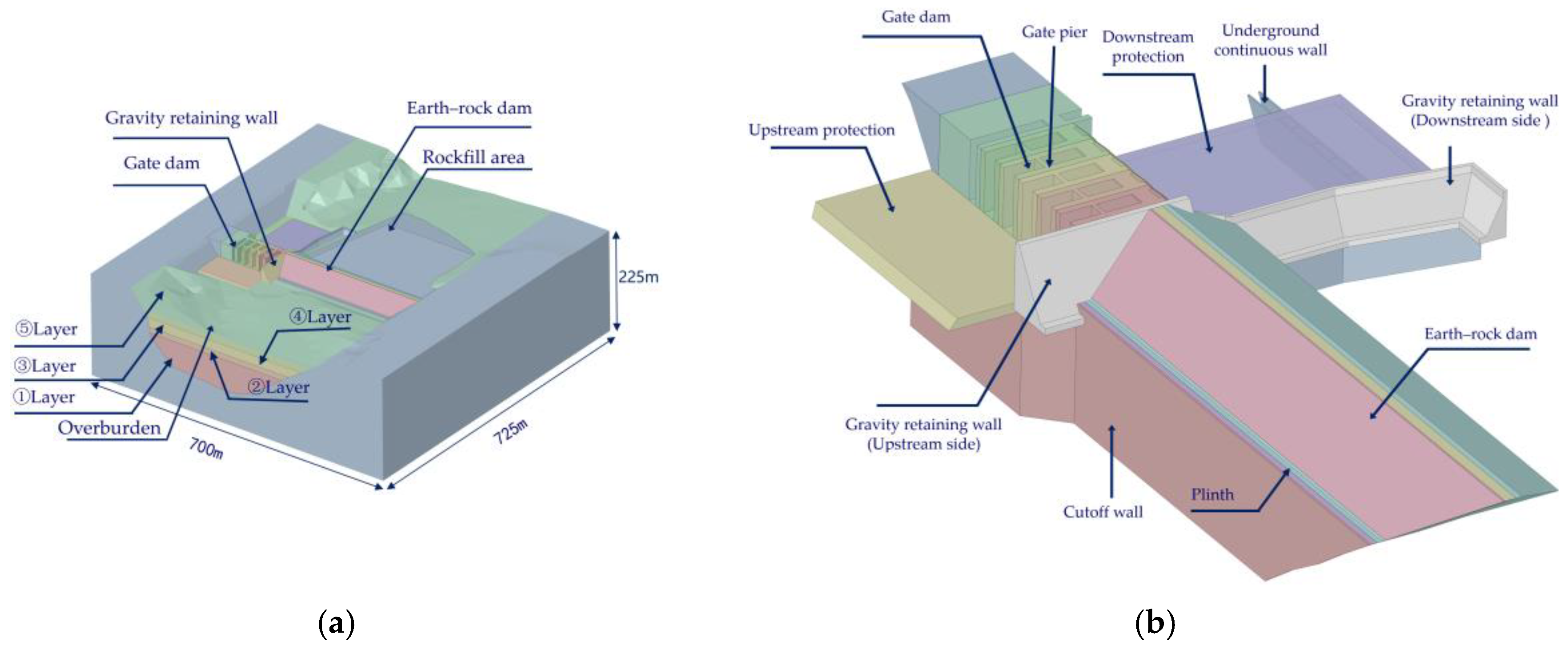
The project examined here is a hybrid hydraulic engineering project consisting of a concrete gate dam and a concrete-face rockfill dam. The main components include the gate dam section, a cutoff wall, an underground continuous wall, a gravity-retaining wall, and a rockfill dam section with a concrete face, which contains multiple layers of covering soil. The project is characterized by numerous irregular structures, intersecting components, and complex connections, posing a serious challenge to conventional modeling methods and requiring extensive simplification in the analysis. Based on the design parameters, this report describes efficient BIM (building information modeling) technology that is used to establish a geometric entity model of the entire dam system, accurately reflecting the spatial characteristics of the terrain and key components, as shown in Figure 2.

3.2. Grid Discretization

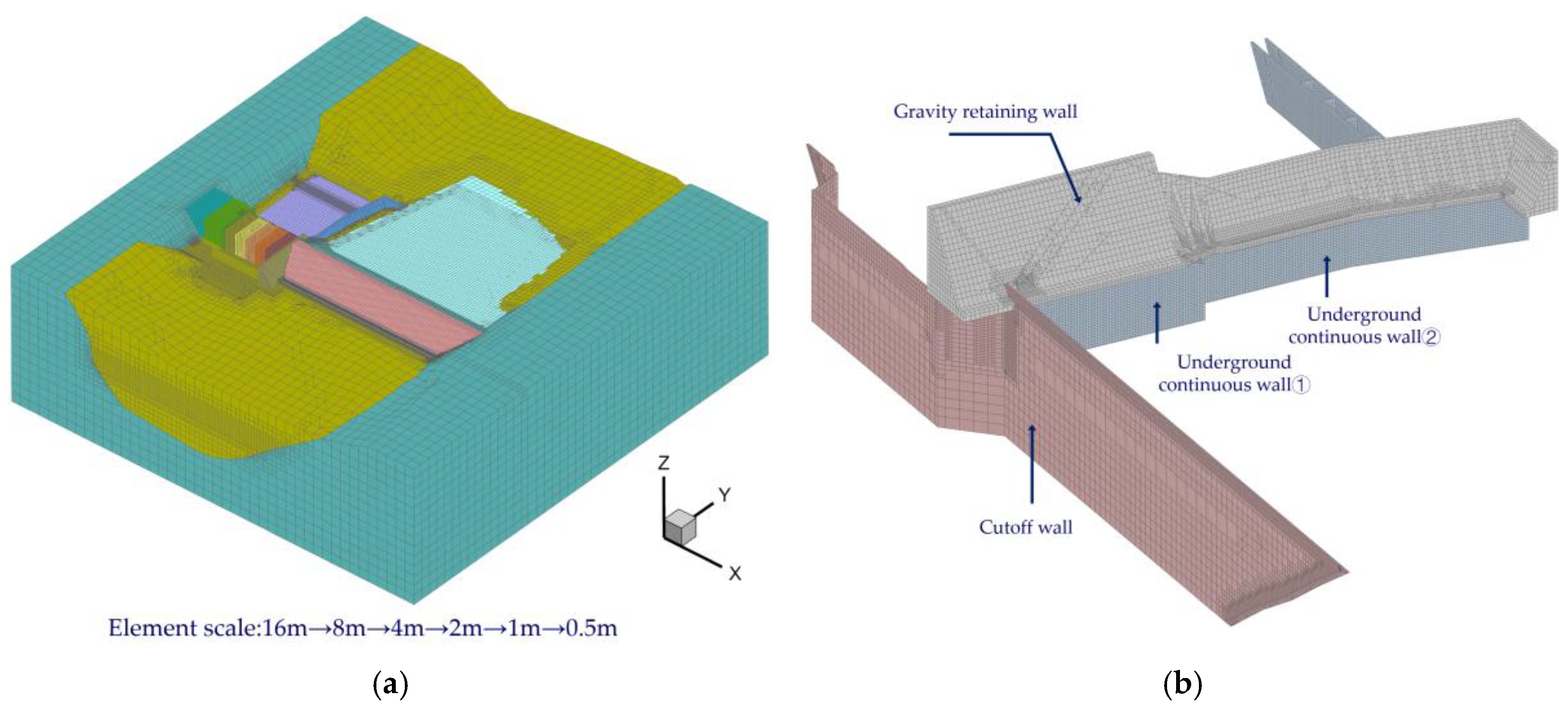
Using the refined modeling method developed by the authors, an efficient cross-scale discretization of the geometric model was achieved. Local grid refinement was performed on key components in dam design, such as gates, cutoff walls, gravity walls, and panels, resulting in a total of 778,195 elements, 842,876 nodes, and more than 2.5 million degrees of freedom, thereby enhancing the reliability of the analysis results. The three-dimensional grid used in this discretization is shown in Figure 3.

3.3. Grid Discretization

Concrete structures are modeled using a linear elastic model, while soil is modeled using an improved generalized plasticity model developed by the authors. Parameters are calibrated based on relevant experimental results (see Table 1), where $G_0$ is the elastic shear modulus; $K_0$ is the elastic bulk modulus; $M_g$ is the slope of the critical state line in the $p^{\prime }-q$ plane; ${\alpha }_g$ is the material constant; $H_0$ is the plastic modulus coefficient; $H_{U0}$ is the initial unloading modulus; and $M_f$, ${\alpha }_f$, $m_s$, $m_v$, $m_l$, $m_u$, $r_d$, ${\gamma }_{DM}$, ${\gamma }_u$, ${\beta }_0$, and ${\beta }_1$ are model parameters. $m_v$ and $m_s$ can be determined based on the initial slope of the stress–strain relationship curve under different confining pressures; $m_l$ and $m_u$ are determined by fitting the stress–strain relationship curves under different confining pressures; and $r_d$ is determined based on cyclic loading tests [22]. The soil–structure interface uses a state-dependent generalized plastic contact model [23]. The aforementioned constitutive models were integrated into the research team’s self-developed high-performance geotechnical engineering analysis software system, GEODYNA8.0. This software has been applied to the seismic analysis of several world-class high dams in China [24,25,26,27,28].

4. Calculation Results and Analysis

4.1. Dam Deformation

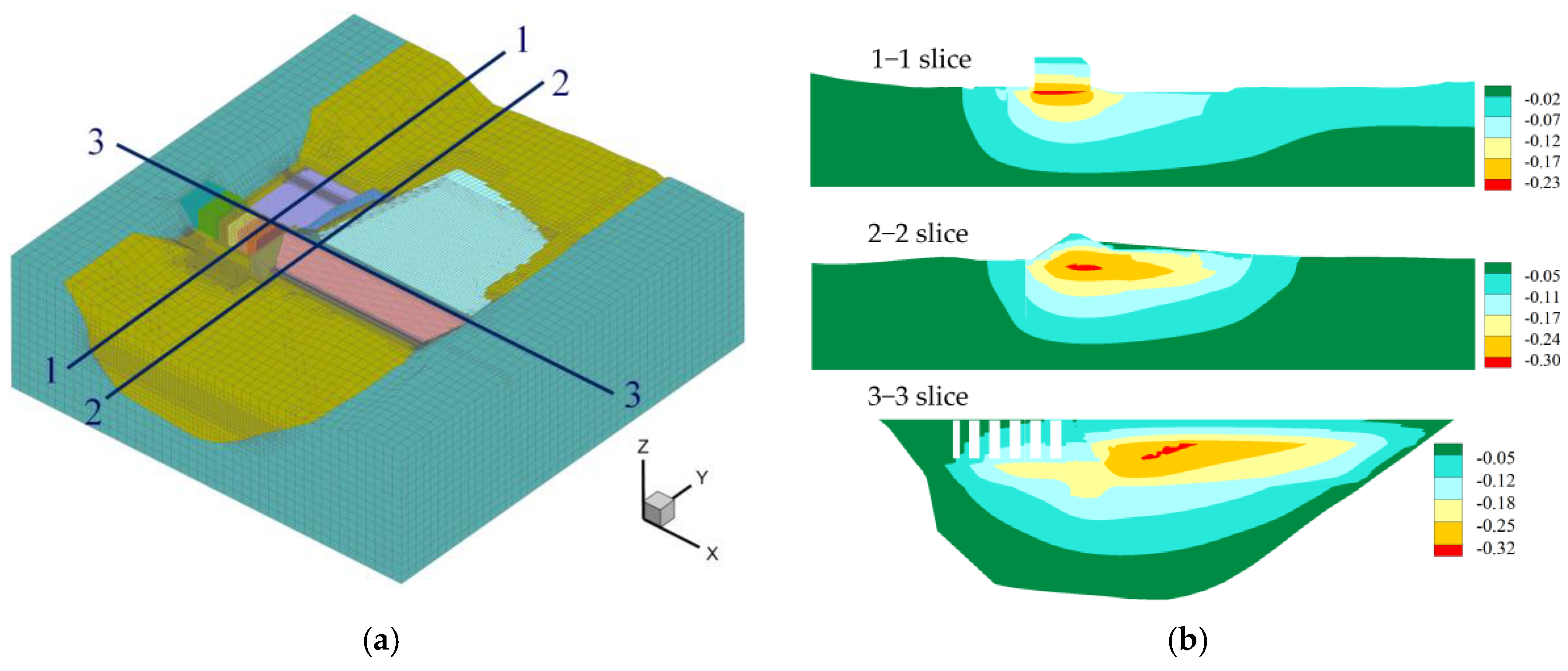
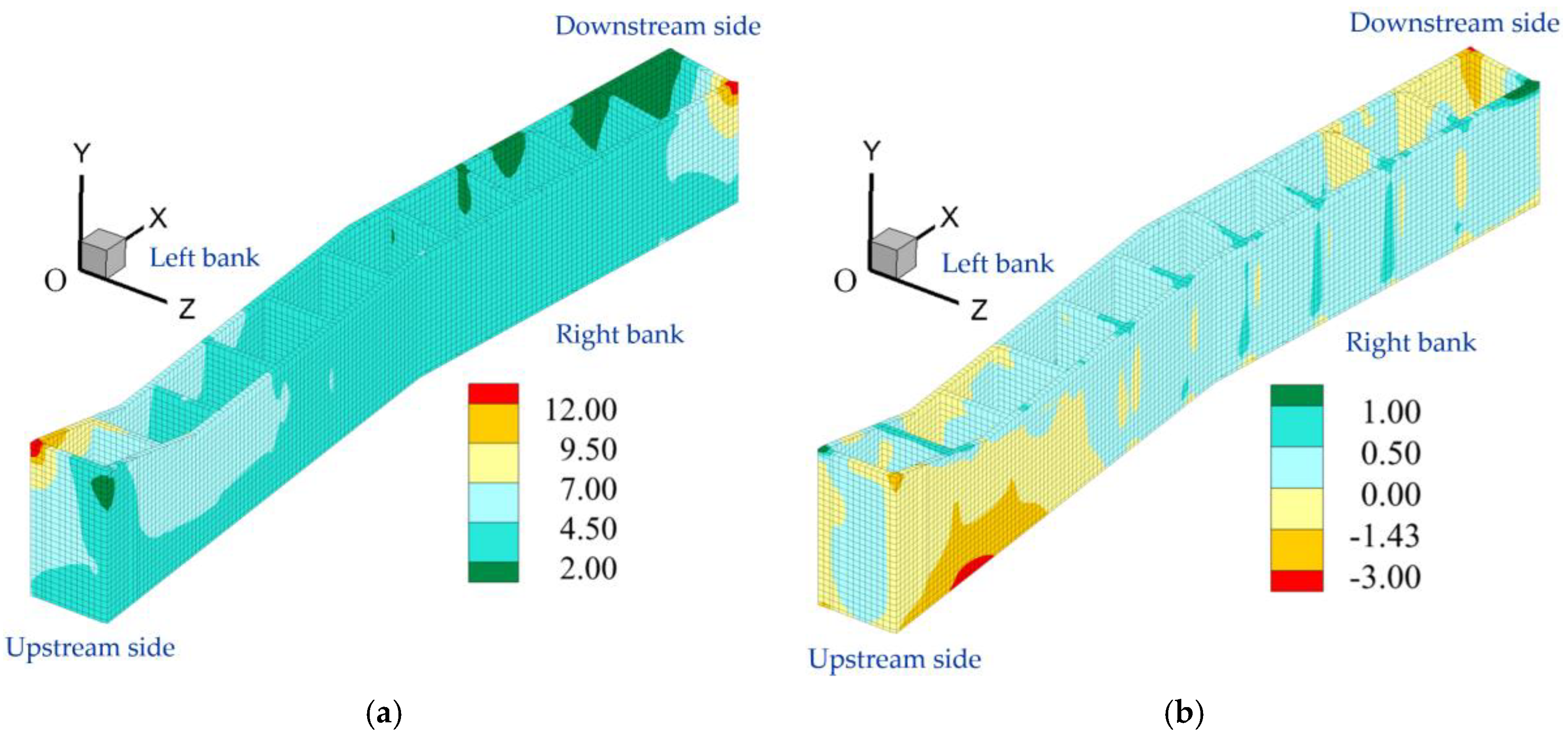
Figure 4 shows the vertical deformation patterns of three representative cross-sections of the mixed dam system, which exhibit two main characteristics: (1) The maximum vertical settlement of the earth–rock dam section is approximately 0.32 m, while that of the gate dam section is approximately 0.23 m. The deformation difference between the two dam sections is approximately 28.1%. This is because the earth–rock dam has a larger volume, resulting in greater soil deformation caused by its construction compared to the gate dam section. (2) The dam exhibits significant non-uniform settlement deformation along the dam axis, primarily due to the uneven spatial distribution of soil layers. The gate dam section has relatively few weak soil layers at the lower section, while the earth–rock dam section has a more extensive distribution of weak soil layers. Additionally, the larger volume of the earth–rock dam section results in relatively greater soil deformation.

4.2. Joint Displacement in the Gate Dam Section

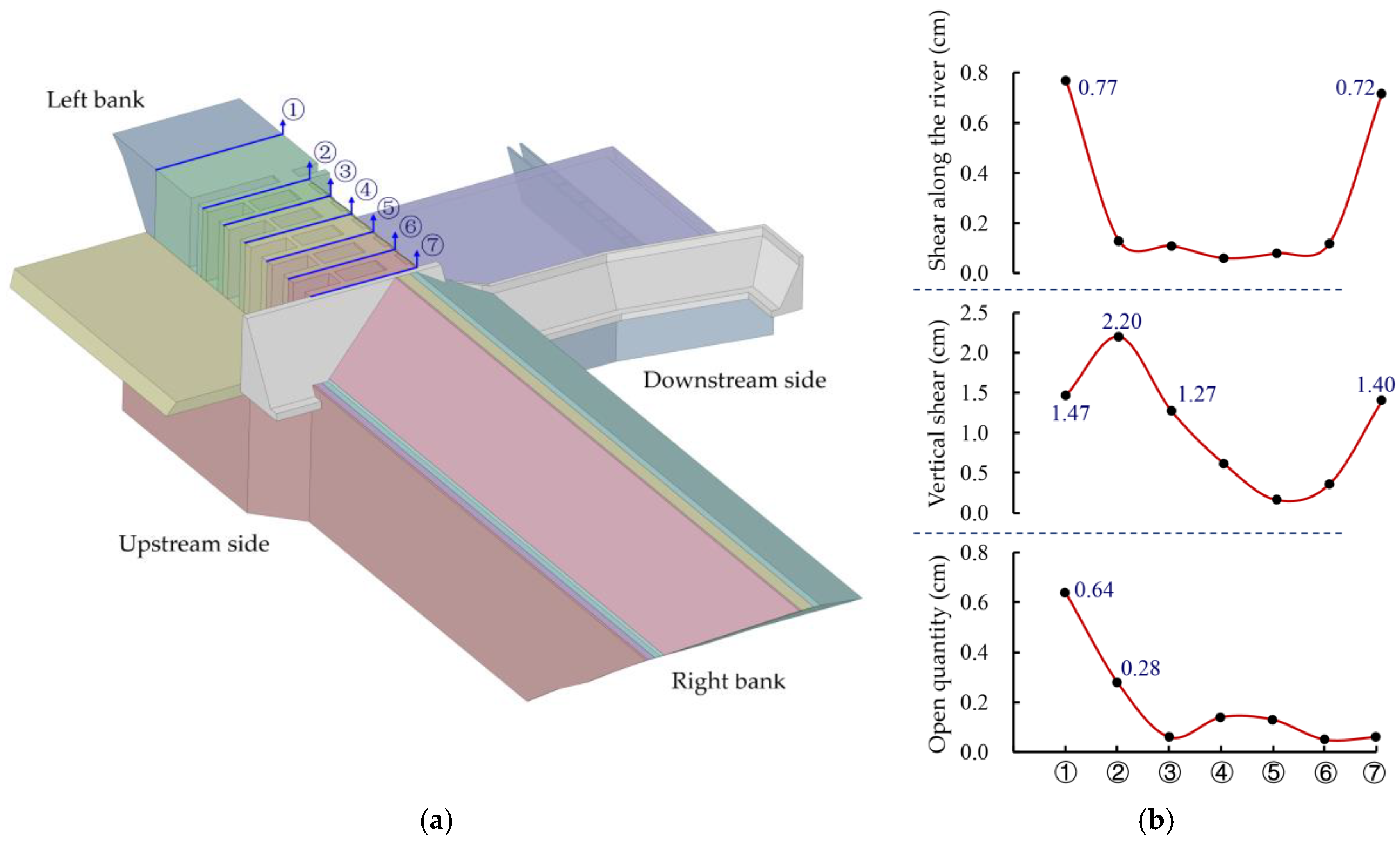
Figure 5 shows the location of the indirect joints between the gate piers in the gate dam section and the deformation patterns of each joint after impoundment. The following can be observed: Joints ① and ⑦ exhibit significant lateral displacement along the river axis; the vertical displacement and opening displacement of joints ①, ②, and ③ on the left bank are relatively large, primarily due to the thickness of the overlying soil layer at the base of the left bank gate piers, increasing gradually along the dam axis, resulting in slight differences in vertical settlement between the gate piers. Additionally, joint ⑦ also exhibits significant vertical displacement, primarily due to the greater vertical deformation of the panel dam section compared to the gate dam section, which causes joint displacement deformation. Overall, the deformation of the joints in all directions is relatively small and remains within the design allowable range.

4.3. Stress and Deformation of the Cutoff Wall

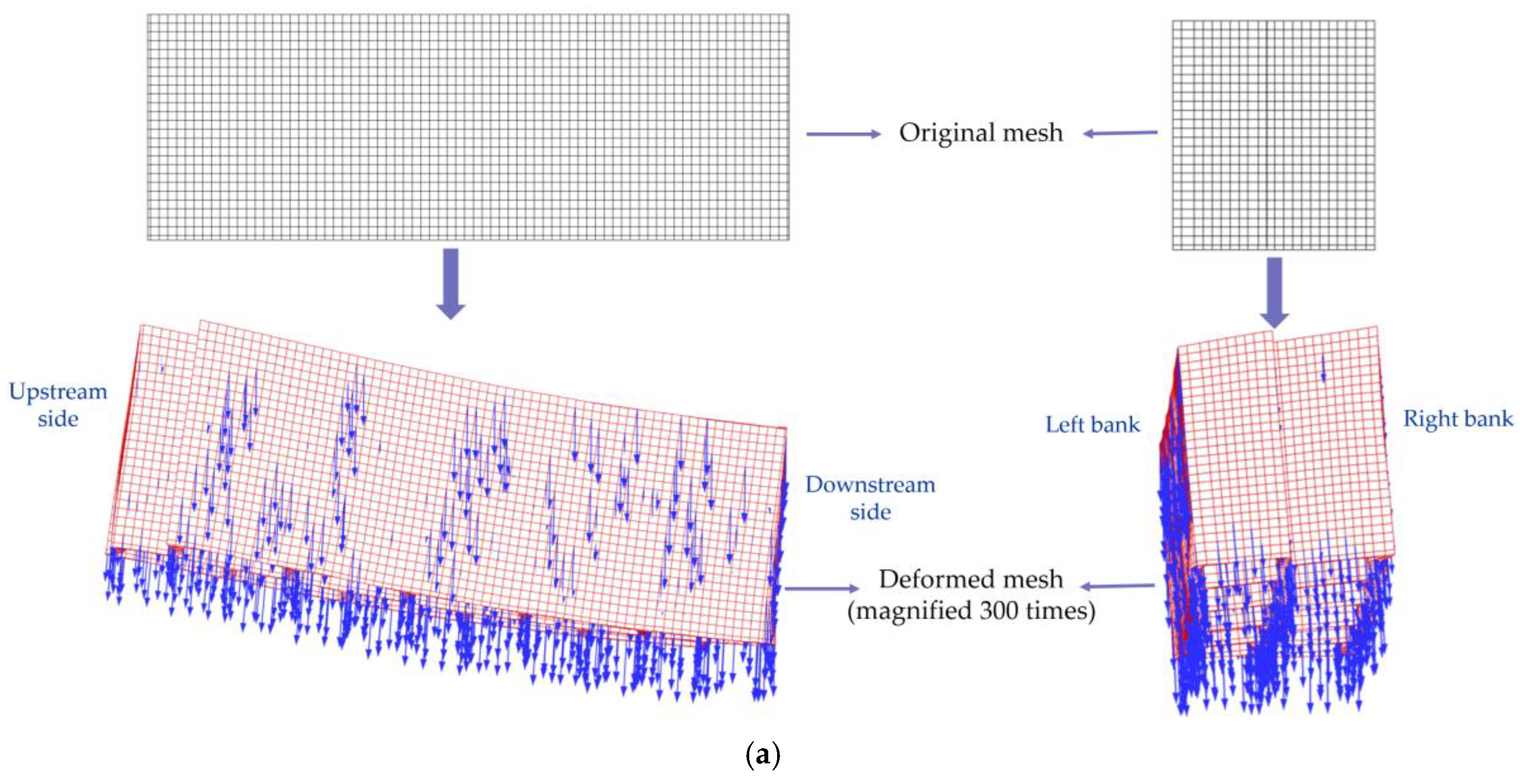
Figure 6 shows the distribution pattern of deformation in the cutoff wall after impoundment. Due to the uplift effect of the bedrock in both banks, the vertical direction is subjected to the gravitational force of the upper gravity retaining wall and the dam body load. The maximum vertical settlement of the cutoff wall occurs in the middle of the river valley, reaching 0.07 m. Due to the influence of vertical settlement deformation, the walls on both banks tend to deform toward the middle of the river valley, with the maximum deformation along the dam axis on the right bank being 0.02 m. 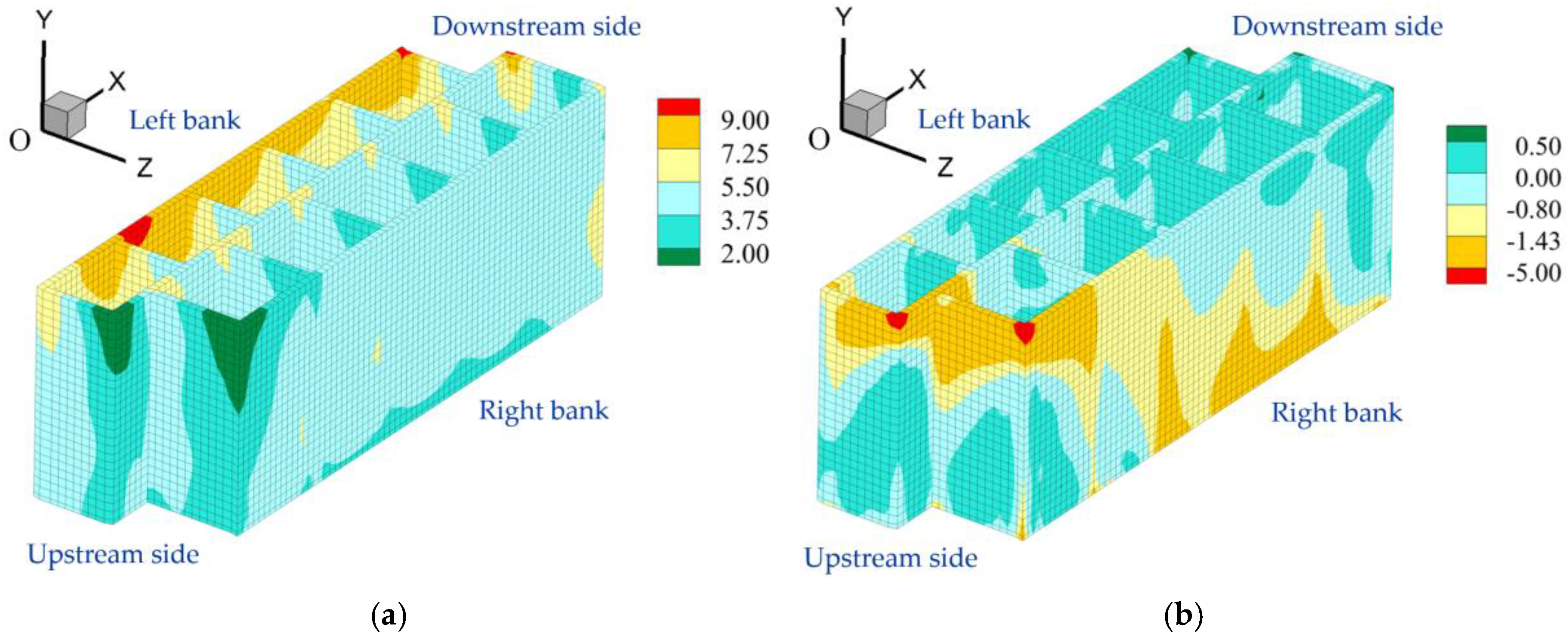Figure 7 shows the stress distribution characteristics of the cutoff wall, with the maximum compressive stress of 9.0 MPa primarily occurring in two regions: ① the lower part of the gravity retaining wall, due to vertical settlement of the cutoff wall causing compressive stress along the dam axis and in the river direction, and ② the bottom of the right bank cutoff wall, primarily due to the strong supporting effect of the bedrock on both banks of the cutoff wall, causing mismatched deformation between the wall bodies and the surrounding soil layers, thus resulting in significant stress concentration at the wall base. Similarly, this uneven settlement deformation pattern also causes a large tensile stress zone at the top of the right bank wall, with a maximum tensile stress of 2.6 Mpa, which can be addressed through reinforcement measures such as adding reinforcing bars.

4.4. Stress and Deformation of Underground Continuous Walls

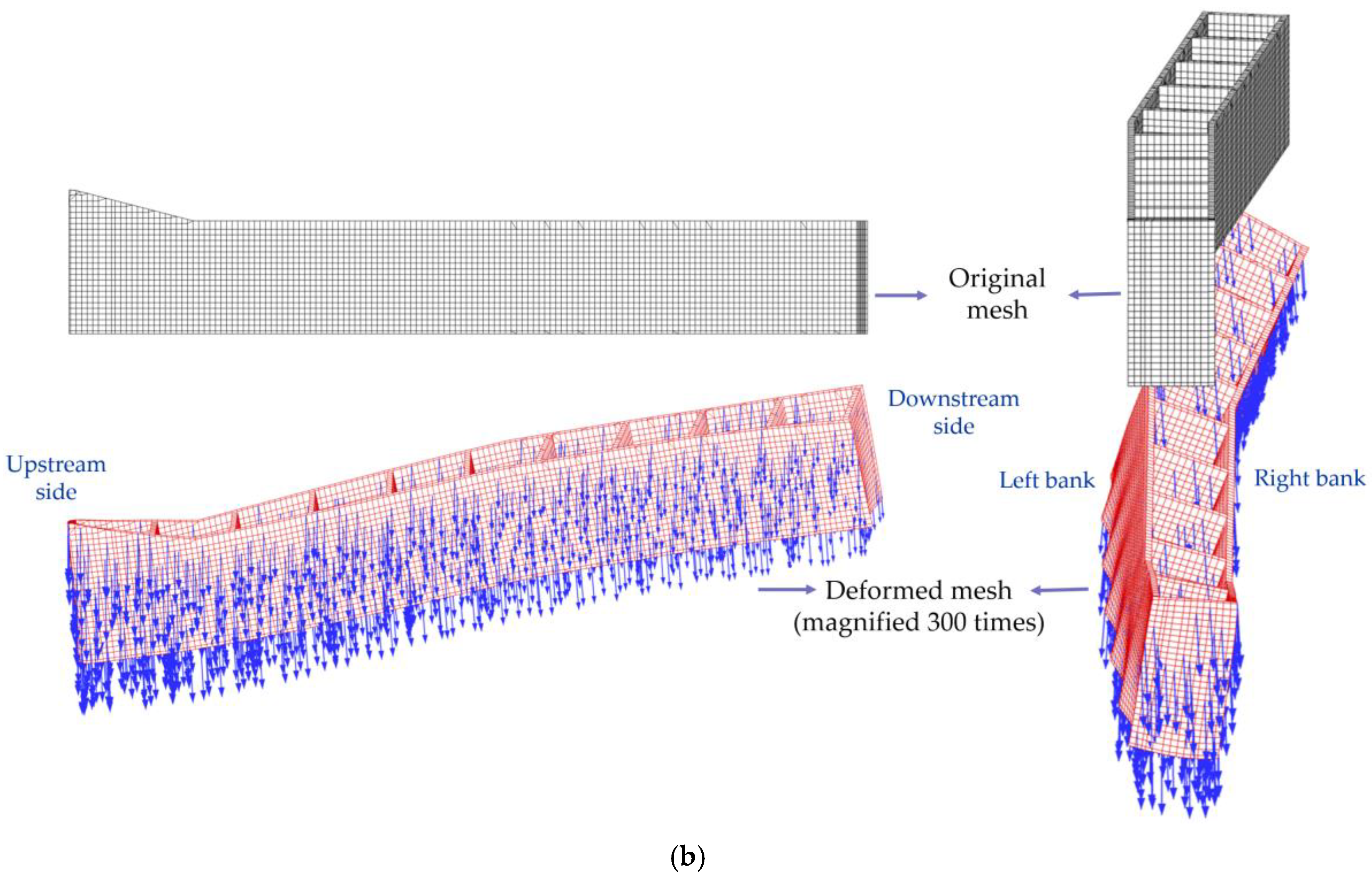
Figure 8 shows the spatial distribution of deformation patterns for the gravity retaining walls. Due to the uneven spatial distribution of loads on the upper part of the underground continuous wall ①, the wall exhibits a spatial distribution characterized by greater deformation on the downstream side and the left bank. Similarly, since the loads in the earth–rock dam section are primarily concentrated at the top of the upstream side of the underground continuous wall ②, the upstream side of the wall experiences greater deformation, accompanied by clockwise rotation in the river direction. Figure 9 and Figure 10 illustrate the stress distribution characteristics of the wall under the aforementioned deformation mode. Firstly, for the underground continuous wall ①, since the upstream side deformation is smaller than the downstream side deformation, the wall bottom exhibits bending deformation in the XOY plane, resulting in tensile stress along the river direction. Secondly, due to the rigid contact between the top and the gravity retaining wall, the upstream side of the wall tends to bend along the XOY plane under this deformation pattern, resulting in significant tensile stress at the top of the wall, with a maximum of 5.0 Mpa, primarily caused by vertical stress. Similarly, for the underground continuous wall ②, due to uneven vertical settlement, the upstream side of the wall bottom exhibits bending deformation in the XOY plane, resulting in tensile stress of 3.0 Mpa, primarily caused by stress parallel to the river.

5. Conclusions

Taking a specific construction project as our background and using independently developed cross-scale detailed modeling and analysis methods combined with a generalized plasticity model of soil, we conducted a comprehensive three-dimensional stress–deformation characteristic analysis of a gate dam and earth–rock dam system with deep overburden. The results show the following:

• Due to the uneven distribution of dam body loads and soil layers, the spatial unevenness of deformation in the mixed dam system is obvious. This is the main reason why the displacement of the indirect joints between the gate piers in the gate dam section is large on both sides of the dam but small in the middle section.
• The vertical cutoff wall in the middle of the river valley is subjected to the gravitational force of the upper gravity retaining wall and the load of the dam body, while the embedded sections on both sides are constrained by the rock foundation. This results in uneven settlement deformation, with more deformation in the middle and less deformation on both sides. This causes a certain amount of tensile stress at the top of the cutoff wall in the right bank, which can be reinforced.
• The spatial non-uniformity of deformation in the underground continuous wall is pronounced. In the region where the maximum vertical deformation occurs, the bottom of the wall exhibits significant tensile stress, primarily caused by in-line stress. Additionally, due to the rigid contact between the top of the wall and the gravity retaining wall, the deformation of the underground continuous wall along the in-line direction is restricted. Consequently, tensile stress appears at the top of the wall on the side with the smallest vertical deformation, primarily caused by vertical stress.

In the future, the authors will investigate the dynamic response characteristics of gate dam and earth–rock dam systems and will explore the impact of liquefaction of weak soil layers on the superstructure. Additionally, by combining a concrete plastic damage model and a generalized plastic constitutive model of soil, the authors will elucidate the failure evolution patterns of concrete structures, such as cutoff walls and gate dams, providing theoretical references for seismic safety assessments of engineered structures.