Submitted:
04 July 2025
Posted:
07 July 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Background: the Lever Rule and the Short-Range Order Configuration Model
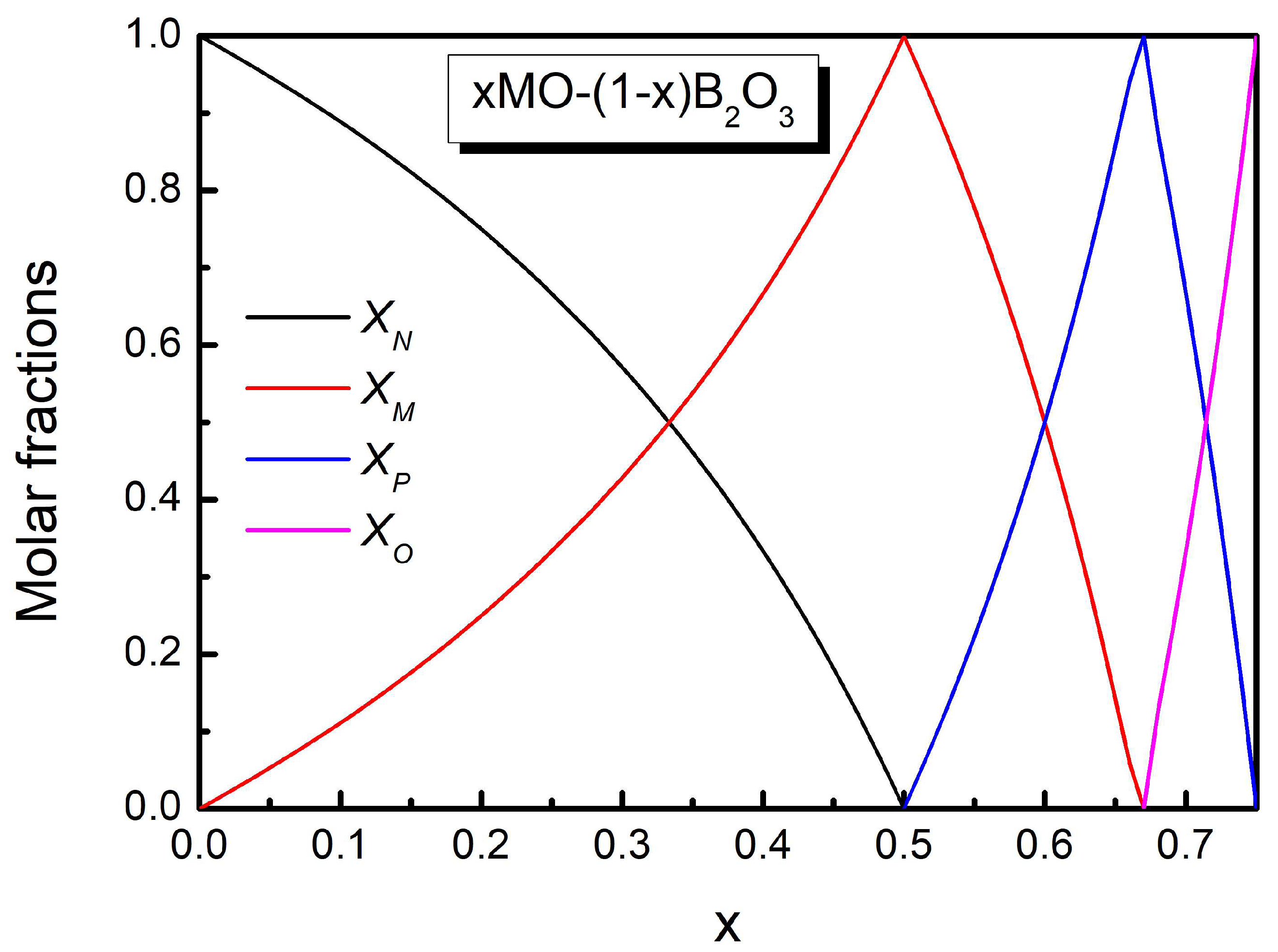
2.1. The Conventional Lever Rule
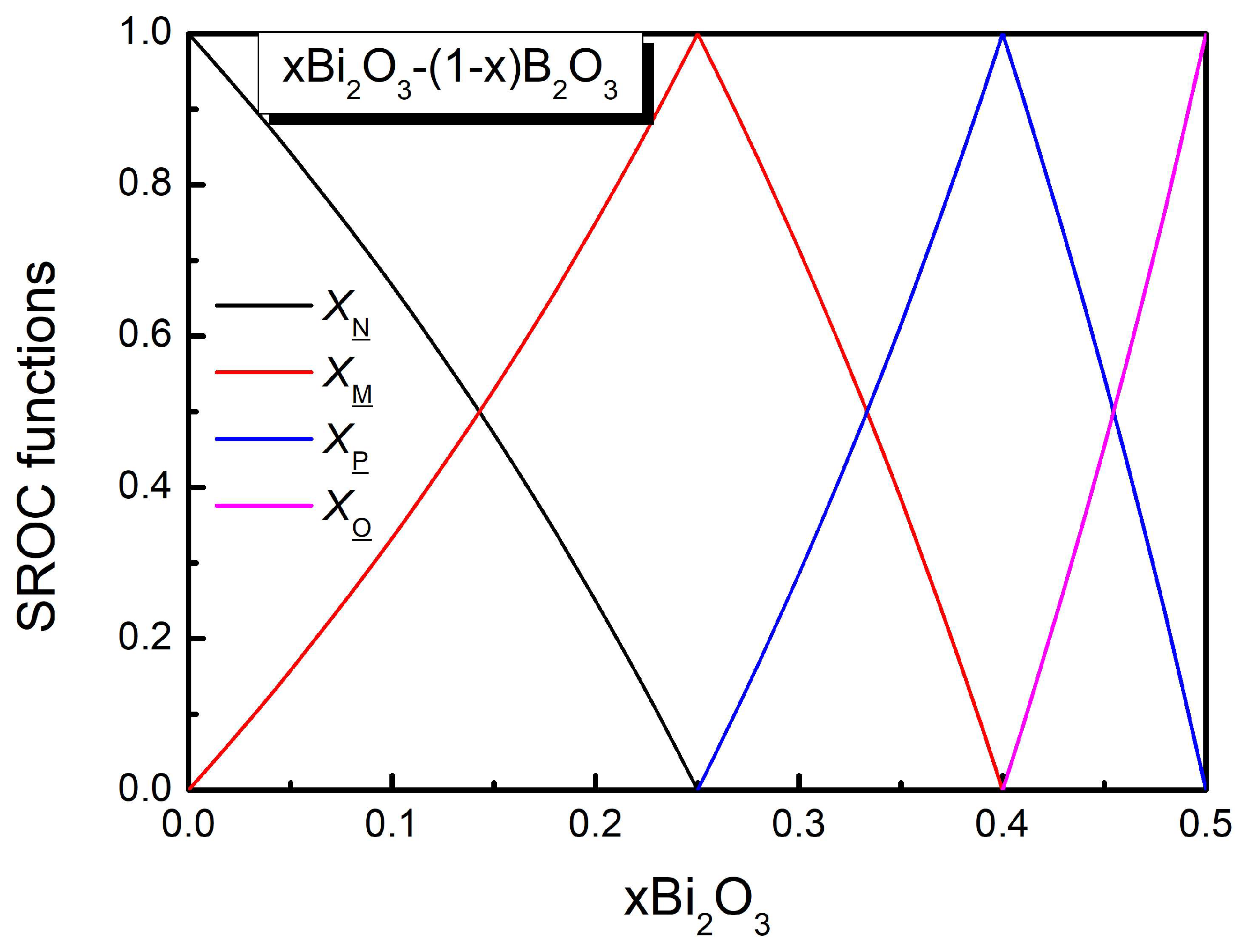
2.2. The Original SROC Model
2.3. Comments on the SROC Model
3. Results and Discussion
3.1. The SROC Model in Bismuth Borate Glasses
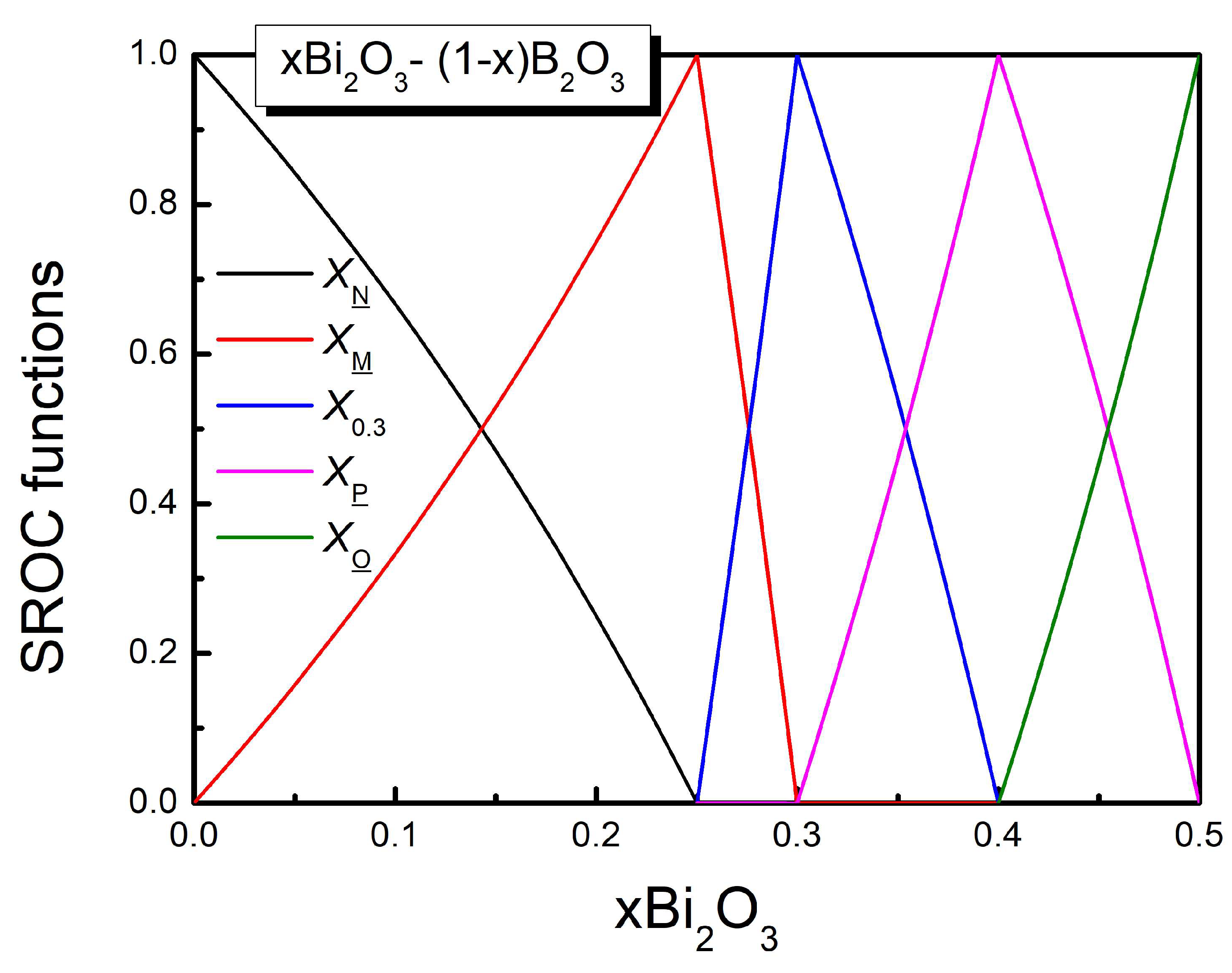
3.2. The Augmented SROC Model, ASROC
4. Conclusions
Author Contributions
Funding
Abbreviations
| SROC | Short-Range Order Configuration |
| ASROC | Augmented Short-Range Order Configuration |
References
- Ashcroft, N.W., M. D. Solid State Physics; 1st ed.; W.B. Saunders Company: Philadelphia, 1976. [Google Scholar]
- Santos, S.N.C.; Almeida, J.M.P.; Paula, K.T.; Tomazio, N.B.; Mastelaro, V.R.; Mendonça, C.R. Characterization of the Third-Order Optical Nonlinearity Spectrum of Barium Borate Glasses. Opt. Mater. 2017, 73, 16–19. [Google Scholar] [CrossRef]
- Venkata Rao, K.; Babu, S.; Venkataiah, G.; Ratnakaram, Y.C. Optical Spectroscopy of Dy3+ Doped Borate Glasses for Luminescence Applications. J. Mol. Struct. 2015, 1094, 274–280. [Google Scholar] [CrossRef]
- Torimoto, A.; Masai, H.; Okada, G.; Kawaguchi, N.; Yanagida, T. Emission Properties of Ce-Doped Alkaline Earth Borate Glasses for Scintillator Applications. Opt. Mater. 2017, 73, 517–522. [Google Scholar] [CrossRef]
- Kirdsiri, K.; Rajaramakrishna, R.; Damdee, B.; Kim, H.J.; Nuntawong, N.; Horphathum, M.; Kaewkhao, J. Influence of Alkaline Earth Oxides on Eu3+ Doped Lithium Borate Glasses for Photonic, Laser and Radiation Detection Material Applications. Solid State Sci. 2019, 89, 57–66. [Google Scholar] [CrossRef]
- Al-Buriahi, M.S.; Sriwunkum, C.; Arslan, H.; Tonguc, B.T.; Bourham, M.A. Investigation of Barium Borate Glasses for Radiation Shielding Applications. Appl. Phys. A 2020, 126, 68. [Google Scholar] [CrossRef]
- Khajonrit, J.; Montreeuppathum, A.; Kidkhunthod, P.; Chanlek, N.; Poo-arporn, Y.; Pinitsoontorn, S.; Maensiri, S. New Transparent Materials for Applications as Supercapacitors: Manganese-Lithium-Borate Glasses. J. Alloys Compd. 2018, 763, 199–208. [Google Scholar] [CrossRef]
- Dua, V.; Arya, S.K.; Singh, K. Review on Transition Metals Containing Lithium Borate Glasses Properties, Applications and Perspectives. J. Mater. Sci. 2023, 58, 8678–8699. [Google Scholar] [CrossRef]
- Ege, D.; Zheng, K.; Boccaccini, A.R. Borate Bioactive Glasses (BBG): Bone Regeneration, Wound Healing Applications, and Future Directions. ACS Appl. Bio Mater. 2022, 5, 3608–3622. [Google Scholar] [CrossRef]
- Krogh-Moe, J. The Infrared Spectra of Some Vitreous and Crystalline Borates. Arkiv Kemi 1958, 12, 475–480. [Google Scholar]
- Krogh-Moe, J. On the Structure of Boron Oxide and Alkali Borate Glasses. Phys. Chem. Glasses 1960, 1, 26–31. [Google Scholar]
- Krogh-Moe, J. Interpretation of the Infra-Red Spectra of Boron Oxide and Alkali Borate Glasses. Phys. Chem. Glasses 1965, 6, 46–54. [Google Scholar]
- Bray, P.J.; O’Keefe, J.G. Nuclear Magnetic Resonance Investigations of the Structure of Alkali Borate Glasses. Phys. Chem. Glasses 1963, 4, 37–46. [Google Scholar]
- Silver, A.H.; Bray, P.J. Nuclear Magnetic Resonance Absorption in Glass. I. Nuclear Quadrupole Effects in Boron Oxide, Soda Boric Oxide, and Borosilicate Glasses. The Journal of Chemical Physics 1958, 3, 984–990. [Google Scholar] [CrossRef]
- Bray, P.J.; Feller, S.A.; Jellison Jr., G. E.; Yun, Y.H. B10 NMR Studies of the Structure of Borate Glasses. Journal of Non-Crystalline Solids 1980, 38–39, 93–98. [Google Scholar] [CrossRef]
- Kamitsos, E.I.; Chryssikos, G.D. Borate Glass Structure by Raman and Infrared Spectroscopies. J. Mol. Struct. 1991, 247, 1–16. [Google Scholar] [CrossRef]
- Varsamis, C.P.; Kamitsos, E.I.; Chryssikos, G.D. Structure of Fast-Ion-Conducting AgI-Doped Borate Glasses in Bulk and Thin Film Forms. Phys. Rev. B 1999, 60, 3885–3898. [Google Scholar] [CrossRef]
- Machowski, P.M.; Varsamis, C.P.E.; Kamitsos, E.I. Dependence of Sodium Borate Glass Structure on Depth from the Sample Surface. J. Non-Cryst. Solids 2004, 345–346, 213–218. [Google Scholar] [CrossRef]
- Chryssikos, G.D.; Kamitsos, E.I.; Patsis, A.P.; Karakassides, M.A. On the Structure of Alkali Borate Glasses Approaching the Orthoborate Composition. Mater. Sci. Eng. B 1990, 7, 1–4. [Google Scholar] [CrossRef]
- Kamitsos, E.I.; Patsis, A.P.; Karakassides, M.A.; Chryssikos, G.D. Infrared Reflectance Spectra of Lithium Borate Glasses. J. Non-Cryst. Solids 1990, 126, 52–67. [Google Scholar] [CrossRef]
- Kamitsos, E.I.; Patsis, A.P.; Chryssikos, G.D. Infrared Reflectance Investigation of Alkali Diborate Glasses. J. Non-Cryst. Solids 1993, 152, 246–257. [Google Scholar] [CrossRef]
- Aguiar, P.M.; Kroeker, S. Boron Speciation and Non-Bridging Oxygens in High-Alkali Borate Glasses. J. Non-Cryst. Solids 2007, 353, 1834–1839. [Google Scholar] [CrossRef]
- Montouillout, V.; Fan, H.; Del Campo, L.; Ory, S.; Rakhmatullin, A.; Fayon, F.; Malki, M. Ionic Conductivity of Lithium Borate Glasses and Local Structure Probed by High Resolution Solid-Sate NMR. J. Non-Cryst. Solids 2018, 484, 57–64. [Google Scholar] [CrossRef]
- Chatzipanagis, K.I.; Tagiara, N.S.; Kamitsos, E.I.; Barrow, N.; Slagle, I.; Wilson, R.; Greiner, T.; Jesuit, M.; Leonard, N.; Phillips, A.; et al. Structure of Lead Borate Glasses by Raman, 11B MAS, and 207Pb NMR Spectroscopies. J. Non-Cryst. Solids 2022, 589, 121660. [Google Scholar] [CrossRef]
- Song, L.; Wang, Y.; Zhai, T.; Sun, B.; Du, Y.; Feller, S.; Yin, W.; Xu, J.; Hannon, A.C.; Zhu, F. Revealing the Microstructure and Structural Origin of Glass-Forming Range of Magnesium Borate Glass. Ceram. Int. 2025, 51, 18966–18977. [Google Scholar] [CrossRef]
- Varsamis, C.P.; Vegiri, A.; Kamitsos, E.I. A Molecular Dynamics Study of Li-Doped Borate Glasses. Condens. Matter Phys. 2001, 4, 119. [Google Scholar] [CrossRef]
- Varsamis, C.-P.E.; Vegiri, A.; Kamitsos, E.I. Molecular Dynamics Investigation of Lithium Borate Glasses: Local Structure and Ion Dynamics. Phys. Rev. B 2002, 65, 104203. [Google Scholar] [CrossRef]
- Vegiri, A.; Varsamis, C.-P.E.; Kamitsos, E.I. Composition and Temperature Dependence of Cesium-Borate Glasses by Molecular Dynamics. J. Chem. Phys. 2005, 123, 014508. [Google Scholar] [CrossRef] [PubMed]
- Sahu, P.; Pente, A.A.; Singh, M.D.; Chowdhri, I.A.; Sharma, K.; Goswami, M.; Ali, Sk.M.; Shenoy, K.T.; Mohan, S. Molecular Dynamics Simulation of Amorphous SiO2, B2 O3, Na2 O–SiO2, Na2 O–B2 O3, and Na2 O–B2 O3 –SiO2 Glasses with Variable Compositions and with Cs2 O and SrO Dopants. J. Phys. Chem. B 2019, 123, 6290–6302. [Google Scholar] [CrossRef]
- Kato, T.; Lodesani, F.; Urata, S. Boron Coordination and Three-membered Ring Formation in Sodium Borate Glasses: A Machine-learning Molecular Dynamics Study. J. Am. Ceram. Soc. 2024, 107, 2888–2900. [Google Scholar] [CrossRef]
- Ohkubo, T.; Sasaki, S.; Masuno, A.; Tsuchida, E. Ab Initio Molecular Dynamics Study of Trivalent Rare Earth Rich Borate Glasses: Structural Insights and Formation Mechanisms. J. Phys. Chem. B 2024, 128, 11800–11813. [Google Scholar] [CrossRef]
- Ohkubo, T.; Urata, S.; Imamura, Y.; Taniguchi, T.; Ishioka, N.; Tanida, M.; Tsuchida, E.; Deng, L.; Du, J. Modeling the Structure and Dynamics of Lithium Borosilicate Glasses with Ab Initio Molecular Dynamics Simulations. J. Phys. Chem. C 2021, 125, 8080–8089. [Google Scholar] [CrossRef]
- Varsamis, C.P.E.; Makris, N.; Valvi, C.; Kamitsos, E.I. Short-Range Structure, the Role of Bismuth and Property–Structure Correlations in Bismuth Borate Glasses. Phys. Chem. Chem. Phys. 2021, 23, 10006–10020. [Google Scholar] [CrossRef] [PubMed]
- Topper, B.; Möncke, D.; Youngman, R.E.; Valvi, C.; Kamitsos, E.I.; Varsamis, C.P.E. Zinc Borate Glasses: Properties, Structure and Modelling of the Composition-Dependence of Borate Speciation. Phys. Chem. Chem. Phys. 2023, 25, 5967–5988. [Google Scholar] [CrossRef] [PubMed]
- Bajaj, A.; Khanna, A.; Chen, B.; Longstaffe, J.G.; Zwanziger, U.-W.; Zwanziger, J.W.; Gómez, Y.; González, F. Structural Investigation of Bismuth Borate Glasses and Crystalline Phases. J. Non-Cryst. Solids 2009, 355, 45–53. [Google Scholar] [CrossRef]
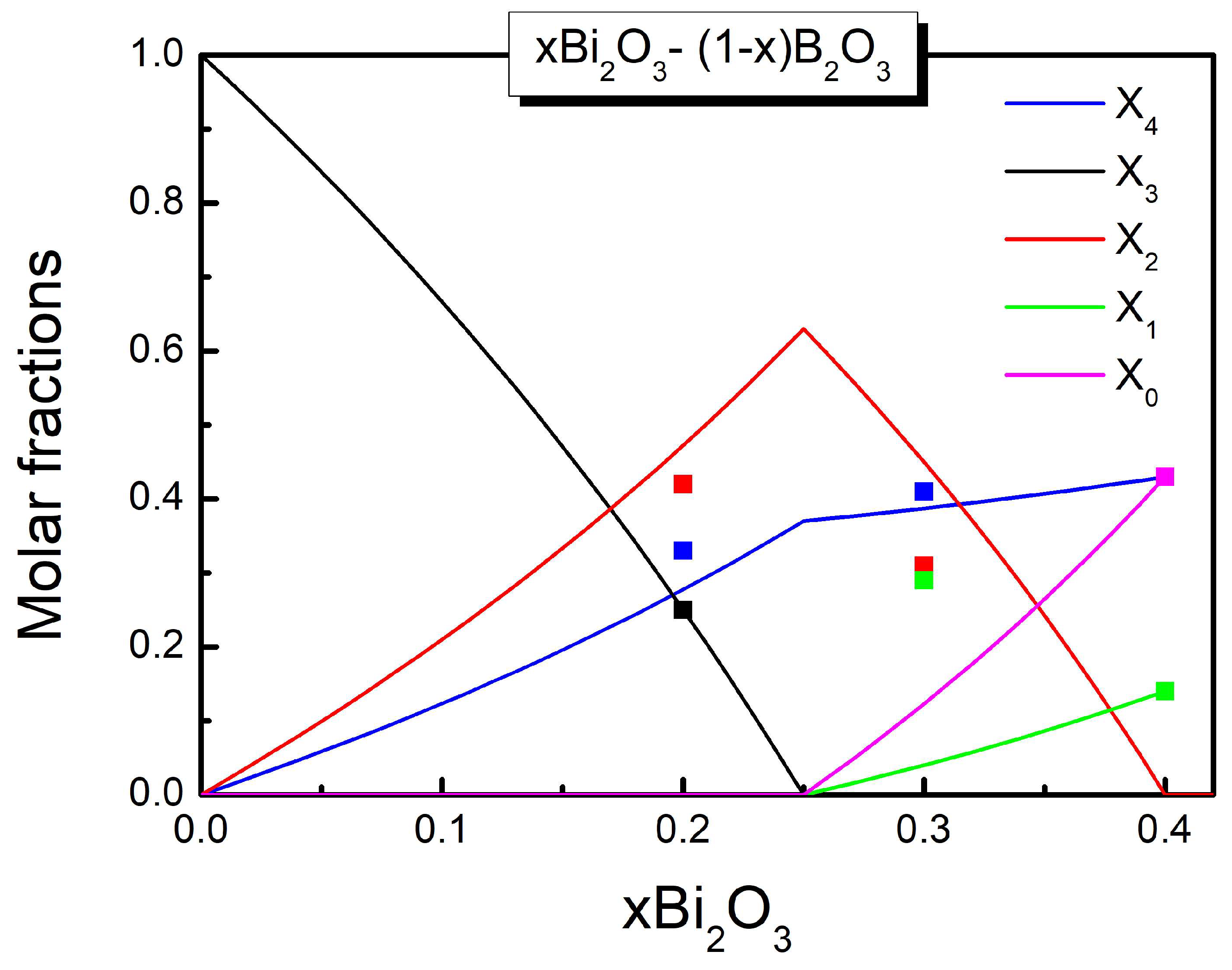
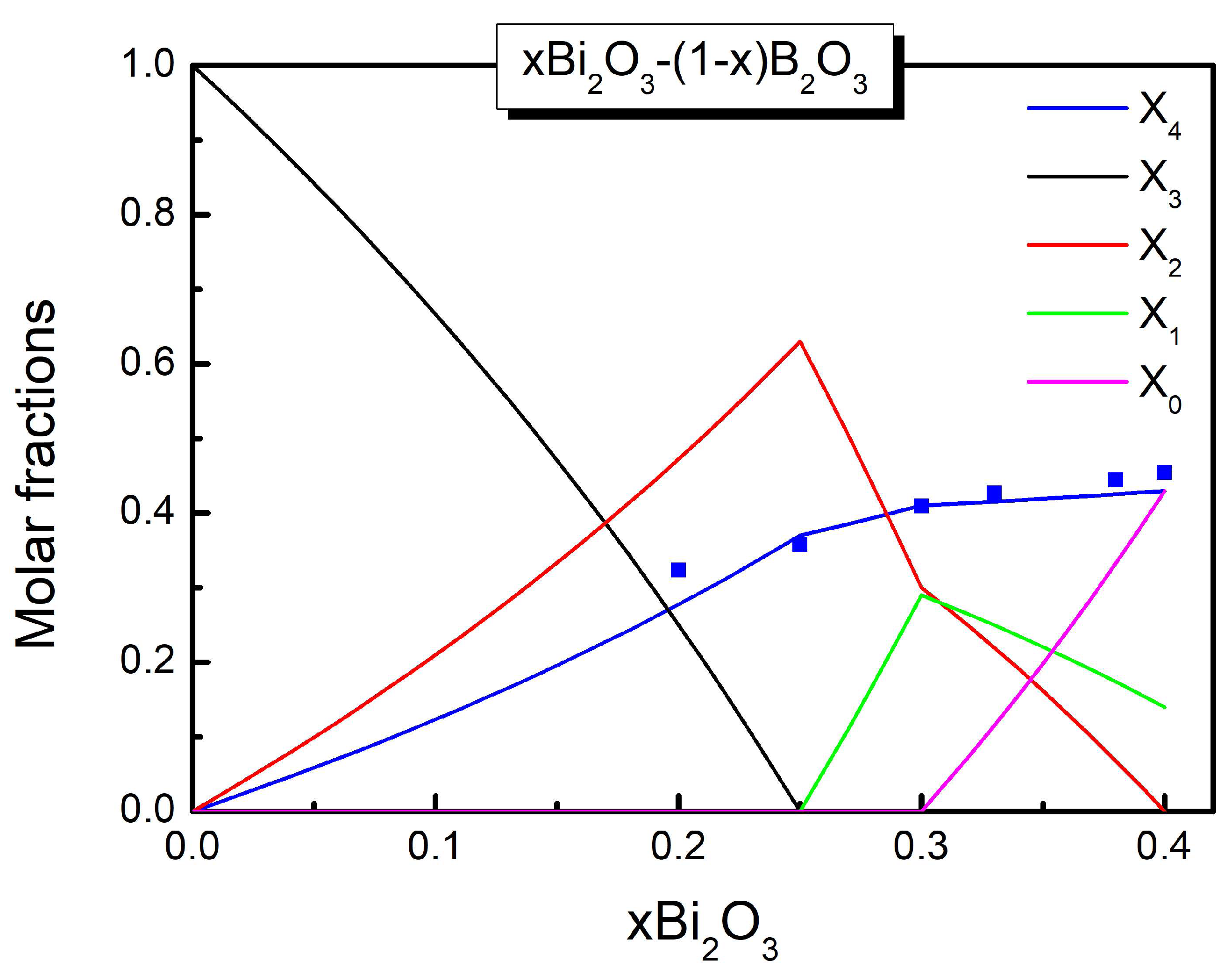
| x | |||||
| 0.20 | 0.250 | 0.330 | 0.420 | - | - |
| 0.30 | - | 0.408 | 0.306 | 0.286 | - |
| 0.40 | - | 0.430 | 0.140 | 0.430 |
| SROC | |||||
| N ( | 0 | 0 | 0 | 1 | 0 |
| M ( | 0 | 0 | 0.63 | 0 | 0.37 |
| P ( | 0.43 | 0.14 | 0 | 0 | 0.43 |
| SROC | |||||
| N (x= | 0 | 0 | 0 | 1 | 0 |
| M (x=0.25) | 0 | 0 | 0.63 | 0 | 0.37 |
| 0.3 (x=0.3) | 0 | 0.29 | 0.30 | 0 | 0.41 |
| P (x=0.4 | 0.43 | 0.14 | 0 | 0 | 0.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




