Maximum Likelihood Estimation of Parameters in the Power Normal Distribution

1. Introduction

The Box-Cox (BC) transformation [9] of a positive random variable is defined by

$$Y=\left\{\begin{array}{cc}{\displaystyle \frac{X^{\lambda }-1}{\lambda },}\hfill & \mathrm{if}\lambda \ne 0\hfill \\ {\displaystyle ln\left(X\right),}\hfill & \mathrm{if}\lambda =0\hfill \end{array}\right.$$

(1)

where $\lambda$ is the transformation parameter. Note that the data must be strictly positive, which implies that Y is bounded below by $-1/\lambda$. When the transformation is successful, Y is approximately normally distributed with mean $\mu$ and standard deviation $\sigma$. The probability distribution of the original variable X is known as the PN distribution, first introduced by Goto and Inoue [8], who also provided expressions for its moments in the form of power series.

The PN probability density function (PDF) is given by

$$f_X\left(x\right)={\displaystyle \frac{x^{\lambda -1}}{\sigma A(\lambda ,\mu ,\sigma )}}\varphi \left({\displaystyle \frac{x^{\left(\lambda \right)}-\mu }{\sigma }}\right),$$

(2)

where $x>0$ and $x^{\left(\lambda \right)}={\displaystyle \frac{x^{\lambda }-1}{\lambda }}$. The function $A(\lambda ,\mu ,\sigma )$ serves as a normalization constant and is defined as $\Phi \left(k\right)$, 1, or $\Phi \left(k\right)$ depending on whether $\lambda$ is positive, zero, or negative, respectively. The parameter k, which acts as a shape parameter of the distribution, is given by ${\displaystyle \frac{1+\mu \lambda }{\sigma \lambda }}$ and therefore depends on all three parameters. Here, $\Phi$ denotes the standard normal cumulative distribution function (CDF), and its derivative $\varphi$ is the standard normal probability density function (PDF). The inverse Box–Cox transformation for a truncated normal (TN) variable Y, when $\lambda \ne 0$, is given by $X={(\lambda Y+1)}^{1/\lambda }$.

The PN distribution in the context of the BC transformation was also studied in [10], where expressions for the mean, variance, and quantile functions were derived, and a quantile-based measure of skewness was introduced to show that the PN family is ordered with respect to the transformation parameter. Furthermore, the same paper demonstrates, using Chebyshev–Hermite polynomials, that the correlation coefficient is smaller on the PN scale.

In [1], a formula for the ordinary moments is provided, and the marginal and conditional probability density functions are derived. Additionally, the correlation curve is computed and fitted to a power law model.

For further information and analysis on the PN distribution, see [2,11], and for the BC transformation, see [5].

This paper is organized as follows. In Section 2, we present the log-likelihood function for the PN distribution and provide formulas for estimating $\mu$ and $\sigma$. We also describe the procedures followed in detail. We recall that the maximum likelihood (ML) estimator of the parameter $\lambda$ is asymptotically normal, and we specify its asymptotic distribution. Subsequently, we derive the recursive relation for the N-R method applied to this maximization problem. Furthermore, we present the gradient vector and the Hessian matrix of the log-likelihood function with respect to the parameters $\lambda$, $\mu$, and $\sigma$, as used in the implementation of the estimation algorithm. In Section 3, we describe the simulation procedure employed to generate the data sets for parameter estimation and then report and interpret the results. Finally, in Section 4, we summarize the main conclusions and suggest directions for future research concerning the PN distribution.

2. Maximum Likelihood Estimation in the PN Distribution

In this section, we revisit the MLE in the context of the PN distribution. Following Goto et al. [4], we consider two estimation methods: the truncated Log-likelihood method ($M_1$) and the exact Log-likelihood method ($M_2$). For the former, we report only the estimation results; for the latter, we provide a full methodological description along with a comprehensive simulation study. Within the $M_2$ approach, we compare two scenarios: one in which all three parameters are estimated jointly ($v_1$), and another in which only $\lambda$ is optimized ($v_2$) while $\mu$ and $\sigma$ are estimated conditionally, as in Goto et al. [4].

Our estimation procedure differs from that of Goto et al. [4] in that we explicitly exploit the fact that the transformed data follow a TN distribution. This enables us to derive explicit formulas for the estimation of $\mu$ and $\sigma$, see [7]. We recall that, unlike in the Normal distribution where these parameters are independent, they are correlated in both the PN and TN distributions. This correlation has important implications for their estimation. If n observations $y_1,y_2,···y_n$ have PN distribution with parameters $\lambda$, $\mu$ and $\sigma$ then the Log-likelihood function is,

$$\begin{array}{cc}\hfill log\left(L(y;\lambda ,\mu ,\sigma )\right)=& -{\displaystyle \frac{n}{2}}ln\left(2\pi \right)-{\displaystyle \frac{n}{2}}ln\left({\sigma }^2\right)\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}\sum _{i=1}^n{\left({\displaystyle \frac{y_i^{\left(\lambda \right)}-\mu }{\sigma }}\right)}^2\hfill \\ \hfill & +(\lambda -1)\sum _{i=1}^{n}ln\left(y_i\right)-nln\left(A\left(k\right)\right)\hfill \end{array}$$

(3)

where $y^{\left(\lambda \right)}={\displaystyle \frac{y^{\lambda }-1}{\lambda }}$. The approach of $M_1$ method is to take $A\left(k\right)=1$ as proposed by [9].

The $M_2$ method takes into account the whole Log- likelihood function. Using method $M_2$ the BC transformed data with the right parameter is expected to be TN distributed. The estimators of $\mu$ and $\sigma$ do not have a closed form solutions but are consistent under the ML context. The estimate can be found solving numerically the non-linear system of equations

$$\left\{\begin{array}{c}{\displaystyle \mu =E\left(Z\right)+\sigma ·\frac{\varphi \left(k\right)}{\Phi \left(k\right)},}\hfill \\ {\displaystyle \sigma =\sqrt{\frac{Var\left(Z\right)}{1-k\frac{\varphi \left(k\right)}{\Phi \left(k\right)}-{\left(\frac{\varphi \left(k\right)}{\Phi \left(k\right)}\right)}^2}}}\hfill \end{array}\right.$$

(4)

where $Z={\displaystyle \frac{Y-\mu }{\sigma }}$. The Wald’s theorem guarantees that the maximum likelihood estimator (MLE) of $\lambda$ is asymptotically normal [13]. Consequently, we have the following result:

$$\sqrt{n}\left(\widehat{\lambda }-{\lambda }_0\right)\stackrel{d}{\to }\mathcal{N}\left(0,{\displaystyle \frac{1}{I\left({\lambda }_0\right)}}\right)$$

(5)

where n is the sample size and ${\lambda }_0$ is the true value of the parameter. The estimator’s standard error is:

$$\mathrm{SE}\left(\widehat{\lambda }\right)={\displaystyle \frac{1}{\sqrt{nI\left(\widehat{\lambda }\right)}}}$$

(6)

where

$$I\left(\lambda \right)=-\mathbb{E}\left[{\displaystyle \frac{{\partial }^2}{\partial {\lambda }^2}}logL\left(\lambda \right)\right].$$

(7)

Unlike in the standard normal case, the estimators correspond to parameters that are no longer orthogonal and become asymptotically correlated; see [12,13] for theoretical details. Although the estimators $\widehat{\lambda }$, $\widehat{\mu }$, and $\widehat{\sigma }$ are known to be asymptotically correlated (see, e.g., [12,13]), this work focuses on studying the estimation accuracy of $\lambda$ as a function of ${\lambda }_g$, while fixing $C{V}_g$ and $k_g$.

Let $\theta ={(\lambda ,\mu ,\sigma )}^{\top }$ denote the parameter vector. The N-R method iterative update is given by:

$${\widehat{\theta }}^{(l+1)}={\widehat{\theta }}^{\left(l\right)}-{\left[{\nabla }^{2}logL\left({\widehat{\theta }}^{\left(l\right)}\right)\right]}^{-1}\nabla logL\left({\widehat{\theta }}^{\left(l\right)}\right).$$

(8)

Explicitly, this becomes:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\widehat{\lambda }}^{(l+1)}\\ {\widehat{\mu }}^{(l+1)}\\ {\widehat{\sigma }}^{(l+1)}\end{array}\right]=\left[\begin{array}{c}{\widehat{\lambda }}^{\left(l\right)}\\ {\widehat{\mu }}^{\left(l\right)}\\ {\widehat{\sigma }}^{\left(l\right)}\end{array}\right]-{\left[\begin{array}{ccc}{\displaystyle \frac{{\partial }^{2}logL}{\partial {\lambda }^2}}& {\displaystyle \frac{{\partial }^{2}logL}{\partial \lambda \partial \mu }}& {\displaystyle \frac{{\partial }^{2}logL}{\partial \lambda \partial \sigma }}\\ {\displaystyle \frac{{\partial }^{2}logL}{\partial \mu \partial \lambda }}& {\displaystyle \frac{{\partial }^{2}logL}{\partial {\mu }^2}}& {\displaystyle \frac{{\partial }^{2}logL}{\partial \mu \partial \sigma }}\\ {\displaystyle \frac{{\partial }^{2}logL}{\partial \sigma \partial \lambda }}& {\displaystyle \frac{{\partial }^{2}logL}{\partial \sigma \partial \mu }}& {\displaystyle \frac{{\partial }^{2}logL}{\partial {\sigma }^2}}\end{array}\right]}^{-1}{\left[\begin{array}{c}{\displaystyle \frac{\partial logL}{\partial \lambda }}\\ {\displaystyle \frac{\partial logL}{\partial \mu }}\\ {\displaystyle \frac{\partial logL}{\partial \sigma }}\end{array}\right]}_{\theta ={\theta }^{\left(l\right)}}\end{array}$$

(9)

where $\left(l\right)$ denotes the iteration number. In case we are only interested in maximizing in $\lambda$ alone then recurrence relation is:

$${\widehat{\lambda }}^{(l+1)}={\widehat{\lambda }}^{\left(l\right)}-{\left({\displaystyle \frac{{\partial }^{2}logL}{\partial {\lambda }^2}}\right)}^{-1}{\left({\displaystyle \frac{\partial logL}{\partial \lambda }}\right)}_{\widehat{\lambda }={\widehat{\lambda }}^{\left(l\right)}}.$$

(10)

The convergence process stops when $\parallel {\theta }^{(l+1)}-{\theta }^{\left(l\right)}\parallel <ϵ$ where $ϵ$ is pre-determined. For the case of ML of $\lambda$ alone the criteria $|{\lambda }^{(l+1)}-{\lambda }^{\left(l\right)}|<ϵ$. The gradient of the log-likelihood with respect to $\lambda$ is given by

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\displaystyle \frac{\partial logL}{\partial \lambda }}& =0\hfill \\ \hfill {\displaystyle \frac{\partial logL}{\partial \mu }}& =0\hfill \\ \hfill {\displaystyle \frac{\partial logL}{\partial \sigma }}& =0\hfill \end{array}\right.\iff \left\{\begin{array}{cc}\hfill {\displaystyle \sum _{i=1}^{n}log\left(y_i\right)-\sum _{i=1}^n{f}_{y_i}\frac{\partial f_{y_i}}{\partial \lambda }-n\frac{\frac{\partial \Phi \left(k\right)}{\partial \lambda }}{\Phi \left(k\right)}}& =0,\hfill \\ \hfill {\displaystyle \frac{1}{\sigma }\sum _{i=1}^n{f}_{y_i}-\frac{n}{\sigma }\frac{\varphi \left(k\right)}{\Phi \left(k\right)}}& =0,\hfill \\ \hfill {\displaystyle \frac{1}{\sigma }\left(-n+\sum _{i=1}^n{f}_{y_i}^2+kn\frac{\varphi \left(k\right)}{\Phi \left(k\right)}\right)}& =0,\hfill \end{array}\right.\end{array}$$

(11)

where,

$$f_y={\displaystyle \frac{y^{\lambda }-1-\mu \lambda }{\lambda \sigma }}={\displaystyle \frac{\frac{y^{\lambda }-1}{\lambda }-\mu }{\sigma }}.$$

(12)

Before getting into the second partial derivatives of the log likelihood we present some derivatives which are important for simplification.

The first and second partial derivatives of $f_y$ with respect to $\lambda$ is

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial f_y}{\partial \lambda }}& ={\displaystyle \frac{y^{\lambda }\left(log\left(y^{\lambda }\right)-1\right)+1}{{\lambda }^2\sigma }}\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^2{f}_y}{\partial {\lambda }^2}}& ={\displaystyle \frac{{\left(log\left(y^{\lambda }\right)\right)}^2-2\left(log\left(y^{\lambda }\right)-1\right)y^{\lambda }-2}{{\lambda }^3\sigma }}.\hfill \end{array}$$

(14)

The first and second partial derivatives of the standard normal CDF with respect to $\lambda$ are

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial \Phi \left(k\right)}{\partial \lambda }}& =\varphi \left(k\right)·{\displaystyle \frac{\partial k}{\partial \lambda }}=-{\displaystyle \frac{\varphi \left(k\right)}{{\lambda }^2\sigma }}\hfill \\ \hfill {\displaystyle \frac{{\partial }^2\Phi \left(k\right)}{\partial {\lambda }^2}}& ={\displaystyle \frac{\partial }{\partial \lambda }}\left(-{\displaystyle \frac{\varphi \left(k\right)}{{\lambda }^2\sigma }}\right)=-{\displaystyle \frac{\left(k-2\sigma \lambda \right)\varphi \left(k\right)}{{\lambda }^4{\sigma }^2}}.\hfill \end{array}$$

(15)

The second derivatives with respect to the three parameters are:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}logL}{\partial {\lambda }^2}}=& -\sum _{i=1}^n\left[{\left({\displaystyle \frac{\partial f_{y_i}}{\partial \lambda }}\right)}^2+f_{y_i}{\displaystyle \frac{{\partial }^2{f}_{y_i}}{\partial {\lambda }^2}}\right]+{\displaystyle \frac{n}{\Phi \left(k\right)}}\left({\displaystyle \frac{{\left(\frac{\partial \Phi \left(k\right)}{\partial \lambda }\right)}^2}{\Phi \left(k\right)}}-{\displaystyle \frac{{\partial }^2\Phi \left(k\right)}{\partial {\lambda }^2}}\right),\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}logL}{\partial {\mu }^2}}=& -{\displaystyle \frac{n}{{\sigma }^2}}+{\displaystyle \frac{n}{{\sigma }^2}}{\displaystyle \frac{\varphi \left(k\right)}{\Phi {\left(k\right)}^2}}\left(k\Phi \left(k\right)+\varphi \left(k\right)\right),\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}logL}{\partial {\sigma }^2}}=& {\displaystyle \frac{1}{{\sigma }^2}}\left(n-3\sum _{i=1}^n{\left({\displaystyle \frac{z_i-\mu }{\sigma }}\right)}^2-n·k·{\displaystyle \frac{\varphi \left(k\right)}{\Phi \left(k\right)}}\left(2+{\displaystyle \frac{k}{\Phi \left(k\right)}}\left(k·\Phi \left(k\right)+\varphi \left(k\right)\right)\right)\right).\hfill \end{array}$$

(16)

The cross second derivatives involving $\mu ,\sigma ,\lambda$ are:

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\partial }^{2}logL}{\partial \mu \partial \sigma }}=& -{\displaystyle \frac{2}{{\sigma }^2}}\sum _{i=1}^n{f}_{y_i}+{\displaystyle \frac{n}{{\sigma }^2}}{\displaystyle \frac{\varphi \left(k\right)}{\Phi \left(k\right)}}\left(1-{\displaystyle \frac{k}{\sigma \Phi \left(k\right)}}(k\Phi \left(k\right)+\varphi \left(k\right))\right),\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}logL}{\partial \mu \partial \lambda }}=& {\displaystyle \frac{1}{\sigma }}\sum _{i=1}^n{\displaystyle \frac{\partial f_{y_i}}{\partial \lambda }}-{\displaystyle \frac{n\varphi \left(k\right)}{{\sigma }^3\Phi {\left(k\right)}^2{\lambda }^2}}(k\Phi \left(k\right)+\varphi \left(k\right)),\hfill \\ \hfill {\displaystyle \frac{{\partial }^{2}logL}{\partial \sigma \partial \lambda }}=& {\displaystyle \frac{2}{\sigma }}\sum _{i=1}^n{f}_{y_i}{\displaystyle \frac{\partial f_{y_i}}{\partial \lambda }}\lambda -{\displaystyle \frac{n}{\sigma {\lambda }^2}}{\displaystyle \frac{\varphi \left(k\right)}{\Phi \left(k\right)}}\left(1-{\displaystyle \frac{1}{\Phi \left(k\right)}}(k\Phi \left(k\right)+\varphi \left(k\right))\right).\hfill \end{array}$$

(17)

3. Simulation Study Results and Discussion

In this simulation study of the PN distribution, we considered a set of values for the parameter $\lambda$ within the interval $[0,1]$, specifically $0.15,0.25,0.5,0.75$, and $0.85$. Following Goto et al. [4], we fixed several values for the coefficient of variation $C{V}_g$, namely $0.75,1,2,4$, and 8. For the shape parameter $k_g$, three values were selected: $1,2$, and 3. While Goto et al. [4] studied the estimation performance as a function of sample size, here we consider a fixed sample size of 200 observations for each parameter combination. It should be noted that some parameter combinations are incompatible; hence, no datasets were generated for those cases. Additionally, certain samples were discarded due to limitations in applying the Kolmogorov–Smirnov test.

The complete data table containing all the information concerning the estimation including the three standard estimation accuracy metrics: the mean bias (MB), the mean squared error (MSE), and the mean absolute relative error (MARE) mentioned in the text are presented in Table A1 in the Appendix. In what follows, we describe how the ML estimates for the parameters were obtained from the valid datasets corresponding to each parameter combination.

As is well known, the choice of initial values and a suitable convergence criterion is crucial for obtaining reliable maximum likelihood (ML) estimates. In our implementation, the search is restricted to the interval $[0,1]$, using a grid with a step size of 0.01. Each grid point serves as an initial value for the ML estimation procedure.

Following this approach, for each dataset we obtain a set of candidate ML estimates. From this set, we select the estimates corresponding to converged solutions with the smallest absolute skewness after the BC transformation. Alternative selection criteria—such as choosing the estimates with the highest ML value or relying on p-values from normality tests (both standard and truncated normal)—did not yield satisfactory results. These methods proved less effective at identifying estimates that preserved the structural properties of the underlying distribution, particularly symmetry.

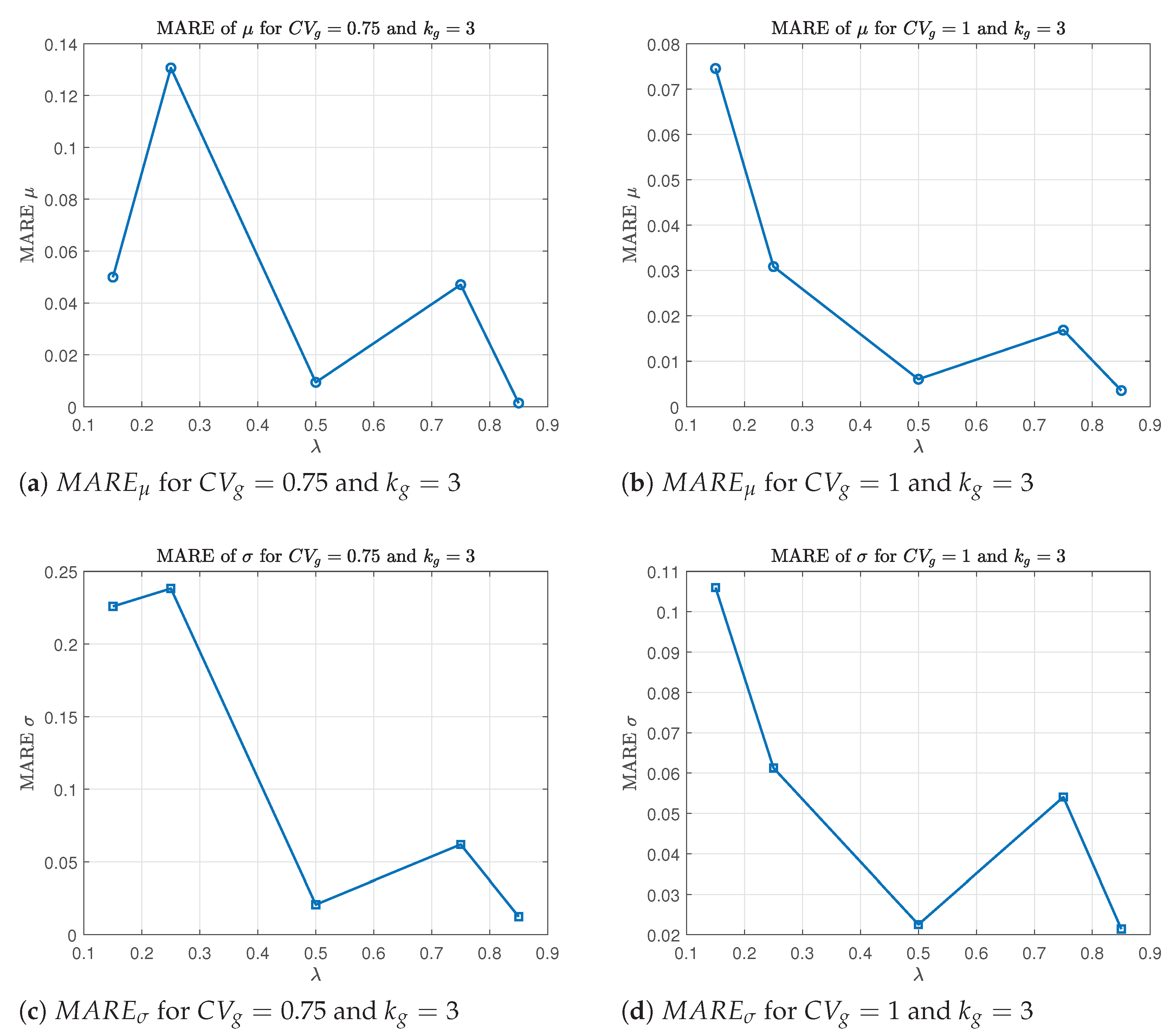
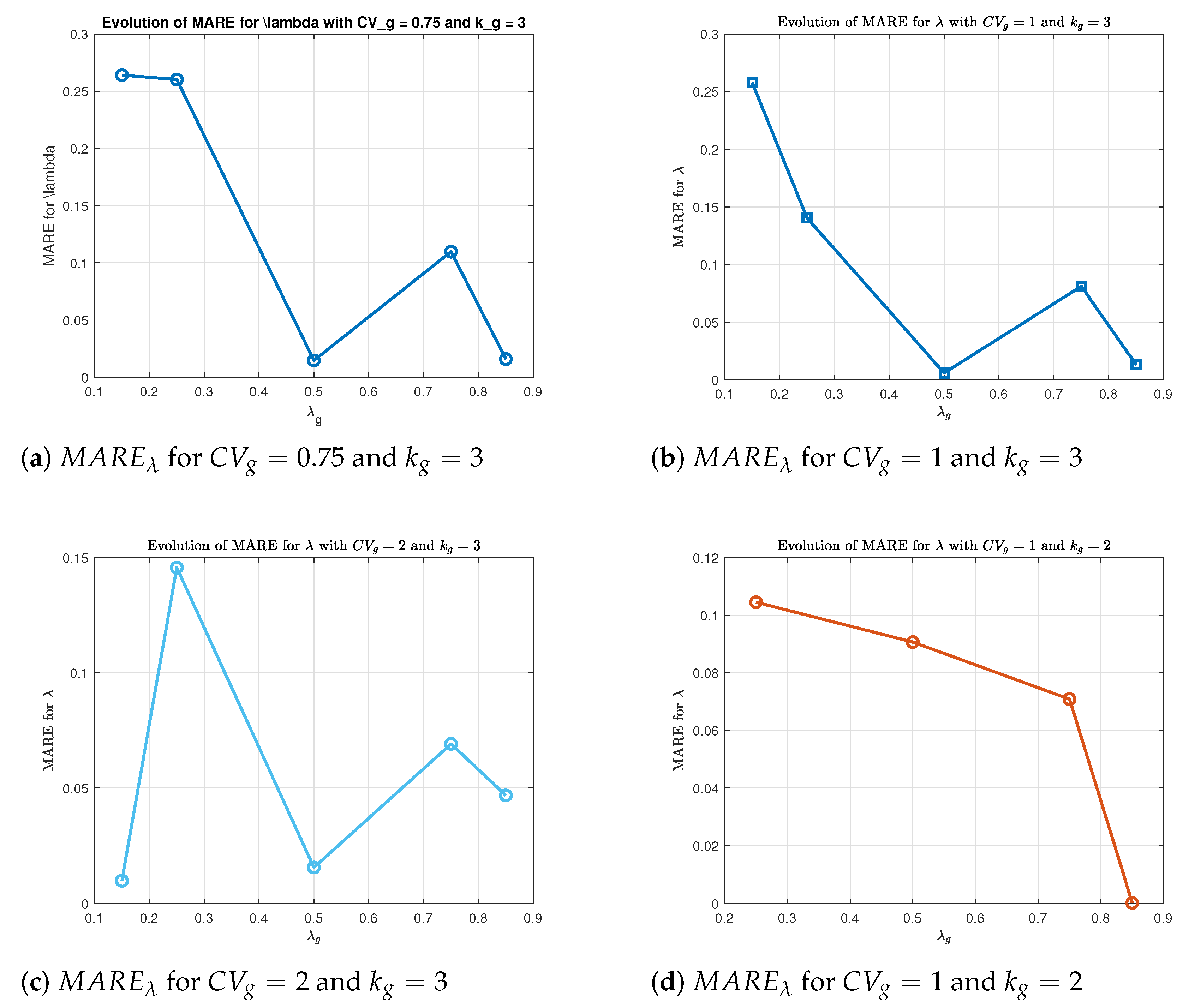
To evaluate how estimation accuracy varies with the parameter values used in the simulations, we analyze the behavior of the estimated parameters $\widehat{\lambda }$, $\widehat{\mu }$, and $\widehat{\sigma }$ as ${\lambda }_g$ increases from 0.15 to 0.85. For comparison purposes, the coefficient of variation $C{V}_g$ and the shape parameter $k_g$ are held fixed (see Figure 1).

For each pair $(C{V}_g,k_g)$, we observe a general trend of decreasing relative error in $\widehat{\lambda }$ as ${\lambda }_g$ increases. This is expected, as the same absolute estimation error in $\lambda$ corresponds to a smaller relative error when ${\lambda }_g$ is large. A similar decreasing trend is also observed for the MARE of $\widehat{\mu }$ and $\widehat{\sigma }$, particularly for smaller values of $C{V}_g$. As ${\lambda }_g$ increases, the BC transformation becomes smoother and more stable, which improves the performance of the maximum likelihood estimation. The reduction in skewness and better approximation to normality help reduce the variability in estimating $\mu$ and $\sigma$, leading to more accurate and reliable parameter estimates.

Figure 2. MARE $\mu$ and $\sigma$ as a function of ${\lambda }_g$ fixing the parameters $C{V}_g$ and $k_g$.

Figure 2. MARE $\mu$ and $\sigma$ as a function of ${\lambda }_g$ fixing the parameters $C{V}_g$ and $k_g$.

By contrast, the MSE curves for the same estimators and parameter settings (not shown) exhibit irregular behavior, often increasing with ${\lambda }_g$ when estimator variability outweighs squared bias, which limits the usefulness of MSE for comparative analysis across the PN parameter space. To provide a comprehensive comparison of the two approaches for maximizing the log-likelihood—estimating all three parameters simultaneously or only $\lambda$—we computed the average MB, MSE, and MARE statistics for each parameter across the entire dataset, as summarized in Table 1.

Estimation results depend on the specific values of the underlying parameters. Some methods perform better than others for certain parameter combinations and worse for others. For this reason, we chose to compare the methods based on the overall average of each error statistic. Note that these statistics themselves are computed as averages over multiple simulated datasets for each parameter combination. The results indicate that maximizing the log-likelihood function with all three parameters simultaneously (the $v_1$ mode) yields the best performance overall. In particular, the average MARE for $\lambda$ shows an improvement of approximately $18\%$ over the classical estimator and about $6.5\%$ over the $v_2$ mode. The average mean bias for $\lambda$ follows a similar trend as the average MARE, although the differences between methods are more pronounced. As for the average statistics associated with $\mu$ and $\sigma$, we observe that method $M_1$, implemented via ML in all three parameters, outperforms the $v_2$ version of the $M_2$ approach. Furthermore, method $M_1$ shows a substantial advantage over both $v_1$ and $v_2$ modes of $M_2$ in terms of the average MSE for $\sigma$.

4. Conclusions and Future Work

In this work, we present in detail methods for estimating the parameters of the PN, which has yet to reveal all of its properties. The quality of the results depends not only on the selected parameter values but also on the specific statistic used to evaluate and compare the maximum likelihood estimates. The foundation of our computational approach is the N-R method, which had to be carefully tuned to ensure proper convergence. The estimation process required extensive experimentation to achieve reliable and satisfactory results.

Classical estimation in the PN distribution, as proposed by Box and Cox [9], was primarily intended to achieve approximate normality of the transformed data. However, the inconsistency of those estimators renders them unsuitable when accurate parameter estimation is the objective. Exact ML estimation was studied by Goto et al. [4], although implemented differently from the approach adopted in this work. We implemented both methods using simultaneous ML estimation of all three parameters. The results indicate an improvement in the estimation of $\lambda$ over the $M_1$ method, although this improvement is not substantial when compared to the $v_2$ mode. In contrast, for the parameters $\mu$ and $\sigma$, we observe a significant enhancement in estimation accuracy under the $M_2$ method relative to the $v_2$ implementation.

Given its close relation to the BC transformation, the correlation structure of variables on the PN scale remains to be fully understood. Under appropriate parameter settings, independent transformation of the marginal variables result in a bivariate approximated normal pair. Understanding this phenomenon may offer practitioners valuable insights into how transformed data under the Box-Cox framework can be analyzed and interpreted.