Submitted:
04 June 2024
Posted:
05 June 2024
You are already at the latest version
Abstract
Keywords:
MSC: 60E05; 62E10; 62F10
1. Introduction
2. The LLU Distribution
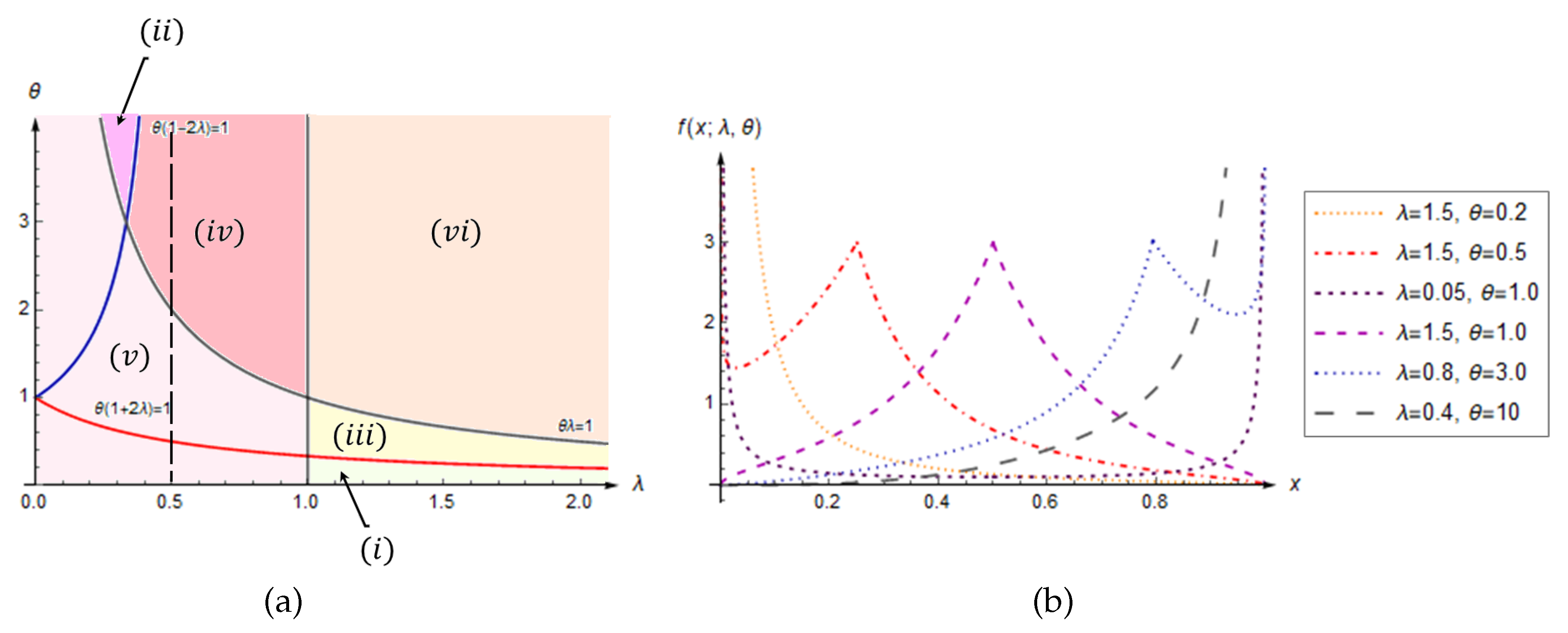
2.1. Definition and Main Properties
- When and , it is decreasing.
- When and , it is increasing.
- When , and , it is left-tailed and right-vanishing.
- When , and , it is right-tailed and left-vanishing.
- When and , it is (both sides) tailed.
- When and , it is (both sides) vanishing.
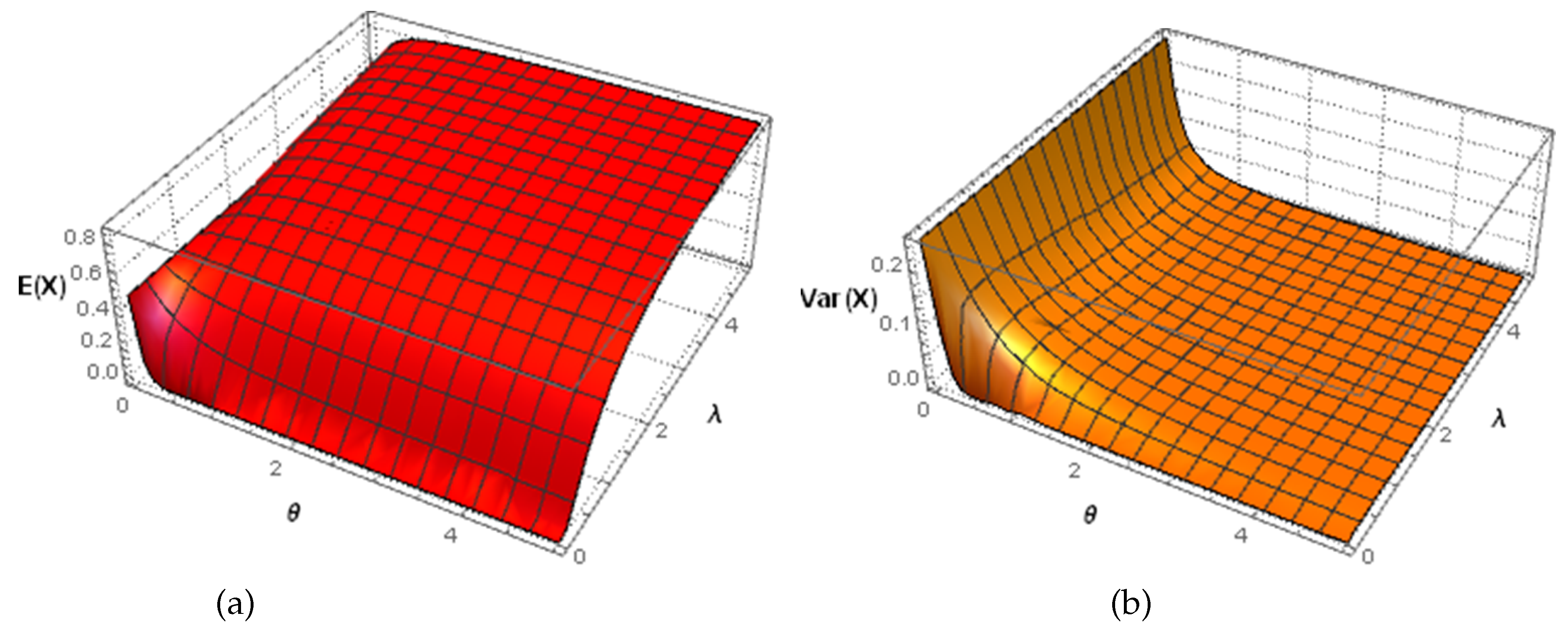
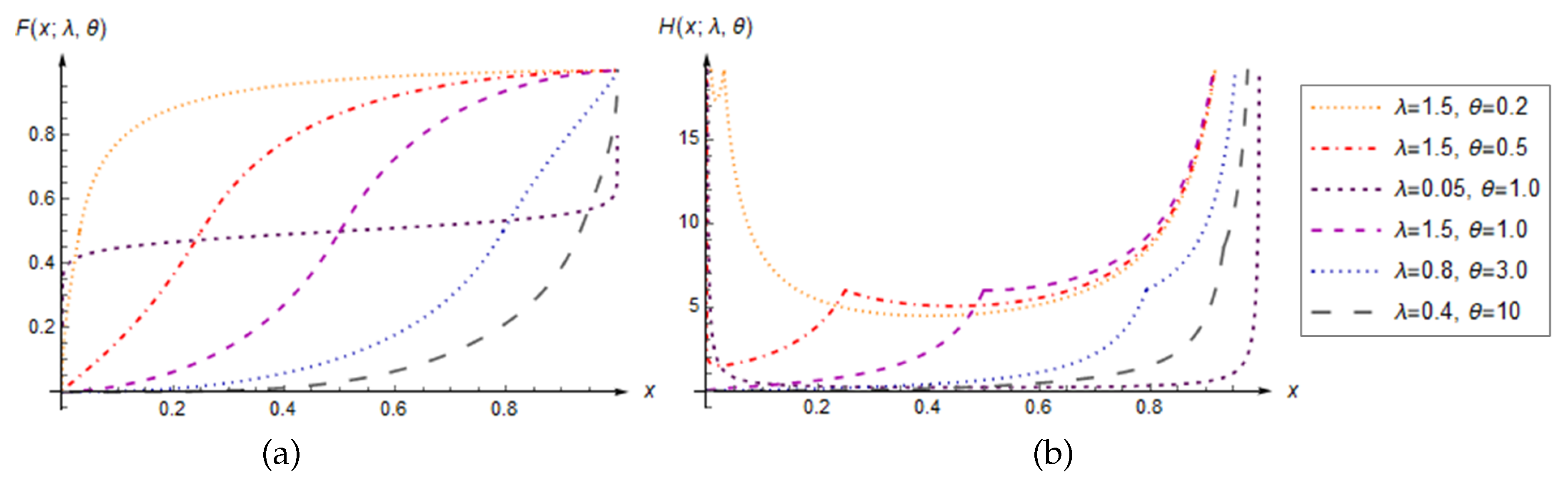
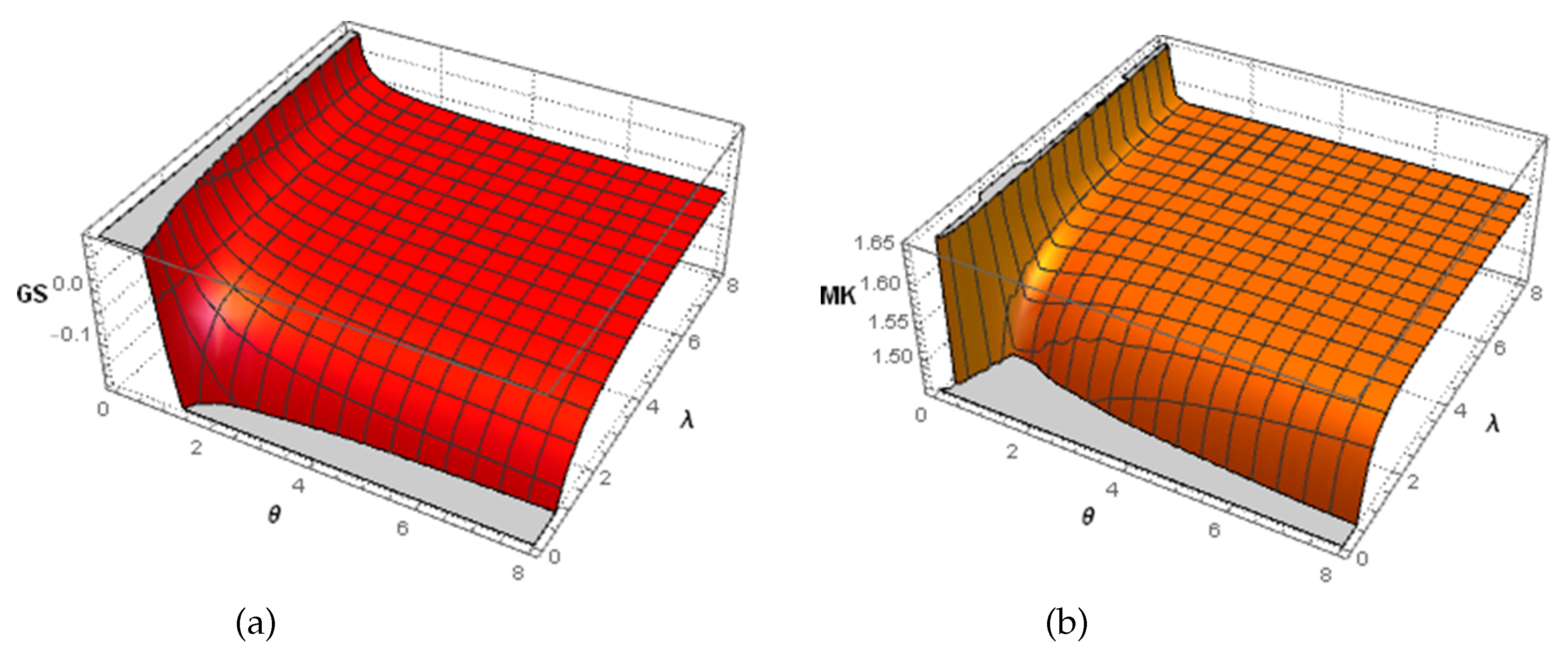
2.2. Cumulative, Hazard and Quantile Function
- When and , it is (both sides) tailed with a local maxima at .
- When and , it is (both sides) tailed without maxima, that is, bathtub-shaped.
- When and , it is left-vanishing with a local maxima at .
- When and , it is increasing.
- The RV X is symmetrically distributed if and only if . Otherwise, X is positively asymmetric when , and negatively asymmetric when .
- The RV X is unimodal, with the mode , if and only if and .
3. Parameters Estimation & Simulation Study
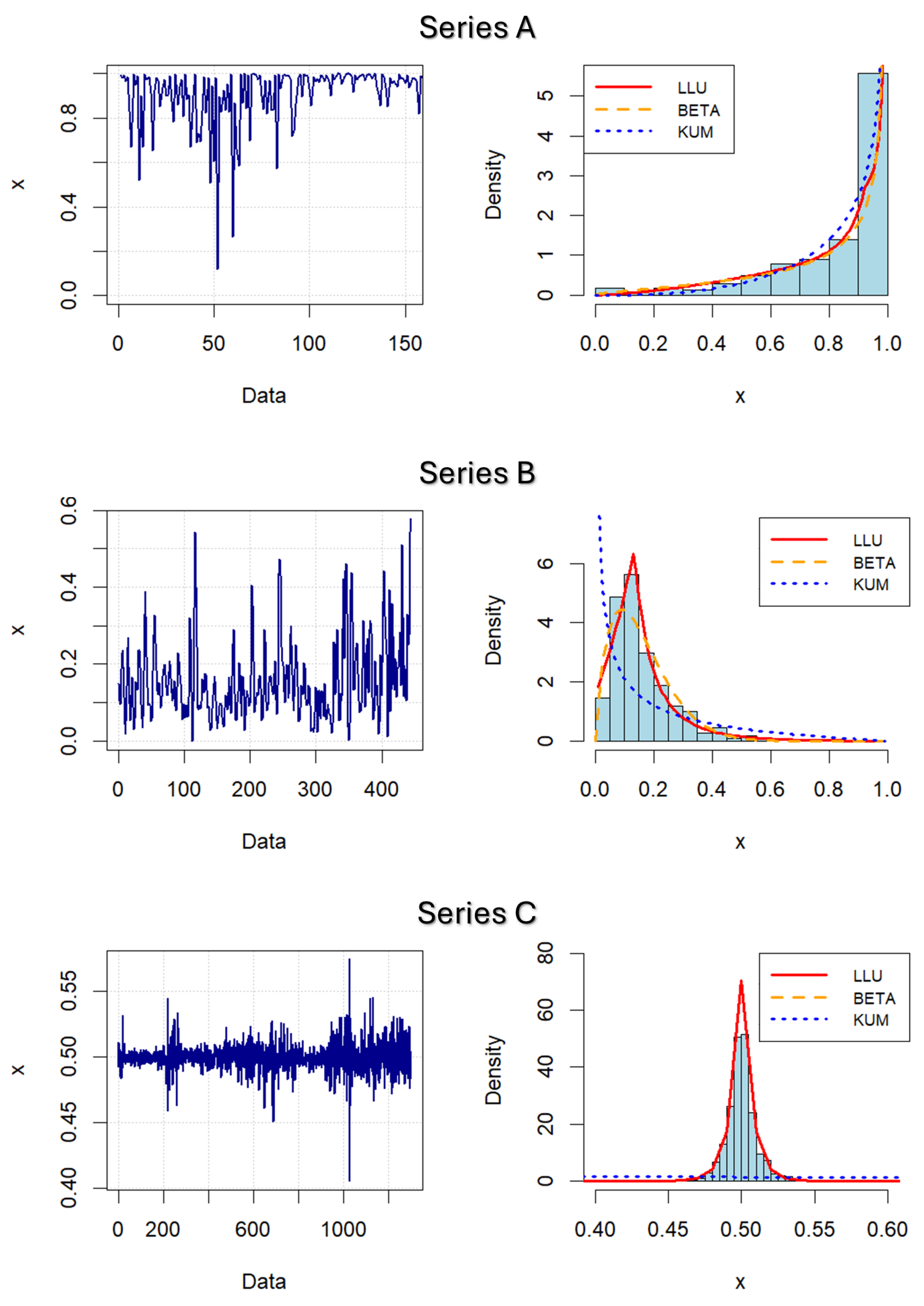
4. Applications of the LLU distribution
5. Conclusion
Author Contributions
Conflicts of Interest
References
- Nakamura, L.R.; Cerqueira, P.H.R.; Ramires, T.G.; Pescim, R.R.; Rigby, R.A.; Stasinopoulos, D.M. A New Continuous Distribution on the Unit Interval Applied to Modelling the Points Ratio of Football Teams. J. Appl. Stat. 2019, 46, 416–431. [CrossRef]
- Hussain, T.; Bakouch, H.S.; Chesneau, C. A New Probability Model With Application to Heavy-Tailed Hydrological Data. Environ. Ecol. Stat. 2019, 26, 127–151. [CrossRef]
- Ghitany, M. E.; Mazucheli, J.; Menezes, A. F. B.; Alqallaf, F. The Unit-Inverse Gaussian Distribution: A New Alternative to Two-Parameter Distributions on the Unit Interval. Commun. Stat. - Theory Methods, 2019, 48, 3423–3438. [CrossRef]
- Mazucheli, J.; Menezes, A. F.; Dey, S. Unit-Gompertz Distribution with Applications. Statistica, 2019a, 79(1), 25–-43. [CrossRef]
- Mazucheli, J.; Menezes, A. F. B.; Chakraborty, S. On the One Parameter Unit-Lindley Distribution and Its Associated Regression Model for Proportion Data. J. Appl. Stat. 2019b, 46(4), 700–714. [CrossRef]
- Gündüz, S.; Mustafa Ç.; Korkmaz, M.C. A New Unit Distribution Based on the Unbounded Johnson Distribution Rule: The Unit Johnson SU Distribution. Pak. J. Stat. Oper. Res. 2020, 16(3), 471–490.
- Afify, A.Z.; Nassar, M., Kumar, D.; Cordeiro, G.M. A New Unit Distribution: Properties and Applications. Electron. J. Appl. Stat. 2022, 15, 460–484.
- Krishna, A.; Maya, R.; Chesneau, C.; Irshad, M.R. The Unit Teissier Distribution and Its Applications. Math. Comput. Appl. 2022, 27(1), 12. [CrossRef]
- Bakouch, H.S.; Hussain, T. ; Tošić, M.; Stojanović, V.S.; Qarmalah, N., Unit Exponential Probability Distribution: Characterization and Applications in Environmental and Engineering Data Modeling, Mathematics 2023, 11(19), Article No. 4207. [CrossRef]
- Korkmaz, M. Ç.; Korkmaz, Z. S. The Unit Log–log Distribution: A New Unit Distribution With Alternative Quantile Regression Modeling and Educational Measurements Applications. J. Appl. Stat. 2023, 50(4), 889–908. [CrossRef]
- Nasiru, S.; Abubakari, A.G.; Chesneau, C. New Lifetime Distribution for Modeling Data on the Unit Interval: Properties, Applications and Quantile Regression. Math. Comput. Appl. 2022, 27, Article No. 105. [CrossRef]
- Nasiru, S.; Abubakari, A.G.; Chesneau, C. The Arctan Power Distribution: Properties, Quantile and Modal Regressions with Applications to Biomedical Data. Math. Comput. Appl. 2023, 28, Article No. 25. [CrossRef]
- Fayomi, A.; Hassan, A.S.; Baaqeel, H.; Almetwally, E.M. Bayesian Inference and Data Analysis of the Unit–Power Burr X Distribution. Axioms 2023, 12, Article No. 297. [CrossRef]
- Condino, F.; Domma, F.; Unit Distributions: A General Framework, Some Special Cases, and the Regression Unit-Dagum Models. Mathematics 2023, 11(13), Article No. 2888. [CrossRef]
- Mazucheli, J.; Menezes, A.F.B.; Fernandes, L.B.; de Oliveira, R.P.; Ghitany, M. E. The Unit-Weibull Distribution as an Alternative to the Kumaraswamy Distribution for the Modeling of Quantiles Conditional on Covariates. J. Appl. Stat. 2019c, 47(6), 954-974. [CrossRef]
- Altun, E. The Log-Weighted Exponential Regression Model: Alternative to the Beta Regression Model. Commun. Stat. - Theory and Methods, 2020, 50(10), 2306–2321. [CrossRef]
- Altun, E.; Cordeiro, G.M. The Unit-Improved Second-Degree Lindley Distribution: Inference and Regression Modeling. Comput. Stat. 2020 35, 259–279. [CrossRef]
- Mazucheli, J.; Bapat, S.R.; Menezes, A.F. A New One-Parameter Unit-Lindley Distribution. Chilean J. Stat. 2020, 11(1), 53–67.
- Krishna, A.; Maya, R.; Chesneau, C.; Irshad, M.R. The Unit Teissier Distribution and Its Applications. Math. Comput. Appl. 2022, 27, Article No. 12. [CrossRef]
- Mustafa, Ç.; Korkmaz, Z; Korkmaz, S. The Unit Log–log Distribution: A New Unit Distribution With Alternative Quantile Regression Modeling and Educational Measurements Applications, J. Appl. Stat. 2023, 50(4), 889–908. [CrossRef]
- Biçer, C.; Bakouch, H.S.; Biçer, H.D.; Alomair, G.; Hussain, T.; Almohisen, A. Unit Maxwell-Boltzmann Distribution and Its Application to Concentrations Pollutant Data. Axioms 2024, 13(4), Article No. 226. [CrossRef]
- Nasiru, S. ; Chesneau, C.; Ocloo, S.K., The Log-Cosine-Power Unit Distribution: A New Unit Distribution for Proportion Data Analysis. Decis. Anal. J. 2024, 10, Article No. 100397. [CrossRef]
- Alsadat, N.; Taniş, C.; Sapkota, L.P.; Kumar, A.; Marzouk, W.; Gemeay, A.M. Inverse unit exponential probability distribution: Classical and Bayesian inference with applications. AIP Advances 2024, 14, Article No. 055108. [CrossRef]
- Stojanović, V.S.; Bojičić, R.; Pažun, B.; Langović, Z. Quasi-Lindley Unit Distribution: Properties and Applications in Stochastic Data Modeling, U.P.B. Sci. Bull., Series A, submitted manuscript.
- Stojanović, V.S.; Jovanović Spasojević, T.; Pažun, B.; Langović, Z. Cauchy-Logistic Unit Distribution: Properties and Application in Modeling Data Extremes, An. Sti. U. Ovid. Co.-Mat., submitted manuscript.
- Norton, R.M. The Double Exponential Distribution: Using Calculus to Find a Maximum Likelihood Estimator. Am. Stat. 1984, 38, 135–136. [CrossRef]
- R. Zieliński, Uniform strong consistency of sample quantiles, Stat. Prob. Lett. 37:2 (1998), 115–119. [CrossRef]
- Dudek, D.; Kuczmaszewska, A. Some Practical and Theoretical Issues Related to the Quantile Estimators, Stat. Papers 2024, in press. [CrossRef]
- Serfling, R.J. Approximation Theorems of Mathematical Statistics, 2nd edition; John Wiley & Sons: New York, NY, USA, 2002.
- Ruckdeschel, P.; Kohl, M.; Stabla, T. ; Camphausen, F. S4 Classes for Distributions. R News, 2006, 6:(2–6). Available online: https://CRAN.R-project.org/doc/Rnews (accessed on 01 May, 2024).
- Gross, L. Tests for Normality. R package version 1.0-2. http://CRAN.R-project.org/package=nortest, 2013. http://CRAN.R-project.org/package=nortest (accessed on 2 May, 2024).
- https://github.com/microsoft/USBroadbandUsagePercentages/tree/master/dataset (accessed on May 12, 2024).
- Kameda, T., et al. South Greenland Site J Ice Core Melt Percent and Temperature Reconstruction. IGBP PAGES/World Data Center for Paleoclimatology, Data Contribution Series # 2004-031, NOAA/NGDC Paleoclimatology Program, Boulder CO, USA, 2004. https://www.ncei.noaa.gov/pub/data/paleo/icecore/greenland/sitej_melt.txt (accessed on 12 May, 2024).
- Nasdaq, https://nasdaq.com (accessed on 12 May, 2024).
- Stojanović, V.S.; Bakouch, H.S.; Ljajko, E.; Božović, I. Laplacian Split-BREAK Process with Application in Dynamic Analysis of the World Oil and Gas Market. Axioms 2023, 12, 622. [CrossRef]
- Jones, M.C. Kumaraswamy’s distribution: A beta-type distribution with some tractability advantages, Stat. Methodol. 2009, 6:1, 70–81. [CrossRef]
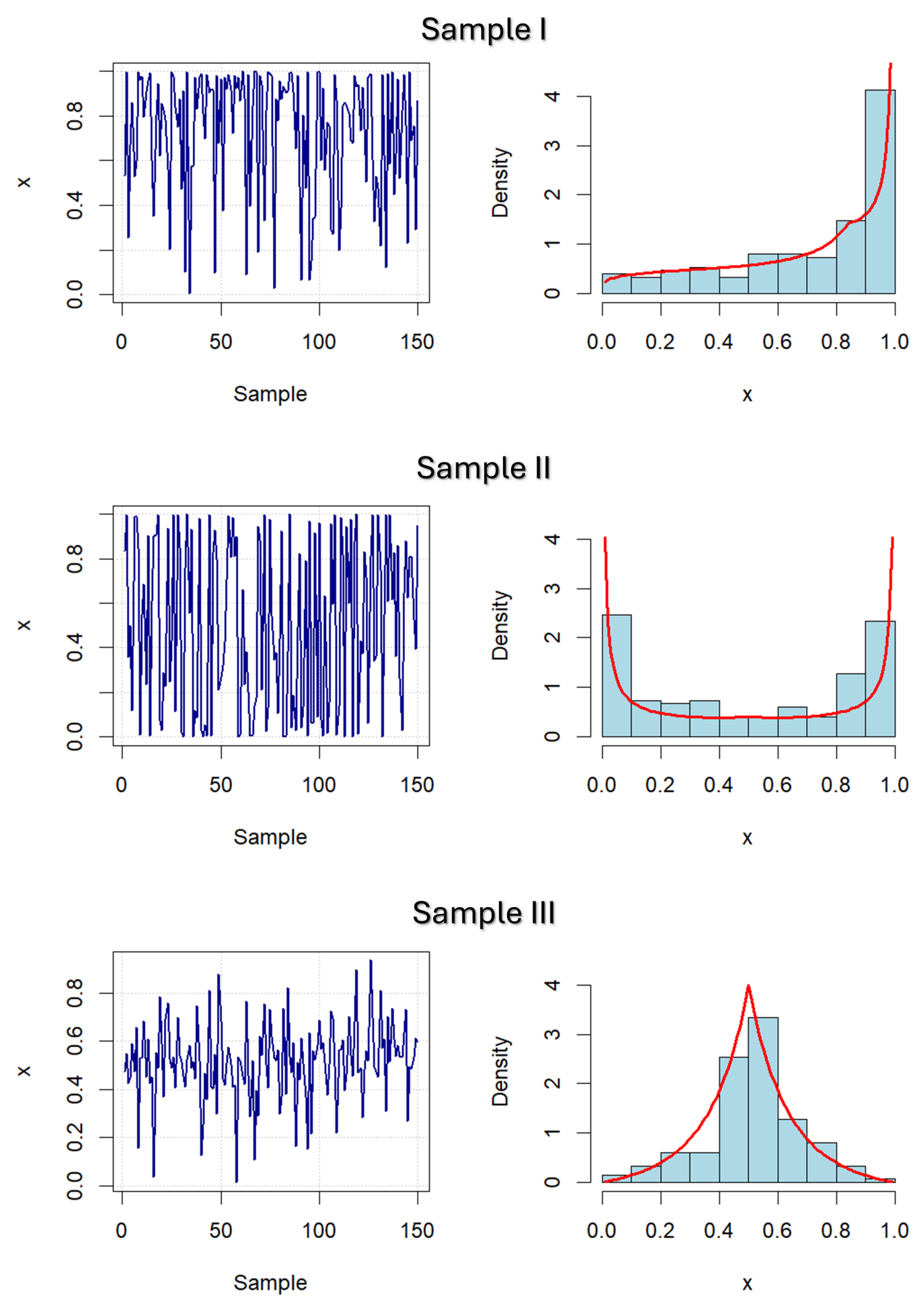
| Statistics | n = 150 | n = 500 | n = 1500 | |||||
|---|---|---|---|---|---|---|---|---|
| Min. | 1.770 | 0.1773 | 2.247 | 0.2190 | 2.676 | 0.2400 | ||
| Mean | 3.210 | 0.2850 | 3.378 | 0.2883 | 3.459 | 0.2928 | ||
| Max. | 5.907 | 0.4094 | 4.099 | 0.3660 | 3.650 | 0.3195 | ||
| SD | 0.0636 | 0.0448 | 0.0332 | 0.0260 | 0.0180 | 0.0150 | ||
| MSEE | 0.0790 | 0.0471 | 0.0722 | 0.0335 | 0.0712 | 0.0269 | ||
| FEE (%) | 8.286 | 15.715 | 3.486 | 11.029 | 1.171 | 8.959 | ||
| 0.8939 * | 1.6913 ** | 0.3090 | 0.6818 | 0.3796 | 0.1678 | |||
| (p-value) | (0.0221) | (2.38) | (0.5553) | (0.0739) | (0.4013) | (0.9359) | ||
| Statistics | n = 150 | n = 500 | n = 1500 | |||||
|---|---|---|---|---|---|---|---|---|
| Min. | 0.5990 | 0.2161 | 0.7375 | 0.2369 | 0.8494 | 0.2602 | ||
| Mean | 1.0254 | 0.3054 | 1.0170 | 0.2987 | 1.0018 | 0.2968 | ||
| Max. | 1.8447 | 0.5394 | 1.4075 | 0.3824 | 1.2316 | 0.3477 | ||
| SD | 0.1907 | 0.0508 | 0.1224 | 0.0252 | 0.0698 | 0.0156 | ||
| MSEE | 0.0254 | 0.1169 | 0.0170 | 0.1019 | 0.0020 | 0.0981 | ||
| FEE (%) | 2.1346 | 34.453 | 0.5739 | 24.476 | 0.2030 | 21.908 | ||
| 1.1064 ** | 1.481 ** | 0.6684 | 0.8172 * | 0.5166 | 0.6030 | |||
| (p-value) | (6.58) | (7.83) | (0.0798) | (0.0341) | (0.1879) | (0.1159) | ||
| Statistics | n = 150 | n = 500 | n = 1500 | |||||
|---|---|---|---|---|---|---|---|---|
| Min. | 0.9036 | 1.4760 | 0.9529 | 1.657 | 0.9698 | 1.860 | ||
| Mean | 1.0048 | 2.0360 | 1.0009 | 2.024 | 1.0003 | 2.016 | ||
| Max. | 2.6290 | 1.1179 | 1.0606 | 2.483 | 1.0262 | 2.243 | ||
| SD | 0.0305 | 0.2603 | 0.0166 | 0.1451 | 9.20 | 0.0767 | ||
| MSEE | 4.78 | 0.2621 | 8.88 | 0.1466 | 2.71 | 0.0782 | ||
| FEE (%) | 0.4783 | 13.106 | 0.0888 | 7.3314 | 0.0271 | 3.9117 | ||
| 0.4960 | 0.8509 * | 0.4029 | 0.2194 | 0.2951 | 0.3024 | |||
| (p-value) | (0.2113) | (0.0282) | (0.3539) | (0.8346) | (0.5930) | (0.5726) | ||
| Paramet./ | Series A | Series B | Series C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Statistics | LLU | BETA | KUM | LLU | BETA | KUM | LLU | BETA | KUM | ||
| 0.2972 | 1.6572 | 3.7527 | 2.5106 | 1.9375 | 0.4843 | 35.459 | 1133.27 | 1.4423 | |||
| 8.4338 | 0.3394 | 0.5241 | 0.3436 | 10.299 | 1.9341 | 0.9999 | 1133.21 | 2.1782 | |||
| MSEE | 0.0091 | 0.0139 | 0.0249 | 2.50 | 3.94 | 0.0205 | 1.31 | 2.28 | 0.0794 | ||
| AIC | -812.13 | -398.61 | -291.23 | -2671.99 | -891.80 | -687.07 | -17785.9 | -8173.7 | -325.18 | ||
| 0.0892 | 0.0797 | 0.1251 * | 0.0541 | 0.0676 | 0.3514 ** | 0.0215 | 0.0760 * | 0.5722 ** | |||
| (p-value) | (0.2534) | (0.3818) | (0.0347) | (0.5354) | (0.2629) | (0.00) | (0.9241) | (0.0108) | (0.00) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





