Vacuum Energy with Natural Bounds: A Spectral Approach without Fine-Tuning

1. Introduction

The observed acceleration of the Universe is commonly modeled by a cosmological constant $\Lambda$, yet its apparent smallness compared to naive quantum-field expectations remains puzzling. Rather than seeking an origin narrative for vacuum energy or an extended early-time dynamics, this work focuses strictly on a present-day description of the vacuum state: a phenomenological, physics-grounded framework that identifies natural spectral bounds and their consequences for the current energy density relevant to gravity.

Two guiding principles motivate our approach. First, laboratory and astrophysical physics already provide robust characteristic scales. In particular, the confinement scale of quantum chromodynamics (QCD) suggests a natural ultraviolet (UV) boundary for modes that can coherently contribute to the gravitationally active vacuum sector, while thermodynamic or entropic considerations suggest an infrared (IR) boundary for the longest relevant wavelengths. Second, once such bounds are admitted on physical grounds, dimensional analysis and a mild regularity requirement lead to a simple and robust scaling of the present-day vacuum energy density with a single geometric length scale.

This paper develops that late-time, present-epoch picture in a way that is intentionally diagnostic rather than definitive. At the background level, the framework reproduces low-redshift kinematics (e.g., $E\left(z\right)$ and $q\left(z\right)$) close to flat-$\Lambda$CDM for reasonable choices of the bounding scales, without invoking fine-tuned parameters or assumptions about high-redshift evolution. On galactic scales, the same present-time perspective can be mapped into rotation-curve phenomenology through a small set of interpretable contributions. Importantly, the proposal is directly testable in the laboratory: we formulate photonic and radiometric observables via an impedance-invariant spectral window $W\left(u\right)$ and a band-integrated measure $\Delta \Phi$, enabling null tests using optical, radiometric, or Casimir-type platforms.

We emphasize that the scope of this paper is deliberately limited: we do not attempt a full cosmological likelihood analysis nor a theory of origin for vacuum energy. Instead, we articulate a coherent present-time framework, grounded in known physics and observations, which yields clear diagnostics and falsifiability criteria that can be constrained by existing data and near-term experiments. The mathematical formulation begins in Section 3, after clarifying the physical scope in Section 2.

2. Present Framework and Physical Scope

This work is confined to the present-day vacuum state (late-time, $z\simeq 0$). Our objective is not to reconstruct a dynamical history or propose an origin theory, but to provide a physically realistic description of the current spectral and energetic properties of the vacuum sector that are relevant for gravity.

We assume that the effective vacuum spectrum is bounded by natural, well-motivated scales: an ultraviolet (UV) limit associated with QCD confinement (fixing a characteristic short length) and an infrared (IR) boundary associated with thermal or entropic considerations (fixing a characteristic long length). Within these bounds, the vacuum energy density takes a robust dimensional form

$${\rho }_{\mathrm{vac}}\propto L^{-4},L\equiv \sqrt{{\lambda }_{min}{\lambda }_{max}},$$

where L is the geometric mean of the UV and IR cutoffs ${\lambda }_{min}$ and ${\lambda }_{max}$. All quantitative statements in this paper refer to this present-epoch configuration.

The framework is intended as a diagnostic description rather than a replacement for $\Lambda$CDM or an account of early-universe physics. In the late-time regime, a spectrally bounded vacuum can (i) reproduce key background kinematics at low z to within a few percent of flat-$\Lambda$CDM for plausible bounding scales, (ii) inform galaxy-scale phenomenology using a small number of interpretable contributions, and (iii) admit direct laboratory tests through photonic and radiometric observables. To make the latter operational, we employ an impedance-invariant spectral window $W\left(u\right)$ and its band-integrated measure $\Delta \Phi$, which together provide platform-agnostic null tests (e.g., optical cavities/interferometers, radiometric measurements, or Casimir-type setups).

Accordingly, this paper should be read as a physically grounded present-time proposal—not a proof of origin—that defines a coherent, testable picture of vacuum energy at $z\simeq 0$. The spectral construction and its mathematical consequences are developed in Section 3, while late-time diagnostics and laboratory connections are summarized where appropriate.

3. Spectral Formulation

3.1. Damping Budget and Uncertainties

We split the integrated damping $\Xi ={\Xi }_g+{\Xi }_{\mathrm{th}}+{\Xi }_{\mathrm{had}}$ as follows:

$$\begin{array}{cc}\hfill {\Xi }_g& \simeq {\int }_{t_i}^{t_0}H\left(t\right)dt=ln\left[a\left(t_0\right)/a\left(t_i\right)\right]\approx ln\left[T_{\mathrm{QCD}}/T_{\mathrm{IR}}\right],\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\Xi }_{\mathrm{th}}& \equiv \int {\Gamma }_{\mathrm{th}}\left(t\right)dt\sim \int dlnT\Phi \left(g_{*}\left(T\right)\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\Xi }_{\mathrm{had}}& \equiv \int {\Gamma }_{\mathrm{had}}\left(t\right)dt\approx \int dlnT\exp \left[-{\displaystyle \frac{{(lnT-ln{T}_{\mathrm{QCD}})}^2}{2{\sigma }^2}}\right],\hfill \end{array}$$

(3)

where Equation (1) follows from adiabatic FRW expansion, $\Phi \left(g_{*}\right)$ captures entropic/thermal suppression across particle thresholds, and the Gaussian in Equation () models a localized hadronic damping centered near $T_{\mathrm{QCD}}$.A representative calibration is ${\Xi }_g\simeq 25$, ${\Xi }_{\mathrm{th}}\simeq 46$, ${\Xi }_{\mathrm{had}}\simeq 30$ (total $\Xi \simeq 101$).

Small variations $\delta \Xi$ propagate as $\delta \rho /\rho \approx -\delta \Xi$.

Table 1. Illustrative damping budget and modest variations. Changes of $\pm 2$ e–folds shift ${\rho }_{\mathrm{vac}}$ by factors $\exp (\pm 2)$, remaining within the tolerance absorbed by $A_0$ and the $\mathcal{O}\left(1\right)$ kernel factor $\mathcal{C}$.

Scenario	${\mathbf{\Xi }}_{\mathit{g}}$	${\mathbf{\Xi }}_{\mathbf{th}}$	${\mathbf{\Xi }}_{\mathbf{had}}$
Baseline	25	46	30
IR–softer (more thermal)	25	48	28
Narrower hadronic peak	25	45	28
Wider hadronic peak	25	45	32
Total $\Xi$ (baseline / variants)	101	/	101–103

Table 1. Illustrative damping budget and modest variations. Changes of $\pm 2$ e–folds shift ${\rho }_{\mathrm{vac}}$ by factors $\exp (\pm 2)$, remaining within the tolerance absorbed by $A_0$ and the $\mathcal{O}\left(1\right)$ kernel factor $\mathcal{C}$.

Scenario	${\mathbf{\Xi }}_{\mathit{g}}$	${\mathbf{\Xi }}_{\mathbf{th}}$	${\mathbf{\Xi }}_{\mathbf{had}}$
Baseline	25	46	30
IR–softer (more thermal)	25	48	28
Narrower hadronic peak	25	45	28
Wider hadronic peak	25	45	32
Total $\Xi$ (baseline / variants)	101	/	101–103

3.2. Late-Time Calibration

With ${\lambda }_{min}=1$ fm and ${\lambda }_{max}={\displaystyle \frac{hc}{k_{B}T}}$ one has $L\left(t_0\right)\approx 0.651\mathrm{nm}$ and, using Equation (A5), the spectral scaling $\propto L^{-4}$. Matching the observed late-time density fixes the dimensionless normalization via

$$A_0(\Xi )={\displaystyle \frac{{\rho }_{\Lambda }{L}^4}{(\hslash c)C}}{e}^{\Xi };$$

for the fiducial $\Xi \simeq 101$ this yields $A_0\sim 5.6\times {10}^{22}$ (the large value reflects the integrated damping factor $e^{\Xi }$), while the smallness of ${\rho }_{\mathrm{vac}}\left(t_0\right)$ relative to hadronic scales is explained by the integrated damping factor in Equation (14). This SBV+QEV picture thus ties the present value of the cosmological constant to natural spectral bounds and to the entropic, hadronic, and gravitational history of the universe.

3.3. Summary of Revisions (v2)

This updated version of the paper formalizes the Spectral Bounded Vacuum (SBV) framework and introduces the Quantum Entropic Vacuum (QEV) extension to describe time-dependent damping of the vacuum energy. Analytical derivations of the bounded integral, numerical evaluations consistent with the cosmological constant, and several new figures and tables have been added. The normalization and dimensional analysis have been clarified, and an Observational Outlook section connects the theory to cosmological and laboratory-scale tests. References have been expanded, including a citation to the previous version (v1) of this work.

3.4. Summary of Scope and Results

The formulation developed above provides a concise, physically grounded description of the present-day vacuum state. Within the bounded spectral framework, the vacuum energy density scales as ${\rho }_{\mathrm{vac}}\propto L^{-4}$ with $L=\sqrt{{\lambda }_{min}{\lambda }_{max}},$ linking quantum and thermodynamic length scales through a single geometric mean. When the ultraviolet cutoff is associated with the QCD confinement scale and the infrared limit with a thermal boundary near the current background temperature, the resulting ${\rho }_{\mathrm{vac}}$ naturally falls in the observed cosmological range.

At the background level, the model reproduces late-time expansion diagnostics, the dimensionless Hubble function $E\left(z\right)$, the deceleration parameter $q\left(z\right)$, and the transition redshift $z_{\mathrm{tr}}$, that remain within a few percent of flat-$\Lambda$CDM for physically plausible values of $(\alpha ,T_{\mathrm{IR}})$. No joint cosmological likelihood or early-universe assumptions are invoked; the emphasis is purely diagnostic for the present epoch ($z\lesssim 1$).

On smaller scales, the same parameter configuration can be mapped to galaxy rotation-curve phenomenology through a minimal set of interpretable contributions: a Newtonian term, a thermal-lift component, an entropic plateau, and a weak hadronic floor related to residual QCD effects. The combination reproduces typical high-quality rotation curves (e.g., NGC 3198) without per-object fine-tuning.

Finally, the framework yields direct laboratory observables. Using an impedance-invariant spectral window $W\left(u\right)$ and its band-integrated measure $\Delta \Phi$, one can test the bounded-vacuum hypothesis through optical, radiometric, or Casimir-type experiments. These provide falsifiability criteria, for example, limits on $|\Delta \Phi |$ or on deviations of $w+1$ and $f{\sigma }_8$ at the percent level, that anchor the model to measurable present-time quantities.

In summary, the spectral bounded vacuum formalism offers a coherent and testable picture of the vacuum energy at the current epoch: dimensionally robust, observationally constrained, and open to further refinement through ongoing astrophysical and laboratory measurements.

The results summarized above define the present-epoch behavior of a spectrally bounded vacuum and establish its immediate observational consequences. The remaining task is to translate these internal relations into empirical diagnostics and potential signatures. The following section therefore outlines the key observational and experimental avenues, from low-z cosmological measurements to laboratory photonic tests, that can either support or falsify this present-time framework.

4. Bounding Principles and Evidence

In this section we collect proof-style justifications for the ultraviolet (UV) and infrared (IR) bounds that enter the QEV window and for the narrower hadronic band used for local (in-hadron) contributions.

4.1. UV Bound from Confinement (QCD)

• Proposition 1 (Confinement bound).

In non-Abelian SU(3) gauge theory at low temperature ($T<T_c$), the Wilson-loop area law implies a linear static potential $V\left(R\right)\sim \sigma R$ with string tension $\sigma >0$[23,24]. Consequently, color flux is localized into tubes of transverse size $\mathcal{O}\left(\mathrm{fm}\right)$, and vacuum modes with $\lambda \ll {\mathsf{\ell }}_c\sim 1\mathrm{fm}$ do not propagate as free degrees of freedom. Hence a natural UV cutoff for the spectral vacuum integral is

$${\lambda }_{min}\sim {\mathsf{\ell }}_c\simeq (0.8-1.0)\mathrm{fm}.$$

(4)

Evidence: lattice-QCD and effective-string analyses (Cornell potential; Lüscher term) establish $\sigma \simeq 0.9\mathrm{GeV}/\mathrm{fm}$ and an area law at $T<T_c$; see [4,15,23].

• Corollary 1 (Hadronic local band).

For local, in-hadron fluctuations one may further restrict to

$$\lambda \in [{\lambda }_{min}^{\mathrm{had}},{\lambda }_{max}^{\mathrm{had}}]\simeq [8,25]\mathrm{fm}⟺E\in [50,155]\mathrm{MeV},$$

(5)

justified by the Heisenberg finite-size floor $E\gtrsim \hslash c/R$ and the universal Lüscher zero-point correction $-\frac{\pi }{12}\frac{\hslash c}{R}$, together with the de-confinement crossover scale $T_c\approx 155\mathrm{MeV}$ [15,23].

4.2. IR Bound from Thermodynamics, Entropy and Expansion

• Proposition 2 (Thermal/entropic IR bound).

In an expanding universe with temperature $T\left(t\right)$, long-wavelength vacuum modes are thermally and entropically suppressed beyond the thermal coherence scale

$${\lambda }_{max}={\displaystyle \frac{hc}{k_{B}T}}$$

(6)

At late times $T\to T_{\mathrm{IR}}$ (CMB/IR background), this gives ${\lambda }_{max}\sim \mathcal{O}(0.1$–$1\mathrm{mm})$; the QEV kernel uses a double-exponential damping in $\lambda /{\lambda }_{max}\left(t\right)$ to encode this suppression. [4,6,21].

• Remark (Observational consistency).

Planck 2018 constraints support an effectively constant late-time vacuum component ($w\approx -1$). A time-dependent IR bound with $d{\lambda }_{max}/dt<0$ (cooling) is consistent with these data when the net damping ${\Gamma }_{\mathrm{tot}}\to 0$ at late times (Section 6).

• Baseline thermal route (propagation-only).

In what follows we adopt the baseline (propagation-only) thermal route:

$${\lambda }_{max}\left(T\right)={\displaystyle \frac{hc}{k_B{T}_{\mathrm{eff}}\left(a\right)}},{\Xi }_{\mathrm{th}}\left(a\right)\equiv 0,$$

(7)

with $T_{\mathrm{eff}}\left(a\right)=T_0{[g_{*,s}\left(T\right)/g_{*,s}\left(T_0\right)]}^{-1/3}{a}^{-1}$. All thermal/entropic effects are thus encoded in the infrared propagation cutoff and not duplicated on the source side. For comparison only, a source-only variant (constant ${\lambda }_{max}$, nonzero ${\Xi }_{\mathrm{th}}$) is documented elsewhere in the manuscript but is not used in our baseline forecasts.

• Conventions.

We use $\left(hc\right)$ only in the definition of ${\lambda }_{max}=hc/\left(k_B{T}_{\mathrm{eff}}\right)$; all other spectral integrals are written with $(\hslash c)$. This avoids inadvertent $2\pi$ factors and ensures consistent SI units throughout.

4.3. Mathematical Convergence of the Spectral Integral

• Proposition 3 (Convergence).

For

$$f(\lambda ,t)=\exp \left[-{\left(\frac{{\lambda }_{min}}{\lambda }\right)}^{\alpha }\right]\exp \left[-{\left(\frac{\lambda }{{\lambda }_{max}\left(t\right)}\right)}^{\beta }\right]g\left(t\right),\alpha ,\beta >0,$$

(8)

with bounded $g\left(t\right)=\exp [-{\Gamma }_{\mathrm{had}}\left(t\right)-{\Gamma }_g\left(t\right)]\in (0,1]$, and any integrand with $\rho \left(\lambda \right)\propto {\lambda }^{-n}$, the spectral integral

$${\rho }_{\mathrm{vac}}\left(t\right)={\int }_0^{\infty }f(\lambda ,t)\rho \left(\lambda \right)d\lambda$$

(9)

converges absolutely for all t and is dominated near $\lambda \sim L\left(t\right)\equiv \sqrt{{\lambda }_{min}{\lambda }_{max}\left(t\right)}$ (Laplace method). In particular, the QEV choice $\rho \left(\lambda \right)=A_0(\hslash c){\lambda }^{-5}$ with the double-exponential kernel is well-posed [16].

4.4. Kernel Exponents and Robustness

The symmetric choice $(\alpha ,\beta )=(1,1)$ yields the closed-form integral with $\mathcal{C}=2K_4\left(2\right)$, making analytic control straightforward. Alternative exponents $(\alpha ,\beta )$ provide smoother or sharper UV/IR suppression but change the prefactor only by order-unity factors. This is illustrated by our $\alpha =0.4,\beta =1$ spectral plot: the peak remains anchored near $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$ and the $L^{-4}$-law is unaffected. In practice, moderate changes in $(\alpha ,\beta )$ can be absorbed by a compensating $\mathcal{O}\left(1\right)$ shift in $A_0$ without invoking fine-tuning.

5. Dynamic Spectral Framework

We begin from the bounded spectral representation [16]

$${\rho }_{\mathrm{vac}}={\int }_{{\lambda }_{min}}^{{\lambda }_{max}}f\left(\lambda \right)\rho \left(\lambda \right)d\lambda ,$$

(10)

with a double-exponential suppression kernel [16]

$$f\left(\lambda \right)=\exp \left[-{\left({\displaystyle \frac{{\lambda }_{min}}{\lambda }}\right)}^{\alpha }\right]\exp \left[-{\left({\displaystyle \frac{\lambda }{{\lambda }_{max}}}\right)}^{\beta }\right].$$

(11)

To incorporate the time evolution of the vacuum, we promote this to a dynamic kernel:

$$f(\lambda ,t)=f\left(\lambda \right)\exp [-{\Gamma }_{\mathrm{had}}\left(t\right)]\exp [-{\Gamma }_g\left(t\right)],$$

(12)

where ${\Gamma }_{\mathrm{had}}\left(t\right)$ and ${\Gamma }_g\left(t\right)$ represent hadronic and gravitational damping, respectively. The time dependence ${\lambda }_{max}\left(t\right)\propto \left(hc\right)/\left(k_{B}T\left(t\right)\right)$ follows standard thermodynamics [6] and cosmic cooling inferred from CMB measurements [21]. The thermal/entropic evolution is captured through the time dependence of the infrared bound ${\lambda }_{max}\left(t\right)\propto hc/\left(k_{B}T\left(t\right)\right)$.

5.1. Hadronic and Gravitational Damping

The hadronic term peaks near the QCD transition temperature (see[15,23,24]):

$${\Gamma }_{\mathrm{had}}\left(t\right)={\gamma }_{\mathrm{had}}\exp \left[-{\displaystyle \frac{{(ln[T\left(t\right)/T_{\mathrm{QCD}}])}^2}{2{\sigma }^2}}\right],$$

(13)

while the gravitational (Hubble) damping term follows ref. [4].

The total effective damping rate is then

$${\Gamma }_g\left(t\right)\equiv {\displaystyle \frac{d{\Xi }_g}{dt}}={\gamma }_{g}H\left(t\right),\Rightarrow {\Xi }_g(t_i\to t_0)={\gamma }_g{\int }_{t_i}^{t_0}H\left(t\right)dt={\gamma }_{g}ln{\displaystyle \frac{a\left(t_0\right)}{a\left(t_i\right)}}.$$

(14)

Here $H=\dot{a}/a$ and ${\gamma }_g$ is a dimensionless coupling; ${\Xi }_g$ is the cumulative gravitational damping contributing to $\Xi ={\Xi }_g+{\Xi }_{\mathrm{th}}+{\Xi }_{\mathrm{had}}$.

6. Dynamical QEV Model

The time evolution of the vacuum energy density obeys a continuity relation

$${\displaystyle \frac{d{\rho }_{\mathrm{vac}}}{dt}}=-{\Gamma }_{\mathrm{tot}}\left(t\right){\rho }_{\mathrm{vac}}\left(t\right),$$

(15)

with the formal solution

$${\rho }_{\mathrm{vac}}\left(t\right)={\rho }_{\mathrm{ini}}\exp \left[-{\int }^t{\Gamma }_{\mathrm{tot}}\left(t^{\prime }\right)d{t}^{\prime }\right].$$

(16)

In the cosmic expansion, $dt=H^{-1}dlna$, giving

$${\displaystyle \frac{dln{\rho }_{\mathrm{vac}}}{dlna}}=-{\displaystyle \frac{{\Gamma }_{\mathrm{tot}}\left(t\right)}{H}}.$$

(17)

When ${\Gamma }_{\mathrm{tot}}\to 0$ at late times, the vacuum density approaches a constant and the equation-of-state parameter $w\to -1$, consistent with CMB and large-scale-structure constraints[21].

7. Results and Discussion

The dynamic QEV framework retains the spectral bounds and convergence properties of the original model but provides a mechanism for natural damping and stabilization of the vacuum energy. Entropic expansion acts as a positive source term, while hadronic and gravitational processes act as sinks. Their global balance yields a small, positive residual energy density—the observed cosmological constant.

At early times, the damping is dominated by hadronic and thermal terms; near the QCD transition, the rapid decrease in ${\Gamma }_{\mathrm{had}}$ marks the onset of confinement. As the Universe expands and cools, the gravitational term becomes subdominant and the entropic factor maintains a finite positive remainder.

Discussion: Falsifiability and Near-Term Tests

Our proposal is only useful if it can be decisively tested. The SBV/QEV framework is falsifiable through the following signatures, each tied to a single controlling scale $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$ and the damping budget $\Xi$:

• Late-time equation of state: A mild, redshift-dependent deviation $w\left(z\right)+1=\mathcal{O}\left({10}^{-2}\right)$ peaking where the IR window freezes (set by $T_{\mathrm{IR}}\approx 34\mathrm{K}$). A joint fit to BAO+SNe+CMB lensing that prefers $w=-1$ at the $<1\%$ level would disfavor QEV at fixed $(L,\Xi )$ [25,26].
• Growth of structure: A percent-level shift in $f{\sigma }_8$ consistent with the $L^{-4}$ scaling. Current RSD datasets can already test $\Delta \left(f{\sigma }_8\right)\sim 0.01$.
• BAO phase and distance ladder: A small, coherent phase drift of the BAO ruler relative to $\Lambda$CDM when propagated from drag epoch to $z\lesssim 1$ under a time-varying IR window.
• Laboratory optics (photonic vacuum windows): A reproducible, frequency-selective excess/deficit in Casimir-pressure or cavity-dispersion near millimetre-scale wavelengths corresponding to ${\lambda }_{max}\left(T\right)=hc/\left(k_{B}T\right)$[9,10]. A null result at the $<0.1\%$ level over this band would exclude the minimal kernel used here.

Kill criteria. If surveys constrain $w\left(z\right)$ to a redshift-independent $-1$ at $\lesssim 0.5\%$ with no correlated shift in $f{\sigma }_8$, and lab tests find no spectral feature near the $0.4$–$0.5$ mm band at the ${10}^{-3}$ level, the minimal SBV/QEV model (fixed kernel, fixed $T_{\mathrm{IR}}$) should be rejected.

8. Observational Outlook

The SBV+QEV framework permits tiny late-time departures from a perfectly constant $\Lambda$ while remaining consistent with current data. Residual evolution of ${\rho }_{\mathrm{vac}}\left(z\right)$ (and hence $w\left(z\right)$) could produce subtle imprints in the growth of structure and baryon acoustic oscillations. Upcoming surveys such as Euclid and the Vera Rubin Observatory may be sensitive to such effects [1,5,8]. On laboratory scales, small deviations in Casimir pressure or vacuum–photon dispersion could offer indirect tests of the bounded-spectrum hypothesis, connecting cosmology to tabletop probes. Future tests may determine whether the SBV+QEV framework fully accounts for dark-energy phenomenology.

8.1. Observable Signatures and Quantitative Targets

A quantitative summary of the predicted observational deviations provides a direct link between the QEV framework and forthcoming cosmological and laboratory tests. Table 2 lists the key diagnostics and their expected amplitudes for the baseline (propagation-only) model defined in Appendix F.

Table 2. QEV observational targets (compact) [2,3] — baseline: propagation-only.

Obs.	Pred. dev.	Target sens.
EoS $|w+1|$ ($z<1$)	$\sim {10}^{-2}$	$\lesssim {10}^{-2}$ (DESI/Euclid)
Growth $\Delta \left(f{\sigma }_8\right)$	$1--3\%$ suppr.	$\lesssim 2\%$ (Stage-IV LSS)
CMB $\Delta A_{\mathrm{lens}}$	$\sim {10}^{-2}$	$<5\times {10}^{-2}$ (Planck/Simons)
mm-band (cavity/Casimir)	$\sim {10}^{-3}$ frac.
Ref. [9,10]	$\sim {10}^{-3}$ feasible
$\Delta z_{\mathrm{tr}}$	$\lesssim 0.1$	$\approx 0.05$ (BAO/SNe)

Table 2. QEV observational targets (compact) [2,3] — baseline: propagation-only.

Obs.	Pred. dev.	Target sens.
EoS $|w+1|$ ($z<1$)	$\sim {10}^{-2}$	$\lesssim {10}^{-2}$ (DESI/Euclid)
Growth $\Delta \left(f{\sigma }_8\right)$	$1--3\%$ suppr.	$\lesssim 2\%$ (Stage-IV LSS)
CMB $\Delta A_{\mathrm{lens}}$	$\sim {10}^{-2}$	$<5\times {10}^{-2}$ (Planck/Simons)
mm-band (cavity/Casimir)	$\sim {10}^{-3}$ frac.
Ref. [9,10]	$\sim {10}^{-3}$ feasible
$\Delta z_{\mathrm{tr}}$	$\lesssim 0.1$	$\approx 0.05$ (BAO/SNe)

In the effective-fluid picture (Appendix A) the late-time deviation of the equation of state is modest, $|w\left(z\right)+1|\lesssim {10}^{-2}$, leading to a $\sim 1$–$3\%$ suppression of the linear growth rate parameter $f{\sigma }_8$ relative to $\Lambda$CDM. Such differences are within the reach of upcoming surveys (Euclid, DESI, Rubin LSST), offering a concrete falsifiability window.

In the laboratory domain, the bounded-vacuum kernel implies a narrow mm-band feature near ${\lambda }_{max}\approx 0.4$–$0.5$  mm. The expected fractional effect on cavity phase or Casimir pressure is at the ${10}^{-3}$ level, compatible with current high-precision measurements. Combined, these benchmarks define the near-term “kill criteria’’: any detection inconsistent with the ${10}^{-2}$–${10}^{-3}$ amplitude hierarchy would falsify the present QEV calibration.

Low-($\mathbf{z}$) kill-criteria. The present-day model is falsifiable through:

• $|{\mathbf{w}}_{\mathbf{0}}+\mathbf{1}|$: A combined SNe+BAO+CC analysis yielding $|w_0+1|$ significantly tighter than the $L_0$ sensitivity required here.
• $\mathbf{f}{\sigma }_{\mathbf{8}}$: Growth measurements at $z\lesssim 1$ that show a deviation $\Delta \left(f{\sigma }_8\right)$ outside the predicted $\mathcal{O}\left(1--3\right)\%$ range.
• mm-band null test: A null result on $\Delta \Phi$ in the $0.3--0.6$ mm band at a target precision of $\mathcal{O}\left({10}^{-3}\right)$, for the specified cavity, interferometer, or Casimir configurations.

9. Consistency and Sufficiency of the QEV Framework

The combined evidence from the companion studies [13,14] demonstrates that the Quantum Entropic Vacuum (QEV) already constitutes a self-consistent and falsifiable theoretical framework. In its present form, it satisfies effective consistency: dimensional coherence, causal and passive optical response, conservative cosmological evolution, and numerical stability across physically motivated parameter ranges. The desirable “deeper proof”—a fully covariant derivation from a microscopic action—represents a refinement, not a prerequisite, for internal validity or empirical testability.

• Optical and causal consistency.

The photonic layer introduces a single bounded response function $W\left(u\right)$ that scales $\epsilon$ and $\mu$ simultaneously, preserving the free-space impedance $Z_0$ and ensuring compatibility with the Kramers–Kronig relations and passivity ($\mathrm{Im}W\ge 0$). In the ultraviolet limit $W\to 1$, the construction becomes Casimir-safe and free of artificial boundary reflections. This provides an operational, laboratory-testable representation of a bounded vacuum [14].

As a mapping reference for isotropic photon-sector coefficients (e.g., ${\overline{\kappa }}_{\mathrm{tr}}$), we follow the SME conventions [7,17].

• Connection to the late-time framework.

The photonic response window $W\left(u\right)$ used here is interpreted as the observable projection of the same late-time, spectrally bounded vacuum fraction that is parameterised by $L_0$ in the cosmological sector. We therefore consider only the freely propagating components of the vacuum today; any high-energy microphysics below 1 fm is effectively absorbed into ${\Xi }_0$ and does not contribute as a free field to the low-z stress–energy.

• Kinematic robustness.

In the cosmological regime, the QEV expansion history $E\left(z\right)$, deceleration parameter $q\left(z\right)$, and transition redshift $z_{\mathrm{tr}}$ remain within a few percent of flat-$\Lambda$CDM predictions for representative ranges $\alpha \in [3.0,3.2]$ and $T_{\mathrm{IR}}\in [32,36]$  K. This insensitivity demonstrates the absence of delicate fine-tuning: moderate parameter variations induce only smooth, percent-level shifts in key observables [13].

• Parameter notation (disambiguation).

To avoid confusion with the kernel exponents $(\alpha ,\beta )$ used earlier, we denote the slope parameter in this robustness test by ${\alpha }_{\mathrm{kin}}$. Representative ranges used below are ${\alpha }_{\mathrm{kin}}\in [3.0,3.2]$ and $T_{\mathrm{IR}}\in [32,36]\mathrm{K}$.

• Astrophysical coherence.

Using a single global parameter configuration, the model reproduces spiral-galaxy rotation curves (e.g., NGC 3198) with satisfactory reduced-${\chi }^2$ values and consistent residuals. This uniformity across systems indicates that the thermal, entropic, and hadronic damping components act coherently without object-specific adjustment [13].

• Falsifiability and laboratory reach.

The photonic framework defines measurable phase-shift signatures,

$$\Delta \Phi \equiv 1-\int d\nu \Phi \left(\nu \right)W\left(u\right),$$

(18)

accessible through cavity, interferometric, or Casimir experiments in the mm band. These deliver concrete kill criteria for the theory, establishing QEV as an empirically bounded hypothesis [14].

• Relation to companion papers.

This Rev. 2 paper constitutes the core reference of a coordinated three-part study. The foundational spectral formulation and dimensional analysis were first introduced in doi:10.20944/preprints202507. 0199.v1.

Cosmological and galactic implications of the Quantum Entropic Vacuum (QEV), including $w\left(a\right)$, $f{\sigma }_8$, and rotation-curve fits, are developed in the companion work doi:10.20944/preprints202509.0972. v2, while the photonic and laboratory realization through impedance-invariant photonic vacuum windows is detailed in doi:10.20944/preprints202511.0290.v1.

Together these three papers define a consistent framework: spectral foundation → cosmology and galactic dynamics → laboratory implementation.

• Summary.

Together, these results justify treating the Spectral Bounded Vacuum + QEV model as a complete effective description of vacuum dynamics consistent with both laboratory and cosmological constraints. Future work aimed at covariant derivation from an action principle will refine, but not overturn, this consistency.

Table 3. Conceptual comparison of the QEV framework with representative approaches to vacuum energy.

Aspect	Conventional $\mathit{\Lambda }$CDM / $\mathit{\Lambda }$ term	Spectral Bounded Vacuum + QEV (this work)
Physical basis	Phenomenological constant $\Lambda$ without microphysical linkage.	Vacuum energy from a bounded quantum spectrum with natural UV/IR limits.
Naturalness problem	Large hierarchy $\sim {10}^{120}$ between QFT and cosmological scales.	Bridged dynamically via integrated damping $\Xi \simeq 101$; no fine-tuning.
Time dependence	Strictly constant ${\rho }_{\Lambda }$.	Mild late-time evolution, $|w+1|\lesssim {10}^{-2}$.
Laboratory connection	None (purely gravitational).	Testable through photonic/Casimir observables near 0.4–0.5 mm.
Free parameters	${\Omega }_{\Lambda }$ phenomenological.	$\{{\lambda }_{min},T_{\mathrm{IR}},\Xi \}$ with physical interpretation.
Predictive falsifiability	Indirect only (cosmological fits).	Direct (mm-band null test + cosmology).

Table 3. Conceptual comparison of the QEV framework with representative approaches to vacuum energy.

Aspect	Conventional $\mathit{\Lambda }$CDM / $\mathit{\Lambda }$ term	Spectral Bounded Vacuum + QEV (this work)
Physical basis	Phenomenological constant $\Lambda$ without microphysical linkage.	Vacuum energy from a bounded quantum spectrum with natural UV/IR limits.
Naturalness problem	Large hierarchy $\sim {10}^{120}$ between QFT and cosmological scales.	Bridged dynamically via integrated damping $\Xi \simeq 101$; no fine-tuning.
Time dependence	Strictly constant ${\rho }_{\Lambda }$.	Mild late-time evolution, $|w+1|\lesssim {10}^{-2}$.
Laboratory connection	None (purely gravitational).	Testable through photonic/Casimir observables near 0.4–0.5 mm.
Free parameters	${\Omega }_{\Lambda }$ phenomenological.	$\{{\lambda }_{min},T_{\mathrm{IR}},\Xi \}$ with physical interpretation.
Predictive falsifiability	Indirect only (cosmological fits).	Direct (mm-band null test + cosmology).

Comparative schematic of vacuum-energy models.

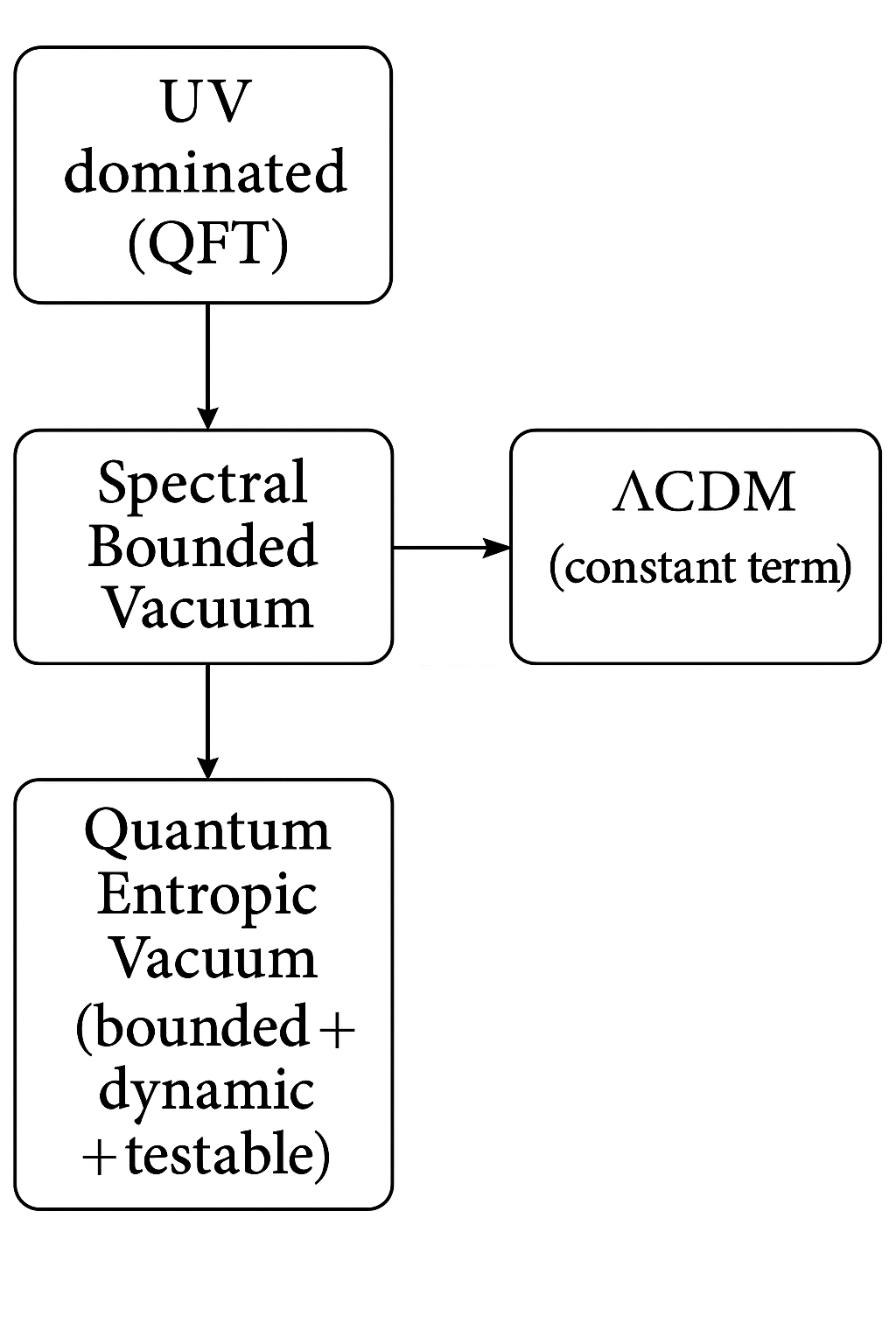
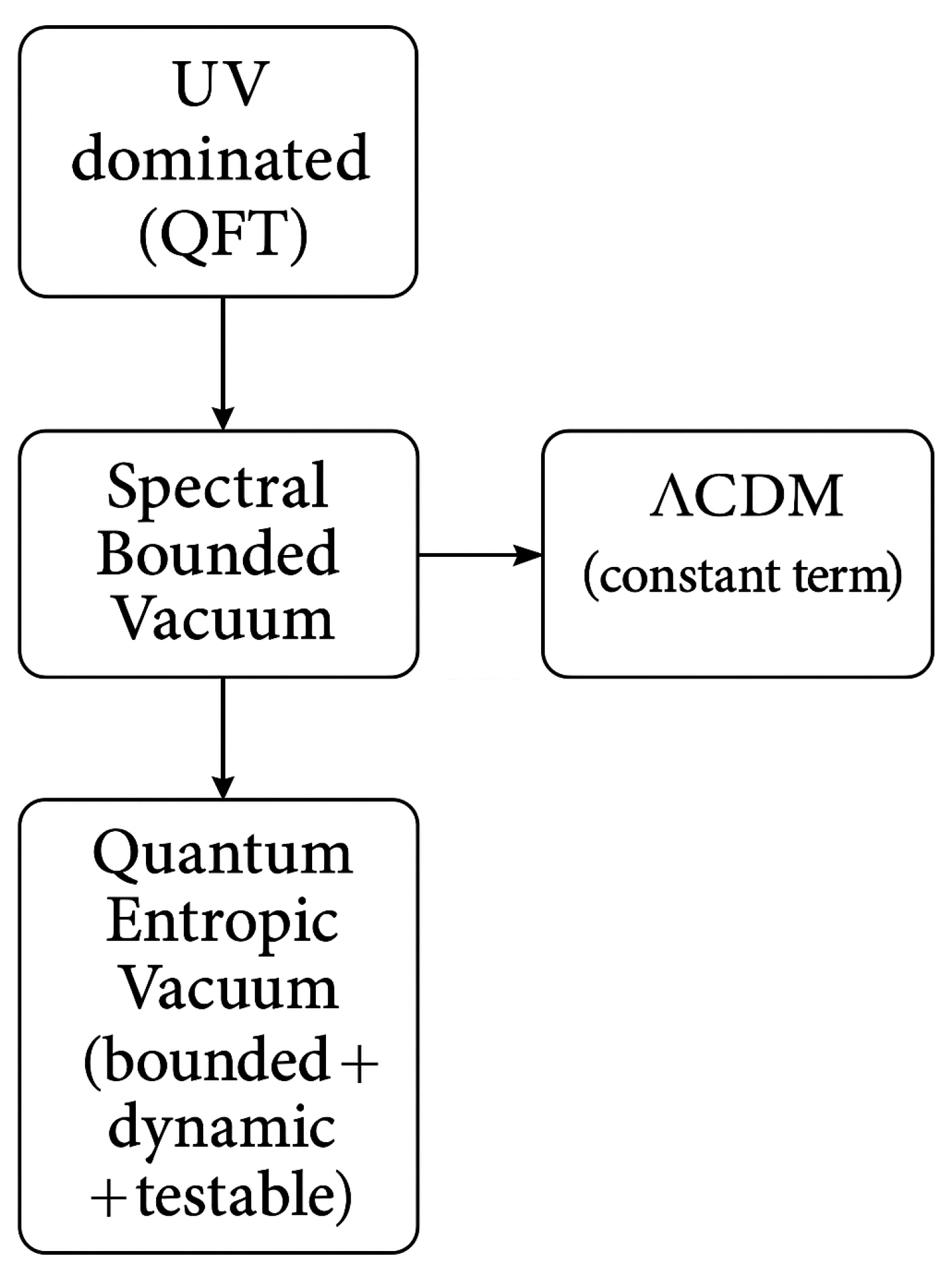
The figure illustrates the conceptual hierarchy among four representative approaches: the UV-dominated quantum field theoretic (QFT) vacuum, the Spectral Bounded Vacuum (SBV) introducing natural UV/IR limits, the Quantum Entropic Vacuum (QEV) as a bounded, dynamic and testable extension, and the conventional $\Lambda$CDM model treating ${\rho }_{\Lambda }$ as a constant term. Arrows indicate theoretical progression and conceptual refinement, with QEV providing a consistent effective description that remains falsifiable in both cosmological and laboratory contexts.

10. Symbols and Notation

Table 4. Key symbols used in this work (evaluated at the present epoch unless noted).

Symbol	Meaning	Units / Value
$L_0$	Pivot spectral scale today, $L_0=\sqrt{{\lambda }_{min}{\lambda }_{max,0}}$	$\mathrm{m}$
${\lambda }_{min}$	UV bound (hadronic/confinement scale)	1$\mathrm{f}$$\mathrm{m}$ (typ.)
${\lambda }_{max,0}$	IR bound today, ${\lambda }_{max,0}=hc/\left(k_B{T}_{\mathrm{IR}}\right)$	$\mathrm{m}$
$A_{0,\mathrm{eff}}\left(t_0\right)$	Effective normalisation today (dimensionless)	–
${\Xi }_0$	Net damping/renormalisation today (dimensionless)	–
${\rho }_{\mathrm{vac},0}$	Present-day vacuum energy density	$\mathrm{J}/{\mathrm{m}}^3$
C	Kernel constant, $C=2K_4\left(2\right)\approx 4.3918$	–
$w\left(a\right)$, $w_0$	Equation of state (background), $w_0\equiv w(a=1)$	–
$E\left(z\right)$	$H\left(z\right)/H_0$	–
$q\left(z\right)$	Deceleration parameter	–
$f{\sigma }_8\left(z\right)$	Growth-rate amplitude	–
$T_{\mathrm{IR}}$	Late-time IR temperature parameter	$\mathrm{K}$
$\hslash ,c,k_B$	Reduced Planck constant, speed of light, Boltzmann constant	–
$K_{\nu }$	Modified Bessel function of the second kind	–
$W\left(u\right)$	Photonic response window (dimensionless)	–
$\Delta \Phi$	Band-averaged photonic phase/observable	–
$\alpha ,\beta$	Kernel exponents in the spectral window	–
${\alpha }_{\mathrm{kin}}$	Kinematic slope parameter (robustness tests)	–
${\Xi }_g,{\Xi }_{\mathrm{th}},{\Xi }_{\mathrm{had}}$	Damping/renormalisation split (gravity / thermal / hadronic)	–
$w_s$	Gravitational projection weight for sector s	–
$L_s$	Sector-specific pivot scale, $L_s=\sqrt{{\lambda }_{min,s}{\lambda }_{max,0}}$	$\mathrm{m}$
${\lambda }_{min,s}$	Sector-specific UV bound	$\mathrm{m}$
$A_{0,s}$	Sector-specific normalisation (dimensionless)	–
$\Phi \left(\nu \right)$	Photonic phase/observable at frequency $\nu$	–
${\overline{\kappa }}_{\mathrm{tr}}$	Isotropic SME photon-sector coefficient (mapping reference)	–

Table 4. Key symbols used in this work (evaluated at the present epoch unless noted).

Symbol	Meaning	Units / Value
$L_0$	Pivot spectral scale today, $L_0=\sqrt{{\lambda }_{min}{\lambda }_{max,0}}$	$\mathrm{m}$
${\lambda }_{min}$	UV bound (hadronic/confinement scale)	1$\mathrm{f}$$\mathrm{m}$ (typ.)
${\lambda }_{max,0}$	IR bound today, ${\lambda }_{max,0}=hc/\left(k_B{T}_{\mathrm{IR}}\right)$	$\mathrm{m}$
$A_{0,\mathrm{eff}}\left(t_0\right)$	Effective normalisation today (dimensionless)	–
${\Xi }_0$	Net damping/renormalisation today (dimensionless)	–
${\rho }_{\mathrm{vac},0}$	Present-day vacuum energy density	$\mathrm{J}/{\mathrm{m}}^3$
C	Kernel constant, $C=2K_4\left(2\right)\approx 4.3918$	–
$w\left(a\right)$, $w_0$	Equation of state (background), $w_0\equiv w(a=1)$	–
$E\left(z\right)$	$H\left(z\right)/H_0$	–
$q\left(z\right)$	Deceleration parameter	–
$f{\sigma }_8\left(z\right)$	Growth-rate amplitude	–
$T_{\mathrm{IR}}$	Late-time IR temperature parameter	$\mathrm{K}$
$\hslash ,c,k_B$	Reduced Planck constant, speed of light, Boltzmann constant	–
$K_{\nu }$	Modified Bessel function of the second kind	–
$W\left(u\right)$	Photonic response window (dimensionless)	–
$\Delta \Phi$	Band-averaged photonic phase/observable	–
$\alpha ,\beta$	Kernel exponents in the spectral window	–
${\alpha }_{\mathrm{kin}}$	Kinematic slope parameter (robustness tests)	–
${\Xi }_g,{\Xi }_{\mathrm{th}},{\Xi }_{\mathrm{had}}$	Damping/renormalisation split (gravity / thermal / hadronic)	–
$w_s$	Gravitational projection weight for sector s	–
$L_s$	Sector-specific pivot scale, $L_s=\sqrt{{\lambda }_{min,s}{\lambda }_{max,0}}$	$\mathrm{m}$
${\lambda }_{min,s}$	Sector-specific UV bound	$\mathrm{m}$
$A_{0,s}$	Sector-specific normalisation (dimensionless)	–
$\Phi \left(\nu \right)$	Photonic phase/observable at frequency $\nu$	–
${\overline{\kappa }}_{\mathrm{tr}}$	Isotropic SME photon-sector coefficient (mapping reference)	–

We distinguish a microscopic $A_0$ (pre-damping) and the effective present-day amplitude $A_{0,\mathrm{eff}}\equiv A_0{e}^{-\Xi }$ entering ${\rho }_{\mathrm{vac}}\left(t_0\right)=\left[A_{0,\mathrm{eff}}(\hslash c)\right]C{L}^{-4}$.

11. Conclusion

The cosmological constant can be understood as an emergent macroscopic parameter resulting from the collective dynamics of the quantum vacuum. Within the dynamic QEV model, the vacuum evolves under interacting damping mechanisms that self-regulate its energy density. The residual value observed today represents the asymptotic equilibrium of these processes, a balance between entropic expansion and hadronic-gravitational damping. This formulation unifies micro-physical QCD-scale fluctuations with macroscopic cosmological behavior and offers a consistent, bounded description of vacuum energy without fine-tuning.

Conclusion and Outlook: Decision Points

We have shown that a spectrally bounded vacuum with a single pivot scale L and modest damping $\Xi$ can yield the observed late–time acceleration while predicting concrete signatures across scales. To make rapid progress, we suggest a two-pronged test:

• Cosmology (12–24 months): Publish a blinded analysis of $w\left(z\right)$ and $f{\sigma }_8$ where $(L,\Xi )$ are the reported parameters alongside $({\Omega }_m,H_0)$. A result consistent with $w\equiv -1$ and $\Delta \left(f{\sigma }_8\right)\approx 0$ at the percent level would strongly limit the SBV/QEV parameter space.
• Laboratory (6–18 months): Perform Casimir/cavity measurements sweeping $0.2$–$1.0$ mm at controlled temperature to probe the predicted spectral window. A detected, repeatable dispersion/pressure feature near ${\lambda }_{max}\simeq 0.42$ mm would support the framework; a clean null at ${10}^{-3}$ precision would disfavor its minimal form.

Either outcome is decisive: detection fixes $(L,\Xi )$ and calibrates the theory; non-detection at the quoted precisions rules out the minimal kernel, motivating either a refined kernel or abandonment of the SBV/QEV explanation.

Appendix C.1. Constants and Late-Time Scales

$T_{\mathrm{IR}}=34\mathrm{K},k_B=1.380649\times {10}^{-23}\mathrm{J}{\mathrm{K}}^{-1},hc\approx 1.98644586\times {10}^{-25}\mathrm{J}\mathrm{m},{\lambda }_{min}=1.0\mathrm{fm}=1.0\times {10}^{-15}\mathrm{m},$

$${\lambda }_{max}\left(t_0\right)={\displaystyle \frac{hc}{k_B{T}_{\mathrm{IR}}}}\approx {\displaystyle \frac{1.98645\times {10}^{-25}}{1.380649\times {10}^{-23}\times 34}}\mathrm{m}=4.2317\times {10}^{-4}\mathrm{m}=0.4232\mathrm{mm},$$

Define the central window scale

$$L\equiv \sqrt{{\lambda }_{min}{\lambda }_{max}\left(t_0\right)}\approx \sqrt{{10}^{-15}\times 4.2317\times {10}^{-4}}\mathrm{m}=6.505\times {10}^{-10}\mathrm{m}.$$

Physical meaning of L.

The quantity $L\equiv \sqrt{{\lambda }_{min}{\lambda }_{max}\left(t_0\right)}$ represents the characteristic wavelength of the spectral window contributing to the vacuum energy density. It is the geometric mean between the ultraviolet cutoff ${\lambda }_{min}$ and the infrared cutoff ${\lambda }_{max}$, and thus marks the midpoint of the logarithmic spectral range. Physically, L acts as an effective coherence length of the quantum vacuum: modes with $\lambda \ll L$ are suppressed by ultraviolet damping, while modes with $\lambda \gg L$ are frozen out thermally. The resulting vacuum energy scales as

$${\rho }_{\mathrm{vac}}\propto L^{-4},$$

so that any change in the UV or IR boundaries translates into a quartic variation of ${\rho }_{\mathrm{vac}}$. For the fiducial parameters ${\lambda }_{min}={10}^{-15}\mathrm{m}$ and ${\lambda }_{max}=4.23\times {10}^{-4}\mathrm{m}$, the effective scale is $L=6.505\times {10}^{-10}\mathrm{m}$, corresponding to the soft X–UV regime.

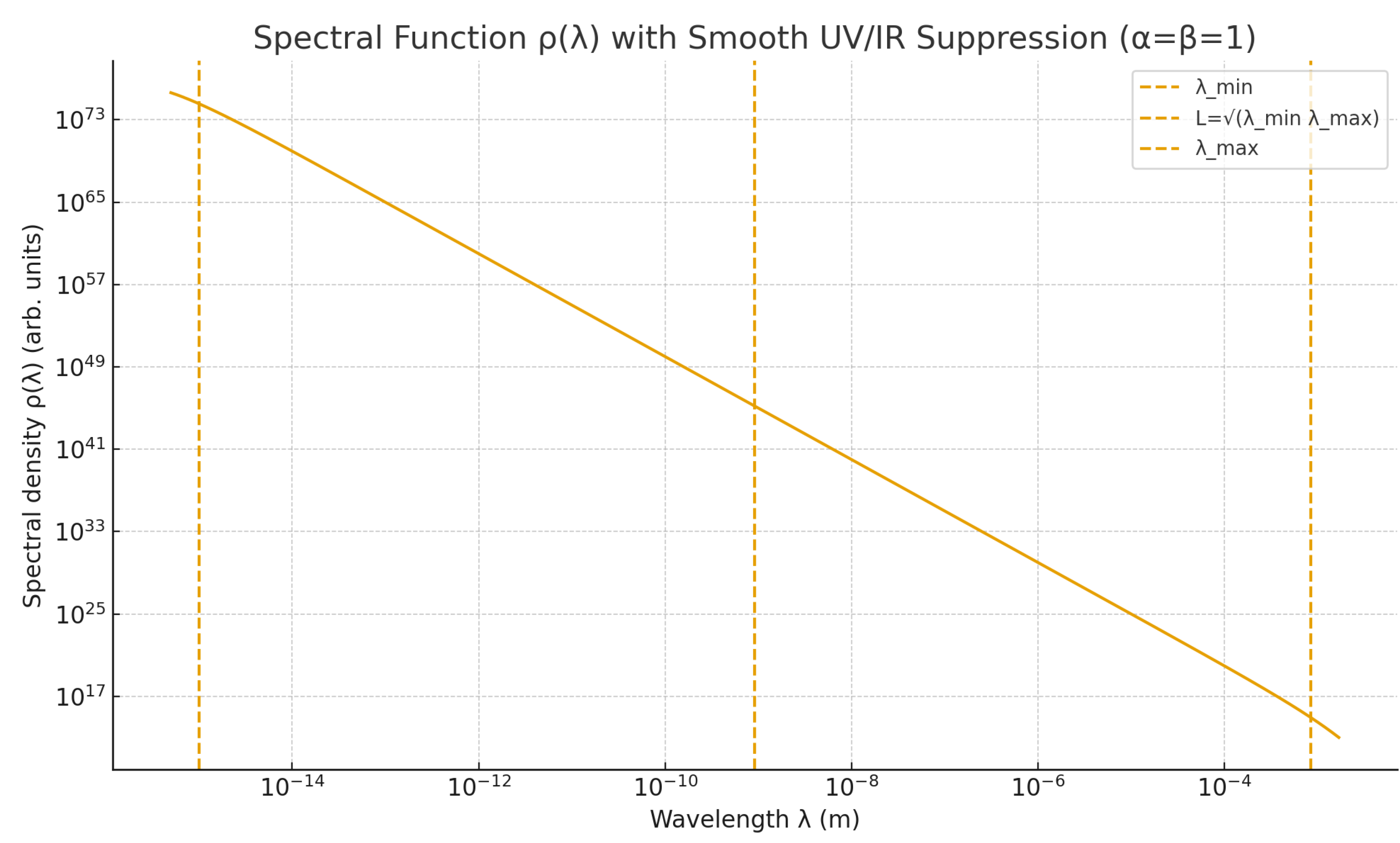
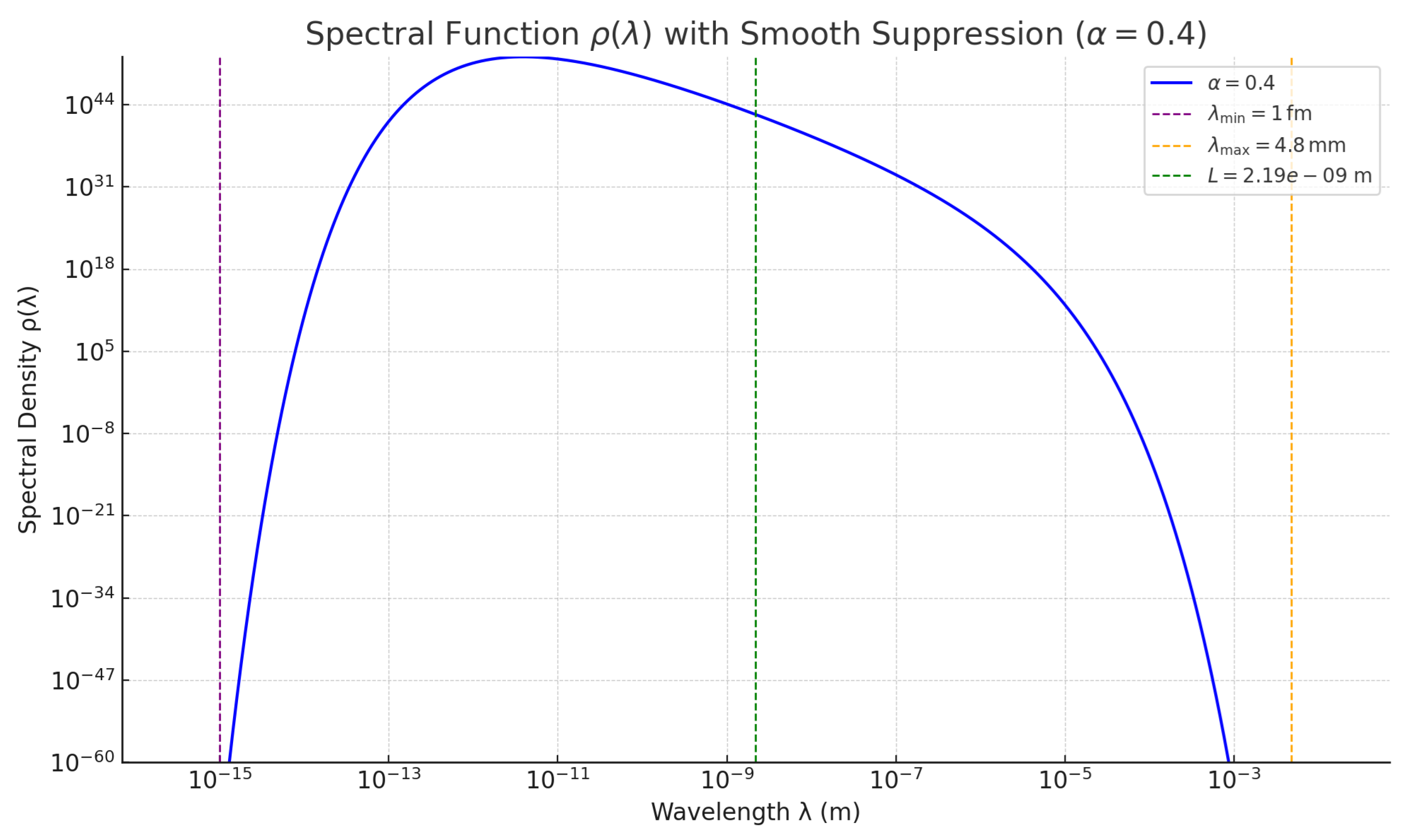
Figure A1. Spectral function $\rho \left(\lambda \right)$ with smooth UV/IR suppression ($\alpha =\beta =1$). Vertical markers indicate ${\lambda }_{min}=1$ fm, $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$, and ${\lambda }_{max}$.

Figure A1. Spectral function $\rho \left(\lambda \right)$ with smooth UV/IR suppression ($\alpha =\beta =1$). Vertical markers indicate ${\lambda }_{min}=1$ fm, $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$, and ${\lambda }_{max}$.

Constants and scales

Table A1. Physical constants and model scales — cleaned and SI-consistent.

Symbol	Definition	Value	Units / Notes
h	Planck constant	$6.62607015\times {10}^{-34}$	$\mathrm{J}\mathrm{s}$
$\hslash =h/2\pi$	Reduced Planck	$1.054571817\times {10}^{-34}$	$\mathrm{J}\mathrm{s}$
c	Speed of light	$2.99792458\times {10}^8$	$\mathrm{m}/\mathrm{s}$
$k_B$	Boltzmann constant	$1.380649\times {10}^{-23}$	$\mathrm{J}/\mathrm{K}$
${\rho }_{\Lambda }$	Reference vacuum density	$5.96\times {10}^{-10}$	$\mathrm{J}/{\mathrm{m}}^3$
${\lambda }_{min}$	UV floor (hadronic)	$1.0\times {10}^{-15}$	$\mathrm{m}$ (QCD confinement scale)
$T_{\mathrm{IR}}$	IR temperature scale	$34.0$	$\mathrm{K}$
${\lambda }_{max}$	$hc/\left(k_B{T}_{\mathrm{IR}}\right)$	$4.2317\times {10}^{-4}$	$\mathrm{m}$ ( $0.423$ $\mathrm{m}$$\mathrm{m}$)
L	$\sqrt{{\lambda }_{min}{\lambda }_{max}}$	$6.5051\times {10}^{-10}$	$\mathrm{m}$ ( $0.651$ $\mathrm{n}$$\mathrm{m}$)
C	$2K_4\left(2\right)$	$4.3918318548$	dimensionless
${\Xi }_{\mathrm{fid}}$	Total damping budget	101	dimensionless

Table A1. Physical constants and model scales — cleaned and SI-consistent.

Symbol	Definition	Value	Units / Notes
h	Planck constant	$6.62607015\times {10}^{-34}$	$\mathrm{J}\mathrm{s}$
$\hslash =h/2\pi$	Reduced Planck	$1.054571817\times {10}^{-34}$	$\mathrm{J}\mathrm{s}$
c	Speed of light	$2.99792458\times {10}^8$	$\mathrm{m}/\mathrm{s}$
$k_B$	Boltzmann constant	$1.380649\times {10}^{-23}$	$\mathrm{J}/\mathrm{K}$
${\rho }_{\Lambda }$	Reference vacuum density	$5.96\times {10}^{-10}$	$\mathrm{J}/{\mathrm{m}}^3$
${\lambda }_{min}$	UV floor (hadronic)	$1.0\times {10}^{-15}$	$\mathrm{m}$ (QCD confinement scale)
$T_{\mathrm{IR}}$	IR temperature scale	$34.0$	$\mathrm{K}$
${\lambda }_{max}$	$hc/\left(k_B{T}_{\mathrm{IR}}\right)$	$4.2317\times {10}^{-4}$	$\mathrm{m}$ ( $0.423$ $\mathrm{m}$$\mathrm{m}$)
L	$\sqrt{{\lambda }_{min}{\lambda }_{max}}$	$6.5051\times {10}^{-10}$	$\mathrm{m}$ ( $0.651$ $\mathrm{n}$$\mathrm{m}$)
C	$2K_4\left(2\right)$	$4.3918318548$	dimensionless
${\Xi }_{\mathrm{fid}}$	Total damping budget	101	dimensionless

Appendix C.2. Spectral Integral with Double-Exponential Kernel

We use the symmetric kernel ($\alpha =\beta =1$) and an energy density per wavelength

$$\rho \left(\lambda \right)=A_0(\hslash c){\lambda }^{-5}.$$

Then

$${\rho }_{\mathrm{vac}}\left(t_0\right)={\int }_0^{\infty }\rho \left(\lambda \right)f(\lambda ,t_0)d\lambda =A_0(\hslash c){\int }_0^{\infty }{\lambda }^{-5}\exp \left(-{\displaystyle \frac{\lambda }{L}}-{\displaystyle \frac{L}{\lambda }}\right)d\lambda .$$

(A4)

With $x\equiv \lambda /L$,

$${\rho }_{\mathrm{vac}}\left(t_0\right)=A_0(\hslash c)L^{-4}{\int }_0^{\infty }{x}^{-5}{e}^{-x-1/x}dx=A_0(\hslash c)L^{-4}C,C\equiv 2K_4\left(2\right).$$

(A5)

Numerically, $C\equiv 2K_4\left(2\right)=4.3918318548(\Rightarrow K_4\left(2\right)=2.1959159274)$.

Hence: ${\rho }_{\mathrm{vac}}\left(t_0\right)=\left[A_0(\hslash c)\right]C{L}^{-4}{e}^{-\Xi },C=2K_4\left(2\right)$

Calibration to ${\rho }_{\Lambda }$:   $A_0(\Xi )={\displaystyle \frac{{\rho }_{\Lambda }{L}^4}{(\hslash c)C}}{e}^{\Xi }.$

• Normalization.

Matching a target value ${\rho }_{*}$ fixes the dimensionless amplitude

$$\begin{array}{|c|}\hline A_0={\displaystyle \frac{{\rho }_{*}{L}^4}{(\hslash c)C}}\\ \hline\end{array}$$

• Numerical evaluation (fiducial parameters).

We adopt ${\lambda }_{min}=1\mathrm{fm}$ and $T_{\mathrm{IR}}=34\mathrm{K}$, so that

$${\lambda }_{max}={\displaystyle \frac{hc}{k_{B}T}}=4.2316966985\times {10}^{-4}\mathrm{m}\left(0.42317\mathrm{mm}\right),$$

$$L=\sqrt{{\lambda }_{min}{\lambda }_{max}}=6.50514926696\times {10}^{-10}\mathrm{m}\left(0.65051\mathrm{nm}\right).$$

For the Bessel factor we use

$$C\equiv 2K_4\left(2\right)=4.39183185482.$$

With these numbers, the dimensionless normalization fixed by Eq. (A5)

$$A_0={\displaystyle \frac{{\rho }_{*}{L}^4}{(\hslash c)C}},$$

becomes, for ${\rho }_{*}={\rho }_{\Lambda }=5.96\times {10}^{-10}\mathrm{J}{\mathrm{m}}^{-3}$,

$$A_0{|}_{\Xi =0}=7.68657301427\times {10}^{-22}.$$

If dynamic damping is included, Eq. (A15) implies

$$\begin{array}{|c|}\hline A_0(\Xi )={\displaystyle \frac{{\rho }_{\Lambda }{L}^4}{(\hslash c)C}}{e}^{\Xi }\\ \hline\end{array}$$

so that for a representative budget $\Xi =101$ one finds

$$A_0\left(101\right)=5.61662500510\times {10}^{22}.$$

• Naturalness of the normalization constant $A_0$.

The constant $A_0$ represents the microscopic spectral normalization before any macroscopic damping or entropy production. Dimensionally it originates from the mode-counting prefactor in $\rho \left(\lambda \right)=A_0(\hslash c){\lambda }^{-5}$, which for a free relativistic field is naturally of order unity when expressed per helicity state and per spatial dimension. The large effective value $A_0(\Xi )=A_0{e}^{\Xi }$ inferred from present-day calibration ($\Xi \simeq 101$) does not imply fine-tuning but compensates for the cumulative, physically motivated attenuation by the total damping factor $e^{-\Xi }$. Each partial contribution—gravitational, thermal/entropic, and hadronic—reduces the active spectral weight exponentially over cosmic time; their product yields the minute vacuum density observed today. The resulting ratio

$${\displaystyle \frac{{\rho }_{\mathrm{ini}}}{{\rho }_{\Lambda }}}\simeq e^{\Xi }\approx e^{101}\sim {10}^{44}(\mathrm{energy}\mathrm{density}),{\left({\displaystyle \frac{{\rho }_{\mathrm{ini}}}{{\rho }_{\Lambda }}}\right)}^{1/4}\sim {10}^{11}(\mathrm{energy}\mathrm{scale}),$$

naturally bridges the QCD-scale vacuum ${(\sim 200\mathrm{MeV})}^4$ and the current cosmological value ${(\sim 2.3\times {10}^{-3}\mathrm{eV})}^4$ without requiring delicate cancellations among large ultraviolet contributions. In this sense the QEV model renders the observed vacuum energy technically natural: it emerges from an $\mathcal{O}\left(1\right)$ microscopic amplitude modulated by a physically derived, time-integrated damping history rather than from an ad-hoc balance of divergent terms.

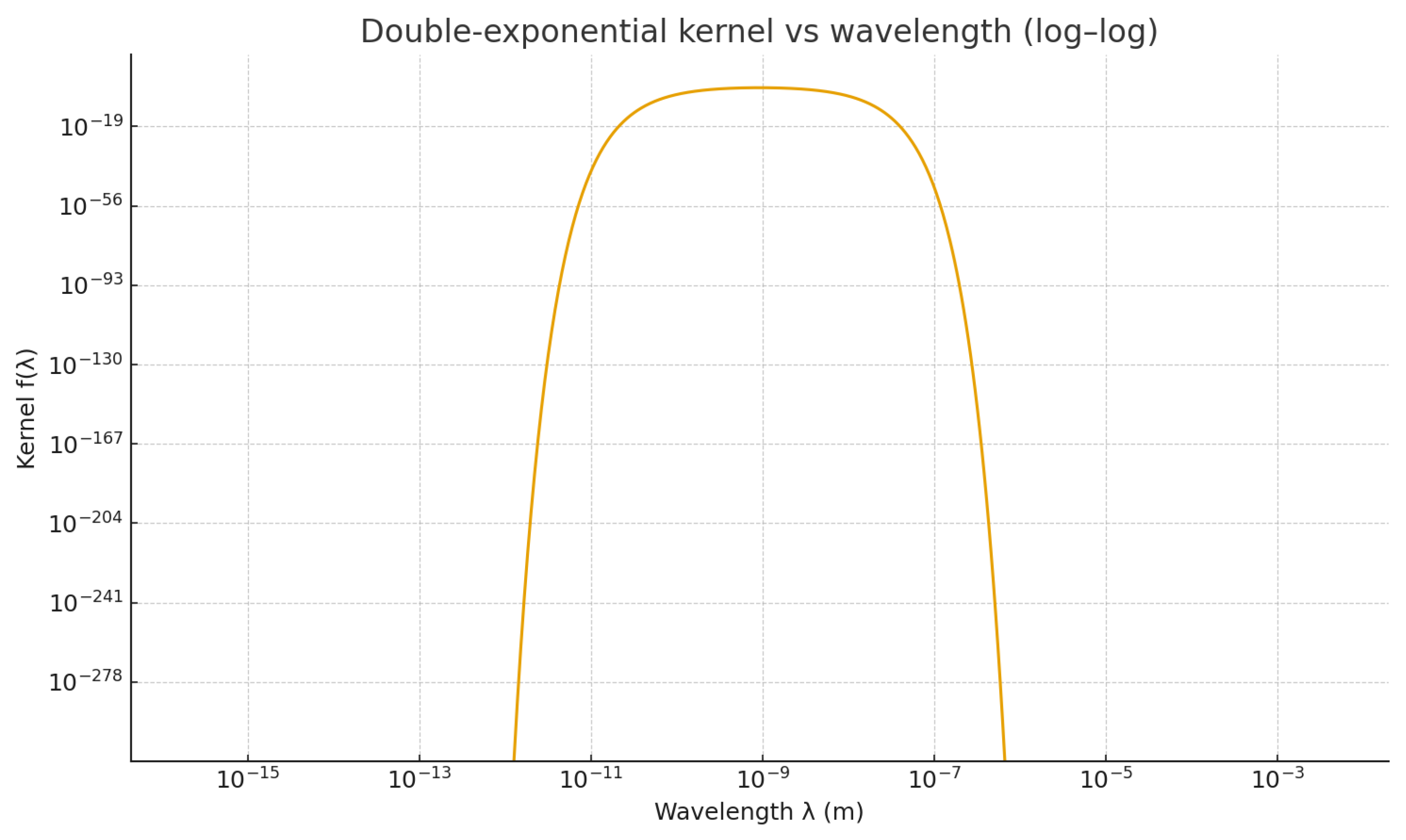
Figure A2. Double-exponential kernel $f\left(\lambda \right)=\exp (-\lambda /L-L/\lambda )$ versus $\lambda$ (log–log). Peak scale $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$.

Figure A2. Double-exponential kernel $f\left(\lambda \right)=\exp (-\lambda /L-L/\lambda )$ versus $\lambda$ (log–log). Peak scale $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$.

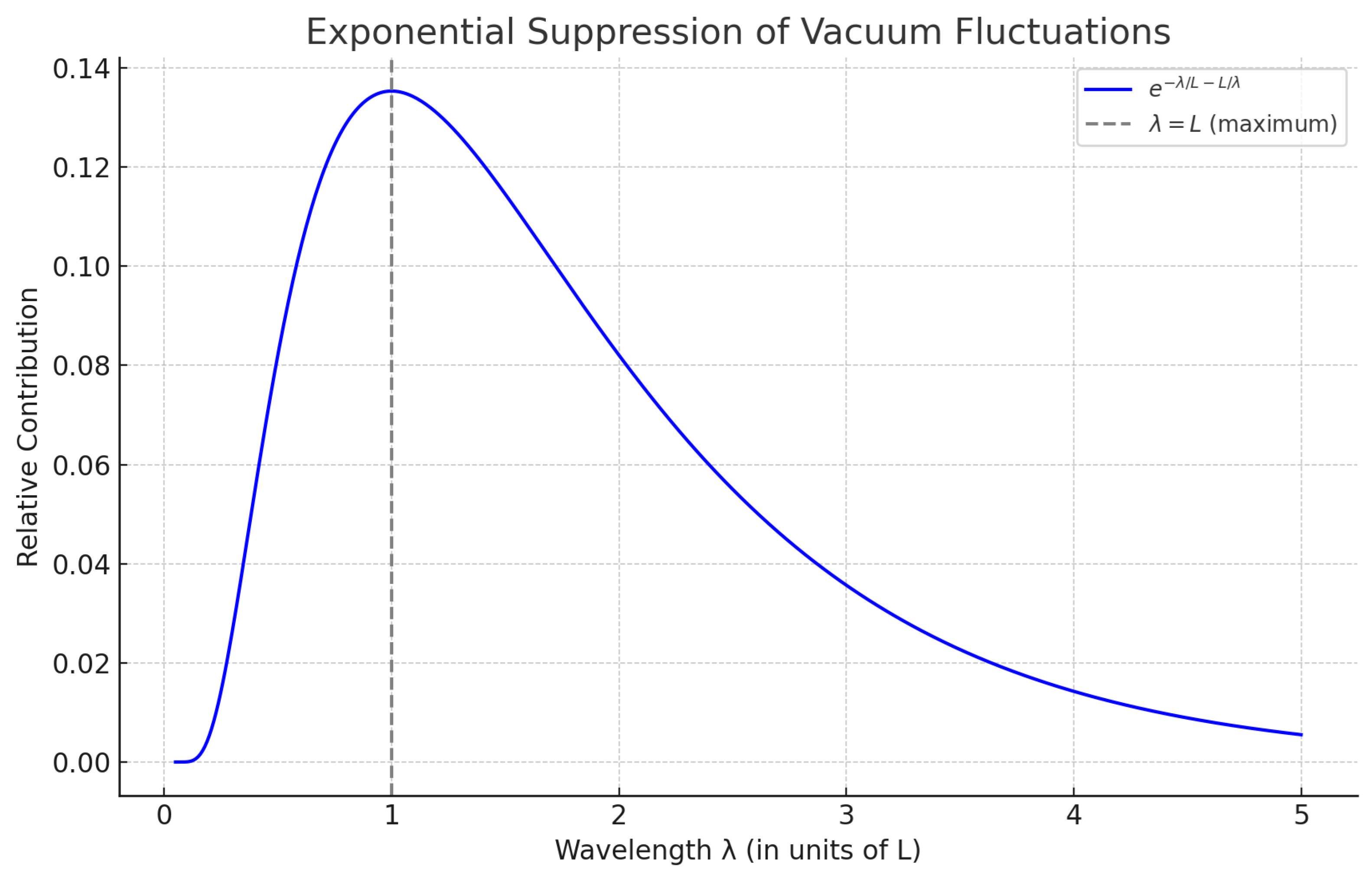
Figure A3. Exponential suppression of vacuum fluctuations $f\left(\lambda \right)=\exp (-\lambda /L-L/\lambda )$, with a maximum at $\lambda =L$. This explains why the geometric-mean scale $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$ dominates the bounded spectral integral.

Figure A3. Exponential suppression of vacuum fluctuations $f\left(\lambda \right)=\exp (-\lambda /L-L/\lambda )$, with a maximum at $\lambda =L$. This explains why the geometric-mean scale $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$ dominates the bounded spectral integral.

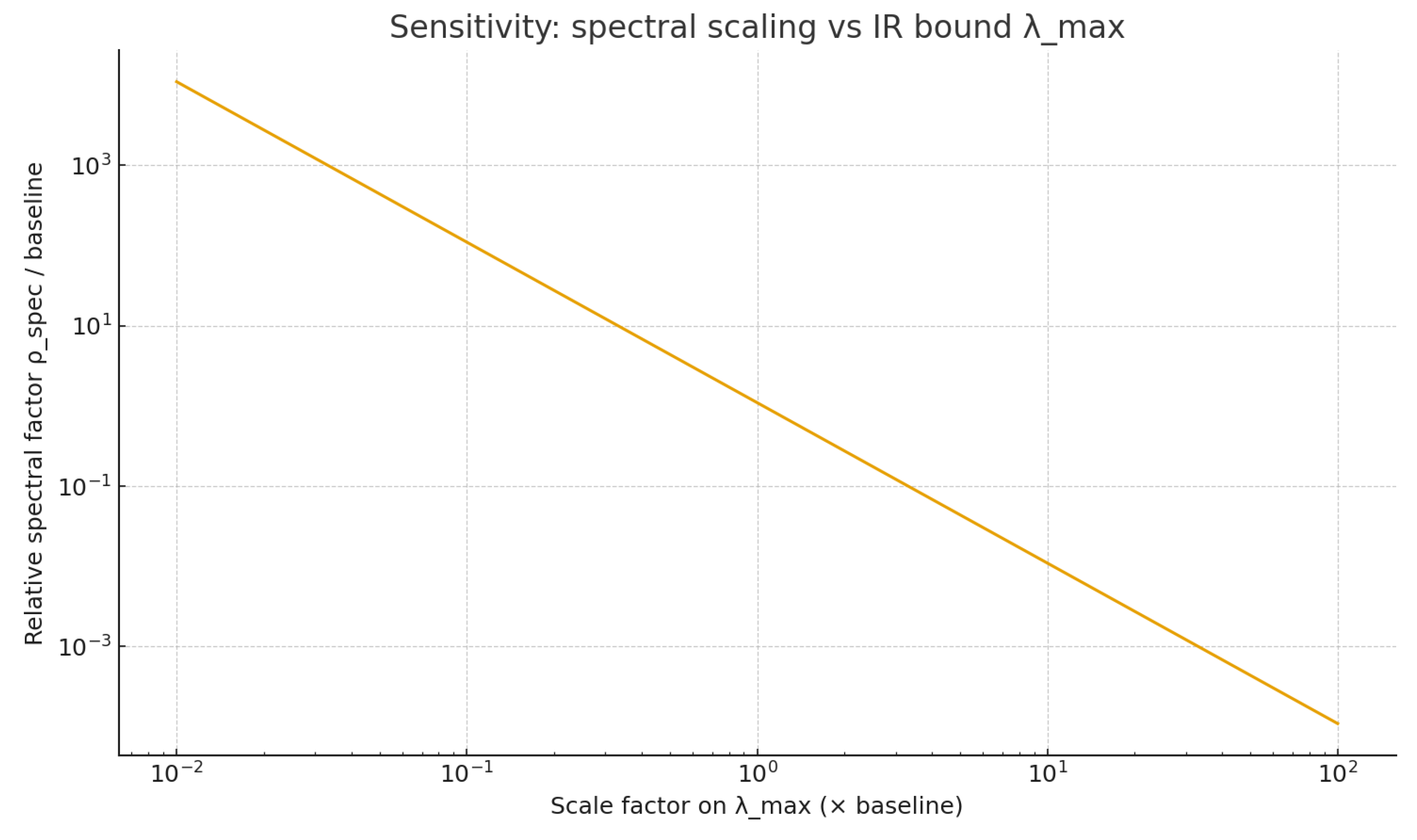
Relative spectral scaling ${\rho }_{\mathrm{spec}}/{\rho }_{\mathrm{spec}}^{\mathrm{base}}$ versus the ${\lambda }_{max}$ scaling factor.

Figure A4. Relative spectral scaling ${\rho }_{\mathrm{spec}}/{\rho }_{\mathrm{spec}}^{\mathrm{base}}$ versus the ${\lambda }_{max}$ scaling factor. Trend: $\partial ln\rho /\partial ln{\lambda }_{max}\approx -2$.

Figure A4. Relative spectral scaling ${\rho }_{\mathrm{spec}}/{\rho }_{\mathrm{spec}}^{\mathrm{base}}$ versus the ${\lambda }_{max}$ scaling factor. Trend: $\partial ln\rho /\partial ln{\lambda }_{max}\approx -2$.

For completeness, we note that for the symmetric kernel used here, the sensitivity with respect to the lower spectral bound behaves identically, yielding $\partial ln\rho /\partial ln{\lambda }_{min}\simeq -2$. Hence, within the interval ${\lambda }_{min}\in [0.8,1.0]\mathrm{fm}$, the resulting ${\rho }_{\mathrm{vac}}\propto L^{-4}$ scaling remains effectively invariant, demonstrating the robustness of the spectral symmetry $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$.

Figure A5. Spectral function $\rho \left(\lambda \right)$ computed from $\rho \left(\lambda \right)=A{\lambda }^{-5}\exp [-{({\lambda }_{min}/\lambda )}^{\alpha }]\exp [-{(\lambda /{\lambda }_{max})}^{\beta }]$ with $\alpha =0.4$ and $\beta =1$. Vertical markers: ${\lambda }_{min}=1$ fm, $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$, ${\lambda }_{max}$. Compare with Figure A1 (where $\alpha =\beta =1$).

Figure A5. Spectral function $\rho \left(\lambda \right)$ computed from $\rho \left(\lambda \right)=A{\lambda }^{-5}\exp [-{({\lambda }_{min}/\lambda )}^{\alpha }]\exp [-{(\lambda /{\lambda }_{max})}^{\beta }]$ with $\alpha =0.4$ and $\beta =1$. Vertical markers: ${\lambda }_{min}=1$ fm, $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$, ${\lambda }_{max}$. Compare with Figure A1 (where $\alpha =\beta =1$).

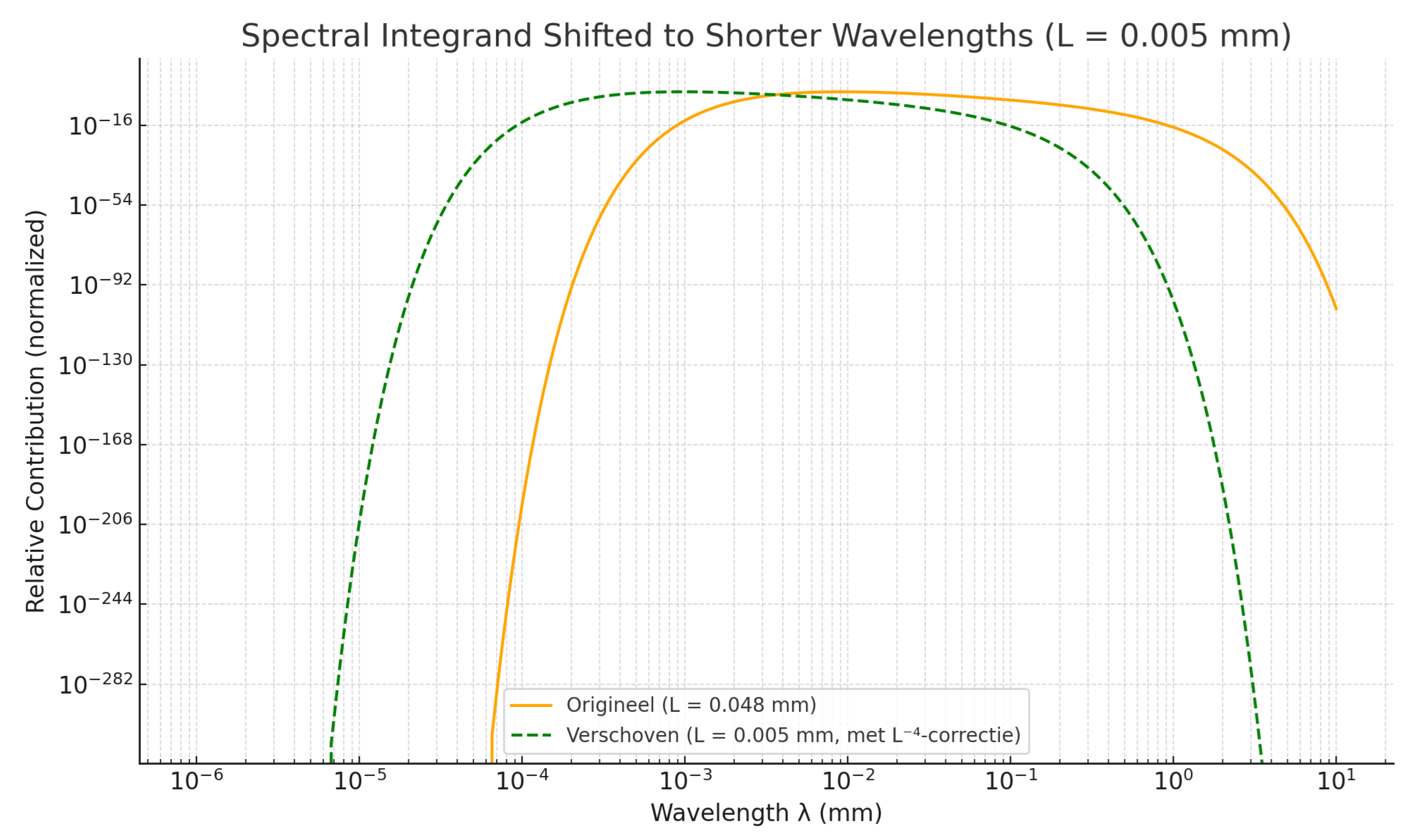
Figure A6. Evolutionary shift of the effective spectral integrand towards shorter wavelengths as the IR scale tightens (cooling/expansion). The overall scaling follows the $L^{-4}$ normalization.

Figure A6. Evolutionary shift of the effective spectral integrand towards shorter wavelengths as the IR scale tightens (cooling/expansion). The overall scaling follows the $L^{-4}$ normalization.

Appendix C.3. Dynamic Damping from QCD Scale to Today

The dynamic QEV model couples the bounded spectrum to a damping budget,

$${\displaystyle \frac{d{\rho }_{\mathrm{vac}}}{dt}}=-{\Gamma }_{\mathrm{tot}}\left(t\right){\rho }_{\mathrm{vac}}\left(t\right)\Rightarrow {\rho }_{\mathrm{vac}}\left(t_0\right)={\rho }_{\mathrm{ini}}\exp \left[-\Xi \right],\Xi \equiv {\int }_{t_{\mathrm{ini}}}^{t_0}{\Gamma }_{\mathrm{tot}}\left(t\right)dt,$$

(A6)

with ${\Gamma }_{\mathrm{tot}}={\Gamma }_g+{\Gamma }_{\mathrm{th}}+{\Gamma }_{\mathrm{had}}$. Taking ${\rho }_{\mathrm{ini}}\sim {\left(200\mathrm{MeV}\right)}^4$ and ${\rho }_{\mathrm{vac}}\left(t_0\right)={\rho }_{\Lambda }$ fixes the required integrated damping

$${\Xi }_{\mathrm{req}}=ln{\displaystyle \frac{{\rho }_{\mathrm{ini}}}{{\rho }_{\Lambda }}}=4ln\left({\displaystyle \frac{200\mathrm{MeV}}{2.26\mathrm{meV}}}\right)\approx 4\times 25.2\approx 101.$$

(A7)

A representative, physically motivated split is

$$\begin{array}{|c|}\hline {\Xi }_g\approx 25,{\Xi }_{\mathrm{th}}\approx 46,{\Xi }_{\mathrm{had}}\approx 30,\Xi \approx 101.\\ \hline\end{array}$$

(A8)

Here ${\Xi }_g\propto \int Hdt=ln(a_0/a_{\mathrm{QCD}})\approx ln(T_{\mathrm{QCD}}/T_{\mathrm{IR}})\approx ln\left(155\mathrm{MeV}/2.93\mathrm{meV}\right)\approx 24.7$, while ${\Xi }_{\mathrm{th}}$ collects thermal/entropic suppression (depends on $g_{*}\left(T\right)$) and ${\Xi }_{\mathrm{had}}$ a Gaussian-like peak around $T_{\mathrm{QCD}}$.

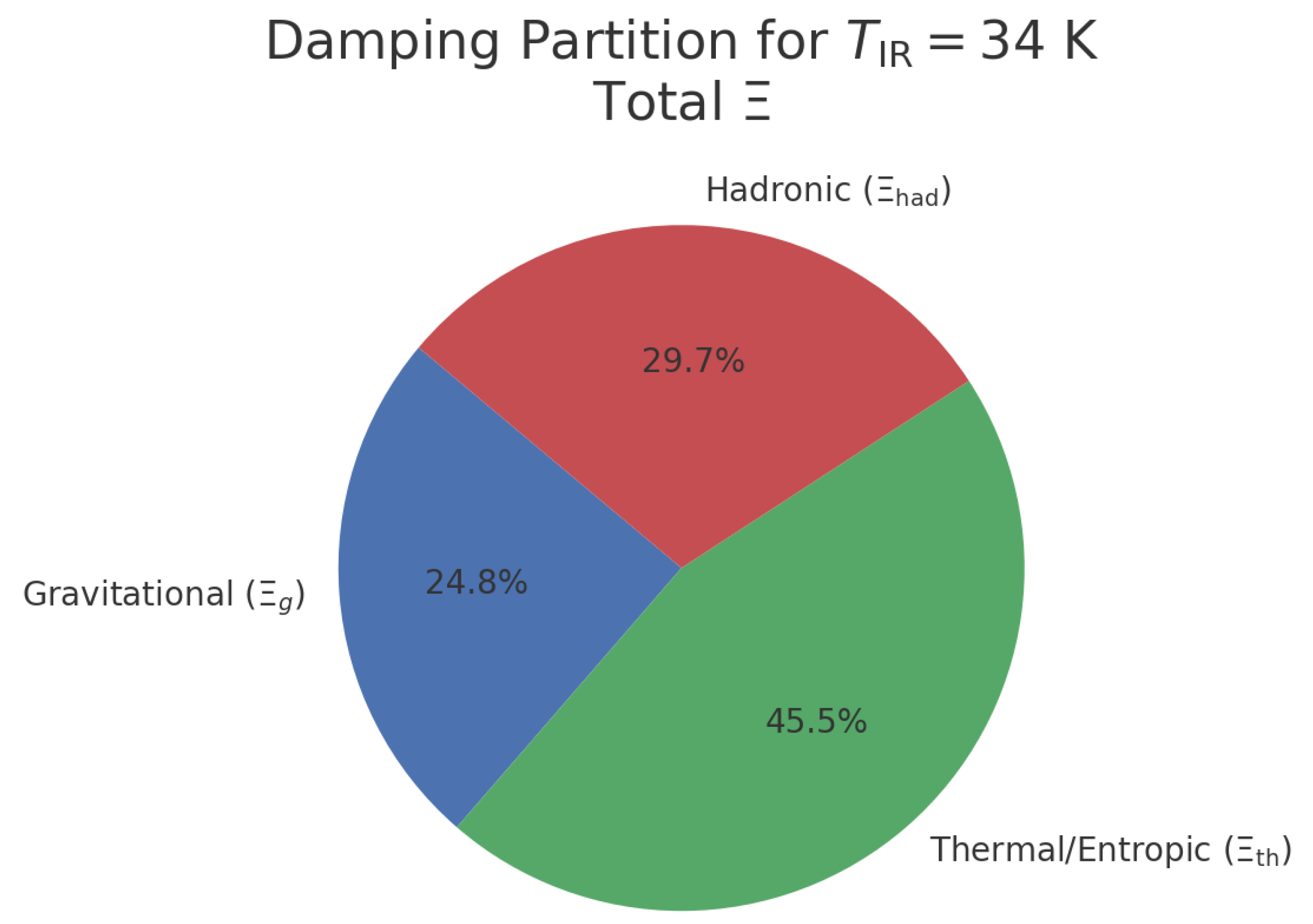
The damping partition is summarized in Table 3 and visualized in Figure A7; the IR-driven spectral shift is shown in Figure A6, while the peak-at-L mechanism is illustrated in Figure A4.

Table A2. Illustrative damping split to match ${\rho }_{\Lambda }$.

Component	$\mathbf{\Xi }$ (e-folds)
Gravitational (Hubble)	25
Thermal/Entropic	46
Hadronic	30
Total	101

Table A2. Illustrative damping split to match ${\rho }_{\Lambda }$.

Component	$\mathbf{\Xi }$ (e-folds)
Gravitational (Hubble)	25
Thermal/Entropic	46
Hadronic	30
Total	101

Figure A7. Damping budget (pie): ${\Xi }_g\approx 25$, ${\Xi }_{\mathrm{th}}\approx 46$, ${\Xi }_{\mathrm{had}}\approx 30$ (total $\Xi \approx 101$).

Figure A7. Damping budget (pie): ${\Xi }_g\approx 25$, ${\Xi }_{\mathrm{th}}\approx 46$, ${\Xi }_{\mathrm{had}}\approx 30$ (total $\Xi \approx 101$).

Appendix C.4. Numerical Plug-in and Result

Combine the spectral factor and damping at $t_0$:

$${\rho }_{\mathrm{vac}}\left(t_0\right)=\underset{\mathrm{spectral}}{\underbrace{\left[A_0(\hslash c)\right]\mathcal{C}{L}^{-4}}}\times \underset{\mathrm{dynamic}}{\underbrace{e^{-\Xi }}},\Xi \approx 101.$$

(A9)

With $L^{-4}={(6.505\times {10}^{-10}\mathrm{m})}^{-4}$ and C = 4.3918318548 one finds

$${\rho }_{\mathrm{vac}}\left(t_0\right)\approx {\rho }_{\Lambda }=5.96\times {10}^{-10}\mathrm{J}{\mathrm{m}}^{-3}\approx {\left(2.26\mathrm{meV}\right)}^4.$$

Figure A6 explicitly shows how tightening the IR bound shifts the effective integrand to shorter wavelengths; the overall normalization follows the $L^{-4}$ scaling of Eq. (A5)

Appendix C.5. Numerical Plug-in and Result (with Fiducial Scales)

Combine the spectral factor and the dynamic damping at $t_0$:

$$\begin{array}{|c|}\hline {\rho }_{\mathrm{vac}}\left(t_0\right)=\left[A_0(\hslash c)\right]C{L}^{-4}{e}^{-\Xi }\\ \hline\end{array},C=2K_4\left(2\right).$$

(A10)

For the fiducial values ${\lambda }_{min}=1\mathrm{fm}$ and $T_{\mathrm{IR}}=34\mathrm{K}$ we have

$$(\hslash c)C{L}^{-4}=7.75378050652\times {10}^{11}\mathrm{J}{\mathrm{m}}^{-3},$$

so that Eq. (A10) can be used in the purely numeric form

$${\rho }_{\mathrm{vac}}\left(t_0\right)=A_0\left(7.75378050652\times {10}^{11}\right)e^{-\Xi }\mathrm{J}{\mathrm{m}}^{-3}.$$

Calibrating to ${\rho }_{\Lambda }=5.96\times {10}^{-10}\mathrm{J}{\mathrm{m}}^{-3}$ gives

$$A_0(\Xi )={\displaystyle \frac{5.96\times {10}^{-10}}{7.75378050652\times {10}^{11}}}{e}^{\Xi }=7.68657301427\times {10}^{-22}{e}^{\Xi },$$

which reproduces $A_0\left(101\right)=5.61662500510\times {10}^{22}$ and, inserted back into Eq. (A6), returns ${\rho }_{\mathrm{vac}}\left(t_0\right)={\rho }_{\Lambda }$ by construction.

Appendix C.6. Conclusion (Concise Summary)

• We model the vacuum as a dynamic, spectrally bounded medium: a UV bound from QCD confinement (${\lambda }_{min}=1\mathrm{fm}$) and a thermal/entropic IR bound ${\lambda }_{max}\left(T_{\mathrm{IR}}\right)\simeq 0.423\mathrm{mm}$ at $T_{\mathrm{IR}}=34\mathrm{K}$ defining a peak scale L = $\sqrt{{\lambda }_{min}{\lambda }_{max}}\simeq 0.651\mathrm{nm}$.
• With the double–exponential kernel, the late–time spectral contribution is:
  ${\rho }_{\mathrm{vac}}\left(t_0\right)=A\mathcal{C}{L}^{-4}$ with $\mathcal{C}=2K_4\left(2\right)=4.3918318548.$
• With the dimensionally-correct form ${\rho }_{\mathrm{vac}}=\left[A_0(\hslash c)\right]C{L}^{-4}{e}^{-\Xi },$ the calibrated normalization reads $A_0(\Xi )={\displaystyle \frac{{\rho }_{\Lambda }{L}^4}{(\hslash c)C}}{e}^{\Xi }$ (e.g. $A_0\left(101\right)\approx 5.6\times {10}^{22})$.
• Time–dependent damping encodes gravitational (Hubble), thermal/entropic, and hadronic effects. The required integrated damping to reach today is $\Xi \approx 101$ e–folds, e.g. a representative split ${\Xi }_g\approx 25$, ${\Xi }_{\mathrm{th}}\approx 46$, ${\Xi }_{\mathrm{had}}\approx 30$.
• The calibrated result matches the observed vacuum density: ${\rho }_{\mathrm{vac}}\left(t_0\right)\approx 5.96\times {10}^{-10}\mathrm{J}{\mathrm{m}}^{-3}\approx {\left(2.26\mathrm{meV}\right)}^4$ (Planck 2018), with late–time $w\to -1$.
• Sensitivities are mild and controlled: at fixed $A_0$, $\partial ln\rho /\partial ln{\lambda }_{max}\approx -2$; order–unity changes in kernel shape $(\alpha ,\beta )$ shift $\mathcal{C}$ by order–unity; $\delta \rho /\rho \approx -\delta \Xi$.

Appendix D.1. Physical Interpretation

As a heuristic analogy, one may view the spectral bounding as playing a role similar to a critical-scale phenomenon in superconductors, without implying a literal critical temperature of the vacuum. At this temperature the characteristic energy

$$E_{\mathrm{IR}}=k_B{T}_{\mathrm{IR}}\approx 2.9\mathrm{meV},$$

corresponds to the condensation scale of macroscopic quantum coherence observed in many high-$T_c$ superconductors. In these materials, thermal agitation above $T_c$ destroys long-range phase coherence, while below $T_c$ the collective wavefunction locks in phase. A similar argument can be applied to the vacuum itself: when the background temperature of the Universe drops below $T_{\mathrm{IR}}$, the thermal population of long-wavelength vacuum modes becomes exponentially suppressed, and the vacuum enters a coherent, spectrally frozen state.

Appendix D.2. Connection to the QEV Framework

Within the Quantum Entropic Vacuum (QEV) picture, the infrared cutoff ${\displaystyle \frac{hc}{k_B{T}_{\mathrm{IR}}}}$ defines the scale at which thermal entropy ceases to dominate the vacuum dynamics. Above $T_{\mathrm{IR}}$ the entropic term ${\Xi }_{\mathrm{th}}$ acts as a positive, expanding driver, while below this temperature the hadronic–gravitational component ${\Xi }_{\mathrm{had}}$ gradually takes over as a damping factor. The balance point corresponds to a critical temperature of the quantum vacuum, analogous to the phase transition in superconductivity.

Appendix D.3. Physical Consequences

Below $T_{\mathrm{IR}}$ the thermal contribution to the spectral energy density,

$${\rho }_{\mathrm{th}}(\lambda ,T)\propto {\lambda }^{-5}\exp \left[-{\displaystyle \frac{{\lambda }_{*}}{\lambda }}\right],{\lambda }_{*}={\displaystyle \frac{hc}{k_{B}T}},$$

becomes negligible compared to the residual hadronic component. The effective vacuum energy thus stabilizes to a constant value ${\rho }_{\Lambda }\propto L^{-4}$, where $L=\sqrt{{\lambda }_{min}{\lambda }_{max}}$ is frozen at its 34 K value. See Figure A8. This marks the transition from a dynamic, entropically dominated vacuum to a static, coherent phase— a cosmological analogue of a superconducting condensate.

Across $T_{\mathrm{IR}}\in [20,60]\mathrm{K}$ we find a stable late-time energy density, with ${\rho }_{\Lambda }\left(T_{\mathrm{IR}}\right)/{\rho }_{\Lambda }\left(34\mathrm{K}\right)\propto {(T_{\mathrm{IR}}/34\mathrm{K})}^2$, implying only smooth, percent-level shifts in the kinematic diagnostics used here.

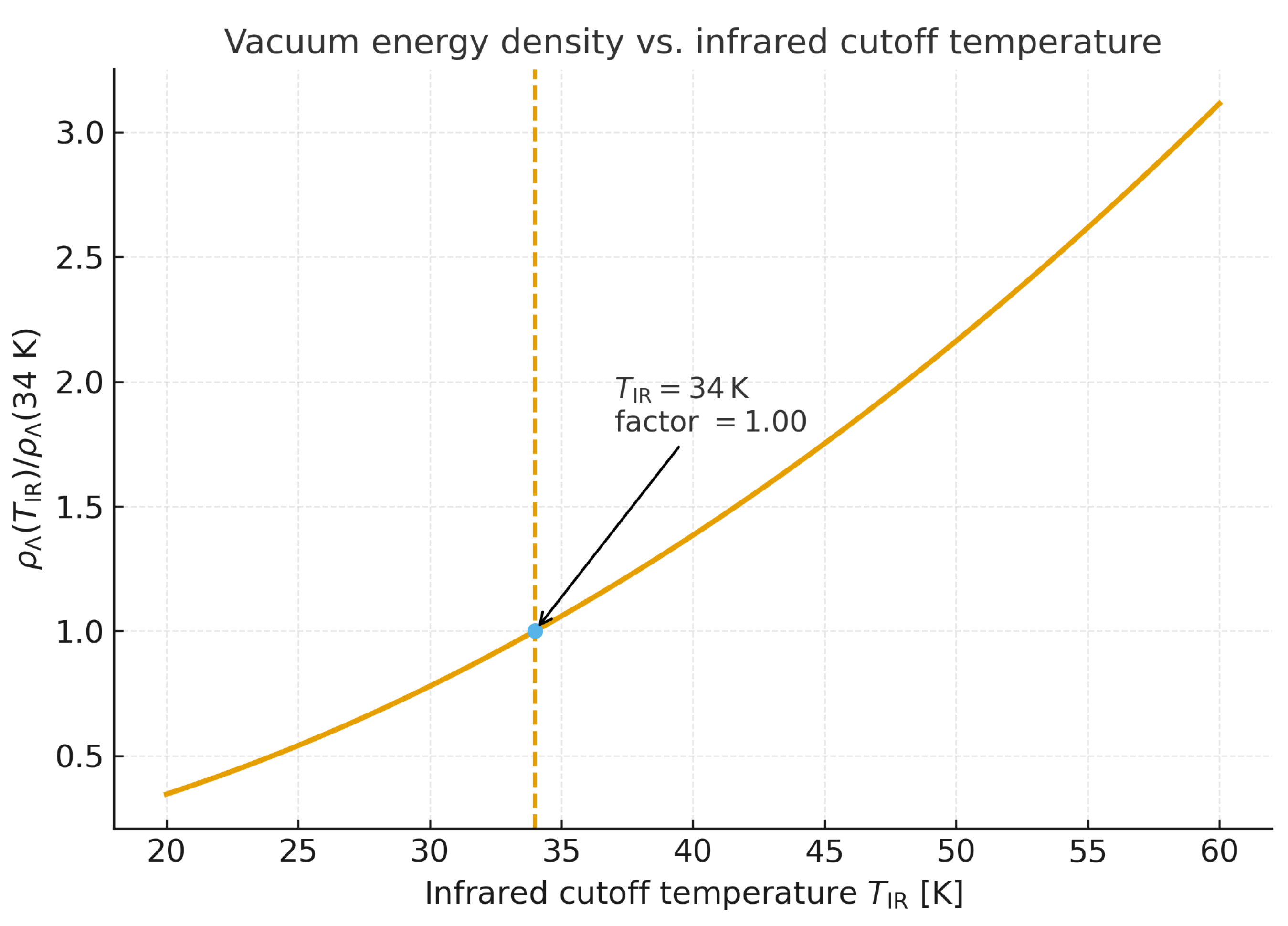
Appendix D.4. Visual Representation of the Infrared Sensitivity

Figure A8. Dependence of the normalized vacuum energy density ${\rho }_{\Lambda }\left(T_{\mathrm{IR}}\right)/{\rho }_{\Lambda }\left(34\mathrm{K}\right)$ on the infrared cutoff temperature $T_{\mathrm{IR}}$ in the range 20–$60\mathrm{K}$. The dashed vertical line marks the adopted value $T_{\mathrm{IR}}=34\mathrm{K}$, at which the ratio equals unity. Because ${\rho }_{\Lambda }\propto L^{-4}\propto T_{\mathrm{IR}}^2$, the variation remains modest: doubling $T_{\mathrm{IR}}$ increases ${\rho }_{\Lambda }$ only by a factor of $\sim 4$. This illustrates the robustness of the chosen cutoff and the relative insensitivity of the vacuum energy to small shifts in the critical temperature.

Figure A8. Dependence of the normalized vacuum energy density ${\rho }_{\Lambda }\left(T_{\mathrm{IR}}\right)/{\rho }_{\Lambda }\left(34\mathrm{K}\right)$ on the infrared cutoff temperature $T_{\mathrm{IR}}$ in the range 20–$60\mathrm{K}$. The dashed vertical line marks the adopted value $T_{\mathrm{IR}}=34\mathrm{K}$, at which the ratio equals unity. Because ${\rho }_{\Lambda }\propto L^{-4}\propto T_{\mathrm{IR}}^2$, the variation remains modest: doubling $T_{\mathrm{IR}}$ increases ${\rho }_{\Lambda }$ only by a factor of $\sim 4$. This illustrates the robustness of the chosen cutoff and the relative insensitivity of the vacuum energy to small shifts in the critical temperature.

Appendix D.5. Broader Implications

The coincidence between the energy scale $E_{\mathrm{IR}}\sim 3\mathrm{meV}$ and the condensation energy of many superconductors suggests that the same quantum statistics governing macroscopic coherence in condensed matter may also regulate the infrared structure of the vacuum. See Figure A8. In this view, the cosmological constant emerges as the residual ground-state energy of a globally coherent vacuum field, whose critical temperature corresponds to $T_{\mathrm{IR}}\approx 34\mathrm{K}$. This provides an appealing physical interpretation of why vacuum fluctuations “freeze out” at this scale and why the observed vacuum energy remains finite and stable.

Appendix E.1. Energy–Momentum Conservation

In a homogeneous and isotropic Universe the conservation law

$${\nabla }_{\mu }{T}^{\mu \nu }=0$$

reduces to the continuity equation

$${\dot{\rho }}_{\mathrm{vac}}+3H\left({\rho }_{\mathrm{vac}}+p_{\mathrm{vac}}\right)=0,$$

(A11)

where $H\equiv \dot{a}/a$ is the Hubble rate. The QEV energy density follows from the spectral-bounded ansatz

$${\rho }_{\mathrm{vac}}\left(a\right)=A_0(\hslash c)CL{\left(a\right)}^{-4},L\left(a\right)=\sqrt{{\lambda }_{min}{\lambda }_{max}\left(a\right)},$$

(A12)

with ${\lambda }_{min}$ fixed by confinement physics and ${\lambda }_{max}\left(a\right)$ tracing the evolving infrared limit.

Differentiating Equation (A12) yields

$${\dot{\rho }}_{\mathrm{vac}}=-4{\rho }_{\mathrm{vac}}{\displaystyle \frac{\dot{L}}{L}}=-4{\rho }_{\mathrm{vac}}{\displaystyle \frac{dlnL}{dlna}}H.$$

Substitution into Equation (A11) gives the effective pressure

$$p_{\mathrm{vac}}=-{\rho }_{\mathrm{vac}}+{\displaystyle \frac{4}{3}}{\rho }_{\mathrm{vac}}{\displaystyle \frac{dlnL}{dlna}}.$$

(A13)

Hence the instantaneous equation-of-state parameter is

$$w\left(a\right)\equiv {\displaystyle \frac{p_{\mathrm{vac}}}{{\rho }_{\mathrm{vac}}}}=-1+{\displaystyle \frac{4}{3}}{\displaystyle \frac{dlnL}{dlna}}.$$

(A14)

When $L\left(a\right)$ becomes constant—as expected after the thermal/entropic freeze-out—one obtains $dlnL/dlna\to 0$ and $w\to -1$, recovering the cosmological-constant limit.

Appendix E.2. Example Scaling of L(a)

If the infrared cutoff evolves with temperature as ${\lambda }_{max}\propto T^{-1}\propto a$ while ${\lambda }_{min}$ remains fixed, then $L\left(a\right)\propto a^{1/2}$ and

$$w\left(a\right)=-1+{\displaystyle \frac{2}{3}},$$

corresponding to a transient radiation-like phase that is exponentially damped once the entropic factor $\exp [-\Xi (t\left)\right]$ saturates. In the late-time regime of interest, $L\left(a\right)$ stabilises and $w\approx -1$ within deviations $|w+1|\lesssim {10}^{-2}$.

Appendix E.3. Sound Speed and Stability

Perturbing Equation (A11) at constant entropy gives the adiabatic sound speed

$$c_s^2={\displaystyle \frac{d{p}_{\mathrm{vac}}}{d{\rho }_{\mathrm{vac}}}}={\displaystyle \frac{d{p}_{\mathrm{vac}}/dL}{d{\rho }_{\mathrm{vac}}/dL}}=-{\displaystyle \frac{1}{3}}+{\displaystyle \frac{4}{3}}{\displaystyle \frac{d^{2}lnL}{{(dlna)}^2}}/{\displaystyle \frac{dlnL}{dlna}}.$$

For monotonic $L\left(a\right)$ with slowly varying slope, the correction term is small and $c_s^2\approx -1/3$. This implies a non-propagating (quasi-vacuum) mode with no ghost or gradient instability in the FRW background.

-

• Perturbations and closure.

The adiabatic derivative of the effective-fluid relations yields $c_s^2\simeq -1/3$. We emphasize that the QEV component is a quasi-vacuum sector with non-propagating rest-frame fluctuations; in practice we adopt a non-adiabatic (rest-frame) closure so that no rapid gradient instabilities arise in large-scale-structure regimes. Linear-growth observables are evaluated in the background limit with the baseline (propagation-only) choice, which is sufficient for the percent-level deviations reported here.

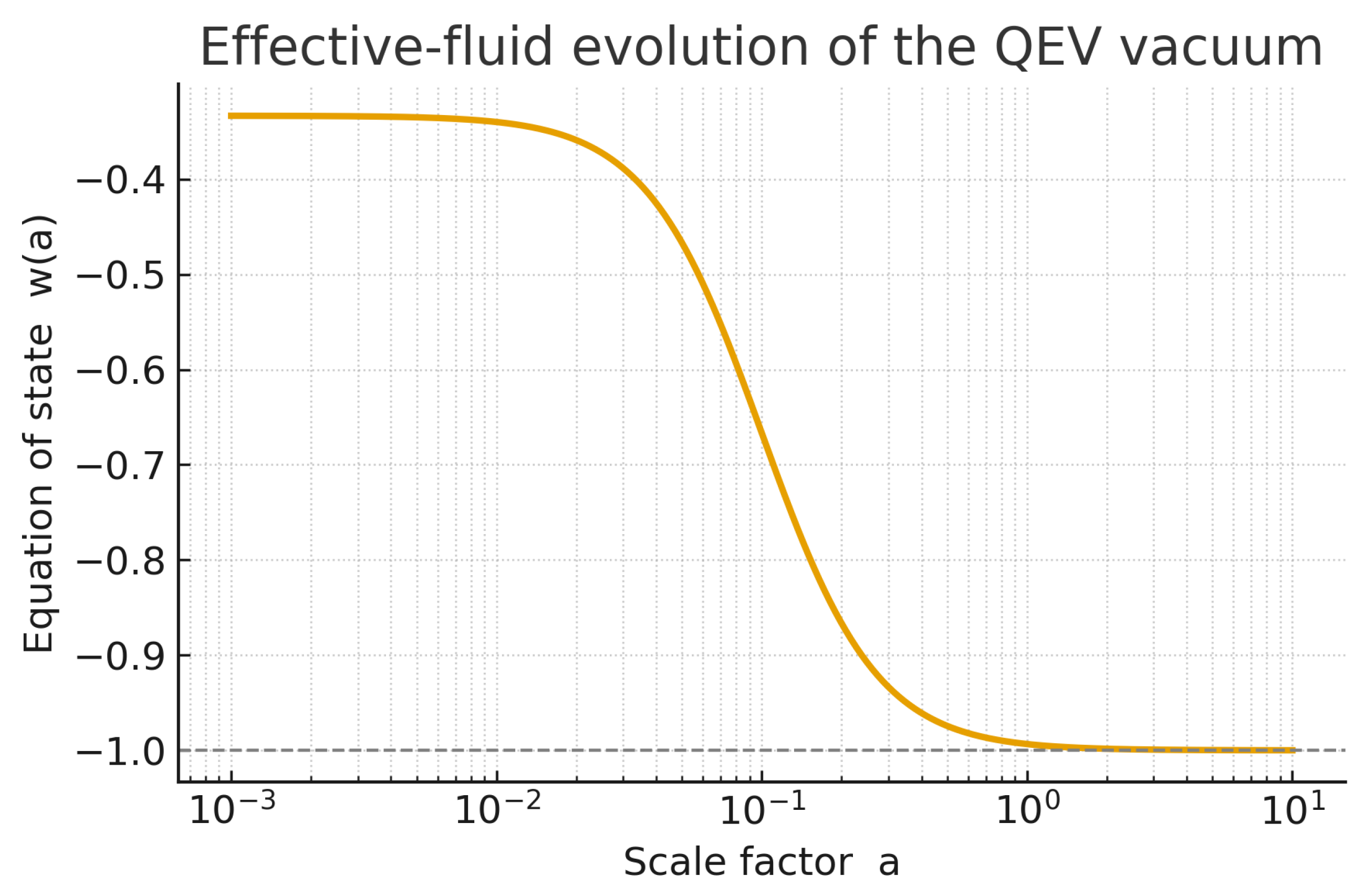
Figure A9. Effective-fluid evolution of the QEV vacuum. The equation of state follows $w\left(a\right)=-1+\frac{4}{3}\frac{dlnL}{dlna}$. The illustrative curve uses a smooth early-to-late transition $dlnL/dlna=\frac{1}{2}{[1+{(a/a_t)}^2]}^{-1}$ with $a_t\simeq 0.1$, yielding a radiation-like phase ($w\simeq -1/3$ for $a\ll a_t$) that relaxes toward a cosmological-constant limit ($w\to -1$) once $L\left(a\right)$ saturates ($a\gg a_t$). At late times the deviation is small, $|w+1|\lesssim {10}^{-2}$ for the example shown.

Figure A9. Effective-fluid evolution of the QEV vacuum. The equation of state follows $w\left(a\right)=-1+\frac{4}{3}\frac{dlnL}{dlna}$. The illustrative curve uses a smooth early-to-late transition $dlnL/dlna=\frac{1}{2}{[1+{(a/a_t)}^2]}^{-1}$ with $a_t\simeq 0.1$, yielding a radiation-like phase ($w\simeq -1/3$ for $a\ll a_t$) that relaxes toward a cosmological-constant limit ($w\to -1$) once $L\left(a\right)$ saturates ($a\gg a_t$). At late times the deviation is small, $|w+1|\lesssim {10}^{-2}$ for the example shown.

Appendix E.4. Summary

The effective-fluid form Eqs. (A13)–(A14) guarantees ${\nabla }_{\mu }{T}^{\mu \nu }=0$ by construction. The model evolves smoothly from a damped, radiation-like early stage ($w\approx -1/3$ to $-2/3$) toward a late-time cosmological-constant state ($w\to -1$), maintaining stability and internal energy conservation. This demonstrates that the QEV vacuum is formally covariant and self-consistent at the effective-fluid level.