Entanglement and Bell Inequalities from a Dynamically Emergent Temporal Structure

1. Introduction

Quantum entanglement remains one of the most striking and conceptually challenging features of quantum theory. When multiple systems share a state that cannot be decomposed into a product of subsystems, they exhibit correlations that persist across spacelike separations. These correlations, experimentally verified to violate Bell inequalities [4,21], are incompatible with any local hidden variable theory, as established by Bell’s theorem [7]. This foundational result continues to provoke debate over the nature of nonlocality, the role of realism, and the completeness of quantum mechanics [8].

Despite its predictive power, standard quantum theory offers no intrinsic account of time or causality. The formalism presupposes a background time parameter, external to the physical system, which is conceptually inadequate in regimes where spacetime geometry and temporal order are expected to emerge dynamically. This limitation becomes especially pressing in contexts such as quantum gravity [30], where background independence is fundamental, and in operational reconstructions of quantum theory that seek intrinsic explanations for temporal structure [34].

Recent proposals—including the Pseudo-Density Operator (PDO) formalism [6,13,25], process matrix frameworks with indefinite causal order [34], and relational quantum mechanics [37]—have sought to treat time and correlations on more equal footing. These approaches reflect a growing recognition that temporality, causality, and entanglement are not separable issues but aspects of a deeper structural foundation yet to be fully articulated.

In this work, we introduce a covariant reformulation of quantum theory centered on a dynamically emergent temporal structure, defined by a smooth, future-directed, unit-norm timelike vector field ${\Phi }^{\mu }\left(x\right)$. This field generates an intrinsic proper-time flow and induces a locally defined foliation of spacetime into spacelike hypersurfaces ${\Sigma }_{\tau }$. We refer to this framework as Chronon Field Theory (ChFT). While the terminology is novel, the motivation aligns with long-standing efforts to reconcile quantum theory with relativistic causality and dynamical notions of time.

ChFT describes the emergence of spacetime geometry from the dynamical alignment of initially uncorrelated domains of ${\Phi }^{\mu }\left(x\right)$. These domains evolve into globally coherent families of integral curves—called Φ-threads—that form a topological and causal scaffold for quantum evolution. Within this structure, entangled states are modeled as coherent field configurations across multiple $\Phi$-threads, with correlations arising from shared causal ancestry rather than from abstract wavefunction amplitudes or acausal influences.

The operational quantum theory built on this structure, which we call Chronon Quantum Mechanics (ChQM), replaces external time with intrinsic evolution along ${\Phi }^{\mu }$. Quantum states are defined on foliation slices ${\Sigma }_{\tau }$, with unitary evolution governed by a Schrödinger-type equation modulated by local geometry and matter content. This formulation is background-independent, respects relativistic covariance, and provides a novel mechanism for the origin and propagation of quantum correlations.

We further argue that the assumptions underpinning Bell’s theorem—particularly global simultaneity and statistical independence—are not fundamental but emergent. In their place, ChFT offers a covariant, locally grounded temporal structure that yields Bell-type correlations through topological and causal coherence. This approach removes the need for nonlocal dynamics, offering instead a geometric account of entanglement consistent with relativistic principles.

In what follows, we develop the formal structure of ChFT and its implications for quantum entanglement and Bell-type phenomena. We propose that ChFT offers a unifying framework in which time, causality, and correlation emerge from the same physical field, laying groundwork for future integration with quantum gravity and spacetime-aware quantum information theory.

2. Theoretical Context

The unresolved tension between quantum theory and relativistic causality continues to motivate the search for reformulations that unify temporal, causal, and measurement structures within a coherent framework [9,27]. Standard quantum mechanics presupposes a fixed spacetime and an external time parameter, offering no intrinsic account of causal ordering. This becomes particularly problematic in regimes where spacetime must be treated dynamically, as in quantum gravity [26,38].

Several frameworks have sought to address these limitations. In quantum field theory (QFT), microcausality and operator locality ensure formal compatibility with special relativity, but they do not resolve the conceptual opacity of entanglement across spacelike separations [18]. Canonical quantum gravity, via the Wheeler–DeWitt equation, effectively eliminates time altogether, leading to the “problem of time” [30]. Covariant approaches, such as spin foams and causal dynamical triangulations, recover spacetime from discrete combinatorial structures but typically lack a detailed account of continuous quantum state evolution [3].

Other proposals explore emergent or internal notions of time from within quantum theory itself. The Page–Wootters mechanism [35] and relational quantum mechanics [37] treat time as a correlation between subsystems. Quantum reference frames [14] and process matrix formalisms with indefinite causal structure [34] suggest more general paradigms in which causal order is not fixed. A particularly relevant development is the pseudo-density operator (PDO) framework [1,11,13,25,31,39,44], which treats temporal and spatial quantum correlations on an equal footing by representing them in a unified operator formalism. PDOs have been used to analyze causally nonseparable processes, to characterize violations of temporal analogues of Bell inequalities, and to extend multipartite and causal inference analyses into the temporal domain. This body of work offers a mathematically precise way to discuss quantum correlations beyond standard spacetime partitions. However, while PDOs elegantly capture the symmetry between spatial and temporal correlations, they remain primarily kinematic tools and do not, by themselves, specify a dynamical spacetime substrate.

Chronon Field Theory enters this landscape by positing a smooth, unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$ as a primitive structure defining an intrinsic, geometrically meaningful flow of time. The integral curves of ${\Phi }^{\mu }$ define $\Phi$-threads—trajectories of proper-time evolution—whose foliation induces a dynamical slicing of spacetime into spatial hypersurfaces ${\Sigma }_{\tau }$. This structure supports a covariant, constraint-preserving Hamiltonian formulation, aligning quantum dynamics with a causal geometry intrinsic to the field itself.

Unlike prior models, ChFT accommodates gauge invariance and constraint consistency while enabling entangled states to emerge from topologically coherent $\Phi$-thread bundles. It thereby bridges conceptual divides between QFT and quantum gravity, while also making new, testable predictions regarding entanglement persistence, decoherence mechanisms, and causal topology.

By integrating quantum evolution with a dynamical causal field, ChFT moves beyond kinematic reconstructions to provide a spacetime-emergent quantum framework—one in which temporal flow, causal order, and quantum correlations arise from a common physical substrate.

3. Foundations of Chronon Quantum Mechanics

The goal of this section is to present the core formalism underlying Chronon Field Theory that directly relates to the theory’s application to quantum entanglement and Bell-type phenomena. While a complete, exhaustive exposition of all foundational elements of ChFT is beyond the scope of this paper, the primary focus is to establish the key mathematical structures and concepts necessary for the interpretation of entanglement in ChFT.

Chronon Quantum Mechanics (ChQM) is founded on a single geometric postulate: the existence of a smooth, future-directed, unit-norm timelike vector field ${\Phi }^{\mu }\left(x\right)$—the chronon field—defined on a four-dimensional differentiable Lorentzian manifold $\mathcal{M}$ with signature $(-+++)$. This vector field intrinsically defines the arrow of time and causal structure without reference to an external time coordinate or preferred foliation. The conditions ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ and ${\Phi }^0>0$ ensure local Lorentzian consistency and global causal orientation.

Each integral curve of ${\Phi }^{\mu }$ is called a Φ-thread, representing a fundamental trajectory of temporal evolution. These $\Phi$-threads endow spacetime with an intrinsic causal ordering, replacing the absolute Newtonian time of standard quantum theory with an endogenous temporal geometry [15].

3.1. Chronon Field and Temporal Foliation

The chronon field ${\Phi }^{\mu }\left(x\right)$ generates a covariant foliation of spacetime into spacelike hypersurfaces ${\Sigma }_{\tau }$, labeled by a scalar function $\tau \left(x\right)$ interpreted as proper time along each $\Phi$-thread. According to the Frobenius theorem, such a foliation exists if and only if the distribution orthogonal to ${\Phi }^{\mu }$ is integrable, which occurs when the twist tensor vanishes:

$${\omega }_{\mu \nu }:=h_{\mu }^{\alpha }{h}_{\nu }^{\beta }{\nabla }_{[\alpha }{\Phi }_{\beta ]}=0,$$

(1)

where $h_{\mu \nu }=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }$ is the spatial projector orthogonal to ${\Phi }^{\mu }$. This irrotational condition ensures that local hypersurfaces exist everywhere orthogonal to ${\Phi }^{\mu }$.

In this hypersurface-orthogonal case, there exists a scalar function $\tau \left(x\right)$ such that

$${\Phi }^{\mu }\left(x\right)=-N\left(x\right)g^{\mu \nu }{\partial }_{\nu }\tau \left(x\right),$$

(2)

where the lapse function $N\left(x\right)$ satisfies the normalization condition

$$N\left(x\right)={[-g^{\mu \nu }{\partial }_{\mu }\tau \left(x\right){\partial }_{\nu }\tau \left(x\right)]}^{-1/2}.$$

(3)

This construction guarantees that $\tau \left(x\right)$ increases monotonically along each $\Phi$-thread and defines a globally coherent temporal parameter. The corresponding level sets ${\Sigma }_{\tau }=\{x\in \mathcal{M}\mid \tau \left(x\right)=\mathrm{const}.\}$ then form a proper-time foliation of the spacetime manifold. Unlike conventional gauge-fixed slicings, this foliation arises dynamically from the field structure itself and is physically intrinsic to the geometry of ${\Phi }^{\mu }$ [15,16].

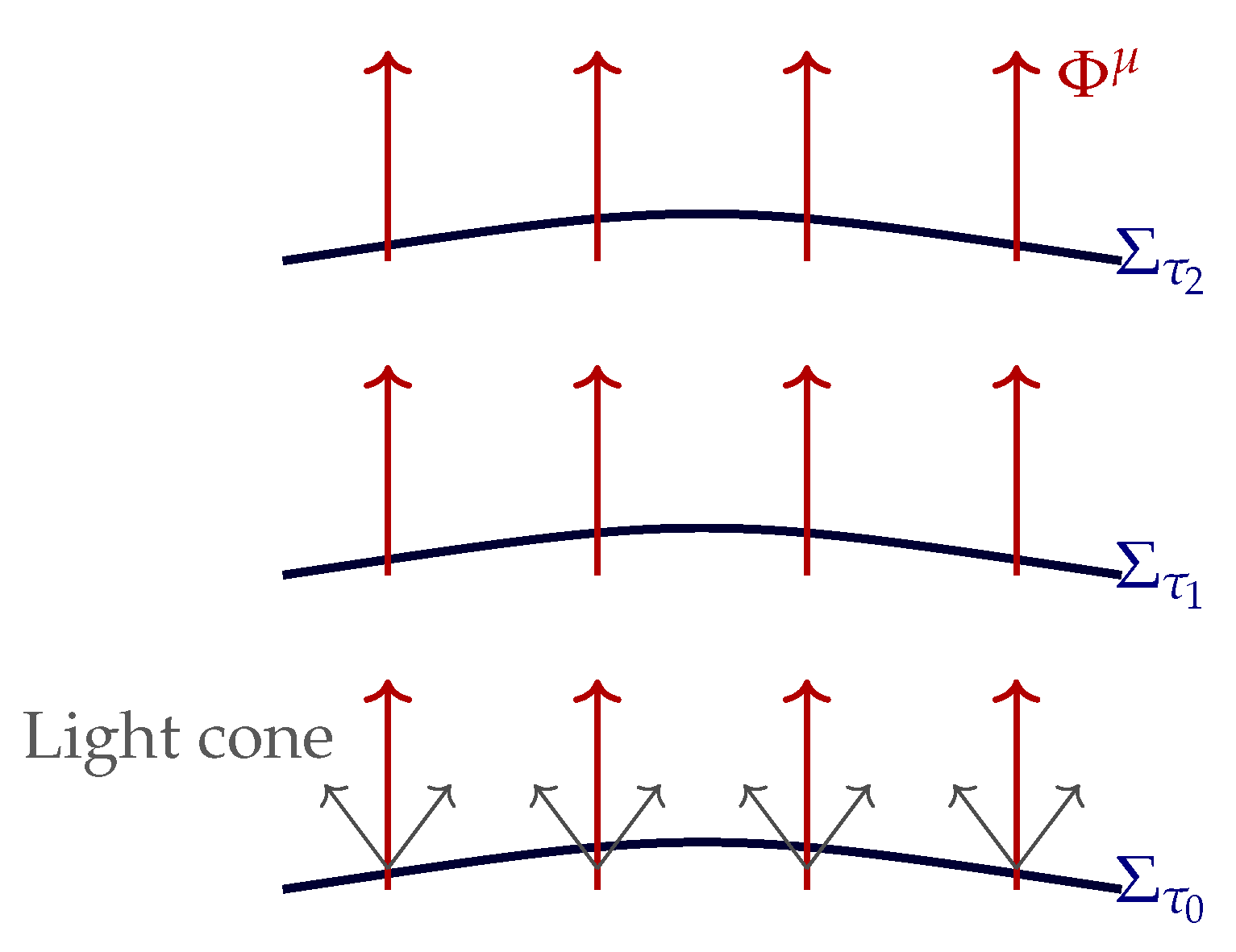
The resulting foliation and intrinsic causal structure are illustrated in Figure 1, where each hypersurface ${\Sigma }_{\tau }$ corresponds to a constant intrinsic time label and is orthogonal to the locally defined time direction ${\Phi }^{\mu }$.

3.2. Hilbert Space Structure and Evolution

Given a foliation of spacetime $\mathcal{M}$ into spacelike hypersurfaces $\left\{{\Sigma }_{\tau }\right\}$ orthogonal to the chronon field ${\Phi }^{\mu }\left(x\right)$, Chronon Quantum Mechanics (ChQM) defines a Hilbert space $\mathcal{H}\left[{\Sigma }_{\tau }\right]$ associated with each leaf ${\Sigma }_{\tau }$. This Hilbert space contains quantum states $\Psi \left[\tau \right]\in \mathcal{H}\left[{\Sigma }_{\tau }\right]$, which are defined on the instantaneous configuration of the field degrees of freedom on the slice.

The dynamics of the quantum state $\Psi \left[\tau \right]$ along the intrinsic proper time $\tau$ are governed by a Schrödinger-type equation that naturally arises from the causal structure of the ${\Phi }^{\mu }$-field and the induced foliation:

$$i\hslash {\displaystyle \frac{d}{d\tau }}\Psi \left[\tau \right]={\widehat{H}}_{\Phi }\left[\tau \right]\Psi \left[\tau \right],$$

(4)

where ${\widehat{H}}_{\Phi }\left[\tau \right]$ is the Hamiltonian operator acting on $\mathcal{H}\left[{\Sigma }_{\tau }\right]$, constructed from the spatial geometry and matter field content on ${\Sigma }_{\tau }$, and depends functionally on the foliation-defining vector field ${\Phi }^{\mu }$.

This evolution follows from the emergent intrinsic temporal flow defined by the ${\Phi }^{\mu }$-field. The equation naturally arises from the geometry of spacetime as encoded in the ${\Phi }^{\mu }$-induced foliation, ensuring that the dynamics respect both the underlying geometry and causality of the theory. In the appropriate limits, this formulation recovers standard quantum mechanics, as the chronon field’s influence becomes negligible. This formulation is background-independent, consistent with gauge-invariant dynamics, and provides a suitable framework for quantum gravity theories [27,36].

To make this structure precise, we define ${\Sigma }_{\tau }$ using the lapse function $N\left(x\right)$ and shift vector $N^i\left(x\right)$ as in the standard Arnowitt-Deser-Misner (ADM) 3+1 decomposition:

$${\Phi }^{\mu }=N{n}^{\mu }+N^i{e}_i^{\mu },$$

(5)

where $n^{\mu }$ is the unit normal to ${\Sigma }_{\tau }$ and $e_i^{\mu }$ form a triad on the slice. In the synchronous gauge where $N^i=0$, evolution is purely orthogonal along ${\Phi }^{\mu }$, and the canonical Hamiltonian takes the form:

$${\widehat{H}}_{\Phi }\left[\tau \right]={\int }_{{\Sigma }_{\tau }}{d}^{3}xN\left(x\right)\left(\widehat{\mathcal{H}}\left(x\right)+{\lambda }^a\left(x\right){\widehat{\mathcal{C}}}_a\left(x\right)\right),$$

(6)

where $\widehat{\mathcal{H}}\left(x\right)$ is the Hamiltonian density and ${\widehat{\mathcal{C}}}_a\left(x\right)$ are the constraint generators associated with local gauge symmetries (e.g., Gauss, diffeomorphism).

Importantly, the total Hamiltonian ${\widehat{H}}_{\Phi }\left[\tau \right]$ is not externally prescribed—it arises from the intrinsic field dynamics and the causal geometry induced by ${\Phi }^{\mu }$. The physical state $\Psi \left[\tau \right]$ must evolve unitarily with respect to $\tau$, provided the lapse function $N\left(x\right)$ and the constraints are appropriately enforced. This condition ensures consistency with the general covariance of the underlying theory.

Moreover, the operator ${\widehat{H}}_{\Phi }\left[\tau \right]$ may be subject to quantum anomalies or regularization ambiguities in field-theoretic implementations. In semiclassical settings, one can extract an effective Hamiltonian by substituting a background configuration of ${\Phi }^{\mu }$, akin to choosing a preferred frame of temporal evolution, while full quantum treatments must treat ${\Phi }^{\mu }$ as a dynamical object entangled with the rest of the field content.

Thus, ChQM offers a formalism where the generator of quantum evolution is emergent from internal field structures, and the passage of time is realized dynamically as flow along a globally coherent chronon field. This framework sidesteps the need for external temporal parameters, aligning the theory with background-independent approaches to quantum gravity [27,30,36].

3.2.1. Recovery in the Weak Field and Smooth Geometry Limits

In both the weak field approximation and the smooth geometry limit, ChFT reduces to standard quantum mechanics, as both limits correspond to regimes in which spacetime approximates flat Minkowski space [27,36]. In these limits, the dynamical evolution of quantum states is governed by the standard Schrödinger equation, with the chronon field ${\Phi }^{\mu }\left(x\right)$ contributing vanishingly small corrections.

Weak Field Approximation: In the weak-field regime, where the chronon field ${\Phi }^{\mu }\left(x\right)$ is small and spacetime curvature is negligible, the foliation induced by ${\Phi }^{\mu }\left(x\right)$ closely approximates the standard time foliation of flat Minkowski spacetime. Here, the hypersurfaces ${\Sigma }_{\tau }$ are essentially the usual Euclidean slices ${\mathbb{R}}^3\times \mathbb{R}$. As a result, the evolution of quantum states follows the conventional time parameter $t=\tau$, and the dynamics are governed by the standard time-dependent Schrödinger equation [40]:

$$i\hslash {\displaystyle \frac{d}{d\tau }}\Psi \left[t\right]=\widehat{H}\Psi \left[t\right].$$

Smooth Geometry Limit: In the smooth geometry limit, where spacetime curvature is negligible, the chronon field ${\Phi }^{\mu }\left(x\right)$ approaches a constant vector field. Consequently, the foliation induced by ${\Phi }^{\mu }\left(x\right)$ becomes indistinguishable from the global foliation of flat Minkowski spacetime. The evolution parameter $\tau$ then becomes identical to the usual time t used in non-relativistic quantum mechanics [27,36]. In this limit, the Hamiltonian ${\widehat{H}}_{\Phi }\left[\tau \right]$ reduces to the standard Hamiltonian $\widehat{H}$, and the evolution equation becomes:

$$i\hslash {\displaystyle \frac{d}{dt}}\Psi \left(t\right)=\widehat{H}\Psi \left(t\right).$$

Thus, in both the weak-field and smooth geometry limits, the dynamics governed by ChFT reduce to those of standard quantum mechanics, with the chronon field ${\Phi }^{\mu }\left(x\right)$ contributing only small corrections that vanish in these limits.

Conclusion: In the weak-field and smooth geometry limits, ChFT naturally recovers the standard framework of quantum mechanics. The evolution of quantum states becomes governed by the standard Schrödinger equation, thereby confirming the consistency of ChFT with conventional quantum theory in these appropriate limits.

3.3. Constraint Structure and Gauge Invariance

As a background-independent and generally covariant theory, Chronon Quantum Mechanics (ChQM) necessarily includes a system of constraints that reflect both internal gauge symmetries (e.g., associated with Yang-Mills fields) and spacetime diffeomorphism invariance. These constraints ensure that the evolution of quantum states $\Psi \left[\tau \right]\in \mathcal{H}\left[{\Sigma }_{\tau }\right]$ remains consistent with the symmetry content of the theory.

The physical Hilbert space is defined by imposing a set of first-class operator constraints:

$${\widehat{C}}_a\left[\tau \right]\Psi \left[\tau \right]=0,\forall a,$$

(7)

where each ${\widehat{C}}_a\left[\tau \right]$ corresponds to a canonical generator of a gauge or diffeomorphism symmetry projected onto the hypersurface ${\Sigma }_{\tau }$. These include, for example:

• the Gauss constraints ${\widehat{G}}^i\left(x\right)$ generating local internal gauge transformations;
• the diffeomorphism constraints ${\widehat{D}}_i\left(x\right)$ generating spatial coordinate shifts within ${\Sigma }_{\tau }$;
• and the Hamiltonian constraint $\widehat{\mathcal{H}}\left(x\right)$, which in standard canonical gravity generates refoliations of spacetime.

The requirement that all observables $\mathcal{O}\left[\tau \right]$ satisfy:

$$[\mathcal{O}\left[\tau \right],{\widehat{C}}_a\left[\tau \right]]=0$$

(8)

ensures that physical quantities are invariant under the gauge transformations of the theory. This condition is essential for preserving diffeomorphism invariance and ensuring that the theory does not depend on arbitrary coordinate or gauge choices.

The chronon field ${\Phi }^{\mu }\left(x\right)$ plays a dual role in this structure. On one hand, it provides the intrinsic temporal flow required to define evolution along $\tau$; on the other, its compatibility with the constraints imposes nontrivial conditions on its dynamics and admissibility. For instance, the requirement that ${\Phi }^{\mu }$ be hypersurface-orthogonal may constrain the matter content and topology of spacetime, while quantum consistency may require ${\Phi }^{\mu }$ to be dynamically coupled to other fields.

This interplay mirrors structures seen in relational quantum gravity approaches, where time and observables must emerge relationally from the underlying field content [15,27,36]. In ChQM, ${\Phi }^{\mu }$ serves as the backbone that connects the constraint algebra to a physical notion of evolution, thereby avoiding the frozen formalism problem typical of canonical quantum gravity.

Together, these constraints and their relation to the chronon field define the kinematical and dynamical foundation of Chronon Quantum Mechanics. They guarantee internal consistency, enforce gauge symmetry, and provide the mathematical machinery needed to explore nonlocal correlations in a causally coherent and covariant framework.

3.4. Emergence and Engineering of $\Phi$-Threads

A foundational assumption of Chronon Quantum Mechanics is that the smooth, timelike vector field ${\Phi }^{\mu }\left(x\right)$ emerges dynamically and organizes into globally coherent structures—$\Phi$-threads—that underpin causal order and entanglement correlations. A natural question arises: is the existence of such structures physically justified, or merely an interpretive device?

We argue that coherent $\Phi$-threads can arise both spontaneously and controllably, based on principles of geometric field dynamics and analogies with established mechanisms in condensed matter and quantum field theory.

First, consider an initial spacetime region with randomized, future-directed ${\Phi }^{\mu }\left(x\right)$ vectors. Provided the field obeys a local action principle favoring minimal twist and curvature (e.g., through a kinetic term like

$$S[\Phi ]=\int \left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }{\Phi }^{\nu }\right)\sqrt{-g}{d}^{4}x,$$

(9)

dynamical relaxation drives the alignment of neighboring vectors to minimize local shear and vorticity. This alignment tendency is mathematically supported by the same Frobenius condition introduced in Eq. (1): hypersurface-orthogonality (required for foliation) is ensured if the twist tensor vanishes,

$${\omega }_{\mu \nu }:=h_{\mu }^{\alpha }{h}_{\nu }^{\beta }{\nabla }_{[\alpha }{\Phi }_{\beta ]}=0,$$

(10)

where $h_{\mu \nu }=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }$ is the spatial projector orthogonal to ${\Phi }^{\mu }$. Here, we revisit this condition not only as a purely geometric requirement, but also as a potential dynamical outcome—for instance, an energetically favored ground state configuration of the chronon field ${\Phi }^{\mu }$ [17].

Spontaneous thread formation parallels known phenomena such as domain alignment in spin systems, defect line formation in nematic media, and phase coherence in Bose-Einstein condensates [29,45]. In these systems, local ordering and symmetry-breaking dynamics produce globally coherent structures, closely analogous to the formation of $\Phi$-threads from locally interacting timelike directions.

Second, $\Phi$-thread configurations can be externally engineered. In experimental systems such as entangled photon sources, superconducting qubits, or trapped ions, coherent evolution is initialized along controlled channels. Within the ChFT framework, such procedures correspond to embedding a designed ${\Phi }^{\mu }\left(x\right)$ configuration that links spatially separated degrees of freedom via a shared causal ancestry. This engineered coherence enables entangled observables to exhibit Bell-type violations even across spacelike separations, as elaborated in Section 6.

Thus, $\Phi$-threads are not speculative artifacts. They emerge naturally from dynamical alignment and can be deliberately constructed through experimental means. This dual pathway enhances the physical plausibility of ChFT and grounds its formal structure in both theoretical justification and operational practice.

4. Entanglement in Chronon Field Theory

In ChFT, entanglement arises not as an abstract algebraic feature of Hilbert space, but as a manifestation of topological and causal coherence among field configurations on a dynamically foliated spacetime. Each entangled state corresponds to a global configuration of fields and $\Phi$-threads that preserve coherence across distant regions of a common proper-time hypersurface ${\Sigma }_{\tau }$ [33,43]. This reformulation places entanglement within a geometric substrate, bridging quantum information theory with relativistic spacetime structure.

4.1. Entangled $\Phi$-thread Configurations

Let ${\mathcal{O}}_1,{\mathcal{O}}_2\subset {\Sigma }_{\tau }$ be disjoint, spacelike-separated open subsets on a common proper-time hypersurface. Consider localized field excitations ${\phi }_1,{\phi }_2$ supported in ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$, respectively. In conventional quantum theory, the pair is considered entangled if the global quantum state $\Psi \left[\tau \right]\in \mathcal{H}\left[{\Sigma }_{\tau }\right]$ cannot be factorized into a simple tensor product ${\psi }_1\otimes {\psi }_2$. In ChFT, however, this notion of entanglement acquires a concrete geometric and topological underpinning grounded in the structure of the dynamical field ${\Phi }^{\mu }\left(x\right)$.

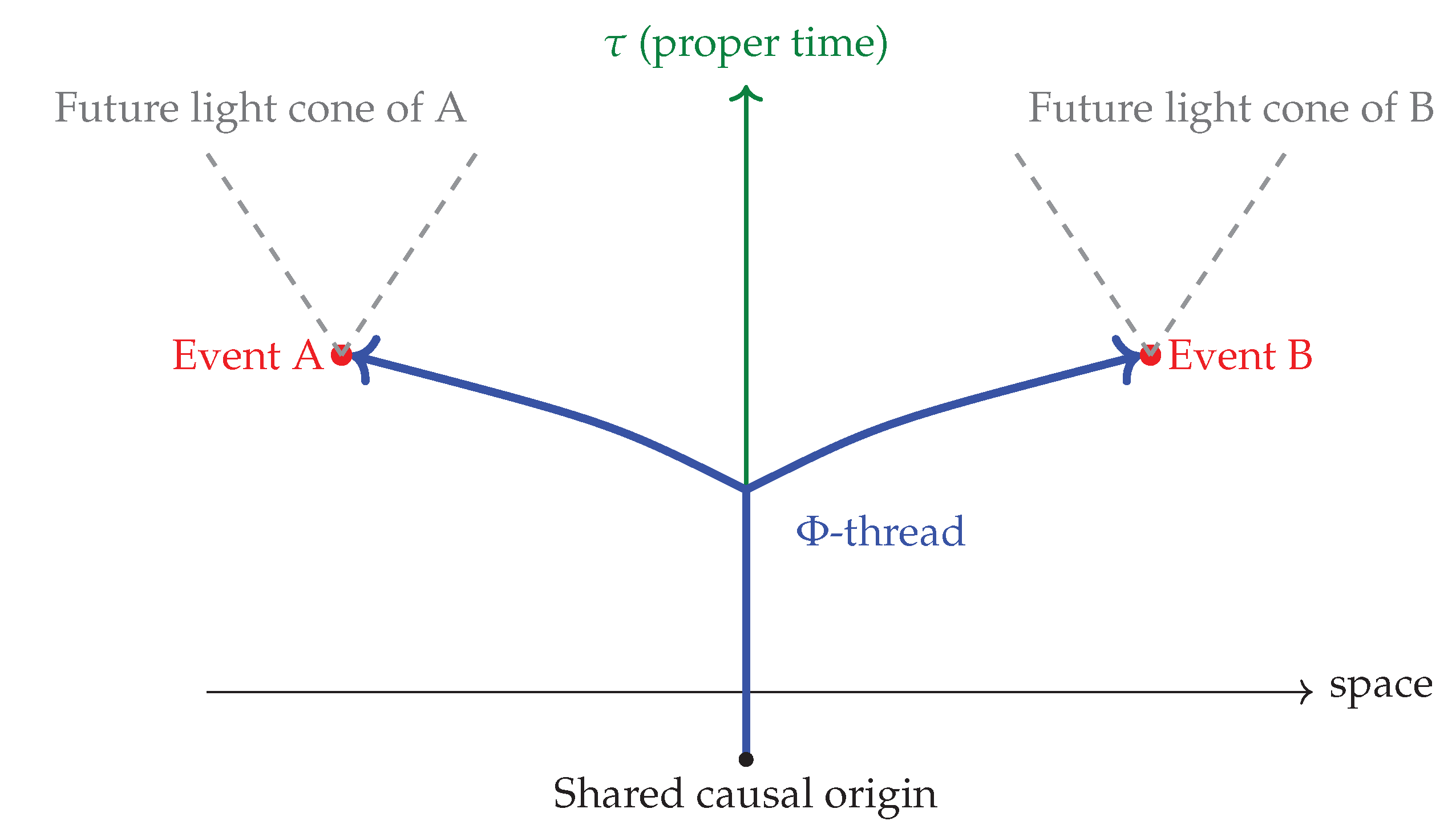
We define ${\phi }_1$ and ${\phi }_2$ to be chronon-entangled if their respective support regions are causally linked through the global configuration of the chronon field. Specifically, this occurs when the integral curves (or $\Phi$-threads) intersecting ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ share a common causal ancestry—either converging to a shared past segment or forming part of a continuous, topologically nontrivial bundle. 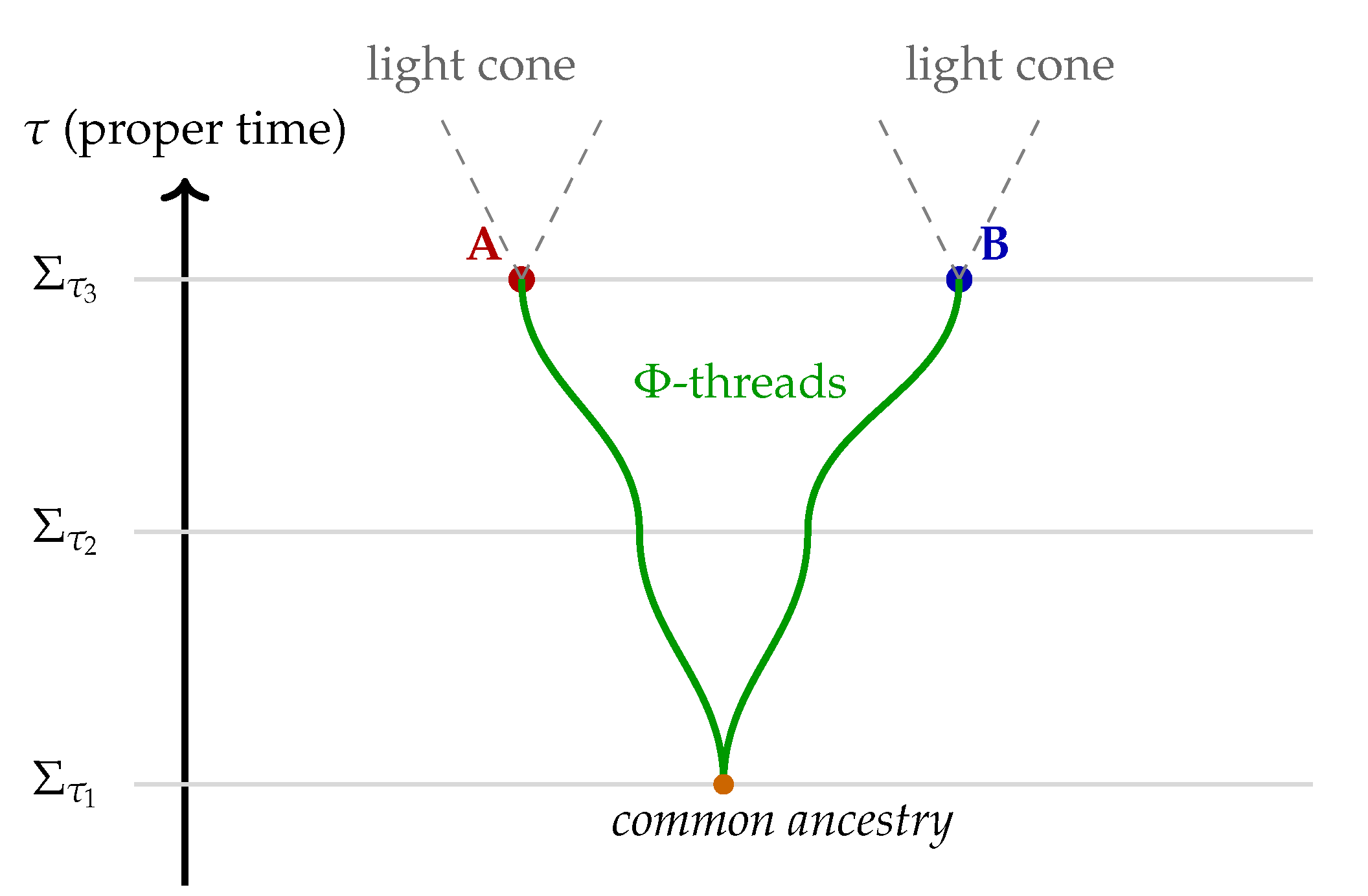This causal linkage is schematically illustrated in Figure 2, where events A and B, though spacelike-separated in the background metric, remain entangled via a shared $\Phi$-thread that preserves coherence across the foliation.

In the continuum limit, such a linkage implies the existence of a non-separable global section of the tangent bundle $\mathcal{T}\mathcal{M}$ satisfying:

$${\Phi }^{\mu }\left(x\right){\partial }_{\mu }\phi \left(x\right)=0\mathrm{along}\mathrm{shared}\mathrm{trajectories}.$$

(11)

This condition ensures that the field excitations remain synchronized under intrinsic evolution along ${\Phi }^{\mu }$.

In topologically nontrivial configurations—e.g., those characterized by nonzero linking number or Hopf index—the integral curves of ${\Phi }^{\mu }$ can form braided or knotted structures. These act as conduits of long-range phase coherence between distant regions, enforcing stable entanglement correlations. Analogous phenomena are observed in entangled vortex filaments in superfluids, topologically ordered photonic lattices, and non-Abelian anyonic systems in fractional quantum Hall platforms [5,28].

The shared ancestry condition may also be formulated in cohomological terms. If the domains ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ lie within the support of a nontrivial cohomology class in $H^1(\mathcal{M},\mathbb{Z})$ dual to a conserved, ${\Phi }^{\mu }$-aligned current, then their field content will exhibit intrinsic phase correlations irrespective of spatial distance. This provides a rigorous topological signature for chronon-mediated entanglement.

In this framework, entanglement ceases to be a purely algebraic property and instead becomes a geometric manifestation of temporally structured, causally coherent field evolution. Bell-type correlations thus emerge not from nonlocal signaling but from shared ${\Phi }^{\mu }$-induced causal ancestry, consistent with Lorentz covariance and compatible with operational no-signaling constraints.

4.2. Topological Sectors and Causal Structure

The space of admissible field configurations in ChFT decomposes into distinct topological sectors $\left\{{\mathcal{C}}_{\alpha }\right\}$, each defined by global invariants of the chronon field ${\Phi }^{\mu }$. These include homotopy classes of maps $\Phi :\mathcal{M}\to S^3$, Chern-Simons numbers, linking numbers, or other topological indices of the $\Phi$-thread bundle. Each sector ${\mathcal{C}}_{\alpha }$ groups chronon configurations sharing the same topological class under smooth deformations.

Quantum states in Chronon Quantum Mechanics (ChQM) can exhibit entanglement not only due to causal ancestry but also via coherent superpositions across distinct topological sectors. Let $\left\{{\mathcal{C}}_{\alpha }\right\}$ denote the set of admissible chronon field configurations classified by topological invariants (e.g., linking number, winding number, or Chern–Simons charge). The corresponding Hilbert space $\mathcal{H}\left[{\Sigma }_{\tau }\right]$ decomposes into orthogonal sector subspaces ${\mathcal{H}}_{\alpha }\left[{\Sigma }_{\tau }\right]$, each supporting quantum states consistent with the topology of ${\mathcal{C}}_{\alpha }$. A general state at proper time $\tau$ can then be expressed as

$$\Psi \left[\tau \right]=\sum _{\alpha }{c}_{\alpha }{\Psi }_{\alpha }\left[\tau \right],{\Psi }_{\alpha }\left[\tau \right]\in {\mathcal{H}}_{\alpha }\left[{\Sigma }_{\tau }\right],$$

(12)

where the complex coefficients $c_{\alpha }\in \mathbb{C}$ encode the probability amplitudes for the system to occupy sector ${\mathcal{C}}_{\alpha }$, satisfying the normalization condition ${\sum }_{\alpha }{\left|c_{\alpha }\right|}^2=1$. Interference between different sector components ${\Psi }_{\alpha }\left[\tau \right]$ leads to long-range quantum correlations supported by topological coherence.

The persistence of such entanglement is tied to the causal and topological structure encoded in ${\Phi }^{\mu }$. Coherent bundles of $\Phi$-threads serve as conduits for phase-preserving evolution across spacetime. Provided that ${\mathcal{O}}_1,{\mathcal{O}}_2\subset {\Sigma }_{\tau }$ remain within a shared topological sector, their quantum correlations can persist dynamically, even in the presence of local perturbations.

Topological robustness plays a crucial role here: while environmental or unitary decoherence may affect local degrees of freedom, transitions between sectors require global topological change—akin to surgery on the thread bundle. This constraint stabilizes chronon-mediated entanglement and defines a new class of geometrically protected quantum correlations.

Thus, ChFT offers a structural framework where quantum entanglement is not grafted onto spacetime but emerges from its causal-topological skeleton. This geometric picture complements algebraic quantum field theory and paves the way toward unified treatments of quantum information and background-independent dynamics.

4.3. Intrinsic Decoherence and $\tau$-Preservation

Unlike standard quantum decoherence, which typically arises from tracing over environmental subsystems, ChFT introduces a notion of intrinsic decoherence—the breakdown of coherence across a given ${\Sigma }_{\tau }$ due to disruption in the global causal structure imposed by ${\Phi }^{\mu }\left(x\right)$.

Such decoherence may result from topological phase transitions, bifurcations or instabilities in the $\Phi$-thread network, or loss of synchrony in the foliation parameter $\tau$[46]. When causal coherence across ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ is disrupted, entanglement can degrade—not through dynamical noise, but via topological disconnection.

However, because ${\Phi }^{\mu }$ evolves under covariant field equations, such decoherence is not arbitrary. So long as foliation-preserving dynamics are maintained, chronon-mediated entanglement remains robust. This feature defines a natural form of causally grounded, dynamically constrained coherence.

In this sense, the foliation structure defined by ${\Phi }^{\mu }$ not only generates entanglement but governs its propagation, resilience, and decay. This intrinsic mechanism differs fundamentally from open system decoherence, and aligns with the broader ambition of ChFT to integrate quantum mechanics with background-independent causal geometry.

The following section demonstrates how this reinterpretation of entanglement resolves key paradoxes raised by Bell’s theorem—without recourse to nonlocality or retrocausality.

5. Revisiting Bell’s Theorem in ChFT

Bell’s theorem demonstrates that no local hidden variable theory can reproduce the statistical predictions of quantum mechanics for entangled systems [7]. The derivation of Bell inequalities relies on three central assumptions: (i) realism — the notion that measurement outcomes are determined by pre-existing properties described by hidden variables $\lambda$; (ii) locality — the assumption that the outcome at one site is independent of the measurement setting at a spacelike-separated site; and (iii) statistical independence — the assumption that the hidden variables are uncorrelated with the choice of measurement settings [8].

Let $A,B\in \{-1,+1\}$ denote measurement outcomes at two spacelike-separated detectors with measurement settings a and b, respectively. Under the above assumptions, Bell derived the Clauser-Horne-Shimony-Holt (CHSH) inequality:

$$|E(a,b)-E(a,b^{\prime })|+|E(a^{\prime },b)+E(a^{\prime },b^{\prime })|\le 2,$$

(13)

where $E(a,b)=\int d\lambda \rho \left(\lambda \right)A(a,\lambda )B(b,\lambda )$ is the expected correlation function integrated over the hidden variable distribution $\rho \left(\lambda \right)$.

Quantum mechanics predicts violations of this inequality up to the Tsirelson bound $2\sqrt{2}$, and this has been repeatedly confirmed in experiments [4,21]. The apparent conflict with local realism has motivated a wide range of interpretive proposals, including retrocausality, superdeterminism, and objective collapse models.

5.1. $\Phi$-thread Reformulation

Chronon Field Theory offers a reformulation of the assumptions underlying Bell’s theorem by replacing background time and absolute simultaneity with a dynamical causal structure. In ChFT, the temporal and causal structure of spacetime emerges from a smooth, future-directed vector field ${\Phi }^{\mu }\left(x\right)$, which defines a covariant foliation into proper-time hypersurfaces ${\Sigma }_{\tau }$. All physical processes, including measurements, are described relative to this intrinsic temporal flow.

Importantly, measurement events in ChFT are not instantaneous acts on a fixed Minkowski slice, but are instead localized interactions that evolve along the integral curves of ${\Phi }^{\mu }$. Thus, two spacelike-separated measurement regions ${\mathcal{O}}_1,{\mathcal{O}}_2\subset {\Sigma }_{\tau }$, while spatially disjoint, may share a common causal ancestry via their embedding in a topologically coherent bundle of $\Phi$-threads.

Within this formulation, the assumption of statistical independence is modified. The global coherence imposed by the dynamical field ${\Phi }^{\mu }\left(x\right)$ induces correlations between spacelike-separated regions—not by signaling, but through a shared geometric history. As a result, the hidden variables $\lambda$ (if such a description is attempted) may not be statistically independent of the settings a and b. This undermines a key assumption required to derive Bell-type inequalities.

Similarly, the assumption of locality, traditionally defined via metric separation, requires re-evaluation. In ChFT, causal relationships are encoded not solely in the metric but in the topology of $\Phi$-threads. Events can be temporally and causally connected through their shared foliation, even if spatially outside each other’s light cones. This geometrically enriched structure invalidates the factorization condition $P(A,B|a,b,\lambda )=P(A|a,\lambda )P\left(B\right|b,\lambda )$, which is essential for Bell’s derivation.

Now we can see that, ChFT does not deny Bell’s reasoning—it recontextualizes it. The core insight is that the violation of Bell inequalities does not require nonlocal dynamics but instead reflects a deeper causal architecture encoded in the chronon field [12,33].

5.2. Joint Probabilities and Inequality Violation

In conventional derivations, joint outcome probabilities are assumed to take a factorizable form:

$$P(A,B|a,b)=\int d\lambda \rho (\lambda \left)P\right(A|a,\lambda )P\left(B\right|b,\lambda ),$$

(14)

where $\lambda$ is drawn from a distribution $\rho \left(\lambda \right)$ assumed uncorrelated with a and b. This factorization, rooted in locality and independence, is central to Bell-type bounds.

In ChFT, the standard locality and statistical independence assumptions of Bell’s theorem are not fundamental but emergent approximations that need not hold globally. The full quantum state at proper time $\tau$ is represented by a global wavefunctional $\Psi \left[\tau \right]\in \mathcal{H}\left[{\Sigma }_{\tau }\right]$, encoding the configuration of all fields on the foliation slice ${\Sigma }_{\tau }$ defined by ${\Phi }^{\mu }$. When measurement observables localized in ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ are operationally implemented in ChFT, they are described by operators ${\widehat{P}}_A^a$ and ${\widehat{P}}_B^b$ acting on the respective subalgebras of observables supported in those regions. The joint probability for outcomes A and B is then computed as

$$P(A,B|a,b)=\langle \Psi \left[\tau \right]|{\widehat{P}}_A^a\otimes {\widehat{P}}_B^b|\Psi \left[\tau \right]\rangle .$$

(15)

Here, ${\widehat{P}}_A^a$ and ${\widehat{P}}_B^b$ are projection-valued measures within the CFT operator algebra, defined intrinsically on the dynamically generated hypersurfaces ${\Sigma }_{\tau }$. This formalism does not presuppose the axioms of standard quantum mechanics for the derivation of Bell inequalities. Instead, the use of projectors follows naturally from the measurement framework internal to CFT, where they emerge from the orthogonal decomposition of state space on each foliation slice ${\Sigma }_{\tau }$ and from the causal structure encoded in ${\Phi }^{\mu }$.

The crucial distinction is that the correlations in Eq. (15) do not originate from Hilbert-space nonlocality within a fixed background, but rather from the causal and topological ancestry encoded in the $\Phi$-thread network. These correlations are inherently non-factorizable: the shared ${\Phi }^{\mu }$-structure links measurement settings and outcomes through a common causal past. In this way, the usual statistical independence assumption of Bell’s theorem is relaxed without requiring superluminal signaling or retrocausal effects. Relativistic causality remains fully respected, since no controllable influence propagates outside the causal structure determined by ${\Phi }^{\mu }$.

In parallel, the pseudo-density operator (PDO) framework has recently offered complementary operational tools for probing temporal nonclassicality, including explicit formulations of temporal Bell inequalities [1] and techniques for inferring causal directionality from quantum statistics [11].

5.3. Causality and No-Signaling in ChFT

A relativistically consistent quantum theory must preserve the no-signaling condition: measurement outcomes at one site cannot be influenced, in an operationally controllable way, by the setting choice at a spacelike-separated site. ChFT satisfies this condition by aligning dynamics with the causal structure defined by the chronon field ${\Phi }^{\mu }\left(x\right)$.

Evolution proceeds along the intrinsic proper time $\tau$, with field configurations evolving deterministically along integral curves of ${\Phi }^{\mu }$. The hypersurfaces ${\Sigma }_{\tau }$ are orthogonal to these curves, and observables are defined with respect to this foliation. On any fixed ${\Sigma }_{\tau }$, two spatially separated regions ${\mathcal{O}}_1,{\mathcal{O}}_2$ cannot influence one another through any physical process allowed by the theory.

Thus, the marginal probability for A is independent of the measurement setting b applied to B:

$$\sum _{B}P(A,B|a,b)=P\left(A\right|a)\forall b,$$

(16)

and likewise for B. These constraints are respected in ChFT because the global state $\Psi \left[\tau \right]$ evolves unitarily along $\tau$, and the causal structure encoded in ${\Phi }^{\mu }$ forbids superluminal communication.

Entanglement correlations in ChFT are rooted in shared causal ancestry rather than instantaneous influence. This geometric reinterpretation reconciles observed quantum correlations with relativistic causality, offering a conservative yet conceptually enriched alternative to standard views [19,34].

In this view, violations of Bell-type inequalities signal not a breakdown of locality, but the inadequacy of background-dependent causal models. ChFT replaces these with a dynamically foliated, globally entangled spacetime geometry that supports causally consistent quantum correlations.

6. Illustrative Model and Simulation

To concretize the abstract structure of ChFT, we present a computational model that simulates the evolution and correlation structure of quantum fields on a discretized spacetime lattice embedded with a synthetic ${\Phi }^{\mu }$ field. This toy model serves as a proof of concept for how non-factorizable entanglement correlations can emerge from causally coherent topological structures, as opposed to instantaneous nonlocal interactions [12,32].

6.1. Conceptual Lattice Model

We consider a four-dimensional hypercubic lattice discretization of spacetime, $\mathcal{L}=({\mathbb{Z}}^4,\Delta )$, where each lattice site $x\in {\mathbb{Z}}^4$ is assigned a normalized integer-valued vector ${\Phi }^{\mu }\left(x\right)$ that determines the direction of intrinsic time evolution. These vectors define directed edges—called $\Phi$-threads—that link each site to its immediate successor $x+{\Phi }^{\mu }\left(x\right)$, forming a discrete foliation of spacetime consistent with the intrinsic causal order defined by ${\Phi }^{\mu }$ [41].

On this lattice, we evolve a complex scalar field $\psi \left(x\right)$ initialized on a proper-time slice ${\Sigma }_0$. The evolution rule is constrained along $\Phi$-threads:

$$\psi (x+{\Phi }^{\mu }\left(x\right))=U\left(x\right)\psi \left(x\right),$$

(17)

where $U\left(x\right)$ is a site-specific unitary operator preserving norm. Phase correlations are introduced through local interactions, with topological constraints designed to preserve entanglement across distant regions. This setup allows us to encode causal connectivity through shared topological ancestry, reflecting one of the core postulates of ChFT. See Figure 3

6.2. Correlation Extraction and Bell-Type Analysis

To examine quantum correlations, we isolate two spatially separated regions ${\mathcal{O}}_1,{\mathcal{O}}_2\subset {\Sigma }_T$, and define projection-valued observables $A_i,B_j$ acting on $\psi$ in these regions. The correlation function

$$E_{ij}=\langle \psi |A_i\otimes B_j|\psi \rangle$$

(18)

is evaluated by ensemble-averaging over field configurations compatible with the same global ${\Phi }^{\mu }$-coherent foliation. In configurations where topologically linked $\Phi$-threads connect ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$, the resulting statistics exhibit Bell-type inequality violations while still satisfying relativistic no-signaling constraints. This illustrates the main thesis of ChFT: that causally coherent field structure—not nonlocal signaling—is responsible for entanglement correlations.

6.3. Field Observables and Visualization

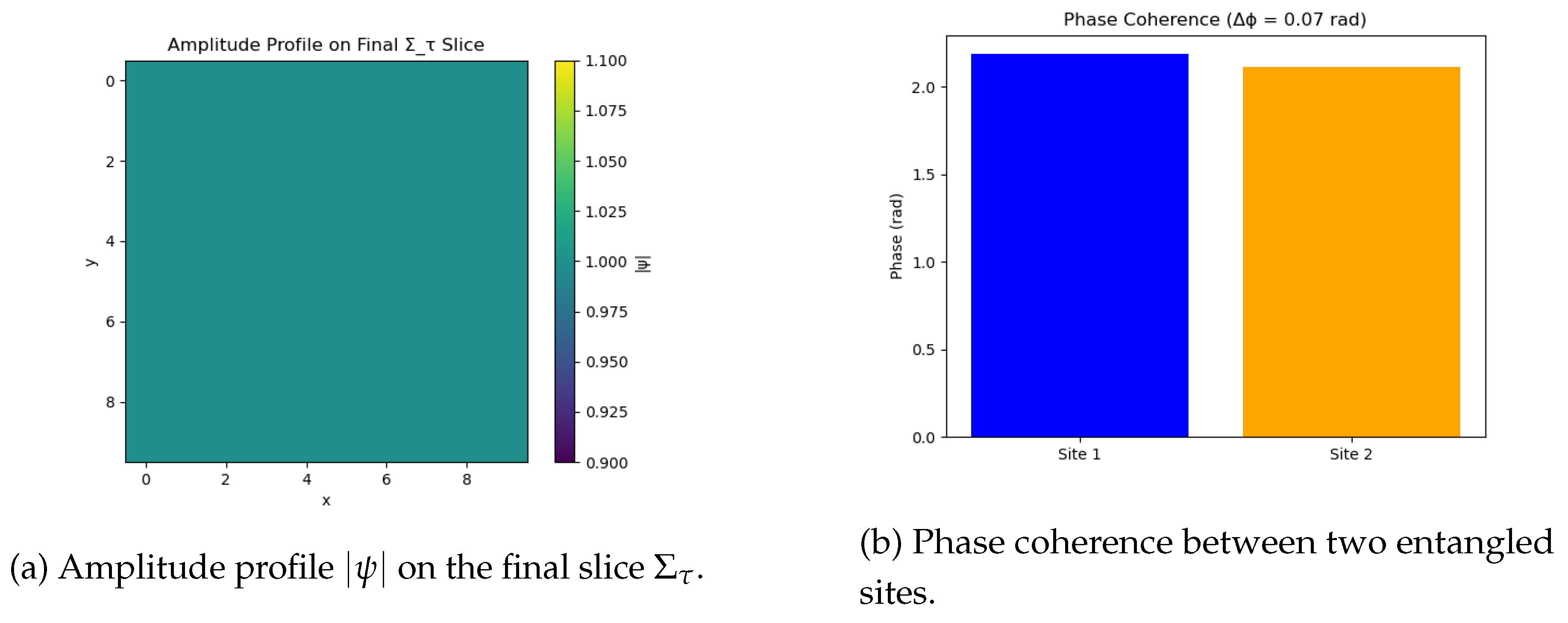
To visualize how entanglement manifests in the scalar field $\psi$, we compute the amplitude and phase profiles across a final foliation slice ${\Sigma }_{\tau }$. Figure 4a shows the norm $\left|\psi \right|$ across the spatial domain, highlighting the uniformity of field propagation along $\Phi$-threads. Figure 4b displays the phase values at two entangled sites, showing near-perfect coherence in the presence of a shared topological history. The small phase offset $\Delta \varphi$ quantifies the residual decoherence due to environmental coupling or topological fluctuations.

These visualizations translate abstract Hilbert space entanglement into concrete geometric and field-theoretic terms. They also illustrate how decoherence is understood in ChFT: not as environmental noise, but as a breakdown in global causal synchrony. Disentanglement corresponds to the rupture or divergence of previously coherent $\Phi$-thread bundles, offering a testable geometric signature of quantum coherence.

6.4. Implications for ChFT and Quantum Foundations

This simulation, though idealized, reinforces the foundational principles of ChFT. It demonstrates that entanglement correlations can arise from intrinsic temporal dynamics and topological causality, not external time or acausal effects. The model provides an intuitive bridge between the mathematical formalism and physical insight, and offers a scalable framework for future computational studies in foliated quantum dynamics, quantum gravity analogs, and topological quantum information.

7. Implications and Outlook

Chronon Field Theory introduces a covariant framework for quantum mechanics grounded in a dynamical temporal structure. By postulating a smooth timelike vector field ${\Phi }^{\mu }\left(x\right)$ as the source of intrinsic causality and proper time, ChFT reconfigures the foundations of quantum theory with broad implications.

7.1. Reinterpreting Quantum Nonlocality

ChFT resolves the tension between quantum nonlocality and relativistic causality by attributing Bell-type correlations to shared causal ancestry in the ${\Phi }^{\mu }$ field. Spatially separated events remain correlated not through acausal influence but through coherent $\Phi$-threads within a common foliation slice ${\Sigma }_{\tau }$. These threads encode persistent topological and causal connectivity, offering a geometric explanation for entanglement that preserves no-signaling.

This recharacterization aligns with causal set theory, algebraic QFT, and frameworks with indefinite causal order [23,34]. Entanglement becomes a manifestation of global causal geometry rather than paradoxical nonlocality.

7.2. Experimental Implications and Predictions

While recovering standard quantum predictions, ChFT suggests deviations under engineered or extreme conditions:

• Foliation-sensitive decoherence: Non-inertial frames or curved geometries may disrupt ${\Phi }^{\mu }$-coherence, altering entanglement lifetimes or interference profiles.
• Topology-dependent fidelity: Entanglement operations relying on incompatible ${\Phi }^{\mu }$-ancestries may exhibit reduced fidelity, especially in multipartite quantum networks.
• Correlation saturation under topological constraints: Compact or nontrivial spacetime topologies may impose global limits on long-range entanglement.

These signatures provide potential tests for the physical reality of intrinsic time and chronon-mediated correlations.

7.3. Theoretical Extensions and Open Problems

ChFT opens several avenues for deeper theoretical development:

• Path integral over foliations: A covariant quantization scheme integrating over ${\Phi }^{\mu }$-compatible geometries could extend ChFT toward quantum gravity and cosmology.
• Category-theoretic formulations: Reformulating ChFT within topos or sheaf-theoretic logic may clarify the theory’s treatment of contextuality and relational time [24].
• Backreaction and matter coupling: Understanding how ${\Phi }^{\mu }$ couples to matter and responds to gravitational dynamics is essential for embedding ChFT in effective field theory.
• Quantum information on $\Phi$-networks: Analyzing computation and communication over ${\Phi }^{\mu }$-defined graph structures could link ChFT to quantum networks and holography.

Altogether, Chronon Field Theory offers a coherent, testable framework reconciling quantum entanglement with causal structure, laying conceptual and technical groundwork for deeper integration with quantum gravity.

8. Discussion and Conclusion

We have introduced Chronon Field Theory as a covariant, background-independent reformulation of quantum mechanics in which time and causality emerge from a dynamical timelike vector field ${\Phi }^{\mu }\left(x\right)$. This field induces a foliation of spacetime into proper-time hypersurfaces ${\Sigma }_{\tau }$, providing a geometrically grounded and locally defined temporal evolution.

Within this framework, quantum dynamics proceed via a Schrödinger-type equation along the intrinsic flow of ${\Phi }^{\mu }$, subject to first-class, gauge-invariant constraints. Entangled states correspond to globally coherent ${\Phi }^{\mu }$-thread configurations, linking disjoint regions through shared causal ancestry. Violations of Bell-type inequalities arise naturally from the breakdown of statistical independence in such non-factorizable geometries. Crucially, the foliation-respecting dynamics preserve no-signaling, ensuring compatibility with relativistic causality.

Beyond its conceptual reinterpretation of entanglement, ChFT accommodates topologically protected causal webs, sector-coherent superpositions, and foliation-sensitive observables. These features suggest concrete experimental signatures, such as decoherence rates dependent on topological sector stability or fidelity plateaus tied to ${\Phi }^{\mu }$-coherent ancestry. We have illustrated the viability of the framework with a discrete simulation of ${\Phi }^{\mu }$ alignment and coherence persistence. The causal-topological picture of entanglement—summarized in Figure 5—highlights how spacelike-separated events can remain correlated through a common temporal backbone, without invoking nonlocal signaling.

By unifying temporal flow, causal order, and quantum correlations within a single dynamical substrate, ChFT offers a constructive alternative to purely kinematic frameworks such as pseudo-density operators and process matrix formalisms. Its built-in compatibility with gauge structures and constraint preservation suggests a natural pathway for embedding quantum theory into a fully dynamical spacetime setting.

Recent PDO-based approaches have advanced the analysis of quantum causal inference and temporal Bell scenarios [1,11], but these remain fundamentally kinematic. In contrast, ChFT supplies a genuine dynamical substrate—the ${\Phi }^{\mu }$ field and its induced foliation—from which correlations and their causal ancestry emerge intrinsically.

Future directions include developing a path-integral quantization of the chronon field, exploring its coupling to matter and gauge sectors, and formulating its algebraic structure within operator algebras on foliated manifolds. On the empirical side, probing how topological constraints shape entanglement decay may provide experimental access to the role of intrinsic time in quantum mechanics. In this way, ChFT opens a concrete route toward reconciling quantum theory with the geometric and causal fabric of spacetime.