The Modelling of Dielectric Relaxation Under Microwave Treatment into Porous Humidified Body

1. The Local Space Averaging

The three-phase macroscopic porous area, volume or cell $P$ of the humidified porous body, as it was mentioned into work [2], consist from the solid $P_S$, liquid $P_L$ and gas $P_G$ , so arbitrary volume of averaging $\Delta V_R$ contains the phases sub volume of the skeleton $\Delta V_S(t)$ (solid phase), water $\Delta V_L(t)$ (liquid phase) and gas $\Delta V_G(t)$ (air and water like phase), which may to changes with time $t$. Sub volumes $\Delta V_L(t)$ and $\Delta V_G(t)$ defines the volume of pores $\Delta V_P(t)=\Delta V_L(t)\cup \Delta V_G(t)$ under condition $\Delta V_R={\displaystyle \sum _{\sigma }\Delta V_{\sigma }}(t)$, where $\sigma =\left\{S,L,G\right\}$ is the index of phase.

The configuration and displacement of phases into area of averaging can rewrite with usage of the characteristics function

$${\vartheta }_{\sigma }(\overrightarrow{r},t)=\left\{{\displaystyle \frac{1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{when}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{r}\in \Delta V_{\sigma }(t)}{0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathrm{when}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{r}\notin \Delta V_{\sigma }(t)}}\right.,\mathrm{here} \sigma =\left\{S,L,G\right\}.$$

(1)

This function also takes into account the time moving of phases for considering body, which can be conditioned by the mass transfer processes or the mechanical deformations. Then $\Delta V_{\sigma }(t)={\displaystyle \underset{\Delta V_R}{\int }{\vartheta }_{\sigma }}(\overrightarrow{r},t)dV$, and volume fraction of $\sigma$- phase of the material can be determined as

$${\theta }_{\sigma }(\overrightarrow{x},t)={\displaystyle \frac{\Delta V_{\sigma }(\overrightarrow{x},t)}{\Delta V_R}},. ({\displaystyle \sum _{\sigma }{\theta }_{\sigma }=1})$$

(2)

Also reviewing the physical quantities of the pore saturation by the liquid ${\eta }_l$ or the gas ${\eta }_g$ correspondingly

$${\eta }_L={\displaystyle \frac{\Delta V_L}{\Delta V_L+\Delta V_G}},\hspace{0.33em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\eta }_g={\displaystyle \frac{\Delta V_G}{\Delta V_L+\Delta V}},\hspace{0.33em}({\eta }_L+{\eta }_G=1).$$

(3)

Then, according to the definition [3] of the local porosity

$$\phi ={\displaystyle \frac{\Delta V_L+\Delta V_G}{\Delta V_R}}=1-{\displaystyle \frac{\Delta V_S}{\Delta V_R}},$$

(4)

for the volume fractions of the phases gets the following relations

$${\theta }_S=1-\phi ,\hspace{0.33em}{\theta }_L=\phi {\eta }_L,\hspace{0.33em}{\theta }_G=\phi (1-{\eta }_L).$$

(5)

Let's define the function $\xi (\overrightarrow{r},t)$ which describe into ranges of R.E.V. (the Representative Averaging Volume [4]) a certain the local value of the physical quantity, which characterize the macroscopic physical volume $P$ of porous body. The space averaging of such quantity in the point $\overrightarrow{x}$ of the macroscopic porous volume into the time moment $t$ determines [3] in the such way

$$\xi (\overrightarrow{x},t)={\displaystyle \frac{1}{\Delta V_R}}{\displaystyle \underset{\Delta V_R}{\int }\xi (\overrightarrow{r},t)}dV.$$

(6)

Similarly, with usage of the characteristic function (1), reproduce the phase

$$〈{\xi }_{\sigma }〉(\overrightarrow{x},t)={\displaystyle \frac{1}{\Delta V_R}}{\displaystyle \underset{\Delta V_R}{\int }\xi (\overrightarrow{r},t)}{�}_{\sigma }(\overrightarrow{r},t)dV$$

(7)

and internal

$${〈{\xi }_{\sigma }〉}^{\sigma }(\overrightarrow{x},t)={\displaystyle \frac{1}{\Delta V_{\sigma }}}{\displaystyle \underset{\Delta V_{\sigma }}{\int }\xi (\overrightarrow{r},t)}{�}_{\sigma }(\overrightarrow{r},t)dV$$

(8)

averaged quantities.

Because take the place the relation

$${\displaystyle \underset{\Delta V_R}{\int }\xi (\overrightarrow{r},t)}{\vartheta }_{\sigma }(\overrightarrow{r},t)dV={\displaystyle \underset{\Delta V_{\sigma }}{\int }\xi (\overrightarrow{r},t)}{\vartheta }_{\sigma }(\overrightarrow{r},t)dV,$$

so phase and internal averaged are interconnected

$${\xi }_{\sigma }(\overrightarrow{x},t)={\theta }_{\sigma }(\overrightarrow{x},t){\xi }_{\sigma }^{\sigma }(\overrightarrow{x},t).$$

Thus, using the method of local spatial averaging, a reviewing heterogeneous porous cell can be described by certain continuous local physical quantities in coordinate and time space. This makes it possible to consider this one as a superposition of the three material continua: skeleton, liquid, and gas. With this approach, the equations of the physical model of a porous cell are written relatively to the specified average values (6-8) and are formally equivalent to the equations for a homogeneous (isotropic) single-phase cell according to the approximation of the model [9] for the continuous solid medium.

2. The Equations of Electrodynamics

For microwave electromagnetic field (E.M.F) according to the theory of dielectric relaxation Botcher-Bordewijk [5] we can review the vector of the generalized dielectric displacement for the known relation

$${\overrightarrow{D}}^{\text{'}}\left(\overrightarrow{r},t\right)=\overrightarrow{D}\left(\overrightarrow{r},t\right)+{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{J}\left(\overrightarrow{r},t^{\text{'}}\right)d{t}^{\text{'}}},$$

(9)

where $\overrightarrow{D}\left(\overrightarrow{r},t\right)={\epsilon }_0\overrightarrow{E}\left(\overrightarrow{r},t\right)+\overrightarrow{P}\left(\overrightarrow{r},t\right)$ is the vector of dielectric displacement, which consider polarization processes into continuous media, $\overrightarrow{P}\left(\overrightarrow{r},t\right)$ and $\overrightarrow{E}\left(\overrightarrow{r},t\right)$ are the vectors of polarization and stretch of electric field, and $\overrightarrow{J}\left(\overrightarrow{r},t\right)$ is the density of polarization current.

From the condition of continuity $\partial \rho /\partial t+\overrightarrow{\nabla }\cdot \overrightarrow{J}=0$ it is following the expression for the density of polarization charge $\rho \left(\overrightarrow{r},t\right)=-{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{\nabla }\cdot \overrightarrow{J}\left(\overrightarrow{r},t^{\text{'}}\right)d{t}^{\text{'}}}$, according to this into the local averaging volume (R.E.V) [2] the microscopic equations of E.M.F. Maxwell-Lorents into homogeneous form [6,7] and boundary conditions have the form

$$\begin{array}{c}\overrightarrow{\nabla }\times \overrightarrow{E}\left(\overrightarrow{r},t\right)=-{\displaystyle \frac{\partial \overrightarrow{B}\left(\overrightarrow{r},t\right)}{\partial t}},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{\nabla }\times \overrightarrow{H}\left(\overrightarrow{r},t\right)={\displaystyle \frac{\partial {\overrightarrow{D}}^{\text{'}}\left(\overrightarrow{r},t\right)}{\partial t}},\\ \overrightarrow{\nabla }\cdot {\overrightarrow{D}}^{\text{'}}\left(\overrightarrow{r},t\right)=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{\nabla }\cdot \overrightarrow{B}\left(\overrightarrow{r},t\right)=0,\end{array}$$

(10a)

where

$${\overrightarrow{E}}_{\sigma }^{\left(t\right)}\left(t\right)={\overrightarrow{E}}_{\sigma \text{'}}^{\left(t\right)}\left(t\right), {\overrightarrow{H}}_{\sigma }^{\left(t\right)}\left(t\right)={\overrightarrow{H}}_{\sigma \text{'}}^{\left(t\right)}\left(t\right),\overrightarrow{D}{\text{'}}_{\sigma }^{\left(n\right)}\left(t\right)=\overrightarrow{D}{\text{'}}_{\sigma \text{'}}^{\left(n\right)}\left(t\right),{\overrightarrow{B}}_{\sigma }^{\left(n\right)}\left(t\right)={\overrightarrow{B}}_{\sigma \text{'}}^{\left(n\right)}\left(t\right)$$

(10b)

Are the conditions of continuity for components and derivatives of the field. Here $\left\{\sigma |\sigma \text{'}\right\}=\left\{S,L,G\right\}\left(\sigma \ne {\sigma }^{\text{'}}\right)$ are denotations of phases, $t$ and $n$ are indexes, which define the tangential and normal components of field on the surfaces $\Delta S_{\sigma \sigma \text{'}}$ of separations of phases accordingly. The system of equations (10a) is satisfied under conditions, that charges and currents of other nature into the investigated closed system are absent.

2.1. The Operators of Dielectric Susceptibility and Conductivity

The constitutive or material equations is proposed to write into following case

$$\begin{array}{c}\overrightarrow{D}\left(\overrightarrow{r},t\right)={\epsilon }_0\widehat{\epsilon }\overrightarrow{E}\left(\overrightarrow{r},t\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{B}\left(\overrightarrow{r},t\right)={\mu }_0\overrightarrow{H}\left(\overrightarrow{r},t\right),\\ \overrightarrow{J}\left(\overrightarrow{r},t\right)=\widehat{\sigma }\left(\overrightarrow{r}\right)\overrightarrow{E}\left(\overrightarrow{r},t\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}тут\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\widehat{\epsilon }=\left(1+\widehat{\chi }\right),\end{array}$$

(11)

where $\widehat{\epsilon }$,$\widehat{\chi }$ and $\widehat{\sigma }$ are operators of dielectric permeability, susceptibility and conductivity of cell correspondingly, ${\epsilon }_0$ and ${\mu }_0$ are dielectric and magnetic constants into vacuum respectively. It is important to note, that under conditions of absence of joules heat releasing at the fixed frequency of E.M.F. and absence of dispersion, into harmonic approximation of the field amplitudes (see Section 2, subsection 2 eqv. (28)) the operators of dielectric permeability and conductivity must have to satisfy the known [7] relation

$${\widehat{\sigma }}_{\omega }=-i\omega {\epsilon }_0\left[{\widehat{\epsilon }}_{\omega }-1\right]=-i\omega {\epsilon }_0{\widehat{\chi }}_{\omega },$$

(12)

where $\omega$ is the index, which point on the fixed frequency of harmonic field. Then the density of polarization current ${\rho }_p=-\overrightarrow{\nabla }\cdot \overrightarrow{P}$ , here $\overrightarrow{P}$ is the polarization vector, is is determined in the usual way.

Let's define the operators of dielectric susceptibility $\chi$ and conductivity $\sigma$ of the considering media in the form of linear integration operators

$$\widehat{\chi }f\left(\overrightarrow{r},t\right)={\displaystyle \underset{-\infty }{\overset{t}{\int }}\chi \left(\overrightarrow{r},t\text{'}\right)}f\left(\overrightarrow{r},t\right){\psi }_P\left(t-t\text{'}\right)dt\text{'}\mathrm{and} \widehat{\sigma }f\left(\overrightarrow{r},t\right)={\displaystyle \underset{-\infty }{\overset{t}{\int }}\sigma \left(\overrightarrow{r},t\text{'}\right)}f\left(\overrightarrow{r},t\right){\psi }_J\left(t-t\text{'}\right)dt\text{'},$$

(13)

where $f\left(\overrightarrow{r},t\right)$ is the arbitrary continuous function of values for the coordinates and time. If $\chi \left(\overrightarrow{r},t^{\text{'}}\right)$ and $\sigma \left(\overrightarrow{r},t\right)$ are local susceptibility and conductivity of medium, then ${\psi }_P\left(t-t\text{'}\right)=-{\dot{\alpha }}_P\left(t-t\text{'}\right)$ and ${\psi }_J\left(t-t\text{'}\right)=-{\dot{\alpha }}_J\left(t-t\text{'}\right)$ are pulse-relaxation functions [5], also ${\alpha }_P\left(t-t\text{'}\right)$ and ${\alpha }_J\left(t-t\text{'}\right)$ are functions of delaying for polarization and current, which describe the reverse processes of relaxation for polarization $\overrightarrow{P}\left(\overrightarrow{r},t\right)$ and current $\overrightarrow{J}\left(\overrightarrow{r},t\right)$ accordingly.

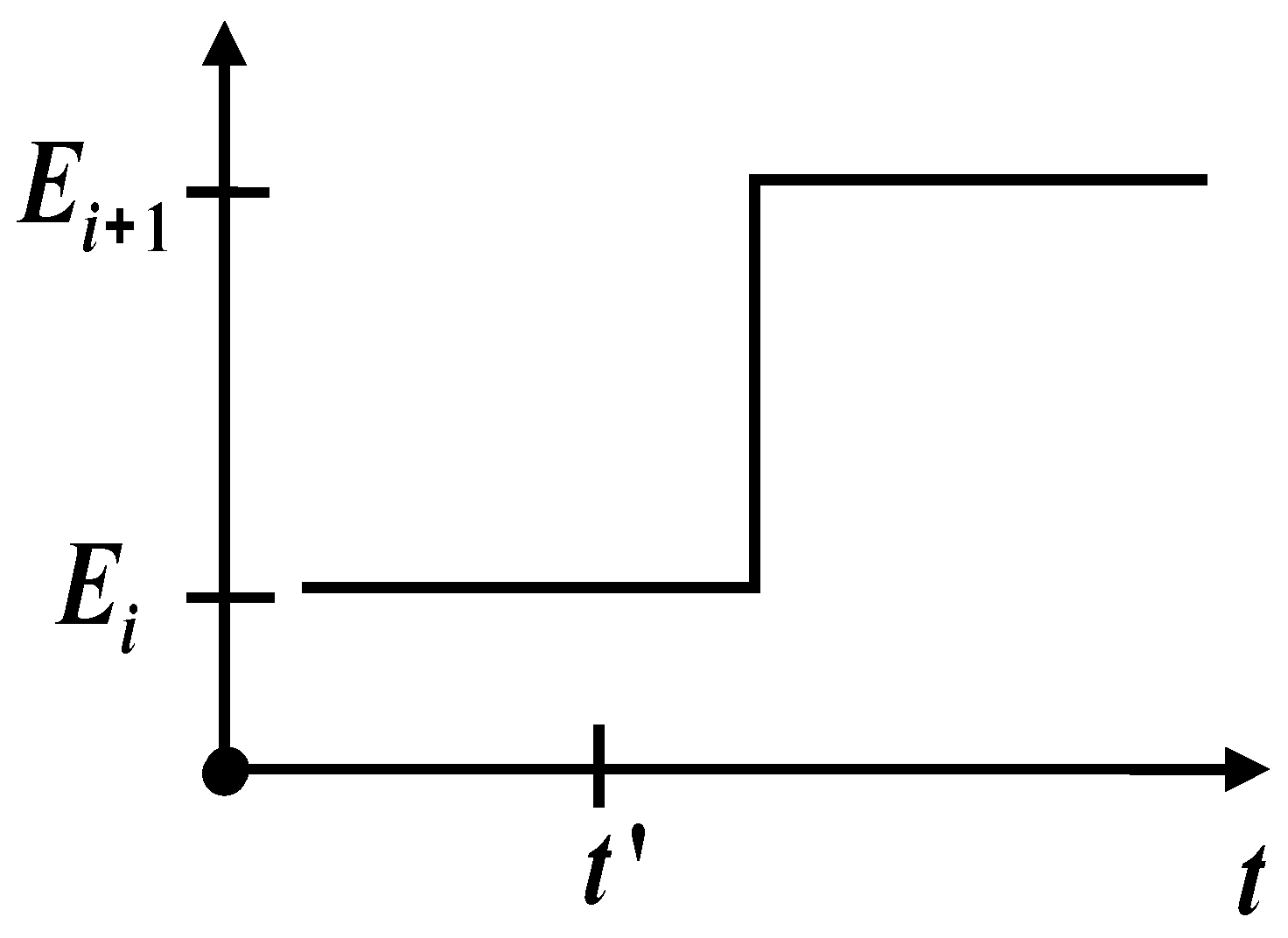
We are considering the linear homogeneous dielectric, for each point of which the principle of superposition of electromagnetic fields is satisfied. It is taking a possibility to modelling of time hopping (Figure 1) of electrical field $\Delta {\overrightarrow{E}}_i^{(+)}=-\Delta {\overrightarrow{E}}_i^{(-)}={\overrightarrow{E}}_{i+1}(\overrightarrow{r})-{\overrightarrow{E}}_i(\overrightarrow{r})>0$ into fixed point $\overrightarrow{r}$ of investigated medium relatively to constant quantity ${\overrightarrow{E}}_i(\overrightarrow{r})$ of electric field stretch into ranges of $\sigma$ - phase of porous material

$$\begin{array}{l}\overrightarrow{E}(\overrightarrow{r},t)={\overrightarrow{E}}_i(\overrightarrow{r})+\Delta {\overrightarrow{E}}_i^{(+)}(\overrightarrow{r})\tau (t-t\text{'})={\overrightarrow{E}}_i(\overrightarrow{r})-\Delta {\overrightarrow{E}}_i^{(-)}(\overrightarrow{r})\tau (t-t\text{'})=\\ \hspace{0.33em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\overrightarrow{E}}_{i+1}(\overrightarrow{r})-\Delta {\overrightarrow{E}}_i^{(+)}(\overrightarrow{r})\left[1-\tau (t-t\text{'})\right]\end{array},$$

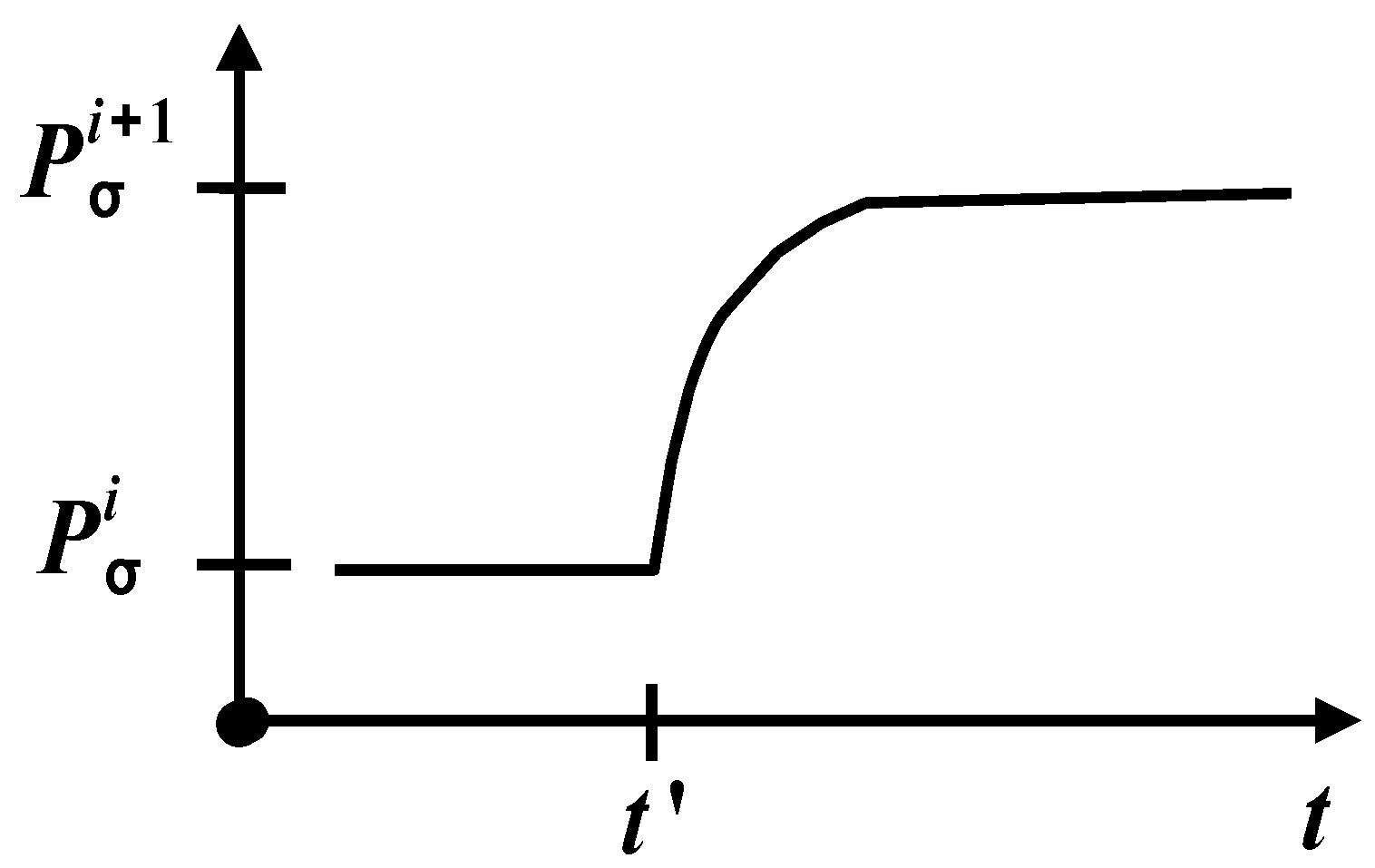
where $\tau (t)=\left\{0,t\le 0;1,t>0\right\}$ is the theta-function of Heaviside [8]. Then the dielectric response of substance for $\sigma$ - phase (Figure 2) can be defined by the relation

$$\begin{array}{l}{\overrightarrow{P}}_{\sigma }(\overrightarrow{r},t)={\epsilon }_0{\chi }_{\sigma }({\overrightarrow{E}}_{i+1}(\overrightarrow{r})-\Delta {\overrightarrow{E}}_i^{(+)}(\overrightarrow{r})\alpha (t-t^{\text{'}}))=\\ \hspace{0.33em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\epsilon }_0{\chi }_{\sigma }({\overrightarrow{E}}_{i+1}(\overrightarrow{r})+\Delta {\overrightarrow{E}}_i^{(-)}(\overrightarrow{r})\alpha (t-t^{\text{'}}))\hspace{0.33em}(t\ge t^{\text{'}})\end{array},$$

(14)

here $\alpha (t-t^{\text{'}})=1-\tau (t-t^{\text{'}})$ is the stepped function of response for polarization, ${\chi }_{\sigma }$ is the static susceptibility of $\sigma$-phase.

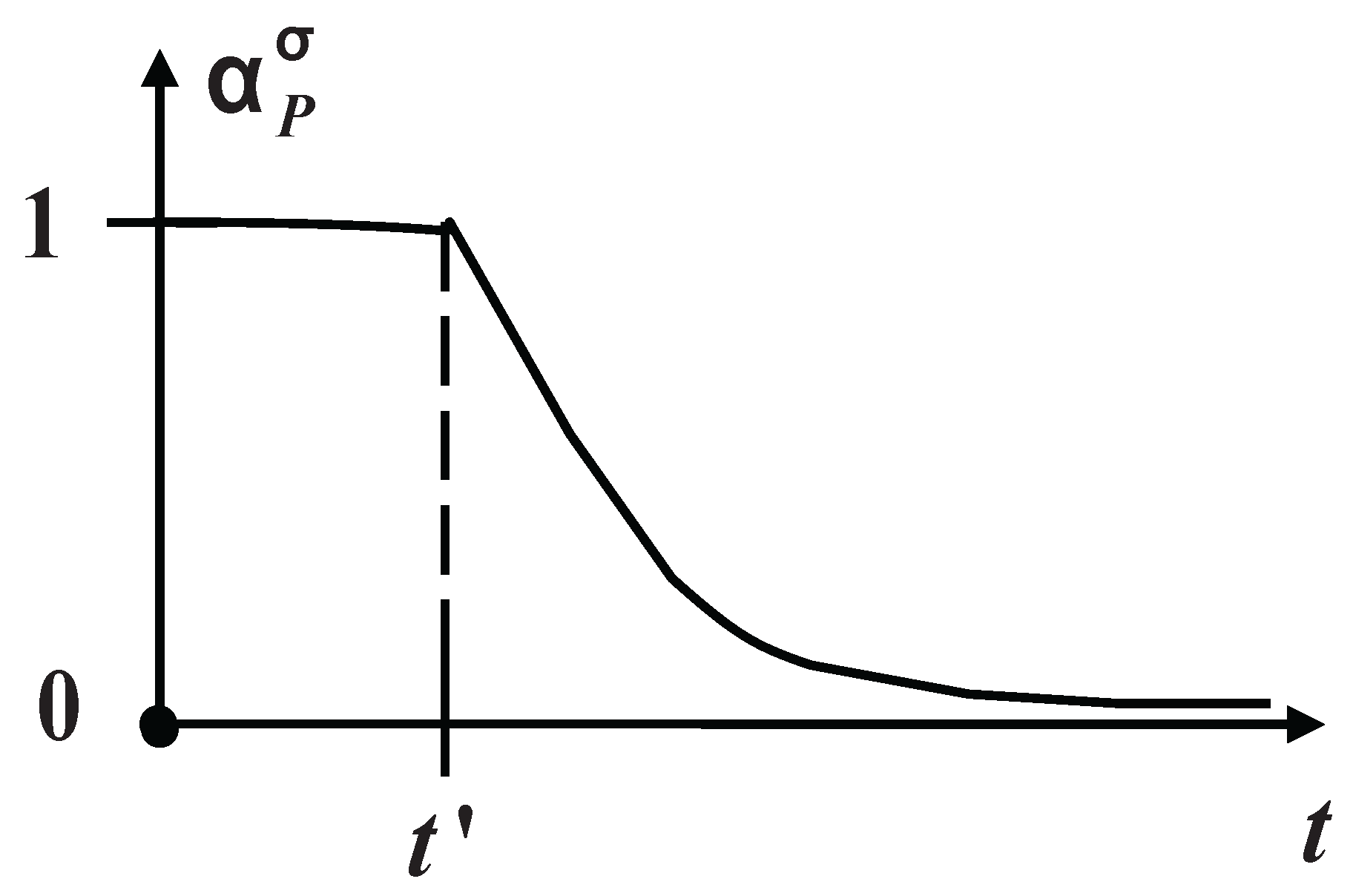
It should be noted, what defined abstractly the step response function of the polarization $\alpha$ for dielectric material of the $\sigma$-phase is displayed by the real function (Figure 3) of polarization delaying

Because$\alpha (\overline{t})=\left\{1,\hspace{0.33em}\overline{t}\le 0;0,\overline{t}>0\right\}$, where $\overline{t}=t-t\text{'}$ is the time offset symbol, when at $\overline{t}=0$ we get ${\alpha }_P^{\sigma }(0)=1$, and when $\overline{t}\to +\infty$ we have ${\alpha }_P^{\sigma }(+\infty )=0$, under executing [5] of a necessary condition ${\displaystyle \int {\alpha }_P^{\sigma }}(\overline{t})d\overline{t}=1$ of normalization.

In the case of the Debay`s type of relaxation [5] we receive the known classical relaxation relation

$${\overrightarrow{P}}_{\sigma }(\overrightarrow{r},t)={\overrightarrow{P}}_{\sigma }(\overrightarrow{r},0){\alpha }_P^{\sigma }(t)={\epsilon }_0{\chi }_{\sigma }\overrightarrow{E}(\overrightarrow{r},0){\alpha }_P^{\sigma }(t).$$

(15)

The local macroscopic field $\overrightarrow{E}(\overrightarrow{r},t)$ can be defined, as superposition of amplitude-vector (coordinate) fields ${\overrightarrow{E}}_i(\overrightarrow{r})$ through the time step-impulse function in the interval $t_i-\Delta t<t\le t_i$ at the arbitrary current $t$ value of time

$$\overrightarrow{E}(\overrightarrow{r},t)={\displaystyle \sum _i{\overrightarrow{E}}_i}(\overrightarrow{r})[\tau (t-t_i+\Delta t)-\tau (t-t_i)],$$

Then a vector of polarization for the medium of $\sigma$-phase the material have viewed

$${\overrightarrow{P}}_{\sigma }(\overrightarrow{r},t)={\epsilon }_0{\chi }_{\sigma }{\displaystyle \sum _i{\overrightarrow{E}}_i(\overrightarrow{r})({\alpha }_P^{\sigma }(t-t_i+\Delta t)-{\alpha }_P^{\sigma }(t-t_i))}.$$

Under boundary limit $\Delta t\to 0$ with considering of material properties for $\sigma$-phase we get the expression for determining of polarization vector

$${\overrightarrow{P}}_{\sigma }(\overrightarrow{r},t)={\epsilon }_0{\chi }_{\sigma }{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{E}(\overrightarrow{r},t^{\text{'}})}\left[-{\displaystyle \frac{\partial {\alpha }_p^{\sigma }(t-t^{\text{'}})}{\partial t}}\right]d{t}^{\text{'}}={\epsilon }_0{\chi }_{\sigma }{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{E}(\overrightarrow{r},t^{\text{'}})}{\psi }_P^{\sigma }(t-t^{\text{'}})d{t}^{\text{'}},$$

(16)

here ${\psi }_p^{\sigma }(t-t^{\text{'}})=-{\dot{\alpha }}_p^{\sigma }(t-t^{\text{'}})$ is the impulse-relaxation function for polarization of $\sigma$-phase.

Similarly by the mirroring of images Figure 1 and Figure 2 relaying to averaged hope of electric field stretch and current along the abscissa axis and shifting for modulus per unit of current relaxation values (see Figure 3) under inverse mapping along the axis we get the expression for determining of the polarization current vector for $\sigma$-phase of material

$${\overrightarrow{J}}_{\sigma }(\overrightarrow{r},t)={\sigma }_{\sigma }{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{E}(\overrightarrow{r},t^{\text{'}})}\left[-{\displaystyle \frac{\partial {\alpha }_j^{\sigma }(t-t^{\text{'}})}{\partial t}}\right]d{t}^{\text{'}}={\sigma }_{\sigma }{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{E}(\overrightarrow{r},t^{\text{'}})}{\psi }_J^{\sigma }(t-t^{\text{'}})d{t}^{\text{'}},$$

(17)

here ${\psi }_J^{\sigma }(t-t^{\text{'}})=-{\dot{\alpha }}_J^{\sigma }(t-t^{\text{'}})$ is the impulse-relaxation function for $\sigma$ -phase polarization current.

According to the local averaging method (see. Section 1, eqv. (6)) it is possible to define the averaged susceptibility $〈\chi 〉$ and conductivity $〈\sigma 〉$ into the local volume of averaging in the such way

$$〈\chi \left(\overrightarrow{x},\overline{t}\right)〉={\displaystyle \sum _{\sigma }{\theta }_{\sigma }}\left(\overrightarrow{x},t\right){\chi }_{\sigma }\left(\overrightarrow{x},\overline{t}\right)і 〈\sigma \left(\overrightarrow{x},\overline{t}\right)〉={\displaystyle \sum _{\sigma }{\theta }_{\sigma }}\left(\overrightarrow{x},t\right){\sigma }_{\sigma }\left(\overrightarrow{x},\overline{t}\right),$$

(18)

here ${\chi }_{\sigma }$ and ${\sigma }_{\sigma }$ is the specific values of susceptibility and conductivity, and${\theta }_{\sigma }\left(\overrightarrow{x},t\right)$ is the volume fraction of $\sigma$-phase correspondingly. Here the times of polarization $\overline{t}$ and heat and mass exchanges processes $t$ are separated because of the transience of polarization processes (${\displaystyle \frac{1}{{\theta }_{\sigma }(x,t)}}{\displaystyle \frac{\partial {\theta }_{\sigma }(x,t)}{\partial t}}<<\omega$, where $\omega$ is the fixed so match frequency of E.M.F. under microwave irradiation) relatively to the slow temporal changes in the heat and mass transfer phenomena.

Into approach of local macroscopic field [9] the space averaged kernels of relaxation for susceptibility and current into range of [4] can rewrite (see also Appendix) through approximate expressions

$$〈\chi 〉\left(\overrightarrow{x},t\right){\psi }_P\left(t-t\text{'}\right)={\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\psi }_P^{\sigma }\left(t-t\text{'}\right)\cong i\omega {\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)\left[1-{\alpha }_P^{\sigma }\left(t-t\text{'}\right)\right],$$

$$〈\sigma 〉\left(\overrightarrow{x},t\right){\psi }_J\left(t-t\text{'}\right)={\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\psi }_J^{\sigma }\left(t-t\text{'}\right)\cong -i\omega {\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)\left[1+{\alpha }_J^{\sigma }\left(t-t\text{'}\right)\right],$$

here ${\psi }_{\alpha }^{\sigma }\left(t-t\text{'}\right)$ and ${\alpha }_{\alpha }^{\sigma }\left(t-t\text{'}\right)$, where $\beta =\{P,J\}$ is the index of conventional designation for vectors of polarization $P$ and current $J$ relatively, the impulse-relaxation functions and functions of response for polarization and current of $\sigma$- phase.

According to (16) and (17) under applying of local averaging method [4] we receive the averaged vectors of the orientational polarization

$$\begin{array}{l}\overrightarrow{P}\left(\overrightarrow{x},t\right)={\displaystyle \underset{-\infty }{\overset{t}{\int }}\chi \left(\overrightarrow{x},t\right){\psi }_P\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)dt\text{'}=}\\ \hspace{0.33em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\epsilon }_0{\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right){\psi }_p^{\sigma }\left(t-t\text{'}\right)dt\text{'}}\end{array},$$

(19)

and the current of polarization into porous media

$$\begin{array}{l}\overrightarrow{J}\left(\overrightarrow{x},t\right)={\displaystyle \underset{-\infty }{\overset{t}{\int }}\sigma \left(\overrightarrow{x},t\right){\psi }_J\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}dt\text{'}\cong \\ \hspace{0.33em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\cong -i\omega {\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}\left[1+{\alpha }_J^{\sigma }\left(t-t\text{'}\right)\right]dt\text{'}\end{array},$$

(20)

here ${\chi }_{\sigma }\left(\omega \right)$ and ${\sigma }_{\sigma }\left(\omega \right)$ is the static susceptibility and conductivity of $\sigma$-phase, which are interconnected through the known [6] relation

$${\sigma }_{\sigma }\left(\omega \right)=i\omega {\epsilon }_0{\chi }_{\sigma }\left(\omega \right).$$

From the received expressions, the vectors of dielectric displacement and current into porous media take the form

$$\overrightarrow{D}\left(\overrightarrow{x},t\right)={\epsilon }_0{\displaystyle \underset{-\infty }{\overset{t}{\int }}{\psi }_D\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}dt\text{'}і \overrightarrow{J}\left(\overrightarrow{x},t\right)={\displaystyle \underset{-\infty }{\overset{t}{\int }}{\psi }_J\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}dt\text{'},$$

(21)

where

$${\psi }_D\left(t-t\text{'}\right)=\delta \left(t-t\text{'}\right)+{\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\psi }_p^{\sigma }\left(t-t\text{'}\right)$$

(22)

and

$${\psi }_J\left(t-t\text{'}\right)=-i\omega {\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)\left[1+{\alpha }_J^{\sigma }\left(t-t\text{'}\right)\right]$$

(23)

Are corresponding impulse-relaxation functions and $\delta \left(t-t\text{'}\right)$ is the Dirace [8] delta function.

Then the functions of delaying for dielectric displacement and polarization current (see Appendix) have the view

$${\alpha }_D\left(t-t\text{'}\right)=1-\tau \left(t-t\text{'}\right)+{\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\alpha }_p^{\sigma }\left(t-t\text{'}\right),$$

(24)

$${\alpha }_J\left(t-t\text{'}\right)=-i\omega {\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\alpha }_J^{\sigma }\left(t-t\text{'}\right)$$

(25)

$$(\underset{t\to t\text{'}}{\lim }{\alpha }_D\left(t-t\text{'}\right)=1+〈\chi 〉\left(\overrightarrow{x},t\right), \underset{t\to +\infty }{\lim }{\alpha }_J\left(t-t\text{'}\right)=-i\omega 〈\sigma 〉\left(\overrightarrow{x},t\right)),$$

where $〈\chi 〉\left(\overrightarrow{x},t\right)={\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)$ and $〈\sigma 〉\left(\overrightarrow{x},t\right)={\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)$ are defined above averaged susceptibility and conductivity accordingly.

During receiving of expressions (22) and (23) for impulse-relaxation functions is taken into account the join (12) between the polarization and current vectors as well, as also reverse relatively to polarization similarity to the relaxation properties of current. According to the definition (9) of generalized displacement vector of $\sigma$- phase the material on the base of relations (16) and (17) it is follows

$$\begin{array}{l}{\overrightarrow{D}}_{\sigma }^{\text{'}}\left(\overrightarrow{x},t\right)=\overrightarrow{D_{\sigma }}\left(\overrightarrow{x},t\right)+{\displaystyle \underset{-\infty }{\overset{t}{\int }}\overrightarrow{J_{\sigma }}\left(\overrightarrow{x},t^{\text{'}}\right)d{t}^{\text{'}}}=\\ \hspace{0.33em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\epsilon }_0{\displaystyle \underset{-\infty }{\overset{t}{\int }}{\psi }_D^{\sigma }\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}dt\text{'}+{\sigma }_{\sigma }{\displaystyle \underset{-\infty }{\overset{t}{\int }}{\displaystyle \underset{-\infty }{\overset{t^{\prime }}{\int }}{\psi }_J^{\sigma }\left(t^{\prime }-{t^{\prime }}^{\prime }\right)\overrightarrow{E}\left(\overrightarrow{x},{t^{\prime }}^{\prime }\right)}}d{t}^{\prime }d{t}^{\prime }\text{'}\end{array}.$$

In the way of integration by parts of second application of sum from the definition of impulse-response function, it is follows

$${\displaystyle \underset{-\infty }{\overset{t}{\int }}{\displaystyle \underset{-\infty }{\overset{t}{\int }}{\psi }_J^{\sigma }\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}}dt\text{'}={\displaystyle \underset{-\infty }{\overset{t}{\int }}\left(1-{\alpha }_J^{\sigma }\left(t-t\text{'}\right)\right)}\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)dt\text{'},$$

then

$${\overrightarrow{D}}_{\sigma }^{\text{'}}\left(\overrightarrow{x},t\right)={\epsilon }_0{\displaystyle \underset{-\infty }{\overset{t}{\int }}{\psi }_D^{\sigma }\left(t-t\text{'}\right)\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)}dt\text{'}+{\sigma }_{\sigma }{\displaystyle \underset{-\infty }{\overset{t}{\int }}\left(1-{\alpha }_J^{\sigma }\left(t-t\text{'}\right)\right)}\overrightarrow{E}\left(\overrightarrow{x},t\text{'}\right)dt\text{'}.$$

From this according to (19) with taking into account received expressions for impulse-response functions (22) and (23) it follows, that space averaged vector of generalized dielectric displacement can be defined in the such way

$$〈{\overrightarrow{D}}^{\text{'}}〉\left(\overrightarrow{x},t\right)={\epsilon }_0\left[1+〈\chi (\overrightarrow{x},t)〉R_P\left(\overrightarrow{x},t\right)\right]\overrightarrow{E}\left(\overrightarrow{r},t\right)+〈\sigma (\overrightarrow{x},t)〉\left[1-R_J\left(\overrightarrow{x},t\right)\right]\overrightarrow{E}\left(\overrightarrow{r},t\right),$$

here $R_P$ and $R_J$ are the relaxation products for polarization and current accordingly, which can be described by the following relations

$$\begin{array}{l}{R}_P\left(\overrightarrow{x},t\right)={\displaystyle \frac{1}{〈\chi (\overrightarrow{x},t)〉}}{\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\displaystyle \underset{-\infty }{\overset{t}{\int }}{\psi }_P^{\sigma }\left(t-t\text{'}\right)dt\text{'}}\cong \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\cong {\displaystyle \frac{i\omega }{〈\chi (\overrightarrow{x},t)〉}}{\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\displaystyle \underset{-\infty }{\overset{t}{\int }}\left[1-{\alpha }_P^{\sigma }\left(t-t\text{'}\right)\right]dt\text{'}}\end{array},$$

(26)

$$R_J\left(\overrightarrow{x},t\right)={\displaystyle \frac{1}{〈\sigma (\overrightarrow{x},t)〉}}{\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right){\displaystyle \underset{-\infty }{\overset{t}{\int }}{\alpha }_J^{\sigma }\left(t-t\text{'}\right)dt\text{'}},$$

(27)

here $〈\chi (\overrightarrow{x},t)〉$ and $〈\sigma (\overrightarrow{x},t)〉$ are averaged according to the relation (18) susceptibility and conductivity of porous body.

With taking into account the known relation ${\sigma }_{\sigma }\left(\omega \right)=i\omega {\epsilon }_0{\chi }_{\sigma }\left(\omega \right)$ [6] for $\sigma$-phase under condition of executing of averaged material or constitutive equation

$$〈\sigma (\overrightarrow{x},t)〉=i\omega {\epsilon }_0〈\chi (\overrightarrow{x},t)〉$$

On the mezoscopic level of the space averaging [4] we're going to more transparent for the physical sense equation

$$\begin{array}{l}〈{\overrightarrow{D}}^{\text{'}}〉\left(\overrightarrow{x},t\right)={\epsilon }_0\left[1+{\displaystyle \frac{〈\sigma (\overrightarrow{x},t)〉}{{\epsilon }_0}}\right]\overrightarrow{E}\left(\overrightarrow{r},t\right)+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+i\omega {\displaystyle \sum _{\sigma }{\chi }_{\sigma }}(\omega ){\theta }_{\sigma }(\overrightarrow{x},t){\displaystyle \underset{-\infty }{\overset{t}{\int }}\left\{1-\left[{\alpha }_P^{\sigma }\left(t-t^{\prime }\right)+{\alpha }_J^{\sigma }\left(t-t^{\prime }\right)\right]\right\}\overrightarrow{E}\left(\overrightarrow{r},t^{\prime }\right)d{t}^{\prime }}\end{array},$$

here ${\alpha }_P^{\sigma }\left(t-t^{\prime }\right)$ and ${\alpha }_J^{\sigma }\left(t-t^{\prime }\right)$ are relaxation functions for polarization (24) and current (25), which needs to determine.

2.2. The Harmonic Approach of Field Amplitude

Into harmonic approach of electric and magnetic fields amplitudes

$$\Phi \left(\overrightarrow{r},t\right)=\mathrm{Re}\left[{\Phi }_{*}\left(\overrightarrow{r},t\right)e^{i\omega t}\right]\equiv \mathrm{Re}\left[{\Phi }_{*}^t\left(\overrightarrow{r}\right)e^{i\omega t}\right],, (\Phi =\left\{\overrightarrow{E},\overrightarrow{H}\right\})$$

(28)

where ${\Phi }_{*}\left(\overrightarrow{r},t\right)\equiv {\Phi }_{*}^t\left(\overrightarrow{r}\right)$ are complex amplitudes, which light varying with the time $t$ function due to moving of liquid phases into porous skeleton, according to the local view of equations E.M.F. (10a) the averaged (mezoscopic) equation are received

$$\begin{array}{c}\overrightarrow{\nabla }\times {\overrightarrow{E}}_{*}^t\left(\overrightarrow{x}\right)=-i{\mathsf{\omega }\mathsf{\mu }}_0{\overrightarrow{H}}_{*}^t\left(\overrightarrow{x}\right),\overrightarrow{\nabla }\times {\overrightarrow{H}}_{*}^t\left(\overrightarrow{x}\right)=i\omega {\overline{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right){\overrightarrow{E}}_{*}^t\left(\overrightarrow{x}\right),\\ \overrightarrow{\nabla }\cdot {\overrightarrow{E}}_{*}^t\left(\overrightarrow{x}\right)=0,\overrightarrow{\nabla }\cdot {\overrightarrow{H}}_{*}^t\left(\overrightarrow{x}\right)=0,\end{array}$$

(29)

with corresponding material relations

$$\begin{array}{c}{\overrightarrow{D}}_{*}^{\mathrm{t}}\left(\overrightarrow{x}\right)={\overline{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right){\overrightarrow{E}}_{*}^t\left(\overrightarrow{x}\right),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overrightarrow{B}}_{*}^t\left(\overrightarrow{x}\right)={\mu }_0{\overrightarrow{H}}_{*}^t\left(\overrightarrow{x}\right),\end{array}$$

(30)

where ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)={\overline{\epsilon }}_t\left(\overrightarrow{x},\omega \right)+{\sigma }_t\left(\overrightarrow{x},\omega \right)/i\omega$ and ${\overline{\epsilon }}_t\left(\overrightarrow{x},\omega \right)={\overline{\epsilon }}_t^{\text{'}}\left(\overrightarrow{x},\omega \right)-i{\overline{\epsilon }}_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)$ are effective dynamical generalized and local complex dielectric permeability (C.D.P), ${\sigma }_t\left(\overrightarrow{x},\omega \right)={\sigma }_t^{\text{'}}\left(\overrightarrow{x},\omega \right)-i{\sigma }_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)$ is the local complex conductance.

Also

$${\chi }_t\left(\overrightarrow{x},\omega \right)={\displaystyle \sum _{\sigma }{\chi }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)L\left[{\psi }_P^{\sigma }\left(t-t\text{'}\right)\right],$$

(31)

$${\sigma }_t\left(\overrightarrow{x},\omega \right)={\displaystyle \sum _{\sigma }{\sigma }_{\sigma }\left(\omega \right)}{\theta }_{\sigma }\left(\overrightarrow{x},t\right)\left(1+L\left[{\alpha }_J^{\sigma }\left(t-t\text{'}\right)\right]\right)$$

are corresponding Laplace [8] images $L\left[f\left(\overrightarrow{r},s\right)\right]={\displaystyle \underset{0}{\overset{+\infty }{\int }}f\left(\overrightarrow{r},t\right)}{e}^{-\mathrm{s}\hspace{0.17em}\mathrm{t}}\mathrm{dt}$ $\left(s=\gamma +i\omega ,\gamma \to 0\right)$ from averaged (22) and (23) relaxation functions.

Because ${\overline{\epsilon }}_t^{\text{'}}\left(\overrightarrow{x},\omega \right)={\epsilon }_0\left\{1+{\chi }_t^{\text{'}}\left(\overrightarrow{x},\omega \right)\right\}$ і ${\overline{\epsilon }}_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)={\epsilon }_0{\chi }_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)$, so real ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}\left(1\right)}\left(\overrightarrow{x},t\right)=\mathrm{Re}\left[{\overline{\epsilon }}_{\omega }\left(\overrightarrow{x},t\right)\right]$ and imaginary ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}\left(2\right)}\left(\overrightarrow{x},t\right)=\mathrm{Im}\left[{\overline{\epsilon }}_{\omega }^{\text{'}}\left(\overrightarrow{x},t\right)\right]$ part of generalized dynamic (C.D.P.) and ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)$ takes the form

$${\overline{\epsilon }}_{\omega }^{\mathrm{eff}\left(1\right)}\left(\overrightarrow{x},\omega \right)={\epsilon }_0\left\{1+{\chi }_t^{\text{'}}\left(\overrightarrow{x},\omega \right)\right\}-{\displaystyle \frac{{\sigma }_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)}{\omega }}, {\overline{\epsilon }}_{\omega }^{\mathrm{eff}\left(2\right)}\left(\overrightarrow{x},\omega \right)={\epsilon }_0\hspace{0.17em}{\chi }_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)+{\displaystyle \frac{{\sigma }_t^{\text{'}}\left(\overrightarrow{x},\omega \right)}{\omega }},$$

(32)

here ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)$ is the effective-generalized complex dynamic dielectric permittivity (C.D.D.P).

By the using of definition (9) of the generalized dielectric displacement vector and complex amplitudes (28) of field, the material equation (30) in the case of composite bodies with low electrical conductivity (C.B.L.C) we can define trough relation

$${\overrightarrow{D}}_{*}^{\text{'}t}(\overrightarrow{r})={\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t){\overrightarrow{E}}_{*}^t(\overrightarrow{r}),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overrightarrow{B}}_{*}^t(\overrightarrow{r})={\mu }_0{\overrightarrow{H}}_{*}^t(\overrightarrow{r}),$$

(33)

where ${\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},\omega )={\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},\omega )-i{\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},\omega )$ is generalized complex dynamical dielectric permeability (G.C.D.D.P), ${\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},\omega )$ and ${\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},\omega )$ are the real and imaginary parts correspondingly.

Because the joules heat exchanges was missing or neglected, so takes ${\sigma }_t^{\text{'}}\left(\overrightarrow{x},\omega \right)=\sigma \left(\overrightarrow{x},\omega \right)$ and ${\sigma }_t^{\text{'}\text{'}}\left(\overrightarrow{x},\omega \right)=0$. According to the relation (30) into taken definitions, we receives

$${\overline{\epsilon }}_t^{\text{'}}(\overrightarrow{r},\omega )={\epsilon }_0\left\{1+{\overline{\chi }}_t^{\text{'}}(\overrightarrow{r},\omega )\right\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{\epsilon }}_t^{\text{'}\text{'}}(\overrightarrow{r},\omega )={\epsilon }_0{\overline{\chi }}_t^{\text{'}\text{'}}(\overrightarrow{r},\omega ),$$

(34)

where real ${\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},t)=\mathrm{Re}[{\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)]$ and imaginary ${\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},t)=\mathrm{Im}\left[{\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)\right]$ part of generalized complex dynamic dielectric permittivity ${\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)$ (G.C.D.D.P.) (33) have the view

$${\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},t)\equiv {\overline{\epsilon }}_t^{\text{'}}(\overrightarrow{r},\omega )={\epsilon }_0\left\{1+{\overline{\chi }}_t^{\text{'}}(\overrightarrow{r},\omega )\right\}, {\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},t)\equiv {\overline{\epsilon }}_t^{\text{'}\text{'}}(\overrightarrow{r},\omega )={\epsilon }_0{\overline{\chi }}_t^{\text{'}\text{'}}(\overrightarrow{r},\omega )+{\displaystyle \frac{\sigma (\overrightarrow{r},\omega )}{\omega }},$$

(35)

here${\overline{\epsilon }}_t(\overrightarrow{r},\omega )={\overline{\epsilon }}_t^{\text{'}}(\overrightarrow{r},\omega )-i\hspace{0.17em}{\overline{\epsilon }}_t^{\text{'}\text{'}}(\overrightarrow{r},\omega )$ is the local complex dynamical permeability.

Also according (28) the dispersion relation [12] are satisfied

$${\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},t)={\overline{\epsilon }}_{-\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},t),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},t)=-{\overline{\epsilon }}_{-\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},t),$$

(36)

here ${\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)={\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},t)-i\hspace{0.17em}{\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},t)$ is the generalized complex dynamical dielectric permeability (G.C.D.D.P).

Under known material or constitutive relations for field equation (33) into (C.B.L.C) relatively to complex amplitudes ofE.M.F. (10a) oтримуємo у наступнoму вигляді

$$\begin{array}{l}\overrightarrow{\nabla }\times {\overrightarrow{E}}_{*}^t(\overrightarrow{r})=-i\omega {\mu }_0{\overrightarrow{H}}_{*}^t(\overrightarrow{r}),\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{\nabla }\times {\overrightarrow{H}}_{*}^t(\overrightarrow{r})=i\omega {\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t){\overrightarrow{E}}_{*}^t(\overrightarrow{r})\\ \overrightarrow{\nabla }\times {\overrightarrow{D}}^{\text{'}}{}_{*}{}^t(\overrightarrow{r})=\overrightarrow{\nabla }\cdot \left[{\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t){\overrightarrow{E}}_{*}^t(\overrightarrow{r})\right]=0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\overrightarrow{\nabla }\cdot {\overrightarrow{H}}_{*}^t(\overrightarrow{r})=0\end{array},$$

(37)

where ${\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)={\overline{\epsilon }}_{\omega }^{\text{'}\left(1\right)}(\overrightarrow{r},t)-i\hspace{0.17em}{\overline{\epsilon }}_{\omega }^{\text{'}\left(2\right)}(\overrightarrow{r},t)$ is the generalized complex dynamical dielectric permeability (G.C.D.D.P), which is defined according to equation (35) under conditions of satisfied of dispersion (36) relations.

2.3. The Space Averaged Equations of Electromagnetic Field

Because into multiphase porous cell electro-physical characteristics change like jumpy on the surface separation of two phases, so generalized complex (dynamical) dielectric permittivity (G.C.D.D.P) ${\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)$ can not be the continues function of coordinate. In general the last one can be defined by the characteristic (phase) function ${\vartheta }_{\sigma }$ (here $\sigma =\left\{S,L,G\right\}$ is point to the index of phase), which is defined according to known relation (Section 1, eqv. (1), through this relation

$${\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)={\epsilon }_{с}^S(\omega ){\vartheta }_S(\overrightarrow{r},t)+{\epsilon }_c^L(\omega ){\vartheta }_l(\overrightarrow{r},t)+{\epsilon }_c^G(\omega ){\vartheta }_G(\overrightarrow{r},t),$$

(38)

where ${\epsilon }_c^{\sigma }(\omega )={\epsilon }_{\sigma }(\omega )+{\sigma }_{\sigma }/i\omega$ is the generalized complex dynamical dielectric permeability (G.C.D.D.G.) for $\sigma$-phase (here ${\sigma }_{\sigma }$ is conductivity of $\sigma$-фази). Because of this the characteristics of field, which is included into the equations (37) of electrodynamics also will be stepping like functions of coordinate. To describe the electromagnetic field in a porous cell, as in a continuous medium by continuous functions, we will use the methods of the theory of local spatial averaging [6]. For this purpose, we assume that the equations of electrodynamics and material relations relative to the specified average (effective) quantities have the same form as in the case of a single-phase (continuous) medium, i.e., they are formally equivalent. Formal equivalence of equations is ensured by fulfilling boundary conditions (10b) at the interface of two media on a microscopic scale at each (current) moment of time, and formal equivalence of material relations is ensured by defining effective electro physical characteristics. Such effective characteristics are established within the averaging region $\Omega$ (R.E.V) [2] and are determined through local properties of the environment based on certain geometric model considerations.

Let's review the simple example of averaging the material relation $\overrightarrow{\nabla }\times {\overrightarrow{D}}^{\text{'}}{}_{*}{}^t(\overrightarrow{r})=\overrightarrow{\nabla }\cdot \left[{\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t){\overrightarrow{E}}_{*}^t(\overrightarrow{r})\right]$, which is the part of equation of E.M.F (37) rewriting relatively to complex amplitudes (28) of filed. Suppose, that into each point of averaging area R.E.V. the electrical field is potential, i.e., $\overrightarrow{E}(\overrightarrow{r},t)=-)\psi (\overrightarrow{r},t)$ [10] $\overrightarrow{E}(\overrightarrow{r},t)=\mathrm{Re}\left[{\overrightarrow{E}}_{*}(\overrightarrow{r},t)\right]=\mathrm{Re}\left[{\overrightarrow{E}}_{*}^t(\overrightarrow{r})e^{i\omega t}\right]$), where $\psi (\overrightarrow{r},t)=\mathrm{Re}\left[{\psi }_{*}^t(\overrightarrow{r})e^{i\omega t}\right]$is the dynamical potential and ${\psi }_{*}^t(\overrightarrow{r})$ is the complex amplitude of dynamical potential. Then joining between complex amplitudes of the generalized dielectric displacement and the stretch of electric field have the view

$${\overrightarrow{D}}^{\text{'}}{}_{*}{}^t(\overrightarrow{r})={\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t){\overrightarrow{E}}_{*}^t(r)=-{\overline{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)){\psi }_{*}^t(\overrightarrow{r}).$$

(39)

According to approach of local macroscopic field into area of averaging $\Omega$ (R.E.V) in each moment of time $t$ the field is homogeneous, i.e., ${\overrightarrow{E}}_{*}^t(\overrightarrow{r})={\overrightarrow{E}}_{*0}^t$, where ${\overrightarrow{E}}_{*0}^t$ is the complex amplitude of external field. Then the expression for amplitude of dynamic potential in this case have the view ${\psi }_{*}^t(\overrightarrow{r})=-{\overrightarrow{E}}_{*0}^t\cdot \overrightarrow{r}$ ($\overrightarrow{r}\in \Omega$).

We are defining the generalized complex dynamical dielectric permeability (G.C.D.D.P) of the cell ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}}(t)$ on the base of equality, that expresses the formal equivalence of material relations

$$\overrightarrow{D}{\text{'}}_{*}^t(\overrightarrow{x})={\overline{\epsilon }}_{\omega }^{\mathrm{eff}}(\overrightarrow{x},t){\overrightarrow{E}}_{*}^t(\overrightarrow{x})=-{\overline{\epsilon }}_{\omega }^{eff}(\overrightarrow{x},t)\nabla {\psi }_{*}^t(\overrightarrow{x}).$$

(40)

According to definition of space average quantity (see Section 1, eqv. (6)) and reviewing relations we have

$$⟨{\overrightarrow{D}}_{*}^{\text{'}t}⟩\left(\overrightarrow{x}\right)=-{\displaystyle \frac{1}{V_R}}{\int }_{V_R}{\bar{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)\nabla {\psi }_{*}^t\left(\overrightarrow{r}\right)d{V}_R={\overrightarrow{E}}_{*0}^t{\sum }_{\sigma }{\theta }_{\sigma }(\overrightarrow{x},t){\epsilon }_c^{\sigma }\left(\omega \right).$$

(41)

Here is taking into account, that space averaged from the gradient of dynamic potential will be

$$⟨\nabla {\psi }_{*}^t⟩\left(\overrightarrow{x}\right)={\displaystyle \frac{1}{V_R}}{\int }_{V_R}\nabla {\psi }_{*}^t\left(\overrightarrow{r}\right)d{V}_R=-{\overrightarrow{E}}_{*0}^t.$$

(42)

After substitution of (41) and (42) into definition of G.C.D.D.P (40) we gets

$${\bar{\epsilon }}_{\omega }^{\mathrm{eff}}(\overrightarrow{x},t)={\sum }_{\sigma }{\theta }_{\sigma }(\overrightarrow{x},t){\epsilon }_c^{\sigma }\left(\omega \right),$$

(43)

where ${\bar{\epsilon }}_{\omega }^{eff}(\overrightarrow{x},t)={\bar{\epsilon }}_t\left(\omega \right)+\bar{\sigma }/i\omega$, here ${\bar{\epsilon }}_t\left(\omega \right)$ and $\bar{\sigma }$ is the effective complex dynamical dielectric permeability and conductivity of the reviewed cell and t is the index which points on the light time dependence of physical quantity.

From the expression (43) it is follows, that quantity ${\overline{\epsilon }}_{\omega }^{\mathrm{eff}}$ subject to neglect of dispersion phenomena into the material depends on constant frequency of external microwave irradiation, , dielectric permeability and volume fraction of cell phases

$$\begin{array}{c}{\bar{\epsilon }}_{\omega }^{\mathrm{eff}}(\overrightarrow{x},t)=f(\omega ;{\epsilon }_c^{\sigma },{\theta }_{\sigma }),\hspace{0.33em}\sigma =\left\{S,L,G\right\}\\ {\epsilon }_c^{\sigma }={\epsilon }_c^{\sigma }\left(\omega \right){\theta }_{\sigma }={\theta }_{\sigma }(\overrightarrow{x},t)\end{array}.$$

It should be noted that under the condition of weak variability of the volumetric characteristics of the porous material the E.G.C.D.D.P. ${\bar{\epsilon }}_{\omega }^{eff}(\overrightarrow{x},t)\cong {\bar{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x}\right)$ can be reviewed, as constant physical quantity in the volume of averaging Ω (R.E.V), which takes the constant into the time interval values.

Taking into account the definition of E.G.C.D.D.P (39) into harmonic approach of local field (28) after applying described above the homogenization [4] on the mezoscopic level into range of R.E.V. considering approach of not interacting clusters we get (see Section 2, subsection 2, eqv. (37)) the averaged equation of field

$$\overrightarrow{\nabla }\times ⟨{\overrightarrow{E}}_{*}^t\left(\overrightarrow{r}\right)⟩=-i\omega {\mu }_0⟨{\overrightarrow{H}}_{*}^t\left(\overrightarrow{r}\right)⟩,\overrightarrow{\nabla }\times ⟨{\overrightarrow{H}}_{*}^t\left(\overrightarrow{r}\right)⟩=i\omega {\bar{\epsilon }}_{\omega }^{\text{'}}(\overrightarrow{r},t)⟨{\overrightarrow{E}}_{*}^t\left(\overrightarrow{r}\right)⟩\overrightarrow{\nabla }\times ⟨{\overrightarrow{E}}_{*}^t\left(\overrightarrow{r}\right)⟩=0,\overrightarrow{\nabla }\cdot ⟨{\overrightarrow{H}}_{*}^t\left(\overrightarrow{r}\right)⟩=0$$

(44)

where $\Phi (\overrightarrow{x},t)=\mathrm{Re}\left[{\Phi }_{*}^t\left(\overrightarrow{x}\right)\right]$ ($\Phi =\left\{\overrightarrow{E},\overrightarrow{H}\right\}$) and ${\bar{\epsilon }}_{\omega }^{\mathrm{eff}}(\overrightarrow{x},t)$ are the light (slowly) changed functions of coordinate and ${\Phi }_{*}^t\left(\overrightarrow{x}\right)$are the complex amplitudes of Е.M.F. into the porous cell. Here time t have the sense of parameter with usage of which can be taken into account the moving of phases.

When obtaining the averaged field equations (44), a relatively simple method of finding the effective electro physical characteristics (the method of local spatial averaging) of a multiphase porous cell was used. Interesting comparative results of the dependence of the G.C.D.D.P on the internal geometry or structure of the composite material of the sample [2] are highlighted in the author's article. For a more adequate description, it is necessary to take into account the dependence of E.G.C.D.D.P not only on the dielectric properties of the phases of the cell, but also on its local microstructure [11], the interaction between phase inclusions [12,13], and their geometric shape and orientation [14].

3. Propagation of Electromagnetic Waves

According to the system of averaged equations E.M.F (44) the wave equation for the Т.Е.М (Transference Electromagnetic Wave) for monochromatic wave in the terms of electric field strength into C.B.L.C have the view

$${\partial }_x^2⟨{\overrightarrow{E}}_{*}^t⟩\left(\overrightarrow{x}\right)+k_0^2{\left[{\bar{n}}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)\right]}^2⟨{\overrightarrow{E}}_{*}^t⟩\left(\overrightarrow{x}\right)=0,$$

(45)

here ${\bar{n}}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},\omega \right)={\bar{k}}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)/k_0=\sqrt{{\bar{\epsilon }}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)}$ is the complex refractive index, ${\bar{k}}_{\omega }^{\mathrm{eff}}\left(\overrightarrow{x},t\right)$ is the effective wave vector into the porous (inhomogeneous) media, $k_0=\omega \sqrt{{\mu }_0{\epsilon }_0}=\omega /c_0$ (where $c_0=1/\sqrt{{\mu }_0{\epsilon }_0}$ is the velocity of light) is the wave vector of electromagnetic wave into vacuum, $\omega =2\pi f$ is the angle frequency of E.M.F. (f is the lineal frequency), μ₀ and ε₀ are correspondingly the magnate and electric constant into vacuum. The analytical solving of such equation is into details described by the author of this paper [15], where is demonstrated the possibility of applying of Wentzel-Kramers-Brillouin (W.K.B.) [16,17] method for founding the analytical solution of wave equation (45) into approach of slowly varying refractive properties of the T.E.M. wave.

4. Compatibility Conditions of the Electromagnetic Field Equations

The closed-form electrodynamic equations were obtained under the conditions of weak variation of the bulk (phase) and dielectric (wave) properties of a three-phase porous wetted material.

$${\displaystyle \frac{1}{{\theta }_{\sigma }(x,t)}}{\displaystyle \frac{\partial {\theta }_{\sigma }(x,t)}{\partial t}}<<{\omega }_0 \mathrm{і} {\displaystyle \frac{1}{{\bar{n}}_{\omega }^{\mathrm{e}\mathrm{f}\mathrm{f}}(x,t)}}{\displaystyle \frac{\partial {\bar{n}}_{\omega }^{\mathrm{e}\mathrm{f}\mathrm{f}}(x,t)}{\partial x}}<<k_{\omega }^{\mathrm{e}\mathrm{f}\mathrm{f}}(x,t),$$

(46)

As well as condition

$${\lambda }_{\omega }^{\mathrm{eff}}(x,t)={\displaystyle \frac{2\pi {\upsilon }_{\omega }^{\mathrm{eff}}(x,t)}{{\omega }_0}}>>l,$$

which determines the possibility of using the effective macroscopic field approximation in the study (determination) of the effective electro physical properties of a porous material according to the method of local spatial averaging.

Here $k_{\omega }^{\mathrm{eff}}(x,t)=2\pi /{\lambda }_{\omega }^{\mathrm{eff}}(x,t)$ and ${\upsilon }_{\omega }^{\mathrm{eff}}(x,t)=c_0/{\bar{n}}_{\omega }^{\mathrm{eff}}(x,t)$ is the wave vector and phase velocity of propagation the electromagnetic (T.E.M.) wave in the modelling media, ${\bar{n}}_{\omega }^{\mathrm{eff}}(x,t)$ is the effective value of refractive index, ${\theta }_{\sigma }(x,t)$ is the volume fraction f $\sigma$-phase, ${\omega }_0$ in the constant angle frequency the microwave field, $l$ is the characteristic length of the volume $\Omega$ (R.E.V) for space averaging.