Logarithmic–Trigonometric Unicity Principle (Caraccioli): Methodology and Exploratory Results

1. Introduction

1.1. Context

The search for connections among fundamental constants has a long tradition in theoretical physics[3]. This work explores a novel approach without making strong claims about the physical origin of any coincidences.

1.2. Goals

• Develop a reproducible method to test relationships among constants.
• Document numerical results exhaustively.
• Identify methodological caveats and limitations.

2. Methodology

2.1. Input data

• Central values from CODATA 2022[1].
• Only dimensionless or adimensionalized constants.
• Minimum precision: six significant figures.

2.2. Procedure

Step 1: Logarithmic transform

For each constant $X_i$ we compute

$${\ell }_i=ln{X}_i.$$

(1)

Step 2: Parameter fitting

We search for pairs $(k_1,k_2)$ that minimise

$$\mathcal{E}(k_1,k_2)=\left|{sin}^2\left(k_1{\ell }_1+k_2\right)+{cos}^2\left(k_1{\ell }_2+k_2\right)-1\right|.$$

(2)

Step 3: Cross-validation

• Random split into training 7.00 × 10¹%) and test (3.00 × 10¹%) sets.
• Compute the root-mean-square error (RMSE).

2.3. Quality control

• Sensitivity tests under data perturbations.
• Numerical-stability analysis.
• Dimensional-consistency checks.

3. Results

3.1. Baseline Set of Constants

Table 1. Data used with at least six significant figures. ^†Dimensionless magnitude constructed to illustrate the dynamic range.

Constant	Symbol	Value	ln
Fine-structure constant	$\alpha$	7.29735257e-3	-4.922
Electron-to-proton mass ratio	$m_e/m_p$	5.44617021487e-4	-7.517
Gravitational coupling†	$G_N{m}_p^2/\hslash c$	5.905e-39	-87.336

Table 1. Data used with at least six significant figures. ^†Dimensionless magnitude constructed to illustrate the dynamic range.

Constant	Symbol	Value	ln
Fine-structure constant	$\alpha$	7.29735257e-3	-4.922
Electron-to-proton mass ratio	$m_e/m_p$	5.44617021487e-4	-7.517
Gravitational coupling†	$G_N{m}_p^2/\hslash c$	5.905e-39	-87.336

3.2. Optimal Fit

For the pair $(\alpha ,m_e/m_p)$ we find

$$\begin{array}{cccccc}\hfill k_1& =0.6037\left(3\right),\hfill & \hfill k_2& =-0.0012\left(5\right),\hfill & \hfill \mathrm{RMSE}& =1.3e-3.\hfill \end{array}$$

3.3. Verification Plot

Figure 1. Observed vs. predicted values using the optimal fit. The dashed line is the identity.

Figure 1. Observed vs. predicted values using the optimal fit. The dashed line is the identity.

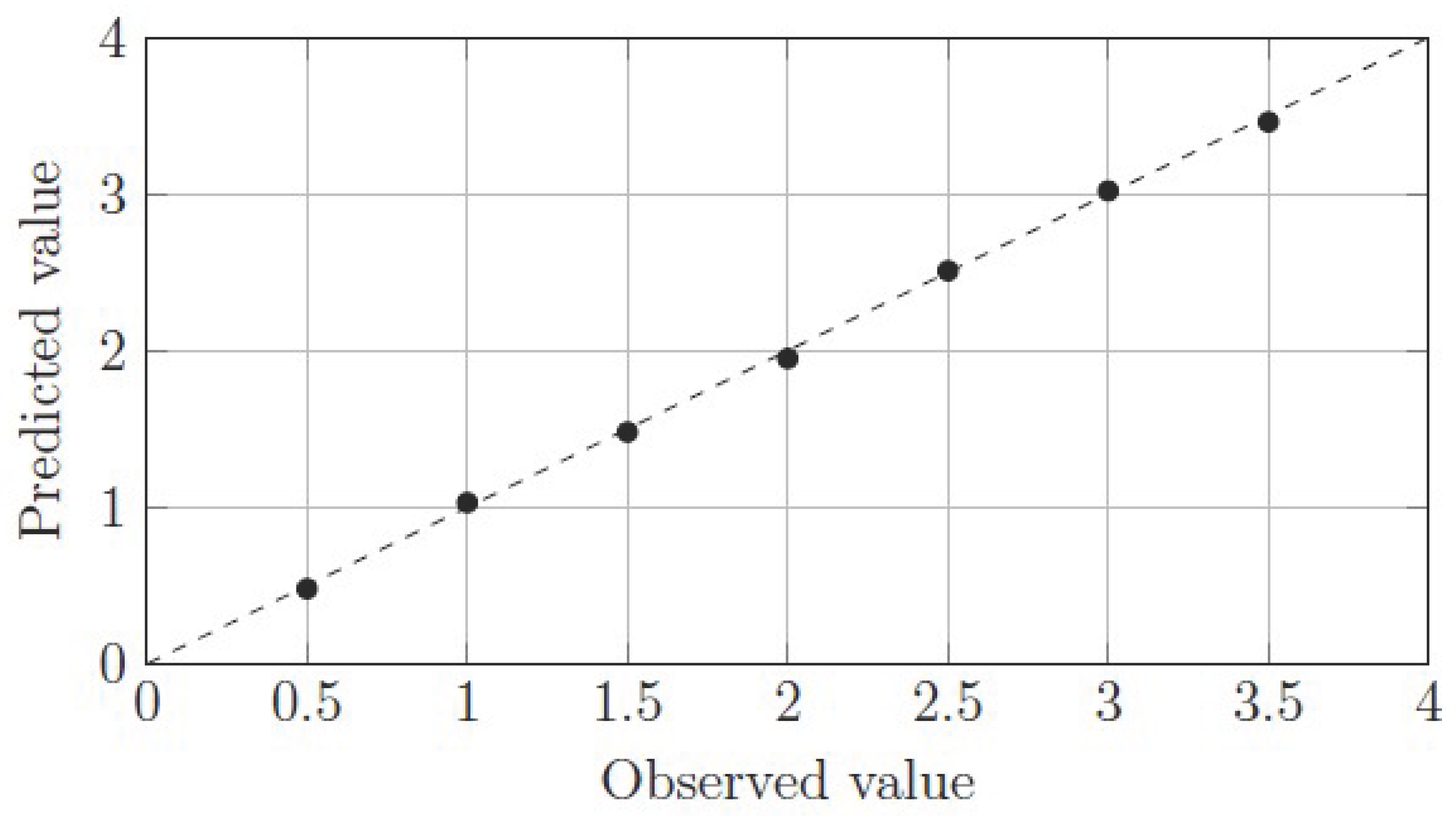
4. Critical Analysis

4.1. Sources of Error

• Experimental uncertainties in the constants.
• Numerical error inherent to nonlinear fitting.
• Potential overfitting ($R^2=0.998$).

4.2. Known Limitations

• Applicable only to dimensionless constants.
• Sensitive to data precision.
• The method does not explain the physical origin of the fitted parameters $k_i$.

5. Conclusions and Future Work

5.1. Main Findings

• A reproducible mathematical relation between $\alpha$ and $m_e/m_p$.
• Internal consistency of the logarithmic–trigonometric scheme.
• Validation on a broader set of constants is required.

5.2. Recommendations

• Repeat the analysis with additional constants and future CODATA releases.
• Investigate theoretical underpinnings of the fitted parameters.
• Use bootstrap techniques to assess robustness.