A Proof of the Reverse Isoperimetric Inequality Using a Geometric-Analytic Approach

1. Introduction

Extended black hole thermodynamics [1,2,3] provides a richer structure of black hole thermodynamics by identifying the cosmological constant $\Lambda$ with pressure as

$$P=-{\displaystyle \frac{\Lambda }{8\pi }}$$

(1)

This is possible for the AdS case for which we have $\Lambda <0$, which implies that $P>0$ as required on physical grounds. The volume is given as

$$\Theta =-{\displaystyle \frac{V_{D-2}{r}_h^{D-1}}{(D-1)}},$$

(2)

where $V_{D-2}$ is the volume of unit sphere and $r_h$ is the horizon radius. This leads to the modified first law with a varying cosmological constant as

$$\delta M={\displaystyle \frac{\kappa }{8\pi G}}\delta A+{\displaystyle \frac{\Theta }{8\pi G}}\delta \Lambda .$$

(3)

$\kappa$ is the surface gravity given as ($k^a$ is the Killing vector)

$$k^a{\nabla }_a{k}^b=\kappa k^b.$$

(4)

The modified first law points to the mass of the AdS black hole as being the enthalpy of spacetime [1]. This has given rise to interesting phenomena concerning black holes, such as Van der Waals fluids [4,5], and heat engines [6].

A varying cosmological constant has been shown to arise from higher-dimensional bulk effects, in which case the varying brane tension $\tau$ induces extended thermodynamics on the brane [7]. The modified first law has been shown to arise robustly via the Extended Iyer-Wald formalism in [8]. In the context of extended phase space, an interesting result is conjectured originally within Einstein’s gravity called the “reverse” isoperimetric inequality (RII) [3], which is formally defined as

$${\left({\displaystyle \frac{(D-1)V}{{\mathcal{A}}_{D-2}}}\right)}^{{\displaystyle \frac{1}{D-1}}}\ge {\left({\displaystyle \frac{A}{{\mathcal{A}}_{D-2}}}\right)}^{{\displaystyle \frac{1}{D-1}}},$$

(5)

where V is the thermodynamic volume1, ${\mathcal{A}}_{D-2}$ is the volume of unit sphere and A is the area of the outer horizon. Equivalently, the inequality can be stated as AdS-Schwarzschild black holes at a fixed geometric2 volume $V^{\prime }$ maximize area or entropy [3]. This means that a round sphere of fixed geometric volume in AdS space maximize area or entropy. It is precisely this statement that we will prove.

The inequality is reversed in the sense that in Euclidean space, a round sphere minimizes area, called simply the isoperimetric inequality [9,10]. The reverse isoperimetric inequality is known to be obeyed for every case except for the charged Bañados-Teitelboim-Zanelli (BTZ) black holes [11,12]. Black holes that violate RII are called superentropic [13,14]. However, these are thermodynamically unstable [15] since they have negative heat capacity at constant volume. RII is a classical result, and some quantum inequalities have also been proposed recently regarding this [16]. Despite the success of RII, it lacks a general proof and remains a conjecture.

In this letter, we provide for the first time a general proof of RII in arbitrary dimension using a two-pronged geometric and analytical approach. The geometric part of the proof establishes a very general statement: In any theory of gravity coupled to matter fields that respects the standard energy conditions leading to gravitational focusing, a round sphere of fixed geometric volume maximizes area or entropy. In the analytic part of the proof, we focus on Einstein’s gravity within which the conjecture is originally formulated. Our complementary two-pronged proof does not invoke any explicit form of the metric function $f\left(r\right)$, but relies solely on the Raychaudhuri inequality, the Obata/Sherif–Dunsby rigidity theorem, and a second-variation analytical check. Hence, it can also be regarded as the first metric-agnostic proof that all spherically symmetric horizons of fixed geometric volume maximize the entropy functional.

The reverse isoperimetric conjecture asserts that, for fixed thermodynamic volume, only the static, spherically symmetric AdS black holes—namely Schwarzschild–AdS and Reissner–Nordström–AdS—saturate the upper bound on horizon entropy. In other words, round spherical horizons maximize area or entropy at fixed geometric volume. Our geometric proof (via the Sherif–Dunsby/Obata rigidity theorem) furthermore demonstrates that any smooth, volume-preserving deformation of a round $S^{D-2}$ forces the geometry back to being round, thereby identifying the round sphere as a stable, maximally entropic extremum. Consequently, when establishing the conjecture analytically in Einstein–Hilbert gravity with $\Lambda <0$, one need only consider $S^{D-2}$ cross-sections. Rotating solutions such as Kerr–AdS possess non-spherical horizon cross-section and, at fixed volume, exhibit strictly lower entropy than their non-rotating counterparts. They therefore do not saturate the entropy bound, and are thus naturally excluded.

The proof is briefly organized as follows: In subsection (Section 2.1), we argue in favor of RII purely on geometric grounds. In Section 2.2, an analytical approach using the second variation of the area is provided. We end the paper with some discussion on potential implications and extensions of the proof. Four appendices (A, B, C and D) are included, which contain important technical aspects and derivations to further elaborate on our proof.

2. AdS-Schwarzschild/RN black holes maximize entropy

To begin the analysis, we perform a 1+1+2 split [17] of spacetime $\mathcal{M}$ (since we are only interested in the properties of hypersurface, it is natural to perform a 1+3 or 1+1+2 decomposition of spacetime) of dimension $D=4$ and apply a proper (non-constant) conformal transformation to the metric of the $(D-1)$-hypersurface $\Sigma$ of $\mathcal{M}$

$$h_{ab}⟶{\Omega }^2\left(\mathcal{X}\right)h_{ab}.$$

(6)

Here, $\mathcal{X}$ are the angular coordinates, so that the spherical symmetry is broken. For example, one can have $\Phi \equiv \Phi \left(\theta \right)$ which explicitly breaks the $SO\left(3\right)$ symmetry. In the 1+1+2 decomposition of the spacetime $\mathcal{M}$, the 3-space orthogonal to the timelike unit vector $u^{\mu }$ is further split into a preferred spacelike direction $e^{\mu }$ and its orthogonal 2-space (or “2-sheet”). One introduces the projection tensors [18]

$$h_{\mu \nu }=g_{\mu \nu }+u_{\mu }{u}_{\nu },N_{\mu \nu }=h_{\mu \nu }-e_{\mu }{e}_{\nu },$$

so that $u^{\mu }{u}_{\mu }=-1$, $e^{\mu }{e}_{\mu }=+1$, and $u^{\mu }{e}_{\mu }=0$. Working on a fixed background (here, Anti-de Sitter) so that $R_{\mu \nu }\left[g\right]$ is held fixed by Einstein’s equations, we vary only the intrinsic 3-metric (or induced metric) $h_{\mu \nu }$ via a (proper) conformal transformation. Spatial indices are then raised and lowered with $h_{\mu \nu }$. This point can be understood as follows: Although the induced metric and bulk metric are related by

$$h_{ab}=g_{ab}+n_a{n}_b,$$

(7)

we hold the bulk metric fixed,

$$\delta g_{ab}=0⟹\delta R_{ab}\left[g\right]=0,$$

(8)

and vary only the hypersurface embedding (or its conformal factor). Concretely, deforming the embedding as

$$X^a\left(\sigma \right)⟶X^a\left(\sigma \right)+\Phi \left(\sigma \right)n^a⟹n^a⟶n^a+\delta n^a,$$

(9)

induces a change in the induced metric via

$$\delta h_{ab}=\delta \left(n_a{n}_b\right)=\left(\delta n_a\right)n_b+n_a\left(\delta n_b\right),$$

(10)

even though $\delta g_{ab}=0$. Therefore,

1.

Bulk metric fixed:$\delta g_{ab}=0\Rightarrow \delta R_{ab}=0.$

2.

Hypersurface varied:$X^a\to X^a+\Phi n^a$ so that $\delta n^a\ne 0$ and hence $\delta h_{ij}\ne 0.$

Thus, we achieve a non-trivial variation of the induced metric $h_{ij}$ while keeping the ambient Ricci tensor $R_{ab}$ fixed by Einstein’s equations.

In addition, we choose to break the spherical symmetry via conformal transformation so that the topology of the hypersurface $\Sigma$ is preserved while breaking the spherical symmetry in a controlled way. We now argue in favor of the round 3-sphere in $\mathcal{M}$ maximizing area or entropy purely on geometric grounds.

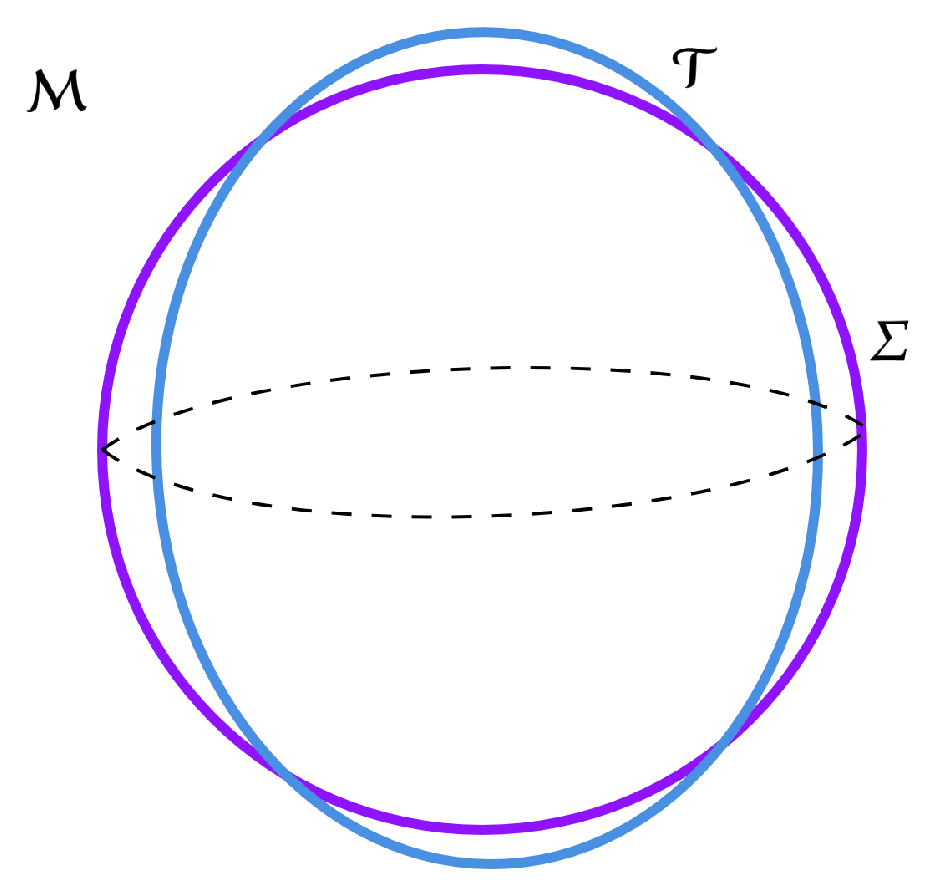
2.1. Sherif-Dunsby rigidity and maximal entropy

Consider a compact 3-manifold $\Sigma$ of spherical topology in the 1+1+2 decomposition of spacetime $\mathcal{M}$. We consider an arbitrary one-parameter family of volume-preserving normal deformations ${\Sigma }_s$, $s\in (-\epsilon ,\epsilon )$, with induced metrics

$$h_{ab}\left(s\right)=e^{2\Phi \left(s\right)}{h}_{ab}\left(0\right),\Phi \left(0\right)=0.$$

Let us represent the deformed 3-sphere (non-Einstein) with $\mathcal{T}$ (see Figure 1). Then on $\mathcal{T}$:

• Identification of the conformal factor: One shows that the infinitesimal conformal factor

  $$\dot{\phi }\left(0\right)={\left.{\displaystyle \frac{d\phi }{ds}}\right|}_{s=0}$$

  coincides with the sheet-expansion scalar $\theta ={\delta }_{\mu }{e}^{\mu }$ in the $1+1+2$ split.
• Gravitational focusing: For the vector $e^a$ of our spacelike 2-sheet, $R_{ab}{e}^a{e}^b<0$, since, $R_{ab}=\Lambda g_{ab}$ and $\Lambda <0$ in an AdS space, the Raychaudhuri-type equation for $\theta$ implies focusing:

  $$\theta =\dot{\phi }\left(0\right)<0\mathrm{everywhere}\mathrm{on}\mathcal{T}.$$
  Hence, the conformal factor is strictly negative as we move along $e^{\mu }$.
• Sherif–Dunsby rigidity: By Theorem VII.4 of Sherif and Dunsby [18] (see Appendix A for details of theorem and its role in our proof), any proper (non-constant), scalar-curvature-preserving conformal transformation

  $${\tilde{h}}_{ab}=e^{2\phi }{h}_{ab}\mathrm{with}\phi <0$$

  on a compact 3-manifold (non-Einstein) forces $(\mathcal{T},{\tilde{h}}_{ab})$ to be isometric to the round $S^3$ (up to a constant scale).

Note that we are using two different expressions of conformal factors: $\Phi$ is the proper conformal factor by which we deform the round 3-sphere. This is not sign-definite. In fact, under volume preservation

$${\int }_{\Sigma }\Phi d\mu =0,$$

(11)

where $d\mu$ is the volume element, and it takes both positive and negative values while $\phi$ is the Yamabe (conformal) factor by which we study the Yamabe problem on the deformed 3-sphere $\mathcal{T}$. This has a strictly negative sign via gravitational focusing3. The discussion leads to an interesting geometrical implication: any non-homothetic, volume-preserving conformal deformation of a compact 3-sphere under the gravitational focusing forces it to be isometric to round 3-sphere. So, the only admissible extremal or stable surface is the round $S^3$. Since stability in the context of thermodynamics is related to maximizing entropy. This establishes a very general statement: In any theory of gravity coupled to matter fields that respects the standard energy conditions leading to gravitational focusing, a round sphere of fixed geometric volume represents a maximally entropic state. Therefore, the reverse isoperimetric inequality is a feature of attractive nature of gravity itself establishing the inequality as a very general statement, a statement about gravity.

This is in stark contrast to the Euclidean isoperimetric case, where no such curvature-driven rigidity exists due to the absence of gravity.

Although the Sherif–Dunsby rigidity theorem can be stated “abstractly” for any 3-metric satisfying its hypotheses, in our gravitational proof we must verify those hypotheses dynamically, and the simplest way to do so is to start from the known round sphere and then deform it. In this case, the conditions for the applicability of the theorem can be dynamically satisfied: The deformed 3-sphere remains compact and the Ricci scalar on the deformed 3-sphere is also positive since the Ricci scalar of the round 3-sphere is positive, any infinitesimal conformal deformation of it by $\Phi$ preserves the positivity.

Bolt-to-horizon identification: By Sherif–Dunsby rigidity the compact Euclidean slice $\mathcal{T}\cong S^3$ is isometric to the round 3-sphere. Introducing standard “latitude” coordinate $\chi \in [0,\pi ]$,

$$d{s}_{S^3}^2=d{\chi }^2+{sin}^2\chi d{\Omega }_2^2,$$

each $\chi =\mathrm{const}$ hypersurface is a round $S_{\chi }^2$ of radius $sin\chi$. In particular the Euclidean “bolt” at

$$\chi ={\displaystyle \frac{\pi }{2}}⟹r=sin\left(\frac{\pi }{2}\right)=1$$

is the unique maximal-area 2-sphere leaf under fixed enclosed 3-volume. Under the Wick rotation back to Lorentzian signature, this bolt maps exactly to the event-horizon cross-section (the $r=r_h$ sphere) of the black hole. Hence maximality of the full $S^3$ immediately implies maximality of the horizon $S^2$.

After the geometric argument, we now turn towards the area variation method to analytically establish this result. For the purpose of analytic calculations, an action must be chosen. In this case, we specifically focus on Einstein’s gravity within which the conjecture is originally formulated.

2.2. Effective Functional and Its Variation

We begin with the Euclidean Einstein–Hilbert action plus Gibbons–Hawking boundary term in D dimension in the presence of cosmological constant

$$\begin{array}{cc}\hfill I\left[g\right]=& -{\displaystyle \frac{1}{16\pi G}}{\int }_{\mathcal{M}}(R-2\Lambda )\sqrt{-g}{d}^{D}x\hfill \\ \hfill & -{\displaystyle \frac{1}{8\pi G}}{\int }_{\partial \mathcal{M}}K\sqrt{\gamma }{d}^{D-1}x.\hfill \end{array}$$

(12)

On an Einstein solution $R_{ab}-\frac{1}{2}R{g}_{ab}+\Lambda g_{ab}=0$ we have $R=\frac{2D}{D-2}\Lambda \equiv \tilde{D}\Lambda$, so under a normal4deformation $X^a\to X^a+\varphi n^a$, the bulk term varies as (Appendix B)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \delta I_{\mathrm{bulk}}=-{\displaystyle \frac{(\tilde{D}-2)\Lambda }{16\pi G}}\left(\int d\tau N\right)\delta V\hfill \\ & =-{\displaystyle \frac{(\tilde{D}-2)\Lambda \beta }{16\pi G}}\delta V,\hfill \end{array}\end{array}$$

(13)

where $\beta$ is the period, N is the lapse and $\delta V$ is the volume variation of $(D-1)$-sphere given as

$$\delta V={\int }_{\Sigma }\sqrt{h}\varphi d^{D-1}x.$$

(14)

where $h_{ab}$ is the induced metric on the spatial hypersurface $\Sigma$.

Furthermore, the variation of the Gibbons–Hawking-York (GHY) term contributes (Appendix B)

$$\delta I_{\mathrm{bdy}}=-{\displaystyle \frac{1}{8\pi G}}\delta A,$$

(15)

where $\delta A$ is the area variation of $(D-2)$-sphere.

Collecting the values above leads to

$$\begin{array}{cc}\hfill \delta I\left[g\right]& =\delta I_{\mathrm{bdy}}+\delta I_{\mathrm{bulk}}\hfill \\ \hfill & =-{\displaystyle \frac{1}{8\pi G}}\delta A-{\displaystyle \frac{(\tilde{D}-2)\Lambda \beta }{16\pi G}}\delta V.\hfill \end{array}$$

(16)

Note that the cosmological constant $\Lambda$ enters the Lagrange multiplier $\lambda$ implementing the volume constraint. This is reminiscent of AdS black holes which have a fixed volume in the extended black hole thermodynamics. We define

$$\begin{array}{cc}\hfill I_{\mathrm{slice}}[\Sigma ]& =-{\displaystyle \frac{A[\Sigma ]}{8\pi G}}-\lambda V[\Sigma ],\hfill \\ \hfill \lambda & ={\displaystyle \frac{(\tilde{D}-2)\Lambda \beta }{16\pi G}}.\hfill \end{array}$$

(17)

so that

$$\delta I_{\mathrm{slice}}=-\delta A-\lambda \delta V.$$

(18)

with $8\pi G=1$. Therefore, the entropy or horizon area, given by the total contribution of bulk+GHY term takes the following form

$$S={\displaystyle \frac{\mathcal{A}}{4}}=-I_{\mathrm{slice}}.$$

(19)

Let us evaluate the first variation of area and volume. Using5

$$\begin{array}{cc}\hfill \delta A& =-{\int }_{\Sigma }H\varphi dV,\hfill \\ \hfill \delta V& ={\int }_{\Sigma }\varphi dV,\hfill \end{array}$$

(20)

where H is the mean curvature (trace of second fundamental form). The stationarity of $\delta I_{\mathrm{slice}}=0$ implies

$${\int }_{\Sigma }(H-\lambda )\varphi dV=0⟹H=\lambda .$$

(21)

For the second variation of a Riemann hypersurface, we have the standard expression

$$\begin{array}{cc}\hfill {\delta }^{2}A& ={\int }_{\Sigma }\left({|\nabla \varphi |}^2-{\left(\right|K|}^2+R_{ab}{n}^a{n}^b){\varphi }^2\right)dV,\hfill \\ \hfill {\delta }^{2}V& =-{\int }_{\Sigma }H{\varphi }^{2}dV.\hfill \end{array}$$

(22)

where ${|\nabla \varphi |}^2$ is the squared norm of the gradient operator, $\mathrm{Ric}(n,n)$ is the ambient manifold Ricci tensor and $K_{ij}$ is the second fundamental form. Thus, we get

$$\begin{array}{cc}\hfill {\delta }^2{I}_{\mathrm{slice}}& =-{\delta }^{2}A-\lambda {\delta }^{2}V\hfill \\ \hfill & =-{\int }_{\Sigma }{|\nabla \varphi |}^{2}dV\hfill \\ & +{\int }_{\Sigma }\left({\left|K\right|}^2+R_{ab}{n}^a{n}^b+H\lambda \right){\varphi }^{2}dV.\hfill \end{array}$$

(23)

In an Einstein background $R_{ab}{n}^a{n}^b=\Lambda$. Therefore, on a round 3-sphere of radius R in an Euclidean AdS space, we obtain

$$\begin{gathered} \begin{array}{c}\hfill \begin{array}{cc}\hfill & {\delta }^2{I}_{\mathrm{slice}}=-{\displaystyle \frac{\ell (\ell +2)}{R^2}}+{\displaystyle \frac{3}{l^2}}\left(1+{\displaystyle \frac{l^2}{R^2}}\right)+{\displaystyle \frac{9}{l^2}}\left(1+{\displaystyle \frac{l^2}{R^2}}\right)-{\displaystyle \frac{3}{l^2}}\hfill \end{array} \\ \begin{array}{c}\hfill =-{\displaystyle \frac{\ell (\ell +2)}{R^2}}+{\displaystyle \frac{12}{R^2}}+{\displaystyle \frac{9}{l^2}}.\end{array}\end{array} \end{gathered}$$

(24)

This equation follows from the fact that the Laplace-Beltrami spectrum on a 3-sphere of radius R is

$${\mu }_{\ell }={\displaystyle \frac{\ell (\ell +2)}{R^2}},$$

(25)

while in an AdS space (Appendix C)

$$\begin{array}{cc}\hfill & R_{ab}{n}^a{n}^b=\Lambda =-{\displaystyle \frac{3}{l^2}},\hfill \end{array}$$

(26)

$$\begin{array}{cc}& K_{ij}=-{\displaystyle \frac{1}{l}}\sqrt{1+{\displaystyle \frac{l^2}{R^2}}}{h}_{ij},H=\mathrm{Tr}K.\hfill \end{array}$$

(27)

Therefore, for $\ell =2$ (quadrupole) modes, which are volume preserving, true shape deformations of the Laplace-Beltrami spectrum and are physical deformations (Appendix D), we get

$${\delta }^2{I}_{\mathrm{slice}}>0,$$

(28)

This shows that the round $S^3$ in an AdS space is a local maximum of horizon area $\mathcal{A}$ (or entropy S) since ${\delta }^2{I}_{\mathrm{slice}}>0\Rightarrow {\delta }^2\mathcal{A}<0$.

In Euclidean space, the Ricci scalar vanishes, and we are left with only the GHY term, which gives the area variation of a standard round $(D-2)$-sphere (the usual isoperimetric problem)

$$\begin{array}{cc}\hfill & {\delta }^2{I}_{\mathrm{slice}}\left(\mathrm{Euclidean}\mathrm{space}\right)=-{\displaystyle \frac{\ell (\ell +2)}{R^2}}+{\displaystyle \frac{3}{R^2}}.\hfill \end{array}$$

(29)

Therefore, for the volume preserving, true shape deforming modes6 ($\ell \ge 2$)

$${\delta }^2{I}_{\mathrm{slice}}(\mathrm{Euclidean}\mathrm{space})<0.$$

(30)

This means that a round 3-sphere in Euclidean space is a local minimum of area, which is the standard isoperimetric inequality in Euclidean spaces. This shows that the reversal of the isoperimetric inequality is due to the structure of spacetime governed by Einstein’s field equation in the curved AdS background.

It is worth mentioning that in the case of horizons, the area is identified with entropy. Therefore, maximizing area (or entropy) leads to stability, unlike the Euclidean isoperimetric inequality, where minimizing area is related to stability. Although we derived the result for Euclidean AdS space in $D=4$, the analysis applies directly to Euclidean AdS space in D-dimension since all the results (gravitational focusing, Sherif-Dunsby rigidity, and second area variation) continue to hold. Therefore, the conclusion naturally extends to any dimension. The extension of the Sherif-Dunsby result can be better understood as follows. Because Obata’s theorem [20] holds on any compact n-manifold ($n\ge 2$), we may replace the 3D Yamabe rigidity of Sherif–Dunsby by its n-dimensional analogue. Concretely, on a D-dimensional spacetime we perform a $1+1+(D-2)$ decomposition and identify the infinitesimal conformal factor with expansion of $(D-2)$ sheet, $\dot{\varphi }=\theta$. Then, via gravitational focusing, we have $\dot{\varphi }<0$ everywhere, and Obata’s theorem then forces the deformed metric to be isometric (up to scale) to the round $S^{D-1}$. Hence, the only volume-preserving extremum of the entropy functional is the round sphere in any dimension.

At this point, it is necessary to analyze another spherically symmetric geometry, the charged (Reissner-Nordström) black hole. It is straightforward to evaluate that adding a charge Q modifies the saddle action as

$$I_{\mathrm{saddle}}={\displaystyle \frac{1}{4G}}(-\mathcal{A}+Q\Psi ),$$

(31)

where $\Psi$ is the electrostatic potential. The term corresponding to the charge Q appears due to the addition of Maxwell’s action to the Einstein-Hilbert action

$$I=I_{EH}-{\displaystyle \frac{1}{16\pi G}}\int \sqrt{-g}{F}_{\mu \nu }{F}^{\mu \nu }{d}^{D}x.$$

(32)

However, the entropy is still given by the usual Bekenstein-Hawking entropy in the fixed Q-ensemble

$$S_{\mathrm{RN}}={\displaystyle \frac{\mathcal{A}}{4G}}.$$

(33)

More precisely, one does a Legendre transform on the bulk Maxwell action by adding the boundary term that fixes the charge, and under these boundary conditions the total Maxwell variation vanishes. Mathematically, the bulk Maxwell action is given as

$$I_{\mathrm{M}}=-{\displaystyle \frac{1}{16\pi G}}{\int }_M{d}^{4}x\sqrt{-g}{F}_{\mu \nu }{F}^{\mu \nu },$$

(34)

whose variation gives

$$\begin{array}{cc}\hfill \delta I_{\mathrm{M}}& =-{\displaystyle \frac{1}{4\pi G}}\underset{\mathrm{EOM}=0}{\underbrace{{\int }_M{d}^{4}x\sqrt{-g}{\nabla }_{\mu }{F}^{\mu \nu }\delta A_{\nu }}}\hfill \\ & +{\displaystyle \frac{1}{4\pi G}}{\int }_{\partial M}{d}^{3}x\sqrt{h}{n}_{\mu }{F}^{\mu \nu }\delta A_{\nu },\hfill \end{array}$$

(35)

where $h_{ij}$ is the induced metric on $\partial M$ and $n^{\mu }$ its outward normal.

To work in the canonical (fixed-Q) ensemble, one adds the boundary term

$$I_{\mathrm{bdy}}=-{\displaystyle \frac{1}{4\pi G}}{\int }_{\partial M}{d}^{3}x\sqrt{h}{n}_{\mu }{F}^{\mu \nu }{A}_{\nu }$$

(36)

which fixes ${\displaystyle Q=\frac{1}{4\pi }{\int }_{S_{\infty }^2}{n}_{\mu }{F}^{\mu t}}$. Under these boundary conditions,

$$\delta \left(I_{\mathrm{M}}+I_{\mathrm{bdy}}\right)=-{\displaystyle \frac{1}{4\pi G}}{\int }_{\partial M}{d}^{3}x\sqrt{h}{A}_{\nu }\delta \left(n_{\mu }{F}^{\mu \nu }\right)=0,$$

(37)

since holding the charged Q fixed at the boundary, implies $\delta \left(n_{\mu }{F}^{\mu \nu }\right)=0$. This shows that the Maxwell sector does not contribute to the variation of the on-shell action in the fixed-Q ensemble and one is left with $\delta I_{\mathrm{slice}}=-\delta A-\lambda \delta V$ as before.

Evidently, this means that a charged, spherically symmetric black hole also maximizes entropy as required by RII. This leads us to conclude the main result of our Letter: Spherically symmetric black holes in AdS space, i.e., AdS-Schwarzschild/RN black holes in any dimension maximize entropy (or horizon area).

3. Conclusions and Discussion

In this work, given the assumptions, we have established a rigorous geometric–analytic proof of the reverse isoperimetric inequality (RII) for black hole horizons in AdS space of arbitrary dimension. On the one hand, the geometric argument based on a $1+1+(D-2)$ decomposition, Raychaudhuri focusing, and the Sherif–Dunsby (or Obata) rigidity theorem shows that any nontrivial, volume-preserving conformal deformation of a compact spherical hypersurface is forced back to the round $S^{D-1}$ by gravitational focusing alone. On the other hand, the analytic approach—via the second variation of the Euclidean gravitational action plus Gibbons–Hawking–York boundary term—demonstrates that quadrupolar ($\ell =2$) perturbations of the round sphere yield ${\delta }^2\mathcal{A}<0$ in Euclidean AdS (but ${\delta }^{2}A>0$ in flat Euclidean space), confirming that the round AdS-Schwarzschild horizon is a local maximum of area (entropy) under volume constraints.

Together, these complementary methods show that, in contrast to the classical isoperimetric inequality in flat space, gravity in a curved background reverses the inequality: among all hypersurfaces of fixed thermodynamic volume, spherically symmetric black holes uniquely maximizes horizon area. This result not only resolves the long-standing conjecture of RII in extended black hole thermodynamics but also highlights the fundamental role of Einstein’s equations and background curvature in governing entropic extremization.

Several avenues for further investigation naturally arise from our proof:

• Effects of Modified Gravity on the RII: In theories beyond Einstein–Hilbert—such as $f\left(R\right)$, Gauss–Bonnet or more general Lovelock gravities, and scalar–tensor models—the gravitational field equations acquire extra curvature-dependent or scalar-coupling terms which modify both the Raychaudhuri focusing condition and the form of the Euclidean action functional. In particular, the Raychaudhuri equation picks up additional contributions from the effective stress–energy of higher-derivative couplings, so that the sheet-expansion scalar $\theta$ no longer obeys the simple $\theta <0$ condition under volume-preserving deformations. Analytically, the second variation

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\delta }^2{I}_{\mathrm{slice}}=-{\delta }^{2}A-\lambda {\delta }^{2}V\hfill \\ & ⟶-{\delta }^{2}A-\lambda {\delta }^{2}V+{\delta }^2{I}_{\mathrm{higher}-\mathrm{curv}}\hfill \end{array}\end{array}$$

  (38)

  acquires extra terms ${\delta }^2{I}_{\mathrm{higher}-\mathrm{curv}}$ coming from variation of the $f\left(R\right)$ or Gauss–Bonnet invariants, altering the stability criterion of the extremal hypersurface. As a result, spherically symmetric black hole solutions in modified gravity may saturate or correct the reverse isoperimetric bound by theory-specific coefficients. A systematic study of these corrections would therefore be required to formulate a generalized RII in alternative theories of gravity.
• Quantum Corrections: Incorporating higher-curvature corrections or quantum effects (e.g., via one-loop determinants or entanglement entropy corrections) may modify the geometric rigidity or the second variation functional, potentially leading to refined ‘‘quantum RII’’ bounds.
• Holographic Perspectives: Given the AdS/CFT correspondence, it would be interesting to interpret our RII proof in the dual field theory, perhaps relating maximal horizon entropy at fixed volume to extremal entanglement or energy constraints in the boundary CFT.
• Beyond Asymptotic AdS: Extending the analysis to asymptotically flat or more exotic asymptotics (e.g., Lifshitz, hyperscaling violation) might reveal whether the reverse isoperimetric phenomenon is unique to constant-$\Lambda$ backgrounds or has broader applicability. Moreover, the RII has been advocated to hold for dS black holes in [21]. So, it is interesting to see if the proof can be extended to this case.
• Violation in the case of superentropic black holes: It is known that superentropic black holes violate RII. As part of the proof we presented, this can be traced to their non-compact hypersurface while the proof requires a compact hypersurface. Nevertheless, a general proof explicitly for non-compact hypersurfaces is an interesting future work.

In summary, our geometric–analytic approach not only proves the reverse isoperimetric conjecture in its full generality but also underscores the deep interplay between curvature, gravitational focusing, and entropy extremization. We anticipate that these insights will inform future studies of black hole thermodynamics, geometric inequalities in curved manifolds, and the fundamental connections between geometry and information in gravitational systems.

Appendix B.1. Calculation of the Variation of the Bulk Term

Since on-shell $R=\tilde{D}\Lambda$ and we hold the metric fixed ($\delta g_{ab}=0$), the only contribution to $\delta I_{\mathrm{bulk}}$ comes from the shift of the integration domain (see Appendix B.2 for a rigorous discussion on shift of integration domain or “thin shell” argument) under

$$X^a\mapsto X^a+\varphi n^a.$$

Hence

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & \delta I_{\mathrm{bulk}}={\displaystyle \frac{1}{16\pi G}}[{\int }_{M+\delta M}(R-2\Lambda )\sqrt{-g}{d}^{D}x\hfill \\ & -{\int }_M(R-2\Lambda )\sqrt{-g}{d}^{D}x]\hfill \\ \hfill & =-{\displaystyle \frac{(\tilde{D}-2)\Lambda }{16\pi G}}\int d\tau {\int }_{\Sigma }N\varphi \sqrt{h}{d}^{D-1}x\hfill \\ \hfill & ={\displaystyle \frac{(\tilde{D}-2)\Lambda }{16\pi G}}\left(\int Nd\tau \right)\delta V.\hfill \end{array}\end{array}$$

(A6)

where

$$\delta V={\int }_{\Sigma }\varphi \sqrt{h}{d}^{D-1}x,\int Nd\tau =\beta .$$

(A7)

Appendix B.2. Boundary-Term Variation for a General York Boundary

We consider the Gibbons–Hawking–York term on a timelike (or spacelike) boundary $\Sigma$,

$$I_{\mathrm{bdy}}=-{\displaystyle \frac{1}{8\pi G}}{\int }_{\Sigma }K\sqrt{\gamma }{d}^{D-1}x,$$

(A8)

where ${\gamma }_{ij}$ is the induced metric on $\Sigma$ and $K={\gamma }^{ij}{\nabla }_i{n}_j$ its extrinsic curvature.

Under an infinitesimal normal deformation

$$\begin{array}{cc}\hfill X^a& ⟶X^a+\varphi \left(x\right)n^a,n_a{n}^a=\pm 1,\hfill \end{array}$$

(A9)

the induced volume element varies as

$$\begin{array}{cc}\hfill \delta \sqrt{\gamma }& =\frac{1}{2}\sqrt{\gamma }{\gamma }^{ij}\delta {\gamma }_{ij}=\sqrt{\gamma }K\varphi ,\hfill \end{array}$$

(A10)

since $\delta {\gamma }_{ij}=2\varphi K_{ij}$ and $K={\gamma }^{ij}{K}_{ij}$. Hence

$$\begin{array}{cc}\hfill & \delta A_{\Sigma }\equiv \delta {\int }_{\Sigma }\sqrt{\gamma }{d}^{D-1}x={\int }_{\Sigma }\delta \sqrt{\gamma }{d}^{D-1}x\hfill \\ & ={\int }_{\Sigma }K\varphi \sqrt{\gamma }{d}^{D-1}x.\hfill \end{array}$$

(A11)

On the other hand, one may view $\delta I_{\mathrm{bdy}}$ as the difference between two boundaries separated by a thin shell of thickness $\varphi$. To first order in $\varphi$,

$$\begin{array}{cc}\hfill \delta I_{\mathrm{bdy}}& =-{\displaystyle \frac{1}{8\pi G}}\left[{\int }_{{\Sigma }^{\prime }}K\sqrt{\gamma }{d}^{D-1}x-{\int }_{\Sigma }K\sqrt{\gamma }{d}^{D-1}x\right]\hfill \\ \hfill & =-{\displaystyle \frac{1}{8\pi G}}{\int }_{\delta \Sigma }K\sqrt{\gamma }{d}^{D-1}x\hfill \\ & \approx -{\displaystyle \frac{1}{8\pi G}}{\int }_{\Sigma }K\varphi \sqrt{\gamma }{d}^{D-1}x=-{\displaystyle \frac{1}{8\pi G}}\delta A_{\Sigma }.\hfill \end{array}$$

(A12)

This is the Eq.(15) of the main text.

To understand the thin shell argument rigorously, introduce Gaussian normal coordinates $(u,x^i)$ in a neighborhood of $\Sigma$:

$$\begin{array}{cc}\hfill d{s}^2& =d{u}^2+{\gamma }_{ij}(u,x)d{x}^{i}d{x}^j,\hfill \\ \hfill n^a& ={\partial }_u,\hfill \\ \hfill \Sigma :u& =0,{\Sigma }^{\prime }:u=\varphi \left(x\right).\hfill \end{array}$$

(A13)

Then the “shell” $\delta \Sigma$ is the set of points $\{(u,x^i)\mid 0\le u\le \varphi \left(x\right)\}$, and its volume element is

$$d{V}_{\mathrm{shell}}=\sqrt{det\left[{\gamma }_{ij}(u,x)\right]}du{d}^{D-1}x.$$

(A14)

The variation of the GHY boundary action is

$$\begin{array}{cc}\hfill \delta I_{\mathrm{bdy}}& =-{\displaystyle \frac{1}{8\pi G}}{\int }_{\delta \Sigma }K\sqrt{\gamma }{d}^{D-1}x\hfill \\ \hfill & =-{\displaystyle \frac{1}{8\pi G}}{\int }_{\Sigma }{d}^{D-1}x{\int }_0^{\varphi \left(x\right)}K(u,x)\sqrt{det\left[{\gamma }_{ij}(u,x)\right]}du.\hfill \end{array}$$

(A15)

Expanding to first order in the small displacement $\varphi$:

$$\begin{array}{cc}\hfill & K(u,x)\sqrt{det\left[{\gamma }_{ij}(u,x)\right]}=K(0,x)\sqrt{det\left[{\gamma }_{ij}(0,x)\right]}+O\left(u\right),\hfill \\ & {\int }_0^{\varphi \left(x\right)}du=\varphi \left(x\right),\hfill \\ & {\int }_0^{\varphi \left(x\right)}K(u,x)\sqrt{det\left[{\gamma }_{ij}(u,x)\right]}du\approx K(0,x)\sqrt{\gamma \left(x\right)}\varphi \left(x\right).\hfill \end{array}$$

(A16)

Hence, to first order,

$$\delta I_{\mathrm{bdy}}=-{\displaystyle \frac{1}{8\pi G}}{\int }_{\Sigma }K\left(x\right)\varphi \left(x\right)\sqrt{\gamma \left(x\right)}{d}^{D-1}x+O\left({\varphi }^2\right).$$

(A17)

Appendix D.1. Transverse–Traceless Gauge and Lichnerowicz Operator

Since the normal deformation $\varphi$ (which is equal to the infinitesimal conformal transformation for an umbilic surface which is the round sphere in our case) corresponds to metric perturbation, it restricts mode choice to those which solves linearized Einstein’s equation. This uniquely picks out $\ell =2$ (quadrupole) modes, which we show now.

Let $g_{ab}$ be the round metric on $S^3$ of radius R, satisfying

$$\begin{array}{cc}\hfill R_{ab}& ={\displaystyle \frac{2}{R^2}}{g}_{ab}.\hfill \end{array}$$

(A24)

Consider a small perturbation

$$\begin{array}{cc}\hfill g_{ab}& \to g_{ab}+h_{ab},\hfill \end{array}$$

(A25)

imposed in transverse–traceless (TT) gauge:

$$\begin{array}{c}\hfill {\nabla }^a{h}_{ab}=0,{h^a}_a=0.\end{array}$$

(A26)

The linearized, source-free Einstein equation on an Einstein manifold $R_{ab}=\Lambda g_{ab}$ reads

$$\begin{array}{cc}\hfill \left({\Delta }_L-2nK\right)h_{ab}& =0,\hfill \end{array}$$

(A27)

where

$$\begin{array}{cc}\hfill & n=3,K={\displaystyle \frac{1}{R^2}},\hfill \end{array}$$

(A28)

$$\begin{array}{cc}& {\Delta }_L{h}_{ab}=-{\nabla }^2{h}_{ab}-2{{{R_a}^c}_b}^d{h}_{cd}+2\Lambda h_{ab}.\hfill \end{array}$$

(A29)

Appendix D.2. Tensor Harmonic Spectrum on S³

One can expand TT–tensors in tensor spherical harmonics $h_{ab}^{(\ell )}$ labeled by $\ell =0,1,2,\dots$, which satisfy

$$\begin{array}{cc}\hfill & {\Delta }_L{h}_{ab}^{(\ell )}={\mu }_{\ell }{h}_{ab}^{(\ell )},\hfill \end{array}$$

(A30)

$$\begin{array}{cc}& {\mu }_{\ell }={\displaystyle \frac{\ell (\ell +2)-2}{R^2}}.\hfill \end{array}$$

(A31)

Inserting into the linearized equation gives the eigenvalue condition

$$\begin{array}{cc}\hfill & {\mu }_{\ell }=2nK⟹\ell (\ell +2)-2=6,\hfill \\ & ⟹\ell =2(\ell =-4\mathrm{discarded}).\hfill \end{array}$$

(A32)

Hence the only nontrivial solution of $({\Delta }_L-2nK)h_{ab}=0$ in TT gauge on $S^3$ is the quadrupole mode $\ell =2$.

Appendix D.3. Exclusion of ℓ=0,1 Modes

• $\ell =0$ (monopole): A constant rescaling

  $$\begin{array}{cc}\hfill h_{ab}& \propto g_{ab}\hfill \end{array}$$

  (71)

  changes the volume rather than shape; in TT gauge ${h^a}_a=0$ forbids such a trace mode.
• $\ell =1$ (dipole): These correspond to infinitesimal diffeomorphisms (Killing vectors) on $S^3$,

  $$\begin{array}{cc}\hfill h_{ab}& ={\nabla }_a{\xi }_b+{\nabla }_b{\xi }_a,\hfill \end{array}$$

  (72)

  which can be entirely removed by a coordinate redefinition. In TT gauge one requires ${\nabla }^a{h}_{ab}=0$, and one finds no non-gauge $\ell =1$ TT tensors.

Therefore, when restricting to physical, source-free metric perturbations of the round $S^3$, only the $\ell =2$ harmonics survive, justifying the truncation to the quadrupole sector in the main text.