Enhancing Supervisory Control with GPenSIM

1. Introduction

Supervisory control theory in the context of Petri nets is a formal framework for modeling, analyzing, and synthesizing controllers for discrete-event systems [1,2]. In this framework, the uncontrolled system (“plant”) is represented as a Petri Net, where places represent system states or conditions, transitions represent events (e.g., actions, tasks), and tokens represent the resources or signals [3]. Control specifications for the desired behaviors (such as a maximum of ten tokens in place p1; buffer control via monitor places [4]) are formalized as linear constraints (e.g., linear inequalities on markings) [5]. A supervisor is synthesized to enforce specifications by either disabling transitions that would violate constraints or monitoring markings (system states) in real-time [2]. The approach for the synthesis of supervisors is based on Place Invariants (P-invariants), which enforce linear constraints on markings (e.g., via control places added to the plant Petri Net) [5], and maximally permissive control by which all legal behaviors are allowed while illegal ones are prevented [6]. Using Petri Nets for supervisory control offers many advantages, such as a graph- based visual front and linear algebraic-based mathematical modeling and analysis on the back end, handling concurrency and resource sharing naturally, and supporting modular supervisor design [3,7,8]. However, it has several limitations, particularly in scalability, expressiveness, and practical implementation (explained in Section 2). Some of these limi- tations can be overcome with extended Petri Nets such as Colored Petri Nets (for complex systems with data/variable dependencies) [9] and Timed Petri Nets and Stochastic Petri Nets (for performance-oriented real-time control) [10]. However, most of the limitations remain unresolved. This paper provides a novel approach based on GPenSIM to address these gaps. The structure of this paper is as follows: Section 2 presents a compact literature review on the limitations of supervisory control based on Petri nets. Section 3 and Section 4 provide formal definitions of Petri nets, as these definitions are expected in works on the modeling of discrete systems. Section 5 introduces GPenSIM, and Section 6 shows how GPenSIM can mitigate some of the limitations of supervisory control. Finally, Section 7 summarizes the findings of this paper.

2. Literature Review

While supervisory control theory based on Petri nets is a powerful framework for discrete-event systems [5,11,12], it has several limitations, particularly in scalability, expressiveness, and practical implementation.

2.1. State-Space Explosion

The computational complexity of synthesizing supervisors grows exponentially with the size of the plant (number of places, transitions, and tokens). This so-called “state-space explosion” is a major problem when Petri nets are used, and also for the synthesis of super- visors [13]. Hence, this problem prevents the applicability of Petri nets for controlling large or complex systems such as industrial automation or multi-agent-based communication systems. One way to eliminate the state-explosion problem is to modularize the monolithic Petri net model into multiple “Petri Modules,” which can be run on multiple host CPUs. Thus, this modular approach eliminates the state-explosion problem as well as reduces the overall simulation time, as multiple CPUs host these modules [14]. However, the monolithic Petri net model must intrinsically possess laminar flow (no criss-crossing connections) so that it can be decomposed into modules. Also, model abstraction has been proposed as a solution [15]. Here, again, abstraction means loss of information; how much information are we willing to sacrifice in order to reduce the number of states—it is a trade-off between depth of information and number of states.

2.2. Scalability in Distributed Systems

Supervisors synthesized by supervisory control theory are meant for centralized control, as there are no measures for distributed control. However, centralized supervisors may not scale well for decentralized or distributed systems due to communication delays and may not work at all in synchronization issues [8]. Hence, Davidrajuh [8] and Yoo and Lafortune [16] propose decentralized or distributed supervisors with localized modular control and minimal coordination between the modules.

2.3. Limited Expressiveness for Nonlinear Constraints

Classical Petri Net-based supervisory control relies on linear constraints (e.g., place invariants), and it does not support nonlinear constraints. Also, there is no way to enforce temporal, priority-based, or conditional constraints (e.g., “If a fire event occurs, disable the machine for 60 seconds”). Some temporal constraints can be enforced using Timed/S- tochastic Petri nets [10]. Also, Basile et al. [6] suggested the use of hybrid methods (such as integrating Petri nets with Automata or logic programming); however, a formal, robust approach does not exist.

2.4. Rigid Enforcement of the Controller

Supervisors synthesized by supervisory control theory often disable all transitions leading to illegal states, which may be too conservative. This excessive conservativeness reduces system flexibility and efficiency, as sometimes the controller blocks legal behaviors unnecessarily. Ghaffari et al. [17] suggested maximally permissive control using the theory of regions as a way to relax the controller’s over-restrictiveness. Yang et al. [18] and Herzig et al. [19] suggested partial observability-aware synthesis to relax the controller.

2.5. Partial Observability Challenges

If some transitions are unobservable, the supervisor cannot always determine the exact system state, and this may lead to incorrect disabling of transitions. Ru and Hadjicostis [20] suggested estimating markings using observers.

2.6. Other Difficulties

There are some other limitations in supervisory control theory based on Petri nets, such as handling unmodeled disturbances. Basile et al. [21] proposed fault-tolerant Petri nets as a remedy and online reconfiguration of supervisors. Also, Wang et al. [10] presented the problem of handling real-time and continuous dynamics in supervisors and suggested an approach based on Timed Petri Nets. Kaid et al. [22] and Al-Ahmari et al. [23] propose a reconfigurable controller to face dynamic changes in the plant. While Petri Net-based supervisory control is a theoretically sound method for synthe sizing controllers for discrete-event systems, its scalability, expressiveness, and adaptability remain challenges. Recent advances (such as hybrid Petri nets and decentralized control) help mitigate these issues, but trade-offs between computational cost and control precision persist.

3. Petri Nets

Petri nets have gone through many versions (extensions and subclasses), mainly to incorporate time and to increase their modeling power [7]. In this section, we provide the formal definitions.

3.1. Definition: P/T Petri Nets

The Place-Transition Petri net (P/T Petri net, for short) is defined as a four-tuple [7,24,25]:

PTN = (P, T, A, M₀),

where, P is a finite set of places, P = {p₁, p₂, . . . , p_np }.

• T is a finite set of transitions, T = {t₁, t₂, . . . , t_nt }. P ∩ T = ∅.
• A is the set of arcs (from places to transitions and from transitions to places). A ⊆ (P × T) ∪ (T × P). The default arc weight W of a_ij (a_ij ∈ A, an arc going from p_i to t_j or from t_i to p_j) is one, unless noted otherwise.
• M is the row vector of markings (tokens) on the set of places. M = [M(p₁), M(p₂), . . . , M(p_np )] ∈ Nⁿp , M₀ is the initial marking. Due to the markings, a PTN = (P, T, A, M) is also called a marked P/T Petri net. P/T Petri nets do not involve time. Hence, P/T Petri nets are insufficient to model engineering systems, as time is one of the key performance indicators (KPI). Hence, Timed Petri net is an extended Petri net incorporating time.

3.2. Definition: Timed Petri Net

The Timed Petri net (TPN, for short) is defined as a five-tuple [26,27]:

TPN = (P, T, A, M, FT),

where,

• (P, T, A, M) is a Marked Petri net,
• FT is a mapping of T into R⁺: ∀t ∈ T, FT(t) ∈ R⁺, FT(t) > 0
• FT(t) is known as the firing times of the transitions and is defined to be greater than zero.

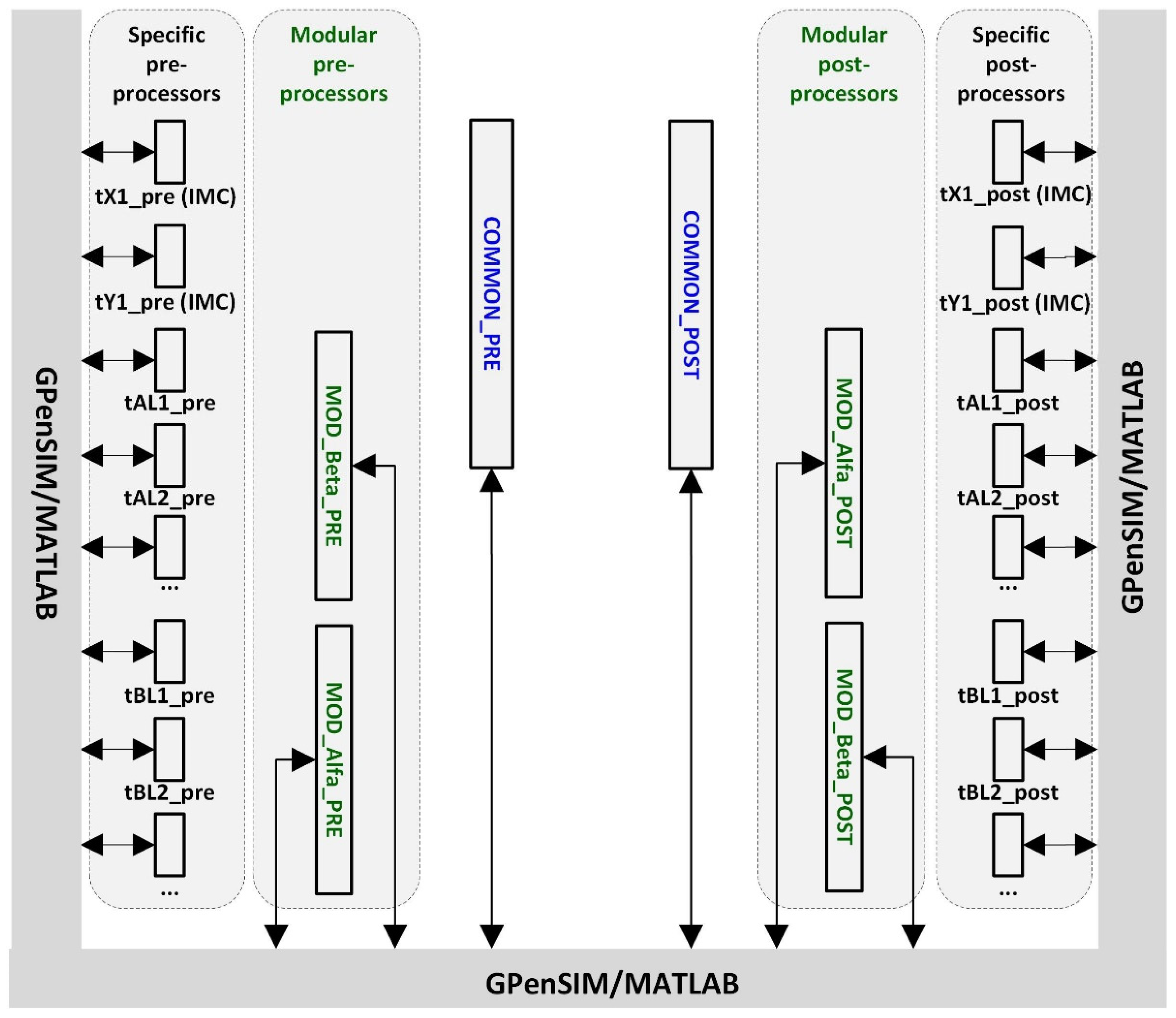
4. Modular Petri Nets

The literature review reveals many definitions of Modular Petri Nets [28,29,30,31,32,33]. Davidrajuh [8,34] proposed a new type of Modular Petri Nets, which is implemented in the software GPenSIM.

Modular Petri Net and Petri Modules

A modular Petri net is composed of one or more Petri modules and zero or more Inter-Modular connectors (IMC). Figure 1 shows the definition of modular Petri nets.

Figure 2 and Figure 3 show the definitions of a Petri module and IMC, respectively.

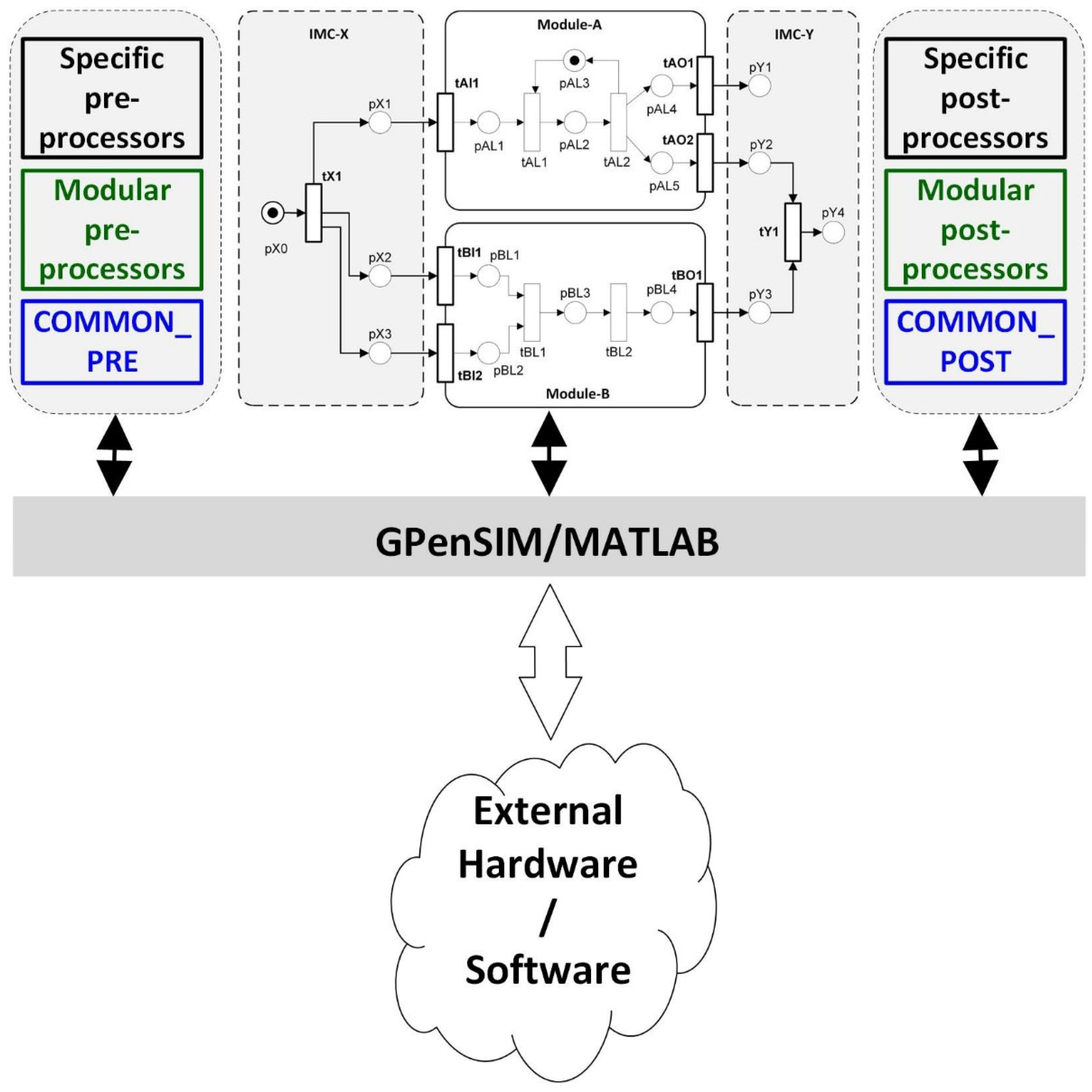
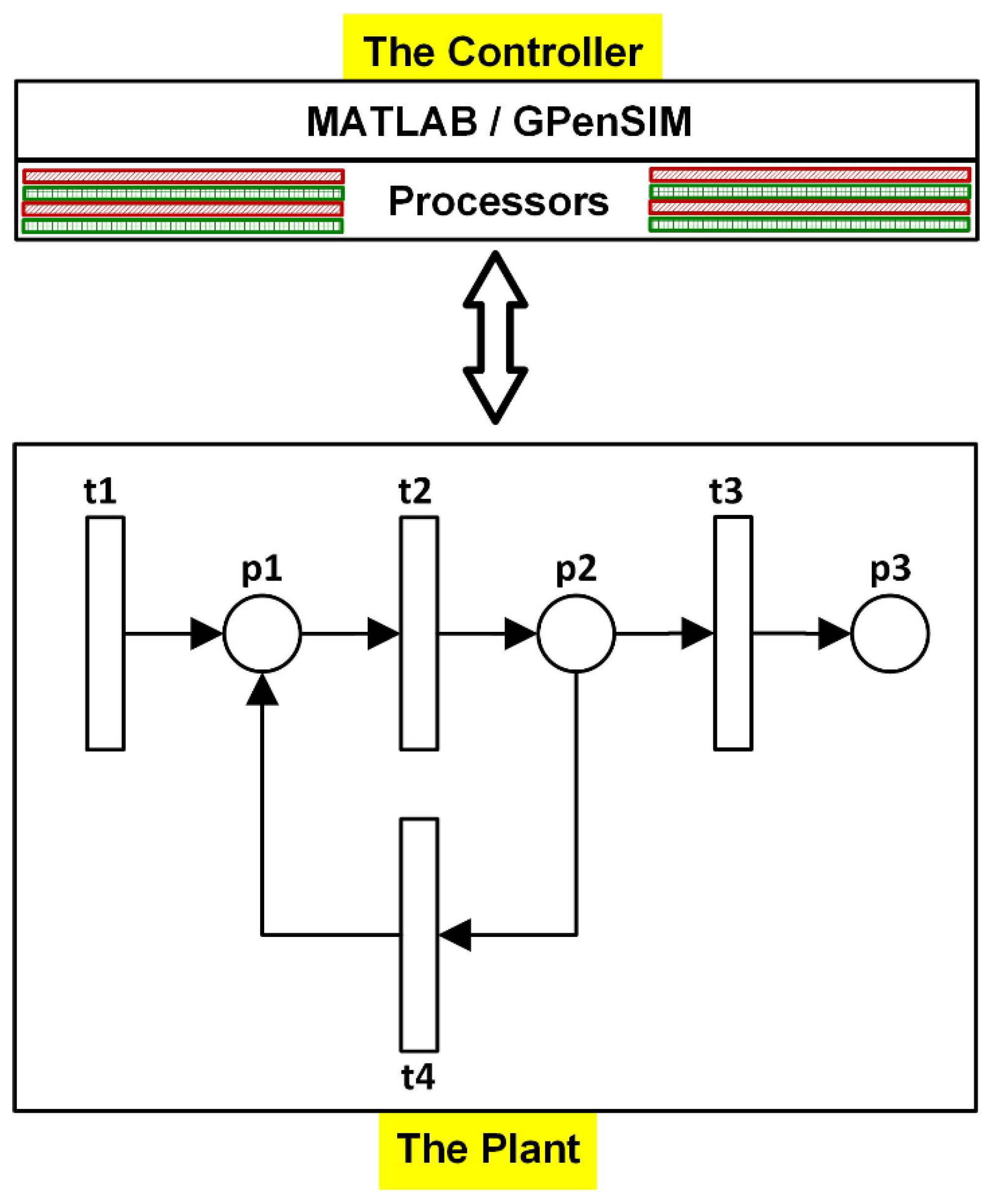
5. GPenSIM: A Modular Petri Net Framework for Scalable Supervisory Control

GPenSIM (General Purpose Petri Net Simulator) is a MATLAB-based Petri net tool developed by the first author of this paper. A C++ programming language-based prototype of GPenSIM was initially developed, called PenSIM (Petri Net Simulator). However, the prototype faced significant limitations in managing interdependencies — both among the Petri net elements and with external systems. To address these challenges, GPenSIM was redeveloped as a MATLAB toolbox, offering improved functionality and flexibility. GPenSIM stands out from other Petri net tools due to its flexibility, integration with MATLAB, and focus on customization [35,36]. GPenSIM provides an interface – the pre-processors and post-processors - that gives a distinctive programming approach to make Petri net models flexible, as explained in the following subsections.

5.1. “The Theory of Connection” Based Design

GPenSIM was designed based on the Theory of Connection. The theory of connection is a concept that appears in different fields (e.g., psychology, sociology, network theory, etc.) with varying interpretations. However, in the context of systems theory, the theory of connection (a.k.a. the principle of interconnectedness) refers to the fundamental idea that elements of a system are interdependent, and their relationships determine the system’s behavior. According to the theory of connection in systems theory, systems are not merely col- lections of parts but networks of dynamic relationships. The connections (flows, feedback loops, dependencies) between elements are as critical as the elements themselves. The concept is interdependence - no element operates in isolation as changes in one element ripple through the system. Also, the connections (loops) create reinforcing, balancing, or stabilizing effects. Additionally, the theory of connection emphasizes Network Structure, meaning the pattern of connections (centralized, decentralized, modular) determines adapt- ability and that systems are defined by their connections to/from the environment (their Boundaries and Openness). The theoretical foundations for the theory of connection were laid by Ludwig von Bertalanffy [37,38], Jay Forrester [39,40], and Fritjof Capra [41,42]. However, GPenSIM was designed following the guidelines provided by the legendary Norwegian professor Øyvind Bjørke in his book on “Manufacturing Systems Theory” [43], and in some follow-up works [44,45,46].

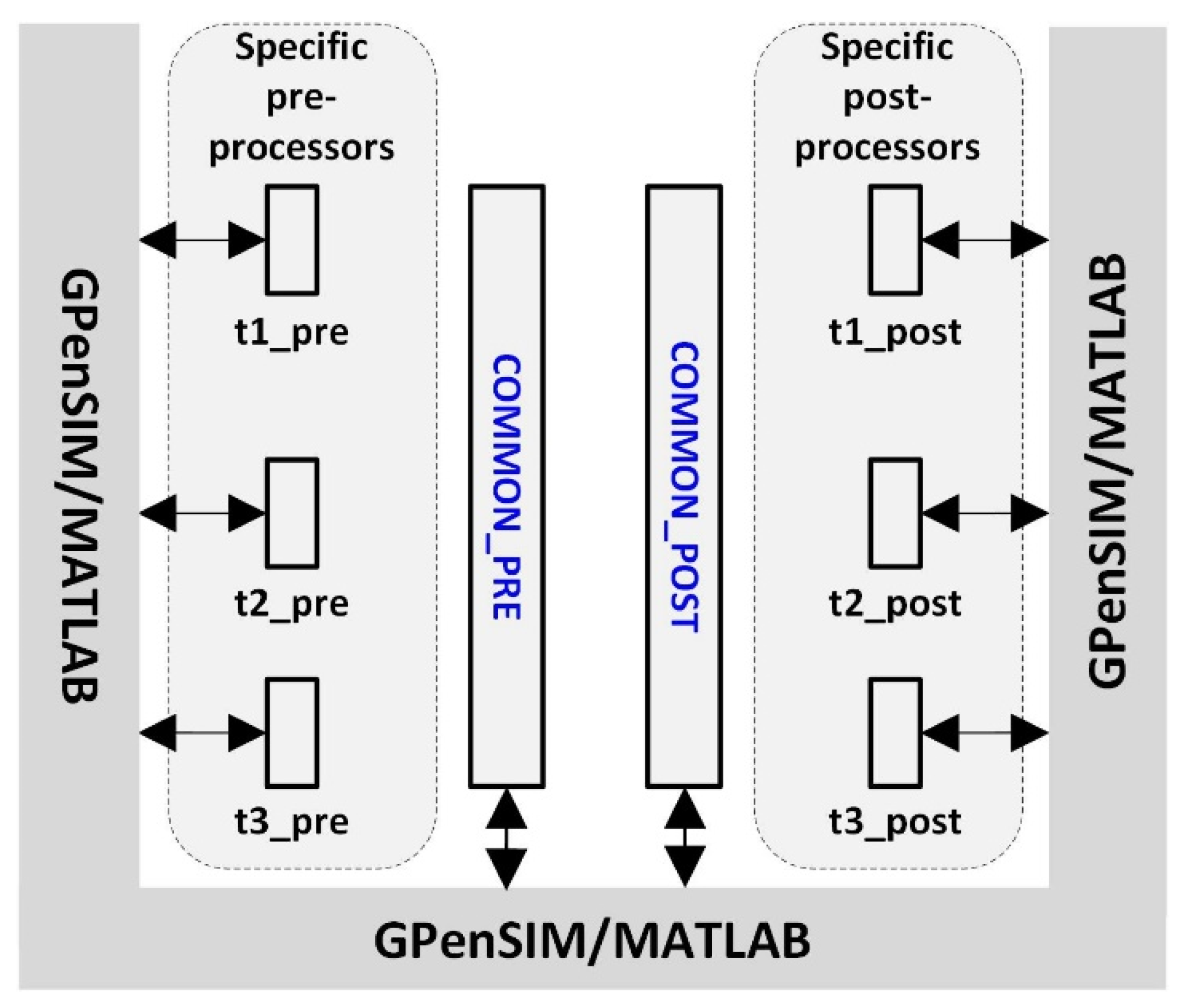
5.2. GPenSIM Processors

Since GPenSIM runs on the MATLAB platform, it allows seamless use of MATLAB’s computational power (matrix operations, advanced statistics, control systems, AI/ML/DL toolboxes) to be integrated with Petri nets. Since MATLAB provides hundreds of functions in virtually any branch of engineering, making Petri net models adapted to different domains becomes easy. Also, after Petri net simulations, modelers can leverage MATLAB’s plotting and data analysis tools for results. At a minimum, implementing a Petri net model with GPenSIM involves four M-files [47,48]:

• Petri Net Definition File (PDF): This file defines the static Petri net graph (places, transitions, and the arcs). This file will be executed only once, for creating a MATLAB structure representing the topological information of this file.
• The Main Simulation File (MSF): This file declares the initial dynamics (e.g., initial tokens, firing times of transitions) and starts the simulations. Once the simulation is started, the GPenSIM compiler takes over to run the simulation. When the simulations are complete, control is passed back to this file so that the simulation results can be analyzed and plotted.
• Pre-processors: Whenever transitions are enabled, pre-processors are executed. Only if the corresponding pre-processors return logical one, the transition will be allowed to start firing.
• Post-processors: Whenever transitions complete firing, post-processors are executed. This means that whenever a transition starts firing and completes firing, there will be a processor file executed by the compiler. Hence, it is the processor files (pre-processors and post-processors) that work as the interface, both intra-model (connecting the elements of the model) and between the model and the external world.

5.3. Integration with MATLAB and the External World

Figure 4 shows a small monolithic (non-modular) Petri net, consisting of four places (p1 to p4) and three transitions (t1 to t3). In GPenSIM, the interface for monolithic Petri net models is different from that of modular Petri nets. For a monolithic Petri net, there are two groups of processors: specific processors and common processors. For example, whenever t1 is enabled, its specific pre-processor t1_pre will be executed if it exists. Also, the common pre-processor COMMON_PRE will be executed if it exists too. Figure 5 shows the processors for the monolithic Petri net shown in Figure 4.

Figure 6 shows a small modular Petri net, consisting of two “Petri Modules,” Module-Alfa 212 and Module-Beta, and two “Inter-Modular Connectors,” IMC-X and IMC-Y. For modular Petri nets, there are three groups of processors - in addition to specific processors and common processors, there are also modular processors. For example, for the modular Petri net shown in Figure 6, whenever tAI1 (an Input Port), tAO1 (an Output Port), or tAL1 (a local transition) is enabled, its modular pre-processor MOD_Alfa_PRE will be executed if it exists. Figure 7 shows the processors for the modular Petri net shown in Figure 6.

In addition to functioning as a standalone offline Petri net simulator, GPenSIM is also designed to function as a real-time Petri net model-based controller. Literature study reveals that some works have used GPenSIM not only as a Petri net simulator but also as a controller [22,35,49]. Figure 8 shows the use of processors as the interface when Petri net models are used to interact with and control external software and hardware.

6. Discussion: Enhancing Supervisory Control with GPenSIM

GPenSIM is grounded in the systems theory principle of interconnectedness, which posits that system behavior emerges from dynamic relationships between components rather than from isolated elements. This principle, rooted in the works of Bertalanffy [37], Forrester [50], and Capra [41], emphasizes: Interdependence: Transitions, places, and tokens interact via feedback loops and dependencies, mirroring real-world discrete-event systems.

• Network Structure: Modular design patterns (centralized vs. decentralized) deter- mine adaptability, aligning with supervisory control challenges in distributed systems (Section 2.2).
• Boundary Dynamics: GPenSIM’s interface - the processors (pre/post-processors) - mod- 234 els interactions between the Petri net and its environment, addressing partial observ- 235 ability (Section 2.5) and unmodeled disturbances (Section 2.6). In the following subsection, we shall see how GPenSIM can help solve some of the difficulties we face in supervisory control theory.

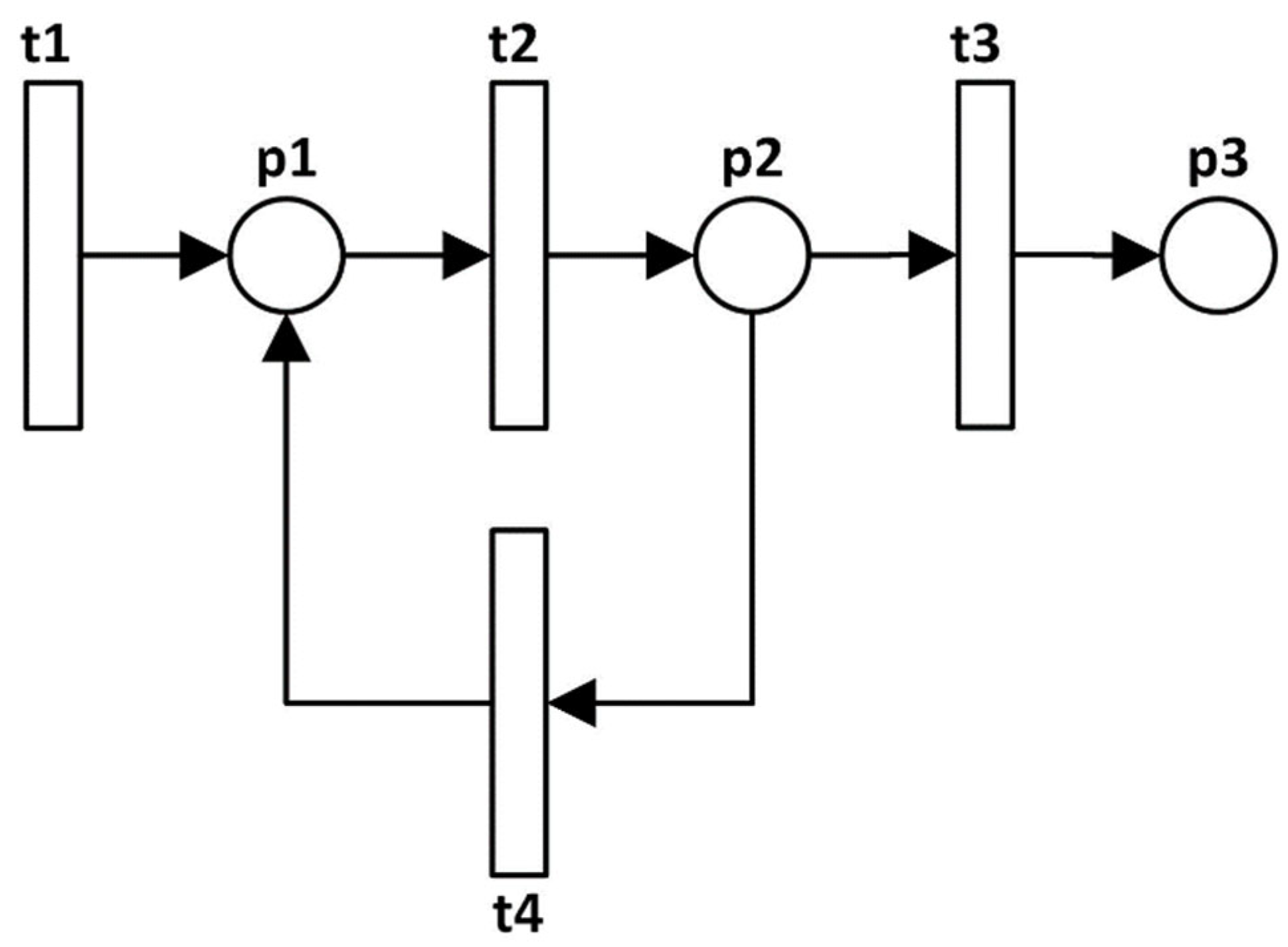
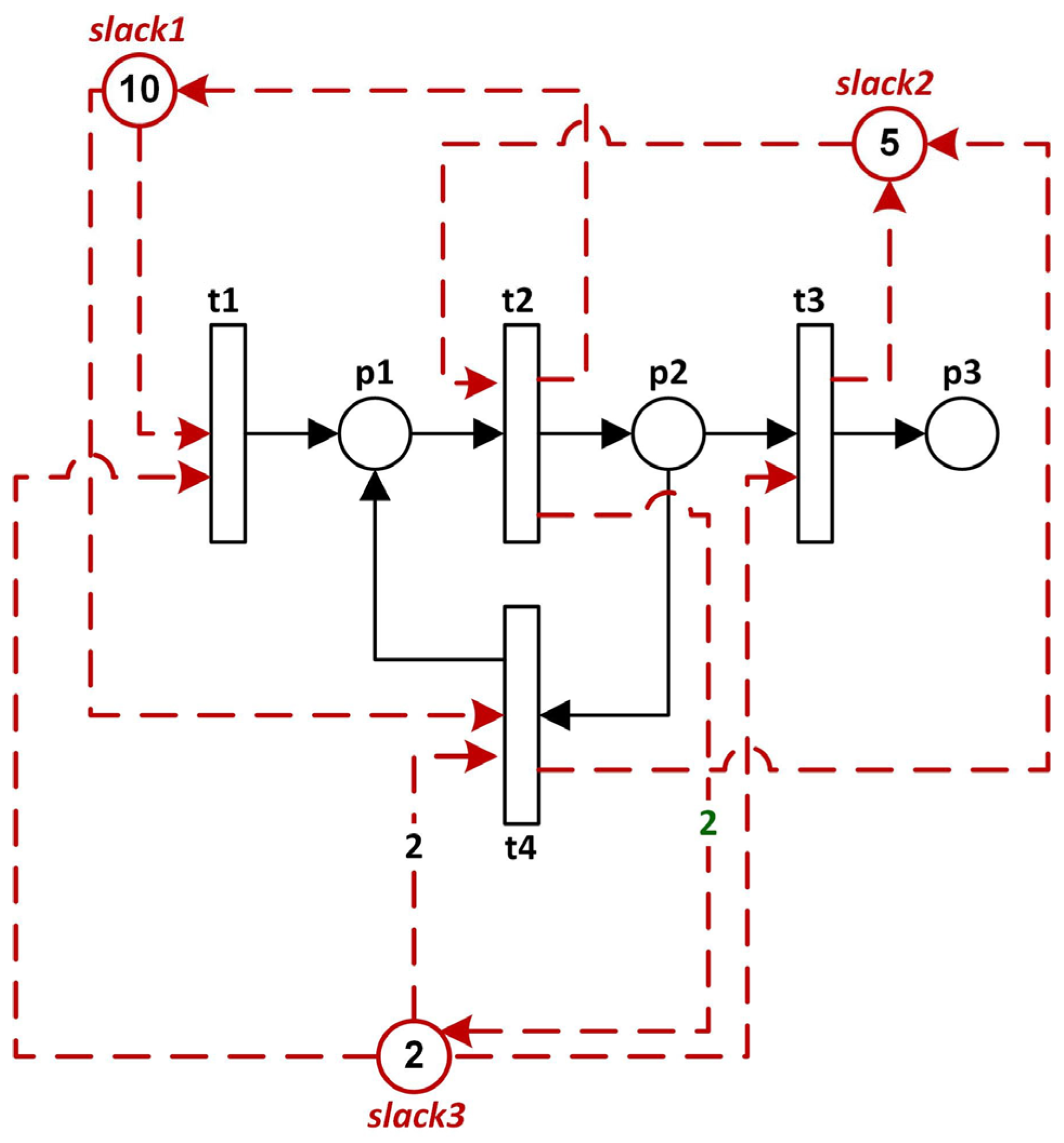
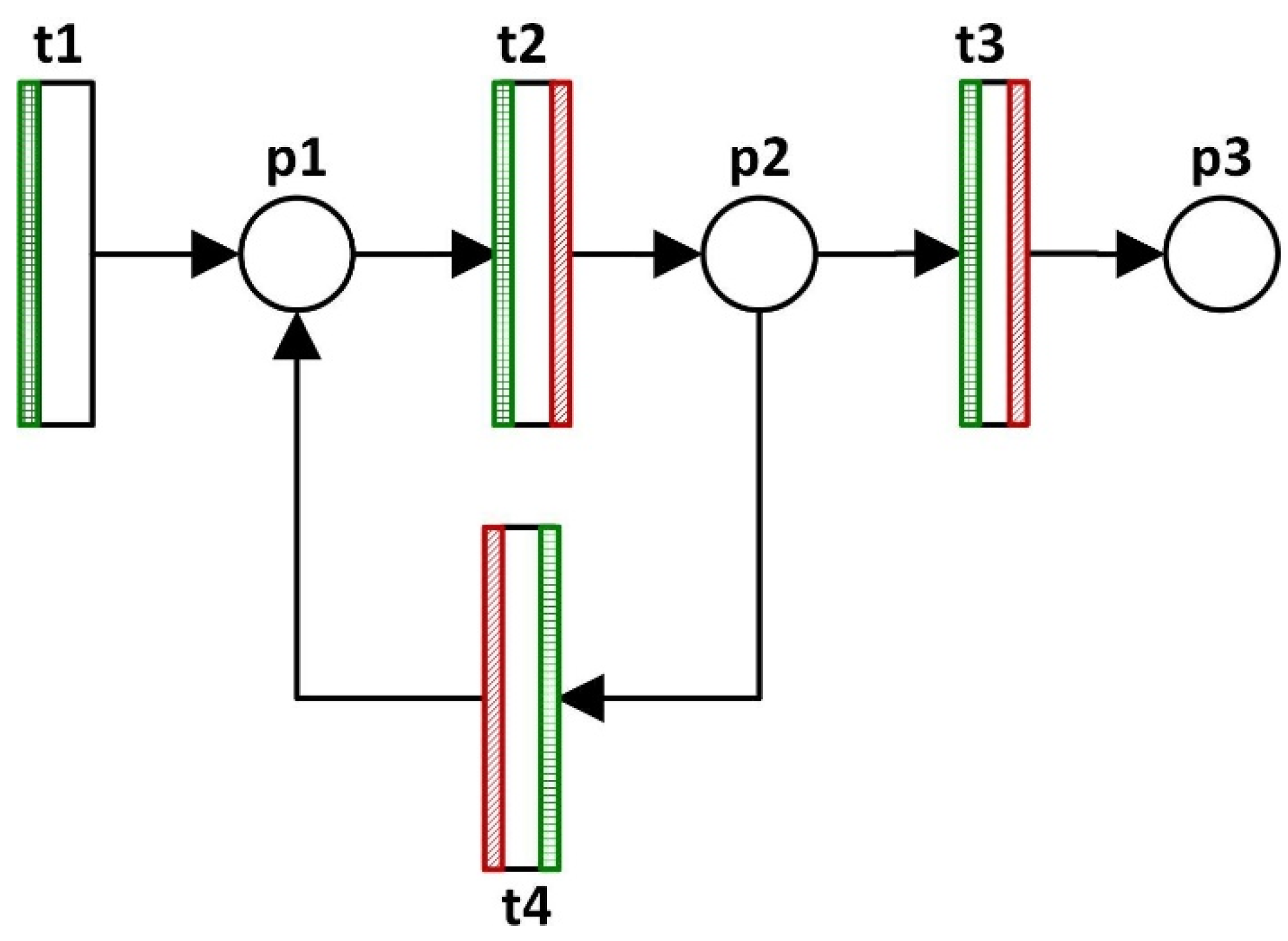
6.1. Reducing State-Space Explosion: Moving Control Logic from Controller to Processors

GPenSIM offers a unique solution to mitigate the state-space explosion problem. As we know, the number of states increases exponentially with the number of places, transitions, and tokens. Hence, embedding a supervisor (a controller with multiple control places and their tokens) on top of a plant to create a controlled system will dramatically increase the total number of states. To address this, GPenSIM provides a unique solution: mapping the controller logic into processors, so that the controlled system consists of the plant and the processors without additional state overhead.

For example, Figure 9 shows a simple plant with three places, four transitions, and no initial tokens. Consider the following three constraints:

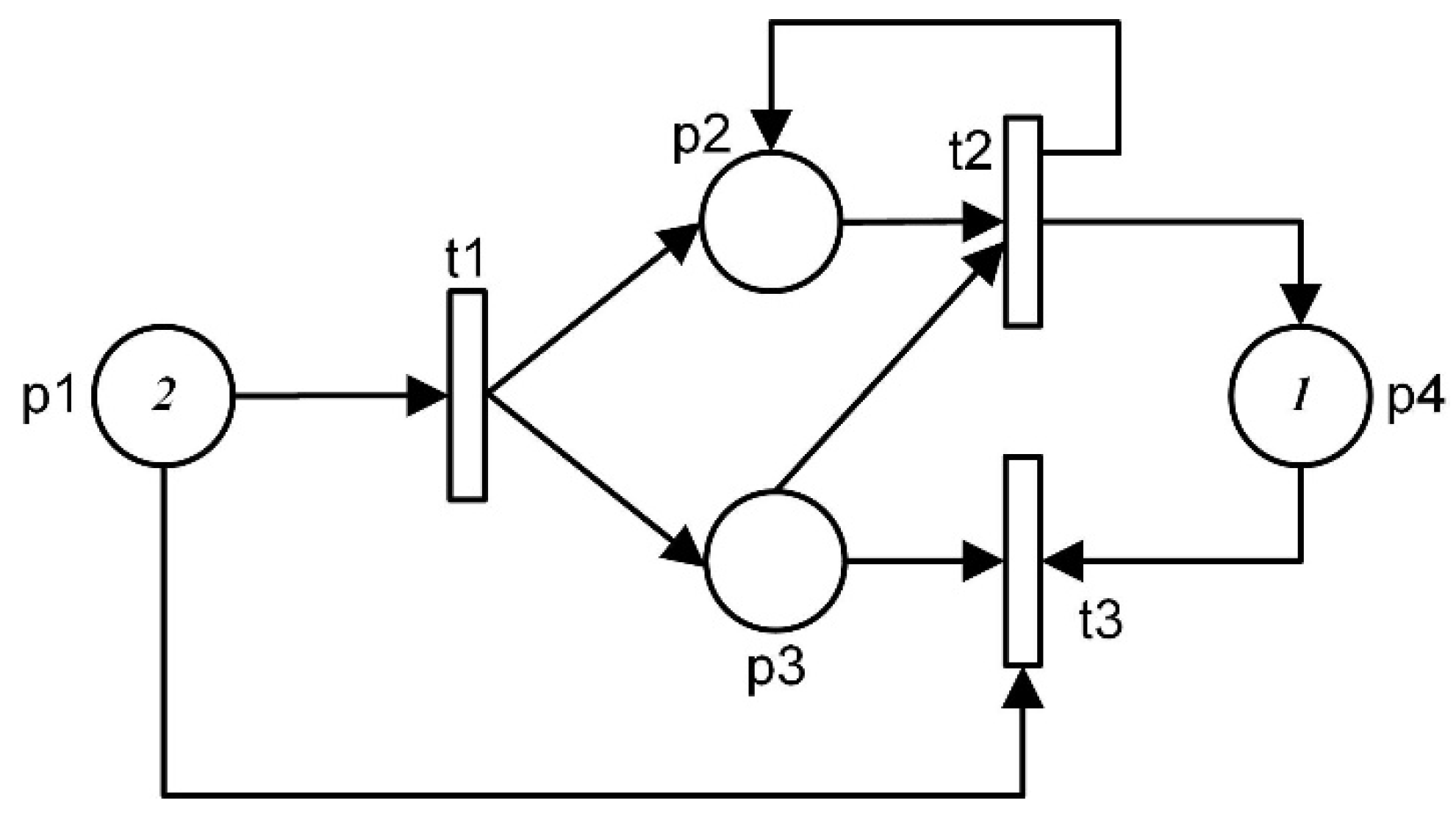
• The number of tokens in p1 must always be less than or equal to 10.
• The number of tokens in p2 must always be less than or equal to 5.
• The difference between the tokens in p1 and p2 must always be less than or equal to 2.

Figure 10 shows the controlled system synthesized using supervisory control theory, assuming all transitions are observable and controllable. The resulting supervisor includes three control places and a total of 17 tokens, which will inevitably cause the state-space of the controlled system to explode.

GPenSIM’s built-in function control2processors maps the supervisor into program code, automatically generating pre-processors and post-processors. This moves the super- visor out of the controlled system, leaving the controlled system as the original Petri net epresenting the plant. Figure 11 shows the controlled system with processors.

Listing 1 shows one of the pre-processors, t2_pre, automatically generated by GPen- SIM’s control2processors function. Listing 2 shows one of the post-processors, t3_post.

Listing 1: Specific pre-processor "t2_pre".

Listing 2: Specific post-processor "t3_post".

In addition to avoiding state-space explosion, GPenSIM’s approach of moving the supervisor’s control logic into processor files offers another advantage. As shown in Figure 12, the controlled system can be implemented in real life as a real-time controller for a physical (real-world) plant. Thus, GPenSIM provides a practical solution for developing industrial supervisory controllers.

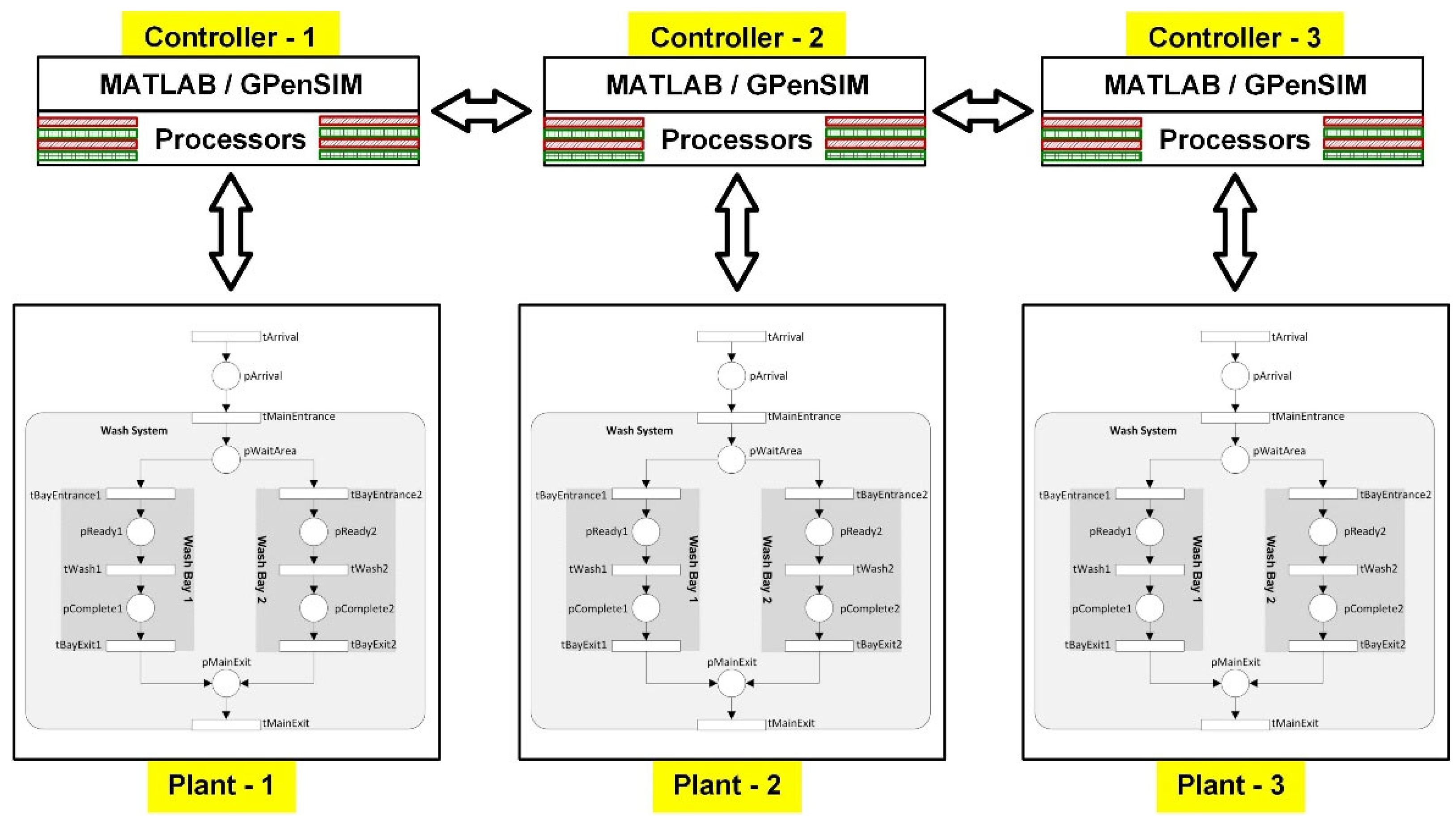
6.2. Increasing Scalability in Distributed Systems

GPenSIM supports modular Petri nets, as defined in [8]. This enables the development of multiple supervisors, each controlling a decentralized plant. These supervisors are implemented as “Petri Modules” that communicate over a shared bus. While operating independently, the distributed supervisors can also collaborate to make global decisions, requiring only minimal coordination between them. Figure 13 illustrates this architecture, showing a set of supervisors managing a decentralized plant.

GPenSIM’s modular architecture directly tackles the state-space explosion problem (Section 2.1) by:

• Decomposition: Partitioning monolithic Petri nets into weakly coupled Petri Modules (Figure 6), enabling parallel execution on multi-core systems. This reduces computational complexity from O(nk ) to O(n) for laminar-flow systems [8].
• Hierarchical Abstraction: Modules can operate at varying granularity levels, trading off detail for scalability—a key consideration in industrial automation [15].

6.3. Enhanced Expressiveness via Programmable Interfaces

Classical Petri nets lack support for nonlinear or temporal constraints (Section 2.3). Classical Petri nets lack support for nonlinear or temporal constraints (Section 2.3). GPenSIM addresses this through programmable processors, enabling:

• Nonlinear constraints (e.g., quadratic, exponential) via MATLAB expressions.
• Temporal/conditional logic (e.g., disabling transitions dynamically).

Example: Enforcing Nonlinear and Temporal Constraints Consider a plant with places p1 and p2. We enforce:

• Quadratic constraint: (p1² + p2 ≤ 100).
• Temporal constraint: Transition t1 is disabled for 60 seconds if p1 exceeds a threshold.

GPenSIM Implementation (version 11):

• Pre-processor for t1 (‘t1_pre.m‘) enforces the quadratic constraint and temporal block-ing:

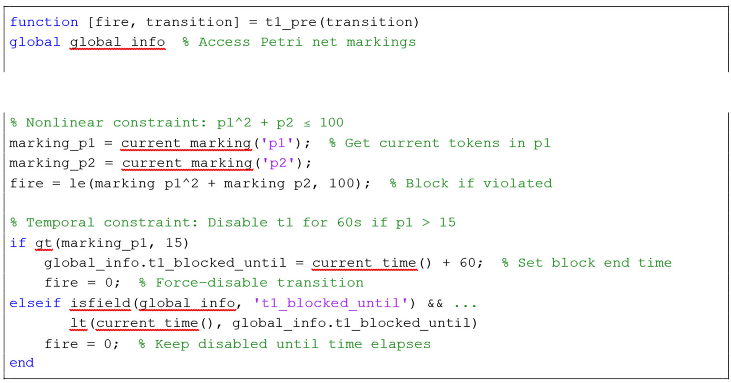
2.

Post-processor for t1 (‘t1_post.m‘) logs violations:

Key features demonstrated in the above code:

• Nonlinear arithmetic: Direct use of MATLAB’s math operators (‘^‘, ‘+‘).
• Dynamic state checks: GPenSIM’s built-in function‘current_marking’ queries real time token counts.
• Temporal control: GPenSIM’s Global variables (‘global_info‘) track blocking dura-tions.
• Integration: Leverages MATLAB’s native functions (e.g., ‘disp’) and GPenSIM’s built-in functions (e.g., ‘current_time‘).

GPenSIM’s approach extends classical Petri nets to hybrid systems without modifying the net structure, addressing the rigidity noted in Section 2.3.

6.4. Mitigating Rigid Control via Adaptive Processors

As noted in Section 2.4, classical supervisory controllers often disable all transitions leading to illegal states, even when some paths could safely proceed. GPenSIM’s processors enable adaptive control by:

• Conditional enabling of transitions based on real-time system state.
• Partial permissions (e.g., allowing transitions only under specific token distributions).

Example: Relaxing Overly Conservative Control Consider a manufacturing system where:

• Plant: Places p1 (raw materials), p2 (workspace), p3 (finished goods).
• Constraint: Avoid workspace overflow (‘p2 ≤ 5‘), but allow temporary violations if p3 is nearly empty (to maintain throughput).

GPenSIM Implementation (version 11):

• Pre-processor for t_work (‘t_work_pre.m‘) dynamically adjusts enforcement:

2.

Post-processor for t_work (‘t_work_post.m‘) logs relaxations:

Key features demonstrated in the code above:

• Context-aware firing: Transitions are blocked only when strictly necessary (e.g., ‘p2 > 5‘ and ‘p3 ≥ 2‘).
• Real-time state checks: Uses GPenSIM’s built-in function‘current_marking‘ to evaluate tokens dynamically.
• Logging: Trades off rigor for throughput while maintaining auditability.
• GPenSIM integration: Leverages GPenSIM’s built-in functions like ‘log_file‘ for traceability.
• Theoretical Alignment: This approach aligns with Ghaffari et al.’s maximally permissive control [17] by minimizing unnecessary restrictions, while GPenSIM’s programmability avoids the complexity of formal region theory.

7. Conclusions

Supervisory control theory based on Petri nets provides a robust framework for discrete-event systems but faces persistent challenges in scalability, expressiveness, and practical implementation. This paper presented GPenSIM, a MATLAB-based modular Petri net tool, as a versatile solution to these limitations; GPenSIM is developed by the first author of this paper. By leveraging modular decomposition, programmable interfaces known as the processors, and integration with MATLAB, GPenSIM addresses three core challenges identified in Section 2, such as State-Space Explosion (Section 2.1), Rigid Enforcement (Section 2.4), and Limited Expressiveness (Section 2.3). Broader Implications of this paper:

• Industrial Applicability: GPenSIM bridges the gap between theoretical models and real-world deployment. Its processors interface with external hardware/software (Figure 8), enabling real-time control synthesis (e.g., Kaid et al.’s work [22]).
• Scalability: Petri Modules (Section 4) distribute control across decentralized systems (Section 6.2), minimizing synchronization delays via Inter-Modular Connectors (Figure 1).
• Theoretical Grounding: GPenSIM embodies the Theory of Connection (Section 5.1), emphasizing dynamic interdependencies between system components - a principle rooted in Bertalanffy’s systems theory [37].

Limitations and Future Work: While GPenSIM advances supervisory control theory, challenges remain:

• Abstraction Trade-offs: Modular decomposition requires laminar-flow models (Section 2.1), limiting applicability to highly interconnected systems.
• Verification: GPenSIM lacks native formal verification tools, though bridges to model checkers like NuSMV [51] offer partial solutions.

Future research could explore:

• Hybrid Systems: Integrating continuous dynamics (e.g., via MATLAB’s Control Toolbox).
• AI/ML Enhancements: Adaptive processors trained on historical data to optimize constraints dynamically.

Final Remarks: GPenSIM redefines supervisory control by prioritizing practicality, scalability, and expressiveness. Its modular architecture and MATLAB integration provide a unified platform for academia and industry, as demonstrated in manufacturing and distributed control case studies (Section 6.4). By addressing the limitations of classical supervisory control theory, GPenSIM not only extends the theoretical boundaries of Petri nets but also delivers a practical toolkit for next-generation discrete-event systems.