1. Introduction
The adventure via arithmetic schooling regularly encounters a substantial conceptual chasm: fractions. For many college students in Key Stages Two and Three (a while 7-14), fractions constitute a powerful barrier, regularly main to confusion, anxiety, and a fragmented expertise that persists into better ranges of arithmetic (Schoenfield, 2020). Despite a long time of studies and pedagogical innovation, a widespread share of college students war with even simple fractional principles, not to mention complicated operations (Stephan, 2020). This continual trouble underscores the want for alternative, greater intuitive, and conceptually strong coaching methodologies.
Traditional methods regularly depend on discrete bodily manipulatives (e.g., fraction circles, bars) or summary numerical algorithms. While those techniques have their place, they can on occasion fail to deliver the underlying proportional relationships and the non-stop nature of fractions, especially while handling equivalence, ordering, and operations that amplify past easy unit fractions. The disconnect among “components of an entire” and the summary notation regularly proves hard for growing mathematical fluency and actual mastery.
This article posits that fractal geometry, a subject historically related to superior arithmetic and herbal phenomena, gives a powerful, but underexplored, pedagogical lens via which to train fractions. Fractals are inherently self-comparable, that means they showcase comparable styles at more and more exceptional scales. This asset immediately mirrors the idea of partitioning an entire into smaller, equal components, and the recursive nature of subdividing the ones components. By visualising and interacting with fractals, college students can increase a deep, embodied expertise of proportionality, equivalence, iteration, and countless subdivision – all center principles in fractional arithmetic.
The purpose of this paper is threefold: first, to articulate the unique conceptual demanding situations college students face with fractions; second, to advocate how a fractal geometric technique can intrinsically deal with those demanding situations, fostering a pathway to mastery; and third, to define essential open issues for destiny studies, advocate a blended theoretical framework that justifies this technique, and speak the function of sensible exercise in consolidating mastering. This exploration seeks to put the foundation for a greater intuitive and enduring expertise of fractions, re-modeling a not unusual place stumbling block right into a gateway for superior mathematical thinking.
2. The Conceptual Challenges of Fractions for Key Stages Two and Three
Students’ problems with fractions are well-documented and multifaceted, regularly stemming from an over-reliance on entire-variety reasoning, a loss of strong conceptual fashions, and the summary nature of the notation, as depicted in Figs.1& 2(c.f.,Tossavainen & Helenius, 2024).
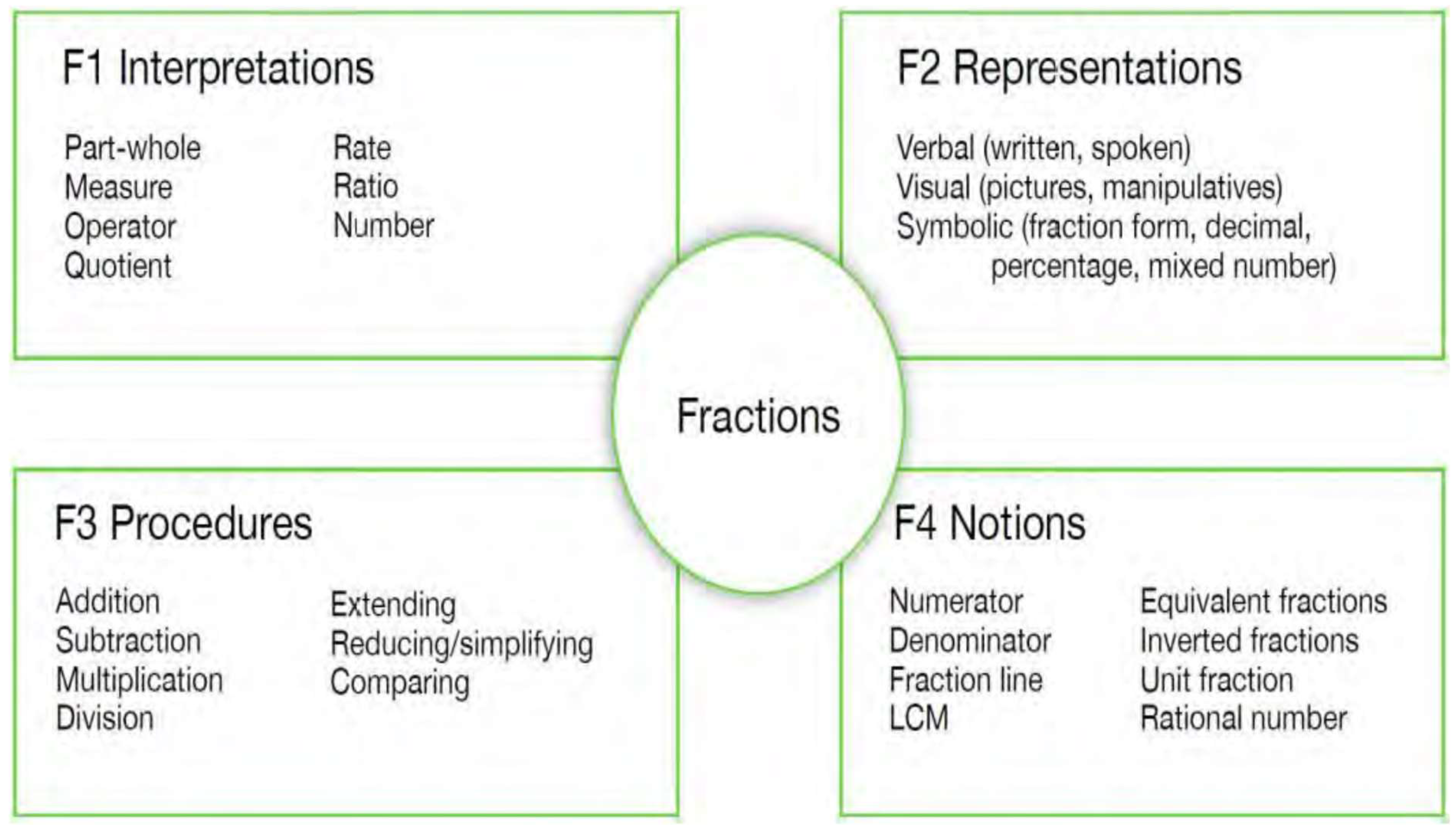
Figure 1.
The framework’s categories and subcategories for examining various fractional aspects.
Figure 1.
The framework’s categories and subcategories for examining various fractional aspects.
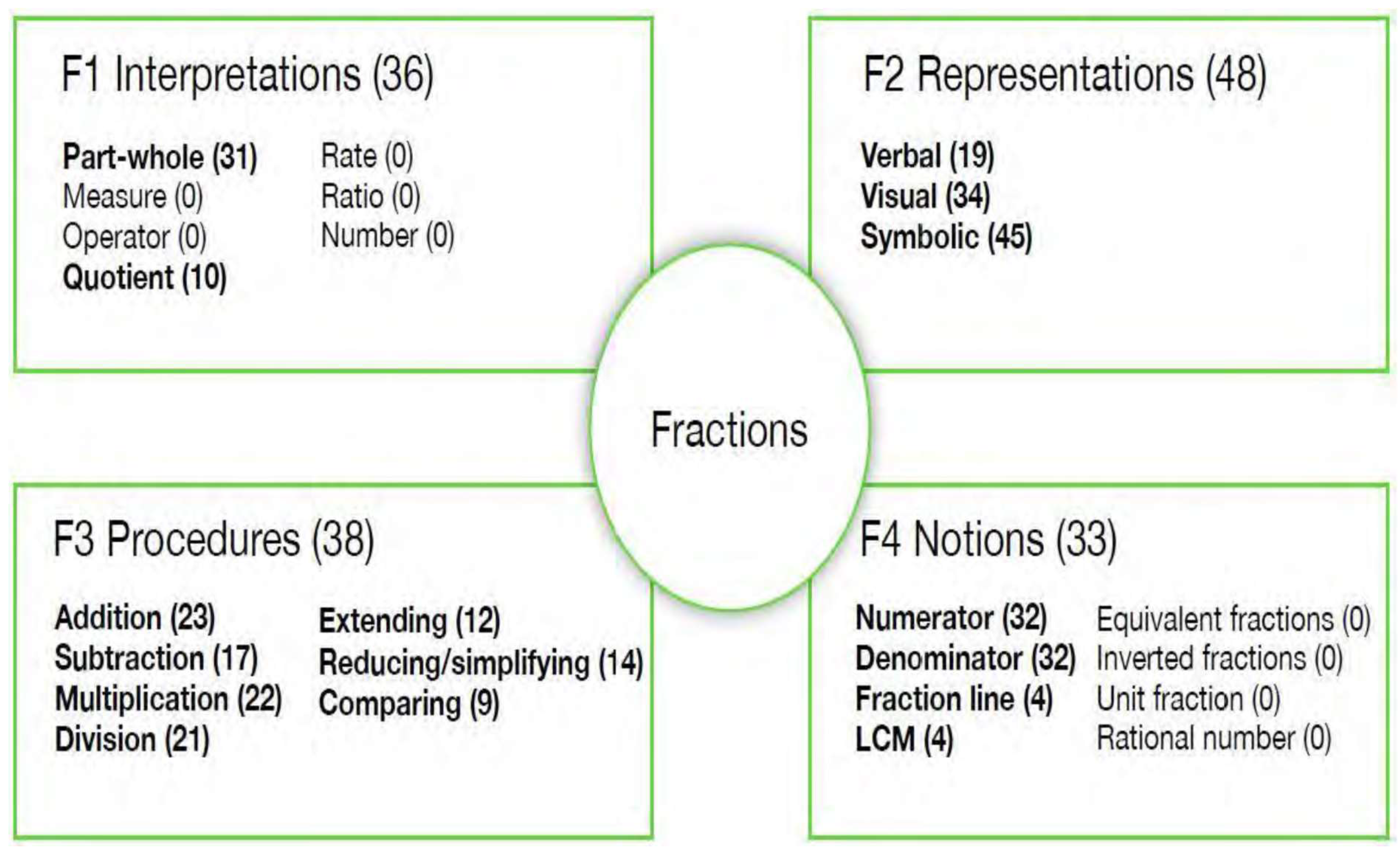
Figure 2.
An example of the fraction’s knowledge held by the student instructors that participated. The number of participants relating to a category or subcategory is indicated by numbers in parenthesis.
Figure 2.
An example of the fraction’s knowledge held by the student instructors that participated. The number of participants relating to a category or subcategory is indicated by numbers in parenthesis.
Key demanding situations include:
2.1. The Whole-Number Bias
Children’s preliminary mathematical expertise is firmly rooted in entire numbers. When brought to fractions, they regularly incorrectly follow homes of entire numbers, along with if
is smaller than
due to the fact three is smaller than four, as visually depicted by
Figure 3 (c.f., Fu et al., 2020). This “entire-variety bias” makes principles like evaluating unit fractions or expertise that multiplying with the aid of using a fragment can bring about a smaller variety counter-intuitive.
2.2. Understanding the Part-Whole Relationship
While “components of an entire” is regularly the preliminary definition of a fragment, college students regularly war to become aware of the “entire” or recognize that the components ought to be same in size. This foundational idea is essential, but regularly superficially grasped, main to mistakes in illustration and interpretation (Wästerlid, 2020). Furthermore, fractions can constitute numerous interpretations past part-entire, along with quotient, ratio, operator, or measure, which provides to the cognitive load, see
Figure 4(Gaidoschik, 2023). Throughout the interviews (Gaidoschik, 2023), the girl, referred to as, Lina, who is extremely shy and talked quietly, seemed to try her hardest to finish the tasks assigned to her.
2.3. Equivalence and Ordering
Grasping that unique fractions can constitute the equal value (e.g., ) is essential however regularly a supply of confusion. Students can also additionally depend on rote algorithms (e.g., multiplying numerator and denominator with the aid of using the equal variety) without expertise because the values are equal. Similarly, ordering fractions (e.g., putting , on a range of line) calls for a robust experience of relative magnitude, that is regularly underdeveloped (Clements et al., 2023).
2.4. Operations with Fractions
Adding, subtracting, multiplying, and dividing fractions introduce new layers of complexity. Adding and subtracting require a not unusual place denominator, an idea regularly finished procedurally without deep expertise of why it’s far necessary. Multiplication and department regularly defy entire-variety logic (e.g., multiplying with the aid of using a fragment much less than one makes the variety smaller; dividing with the aid of using a fragment much less than one makes the variety larger), contributing to substantial cognitive dissonance (Amo-Asante, & Bonyah, 2023).
2.5. Abstract Notation and Symbolism
The notation is rather summary. Students war to attach this image to concrete portions and actions. The numerator and denominator are regularly dealt with as separate entire numbers in place of additives of an unmarried numerical entity representing a quantity.
These demanding situations spotlight the want for a pedagogical technique that gives concrete, dynamic, and visually wealthy fashions that intrinsically illustrate the proportional, recursive, and non-stop nature of fractions, thereby constructing strong conceptual expertise earlier than procedural fluency.
3. Fractal Geometry as a Pedagogical Tool for Fractions
Fractal geometry gives a completely unique and compelling framework for addressing the challenges. Fractals are geometric shapes that showcase self-similarity, that means they seem the identical at any scale (Mageed & Bhat, 2022; Mageed & Mohamed, 2023; Mageed, 2023a; Mageed, 2024a ; Mageed, 2024b; Mageed, 2024c: Mageed, 2024d; Mageed, 2024e), as magnificently demonstrated by
Figure 5 (Mageed, 2025c) . This property, in conjunction with their recursive production, affords effective visible metaphors and urban examples for essential fractional principles.
3.1. Self-Similarity and Parts of a Whole
The self-comparable nature of fractals(Mageed , 2025 a; Mageed , 2025 b; Mageed & Nazir, 2024; Mageed, 2024a ; Mageed, 2024f; Mageed, 2024g: Mageed, 2024h; Mageed, 2024i) immediately mirrors the concept of an entire being composed of smaller elements which can be proportional to the whole. Consider the Sierpinski Triangle(Tan et al., 2022; Zhao et al., 2024), built through beginning with an equilateral triangle, dividing it into 4 smaller equilateral triangles, and getting rid of the crucial one. The Sierpinski triangle is another fractal that demonstrates the self-similarity trait. An example of a three-way recursive algorithm is the Sierpinski triangle. A Sierpinski triangle can be drawn by hand in a straightforward manner. Take one big triangle as a starting point. Connect the midpoints of each side of this huge triangle to create four new triangles. Use the same process for each of the three corner triangles, ignoring the middle triangle you just made. This process is applied recursively to the three smaller corner triangles in each subsequent set of triangles. If you have a sharp enough pencil, you can use this process indefinitely. You might wish to try drawing the Sierpinski triangle yourself using the technique explained before reading on. This system is then recursively implemented to the last 3 triangles, as demonstrated by
Figure 6 (c.f., Runestone Academy, 2025)
Visualizing Unit Fractions: Each generation vividly demonstrates how a “whole” (the preliminary triangle) is split into a selected quantity of identical elements (4), and a sure “fraction” of it’s far eliminated or retained(Mageed , 2025 a; Mageed , 2025 b; Mageed & Nazir, 2024; Mageed, 2024a ; Mageed, 2024f; Mageed, 2024g: Mageed, 2024h; Mageed, 2024i).The last elements constitute fractional portions (e.g., three/four of the location stays after the primary generation).
Recursive Partitioning: The non-stop subdivision illustrates the endless divisibility inherent in fractions, shifting past the discrete “elements” and closer to a non-stop quantity( Li et al., 2022). This enables counter the whole-quantity bias through displaying that segments may be infinitely refined.
3.2. Scaling and Equivalence
Fractals inherently contain scaling(Mageed & Bhat, 2022; Mageed & Mohamed, 2023; Mageed, 2023a; Mageed, 2024a ; Mageed, 2024b; Mageed, 2024c: Mageed, 2024d; Mageed, 2024e). As one zooms right into a fractal, the styles repeat, however at a distinctive scale. This affords an intuitive manner to recognize equivalence.
Koch Snowflake: This fractal is built through beginning with an equilateral triangle, dividing every aspect into 3 segments, and changing the center section with segments forming an outward equilateral triangle(Mageed & Bhat, 2022; Mageed & Mohamed, 2023; Mageed, 2023a; Mageed, 2024a ; Mageed, 2024b; Mageed, 2024c: Mageed, 2024d; Mageed, 2024e). Each generation will increase the fringe at the same time as preserving the general shape. This system obviously illustrates that of a section is being manipulated, and that smaller pieces (e.g., or of the unique section) relate proportionally to the bigger whole. Students can visually see that editing elements proportionally keeps the “essence” of the shape, analogous to half being equal to through scaling up the quantity of elements.
3.3. Infinite Iteration and Density
The endless nature of fractal production enables to bring the density of rational numbers. Between any fractions, there may be an endless quantity of different fractions (Mageed & Bhat, 2022; Mageed & Mohamed, 2023; Mageed, 2023a; Mageed, 2024a ; Mageed, 2024b; Mageed, 2024c: Mageed, 2024d; Mageed, 2024e). While this will be a tough idea to grasp, the non-stop system of including element in fractals (e.g., producing increasingly problematic branches in a fractal tree) affords a visible analogue for this density.
3.4. Operations with Fractals
While direct utility of operations on complicated fractals is probably too superior for KS2/3, simplified fractal-like systems may be used (Yu et al., 2023).
Addition/Subtraction: Imagine a fractal bar. If a bar is split into fifths (López, 2021), and -fifths are shaded, then every other -fifths are shaded, college students can visually integrate those sections. The recursive nature approach that if is itself a smaller fractal, college students can see how combining those “sub-fractals” provides to the bigger whole.
Multiplication: “Of “ in fractions approach multiplication(López, 2021). Consider taking half of a section. If a fractal is built in ranges in which every level represents a fragment of the preceding level, college students can see how a fragment of a fragment works. For example, if a department splits into 3 smaller branches, after which every of these splits into , takingof half of the unique “increase potential” may be visualised.
3.5. Beyond the Visual: Connection to Number Lines
Fractals also can be used to beautify knowledge of fractions on various line. The production of a Cantor Set (Athreya et al., 2019), for instance, includes again and again getting rid of the center of line segments. This system inherently locations fractional factors on a line, demonstrating how a non-stop line may be partitioned and the way fractions occupy specific, but infinitely divisible, factors.
By attracting college students with the production Filipczak & Nowakowski, 2023), observation, and manipulation of easy fractal styles (e.g., thru drawing, paper folding, or virtual tools), educators can offer a concrete, dynamic, and aesthetically attractive access factor into the summary international of fractions. This technique leverages visible-spatial reasoning and sample recognition, which can be regularly robust in younger learners, to construct a stronger conceptual foundation.
4. Teaching Fractions for Mastery
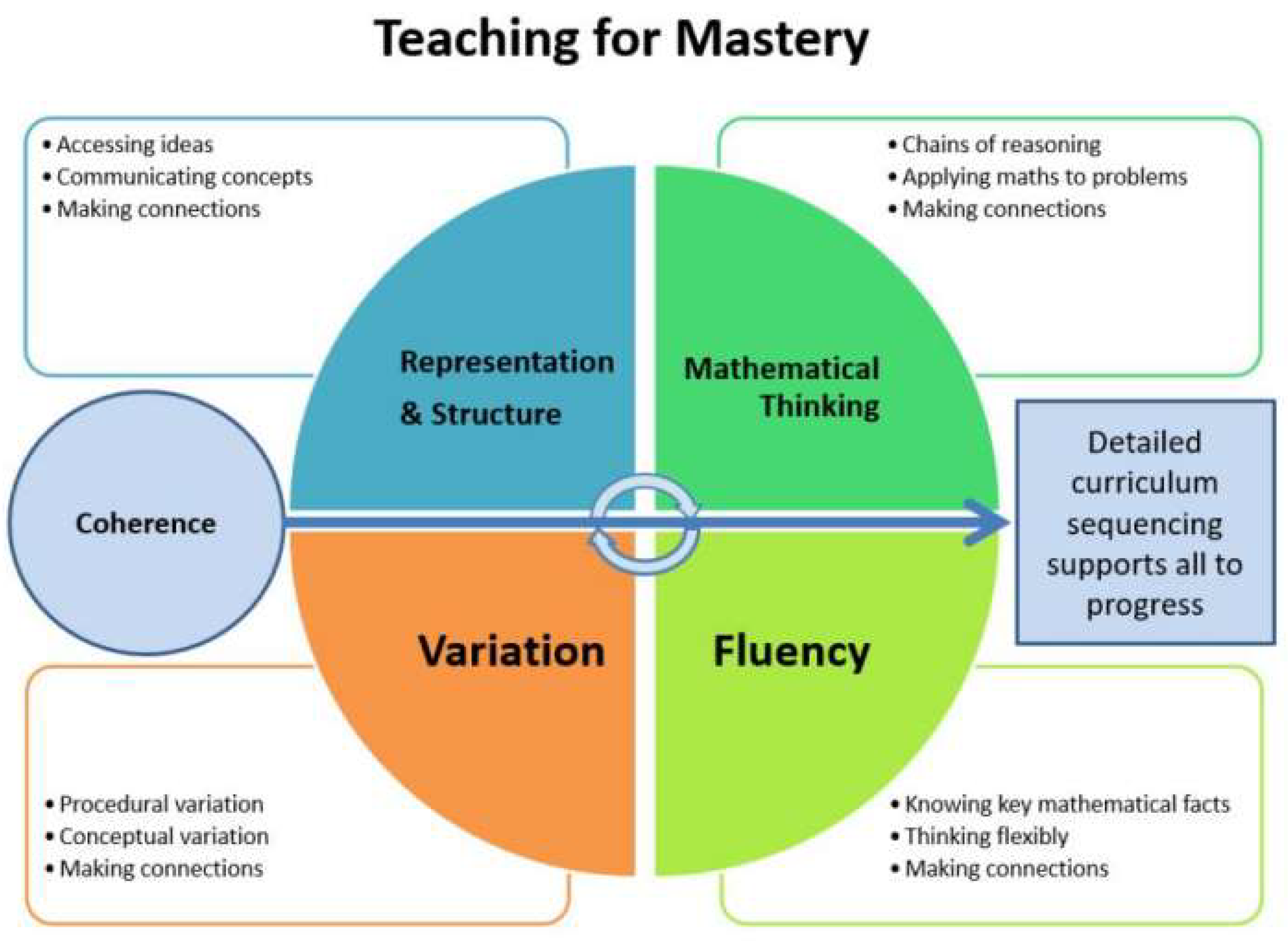
The idea of “mastery” in arithmetic schooling refers to a deep, flexible, and transferable knowledge of a topic, instead of superficial information or rote utility of procedures (Acuña & Blacklock, P.J., 2022; NCETM, 2017; NCETM, 2022; NCETM, 2023). It implies now no longer simply the capacity to carry out calculations correctly, however, additionally to explain principles, resolve issues in various contexts, and practice information to new situations, as in
Figure 7(c.f., NCETM, 2017). For fractions, mastery approach:
Conceptual Understanding(Barrera & Shah, 2023): Knowing what a fragment represents (a couple of interpretations).
Procedural Fluency (William et al., 2023): Performing operations as it should be and efficiently.
Strategic Competence( Fric et al., 2023): Selecting suitable techniques for problem-solving.
Adaptive Reasoning (Lestari et al., 2022): Justifying answers and making logical connections.
Productive Disposition(Awofala et al., 2022): Developing a tremendous mind-set closer to fractions and seeing their relevance.
A fractal geometric technique aligns strongly with the ideas of mastery studying. By imparting a rich, visible, and interactive context, it encourages college students to:
Explore and Discover: Students assemble fractals(Tzanaki et al., 2024; Pan et al., 2025), actively coming across styles and relationships, instead of passively receiving rules. This lively engagement fosters deeper knowledge.
See the “Why”: The inherent self-similarity and recursive nature of fractals obviously explain why equal fractions work, or why sure operations result in unique outcomes (Tzanaki et al., 2024; Pan et al., 2025), shifting past mere procedural memorisation.
Develop Intuition: The visible and dynamic nature of fractals enables construct an intuitive experience of fractional portions and their relative magnitudes(Tzanaki et al., 2024; Pan et al., 2025), addressing the whole-quantity bias.
Connect Concepts: Fractals can bridge reputedly (Tzanaki et al., 2024; Pan et al., 2025)disparate mathematical ideas, connecting geometry, quantity theory, or even early algebraic thinking (through recursive rules).
Traditional mastery studying cycles contain pre-evaluation, instruction, formative evaluation, corrective instruction (for the ones now no longer but at mastery), and enrichment (for the ones who’ve done mastery) (Akpan, 2020). Incorporating fractals into this cycle could imply designing fractal-primarily based totally sports for instruction, the use of fractal representations in evaluation tasks, and using fractal manipulations for focused corrective instruction, permitting college students to revisit principles from a distinctive, regularly greater intuitive, attitude till deep knowledge is done.
5. Open Problems and Research Questions
While promising, a fractal geometric technique to coaching fractions isn’t without its demanding situations and calls for huge empirical validation. Several open troubles and studies questions want to be addressed:
5.1. Empirical Efficacy and Long-Term Impact
Primary Question: Does the combination of fractal geometry into fraction coaching (Zhao et al., 2024)appreciably enhance college students’ conceptual expertise(Corrêa & Rangel, (2021), procedural fluency, and problem-fixing skills as compared to standard methods?
Longitudinal Studies(Bleidorn et al., 2022): What is the long-time period effect of this technique on mathematical confidence, retention of fractional ideas, and next getting to know in algebra and better arithmetic?
Specificity of Impact (Shanty, 2023): Are positive fractional ideas (e.g., equivalence, multiplication) extra correctly taught thru fractals than others (e.g., subtraction with not like denominators)?
5.2. Curriculum Integration and Teacher Training
Curriculum Mapping(Cooper et al., 2024): How can fractal geometry be seamlessly incorporated into present Key Stage Two and Three arithmetic curricula without overwhelming instructors or displacing vital content? At what age/level are college students cognitively equipped for summary fractal ideas?
Teacher Readiness(Nurzen, 2022): What stage of schooling do instructors require to correctly put in force this technique? Many instructors might also additionally have restricted publicity to fractal geometry; what expert improvement fashions are handiest?
Resource Development (Ferrari et al., 2023): What specific, accessible, and tasty educational materials (virtual tools, bodily manipulatives, lesson plans) are had to guide this technique?
5.3. Accessibility and Equity
Diverse Learners (Kumi-Yeboah et al., 2020): How powerful is the fractal technique for college kids with extraordinary getting to know styles, unique instructional needs, or from numerous linguistic and cultural backgrounds? Does it lessen getting to know disparities or inadvertently create new ones?
Cognitive Load Management(Behari, 2023): While supposed to lessen cognitive load, complicated fractals can themselves be challenging. How can the complexity be scaffolded as it should be for extraordinary age corporations and skills?
5.4. Assessment Methods
Measuring Mastery(Porter et al., 2020): How can mastery of fractions, mainly the conceptual expertise fostered with the aid of using fractals, be correctly assessed? Traditional checks might not seize the intensity of expertise won thru this technique.
Authentic Assessment (McArthur, 2023): What varieties of proper assessment (e.g., layout projects, presentations, motives of fractal properties) are suitable for comparing getting to know inside this framework?
5.5. Technology and Implementation
Digital Tools (Dansca et al., 2023): What function do virtual tools (e.g., interactive fractal generators, simulation software) play in facilitating getting to know, and the way can they be designed to maximize their pedagogical effect?
Scalability(Piccoli et al., 2020): How can this technique be scaled from pilot research to significant implementation throughout faculties and academic systems?
Addressing those open troubles thru rigorous studies is critical for figuring out the viability and significant applicability of a fractal geometric technique to coaching fractions.
6. A Combined Theoretical Framework
To robustly underpin the fractal geometric technique to coaching fractions (Hearne, 2021), a synthesis of numerous outstanding getting to know theories gives a complete theoretical framework. This mixed attitude highlights how fractals can facilitate deep conceptual expertise and mastery.
6.1. Cognitive Load Theory
Cognitive Load Theory (Sweller, 2020) posits that getting to know is handiest whilst educational layout minimises extraneous cognitive load (needless intellectual attempt) and optimises intrinsic cognitive load (attempt associated with the complexity of the fabric itself) and germane cognitive load (attempt invested in schema creation).
Application(Copur-Gencturk, 2021): Fractions, particularly operations, regularly impose excessive intrinsic cognitive load because of their summary nature and the counter-intuitive software of whole-variety rules. Fractal representations can appreciably lessen extraneous load with the aid of using supplying a single, coherent, visible version that unifies more than one fractional idea (part-whole, equivalence, operations). By seeing the relationships embedded inside a self-comparable structure(Harkotte, 2022), college students might also additionally require much less intellectual attempt to manipulate disparate portions of information, hence releasing up operating reminiscence for schema creation (germane load). The visible nature additionally reduces the split-interest impact regularly visible whilst college students need to combine text, numbers, and diagrams separately.
6.2. Constructivism
Constructivism emphasises (Kouicem, 2020) that rookies actively assemble their personal expertise and information of the sector thru experiencing matters and reflecting on the ones experiences.
Application: The fractal technique is inherently constructivist (Rodriguez & Towns, 2021). Students aren’t passively pointed out fractions; instead, they interact withinside the creation of fractals (e.g., thru drawing, paper folding, the use of virtual generators). This lively engagement permits them to find out the inherent fractional relationships (e.g., that of a duration eliminated from a phase creates a selected pattern (Rodriguez & Towns, 2021), or that every generation represents a fragment of the preceding level). The technique of constructing and editing fractals permits for assimilation and lodging of recent fractional schemas.
6.3. Inactivism
Inactivism (Ertl, 2024) argues that cognition arises from the dynamic interplay among an appearing organism and its environment. Knowledge isn’t simply represented internally however is enacted thru sensorimotor activity.
Application: Beyond simply visualising, the act of making fractals (e.g., drawing iterations of a Koch snowflake, folding a Sierpinski gasket) embodies fractional procedures. The learner’s frame and movements come to be essential to expertise(Taylor, 2023). For instance(Cui et al., 2023), the repeated movement of dividing a line phase into thirds and manipulating the center segment bodily instantiates the idea of and its function in developing a brand-new structure. This “getting to know with the aid of using doing” strengthens the conceptual hyperlinks among bodily movement and summary mathematical ideas.
6.4. Embodied Cognition
Closely associated with inactivism, embodied cognition(Agostini & Francesconi, 2021) posits that our cognitive procedures are deeply rooted in our physical interactions with the sector and our sensory experiences.
Application: When college students bodily manage fractal patterns (e.g., reducing paper triangles for a Sierpinski gasket, the use of blocks to construct a fractal pyramid) (Abrahamson et al., 2020; Soto-Andrade et al., 2022), they’re constructing intellectual fashions grounded in sensorimotor experience. The spatial reasoning worried in expertise self-similarity and scale inside a fractal is without delay tied to the frame’s interplay with space(Abrahamson et al., 2020; Soto-Andrade et al., 2022). This bodily grounding could make summary fractional ideas extra tangible and much less vulnerable to summary errors(Abrahamson et al., 2020; Soto-Andrade et al., 2022). The “feel” of dividing something into identical parts(Abrahamson et al., 2020; Soto-Andrade et al., 2022), even if represented geometrically, may be profound.
6.5. Zone of Proximal Development (ZPD)
The ZPD (Xi & Lantolf, 2021) defines the variety of duties that a learner can carry out with the assist and steerage of an extra informed other, however cannot but carry out independently.
Application: Teachers can strategically introduce fractal standards inside college students’ ZPD. For instance(Gehlot, 2021), initially, college students are probably capable of discover unit fractions inside an easy fractal pattern. With scaffolding (e.g., instructor questions, peer collaboration, virtual tips), (Smirnov et al., 2019) they could then flow to expertise equivalence thru scaling or follow operations to multi-level fractal constructions. The visible nature of fractals lets in instructors to factor to precise elements and processes (Berry, 2017), making the scaffolding extra concrete and centered, allowing college students to development from what they could do with help to what they could do independently.
By integrating those theoretical perspectives, the fractal geometric technique actions past a trifling academic approach to a deeply rooted pedagogical philosophy that leverages essential factors of human cognition and studying to cope with a perennial mission in arithmetic education.
7. Intelligent Practice
Intelligent exercise refers to the strategic utility of exercise sports designed to maximize studying and retention, regularly leveraging concepts from cognitive technology along with spaced repetition, interleaving, and adaptive remarks (Alvarez-Blanco et al., 2023). Integrating smart exercise with a fractal geometric technique can considerably decorate the effectiveness of fraction coaching for mastery.
7.1. Spaced Repetition
Instead of massed exercise (doing many comparable troubles at once) (Jacinto et al., 2024), spaced repetition includes revisiting standards and capabilities at growing durations over time. This strengthens reminiscence consolidation.
Integration: After preliminary coaching the use of fractals, next exercise periods have to characteristic fractal-primarily based totally troubles on fractions however spaced out over days or weeks. For example, a scholar may study equal fractions the use of Sierpinski triangles(Sierpinska, 2019). A week later, they could come across troubles in which they want to discover equal fractions inside a Koch snowflake(Golding, 2021), and a month later, discover equal ratios in a fractal tree. The numerous context (distinct fractals) blended with spaced durations reinforces the center idea.
7.2. Interleaving
Interleaving (Firth et al., 2021) includes blending distinct forms of troubles or standards inside an unmarried exercise consultation, as opposed to blockading them through type. This forces novices to discriminate among trouble sorts and choose suitable techniques, main to deeper expertise and higher transfer.
Integration: An exercise consultation may want to contain figuring out fractional elements of a fractal (Marýan et al., 2023), then ordering fractions represented through distinct fractal scales, observed through a trouble requiring addition of fractions associated with a multi-level fractal creation. This contrasts with doing 10 “discover the fractional component” troubles consecutively(Marýan et al., 2023). The visible cues from the fractals can assist college students make connections throughout trouble sorts.
7.3. Adaptive Feedback and Personalisation
Intelligent exercise structures regularly offer immediate(Qi et al., 2023), centered remarks and adapt to the man or woman learner’s development, presenting extra help in which wanted and extra tough troubles while ready.
Integration: Digital fractal mills may be designed to be adaptive. If a scholar struggles to discover inside a Sierpinski tetrahedron(Lim et al., 2021), the gadget may want to offer tips through highlighting sections or simplify the fractal temporarily. If they grasp it quickly, the gadget may want to introduce extra complicated fractal styles or require them to carry out operations on fractal quantities (Lim et al., 2021). This lets in for personalized pacing and help, making sure all college students are challenged appropriately.
7.4. Varied Examples and Non-Examples
Exposure to an extensive variety of examples and non-examples enables novices to generalise standards and keep away from over-generalisation.
Integration: Intelligent exercise structures may want to gift a numerous array of fractals (e.g., Mandelbrot set, Julia set, Barnsley fern, Dragon curve, easy self-comparable polygons)( Tharaniya et al., 2024; Bunimovich & Skums, 2024) and fractal-like styles. Students might want to discover which styles exhibit fractional self-similarity and follow fractional expertise to them. This range guarantees that scholars recognize fractions(Tharaniya et al., 2024; Bunimovich & Skums, 2024) as a standard mathematical idea, now no longer simply tied to at least one precise fractal representation.
7.5. Retrieval Practice
Retrieval exercise, or the act of recalling statistics from reminiscence(Carpenter et al., 2022), is one of the best studying techniques.
Integration: Practice sports must regularly require college students to remember and follow fractional standards without searching up rules. For example, “Draw the subsequent new release of this fractal and label the fractional elements of the location” or “If this fractal represents a whole (Shcherbatykh & Polyakova, 2020) what fraction does this highlighted component constitute?” These open-ended, fractal-primarily based totally retrieval cues beef up reminiscence traces.
By strategically weaving those smart exercise methodologies right into a curriculum that leverages fractal geometry(Fuat et al., 2025), educators can create effective studying surroundings that promotes energetic creation of knowledge, deep conceptual expertise, and long-time period retention of fractional mastery.
8. Practical Implications and Classroom Strategies
Implementing a fractal geometric technique (Buehl, 2023) to coaching fractions calls for a shift in pedagogical technique and the combination of latest sports. Here are a few realistic implications and lecture room techniques for Key Stages Two and Three:
8.1. Key Stage Two (Ages 7-11)
At this level, the point of interest must be on constructing foundational expertise of unit fractions, equal fractions, and easy addition/subtraction, mostly through visible and tactile sports.
Paper Folding Sierpinski Gasket(Morska & Rogerson, 2023): Students can begin with a rectangular or equilateral triangle and again and again fold it into smaller self-comparable shapes, figuring out the fractions of the location or perimeter at every level.
“Fractal Pizza/Cake(Granville, 2022)”: Use round reduce-outs or draw circles. Repeatedly divide them into halves, quarters, eighths, etc., demonstrating how every new reduce creates “of of a “ or “of of a quarter,” certainly linking to fractional multiplication standards like = Koch Line Segments: Start with a line segment (e.g., 27 cm). Students divide it into 3 identical elements (nine cm every), then discover one-third. They can then “construct out” the Koch curve concept through changing the center third, extending the idea of duration and perimeter in a fractional way.
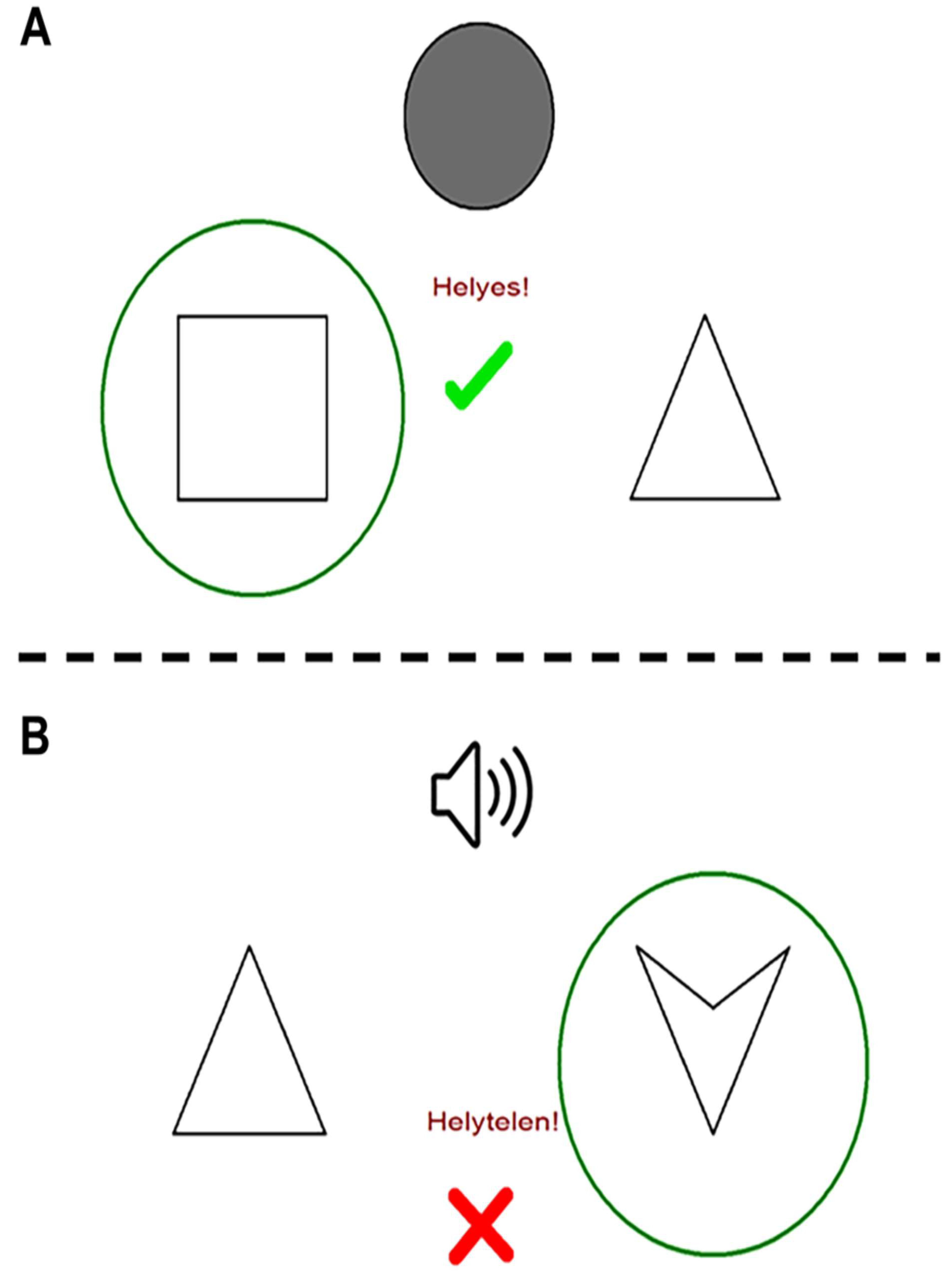
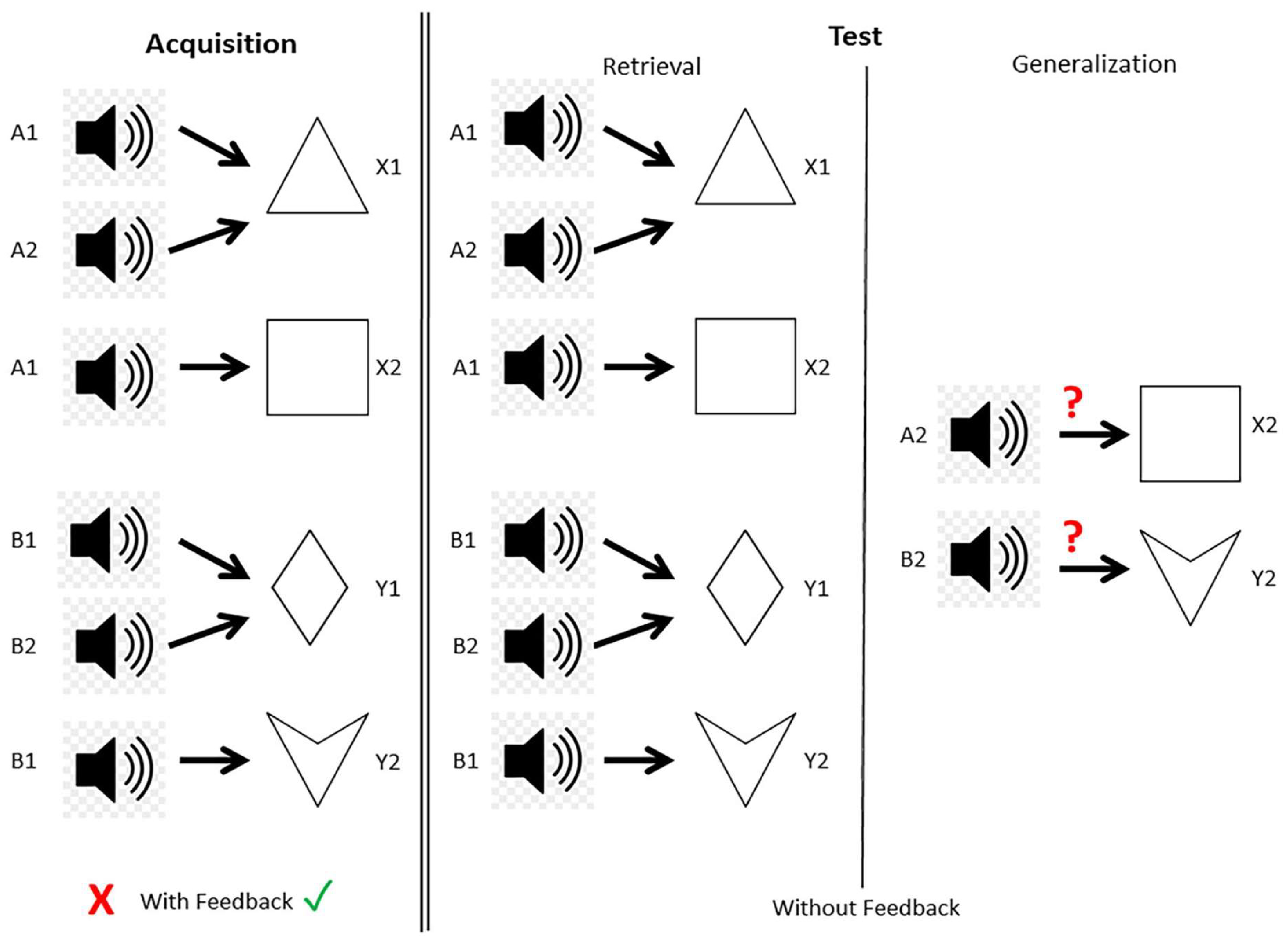
Visual Equivalence(Tót et al., 2025): Create units of fractal “constructing blocks” (e.g., small squares representing of a bigger rectangular). Students can discover how combining distinct numbers of those small blocks can constitute , , or , visually reinforcing equivalence, as visually illustrated by Figs.8-12(c.f., Tót et al., 2025) .
Figure 8.
An experiment with Polygon (A) and SoundPolygon (B) during the acquisition stage.
Figure 8.
An experiment with Polygon (A) and SoundPolygon (B) during the acquisition stage.
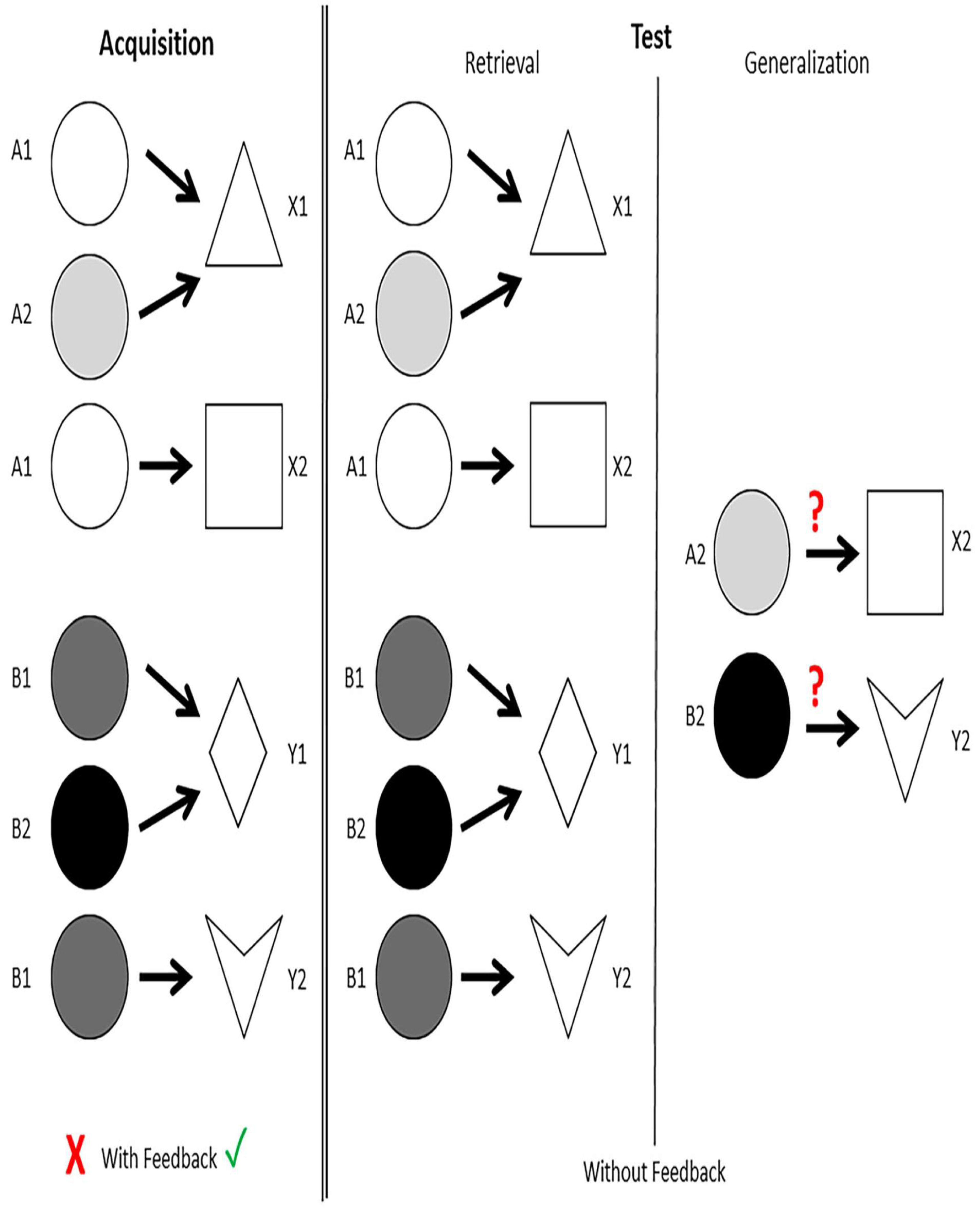
Figure 9.
overview of the Polygon test’s structure. White (A1), light grey (A2), dark grey (B1), and black (B2) are the predecessors, which are circles in greyscale. A triangle (X1), a square (X2), a rhombus (Y1), and a concave deltoid (Y2) are the consequents, which are basic geometric shapes. There are two stages to the test: the acquisition phase, which includes feedback, and the test phase, which does not. Participants must then apply the equivalency rule to fresh stimulus pairs and recall the previously learnt associations.
Figure 9.
overview of the Polygon test’s structure. White (A1), light grey (A2), dark grey (B1), and black (B2) are the predecessors, which are circles in greyscale. A triangle (X1), a square (X2), a rhombus (Y1), and a concave deltoid (Y2) are the consequents, which are basic geometric shapes. There are two stages to the test: the acquisition phase, which includes feedback, and the test phase, which does not. Participants must then apply the equivalency rule to fresh stimulus pairs and recall the previously learnt associations.
Figure 10.
An overview of the SoundPolygon test’s structure. The sounds of a cat (A1), a guitar chord (A2), a car (B1), and a woman’s voice (B2) are the antecedent stimuli. The structure is congruent with the Polygon test, and the consequents are identical.
Figure 10.
An overview of the SoundPolygon test’s structure. The sounds of a cat (A1), a guitar chord (A2), a car (B1), and a woman’s voice (B2) are the antecedent stimuli. The structure is congruent with the Polygon test, and the consequents are identical.
Figure 11.
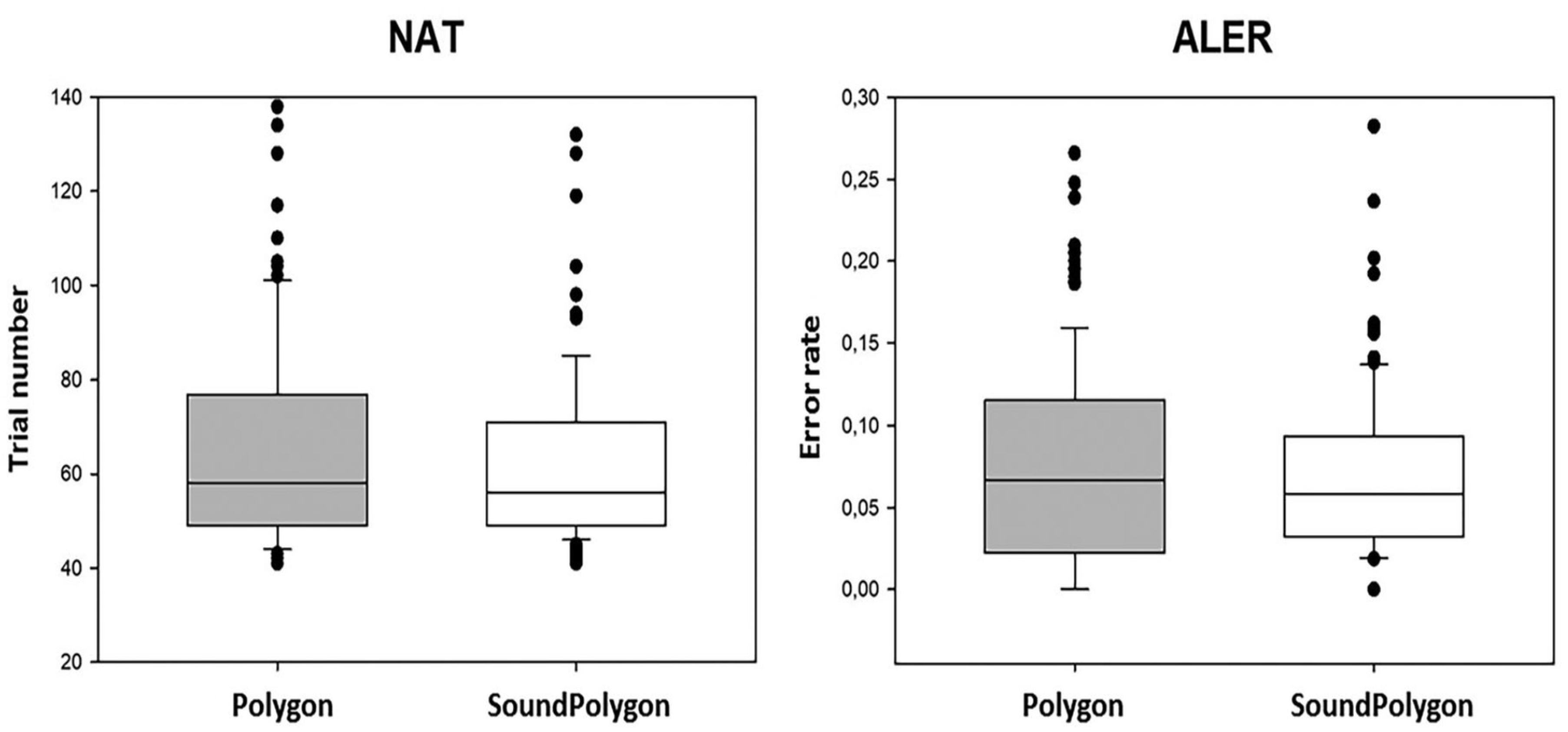
performance in the two tests’ acquisition phase. Acquisition learning error rates are represented by ALER, and the number of trials in the acquisition phase is represented by NAT. The boxes’ upper and lower margins, respectively, represent the top and bottom quartiles. The median is indicated by the line inside the boxes. The 90th and 10th percentiles are indicated by the upper and lower whiskers, respectively. The outliers are shown by the dots above and below the whiskers.
Figure 11.
performance in the two tests’ acquisition phase. Acquisition learning error rates are represented by ALER, and the number of trials in the acquisition phase is represented by NAT. The boxes’ upper and lower margins, respectively, represent the top and bottom quartiles. The median is indicated by the line inside the boxes. The 90th and 10th percentiles are indicated by the upper and lower whiskers, respectively. The outliers are shown by the dots above and below the whiskers.
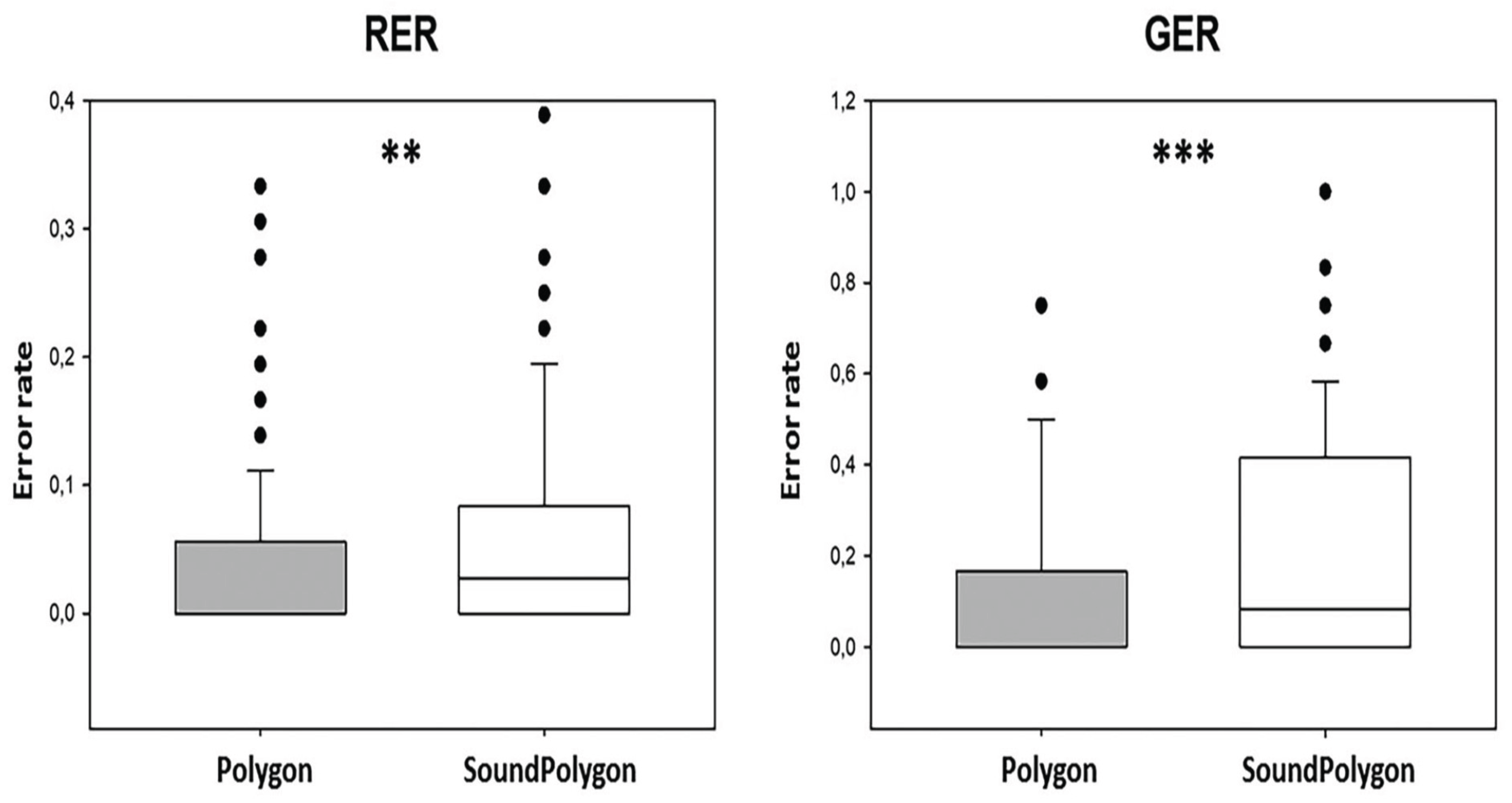
Figure 12.
performance in the two tests during the test phase. RER stands for retrieval error rate; GER is for generalisation error rate. The significant difference is indicated by asterisks: ** at the
level and *** at the
level. The remaining customs are identical to those shown in
Figure 9.
Figure 12.
performance in the two tests during the test phase. RER stands for retrieval error rate; GER is for generalisation error rate. The significant difference is indicated by asterisks: ** at the
level and *** at the
level. The remaining customs are identical to those shown in
Figure 9.
Digital Explorations (Lynch & O’Mara, 2019): Introduce easy online fractal mills in which college students can extrude new release numbers and have a look at the ensuing fractional partitions.
8.2. Key Stage Three (Ages 11-14)
Building on KS2 foundations, KS3 can discover extra complicated fractions, operations, decimals, percentages, and doubtlessly early algebraic fractions(Karakuş & Baki, 2021), that specialize in conceptual know-how and problem-fixing.
Fractal Dimension Introduction(Mageed, 2025c, Mageed, 2024j; Mageed, 2024k; Mageed, 2024l; Mageed, 2024m): Introduce the concept of fractal size informally. While now no longer without delay approximately fractions, the idea that a few fractals have non-integer dimensions (e.g., Sierpinski triangle ≈1.58) may be a charming extension, prompting questions on portions among integers and reinforcing the continuum of numbers.
Fibonacci Sequence and Fractal Trees (Retaningsih, 2024): Explore how the Fibonacci series and the golden ratio seem in nature’s fractal-like structures (e.g., branching patterns). Students can join this to ratio and proportion, and doubtlessly to the convergence of fractional sequences.
Recursive Rules and Algebraic Fractions: Introduce easy recursive guidelines for producing fractals (e.g., “Take of the modern-day period and upload new segments”). This may be a(Mageed, 2025c, Mageed, 2024j; Mageed, 2024k; Mageed, 2024l; Mageed, 2024m) herbal bridge to algebraic questioning and know-how how fractions are embedded in iterative processes. For example, if a system keeps of an amount at every step, after steps, the final amount is the unique.
Fractals at the Number Line: Use the Cantor Set creation to illustrate how (Mageed, 2025c, Mageed, 2024j; Mageed, 2024k; Mageed, 2024l; Mageed, 2024m) fractional factors exist at numerous scales and the way subsets of a line may be shaped thru fractional removals. This allows deepen know-how of the density of rational numbers.
Problem Solving with Fractional Parts of Fractals(Shah et al., 2024): Design issues in which college students must calculate the location or perimeter of a fractal after a sure variety of iterations, main to sums of fractional collection or geometric progressions. For instance, “What fraction of the unique location stays in a Sierpinski triangle after three iterations?”
Advanced Digital Tools(Borcherds et al., 2025): Utilise software program like GeoGebra or Python with easy Turtle snap shots to programmatically generate fractals, permitting college students to govern parameters and have a look at the effect on fractional relationships. This introduces computational questioning along mathematical concepts.
8.3. General Strategies
Concrete-Representational-Abstract (CRA) Sequence(Flores & Milton, 2020): Begin with concrete fractal manipulatives (paper folding), pass to representational drawings/diagrams of fractals, and subsequently connect with summary numerical notation.
Visualisation and Discussion (Wang et al., 2025): Always inspire college students to explain what they see taking place to the fractional elements as fractals are constructed. Use wealthy mathematical language all through discussions.
Collaborative Learning (Yang, 2023): Group sports for building fractals or fixing fractal-primarily based totally fraction issues can foster peer mastering and shared know-how.
Cross-Curricular Links(Honzik et al., 2020): Connect fractals to art, nature, and generation to expose the real-international relevance and splendour of arithmetic.
By embracing those realistic strategies, educators can rework the coaching of fractions into a fascinating, intuitive, and conceptually enriching experience, laying a sturdy basis for mathematical mastery.
Conclusion
Fractions continue to be a perennial task in arithmetic education, regularly hindering college students’ development and confidence. This article has argued for the untapped ability of fractal geometry as a effective pedagogical device to cope with those deep-seated difficulties, mainly for Key Stages Two and Three. The inherent self-similarity, scaling, and recursive nature of fractals provide intuitive visible and structural analogues for center fractional concepts, from the part-complete dating and equivalence to complicated operations. By attractive with fractal constructions, college students can broaden an embodied and conceptual know-how that transcends rote memorisation, fostering authentic mastery.
While the theoretical blessings are compelling, the implementation of a fractal geometric technique offers numerous open issues, mostly regarding empirical efficacy, seamless curriculum integration, powerful instructor training, and making sure accessibility for various learners. These regions call for rigorous studies and collaborative improvement to translate ability into extensive pedagogical effect.
Nevertheless, supported with the aid of using a blended theoretical framework drawing on cognitive load theory, constructivism, inactivism, embodied cognition, and Vygotsky’s Zone of Proximal Development, the fractal technique is located to beautify mastering significantly. Furthermore, the strategic integration of smart exercise methodologies—together with spaced repetition, interleaving, adaptive feedback, and sundry examples—can fortify and consolidate this deep mastering, making sure long-time period retention and bendy utility of fractional knowledge.
Ultimately, with the aid of using embracing the visible beauty and structural intensity of fractal geometry, arithmetic educators have a possibility to revolutionise the manner fractions are taught. This technique guarantees to convert a not unusual place supply of mathematical tension into a fascinating adventure of discovery, equipping college students with a sturdy and intuitive know-how of fractions that serves as a cornerstone for destiny mathematical success. Further studies and pedagogical innovation on this promising location aren’t simply useful however critical for fostering a technology of mathematically gifted and assured learners.
References
- Abrahamson, D., Nathan, M. J., Williams-Pierce, C., Walkington, C., Ottmar, E. R., Soto, H., & Alibali, M. W. (2020, August). The future of embodied design for mathematics teaching and learning. In Frontiers in Education (Vol. 5, p. 147). Frontiers Media SA.
- Acuña, K., & Blacklock, P. J. (2022). Mastery Teachers: How to Build Success for Each Student in Today’s Classrooms. Journal of Higher Education Theory & Practice, 22(1).
- Agostini, E., & Francesconi, D. (2021). Introduction to the special issue “embodied cognition and education”. Phenomenology and the Cognitive Sciences, 20(3), 417-422.
- Akpan, B. (2020). Mastery Learning—Benjamin Bloom. Science Education in Theory and Practice: An Introductory Guide to Learning Theory, 149-162.
- Amo-Asante, K., & Bonyah, E. (2023). Building students’ conceptual understanding of operations on fractions using manipulatives: A junior high school perspective. Mediterranean Journal of Social & Behavioral Research, 7(3), 151-159.
- Athreya, J. S., Reznick, B., & Tyson, J. T. (2019). Cantor set arithmetic. The American Mathematical Monthly, 126(1), 4-17.
- Awofala, A. O., Lawal, R. F., Arigbabu, A. A., & Fatade, A. O. (2022). Mathematics productive disposition as a correlate of senior secondary school students’ achievement in mathematics in Nigeria. International Journal of Mathematical Education in Science and Technology, 53(6), 1326-1342.
- Bahari, A. (2023). Challenges and affordances of cognitive load management in technology-assisted language learning: A systematic review. International Journal of Human–Computer Interaction, 39(1), 85-100.
- Barrera, K. G., & Shah, D. (2023). Marketing in the Metaverse: Conceptual understanding, framework, and research agenda. Journal of Business Research, 155, 113420.
- Berry, M. (2017). QuickStart Computing: Subject Knowledge Enhancement for secondary teachers. British Computer Society.
- Bleidorn, W., Schwaba, T., Zheng, A., Hopwood, C. J., Sosa, S. S., Roberts, B. W., & Briley, D. A. (2022). Personality stability and change: A meta-analysis of longitudinal studies. Psychological bulletin, 148(7-8), 588.
- Borcherds, M., Derflinger, F., Kovács, Z., & North, B. (2025). Teaching programming through mathematics: the PyGgb platform. International Journal of Mathematical Education in Science and Technology, 1-16.
- Bunimovich, L., & Skums, P. (2024). Fractal networks: Topology, dimension, and complexity. Chaos: An Interdisciplinary Journal of Nonlinear Science, 34(4).
- Clements, D.H., Lizcano, R. and Sarama, J., 2023. Research and pedagogies for early math. Education Sciences, 13(8), p.839.
- Cooper, B., Cowie, B., & Furness, J. (2024). Curriculum mapping as a boundary encounter: meeting the demands of multiple agendas. Educational Research for Policy and Practice, 23(2), 229-250.
- Copur-Gencturk, Y. (2021). Teachers’ conceptual understanding of fraction operations: results from a national sample of elementary school teachers. Educational Studies in Mathematics, 107(3), 525-545.
- Corrêa, P. D., & Rangel, L. (2021). The teaching of fractions–Emerging questions from the combined reading of Brazilian and Canadian curricular documents. International Journal for Cross-Disciplinary Subjects in Education (IJCDSE), 12(2).
- Cui, Z., Ng, O. L., & Jong, M. S. Y. (2023). Integration of computational thinking with mathematical problem-based learning. Educational Technology & Society, 26(2), 131-146.
- Dancsa, D., Štempeľová, I., Takáč, O., & Annuš, N. (2023). Digital tools in education. International Journal of Advanced Natural Sciences and Engineering Researches, 7(4), 289-294.
- Dreyfus, T., Apkarian, N., Rasmussen, C., & Tabach, M. (2023). Collective and Individual Mathematical Progress: Layering Explanations in the Case of the Sierpiński Triangle. International Journal of Research in Undergraduate Mathematics Education, 9(3), 694-722.
- Ertl, T. (2024). Artistic Inactivism. Some Remarks on the Importance of Doing Nothing and Discussing Everything. Revista de Estudios Globales y Arte Contemporáneo, 10(1), 81-104.
- Ferrari, C., Fleet, C., Ohshiro, K., Alfaro Arias, V., Hao Xu, E., & Hurst, A. (2023). Tangible progress: Tools, techniques, and impacts of teaching web development to screen reader users. ACM Transactions on Accessible Computing, 16(1), 1-33.
- Filipczak, T., & Nowakowski, P. (2023). Conditions for the difference set of a central Cantor set to be a Cantorval. Results in Mathematics, 78(5), 166.
- Fink, L. D., Davis, J. R., & Arend, B. D. (2023). Facilitating seven ways of learning: A resource for more purposeful, effective, and enjoyable college teaching. Routledge.
- Firth, J., Rivers, I., & Boyle, J. (2021). A systematic review of interleaving as a concept learning strategy. Review of Education, 9(2), 642-684.
- Fric, U., O’Gorman, W., & Rončević, B. (2023). Strategic competence model for understanding smart territorial development. Societies, 13(3), 76.
- Fu, X., Li, X., Xu, P., & Zeng, J. (2020). Inhibiting the whole number bias in a fraction comparison task: An event-related potential study. Psychology Research and Behavior Management, 245-255.
- Fuat, F., Senja, M., & Labh, A. (2025). Exploring Mathematical Creativity in the Crafting of Hex Flange Nuts: Drawing Regular Hexagons. Journal of Teaching and Learning Mathematics, 2(2), 122-142.
- Gaidoschik, M. (2023, July). Inclusive teaching for part-whole understanding: A case study and related reflections on desirable frameworks. In Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13) (No. 4). Alfréd Rényi Institute of Mathematics; ERME.
- Golding, J. (2021). The lure of infinity. Mathematics in School.
- Granville, A. (2022). In Mathematics, As In Art. Journal of Humanistic Mathematics, 12(2), 426-429.
- Harkotte, M., Contreras, M. P., Inostroza, M., & Born, J. (2022). Effects of information load on schema and episodic memory formation. Frontiers in Behavioral Neuroscience, 16, 923713.
- Honzík, L., Frank, J., & Dvořáková, R. (2020). Cross-curricular relations in the teaching of mathematics and other subjects at elementary school. In ICERI2020 Proceedings (pp. 1568-1576). IATED. https://runestone.academy/ns/books/published/pythonds3/Recursion/SierpinskiTriangle.html#fig-sierpinski.
- Jacinto, A. S., de Medeiros, F. P. A., & de Sousa, M. P. (2024, October). An Approach to Spaced Repetition Methodology for Teaching Markup and Scripting Programming Languages. In 2024 IEEE Frontiers in Education Conference (FIE) (pp. 1-9). IEEE.
- Karakuş, F., & Baki, A. (2021). From chaotic to order: Using chaos game in mathematics teaching. Turkish Journal of Computer and Mathematics Education (TURCOMAT), 12(1), 1-21.
- Kouicem, K. (2020). Constructivist theories of Piaget and Vygotsky: Implications for pedagogical practices. dirasat nafsiyat wa tarbawiyat, 13(3), 359-372.
- Kumi-Yeboah, A., Kim, Y., Sallar, A. M., & Kiramba, L. K. (2020). Exploring the use of digital technologies from the perspective of diverse learners in online learning environments. Online Learning, 24(4), 42-63.
- Lestari, K. E., Utami, M. R., & Yudhanegara, M. R. (2022). Exploratory Analysis on Adaptive Reasoning of Undergraduate Student in Statistical Inference. International Journal of Instruction, 15(4).
- Li, T., Lei, L., Bhattacharyya, S., Van den Berge, K., Sarkar, P., Bickel, P. J., & Levina, E. (2022). Hierarchical community detection by recursive partitioning. Journal of the American Statistical Association, 117(538), 951-968.
- Lim, Y. S., Wang, P. C., Yeo, J. J., & Yu, S. C. M. (2021). Experimental and numerical studies for flow over a Sierpinski tetrahedron for potential windbreak application. Journal of Wind Engineering and Industrial Aerodynamics, 216, 104712.
- López, L. L. L. (2021). Fractal education inquiry. Discourse: Studies in the Cultural Politics of Education, 42(2), 251-266.
- Lynch, J., & O’Mara, J. (2019). Morphologies of knowing: Fractal methods for re-thinking classroom technology practices. In Practice methodologies in education research (pp. 166-186). Routledge.
- Mageed, I. A. (2023a, November). Fractal Dimension (Df) of Ismail’s Fourth Entropy (with Fractal Applications to Algorithms, Haptics, and Transportation. In 2023 international conference on computer and applications (ICCA) (pp. 1-6). IEEE.
- Mageed, I. A. (2024a). The Fractal Dimension Theory of Ismail’s Third Entropy with Fractal Applications to CubeSat Technologies and Education. Complexity Analysis and Applications, 1(1), 66-78.
- Mageed, I. A. (2024b). Fractal Dimension of the Generalized Z-Entropy of The Rényian Formalism of Stable Queue with Some Potential Applications of Fractal Dimension to Big Data Analytics.
- Mageed, I. A. (2024c). Fractal Dimension (Df) Theory of Ismail’s Entropy (IE) with Potential Df Applications to Structural Engineering. Journal of Intelligent Communication, 3(2), 111-123.
- Mageed, I. A. (2024d). A Theory of Everything: When Information Geometry Meets the Generalized Brownian Motion and the Einsteinian Relativity. J Sen Net Data Comm, 4(2), 01-22.
- Mageed, I. A. (2024e). The Generalized Z-Entropy’s Fractal Dimension within the Context of the Rényian Formalism Applied to a Stable M/G/1 Queue and the Fractal Dimension’s Significance to Revolutionize Big Data Analytics. J Sen Net Data Comm, 4(2), 01-11.
- Mageed, I. A. (2024j). Do You Speak The Mighty Triad?(Poetry, Mathematics and Music) Innovative Teaching of Mathematics. MDPI preprints.
- Mageed, I. A. (2025c). Fractals Across the Cosmos: From Microscopic Life to Galactic Structures.
- Mageed, I. A.(2025a). The Hidden Poetry & Music of Mathematics for Teaching Professionals: Inspiring Students through the Art of Mathematics: A Guide for Educators. Eliva Press. https://www.elivabooks.com/en/book/book-1450104825.
- Mageed, I. A., & Bhat, A. H. (2022). Generalized Z-Entropy (Gze) and fractal dimensions. Appl. math, 16(5), 829-834.
- Mageed, I. A., & Mohamed, M.(2023). Chromatin can speak Fractals: A review.
- Mageed, I.A. (2024f). Do You Speak The Mighty Triad?(Poetry, Mathematics and Music) Innovative Teaching of Mathematics. MDPI Preprints.
- Mageed, I.A. (2024g). The Mathematization of Puzzles or Puzzling Mathematics Innovative Teaching of Mathematics. Preprints. [CrossRef]
- Mageed, I.A. (2024h). Let’s All Dance and Play Mathematics Innovative Teaching of Mathematics. Preprints. [CrossRef]
- Mageed, I.A. (2024i). AI-Generated Abstract Expressionism Inspiring Creativity Through Ismail A Mageed’s Internal Monologues in Poetic Form. Preprints. [CrossRef]
- Mageed, I.A. (2024k). The Mathematization of Puzzles or Puzzling Mathematics Innovative Teaching of Mathematics. Preprints. [CrossRef]
- Mageed, I.A. (2024l). Let’s All Dance and Play Mathematics Innovative Teaching of Mathematics. Preprints. [CrossRef]
- Mageed, I.A. (2024m). AI-Generated Abstract Expressionism Inspiring Creativity Through Ismail A Mageed’s Internal Monologues in Poetic Form. Preprints. [CrossRef]
- Mageed, I.A. (2025b). The Hidden Dancing & Physical Education of Mathematics for Teaching Professionals. Eliva Press. https://www.elivabooks.com/en/book/book-7724827898.
- Mageed, I.A. and Nazir, A.R. (2024). AI-Generated Abstract Expressionism Inspiring Creativity through Ismail A Mageed’s Internal Monologues in Poetic Form. Annals of Process Engineering and Management, 1(1), pp.33-85.
- Marýan, M., Opachko, M., & Seben, V. (2023). METHODS OF THE FRACTAL APPROACH IN SCIENCE EDUCATION: INNOVATIVE TECHNOLOGY AND CONCEPTS OF COMPUTER MODELING.
- McArthur, J. (2023). Rethinking authentic assessment: work, well-being, and society. Higher education, 85(1), 85-101.
- Morska, J., & Rogerson, A. (Eds.). (2023). Symposium Proceedings Innovative Teaching Practices: Held at the Queen’s College Oxford University, UK August 14-18, 2023 (Vol. 9). WTM-Verlag Münster.
- NCETM. (2017). Five big ideas in teaching for mastery. https://www.ncetm.org.uk/teaching-for-mastery/mastery-explained/five-big-ideas-in-teaching-for-mastery/.
- NCETM. (2022). The essence of mathematics teaching for mastery. https://www.ncetm.org.uk/teaching-for-mastery/mastery-explained/the-essence-of-mathematics-teaching-for-mastery/.
- NCETM. (2023). Supporting research, evidence and argument. https://www.ncetm.org.uk/teaching-for-mastery/mastery-explained/supporting-research-evidence-and-argument/.
- Nurzen, M. (2022). Teacher readiness in implementing the merdeka curriculum in Kerinci Regency. Edunesia: Jurnal Ilmiah Pendidikan, 3(3), 313-325.
- Pan, W., Wu, W., Ming, H., Kim, D. K., Yang, Z., & Ma, Y. (2025). Toward the fractal dimension of classes. ACM Transactions on Software Engineering and Methodology, 34(2), 1-50.
- Piccoli, G., Bartosiak, M. Ł., Palese, B., & Rodriguez, J. (2020). Designing scalability in required in-class introductory college courses. Information & Management, 57(8), 103263.
- Porter, T., Molina, D. C., Blackwell, L., Roberts, S., Quirk, A., Duckworth, A. L., & Trzesniewski, K. (2020). Measuring Mastery Behaviours at Scale: The Persistence, Effort, Resilience, and Challenge-Seeking (PERC) Task. Journal of Learning Analytics, 7(1), 5-18.
- Qi, X., Sun, G., & Yue, L. (2023). Applying self-optimised feedback to a learning management system for facilitating personalised learning activities on massive open online courses. Sustainability, 15(16), 12562.
- Retnaningsih, R. (2024). Fractal Geometry, Fibonacci Numbers, Golden Ratios, And Pascal Triangles as Designs. The Journal of Academic Science, 1(1), 51-66.
- Rodriguez, J. M. G., & Towns, M. H. (2021). Analysis of biochemistry students’ graphical reasoning using misconceptions constructivism and fine-grained constructivism: why assumptions about the nature and structure of knowledge matter for research and teaching. Chemistry Education Research and Practice, 22(4), 1020-1034.
- Runestone Academy. (2025).Sierpiniski triangle. Online Source [Last accessed 15/06/2025].
- Schoenfeld, A. H. (2020). Mathematical practices, in theory and practice. ZDM, 52(6), 1163-1175.
- Shanty, N. O. (2023). Fıfth Grade Students’ Learning of Multiplication of Fractions Based on Realistic Mathematics Education (Doctoral dissertation, Middle East Technical University (Turkey)).
- Shcherbatykh, S. V., & Polyakova, A. Y. (2020). Modern educational technologies in a fractal approach implementation in the math lessons (on the example of learning a probability-statistical line elements). International Journal of Criminology and Sociology, 9, 1709-1723.
- Sierpinska, A. (2019). Materials for teaching a course on research in mathematics education about students’ difficulties in mathematics. Retrieved from Academia. edu: https://www. academia. edu/39941494/Materials_for_teaching_a_course_on_research_in_mathematics_education_about_students_difficulties_in_mathematics.
- Soto-Andrade, J., Díaz-Rojas, D., & Valdés-Zorrilla, A. (2022, October). Embodiment and metaphorising in the learning of mathematics. In IOP Conference Series: Materials Science and Engineering (Vol. 1261, No. 1, p. 012021). IOP Publishing.
- Stephan, M. (2020). Teacher-centered teaching in mathematics education. Encyclopedia of mathematics education, 836-840.
- Sweller, J. (2020). Cognitive load theory and educational technology. Educational technology research and development, 68(1), 1-16.
- Tan, L., Yang, J., Kang, J., & Xu, H. (2022, October). Diffusive surface design using Sierpinski triangle fractal structures. In Proceedings of the International Congress on Acoustics. International Congress on Acoustics (ICA).
- Taylor, T. (2023). Using Triangle Sierpinski Relatives to Visualize Subgroups of the Symmetries of the Square. In Bridges Conference Proceedings (pp. 27-31).
- Tharaniya, P., Jayalalitha, G., Raj, P., & Sundaravadivazhagan, B. (2024). Advanced Fractal Graph Theory and Applications. CRC Press.
- Tossavainen, A., & Helenius, O. (2024). Student Teachers’ Conceptions of Fractions: A Framework for the Analysis of Different Aspects of Fractions. Mathematics Teacher Education and Development, 26(1), 4.
- Tót, K., Eördegh, G., Harcsa-Pintér, N., Bodosi, B., Kéri, S., Kiss, Á., ... & Nagy, A. (2025). Simplified Visual Stimuli Impair Retrieval and Transfer in Audiovisual Equivalence Learning Tasks. Brain and Behavior, 15(2), e70339.
- Tzanaki, E., Bessas, N., Vavougios, D., & Plagianakos, V. (2024). An Interdisciplinary Educational Proposal in Junior High School: The Fractal Geometry in Science, Computer Science and Art Lessons. International Journal of Emerging Technologies in Learning (iJET), 19(3), 35-45.
- Wang, P., Chen, F., Wang, D., & Chen, G. (2025). Enhancing students’ dialogic reflection through classroom discourse visualisation. International Journal of Computer-Supported Collaborative Learning, 1-23.
- Wästerlid, C. A. (2020). Conceptual subitizing and preschool class children’s learning of the part-part-whole relations of number. Problems of Education in the 21st Century, 78(6), 1038-1054.
- Xi, J., & Lantolf, J. P. (2021). Scaffolding and the zone of proximal development: A problematic relationship. Journal for the Theory of Social Behaviour, 51(1), 25-48.
- Xu, H., & Ball, R. (2024). Indigenous Mathematics: From Mainstream Misconceptions to Educational Enrichment. Canadian Journal of Science, Mathematics and Technology Education, 24(2), 160-175.
- Yang, X. (2023). A historical review of collaborative learning and cooperative learning. TechTrends, 67(4), 718-728.
- Zhao, G., Zhang, Y., & Wu, Y. (2024). Implementation effect, long-term mechanisms, and industrial upgrading of the low-carbon city pilot policy: an empirical study based on city-level panel data from China. Sustainability, 16(19), 8316.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).