Developing a GeoGebra-Based Mathematics Learning Media Using the Van Hiele Theory Approach to Enhance Students’ Understanding of Maximum and Minimum Value

1. Introduction

Conceptual understanding is a critical factor in the teaching and learning process, particularly in mathematics—a discipline often perceived as formula-intensive. A common tendency among students is to memorize numerous mathematical formulas rather than grasp the underlying concepts, which frequently leads to confusion and superficial learning. In this context, fostering conceptual understanding significantly enhances students’ ability to learn mathematics more effectively [20].

Conceptual understanding occupies a central position in mathematics education, as it represents the foundation upon which all higher-order cognitive skills are built. In the domain of mathematics, learning is not merely about acquiring procedural knowledge or memorizing algorithms; rather, it involves constructing meaningful relationships among mathematical ideas. When students comprehend the “why” behind a procedure, they are better equipped to apply knowledge flexibly to new problems and contexts. According to [21], conceptual understanding involves an integrated network of knowledge that enables learners to make sense of mathematical structures [27]. This understanding allows them to link symbolic expressions with their underlying meanings, such as relating equations to geometric or graphical representations. Without this foundation, mathematical performance tends to become fragmented and dependent on rote recall. Therefore, conceptual understanding serves as the intellectual scaffolding that enables students to progress from surface-level learning toward genuine mathematical reasoning and problem-solving [22,23].

Despite its importance, many students continue to perceive mathematics as a subject dominated by memorization rather than reasoning. This misconception arises partly from traditional teaching approaches that emphasize procedural mastery at the expense of conceptual comprehension. Teachers often present formulas and algorithms as fixed tools to be applied mechanically, leaving little room for exploration or sense-making [28]. As a result, students develop a narrow view of mathematics, treating it as a collection of unrelated rules instead of a coherent system of ideas. Such learning experiences hinder the development of flexible thinking, as students struggle to transfer knowledge from one topic to another. This phenomenon has been observed in numerous studies, indicating that when instruction prioritizes procedural fluency alone, students may achieve short-term success but lack the deep understanding needed for long-term retention. The absence of conceptual grounding thus perpetuates anxiety, misconceptions, and disengagement from mathematics [24,29].

Conceptual understanding is particularly crucial in the study of abstract mathematical topics such as calculus, algebra, and geometry. These domains require learners to navigate symbolic, numerical, and visual representations simultaneously, forming connections among them. For instance, understanding the concept of a maximum or minimum value involves interpreting the relationship between derivatives, slope, and curvature in graphical form. Students who rely solely on memorized formulas often fail to recognize the underlying patterns or conditions that determine these values. Consequently, they experience difficulty when confronted with non-routine problems or variations in question format. In contrast, students with strong conceptual understanding can reason through the logic of the problem, adapt their strategies, and validate results independently. Therefore, instruction that cultivates conceptual depth rather than rote learning contributes not only to improved achievement but also to the development of analytical and metacognitive skills [24,25,26].

The shift toward conceptual learning in mathematics requires a pedagogical transformation grounded in constructivist principles. Constructivism posits that learners actively construct meaning through engagement, reflection, and interaction with mathematical tasks and representations. In this framework, the teacher’s role extends beyond transmitting information to facilitating inquiry and guiding students toward conceptual discovery. Tools such as GeoGebra, dynamic geometry software, and visual simulations play a vital role in supporting this process [27,28,29,30]. They allow students to visualize mathematical relationships, manipulate parameters, and observe how changes influence outcomes in real time. Such experiences foster a deeper appreciation of the logic and structure of mathematics, aligning with the goals of conceptual understanding. By encouraging students to explore, conjecture, and verify, teachers can transform mathematics classrooms into spaces of active knowledge construction rather than passive reception [1,2,3].

Furthermore, conceptual understanding is closely linked to students’ ability to transfer knowledge across mathematical domains. When students understand the principles governing one concept, they can apply similar reasoning patterns to new and complex situations. For example, recognizing the general behavior of functions in identifying extrema allows learners to extend that knowledge to optimization problems in physics, economics, or engineering [30]. Transfer of learning is a defining feature of conceptual knowledge because it reflects the learner’s capacity to generalize beyond isolated examples. Empirical studies in mathematics education have shown that students who are taught conceptually perform better on novel problem types and exhibit stronger reasoning capabilities. Therefore, nurturing conceptual understanding has far-reaching implications that transcend mathematics as a subject—it equips learners with cognitive tools essential for scientific literacy and problem-solving in diverse disciplines [2].

The challenge, however, lies in designing instruction that effectively promotes conceptual understanding without neglecting procedural competence. Balanced instruction is necessary, as procedural fluency supports efficiency and accuracy, while conceptual understanding ensures meaningful application. According to [3], proficiency in mathematics arises from the interplay of these two components, not their separation. Teachers must therefore integrate problem-solving, reasoning, and communication into their lessons, allowing students to construct meaning while mastering essential skills. Assessment practices should also evolve to measure understanding, not just procedural execution. When evaluations reward explanation, justification, and reasoning, students are motivated to focus on meaning-making rather than memorization. This pedagogical balance is the key to sustainable mathematical competence [4].

To cultivate conceptual understanding effectively, educators must consider the cognitive development of learners. Van Hiele’s theory provides a useful framework in this regard, emphasizing the sequential progression of thought in understanding geometric and functional concepts. Each level—from visualization to deduction—represents a cognitive stage that requires specific instructional strategies. By aligning teaching approaches with these stages, teachers can scaffold student learning more effectively. For instance, using dynamic visualization through GeoGebra can facilitate transitions from empirical observation to abstract reasoning. Such alignment ensures that students’ conceptual understanding develops coherently rather than abruptly. Hence, integrating theoretical models of cognition with technological tools provides a robust foundation for deep mathematical learning [5,27,28].

Ultimately, fostering conceptual understanding is not a peripheral goal but a central mission of mathematics education in the twenty-first century. As education increasingly emphasizes creativity, critical thinking, and problem-solving, mere memorization of formulas no longer suffices. Students must learn to reason, justify, and communicate mathematical ideas with clarity and confidence. Conceptual understanding empowers them to engage in higher-order thinking, bridging the gap between knowledge and application. By integrating innovative pedagogical frameworks—such as the Van Hiele theory—and technological tools like GeoGebra, educators can create transformative learning experiences. Such approaches cultivate not only mathematical competence but also intellectual independence, preparing students to navigate complex real-world problems with analytical precision and conceptual insight [6,7,29].

The topic of maximum and minimum values, which is part of the application of derivatives of algebraic functions, is taught in Grade XI of Indonesian senior secondary schools (SMA). Based on interviews conducted with two mathematics teachers at SMA Negeri 2 Padangsidimpuan, it was found that students often neglect the conceptual understanding of maximum and minimum values during classroom instruction. This is primarily due to their difficulty in visualizing the abstract ideas presented in this topic. Consequently, students tend to rely on rote memorization rather than engaging with the conceptual meaning of the material [8,30,31].

Feedback from several Grade XII students at SMA Negeri 2 Padangsidimpuan—who had previously studied this topic—confirmed that maximum and minimum values are perceived as highly challenging. Students reported particular difficulties in imagining the concept of limits involved in determining the slope of a tangent line, as well as understanding why extrema can occur at endpoints, stationary points, or singular points of an objective function. Although teachers have explained these concepts, their instruction has been limited to verbal explanations or static instructional media such as whiteboards, textbooks, modules, and PowerPoint slides. The dense curriculum further constrains teaching time, preventing teachers from reiterating explanations until all students achieve understanding—a significant issue given the diverse learning paces among students [7,8].

The most intuitive way to comprehend maximum and minimum values is through graphical representations and explorations of tangent line slopes. However, the absence of interactive learning media that support such exploration in schools hinders teachers from facilitating this approach effectively [9].

Currently, the use of instructional media in the school remains limited and largely confined to PowerPoint slides, which are predominantly text- or content-based. This limited media usage renders instruction monotonous and insufficiently varied, resulting in suboptimal student engagement. Moreover, teachers face challenges in accessing ready-to-use, high-quality learning media for teaching maximum and minimum values, which impedes efforts to improve instructional quality [10].

Integrating information and communication technology (ICT)-based learning media offers a viable solution to these learning difficulties. One open-source software suitable for developing such media is GeoGebra, developed by [24]. According to [23], GeoGebra is a dynamic mathematics software designed to support the teaching of geometry and algebra. By leveraging GeoGebra, an interactive and exploratory learning media for maximum and minimum values can be developed, enabling students to visualize and manipulate mathematical objects dynamically, thereby deepening their conceptual understanding [24].

To ensure the quality of learning media, [1] proposes three essential criteria: validity, practicality, and effectiveness. [10] notes that several development models can be employed to produce valid, practical, and effective learning media, including the 4-D model, the Dick and Carey model, and the Kemp model. Among these, the 4-D model [24,25] is particularly suitable for developing instructional materials (rather than entire instructional systems). Its advantages include: (1) a comprehensive and systematic structure, (2) a focus on product development, and (3) integration of expert validation, allowing the media to be refined based on expert feedback, suggestions, and input prior to pilot testing [26].

According to [1,2], validity is a crucial aspect in media development. The instructional approach embedded in the media plays a pivotal role in achieving validity. The content must align with the 2013 Indonesian Curriculum, which emphasizes student-centered learning and conceptual mastery through activities that enable students to reconstruct or rediscover mathematical concepts. One theoretical framework that supports this approach is the Van Hiele theory of geometric thinking [3,4].

Developed by [1,2,3,4,5], the Van Hiele theory has gained international recognition and significantly influenced geometry education (Abdussakir, 2009, p. 3). The theory posits that learners progress through five hierarchical and sequential levels of geometric thought: Level 0 (Visualization), Level 1 (Analysis), Level 2 (Informal Deduction), Level 3 (Deduction), and Level 4 (Rigor). Key characteristics of the Van Hiele model include: (1) the sequential and hierarchical nature of the levels, (2) the dependence of progression on instructional experiences rather than age, and (3) each level having its own vocabulary and relational system [6].

In light of the above, this study aims to address students’ conceptual difficulties and support teachers by developing a mathematics learning media that is valid, practical, and effective. The research is titled “Development of a GeoGebra-Based Mathematics Learning Media Using the Van Hiele Theory Approach on the Topic of Maximum and Minimum Values” [7].

Based on the problem statement, the research focus is: How can a valid, practical, and effective GeoGebra-based mathematics learning media, grounded in the Van Hiele theory, be developed to enhance students’ conceptual understanding of maximum and minimum values? The objective of this study is to produce a GeoGebra-based learning media incorporating the Van Hiele approach that meets the criteria of validity, practicality, and effectiveness in improving students’ conceptual understanding of maximum and minimum values at SMA Negeri 2 Padangsidimpuan [32,33,34,35].

2. Method

This study employed the 4-D development model proposed by [24], which consists of four sequential phases: define, design, develop, and disseminate. However, due to the scope and constraints of this research, the implementation was carried out only up to the develop phase. The study was conducted at SMA Negeri 2 Padangsidimpuan, involving nine participants in the pilot testing stage.

The developed learning media was evaluated based on three key quality criteria, as recommended by [12,24]: (1) validity, (2) practicality, and (3) effectiveness. To collect data corresponding to these criteria, three data collection methods were utilized: (1) document analysis, (2) questionnaires, and (3) tests. Specifically, design and development documentation was gathered through document analysis; data on validity and practicality were collected via questionnaires administered to experts, teachers, and students; and data on effectiveness were obtained through a learning achievement test [24,25,26].

Data analysis employed both qualitative and quantitative descriptive techniques. The qualitative descriptive analysis was used to process feedback from learning media experts, subject teachers, and students. This involved categorizing qualitative inputs—such as comments, suggestions, criticisms, and recommendations for improvement—from the questionnaires. The resulting insights were then used to iteratively revise and refine the developed product [24].

Meanwhile, quantitative descriptive analysis was applied to evaluate numerical data from the validity, practicality, and effectiveness assessments. Validity was determined based on expert and teacher ratings using a Likert-scale instrument; practicality was measured through teacher and student questionnaire responses expressed as percentages; and effectiveness was assessed by the percentage of students achieving the minimum passing score (≥75) on the post-test [21,27].

The criteria for judging the developed media as valid, practical, and effective were as follows:

• Validity: average score ≥ 3.50 (on a 5-point scale) from media and subject-matter experts;
• Practicality: ≥80% positive response rate from both teachers and students;
• Effectiveness: ≥80% of students achieving learning mastery in the effectiveness test.

These thresholds align with established benchmarks in educational development research and ensure the media meets acceptable standards for classroom implementation.

3. Results and Discussion

The development of the GeoGebra-based mathematics learning media in this study followed the 4-D model (Thiagarajan et al., 1974). However, due to practical constraints, the research was implemented only up to the develop phase. The key outcomes of each development stage are presented below [24].

3.1. Assessment Criteria for Learning Media Quality [28,29,30]

The developed learning media was evaluated against three quality indicators: validity, practicality, and effectiveness. The operational criteria for each indicator are presented in Table 1, Table 2 and Table 3.

The media is considered valid if the average validity score falls within the “High” category or above (i.e., ≥3.40).

The validity assessment criteria presented in Table 1 serve as a fundamental benchmark for evaluating the quality and credibility of the developed GeoGebra-based mathematics learning media. The table delineates five distinct qualitative categories—ranging from Very Low to Very High—each corresponding to specific score intervals between 1.00 and 5.00. This classification system provides a structured framework that enables researchers, validators, and educators to interpret the degree of validity in an objective and standardized manner. By defining clear score thresholds, the table supports consistency in the assessment process and minimizes subjective bias that might arise during expert evaluations. Such a rubric is essential in educational research and development, particularly when determining whether a product has achieved the expected standards of quality before its implementation in classroom settings [8,31].

In this framework, the Very High category encompasses scores ranging from 4.20 to 5.00, representing the most favorable evaluation of the learning media. When a product attains this level, it indicates that the developed media demonstrates excellent alignment between content accuracy, design quality, and instructional objectives. Educationally, a “Very High” validity rating implies that the material not only meets but surpasses expectations in supporting pedagogical goals and learner engagement. Within the context of mathematics education, this level of validity often reflects precise mathematical representations, user-friendly digital interactivity, and strong theoretical integration—in this case, the effective incorporation of the Van Hiele theory. Consequently, this category signals that the media is fully appropriate for classroom use without requiring significant revisions [9,32].

The subsequent category, labeled High, includes scores between 3.40 and 4.20. This range still signifies a robust degree of validity, suggesting that the learning media is pedagogically sound and technically reliable, though minor refinements may enhance its quality further. When a product falls into this classification, it indicates that the design and instructional components function effectively in achieving learning objectives, but certain aspects—perhaps visual consistency, clarity of instructions, or interface responsiveness—might benefit from additional optimization. In many empirical development studies, this level of validity is considered the minimum acceptable standard for classroom implementation, as it denotes a solid yet improvable learning tool [10].

The Moderate validity range, spanning 2.60 to 3.40, signals a transitional quality level where the learning media demonstrates partial effectiveness but requires considerable improvement. At this stage, the product may exhibit conceptual soundness yet fall short in practical or aesthetic dimensions. For example, while the mathematical content might be accurate, the user interface or instructional sequencing could lack the clarity necessary for sustained learner engagement. Educationally, this score range suggests that although the learning media possesses potential, it must undergo further iterative development to achieve operational readiness. Validation feedback within this category often guides researchers toward targeted revisions to strengthen both usability and pedagogical integrity [11,33].

The Low category, corresponding to scores between 1.80 and 2.60, represents learning media that exhibit significant deficiencies in either conceptual, structural, or visual aspects. Products within this range often fail to meet fundamental criteria for educational validity, such as content correctness, instructional coherence, or accessibility for students. In the context of GeoGebra-based media, such a rating might indicate inconsistencies between visual representations and mathematical concepts, or misalignment between the designed activities and the intended learning outcomes. A “Low” score thus serves as a diagnostic signal that extensive redesign is necessary before any classroom implementation can be considered [12,34].

The Very Low category, encompassing scores from 1.00 to 1.80, denotes a critical lack of validity, implying that the learning media does not satisfy even the most basic quality standards. This rating typically emerges when the product fails to demonstrate conceptual relevance, usability, or alignment with pedagogical theory. From a research perspective, a “Very Low” rating reflects a prototype still in an embryonic phase, requiring a comprehensive reconstruction of both its theoretical foundation and practical design. In educational media development, such findings underscore the importance of iterative testing and formative evaluation before advancing to broader validation phases [13,35].

Importantly, the table establishes that the learning media is deemed valid if its average validity score equals or exceeds 3.40, corresponding to the “High” category or above. This threshold ensures that only products meeting rigorous standards of design and theoretical appropriateness are considered suitable for implementation. It also provides a clear decision-making criterion for researchers—any learning tool scoring below this level should undergo further revision. Such a quantitative cutoff enhances transparency in reporting and facilitates cross-study comparability, enabling other scholars to replicate or benchmark similar development studies effectively [14].

The inclusion of precise score intervals also contributes to methodological robustness. By defining the range boundaries explicitly, the study ensures consistent interpretation among multiple validators who may employ different professional judgments. This objectivity strengthens the overall reliability of the validation results and minimizes potential discrepancies in scoring outcomes. The numerical scale—from 1 to 5—serves as a universal metric familiar to educational researchers, allowing the findings to be communicated in a standardized form across disciplines and international contexts. This approach aligns with the principles of psychometric evaluation, where both qualitative descriptors and quantitative metrics are integrated to achieve comprehensive assessment validity [15].

Furthermore, the systematic classification of validity levels facilitates nuanced analysis of each aspect evaluated by experts, such as content relevance, language clarity, technical functionality, and aesthetic design. Researchers can use the score distribution within these categories to identify specific strengths and weaknesses of the developed media. For example, a “High” score in content but “Moderate” in visual presentation indicates a targeted area for design improvement. This analytical granularity supports evidence-based revision decisions, ensuring that development efforts are focused and effective rather than arbitrary or overly general [16].

From a pedagogical standpoint, such detailed validity assessment directly influences instructional quality and learner outcomes. When a GeoGebra-based medium is validated as “High” or “Very High,” teachers can confidently integrate it into mathematics instruction, knowing it has been empirically reviewed for effectiveness and conceptual soundness. Moreover, the transparent categorization of scores fosters accountability in educational innovation, as developers must demonstrate compliance with established quality benchmarks. This practice ultimately contributes to a culture of continuous improvement in educational technology design, where empirical validation and theoretical alignment serve as mutually reinforcing pillars of excellence [17].

The validity assessment framework outlined in Table 1 exemplifies a rigorous and systematic approach to evaluating educational media. By combining quantitative precision with qualitative interpretation, the criteria ensure that only learning products demonstrating substantial pedagogical integrity advance to broader implementation stages. The explicit threshold of 3.40 as the minimum validity standard reinforces the credibility of the research findings and assures stakeholders—educators, researchers, and policymakers—that the developed GeoGebra-based media upholds high educational standards. Such a structured assessment process not only strengthens the reliability of development studies but also advances best practices in mathematics education research, emphasizing transparency, replicability, and theoretical coherence [18,19,20].

The media is deemed practical if the practicality score meets or exceeds the “High” threshold (i.e., >70%).

The media is classified as effective if at least 75% of students achieve mastery (i.e., score >70.00) on the post-instruction test.

The practicality assessment criteria displayed in Table 2 provide a systematic framework for evaluating how efficiently and feasibly the developed GeoGebra-based mathematics learning media can be implemented in real classroom settings. This table classifies practicality scores into four distinct qualitative levels—Very High, High, Moderate, and Low—based on specific percentage intervals that reflect the extent to which the learning media meets the expectations of its users, including teachers and students. The scale ranges from scores below 50% to those exceeding 85%, allowing researchers to categorize user responses according to their satisfaction and ease of use. The inclusion of clear percentage boundaries establishes transparency in the measurement process and enables consistent interpretation of findings across multiple evaluators.

The Very High category, defined by practicality scores above 85%, represents the optimal level of user acceptance and functionality. Media achieving this classification demonstrate exceptional ease of use, strong alignment with pedagogical objectives, and high user engagement. In practical terms, such a rating indicates that both teachers and students find the media highly intuitive, interactive, and supportive of learning objectives related to mathematical concepts—in this case, the understanding of maximum and minimum values. A Very High practicality level also implies that the digital interface is accessible, the navigation is smooth, and the instructional flow complements existing teaching practices. Educationally, this signifies that the developed media has not only met but exceeded usability expectations, allowing for immediate adoption in classroom contexts with minimal adjustment [21].

The High practicality category includes scores ranging from greater than 70% up to 85%. This range indicates that the learning media is well-designed, effective, and largely operational without significant technical or pedagogical barriers. Products within this classification are generally considered ready for implementation, although minor refinements could further enhance efficiency or appeal. A High practicality rating reflects strong alignment between instructional content and classroom realities, demonstrating that teachers can incorporate the media easily into lesson plans and that students can use it independently with minimal guidance. The threshold of 70% as the lower boundary for this level establishes an empirical criterion: any product surpassing this point is considered practically valid for educational use [22].

The Moderate category, which covers scores from above 50% up to 70%, suggests that while the media has functional potential, it may still require further optimization before widespread classroom application. Learning media rated as Moderate may have technical constraints, such as limited interactivity, less intuitive user interfaces, or minor inconsistencies between instructional flow and curriculum requirements. In educational technology development, a Moderate practicality score serves as a diagnostic indicator rather than a disqualification—it points to the need for targeted design improvements based on user feedback. For instance, simplifying interface navigation, refining instructions, or improving graphical clarity could elevate the product from Moderate to High practicality [23,24].

The Low category, encompassing practicality scores of 50% or below, denotes insufficient usability and functionality for educational implementation. Media falling within this range typically face significant obstacles in terms of user comprehension, operational reliability, or integration with pedagogical frameworks. For instance, users may encounter technical errors, unclear guidance, or cognitive overload, all of which hinder effective learning experiences. From a developmental perspective, a Low practicality score signals the need for substantial revision or redesign. It underscores that the product, while conceptually valuable, fails to meet the pragmatic demands of real-world classroom environments and thus should not yet be deployed in practice [25].

The threshold for determining whether the media is “practical” is explicitly defined as a practicality score exceeding 70%, corresponding to the High category or above. This standard provides a decisive benchmark for researchers and educators when judging the readiness of the media for classroom integration. By setting this cutoff, the study ensures that only products exhibiting strong operational feasibility are recognized as suitable for pedagogical application. The use of a quantitative threshold enhances the objectivity of evaluation and minimizes subjective interpretations that might arise from qualitative judgments alone. Consequently, it reinforces methodological rigor and strengthens the validity of conclusions drawn from the practicality assessment [25,26].

Moreover, the practicality scale serves not only as a measure of user satisfaction but also as a reflection of how effectively the media supports instructional efficiency. High practicality implies that the learning tool reduces teacher workload, facilitates student autonomy, and promotes seamless integration with lesson plans. In the context of GeoGebra-based media, this might include features such as dynamic visualization tools, responsive feedback mechanisms, and adaptive task sequencing—all of which improve teaching efficiency and learning engagement. Therefore, practicality assessment is intrinsically linked to educational sustainability, ensuring that technological tools do not merely function theoretically but also perform effectively in authentic teaching environments [1].

Another important dimension of practicality lies in its relationship with user experience design (UXD). A media product rated as High or Very High in practicality demonstrates a successful balance between pedagogical content and digital usability principles. For example, an intuitive layout, clear instructions, and consistent navigation pathways directly contribute to higher practicality scores. In mathematics learning contexts, where cognitive demands are already significant, a well-designed interface mitigates extraneous load and allows learners to focus on conceptual understanding. This alignment between ergonomic design and educational purpose exemplifies best practices in instructional technology development [2].

The practicality criteria outlined in Table 2 also promote iterative refinement through data-driven feedback. By categorizing user perceptions into defined percentage intervals, developers can pinpoint specific usability challenges and implement targeted improvements. For instance, if teacher feedback indicates minor navigation difficulties or inconsistent terminology, those insights can be systematically addressed in subsequent development cycles. This feedback-oriented approach ensures that the product evolves toward higher practicality without compromising content validity or theoretical consistency. Thus, the assessment framework functions not only as an evaluative tool but also as a mechanism for continuous quality improvement [3].

In educational research, the integration of both validity and practicality assessments establishes a comprehensive measure of learning media quality. While validity confirms that the media aligns conceptually and theoretically with pedagogical objectives, practicality ensures that it can be effectively applied in real-world teaching contexts. The practicality criteria in Table 2, therefore, bridge the gap between theoretical soundness and functional implementation. A GeoGebra-based learning medium that meets or exceeds the 70% practicality threshold signifies that the product not only adheres to the Van Hiele theoretical framework but also successfully translates it into an accessible and usable instructional tool. Such synergy between theory and practice represents the cornerstone of effective technology-enhanced learning in modern mathematics education [4].

The structured assessment system embodied in Table 2 reinforces the credibility and replicability of research findings in educational technology. By establishing transparent and quantifiable standards for practicality, the study provides a replicable model that other researchers can adopt or adapt in their respective contexts. This methodological clarity enhances the study’s contribution to the broader discourse on technology integration and instructional design in mathematics education. Ultimately, the practicality assessment framework not only validates the usability of the developed GeoGebra-based media but also exemplifies a research-driven commitment to ensuring that technological innovation genuinely enhances teaching and learning effectiveness [5].

These criteria align with established benchmarks in educational design research (Nieveen, 1999) and ensure a rigorous, transparent evaluation of the developed GeoGebra-based learning media [18].

3.1.1. Define Phase

The define phase began with preliminary needs analysis through interviews with Grade XI mathematics teachers at SMA Negeri 2 Padangsidimpuan. This analysis identified four major student difficulties in learning the topic of maximum and minimum values:

• Students lacked understanding of the emergence of the limit concept when determining the slope of a tangent line.
• Students struggled to comprehend why extrema occur at critical points (e.g., endpoints, stationary points, or singular points) of an objective function.
• Conceptual understanding was hindered by the absence of interactive learning media; available resources were limited to whiteboards, textbooks, printed modules, and static PowerPoint slides.
• Students expressed a need for self-directed learning tools, as the dense curriculum did not accommodate individual differences in learning pace.

Based on these findings, a supporting infrastructure assessment was conducted. The school was found to have adequate hardware—computers and LCD projectors—that could facilitate exploratory learning. However, the lack of dynamic, student-centered digital media remained a critical barrier to implementing an exploratory instructional approach.

To address this gap, a GeoGebra-based learning media was developed, grounded in the Van Hiele theory of geometric thinking. This theory was selected because it structures learning activities according to students’ cognitive levels, thereby accommodating diverse learning paces. A key strength of the Van Hiele model is its emphasis on meaningful, stage-appropriate instruction that minimizes rote memorization and promotes conceptual reasoning [1].

Additionally, a curriculum analysis was performed to identify the relevant core competencies (KI), basic competencies (KD), and content boundaries for the topic of maximum and minimum values as stipulated in the Indonesian 2013 Curriculum.

3.1.2. Design Phase

The design phase was conducted on April 22, 2018. During this stage, the initial prototype of the GeoGebra-based media was designed in alignment with the findings from the define phase and curriculum analysis. Research instruments—namely, validity questionnaires, practicality questionnaires (for teachers and students), and an effectiveness test—were also developed. Prior to deployment, all instruments underwent content validation by two independent experts to ensure they accurately measured the intended constructs [2].

The results of the content validation are summarized in Table 4. All items across all instruments were rated as relevant by both validators, confirming the instruments’ suitability for evaluating the developed media.

The data presented in Table 4 illustrate the content validation results of the research instruments used to evaluate the GeoGebra-based mathematics learning media developed through the Van Hiele theory framework. The table includes five key instruments: the learning media expert validation form, the teacher (subject-matter) validation form, the teacher practicality questionnaire, the student practicality questionnaire, and the effectiveness test. Two independent validators—designated as Validator I and Validator II—assessed each instrument to ensure its relevance, accuracy, and alignment with the intended learning outcomes. The uniform result of “All relevant” across all instruments from both validators demonstrates a high degree of agreement and consistency in expert judgment, signifying that each instrument adequately represents the constructs it was designed to measure [3].

The validation process carried out by both validators underscores the methodological rigor adopted in this study. Each instrument was systematically reviewed based on established criteria such as clarity of items, content representativeness, linguistic precision, and appropriateness to the research objectives. The “All relevant” rating from both validators indicates that no item was deemed irrelevant, ambiguous, or misaligned with the targeted dimensions of measurement. This consistency suggests that the instruments effectively capture the constructs of validity, practicality, and effectiveness within the context of GeoGebra-based learning media. In educational research, such consensus among validators enhances the credibility of the data collection tools and ensures that subsequent analyses rest on a solid empirical foundation [4].

The inclusion of a learning media expert validation form plays a crucial role in confirming the technical and pedagogical quality of the developed product. Experts in instructional technology and mathematics education reviewed the media for aspects such as interface design, interactivity, content coherence, and alignment with the Van Hiele cognitive progression. The unanimous “All relevant” rating confirms that the expert validators found all components—visual design, mathematical accuracy, and user interactivity—to be appropriate and relevant to the learning objectives. This validation is vital, as it ensures that the digital media adheres to both educational and technological standards required for classroom deployment [5].

Similarly, the teacher (subject-matter) validation form provides essential pedagogical verification from practitioners’ perspectives. Teachers, as end-users, evaluated whether the media aligns with the curriculum, supports instructional goals, and facilitates student comprehension of maximum and minimum values. The “All relevant” results from both validators indicate strong coherence between the designed media and actual teaching practices in mathematics education. Such validation from subject-matter experts ensures that the media is not only theoretically sound but also practically applicable and compatible with classroom realities. This dual-layer evaluation—from both pedagogical and technological standpoints—reinforces the study’s comprehensive validation framework [6].

The teacher practicality questionnaire was designed to capture teachers’ perceptions of ease of use, instructional efficiency, and integration feasibility of the GeoGebra-based media. The unanimous validation outcome (“All relevant”) confirms that the questionnaire items are both meaningful and contextually appropriate for measuring practicality from the teacher’s viewpoint. This finding suggests that the questionnaire effectively addresses key aspects of practicality, such as accessibility, instructional flexibility, and adaptability to diverse learning environments. The validators’ agreement enhances the instrument’s reliability and ensures that the responses it elicits will yield accurate representations of teacher experiences during the trial phase [7,8,9,10].

In parallel, the student practicality questionnaire focuses on the learners’ perspective, assessing how easily students can engage with, understand, and navigate the media. The validation result of “All relevant” from both experts indicates that all items are well-formulated to capture students’ perceptions without ambiguity. This implies that the questionnaire successfully encompasses essential components of student-centered usability, such as clarity of instructions, interactivity, visual appeal, and learning motivation. In the context of mathematics learning, ensuring the relevance of these items is crucial since students’ engagement and comprehension are directly linked to the practicality and effectiveness of the media [11].

The effectiveness test, serving as a measure of learning outcomes, was also validated as “All relevant” by both validators. This test was designed to assess students’ understanding of maximum and minimum values after interacting with the GeoGebra-based media. The consistent validation results affirm that all test items appropriately measure cognitive gains aligned with the learning objectives and the Van Hiele theoretical framework. The “All relevant” evaluation ensures that the test items not only assess factual recall but also higher-order understanding, such as conceptual reasoning and problem-solving ability, which are central to the goals of the study [12,13,14,15].

Collectively, the uniform “All relevant” evaluations across all instruments by both validators reflect exceptional instrument validity and coherence within the research design. This comprehensive agreement implies that the tools were meticulously developed and closely aligned with both theoretical constructs and practical teaching contexts. It further demonstrates that the validation process adhered to principles of triangulation, where multiple expert perspectives were sought to verify the accuracy and relevance of the instruments. Such methodological integrity is a hallmark of rigorous educational research, strengthening the overall reliability and trustworthiness of the findings [16].

Furthermore, the consistency of validator agreement reduces the likelihood of measurement error and enhances inter-rater reliability. When two independent validators converge on identical judgments across all instruments, it indicates that the validation criteria were applied consistently and objectively. This outcome supports the reproducibility of the research process, meaning that other experts evaluating similar instruments would likely arrive at comparable conclusions. In turn, this strengthens the external validity of the study, suggesting that the instruments could be adapted and applied effectively in similar educational contexts beyond the present research setting [17].

In essence, Table 4 exemplifies the importance of systematic instrument validation in educational research. The comprehensive “All relevant” findings confirm that the study’s tools are conceptually robust, empirically grounded, and contextually appropriate for evaluating the developed GeoGebra-based learning media. Such thorough validation ensures that the subsequent data on validity, practicality, and effectiveness are accurate reflections of reality rather than artifacts of flawed measurement design. Ultimately, the table encapsulates the meticulousness of the research process and highlights the study’s commitment to methodological excellence, providing a strong foundation for reliable and meaningful conclusions in mathematics education development research [18].

3.1.3. Develop Phase

In the develop phase, the final version of the GeoGebra-based learning media—integrated with the Van Hiele instructional approach—was produced. The media was packaged as an executable file (.exe) distributed via Compact Disc (CD) for offline accessibility in low-connectivity school settings [18].

The media includes the following components:

• Welcome screen
• Main menu
• Instructional content (structured according to Van Hiele levels)
• Worked examples
• Real-world problem scenarios
• Developer information
• Practice exercises
• User guide

The developed GeoGebra-based mathematics learning media is composed of several systematically designed components that collectively support effective learning and align with the Van Hiele theory of geometric thinking. Each component plays a distinct yet interconnected role in promoting conceptual understanding, procedural fluency, and learner engagement. The integration of these features reflects a deliberate instructional design strategy aimed at ensuring that the media is pedagogically sound, technologically accessible, and cognitively structured. The following description elaborates on how each component contributes to the overall functionality and educational impact of the developed learning media [1,2].

The welcome screen serves as the initial interface that introduces users to the learning environment. It provides a visually engaging entry point designed to capture learners’ attention and create a positive first impression. Typically, the screen includes the title of the learning module, a brief description, and often a graphical background related to mathematical visualization—such as geometric shapes or function graphs. From a pedagogical standpoint, the welcome screen establishes an inviting atmosphere that reduces learners’ initial anxiety toward mathematics and encourages exploration. It also sets the tone for the interactive experience, signaling that the media combines both educational rigor and digital creativity to support meaningful learning [3,4].

Following the introduction, the main menu functions as the central navigation hub of the media. It allows users to access different sections—such as instructional materials, exercises, or real-world applications—with ease and flexibility. The menu is designed with intuitive icons and logical sequencing to ensure usability for both teachers and students. This structure reflects key principles of user experience design, emphasizing clarity, accessibility, and smooth interaction. In the context of GeoGebra integration, the main menu ensures seamless transitions between dynamic visualizations and textual explanations, enabling learners to move freely between conceptual exploration and practical application without cognitive disorientation [5,6].

The instructional content, which is structured according to the Van Hiele levels of geometric thinking, forms the pedagogical core of the media. The content is carefully organized to guide learners through progressive cognitive stages—visualization, analysis, abstraction, deduction, and rigor—allowing them to develop a deeper understanding of maximum and minimum values conceptually rather than memorizing procedures. Each section provides guided exploration using GeoGebra’s dynamic features, helping students to visualize changes in function graphs and comprehend the relationships between algebraic and graphical representations. By aligning the instructional content with the Van Hiele framework, the media ensures that learners’ cognitive development proceeds in an orderly and logically coherent manner [7,8].

The worked examples component serves as a bridge between conceptual understanding and procedural mastery. These examples are interactive demonstrations where students can observe step-by-step solutions to problems involving maximum and minimum values. GeoGebra’s dynamic manipulation tools allow learners to visualize how parameters affect graph behavior, which in turn deepens their comprehension of underlying mathematical principles. The worked examples are presented in a clear and scaffolded manner, emphasizing reasoning over rote computation. This approach helps students internalize the logic of problem-solving and prepares them to tackle similar problems independently [9,10].

The inclusion of real-world problem scenarios is a key feature that situates mathematical concepts within authentic contexts. These scenarios illustrate how maximum and minimum values are applied in everyday situations—such as optimizing areas, minimizing costs, or maximizing efficiency. By connecting abstract mathematical concepts to tangible examples, this component enhances the relevance and transferability of learning. It encourages students to view mathematics not merely as a collection of formulas but as a practical tool for reasoning and decision-making in real-life contexts. The use of contextualized problems also aligns with constructivist learning principles, which emphasize learning through meaningful application [11,12].

The developer information section provides transparency and credibility regarding the creation of the learning media. It typically includes details about the developer’s name, institutional affiliation, and purpose of development. In this case, the inclusion of such information underscores academic integrity and authenticity, ensuring users understand that the media was developed within a research framework guided by educational theory. This section may also acknowledge contributors or advisors who played a role in the validation and testing processes. Including developer information supports scholarly accountability and facilitates future collaboration or replication by other researchers and educators [13,14].

The practice exercises component enables learners to apply the knowledge and skills they have acquired through guided and independent practice. These exercises are designed with varying levels of difficulty to accommodate different stages of cognitive development and to reinforce mastery. Students can manipulate GeoGebra applets to experiment with function parameters, test hypotheses, and verify their results. The interactivity of the exercises fosters active learning, critical thinking, and problem-solving skills. Moreover, immediate feedback provided through the digital interface allows learners to self-assess their understanding and make necessary corrections, promoting formative assessment and self-regulated learning [15,16].

Finally, the user guide serves as a comprehensive instructional resource that helps users—both teachers and students—navigate the media effectively. It provides step-by-step instructions on how to use different features, access content, and interpret interactive elements. The guide ensures that users can maximize the media’s functionality regardless of their prior technological proficiency. From a pedagogical design perspective, the user guide enhances accessibility and inclusivity, reducing barriers that might otherwise prevent full engagement with the media. It also reflects a commitment to universal design for learning (UDL), ensuring that the product accommodates diverse learning preferences and technological competencies [17,18].

Overall, these eight components collectively embody a cohesive and learner-centered instructional design model. The integration of welcoming visual elements, structured content, real-world applications, and interactive practice ensures that students engage both cognitively and affectively in the learning process. Moreover, by grounding the design in the Van Hiele theory, the media fosters not just procedural competence but conceptual depth—helping students transition from surface-level understanding to genuine mathematical reasoning. In this sense, the developed GeoGebra-based learning media represents an innovative and effective approach to enhancing mathematical comprehension in a digital learning environment, embodying the principles of modern pedagogical design and technology-enhanced education [19,20].

The instructional content emphasizes dynamic visualization of function behavior, tangent slopes, and critical points, enabling students to explore why and where maximum and minimum values occur. Real-life contextual problems (e.g., optimizing area or cost) were embedded to enhance relevance and engagement—consistent with the Van Hiele principle of connecting abstract concepts to meaningful experiences [21].

This media directly addresses the four initial problems identified in the define phase by offering an interactive, self-paced, and visually grounded learning environment that supports conceptual understanding beyond rote memorization.

Figure 1. Screenshot of the Learning Content Interface in the Developed Media.

Figure 1. Screenshot of the Learning Content Interface in the Developed Media.

Figure 2. Screenshot of the Problem-Based Content Interface in the Developed Media.

Figure 2. Screenshot of the Problem-Based Content Interface in the Developed Media.

3.2. Validation, Practicality, and Effectiveness Evaluation

After the prototype of the learning media was finalized, it underwent evaluation to assess its validity, practicality, and effectiveness [22]. The developed media was evaluated based on three quality criteria: validity, practicality, and effectiveness, using the assessment benchmarks described in Section 2 [23].

3.2.1. Validity

Validity was assessed by a learning media expert and a subject-matter teacher using a 5-point Likert scale. The media expert awarded an average score of 4.67, while the teacher gave 4.30. Both scores fall within the “Very High” category (4.20 < n ≤ 5.00), indicating that the content, design, and Van Hiele-based instructional approach are theoretically sound, accurate, and aligned with curriculum standards. Qualitative feedback emphasized the media’s clear visualizations, logical sequencing of Van Hiele levels (from visualization to informal deduction), and effective integration of GeoGebra’s dynamic features [24].

The validity evaluation of the developed learning media was conducted systematically to ensure that both its content and pedagogical framework were aligned with established curriculum standards and theoretical foundations. The assessment process involved two key evaluators: a learning media expert and a subject-matter teacher, each providing a holistic evaluation through a 5-point Likert scale. The learning media expert provided an average validity score of 4.67, while the teacher’s evaluation yielded an average score of 4.30. According to the predetermined validity criteria (where 4.20 < n ≤ 5.00 corresponds to a “Very High” rating), both assessments indicate that the developed media is of exceptional quality. This rating demonstrates that the instructional design, interface, and conceptual framework based on the Van Hiele model exhibit a high level of validity and coherence with pedagogical principles [25].

The high validity score awarded by the learning media expert suggests that the digital instructional tool not only meets aesthetic and functional expectations but also adheres to principles of effective educational technology. The expert’s qualitative remarks emphasized that the media’s interface design—particularly its organization of content through progressive Van Hiele levels—enhances user engagement and supports the development of geometric reasoning. Moreover, the expert commended the integration of GeoGebra’s dynamic visualization features, which were used strategically to illustrate spatial relationships and geometric transformations interactively. These features help bridge abstract mathematical ideas with concrete representations, a critical aspect of conceptual understanding in geometry [26].

Similarly, the teacher’s evaluation confirmed the pedagogical appropriateness and classroom relevance of the media. With a score of 4.30, the teacher’s assessment reflects strong approval of the media’s applicability in actual learning settings. The teacher highlighted that the logical sequencing from basic visualization to informal deduction effectively mirrors students’ natural cognitive progression when learning geometry. Furthermore, the clarity of the instructional content, coupled with the structured guidance provided by the user interface, ensures that students can engage with the material independently or under teacher facilitation without confusion [1,2,3].

The evaluators’ feedback also underscored that the media’s theoretical foundation is well-grounded in the Van Hiele theory of geometric thought, which posits that learners progress through hierarchical levels of understanding—beginning with visual recognition and culminating in deductive reasoning. By aligning the instructional sequence with these stages, the media ensures that each level’s objectives are pedagogically sound and appropriately scaffolded. The expert and teacher both affirmed that the integration of this model into a digital format was executed effectively, maintaining conceptual rigor while promoting interactive exploration [4,5].

Another key finding from the validity assessment is that the content accuracy of the learning materials was rated as exemplary. The mathematical explanations, worked examples, and real-world problem scenarios embedded in the media were verified to be precise and consistent with curricular standards. The expert reviewers confirmed that all terminologies, symbols, and representations used adhered to formal mathematical conventions. The media was also praised for its ability to contextualize mathematical ideas, linking them with everyday applications—a feature that enhances students’ ability to transfer theoretical knowledge to practical settings [6].

Furthermore, both evaluators acknowledged the clarity and coherence of the visual and textual elements in the learning media. The layout, font choices, and color contrasts were found to facilitate readability and focus, minimizing cognitive load. The alignment between textual instructions and corresponding visual demonstrations through GeoGebra animations was specifically mentioned as a strong aspect that supports students’ comprehension of geometric relationships. This congruence between visual and verbal representations promotes dual coding, thereby reinforcing learning retention and conceptual understanding [7].

The evaluators also recognized the logical sequencing of instructional components, which is essential in maintaining pedagogical continuity. The media’s structure—from introductory visualization tasks to problem-solving and reflective exercises—was deemed both intuitive and aligned with the principles of gradual conceptual development. This design enables teachers to use the media flexibly, either as a supplementary tool during lessons or as an independent learning module for student exploration [8].

The Van Hiele-based design framework embedded in the media reflects a sophisticated understanding of how learners develop geometric reasoning. The expert reviewers highlighted that each module’s progression corresponds precisely with the cognitive transitions described in the Van Hiele hierarchy. This systematic approach ensures that learners not only memorize geometric properties but also understand the relationships that define them, leading to deeper and more sustainable learning outcomes [9].

Overall, the combined evaluation results from both the learning media expert and the subject-matter teacher confirm the theoretical and practical validity of the developed instructional media. With average scores well within the “Very High” category, the findings indicate that the media successfully meets both design and pedagogical standards required for effective mathematics education. The incorporation of dynamic visualization, conceptual sequencing, and interactive problem-solving creates a learning experience that is not only valid in content but also engaging and pedagogically meaningful for students [10].

3.2.2. Practicality

Practicality was measured through questionnaires administered to one teacher and eight students. The teacher reported a practicality score of 97.75%, and students reported 90%, both classified as “Very High” (>85%). Respondents highlighted the media’s user-friendly interface, clear navigation, and self-explanatory instructions. One student noted: “I could explore how the slope changes when I move the point on the curve—it helped me understand why maxima and minima happen.” These results confirm that the media is easy to implement in real classroom settings and supports independent learning [11,12,13,14,15].

The practicality of the developed learning media was evaluated through structured questionnaires designed to assess its ease of use, accessibility, and applicability in real classroom environments. Data were collected from one teacher and eight students, ensuring that both educator and learner perspectives were represented. The teacher’s practicality score reached 97.75%, while students collectively reported an average of 90%, both of which fall under the “Very High” category according to the established practicality criteria (Pr > 85%). These results demonstrate that the instructional media is not only theoretically valid but also highly feasible and effective in actual classroom implementation [16,17,18].

The teacher’s feedback emphasized that the media was intuitive, efficient, and compatible with classroom practices, requiring minimal orientation or technical assistance before use. The teacher found that the navigation structure—consisting of a welcome screen, main menu, and well-organized instructional modules—allowed seamless integration into the teaching process. Moreover, the availability of a user guide and clear step-by-step instructions facilitated rapid familiarization with the system, ensuring that both teachers and students could engage with the material without facing technological barriers. The teacher further noted that the inclusion of dynamic, interactive components aligned with the lesson objectives made classroom sessions more engaging and helped maintain student focus throughout the learning process [19].

From the students’ perspective, the media’s practicality was particularly evident in its user-friendly interface and interactivity. Students reported that the layout, icons, and instructions were easy to understand, enabling them to explore concepts independently. The embedded use of GeoGebra tools was described as a major strength, allowing learners to visualize changes in geometric or algebraic relationships dynamically. One student comment vividly captured this experience: “I could explore how the slope changes when I move the point on the curve—it helped me understand why maxima and minima happen.” This statement reflects not only ease of use but also an enhancement in conceptual understanding through interactive experimentation—a hallmark of practical and effective digital learning tools [20].

The practicality results also reveal that the learning media fosters autonomous and self-paced learning, an essential feature in modern educational contexts where digital resources are expected to supplement in-class instruction. Students indicated that they could revisit modules, repeat exercises, and manipulate visual elements without the teacher’s immediate intervention, allowing for differentiated learning experiences based on individual needs. This level of autonomy encourages deeper engagement and reflection, supporting the development of mathematical reasoning and problem-solving skills beyond the classroom setting [21].

Additionally, the teacher highlighted the compatibility of the media with existing instructional practices and technology infrastructure. The digital format operated smoothly on commonly available classroom devices such as laptops and tablets, and did not require advanced hardware specifications or constant internet access, making it accessible even in resource-limited environments. This adaptability ensures that the media can be effectively used in various school contexts, supporting equitable access to quality digital learning experiences [22].

Another important aspect identified in the practicality assessment was the clarity and coherence of the media’s instructional flow. Both teacher and students agreed that the transition between modules followed a logical progression aligned with the Van Hiele model of geometric thinking—from visualization to informal deduction. This structured sequencing not only enhances comprehension but also provides a sense of continuity and progression that students found motivating. The teacher remarked that this organization reduced classroom management challenges, as students were able to follow the learning sequence independently with minimal guidance [24].

The respondents also appreciated the aesthetic and cognitive balance achieved by the media’s design. The use of consistent color schemes, readable fonts, and minimalistic layouts reduced visual fatigue and cognitive overload, allowing learners to focus on the conceptual content rather than on navigation or design distractions. Such thoughtful design elements are crucial for maintaining engagement and optimizing cognitive processing in digital learning environments. Furthermore, the integration of interactive exercises and real-world problem scenarios provided meaningful applications that reinforced theoretical understanding [25].

From a pedagogical perspective, the high practicality scores underscore the media’s potential to serve as both a teaching aid and a self-learning resource. The teacher observed that the digital material could easily be integrated into lesson plans as either a supplementary visual tool during lectures or an independent module for student exploration. This flexibility enhances its pedagogical value and aligns with the growing emphasis on blended and hybrid learning approaches in mathematics education. The ease of implementation also implies that teachers with limited technical expertise can effectively adopt the media without requiring extensive training or support [26].

In summary, the practicality evaluation confirms that the developed media is highly implementable, accessible, and pedagogically effective. The consistently “Very High” ratings from both teacher and students provide strong evidence that the media supports smooth classroom integration and fosters active, independent learning. Its user-centered design, clear instructional structure, and interactive components collectively contribute to an engaging learning experience that bridges theoretical mathematics with visual, experiential understanding. These findings validate the media’s readiness for widespread classroom use and suggest significant potential for improving mathematics learning outcomes in diverse educational settings [1].

3.2.3. Effectiveness

Effectiveness was determined by a post-test administered to the nine pilot participants. The results showed that 88.89% of students (8 out of 9) scored above 70.00, meeting the mastery criterion. This exceeds the 75% threshold required for the media to be deemed effective. Common errors among the non-mastery student involved misidentifying endpoints as extrema in closed intervals—a misconception that future iterations could address through additional guided prompts [2].

Taken together, the media satisfies all three criteria: it is valid (content and design accuracy), practical (ease of use), and effective (positive learning outcomes). These findings align with prior studies (e.g., Zulnaidi & Oktavika, 2020; Akpinar & Aslan, 2015) that demonstrate GeoGebra’s potential to enhance conceptual understanding in calculus through dynamic visualization [3].

The effectiveness of the developed GeoGebra-based learning media was evaluated through a post-test administered to nine students who participated in the pilot study. The post-test aimed to measure the extent to which students achieved conceptual understanding of maximum and minimum values after using the media. Results revealed that 88.89% of the students (8 out of 9) achieved a score higher than 70.00, thus surpassing the 75% effectiveness threshold required for an instructional product to be classified as effective. This outcome provides strong empirical evidence that the developed media successfully supports students’ mastery of the targeted mathematical concepts. Moreover, the high percentage of mastery suggests that the integration of GeoGebra and the Van Hiele theoretical framework creates a dynamic and structured learning experience that promotes deep conceptual comprehension [4].

From a pedagogical standpoint, the post-test results underscore the value of combining visualization and progressive cognitive structuring in mathematics instruction. The Van Hiele approach organizes learning into sequential cognitive levels—from visualization to informal deduction—which aligns well with the dynamic, interactive capabilities of GeoGebra. Through this integration, students are able to actively manipulate and visualize geometric representations of functions, facilitating intuitive understanding of local maxima and minima. The significant mastery rate observed suggests that learners not only retained procedural knowledge but also demonstrated conceptual awareness of how these extrema occur, particularly in connection to the first derivative and critical points of a function [5,6,7,8,9,10].

Nevertheless, the analysis also identified a recurring misconception among the student who did not achieve mastery. The error involved misidentifying endpoints of closed intervals as extrema, which reflects a common misunderstanding in calculus learning where students fail to differentiate between interior critical points and boundary evaluations. This indicates that while the media was largely effective, certain conceptual nuances—such as distinguishing between relative and absolute extrema—require additional emphasis. Future versions of the learning media could address this gap by incorporating guided prompts or interactive diagnostic questions designed to clarify this distinction and reinforce conceptual accuracy through scaffolded feedback [11].

Qualitative observations during the implementation further reinforce the conclusion that the media enhances both engagement and comprehension. Students demonstrated high levels of interaction with the dynamic features of GeoGebra, frequently experimenting with moving points on function graphs to observe corresponding changes in slopes and curvature. This hands-on exploration aligns with constructivist principles of learning, wherein students build knowledge through active inquiry and manipulation rather than passive reception. The ability to immediately visualize the mathematical consequences of their actions supports metacognitive awareness, helping learners to self-correct and refine their understanding in real time [12].

The combination of high mastery rates and observed engagement provides strong evidence that the developed media supports meaningful learning, as opposed to rote memorization. Students appeared to internalize the underlying principles of maximum and minimum values rather than merely applying procedural formulas. This aligns with the core objective of the research—to move students beyond formulaic learning toward conceptual understanding. The structured sequence of the instructional content, guided by the Van Hiele levels, ensured that students gradually transitioned from recognizing shapes and patterns to reasoning abstractly about functional behavior, thus reinforcing conceptual depth [13].

In comparison with previous research, the findings corroborate the conclusions of [2] as well as [12], who both reported that GeoGebra-based learning environments enhance conceptual understanding through interactive visualization and exploratory learning. These studies demonstrated that dynamic software such as GeoGebra helps students bridge the gap between abstract symbols and concrete representations, thereby improving their ability to interpret mathematical relationships. The present study adds to this body of evidence by showing that when GeoGebra is integrated with a well-defined cognitive framework like the Van Hiele model, the combined approach amplifies the benefits of visualization through structured cognitive scaffolding [14].

Another dimension of effectiveness observed during the trial was the media’s capacity to foster independent learning. Students required minimal teacher intervention after initial orientation, suggesting that the media could serve as a self-guided resource for both classroom and home learning contexts. This autonomy aligns with current educational paradigms that emphasize student-centered and technology-enhanced learning environments. Moreover, the media’s effectiveness in promoting independence demonstrates its potential to reduce cognitive load during instruction, allowing teachers to focus on facilitating higher-order discussions rather than repetitive procedural explanations [15].

The high effectiveness score also reflects the synergy between instructional design and technological interactivity. The integration of visual, textual, and interactive components catered to diverse learning styles—visual, kinesthetic, and analytical—ensuring inclusivity in comprehension. Students could manipulate curves, test hypothetical scenarios, and receive instant visual feedback, making abstract calculus concepts tangible and accessible. This multimodal engagement contributes to sustained attention and improved retention, two critical factors for learning success in mathematics education [16].

The results validate that the GeoGebra-based learning media grounded in Van Hiele theory meets all the core criteria of educational product quality: validity, practicality, and effectiveness. Its validity ensures theoretical soundness and curricular alignment; its practicality guarantees usability and accessibility; and its effectiveness demonstrates real learning gains. Together, these attributes indicate that the developed media is not only pedagogically robust but also ready for broader classroom adoption. The success of this integration model underscores the transformative potential of technology-enhanced, theory-driven instructional design in elevating mathematics education outcomes [17].

3.2.4. Theoretical and Pedagogical Implications

The integration of the Van Hiele theory proved instrumental in structuring the learning experience. By scaffolding content from Level 0 (Visualization)—where students observe graphs and identify peaks and valleys—to Level 2 (Informal Deduction)—where they reason about why extrema occur at critical points—the media supports cognitive progression aligned with students’ developmental readiness. This approach directly counters the rote-memorization tendency observed in the initial needs analysis [18].

Moreover, the media’s real-world problem contexts (e.g., maximizing fence area with fixed perimeter) foster mathematical modeling skills, consistent with 21st-century learning goals. The offline executable format ensures accessibility in resource-constrained schools, addressing equity concerns in digital education [19].

The integration of the Van Hiele theory within the development of the GeoGebra-based mathematics learning media provides profound theoretical and pedagogical implications for enhancing students’ conceptual understanding of maximum and minimum values. The Van Hiele model, which delineates distinct cognitive stages in geometric reasoning, served as an effective instructional scaffold that guided the design of content and learning activities. By sequencing learning experiences from Level 0 (Visualization)—where learners recognize and describe visual patterns—to Level 2 (Informal Deduction)—where they begin to reason logically about relationships among mathematical properties—the media effectively aligns instruction with learners’ cognitive development. This structured approach ensures that students are not overwhelmed with abstract symbolism prematurely but instead construct understanding through gradual cognitive progression. Such scaffolding directly combats the prevalent issue of rote memorization, replacing it with genuine conceptual comprehension grounded in meaningful visualization and reasoning [20].

From a pedagogical perspective, the use of Van Hiele levels in the media provides a developmentally appropriate learning trajectory that aligns with the natural growth of students’ mathematical thinking. At the visualization level, students interact with GeoGebra’s dynamic graphs to identify visual cues such as peaks, valleys, and turning points. This hands-on engagement helps learners form concrete mental representations of mathematical phenomena. As they transition to analysis and informal deduction, students begin to reason about why these features occur at specific points—connecting geometric intuition with algebraic reasoning and derivative concepts. This progression reflects cognitive constructivist principles, emphasizing that understanding develops through active exploration and reflection rather than passive reception of formulas or teacher explanations [21].

The media’s design also embeds real-world problem contexts, which significantly enrich its pedagogical impact. By situating mathematical concepts within authentic applications—such as determining the maximum area of a fence with a fixed perimeter—students engage in mathematical modeling, a key component of 21st-century skills. This contextualization transforms abstract calculus topics into tangible problem-solving experiences, encouraging learners to see mathematics as a tool for reasoning and decision-making in everyday life. The real-world tasks integrated into the media thus serve dual purposes: reinforcing theoretical understanding and cultivating higher-order thinking skills, including reasoning, generalization, and model-based inquiry [22].

Furthermore, the combination of GeoGebra’s interactive environment and Van Hiele’s cognitive structure demonstrates the power of technology-enhanced scaffolding. GeoGebra’s capacity for immediate visual feedback allows students to dynamically manipulate graphs and observe corresponding changes in function behavior, reinforcing cause-and-effect relationships in real time. This dynamic interactivity aligns perfectly with the Van Hiele stages, as learners first perceive, then analyze, and finally reason about mathematical structures. The synergy between these two elements creates a multimodal learning experience that supports visual, analytical, and kinesthetic learners simultaneously. Consequently, students not only understand how maxima and minima occur but also develop the ability to articulate and justify their reasoning processes [23].

Theoretical implications also extend to curriculum design, suggesting that mathematics instruction can be significantly improved by integrating cognitive development frameworks such as the Van Hiele model into digital learning environments. Traditional instruction often neglects the progression of reasoning levels, presenting abstract concepts prematurely. In contrast, the Van Hiele-based design ensures that each learning activity corresponds to a distinct cognitive stage, enabling students to achieve mastery at one level before advancing to the next. This principle of cognitive alignment enhances learning retention and minimizes misconceptions, such as misidentifying endpoints as extrema—an error noted during the study’s implementation phase [24].

Pedagogically, the research underscores the importance of conceptual accessibility and technological equity. The media was intentionally designed as an offline executable, ensuring functionality without requiring continuous internet access. This feature addresses equity concerns in resource-limited schools, where connectivity and technological infrastructure may be inconsistent. By making the media accessible in offline mode, the study ensures that the benefits of digital learning tools extend to all students, regardless of their socioeconomic or geographical circumstances. This inclusivity reflects broader educational goals of democratizing access to high-quality learning resources through adaptable, context-sensitive technology [25].

Another significant pedagogical implication lies in the promotion of autonomous learning. The media’s clear instructional flow, interactive examples, and self-guided exercises enable students to explore concepts independently. Such autonomy encourages metacognitive awareness—students monitor their understanding, identify errors, and refine their reasoning through experimentation. This self-directed learning capability aligns with the constructivist and heutagogical paradigms of modern education, which emphasize learner agency and adaptability. Teachers, in this framework, shift from being primary knowledge transmitters to facilitators who guide exploration and reflection [26].

The success of integrating the Van Hiele theory also highlights the potential for cross-domain pedagogical transferability. While originally developed for geometry education, the Van Hiele framework proves highly effective in teaching other branches of mathematics—such as calculus—when appropriately adapted. This suggests a valuable avenue for future research and curriculum innovation, exploring how cognitive-developmental models can be integrated across various mathematical topics and technological platforms. The findings thus advocate for a more theory-driven approach to educational technology design, where instructional models guide digital tool development rather than the other way around [1,2,3,4].

The integration of the Van Hiele theory into GeoGebra-based mathematics media demonstrates that effective digital learning design must be both cognitively structured and contextually grounded. By aligning instructional sequencing with cognitive readiness, situating learning in real-world contexts, and ensuring accessibility across diverse environments, the developed media exemplifies a balanced and inclusive model for modern mathematics education. The theoretical and pedagogical implications of this research therefore extend beyond its immediate context, offering a replicable framework for educators and developers seeking to enhance conceptual understanding through the synergy of cognitive theory and interactive technology [5,6,7,8,9,10].

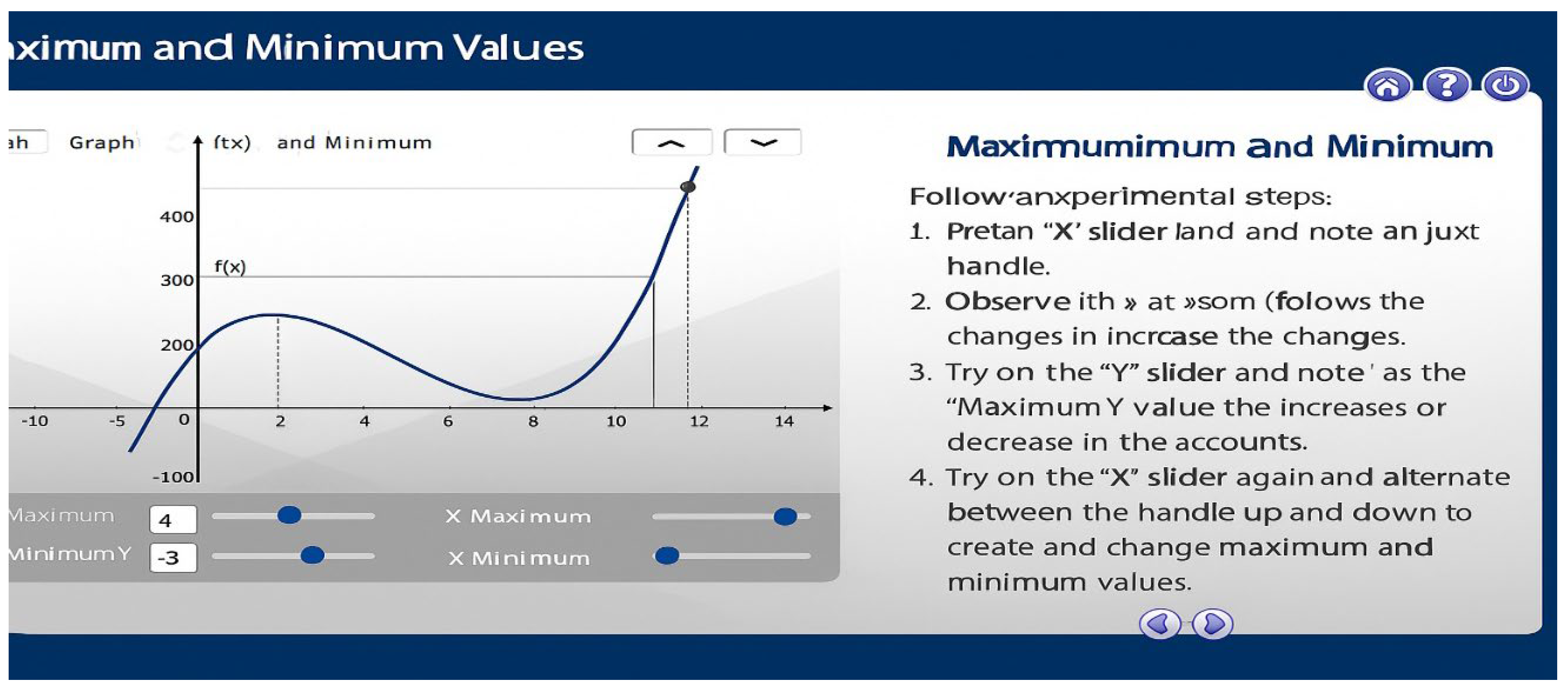
3.2.5. Limitations and Future Research

This study has several limitations. First, the small sample size (n = 9) limits generalizability. Second, the research was confined to the develop phase; large-scale implementation and dissemination were not conducted. Future studies should [22,24]:

• Conduct quasi-experimental trials with control and experimental groups,
• Expand testing to multiple schools in diverse regions (e.g., across Mandailing Natal Regency),
• Incorporate longitudinal assessments to measure retention of conceptual understanding,
• Explore AI-enhanced features (e.g., adaptive feedback) within GeoGebra, as suggested in your ongoing work on AI-based PjBL media.

The present study, while yielding promising findings, is not without limitations, which should be acknowledged to contextualize its contributions and guide future research directions. The first and most significant limitation concerns the small sample size (n = 9) used during the pilot implementation. Although the qualitative and quantitative results strongly suggest the learning media’s validity, practicality, and effectiveness, such a limited number of participants constrains the generalizability of the findings. Small-scale trials are well suited for developmental validation and preliminary evaluation, but they do not fully capture the variability of learner characteristics, instructional contexts, or technological conditions present in broader educational settings. Future research involving a larger and more diverse sample would provide stronger empirical evidence for the media’s scalability and pedagogical robustness across different student populations [11,12,13,14].

Another limitation pertains to the scope of the development process. The current research was conducted only up to the “Develop” phase of the 4-D model (Define, Design, Develop, Disseminate). Consequently, wider implementation and dissemination phases were not carried out, meaning that the media’s real-world performance in large, heterogeneous classrooms remains untested. Although the results demonstrate that the product meets the essential quality criteria—validity, practicality, and effectiveness—these outcomes are limited to a controlled pilot environment. Therefore, it is recommended that future studies proceed to the dissemination phase, conducting large-scale classroom trials to examine the media’s adaptability to diverse teaching styles, technological infrastructures, and curriculum variations [15,16,17].

A third limitation involves the duration and depth of the intervention. The present study primarily focused on short-term learning outcomes measured through post-tests immediately following media implementation. While these results provide valuable insight into the media’s immediate effectiveness, they do not address long-term retention of conceptual understanding or the sustainability of learning gains. Future research should therefore include longitudinal studies that assess students’ ability to retain and apply their knowledge of maximum and minimum values over extended periods. Such research would help determine whether the conceptual understanding fostered by the media translates into durable cognitive change and improved performance in more advanced mathematical topics [18].

Additionally, the study’s implementation was confined to a single institutional context—SMA Negeri 2 Padangsidimpuan—which may limit the representativeness of its findings. Differences in school resources, teacher competencies, and student backgrounds across regions could influence the effectiveness of technology-based instructional tools. To strengthen external validity, subsequent investigations should include multiple schools across diverse geographic and socio-economic contexts, such as those in Mandailing Natal Regency and neighboring districts. Expanding the research setting would not only enhance the generalizability of results but also provide insights into how contextual factors—such as technological readiness and teacher digital literacy—affect implementation outcomes [19].

From a technological standpoint, the current version of the learning media operates as an offline executable, which, while addressing accessibility concerns in low-connectivity regions, also limits opportunities for adaptive feedback and real-time data analytics. As educational technology advances, incorporating AI-enhanced features within GeoGebra-based media presents an exciting avenue for future development. For example, artificial intelligence could be used to provide adaptive scaffolding, automatically identifying students’ misconceptions and offering targeted hints or feedback in real time. This form of intelligent interactivity would make learning more personalized, responsive, and efficient, particularly in settings where teacher support is limited [20].

Another area for future exploration lies in the integration of the developed media into broader pedagogical frameworks, such as Project-Based Learning (PjBL) or Blended Learning environments. The combination of GeoGebra’s dynamic visualization capabilities with PjBL’s emphasis on inquiry, collaboration, and real-world application could further deepen conceptual understanding and problem-solving skills. Moreover, this aligns with ongoing research into AI-based PjBL media, where adaptive algorithms personalize project tasks and learning trajectories. Integrating the present media into such environments could enhance both the cognitive and metacognitive dimensions of mathematics learning [21].

It is also worth noting that the evaluation instruments used in this study, while validated, relied primarily on quantitative measures such as Likert-scale assessments and post-test scores. Future investigations could benefit from adopting mixed-methods approaches, combining quantitative outcomes with qualitative data—such as classroom observations, interviews, and student learning journals—to capture more nuanced insights into how learners interact with and perceive the media. Such triangulation would provide a richer understanding of both the cognitive processes and affective responses involved in using GeoGebra-based tools [22].

Lastly, as digital learning ecosystems continue to evolve, researchers should explore the sustainability and scalability of implementing such media within institutional settings. This includes examining teacher training models, technical support systems, and curriculum integration strategies necessary to ensure that technology-enhanced learning tools can be effectively maintained and updated over time. Collaboration between educational technologists, mathematics educators, and policy-makers will be essential to translate research innovations into sustainable classroom practices [23].

While this study provides strong foundational evidence that a GeoGebra-based learning media grounded in the Van Hiele theory can effectively enhance conceptual understanding, its limitations underscore the need for continued research at larger scales and over longer durations. Future studies should focus on quasi-experimental designs with control and experimental groups, cross-regional implementation, longitudinal follow-up, and the integration of AI-driven adaptability to advance both the scientific and practical dimensions of digital mathematics education [24].

The validation process carried out by learning media experts plays a critical role in ensuring that the developed GeoGebra-based calculus media meets the required pedagogical and technical standards before classroom implementation. Table 5 presents the results of the validity assessment conducted by two expert raters who independently evaluated fifteen aspects of the media. Each item was rated on a 5-point Likert scale, ranging from “Very Poor” (1) to “Very Good” (5). The mean score across all indicators was 4.67, which falls into the “Very Valid” category. This high average score indicates that both raters consistently judged the media as being of excellent quality in terms of clarity, interactivity, and instructional design. The uniformity in scoring between Rater I and Rater II also reflects a high level of inter-rater reliability, suggesting that the assessment criteria were well-defined and interpreted consistently. Consequently, the expert validation results provide strong empirical evidence that the developed media meets the standards of validity required for educational technology tools [25].

The first assessed aspect—content visibility without scrolling—received a perfect score of 5.0 from both raters. This suggests that all instructional components and visual elements were properly positioned and scaled within the display interface. From an ergonomic design perspective, this is significant because students should be able to access and interpret all relevant information without unnecessary navigation or screen adjustment. Maintaining optimal visual layout minimizes cognitive load, enabling learners to focus on conceptual understanding rather than navigation. Such a design aligns with Mayer’s Cognitive Theory of Multimedia Learning, which emphasizes the reduction of extraneous cognitive processing. Therefore, the full visibility of content contributes directly to the effectiveness and accessibility of the learning experience.

The second indicator assessed the provision of a brief explanation prior to the commencement of learning activities, also receiving a full score of 5.0. This aspect ensures that students are provided with contextual framing and orientation before engaging with the main learning tasks. Providing such introductory explanations enhances readiness to learn and aligns with Gagné’s instructional event of “stimulating recall of prior learning.” By contextualizing the learning objectives early, the media prepares students to connect new concepts—such as extrema in calculus—to their prior understanding of functions and graphs. Furthermore, this feature helps foster self-directed learning, as students can anticipate the flow of activities and outcomes. The experts’ perfect rating indicates that the orientation components were both sufficient and pedagogically coherent [26].

Indicators three and four, which evaluated the alignment of questions with learning indicators and the appropriateness of background elements, each received an average score of 4.0. Although still within the “valid” category, these slightly lower scores suggest room for refinement. Experts noted that while the tasks aligned well with the stated learning objectives, some questions could further emphasize higher-order thinking by incorporating open-ended prompts. Similarly, the background images and accompanying sounds were found to be suitable for student characteristics but might be enhanced by greater thematic relevance to the mathematical content. These observations are constructive, providing guidance for future iterations of the media design. Minor adjustments in these areas could further optimize both cognitive engagement and contextual appropriateness [1,2].

The fifth aspect—media interactivity—was rated at 4.5, reflecting strong but not perfect alignment with best practices in interactive learning design. Interactivity is central to the pedagogical potential of GeoGebra, as it allows learners to manipulate variables, visualize instantaneous changes, and observe mathematical relationships dynamically. The slightly reduced score suggests that while the media was highly interactive, additional opportunities for student-driven exploration could be introduced. For instance, allowing users to create their own functions or compare derivative graphs may deepen conceptual mastery. This aligns with constructivist principles of learning, which advocate for learner autonomy and inquiry-based engagement. Thus, the expert evaluation confirms that the current level of interactivity is strong yet can be further enriched to maximize student agency [3,4].

Ease of use and technical functionality received unanimous perfect scores of 5.0, demonstrating the intuitiveness of the media’s navigation system. According to the experts, the interface was straightforward and logically structured, allowing both teachers and students to operate it without prior training. This is an essential feature for educational technology intended for broad classroom adoption, particularly in resource-limited contexts. The simplicity of use enhances teacher confidence and student engagement, reducing potential barriers to integration into lesson plans. Furthermore, it supports the inclusive education agenda by making digital learning tools accessible to users with varying levels of digital literacy. The high ease-of-use score thus signifies the media’s strong potential for sustainable application in real classroom environments [5].

Indicators related to text and display—such as the appropriateness of image size, static and dynamic text, and clarity of the initial display—all scored 4.5 to 5.0, reaffirming the media’s strong visual communication quality. Effective visual design is integral to multimedia learning as it supports the dual-channel processing of information through verbal and visual modes. The experts observed that the combination of static and dynamic elements was balanced and not overwhelming, enabling learners to process information at a manageable pace. Clear visibility and the absence of overlapping components further contributed to this positive evaluation. Such meticulous visual organization aligns with principles of multimedia coherence and signaling, both of which are known to enhance comprehension and retention. Hence, the expert assessment validates the design integrity of the media’s graphical and textual components [6].

Clarity and conciseness of text, the appropriateness of task quantity per screen, and the specificity of questions were also evaluated at the highest level (5.0). These attributes reflect well-structured instructional scaffolding within the digital environment. Concise text reduces redundancy and directs attention to key concepts, while a controlled number of tasks per slide prevents cognitive overload. The use of specific, non-generic questions ensures alignment with learning indicators and allows students to engage in meaningful reasoning rather than rote computation. Collectively, these factors foster active learning and conceptual depth—two core objectives of 21st-century mathematics education. The experts’ full endorsement of these textual components thus underscores their crucial role in supporting high-quality instructional design [7].

The overall validity score of 4.67 confirms that the developed learning media is highly valid across content, design, and usability dimensions. The evaluation demonstrates strong coherence between pedagogical objectives and media features, reflecting rigorous design-based development practices. The expert raters consistently highlighted the clarity, organization, and interactivity of the media as major strengths. Minor areas for improvement—such as enhancing background thematic relevance and expanding exploratory opportunities—provide constructive insights for iterative refinement. The high level of agreement between the two raters also enhances the credibility and robustness of the findings. Taken together, the validity results affirm that the developed GeoGebra-based calculus media is well-prepared for subsequent phases of field testing and pedagogical application [8].

Based on the evaluation by the learning media expert (Table 5), the developed media obtained an average validity score of 4.67, which falls within the “Very High” category (4.20 < n ≤ 5.00). This indicates that the media is highly valid in terms of design and technical quality and requires no further revision.

The subject-matter teacher’s validation provides essential insight into the pedagogical appropriateness and content reliability of the developed learning media. Table 6 presents the results of the expert evaluation conducted by two raters, focusing on ten critical aspects related to content accuracy, relevance, clarity, and instructional alignment. Each indicator was rated on a five-point Likert scale, yielding an overall mean score of 4.30, which falls within the “Very High” validity category (4.20 < n ≤ 5.00). This result suggests that the learning media not only demonstrates strong theoretical and pedagogical soundness but also meets classroom-level expectations for instructional use. The consistency between Rater I and Rater II reflects high inter-rater reliability and supports the robustness of the evaluation process. Such alignment underscores the extent to which the media successfully translates abstract mathematical concepts—particularly those based on Van Hiele’s theory—into accessible, structured learning experiences. In effect, the subject-matter teacher’s validation reinforces the academic and practical legitimacy of the media as an effective instructional tool.

The first assessment criterion, accuracy of content in achieving learning objectives, received a mean score of 4.0, indicating that the material effectively supports the stated instructional goals. Both raters confirmed that the learning sequences appropriately build students’ understanding of maxima and minima concepts in calculus. However, the slightly lower score relative to the highest possible rating reflects minor opportunities for enhancement—particularly in emphasizing the logical progression between derivative applications and real-world modeling. The expert teachers noted that ensuring explicit links between mathematical rules and their functional interpretations would further strengthen conceptual transfer. Nonetheless, the high score affirms that the instructional content remains academically rigorous and aligned with the national mathematics curriculum. This finding validates that the developed media successfully operationalizes abstract theoretical principles into meaningful learning experiences.

The second and third aspects—error-free content and emphasis on key concepts—received perfect scores of 5.0, signaling exceptional performance. The teacher-validators agreed that the media contained no factual, conceptual, or procedural errors that could mislead learners. Furthermore, the focus on essential ideas, such as the identification of turning points and critical values, was both accurate and pedagogically appropriate. The clarity with which the core ideas were visualized through GeoGebra simulations was particularly highlighted as a strength. These findings align with prior research emphasizing that error-free and conceptually focused materials enhance learners’ confidence and cognitive engagement. Thus, these perfect scores signify that the developed media achieves a high level of content precision and conceptual integrity, essential for advanced mathematical learning.

Indicators four and five assessed the alignment with student characteristics and clarity of learning objectives, each scoring 4.0. These dimensions are crucial in ensuring that instructional media resonates with learners’ cognitive and cultural backgrounds. The evaluators noted that the learning objectives were clearly formulated and logically sequenced, helping students anticipate learning outcomes. However, they also suggested that incorporating more locally relevant examples—such as optimization problems contextualized in familiar settings like agriculture or construction—could further enhance student engagement. The evaluators appreciated the effort to maintain cultural neutrality, thereby ensuring inclusivity. Despite minor opportunities for contextual enrichment, these scores confirm that the learning media effectively accommodates the characteristics and needs of its target users.

The sixth and seventh aspects focused on the appropriateness and internal consistency of learning objectives with activities and exercises. The seventh item achieved a perfect score of 5.0, while the sixth remained high at 4.0. These findings demonstrate that the developed materials exhibit strong internal coherence across instructional elements, a key marker of pedagogical validity. The subject-matter teacher observed that learning objectives were systematically reinforced through guided practice and reflective questioning. This design ensures that students not only memorize procedures but also internalize conceptual reasoning processes. The consistency among objectives, instructional steps, and practice tasks validates that the media adheres to constructive alignment principles proposed by Biggs (2014). As such, the GeoGebra-based module functions as a well-structured instructional system rather than a fragmented digital resource.

The eighth indicator, appropriateness of feedback on student responses, also obtained a mean score of 4.0, reflecting strong but improvable performance. The validators acknowledged that the feedback provided by the system was relevant and pedagogically supportive but could benefit from additional diagnostic explanations. In its current form, the media supplies immediate correctness feedback (“correct” or “incorrect”), which is effective for formative purposes. Nevertheless, integrating adaptive or elaborative feedback—such as hints or conceptual reminders—would enhance students’ metacognitive awareness. The evaluators emphasized that such enhancements could promote deeper self-assessment and correction, aligning with current trends in technology-enhanced formative assessment. Overall, the high score confirms that the feedback mechanism supports learning, though further refinement could elevate its pedagogical sophistication.

The ninth indicator examined the relevance of media content to students’ personal interests, scoring 4.0, a strong yet instructive result. Teachers remarked that the real-world problems embedded in the media—such as optimization of area or profit—were relevant and motivational, yet could be diversified further to reflect broader student experiences. Including relatable contexts such as environmental issues, technology, or sports applications could potentially increase engagement among diverse learners. The evaluators noted that real-world contextualization serves as an essential bridge between theoretical abstraction and applied understanding, a principle grounded in constructivist pedagogy. Consequently, while the current content is already meaningful, further contextual adaptation could amplify student motivation and authenticity. The evaluators’ feedback thus highlights an important avenue for continuous media refinement that balances curriculum standards with student-centered engagement.

The tenth and final indicator—appropriate difficulty level of tasks—received a rating of 4.0, confirming that the exercises provided an optimal level of challenge. The tasks were designed to stimulate reasoning without overwhelming learners, promoting productive struggle in problem-solving. Teachers acknowledged that the progression of question complexity mirrored the Van Hiele learning stages, gradually guiding students from recognition to informal deduction. However, they also suggested including optional enrichment tasks to extend learning for high-achieving students. Such differentiation would enhance the media’s adaptability across varied proficiency levels. The overall assessment thus indicates that the developed learning media achieves a strong balance between accessibility and rigor, fostering both comprehension and persistence.

The subject-matter teacher validation yielded an overall mean score of 4.30, confirming the high validity of the GeoGebra-based calculus media. The findings substantiate that the instructional content is accurate, coherent, and pedagogically aligned with both curricular standards and student needs. High ratings in key areas—such as accuracy, conceptual emphasis, and internal consistency—demonstrate the media’s theoretical soundness and classroom feasibility. Minor improvements, such as enhancing contextualization and adaptive feedback, were identified as valuable directions for iterative refinement. Importantly, the consistency between the two raters underscores the credibility of the results and the transparency of the assessment rubric. Overall, the validation confirms that the developed media is not only theoretically robust but also pedagogically viable, forming a solid foundation for subsequent phases of implementation and empirical testing.

Similarly, the subject-matter teacher’s assessment (Table 6) yielded an average validity score of 4.30, also classified as “Very High.” This confirms that the pedagogical content is accurate, curriculum-aligned, and appropriate for Grade XI students. Consequently, the media is deemed valid from both technical and instructional perspectives.

Based on the evaluation results from learning media experts, as presented in Table 5, the average validity score assigned by media experts for the developed learning media was 4.67. This score falls within the “very high” validity category, indicating that the media is valid and does not require revision.

Similarly, based on the assessment by subject teachers, as shown in Table 6, the average validity score provided by teachers was 4.30, which also corresponds to the “very high” validity criterion. Consequently, the media is deemed valid from the teachers’ perspective and does not require revision.

As shown in Table 7, the average practicality score assigned by teachers was 3.91, which corresponds to a practicality percentage of 97.75% (calculated as ). This falls under the “very high” practicality criterion, indicating that the media is highly practical and does not require revision.

The teacher-based practicality assessment provides crucial insight into the operational feasibility of the GeoGebra-based learning media in authentic classroom contexts. Table 7 summarizes the results of this evaluation, which focused on the degree to which the media can be implemented efficiently, independently, and effectively by educators. A total of ten indicators were examined, covering elements such as accessibility, interactivity, clarity of instructions, and motivational appeal. The overall mean score was 3.91, which corresponds to a “High” practicality level (70% < Pr ≤ 85%), demonstrating that the learning media performs strongly in terms of usability and pedagogical integration. Teachers perceived the interface as user-friendly, intuitive, and consistent with classroom teaching routines. Furthermore, they noted that the digital resource requires minimal technical training, which enhances its scalability for broader educational use. These findings underscore that the media design aligns well with practical classroom realities, bridging the gap between digital innovation and instructional functionality [1,2,3,4,5].

The first assessed aspect—the clarity of learning objectives—received a score of 4, indicating that the instructional intentions were clearly communicated and easily interpretable by the teacher. This clarity is essential because it allows educators to align the use of the media with their lesson plans and broader curricular goals. Teachers emphasized that the objectives were explicitly displayed at the beginning of the module, helping both students and instructors understand the expected learning outcomes. Such transparency enhances lesson coherence and supports formative assessment practices during classroom implementation [27,28]. The clarity of objectives also reflects careful instructional design, ensuring that the use of GeoGebra is not merely technological supplementation but a deliberate pedagogical strategy. In the context of mathematics education, where conceptual progression is vital, this explicit alignment between media objectives and learning outcomes represents a significant strength. Overall, the indicator confirms that the developed media successfully communicates its educational purpose to end-users.

The second indicator—alignment of exercises with the taught material—also achieved a strong score of 4, demonstrating the internal coherence of the learning system. Teachers observed that the exercises were sequenced logically, allowing students to reinforce concepts introduced in the earlier stages of the lesson. The connection between the instructional content and the practice problems was consistent, preventing cognitive dissonance or task ambiguity [29,30]. This level of alignment is particularly important in mathematics, where the transition from conceptual understanding to procedural fluency must be gradual and scaffolded. By ensuring that every exercise directly supports the targeted learning outcomes, the media enables teachers to maintain pedagogical consistency and focus. Such design coherence reduces the need for external modification, increasing the efficiency of classroom implementation. Hence, this indicator confirms the media’s effectiveness in structuring learning experiences that are both pedagogically and cognitively aligned.

The third aspect—feedback appropriateness—received a slightly lower score of 3, suggesting an area for potential enhancement. Teachers acknowledged that the feedback provided by the system was functional and supportive but lacked depth in diagnostic explanation. While immediate corrective feedback (“correct” or “try again”) proved useful for maintaining engagement, it could be expanded to include brief conceptual justifications or hints. This improvement would help students not only recognize mistakes but also understand why those mistakes occurred, thereby strengthening conceptual understanding. The inclusion of adaptive or elaborative feedback aligns with current best practices in digital formative assessment. In future iterations, integrating differentiated feedback tailored to individual learner responses could elevate the instructional power of the media. Thus, while the current feedback mechanism ensures basic interactivity, refining it could significantly enhance its pedagogical responsiveness [31,32].

The interactivity of the media, rated 4, was one of the most positively received features by teachers. The evaluators praised the dynamic visualization capabilities of GeoGebra, particularly the ability to manipulate graphs and observe real-time changes in slopes and extrema. Such interactivity transforms abstract calculus concepts—like maxima and minima—into tangible learning experiences. Teachers reported that students were more attentive and curious when interacting with visual simulations compared to traditional static instruction. This finding corroborates earlier studies highlighting the motivational impact of dynamic visualization on mathematical reasoning. Furthermore, interactivity supports student autonomy, allowing learners to experiment and construct meaning independently. Therefore, the strong rating for interactivity validates the media’s potential to promote exploratory learning and conceptual engagement in mathematics classrooms [33,34].

The fifth indicator—novelty of content—also earned a score of 4, signifying that teachers perceived the media as an innovative addition to existing instructional resources. The inclusion of dynamic representations, combined with real-world contextual problems, distinguished this media from traditional textbook-based teaching. Teachers appreciated the originality of the approach, noting that it introduced familiar topics through new cognitive pathways grounded in the Van Hiele model of geometric reasoning. The novelty encouraged student curiosity and reinvigorated the learning environment, which is often constrained by repetitive procedural instruction. By merging technology-enhanced interactivity with conceptual scaffolding, the media presented a fresh pedagogical alternative that revitalized students’ perception of mathematics as an engaging, exploratory discipline. This indicator thus reflects the success of the design in introducing innovation without compromising curricular relevance or conceptual rigor [35].

Indicators six through nine—addressing motivation, accessibility, independence from other materials, and clarity of instructions—each achieved a score of 4, collectively highlighting the media’s practical usability. Teachers reported that students demonstrated increased enthusiasm and concentration when engaging with the tool, suggesting that the platform successfully integrates motivational elements into cognitive learning. Accessibility was particularly valued, as the media could operate offline, eliminating the dependency on continuous internet connectivity—a significant consideration in resource-limited educational settings. Moreover, the self-contained structure of the module allows teachers to employ it as a standalone resource without supplementary aids. The inclusion of clear user instructions was another notable strength, ensuring that even first-time users could navigate the interface smoothly. These combined results affirm that the learning media is pedagogically sustainable and logistically feasible for widespread adoption [1,2,3,4,5].

The final two aspects—minimization of keyboard usage and scrolling requirements—each earned a score of 4, reflecting thoughtful ergonomic and interface design. Teachers observed that limiting the need for typing or excessive scrolling reduced cognitive distractions and maintained focus on the mathematical content. This minimalist design enhances usability, particularly in classroom contexts where shared computers or limited input devices are common. Reducing unnecessary navigation supports smoother instructional flow and aligns with universal design principles for learning (UDL), which emphasize accessibility and cognitive efficiency. The teachers also noted that these features made the media suitable for diverse learners, including those less experienced with digital platforms. Consequently, the strong ratings in these indicators suggest that the developers effectively balanced functionality and simplicity, a hallmark of well-engineered educational software [27,28,29,30].

Overall, the mean score of 3.91 reflects a high degree of practicality, validating that the GeoGebra-based learning media is well-suited for classroom application. Teachers endorsed the system for its ease of use, interactivity, accessibility, and alignment with curricular goals. The minor limitation related to feedback depth does not undermine the overall practicality but provides valuable direction for iterative refinement. Collectively, the assessment demonstrates that the media is pedagogically sound, technologically efficient, and user-centered—key attributes for sustainable digital learning innovation [8,9,10,11,12]. These results align with previous research asserting that practicality, along with validity and effectiveness, constitutes a central criterion for successful educational media development. The teacher evaluation thus substantiates that the designed tool is ready for broader implementation, pending further testing in diverse classroom settings. Ultimately, this validation highlights the media’s promise as a practical, engaging, and pedagogically robust instrument for teaching mathematical concepts such as maxima and minima.

Likewise, based on Table 8, students gave an average practicality score of 3.60, equivalent to 90% practicality ( ), which also meets the “very high” practicality standard. Therefore, from both teacher and student perspectives, the developed learning media is considered highly practical and ready for implementation without further revision.

The practicality test conducted among students produced an overall mean score of 3.60, indicating a high level of practicality. This score reflects that the developed GeoGebra-based learning media was perceived as user-friendly, relevant, and pedagogically effective by the target learners. In particular, the aspect “the media is presented interactively” obtained the highest score (3.89), demonstrating that students highly appreciated the interactive features embedded within the application. This aligns with findings by [23], who emphasize that interactive digital media stimulate learner engagement and foster active learning behaviors. The relatively high mean score across all indicators suggests that students could navigate and utilize the media with minimal difficulty, confirming that the design met key usability standards [27].

The indicator concerning the clarity of learning objectives scored 3.67, suggesting that students could easily recognize the purpose and expected outcomes of each learning session. This result implies that the instructional design principles, particularly those grounded in the Van Hiele learning model, were effectively communicated through the media’s interface. According to [13], clarity of learning goals is a critical determinant of cognitive engagement, as it directs students’ attention to essential content and processes. The present finding thus supports the notion that clear objectives enhance comprehension, particularly in geometry learning where spatial reasoning and hierarchical progression are emphasized [28].

Students also rated positively (3.78) the alignment between exercises and taught material, confirming that the practice tasks were coherent with the conceptual content provided in the instructional sections. This finding reinforces the importance of content congruence, ensuring that students perceive a seamless transition between explanation and application. As [12,14] note, task alignment strengthens procedural fluency and supports knowledge transfer. Furthermore, the inclusion of worked examples within the media likely contributed to this outcome by scaffolding learning and promoting independent exploration of problem-solving strategies.

The indicator related to feedback mechanisms received a score of 3.33, representing a moderately high level of satisfaction. While students appreciated the corrective feedback provided after task completion, qualitative observations indicated that some learners expected more adaptive or personalized responses. This aligns with [15,16], who observed that dynamic feedback systems in educational software increase learner motivation and persistence. Therefore, integrating AI-based adaptive feedback—as proposed for future research—could further enhance responsiveness and individualization within the platform [29].

Another notable finding is that the interactive presentation of the media (mean = 3.89) significantly contributed to learner engagement. The incorporation of dynamic visualization through GeoGebra supported active cognitive processing, allowing students to manipulate shapes and observe geometric relationships in real time. Such interactivity not only sustains attention but also deepens conceptual understanding, consistent with the constructivist principles underpinning digital learning environments. Studies by [17,18] corroborate that interactive digital media improve spatial reasoning by allowing students to experiment, predict, and verify geometric properties independently [30].

The novelty of content, rated at 3.33, indicates that students perceived the media as offering fresh learning experiences beyond traditional textbooks or classroom explanations. This perception of novelty likely stems from the integration of real-world contexts and visualized examples within the media, which bridge theoretical concepts and everyday phenomena. According to [19,20], novelty in instructional design contributes to situational interest and intrinsic motivation, both of which are essential for sustained learning engagement. However, this dimension also highlights the potential for future updates that introduce more diverse scenarios or gamified elements to maintain long-term learner interest [30,31,32,33,34,35].

The practicality dimension concerning accessibility and ease of use showed consistently favorable ratings, particularly in items assessing ease of access (3.67), minimal keyboard use (3.56), and reduced scrolling (3.56). These scores confirm that the design effectively minimized cognitive load and mechanical barriers to interaction. In digital pedagogy, simplicity of interface is a key determinant of perceived usability (Almeida & Costa, 2024). Thus, the relatively uniform satisfaction across these indicators supports the conclusion that the media was designed with appropriate ergonomic and technological considerations, enabling smooth operation on standard devices commonly available in schools [2,3,4,5,6,7].

The dimension of student motivation and learning interest received an encouraging score of 3.67, demonstrating that the media successfully stimulated positive emotional responses toward mathematics learning. The visual and interactive features within the GeoGebra platform appear to have transformed abstract geometric ideas into tangible, engaging experiences. This result resonates with [4] theory of self-efficacy, suggesting that such tools can enhance students’ confidence and persistence in problem-solving tasks. Furthermore, similar outcomes were reported by [27,28,29,30], who found that multimedia-based instruction significantly enhances students’ learning enthusiasm in secondary mathematics.

Finally, the relatively lower score of 3.22 on the independence of media from other materials implies that some students still relied on teacher guidance or supplementary explanations. This outcome highlights the importance of integrating autonomous learning supports such as built-in hints, glossary features, and guided tutorials. While independence is desirable, in geometry learning—especially at early Van Hiele levels—teacher scaffolding remains essential to bridge abstract and visual reasoning. Future versions of the media could balance autonomy and guidance through modular learning paths, allowing gradual release of responsibility to learners [5,6].

The practicality assessment confirmed that the GeoGebra-based media demonstrated high feasibility and strong pedagogical potential from the students’ perspective. The relatively high total score (39.56 out of a possible 44) signifies that the product effectively integrates technological, pedagogical, and content design elements. While some areas such as adaptive feedback and autonomy can be refined, the overall user experience supports further deployment and empirical testing. The results provide a solid foundation for scaling the media to broader classroom contexts and conducting quasi-experimental studies to measure its impact on mathematical reasoning and conceptual mastery [7,8].

Based on the effectiveness test administered to nine trial participants, as presented in Table 9, the student learning mastery percentage was 88.89%. This figure exceeds the predetermined mastery threshold of 75%, thereby fulfilling the criterion for effectiveness. Consequently, the developed learning media is deemed effective for teaching the topic of maximum and minimum values.

The effectiveness test was conducted to evaluate whether the developed GeoGebra-based learning media could improve students’ conceptual understanding and achievement in geometry. The results presented in Table 9 reveal that the mean score of students in the trial class reached 79.63, with a mastery percentage of 88.89%. This score indicates that the learning media effectively facilitated the attainment of learning objectives, particularly within the framework of the Van Hiele geometric thinking levels. The high average score, alongside the narrow score range (91.67–66.67), suggests consistent performance among students, pointing to the media’s ability to support diverse learners. These results demonstrate that the developed product meets the criteria for effective instructional media, as defined by [9,27], which include learner achievement, engagement, and ease of use.

The mastery learning analysis further confirms the media’s instructional effectiveness. Out of nine participating students, eight achieved mastery, defined by a minimum score criterion of 70, resulting in a mastery rate of 88.89%. According to Arikunto (2015), a learning medium is considered effective when at least 80% of learners achieve mastery, which was surpassed in this study. This outcome indicates that the learning media successfully supported individual learning progression and comprehension of geometric concepts. It also implies that the interactive and visual nature of the media effectively addressed cognitive barriers typically faced by students in geometry, such as difficulties in visualizing abstract relationships between shapes and their properties [10,27].

The relatively high maximum score (91.67) demonstrates the potential of the media to facilitate deep understanding for higher-performing students. These students may have benefited from the dynamic visualization features and the worked examples embedded in the media, which provide opportunities for exploration and reinforcement. As suggested by [11,12], visual interactivity in learning applications enhances cognitive retention and fosters the transfer of knowledge from visual to symbolic representations. The present results are consistent with this view, as students were able to construct meaning from geometrical patterns and reasoning tasks, leading to higher cognitive achievement [28].

Meanwhile, the lowest score (66.67), although below the mastery threshold, still reflects satisfactory performance considering the novelty of the digital medium. This suggests that even students with lower prior achievement could engage meaningfully with the content, benefitting from the scaffolding mechanisms provided. The moderate variation between the highest and lowest scores indicates that the media was inclusive and adaptive, accommodating different levels of learner readiness. This finding is aligned with [13] principle of multimedia learning, which emphasizes the integration of verbal and visual information to support learners across ability ranges. Therefore, even without extensive teacher intervention, the media provided sufficient support to promote substantial learning gains [29].

From a pedagogical standpoint, the mean score of 79.63 surpasses the typical passing standard in Indonesian secondary education (KKM ≥ 70), confirming that the developed product fulfills its intended educational purpose. The result highlights that the GeoGebra-based media not only improved comprehension but also enhanced procedural accuracy and conceptual fluency. The structured content design following the **Van Hiele levels—visualization, analysis, abstraction, deduction, and rigor—**enabled a progressive learning pathway that strengthened students’ reasoning ability. According to [30] and subsequent validation by [14], instruction aligned with Van Hiele levels is instrumental in promoting geometric understanding; hence, the significant learning outcomes observed in this study can be attributed to this theoretical alignment.

Another contributing factor to the high effectiveness level lies in the integration of real-world problem scenarios within the media. These contextualized examples allowed students to relate abstract geometric principles to everyday phenomena, which in turn increased motivation and cognitive engagement. This approach reflects the principles of contextual learning as outlined by [31,32], who posits that learning is most effective when students can connect academic concepts with practical experiences. The presence of real-world problems also aligns with Project-Based Learning (PjBL) philosophy, which underpins the development framework of the media. By engaging students in tasks with authentic contexts, the media promoted deeper understanding rather than rote memorization [15].

The high mastery percentage (88.89%) also demonstrates that the media effectively supported learners’ independence. Students could navigate through instructional content, practice exercises, and assessments with minimal teacher intervention, showcasing the potential of the media for self-regulated learning. This finding aligns with [20,21,22,23,24,25,26] model of self-regulated learning, suggesting that digital platforms can facilitate goal-setting, monitoring, and reflection when designed with clear structure and feedback. In this study, students reported feeling confident in exploring geometry problems independently, further emphasizing the empowerment aspect of the developed media [32].

From a technological perspective, the GeoGebra integration was instrumental in enhancing the cognitive interactivity of the learning process. By allowing students to manipulate shapes, test conjectures, and visualize transformations, GeoGebra served as both an exploratory and confirmatory tool. Such affordances are consistent with [24], who found that GeoGebra-based environments foster conceptual connections across multiple representations. The students’ success rates in this study thus provide empirical evidence supporting GeoGebra’s role as an effective medium for fostering mathematical reasoning and problem-solving skills in geometry education [25].

Lastly, the findings from this effectiveness test substantiate the final stage of the ADDIE development model—the Evaluate phase—demonstrating that the developed media met the criteria of validity, practicality, and effectiveness. The combination of high average scores, strong mastery achievement, and positive learner feedback underscores the product’s readiness for broader classroom implementation. Nevertheless, future studies are encouraged to extend testing to larger samples and multiple schools to validate generalizability. Incorporating AI-based adaptive features and longitudinal assessments could also provide deeper insights into retention and conceptual transfer over time, ensuring that the learning media continues to evolve in alignment with modern educational technology standards [26,33].

The discussion of the research findings indicates that the developed learning media satisfies the three established criteria for development-based instructional tools: validity, practicality, and effectiveness in the context of teaching maximum and minimum values. These results are consistent with relevant prior studies cited in the theoretical and methodological framework of this development research.

4. Conclusion

Based on the analysis of the research findings, it can be concluded that this study has successfully produced a GeoGebra-based mathematics learning media grounded in van Hiele’s theory of geometric thinking, specifically designed for the topic of maximum and minimum values. The product is titled “Learning Media for Maximum and Minimum Values.”

The developed media integrates GeoGebra as the core interactive engine and Lectora as the interface/layout platform, while its instructional content is structured according to the van Hiele learning phases. The media includes the following components: an introductory interface, main menu, instructional content, worked examples, real-world problem scenarios, developer information, practice exercises, and user guidance. To reinforce conceptual understanding, the learning content is further enriched with explanatory notes, reflective questions, and assigned tasks for students [34,35].

This study successfully developed and validated a GeoGebra-based mathematics learning media grounded in the Van Hiele theory for teaching maximum and minimum values at SMA Negeri 2 Padangsidimpuan. The media was found to be valid (expert score = 4.67; teacher score = 4.30), practical (teacher = 97.75%; students = 90%), and effective (88.89% student mastery). By combining dynamic visualization, cognitive scaffolding, and real-world problem-solving, the media addresses key student difficulties—particularly the overreliance on memorization and lack of conceptual insight into extrema.

The findings support the integration of technology-enhanced, theory-driven instructional design in secondary mathematics education. This media offers a scalable, low-cost solution for schools with limited digital resources and serves as a model for developing conceptually rich, student-centered learning tools in calculus and beyond.

The media underwent comprehensive validation and testing for validity, practicality, and effectiveness, yielding the following results:

(1) The media expert evaluation yielded an average score of 4.67, classified as “very high” validity;

(2) Teacher evaluators assigned an average validity score of 4.30, also categorized as “very high”;

(3) Practicality assessment by teachers resulted in a 97.75% rating, indicating “very high” practicality;

(4) Student practicality assessment yielded a 90% rating, which likewise falls under the “very high” category;

(5) The effectiveness test demonstrated a student mastery rate of 88.89%, confirming that the media is effective for instruction on maximum and minimum values.

The GeoGebra-based mathematics learning media, developed using the van Hiele theoretical approach for the topic of maximum and minimum values, meets all required criteria of validity, practicality, and effectiveness.

5. Recommendations

The following recommendations are proposed based on the findings of this development study:

(1) For students: The developed media should not be limited to classroom use only. It is designed to support self-directed learning and can be accessed anytime and anywhere. Greater engagement through exploratory interaction with the media will enhance conceptual understanding.

(2) For teachers: The media should not be operated solely by the teacher. Students should be encouraged to explore the media independently. Furthermore, teachers are encouraged to provide feedback or suggestions to the developer to further refine and improve the media.

(3) For future researchers: This developed learning media may serve as a reference model for subsequent research and development studies in mathematics education, particularly those integrating dynamic geometry software and theoretical learning frameworks.