Stepping Stones: Adopting a Fading Programme Design to Promote Teachers’ Use of Metacognitive Strategies for Mathematical Problem-Solving

1. Introduction

The potential benefits of metacognition are well-established both generally [1,2,3] and for mathematical problem solving more specifically [4,5]. However, metacognition is often neglected in policy and practice [2], with some research suggesting that teachers’ own understanding of metacognition is lacking, leading to misconceptions and weak implementation [6]. This, combined with a lack of support and guidance for teachers [7], means that its potential for impact remains unfulfilled.

In exploring ways to promote the development of teachers’ understanding and use of metacognitive strategies for mathematical problem solving, this article reports the impact of an innovative, fading programme - ‘Stepping Stones’ - as part of a multi-faceted professional development (PD) offer. The article discusses research from a pilot evaluation across five English primary schools in response to one central research question: how did Stepping Stones influence teachers’ understanding and use of metacognitive strategies for mathematical problem solving? This question was further divided into two sub-questions: a) did teachers’ deployment of metacognitive strategies vary as the programme faded; and b) how did teachers perceive the acceptability of the fading design?

The article begins with an overview of existing literature regarding metacognition and its role in mathematical problem solving before discussing implementation in school contexts. We then briefly discuss research around PD for teachers and provide an overview of the Stepping Stones programme. From there, we explain the research design and methodology, before the results and discussion in which we respond to the research question by exploring both teachers’ deployment of metacognitive strategies and their perceptions around the acceptability of the fading programme model.

1.1. Metacognition

Often simplistically defined as ‘thinking about thinking’, metacognition is widely acknowledged to significantly influence learning outcomes [1,2,3,6,8]. First defined by Flavell [9], metacognition involves planning, monitoring, regulating and evaluating performance whilst completing a task [1], and can encompass a range of classroom activities, including ‘comparing different students’ approaches to problem solving and decision making; identifying what is known, what needs to be known, and how to produce that knowledge; or having students think aloud while solving problems’ [10].

There is evidence that interventions targeting development of metacognitive strategies are associated with large effects across age and attainment ranges [2,11,12]. Furthermore, several authors highlight the link between metacognition and motivation [1,13,14] indicating that increased examination and reflection upon the learning processes unpinning successful task-completion can encourage pupils’ self-belief, leading to increased resilience and perseverance in the face of setbacks [14].

1.2. Implementation in School Contexts

Despite broad consensus regarding the potential value of metacognition for pupil outcomes, these approaches are under-developed in school contexts due to their relative absence in national policies and curricula (Perry et al., 2019). Widespread teaching, particularly in primary education contexts, may also have been curtailed by debate surrounding the age at which pupils are capable of metacognition, with some authors suggesting that children under the age of eight have limited capacity for metacognition [1,9]. However, in recent years this view has been increasingly challenged, with those such as Whitebread et al. [15] finding both verbal and non-verbal indicators of metacognition in children from the age of three. Whilst this may appear encouraging, some sources indicate that metacognition does not necessarily increase with age [1,16] and that some pupil groups, including socio-economically disadvantaged pupils, may be less likely to acquire metacognitive knowledge and skills without explicit teaching [6], thus rendering particularly important the question of how best to promote the development of metacognition within classroom contexts.

In their systematic review of the literature, Muijs and Bokhoe [6] emphasise the importance of both direct and indirect approaches for promoting the development of pupils’ metacognition, including explicit instruction and teacher modelling, alongside opportunities for guided practice, dialogue and scaffolded inquiry. Veenman and Beishuizen [17] also highlight the importance of embedding the teaching of metacognition within curriculum content, maintaining that discrete teaching may inhibit pupils’ capacity to transfer metacognitive knowledge and skillfulness between contexts.

Prominent within the literature are references to the value of thinking aloud, whereby teachers model their approach to a task alongside their metacognitive planning, monitoring and evaluation of their chosen strategies [6,18,19,20]. When modelling, Muijs and Bokhove [6] particularly endorse deployment of worked examples, whereby teachers adopt a staged approach, reviewing problems step-by-step to articulate thought-processes and the rationale underpinning the use of specific cognitive and metacognitive strategies, before gradually reducing scaffolding to increase pupil independence. However, some studies have highlighted that the use of explicit modelling is relatively infrequently used by teachers [18,20], suggesting that its potential for impact may yet be unrealised.

The role of peer-discussion and collaboration is also significant to the development of metacognition both generally [1,21], and for mathematics specifically [22,23,24]. For example, Schwartz et al. [21] suggest that metacognition may be developed through articulating and explaining reasoning, a view which is supported, albeit loosely, by the work of several other researchers including Cross and Paris [25] and Hennessey [26] as well as Lai [1], who describe the benefits of peer interactions in constructing and refining metacognitive knowledge and regulation. Indeed, Schraw [20] believes that pupils may well provide better role models for metacognition than teachers themselves, arguing that ‘Frequently, students are better able to model cognitive and metacognitive skills, and provide a powerful rationale for these skills within the student’s zone of proximal development’ (p. 118). However, there is a note of caution evident in the work of those such as Stein et al. [27] who note that facilitating such discussions requires considerable skill.

1.3. Metacognition and Mathematical Problem Solving

Numerous studies cite the importance of metacognition in promoting competence in mathematics [6,22,24,28]. Indeed, some authors suggest that supporting pupils’ understanding of the learning process is of particular import given perceptions of success in mathematics as a supernatural power, which Picker and Berry [29] suggest is a consequence of “the general invisibility to pupils of the mathematical process, for with the process hidden, mathematical facility looks more like a power than an ability which anyone has the possibility to learn” (p. 88). This is supported by a considerable body of evidence emphasising the importance of teaching pupils to think through mathematics to deepen understanding [30,31,32,33].

Mathematical problem solving is highly prized by both educators and employers, however several sources raise concerns that the current English curriculum and assessment system fails to adequately support pupils to develop this important skill [34]. This has led some to advocate a shift away from rote and procedural forms of learning, towards greater emphasis upon metacognition to promote flexibility and independence [34,35]. The link between metacognition and improved mathematical problem solving is well-established [36,37]. Mathematical problem solving involves an initial assessment of the problem, and subsequent planning, monitoring and evaluation of the approach used to address it, and can therefore be seen to align closely with the metacognitive process [37,38]. Similarly, several sources emphasise the importance of encouraging pupils to identify and compare multiple types of mathematical problems, and the strategies deployed to approach these [33,36,39] to build knowledge and confidence in approaching novel and unfamiliar problems.

However, despite their acknowledged importance, evidence suggests that both metacognition and problem solving are neglected in the broader mathematics curriculum [40] and teacher PD [34,40,41]. Ofsted’s [40] review of 50 English schools reported insufficient opportunities to explain or justify approaches to problem solving, or describe relationships, impeding the development of deeper understanding. Ofsted [39,40] also highlight the need for greater consideration of progression, sequencing problems to enable pupils to engage with increasingly complex examples over time. This under-representation is also reflected in pupil outcomes. For example, when considering international trends in mathematics learning for Year 9 pupils (aged 13-14 years), England’s Department for Education (DfE) [41] suggested that recent improvements in international league tables have been driven by improvements in number, data and probability, and identified relatively weak outcomes for mathematical reasoning, which underpins problem solving. Combined, these studies underscore the need for a more defined and coherent approach to metacognitive development to promote pupils’ mathematical problem solving.

1.4. Teacher Professional Development

Existing research is clear that PD - defined as ‘structured, facilitated activity for teachers intended to increase their teaching ability’ [42] - can positively impact pupil outcomes [43,44,45] with some sources suggesting that teacher quality accounts for up to 40 per cent of variance in learning [46]. PD is often looked upon favorably by teachers and policymakers [47] and attracts high-levels of investment both in England [48] and internationally [49]. Despite this, research on what PD is, what it looks like and how it should be delivered has been relatively limited [42,50]. This is of particular importance given that the impacts of individual approaches vary considerably, underscoring the potential value of better-distinguishing between more - and less – effective PD models [42].

Whilst it must be noted that those such as Asterhan and Lefstein [51] challenge the assumption that it is possible to identify generally effective feature of PD, and whether this is even desirable, recent years have seen a marked increase in studies attempting to review impact and identify commonalities in what makes PD effective [42,50]. However, these efforts have been impeded by the multitude of different definitions and designs deployed within studies regarding teachers’ PD, limiting comparison of their relative effectiveness [42] and rendering it difficult to reach conclusions about which features matter most [50].

Various sources emphasise the importance of incorporating multiple complementary mechanisms, or activities, when designing PD [42], suggesting that their deployment is more closely related to successful outcomes than factors identified by previous reviews, such as duration of activity [43]. Common mechanisms include sequencing PD to manage cognitive load and provide opportunities to revisit and consolidate prior learning [42,43] as well as motivating teachers through presenting information from credible sources - such as research evidence - [42,52], and establishing a shared purpose and goal setting [42,43]. Existing literature also highlights the importance of promoting understanding of specific teaching techniques through modelling and instruction [42,43,53], feedback [43], collaboration and peer-support [53,54], and emphasises the importance of reflection and repetition of desired behaviours when seeking to embed and sustain change [42]. Beyond consideration of mechanisms, Cordingley et al. [43] and Popova et al. [55] underscore the importance of developing both subject and pedagogic content within PD, emphasising that different subjects require radically different pedagogies [56,57], thus highlighting the importance of carefully considering content and context, as well as the mechanisms adopted for PD delivery.

2. Materials and Methods

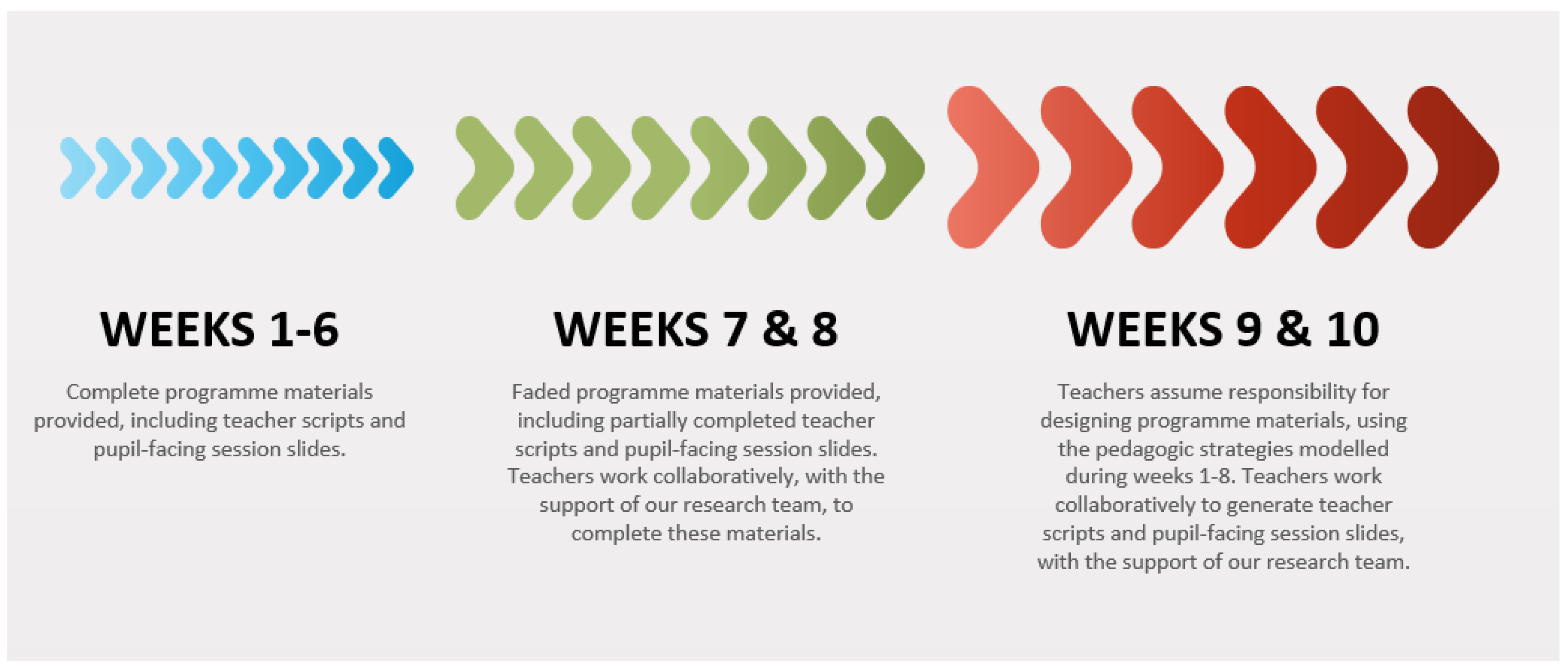
2.1. The Current Study

Combining findings from research into metacognition and teacher PD, we developed a programme and accompanying PD offer to enhance teachers’ understanding and use of metacognitive strategies to develop mathematical problem solving. This programme drew upon earlier work from one member of our research team, employing metacognitive strategies with 9–11-year-old pupils [28,58]. The refined programme – ‘Stepping Stones’ - was piloted with 6-7 year old pupils in five primary schools in England (6 x Year 2 classes, and 1 x mixed Year 1/2 class) across ten weeks between January and March 2024, drawing upon the findings of Perry et al. [11] who found larger effects for metacognitive interventions delivered in ten or more sessions. Intended to supplement the daily mathematics lesson, sessions lasted between 15 and 20 minutes in duration and were delivered as a whole class intervention, three times per week. Framed within the context of a visual metaphor, stepping stones, the programme prompted teachers and pupils to focus attention on the learning process, and to understand and implement metacognitive approaches into mathematics teaching. Drawing upon research from well-evidenced strategies for promoting metacognitive development, we incorporated models for metacognitive talk, including thinking aloud and debriefing questions to structure pupils’ reflections regarding the planning, monitoring and evaluation of learning [6,20]. These strategies were complemented through use of worked examples to support pupils to critique approaches to learning, whilst reducing demands upon cognitive load [6,11,36].

All materials were developed by two members of our research team, including detailed teacher scripts and pupil-facing session slides, and an accompanying PD offer to promote the development of professional understanding. Teachers were supported in three face-to-face training sessions, and in one school visit from one member of the research team to observe programme sessions in action and provide targeted feedback and support. However, in addition to these discrete PD sessions, we intended the programme materials themselves to form part of the comprehensive learning offer, serving as worked examples – complete part-by-part demonstrations of a particular approach [11] – to model metacognitive strategies in action. Stepping Stones can therefore be seen to deploy worked examples in two distinct ways: firstly, as a means of supporting pupils’ understanding of approaches used for specific mathematical problems, and secondly, as a vehicle for teachers’ PD to develop understanding of pedagogic techniques to promote metacognitive thinking.

A central principle of Stepping Stones was the fading approach it adopted. For the initial six weeks of the programme, all session plans and resources were provided for teachers by our research team, however, in the final four weeks of delivery, the scaffolding offered by the materials faded, prompting teachers to assume increasing responsibility for session planning. This fading process is represented below, in Figure 1. Although faded worked examples are well-established in the literature regarding skills acquisition as a means of managing learners’ cognitive load [59,60] to our knowledge this is their first application in a teacher PD context. At the outset of this study, our working hypothesis was that the fading design would prompt the gradual transition from heavily-scaffolded use of metacognitive strategies towards teachers’ more independent application as they planned and created their own programme materials in the final four weeks of delivery.

This fading process was facilitated by support from both peers and two members of our research team, providing opportunities to integrate numerous mechanisms associated with effective PD, including guidance and instruction [42,43,53], feedback [43], collaboration, and peer-support [53,54]. Time for this collaboration was incorporated into PD sessions, acknowledging the many demands upon teacher workload and the associated challenges for professional learning. During the second PD session, teachers worked collaboratively to plan sessions for delivery during weeks 7 and 8 from partially completed plans and programme materials, and in the third PD session, teachers wholly planned sessions for delivery during weeks 9 and 10 using blank materials, following the structure and teaching techniques employed in previous weeks.

2.2. Research Design

Employing a convergent mixed-methods design [61], this study comprised quantitative data to track changes in teachers’ experiences and learning outcomes across the delivery period, including the degree of variance in teachers’ deployment of metacognitive strategies as the programme faded. Concurrently, qualitative data was used to explore teachers’ perceptions concerning acceptability of the programme and its features. Ethical approval for this work was obtained from the host organisation (application number 10332). The data were originally collected as part of an Education Endowment Foundation (EEF)-funded Innovation project – with two members of the research team responsible for the design, delivery and management of the project. Upon completion of the project for the EEF, the project report was used to conduct further data analysis for this study, in line with the EEF’s publication screening processes. All shared data was anonymised, prioritising particpants’ rights to annonymity and confidentiality.

The research design was underpinned by a critical realist framework [62,63]. Selection of this approach was driven by complexities found in studies that report challenges to teachers’ understanding and implementation of metacognitive strategies in the classroom [13,64]. Metacognition involves the creation of internal mental processes that are not directly observable, such as planning, monitoring and evaluating one’s own thinking. The adoption of a critical realist approach provided a framework to unpack these ‘deep’ mechanisms to reveal more about teachers’ metacognitive practices. By this means, quantitative data were treated as the ‘empirical’ layer of the study, where frequency counts and associations of metacognitive strategies across the fading programme established a base-layer to identify previously unobserved and unknown patterns. Through discovery of these underlying mechanisms, quantitative data revealed an ‘actual’ snapshot of the absence and presence of these strategies with some understanding of their use in shared planning activities. Qualitative data contributed evidence to capture the ‘real’ and offered explanatory insights into the underlying causes of how teachers interpreted the programme design.

2.3. Data Collection and Sample

Using a purposive sampling strategy, seven teachers from five primary schools in Northeast England were recruited via an open expression of interest shared by various mathematics education organisations across the region. The sampled teachers all worked full time and had varying levels of teaching experience. Specifically, one teacher was in their first year of teaching, two teachers had at least three years of experience, and four had been teaching for ten or more years. Programme delivery was free to schools, and each school received a payment of £3,000 from the Education Endowment Foundation for taking part.

Impact was evaluated via multiple data collection points and methods. This convergent mixed methods approach permitted in-depth analysis and triangulation of data, centering around understanding teachers’ metacognitive practices and facilitating greater insights into the underlying factors influencing their experiences and engagement. These multiple forms of data are summarised in Table 1.

Pre-, mid- and post-programme surveys included a series of open (qualitative) and closed (quantitative) questions, such as: “How do you currently teach problem solving in Year 2?” and “How confident do you feel about teaching pupils to solve problems (1 = not confident at all; 5 = very confident)” to understand more about teachers’ experiences and reflections. Of the seven teachers sampled in the pilot, n = 5 completed the pre-survey; n = 7 completed the mid-survey and n = 6 the post survey. We also collected feedback following each of the three PD sessions, with completion rates of n = 5 following session 1, n = 5 following session 2, and n = 6 following session 3. Teachers were asked to rate their levels of confidence (1 = not confident at all; 5 = extremely confident) and consider the impact upon their learning, including by identifying the most useful elements of the training.

Visits to each participating school were scheduled during the second week of teaching, providing an opportunity for members of our research team to observe Stepping Stones delivery. The visits provided an opportunity to review fidelity of implementation, as well as acceptability to teachers and schools. Structured observations used a five-item checklist to assess the degree to which key programme features were implemented (1 = not implemented; 2 = partially implemented; 3 = fully implemented). As the programme faded (weeks 7-10), a second checklist was used to review teacher-generated materials as teachers became more responsible for, and assumed ownership of, these sessions. This checklist featured nine key strategies, including models for metacognitive talk such as, thinking aloud and use of debriefing questions to structure pupils’ planning, monitoring and evaluation of learning, as well as use of worked examples to support pupils to critique approaches to learning. Each review took approximately 15 minutes to complete and was supplemented with field notes and brief comments.

Finally, semi-structured interviews were conducted with participating teachers. Two interviews were completed with two pairs of teachers while three individual interviews were arranged with the remaining teachers. All interviews lasted up to 30 minutes with an extended focus on programme design and collected concurrently alongside other data collections.

As part of quality assessment, independent external review established the face validity of the pre-, mid- and post-programme survey questions, checklists, and interview protocol (Appendix I) before data collection commenced. This process ensured that key features of the programme remained a central focus of the review.

2.4. Quantitative Data Analysis

Quantitative data from surveys and checklists were prepared and entered in the Social Package for Statistical Sciences (SPSS, version 29). Frequency counts of teachers’ responses and observations to quantitative components of the pre-, mid,- and post-programme surveys, training session feedback surveys, and programme implementation and teacher-generated materials checklists were collated and analysed alongside qualitative data from open response questions. These data were assessed concomitantly, ensuring a parallel and equitable analysis of multiple sources to accurately report teachers’ views and experiences.

Two ordinally coded checklists were used in this study: one for observation of programme implementation (1 = not implemented; 2 = partially implemented; 3 = fully implemented) and another for review of teacher-generated materials (1 = missing; 2 = brief information included; 3 = detailed information included). The review of programme implementation was based on five observations of programme delivery, while nine reviews of teacher-generated materials were recorded in total (review of three sessions for each of weeks 7, 8, and 9). Review of teacher-generated materials for sessions 10-12 of week 10 were excluded from the final analysis due to time constraints in the final PD session, which prevented the completion of materials within the allotted time. This is considered in further detail in the Results and Discussion below. Initial analysis included inspection of frequency counts for each checklist to determine how features of the programme were implemented and how often they were included in teacher-generated materials. For the observation of programme implementation, a total score of 15 would indicate features were ‘fully implemented’, while for the teacher-generated materials checklist, a total count of 27 would represent ‘detailed information included’ for each feature.

Descriptive statistics (frequency counts and mean ranks) were used to understand patterns and trends from data recorded in the checklists. Further analysis was performed on the teacher-generated materials checklist using the Goodman and Kruskal Gamma test [65] to investigate the association of the nine programme features in teachers’ planning across the nine sessions held between weeks 7-9. The test investigated the existence of concordant or discordant pairs from ordinally ranked observation data for each session over the specified time. The test provides an estimate of the strength of association between the variables with sign (e.g., positive ties or negative ties). The coefficient ranges between measures of -1 to 1, where -1 represents a perfect negative association and 1 being a perfect positive association [66]. Whilst the test is non-parametric by design, there is an assumption that ties have a monotonic relationship, whether positive or negative. Following an inspection of a visual plot, we inspected the ties for each of the nine checklist items on the number of observations (n =9) (weeks 7-9) and concluded there to be a monotonic relationship.

2.5. Qualitative Data Analysis

A six-phase thematic analysis (TA) process [67] was adopted to explore patterns across the qualitative datasets. This process was undertaken by all four members of our research team, working together through the six phases. This gave time to move freely back and forth between the phases, as required for the reflexive aspect of TA. Observation and survey data was collected throughout the delivery period, with final interviews conducted between one and two weeks following conclusion of the programme. The two members of our research team most closely involved in the design and delivery of Stepping Stones initiated the familiarisation phase of analysis [67], therefore it is important to acknowledge the influence of our subjective opinions, influences and overlapping identities (designer, deliver and researcher), particularly in this first engagement with the data.

Following this initial phase, the two remaining members of our research team provided support further for analysis. When moving into the later stages of TA, having both insider and outsider perspectives allowed for thoughtful and complex discussions and analysis, with insider perspectives affording opportunities to bring the data to life, understanding the situations and stories behind the words, whilst outsider perspectives offered fresh viewpoints and perceptions. These different perspectives also encouraged us to shift between inductive modes, where analysis and theme development are driven by the data, and deductive modes, where existing theoretical concepts provide a lens through which to read the data [67]. This flexibility in approach allowed for rich discussion and added further depth to our analysis.

For our familiarisation of the data and initial coding we used both paper and electronic copies of the data. We also completed this at various locations, collaboratively in rooms at the university campus as well as from home over Microsoft Teams. We were conscious that these change of modes could potentially affect each of our moods and therefore the analytical process. Initially, we produced 18 different codes together in the same room. After a two-week break, we came back to the data and began to cluster these codes into four potential broad patterns of meaning. After further discussion, a review of the codes and the complete dataset, we further refined to three broad areas comprising of professional development design, feelings of increased ownership, and the value of collaboration. Throughout phases three, four, and five we moved between our initial themes, developing and reviewing them and eventually defining, refining and naming them.

Whilst our sample size limits any claims to generalisability, this is neither unexpected nor was it an aim of this study. Instead, when considering the analysis presented in this paper, we hope to enable readers to consider the transferability of insights presented here [67]. As such, it is the responsibility of the reader to determine the extent to which our findings may apply to their own contexts.

3. Results

Combined, our results respond to the central research question by considering how Stepping Stones influenced teachers’ understanding and use of metacognitive strategies for mathematical problem solving. We also explore teachers’ experience of the fading approach through examining two further sub-questions: a) did teachers’ deployment of metacognitive strategies vary as the programme faded; and b) how did teachers perceive the acceptability of the fading design? Our analysis of the quantitative and qualitative data has identified three themes: building knowledge and confidence captures teachers’ perceptions and understanding of planning and teaching metacognitive strategies for mathematical problem solving; ownership and ‘buy in’ reports upon teachers’ views around the importance of metacognition, the impact the fading design had upon attitudes towards the programme and the strategies therein; and the value of collaboration speaks to the extent to which teachers valued working with each other as well as the research team.

These themes align with the wider literature regarding principles for effective design and delivery of PD more broadly, suggesting that the fading model implemented through Stepping Stones provided a successful means of enhancing teachers’ understanding and use of metacognitive strategies for mathematical problem solving. These themes will be discussed in turn below, drawing upon data in the form of verbatim quotations from teachers and complemented with descriptive statistics from the quantitative analysis.

3.1. Building Knowledge, Confidence and Capacity

Teachers suggested that opportunities to engage with underpinning research regarding both metacognition and mathematical problem solving increased their motivation to deliver Stepping Stones.

“sometimes you might try things in your own classroom and you never really know how it’s working […] It’s been really lovely trying something new and talking about the theory behind it to start with because then it gives you a reason why you want to do it as well” (Teacher C, final interview).

“I hadn’t even really thought about the fact that we never really teach problem solving. We expect children to be able to do it, but we never actually explicitly teach it. And then I thought especially those pupil premium children, their metacognition isn’t as developed as others and it really got us thinking that it’s definitely something we need to do” (Teacher T, final interview).

In addition to motivation, there was a demonstrable increase in teachers’ self-reported knowledge of the evidence base for metacognition following participation in the programme. Pre-programme surveys indicated that five teachers perceived their knowledge as ‘not familiar at all,’ whereas post-programme surveys revealed that six teachers reported increased familiarity of knowledge of metacognitive strategies. Similar patterns were observed in responses concerning teachers’ confidence in teaching problem-solving, with post-programme results indicating that four teachers reported feeling ‘extremely confident’ while two teachers felt indifferent or slightly confident.

This was also reflected across the qualitative data. For one teacher in their first year of teaching, programme delivery afforded opportunities to revisit and reinforce knowledge obtained from statutory early career training. However, for more established teachers, PD and programme content developed understanding of both metacognition and mathematical problem solving, reinforcing wider literature which suggests that these elements of pedagogy are currently under-represented within both educational policy and practice [2,34,38,40].

“I knew the word metacognition and I didn’t know a lot about it before I came on the course. So for me, it was useful in terms of enabling me to know how to teach the children to plan and when to work through a problem and to be able to do that with a little bit of support and then independently” (Teacher T, final interview).

“Stepping Stones has enabled me to understand how to explicitly teach problem solving. The course has helped me to understand different approaches to teaching problem solving through worked examples, faded worked examples and mistakes” (post-programme survey, Q7a)

Teachers particularly praised the consistent structure of Stepping Stones sessions, emphasising their value in building familiarity and confidence. For example, teachers reported the benefits of repeatedly applying techniques such as highlighting key words to support their discussion when seeking to understand problem solving tasks.

“it’s nice that the programme repeats itself, so we start with the highlighting and then we move on to unpicking the question. I think having that repeated process constantly has been really good for supporting my disadvantaged children who don’t remember as much” (Teacher S, final interview).

In addition to building knowledge of these concepts, programme materials, and the way in which the support provided faded over time, offered a model which scaffolded teachers’ application of metacognitive strategies into classroom practice. Early provision of complete programme materials, including scripts and pupil-facing session slides, enabled teachers’ to implement the programme with fidelity to our intended design. This was evident from observations during the initial weeks of delivery. Results from Table 2 reveal moderate to high levels of implementation of seven out of nine strategies observed as part of school visits. Two strategies, “15-20 mins session delivered” and “Programme slides used,” were fully implemented (100%) and ranked highest compared to the other strategies. High implementation rates were also observed for “Problem-solving objective shared with the class” and use of “Mixed-attaining trios” to promote peer-discussion, both at 93%. Whereas “Expectations for discussion” and “Strategies for problem-solving” were implemented in 87% of the observations, demonstrating a substantial but slightly lower implementation rate. The strategies “River used” and “Alternating worked example” showed the lowest implementation rates, at 60% and 53% respectively. Fieldnotes suggest that during the setting visits, most teachers did not use the optional alternating worked examples to extend sessions. However, they reported using them within other sessions. In sum, we interpret these results as an indicator of consistent and strong adherence to these specific strategies throughout delivery.

As the programme progressed, teachers’ qualitative responses indicated that increased confidence enabled them to deviate from the scripts and increasingly tailor metacognitive discussions to respond to points of interest raised by their pupils.

“the first couple of weeks, I used [the scripts] like gospel and reading them when I was getting the kids to talk. But then I’ll be honest, the last two weeks I haven’t even really looked at them. I’ve looked at them at the start and said alright, it’s a complete problem or a faded problem or a mistake, just so that I know what’s coming next” (Teacher C, final interview).

“The PowerPoints were brilliant. I didn’t use the teacher script and I did for the first week but I kind of went through the slides obviously before I taught it and I just thought about if I was teaching this what would be my questions because I think my questions would be sometimes different from what was in the teacher’s script and really because the way that the slides are set out and there were lots of opportunities for further discussion. So, me and the children ended up going off on a tangent so I didn’t want to be held to a script, I wanted to teach it the way I want to teach it” (Teacher S, final interview).

The gradual decrease in teachers’ reliance upon session scripts is echoed in the quantitative data. Table 3 presents results from observations of the key features of the Stepping Stones programme. The results from three of the checklist items indicate a strong, negative statistically significant association between Learning Intentions (G = -.857), Teacher Overview (script) (G = -1.00) and Think Aloud (G = -.750) checklist items and the number of planning sessions. More specifically, the proportion of concordant pairs is 85% (Learning Intentions) and 75% (Think Aloud) lower than the proportion of discordant pairs from our analysis.

Analysis indicates that data returned in response to the checklist item regarding teacher scripts represents a perfect negative pattern. This suggests that in the latter weeks of delivery, as the scaffolding offered by programme materials fades and teachers have built considerable familiarity with pedagogic techniques, there is a shift from the inclusion of ‘detailed information’ towards ‘brief information’. The change, initiated at the points at which teachers assume greater responsibility for session planning, represents a small shift backwards when comparing a hypothetical shift from ‘detailed information’ to ‘missing’. Our analysis suggests that although a decrease in the level of detail occurred, the core components of these planning elements remained present, albeit in a less developed form. Although it might initially seem that the reduced scaffolding led to teachers being less detailed in their metacognitive strategies, a closer analysis of both our qualitative and quantitative data reveals the opposite. In fact, their increased confidence in the strategies enabled them to produce less-detailed scripts:

“I think the more we’ve got in the way of it and I’m able to speak from me, the more I know what I’m asking. We don’t need the scripts as much because, well, we’ve done it for 10 weeks” (Teacher T, final interview).

Teachers also highlighted the value of worked examples in delivering clear models, allowing pupils to revisit a shared reference point when undertaking subsequent problem solving tasks with their peers.

“So they know that we’re gonna get through these steps. We’re gonna learn how to do it, and then we’re gonna have a go. So I think that was really useful for them as well and gave the other ones a great model of how to solve the problem. So even if there weren’t 100% sure they could look go right, well, we’ll do this one. But they were looking back at the steps on the river to have a go at their problem” (Teacher L, final interview).

This supports existing literature regarding the role of worked examples in scaffolding the gradual release of responsibility from teacher to pupils (Webb et al., 2019), focusing attention upon recognising and articulating approaches used for problem solving [36] and effectively managing cognitive load [68,69] in preparation for pupils’ independent problem solving. Similarly, teachers’ accounts emphasied the importance of worked examples not solely in pupil-facing materials, but also to support their own professional learning. For example, teachers echoed participants elsewhere in the literature [42,70] in commending the incorporation of live modelling of teaching techniques during initial PD, suggesting the importance of this approach in building confidence and shared understanding: “we came away from that first session, though already with like a vision of how it was going to work in the school” (Teacher K, final interview).

It is important to note that teachers also recognised that opportunities for collaborative planning of future programme sessions, “meant very little extra teacher load was needed” (post-programme survey, 11a), with “no extra work to be done and no extra resources to be made” (Teacher L, final interview). Responses indicated that this may have contributed towards their perceptions of the acceptability of the programme, suggesting that: “there’s nothing better than coming away from training and doing something that you can actually immediately put in” (Teacher L, final interview). This suggests the importance of protecting time for discussion and scaffolded application of when encouraging the implementation of new techniques and approaches.

There was also some indication that teachers increasingly applied metacognitive strategies such as thinking aloud, worked examples, and questions to elicit metacognitive thinking beyond the Stepping Stones programme itself, integrating these into their wider classroom practice.

“I feel I am much more confident in using items such as, Think Alouds and worked examples in my practice and I have started using them across my teaching” (post-survey, 8a).

“I definitely hear myself thinking, but why? ‘Tell me you know that because…’ and those types of stem sentences definitely carry through” (Teacher K, final interview).

“it made me think a little bit more about small steps. So I think sometimes I think about doing a worked example, but I don’t think about all the small steps where that’s what the problem solving really did because there was 5-6 steps to it. Sometimes it was going in a lot smaller steps than I would probably think of myself, which is really good because then it affected my practice in a good way. So I kind of use a lot of the strategies that we’ve done in Stepping Stones to help me in my work as well, which is really good.” (Teacher C, final interview).

Again, this is in line with findings across literature relating to PD, advocating the value of repetition in promoting the formation of habits, leading to sustained integration of new techniques and approaches [42,71].

3.2. Increased ownership and ‘buy in’

Teachers confirmed the acceptability of the fading design, indicating that this led to increased feelings of ownership and responsibility for subsequent delivery, as well as supporting understanding of the underpinning rationale for pedagogic intentions within sessions.

“I think it’s really nice to have that ownership of the system to it as well. And then coming back into school and obviously I work with another year group partner, so then me telling them and saying, oh, well, we’ve one this because of this reason and this is how it’s going to work” (Teacher C, final interview).

“I think that was really beneficial with the teaching of it and the implementation of it, like understanding where it’s all come from and doing it yourself. Especially writing the script because it gave… It allowed us to realise what we do need in the script and what we can skip out” (Teacher L, final interview).

These accounts suggest that collaborative planning empowered teachers, equipping them to offer guidance and explanations to colleagues to enhance their understanding of programme content and delivery. As they assumed greater responsibility for planning sessions within the faded programme design, teachers additionally reported tailoring content according to the specific needs of their pupils. This may have been because 3 out of the 5 teachers surveyed thought the average level of understanding of problem solving and reasoning in class was slightly below the expected standard (pre-programme survey, Q13). Adaptations by teachers included minor changes to “some of the wording so the children can understand a bit better” (mid-programme survey, Q8) and supplementing programme materials with additional resources and manipulatives, as well as larger changes to the degree of challenge presented by the mathematical problems themselves:

“I think probably since the people on the course started developing them, they’ve become a bit easier and I don’t know if that’s just because it’s done by the year 2 teachers kind of with their kids in mind.” (Teacher C, final interview).

These accounts evidence teachers’ sensitive and nuanced adjustments to programme content, resonating with the work of Thompson and Wiliam [72], Lendrum & Humphrey [73] and Sims et al. [42] regarding the potential value of creating space for small alterations to better meet the needs of pupils, and contrasting with previous studies maintaining the importance of maintaining absolute fidelity to original design [74].

Teachers’ positive experiences led some to signal their intention to continue using Stepping Stones beyond the conclusion of the programme. For example, 5 teachers indicated they would very likely continue using the programme in the future (post-programme survey, Q25). In some cases, teachers also indicated that their experiences of scaffolded planning through the fading programme encouraged them to plan additional weeks of the programme, beyond the end of the formal teaching period.

“I am going to continue this in summer term and plan and prepare my own slides. I am planning on using the programme with next year’s year 2 cohort too” (post-programme survey, Q25a)

Similarly, participating teachers reported interest from wider colleagues and that, in some cases, colleagues in other year groups were seeking to introduce mathematical problem solving sessions based upon the Stepping Stones model.

“I’ve had an ECT and another staff member observe from our school and the ECT was from year four and she thinks that she would like to roll it out in year four as a quick 10 minutes. Let’s identify the key facts and things. So I’m in discussions with our SLT at the minute to see whether or not we might be able to do it across the school like say three times a week” (Teacher S, final interview)

“I think having a conversation with [Maths Lead] because she’s been really, really excited by it and she’s been thinking about how she can do things like it with Year 6. She’s been having a go’ (Teacher C, final interview)

3.3. The Value of Collaboration

References to the value of collaboration were common to all teachers. This encompassed the impact of collaboration in developing understanding of Stepping Stones, echoing findings from Allen and Penuel [53] regarding the link between collaboration and sense-making. Teachers’ accounts also suggested that opportunities for collaboration and co-construction enhanced relationships between teachers, and between teachers and the research team, with some indication that this may have been encouraged by the fading design, which incorporated opportunities for authentic and open involvement in collaborative planning and reflection as a core focus of PD sessions.

“The collaboration was so useful because I felt sometimes like I wasn’t as valuable as the other teachers, but only because it was… It was really nice to hear experienced teachers feedback on the way they do maths or the way they do something else and it was nice to even make our own and sit with somebody else and say like, ‘I would have done it this way with my class’. But they’ve done it a completely different way and it was really nice to hear that different ways of doing things in maths. I thought that was so useful. When I came back to my headteacher I said, ‘Ohh, it was amazing’” (Teacher J, final interview).

“both of you were absolutely brilliant in your delivery and you kind of opened it up to the floor more than enough because sometimes on some courses that you go to you get talked to a lot. And although they ask for questions, they don’t really want me to answer, they want to answer themselves, whereas I think this was very much you really wanted to hear what we wanted to do and really wanted us to get involved” (Teacher C, final interview).

Teachers particularly endorsed the decision to undertake collaborative planning sessions in-person, rather than online, supporting the work of McConnell et al. [75] regarding teachers’ preference for face-to-face formats for PD activities [75,76]

“I know we did talk about the planning stage where that might have been better just at school, but it wasn’t. It was lovely to be altogether and share our ideas, so I did think the group discussions and the group meetings were brilliant” (Teacher S, final interview).

Accounts from some teachers suggested that this preference for in-person collaboration may stem from the availability of support from the research team.

“Really good opportunity to plan with K present for support” (Training session 3 feedback).

“The two sessions we had with K and W really helped break down the planning process” (post-survey, 8a).

This connects with the findings of Perry and Booth [77] regarding the importance of the role of facilitator within professional learning, alongside helping to address the current absence of studies providing examples of facilitated activity when working with groups of teachers identified by Hadar and Brody [78].

Teachers’ acknowledged time as both a barrier and enabler of successful collaboration. Overall, the timing and sequencing of PD sessions was endorsed by teachers, suggesting that this was well-balanced to ensure appropriate opportunities to apply new techniques in practice before gathering together to share feedback and engage with ongoing support both from peers, and the research team.

“I think the frequency of seeing each other actually was enough to not need anything else. Because we’ve seen you probably once a month, I think I felt like that if we did have a problem then we knew how to reach you […] There’s a lot of work gone into it, you weren’t just handed it and said go and have a go because it was like the sessions where we caught up fell nicely within a week of us being able to give it a go, get back, feedback. Then the sessions we planned together. They weren’t immediately the week after. So, then that fed into those weeks and then we came back together again” (Teacher K, final interview).

However, particularly during the final PD session – when teachers were required to independently plan sessions for weeks 9 and 10 of the programme without the scaffolding from partially-completed materials – teachers expressed a desire for more time for collaborative planning to ensure that all resources were completed.

“you and W were both there supporting and any questions we had you were there to help and support. I think it was just the time, just the amount of time for it, you know. You gave us materials, like all of the things that you use like the puzzles and the problems. […] I don’t think we could have had any more support really. I think it was just the time” (Teacher T, final interview)

The need for increased planning time as the programme materials faded and teachers assumed greater responsibility for the preparation of resources was also evident from review of teacher-generated materials, which demonstrated that both session slides and teacher scripts for the final week of the programme – week 10 – were incomplete due to insufficient time to complete these collaboratively during the final training session. However, teachers’ responses demonstrated varying perceptions of the reasons why additional time was needed, including the need for greater time to think through the mathematical content of problems, and to navigate the online software used to create pupil-facing resources.

“me and my partner didn’t get the second slides done. So we only got the one session done. So I do think a little bit more time to plan both of them in that session would have been useful for me to break it down and think about it myself” (Teacher J, final interview)

“I think time one is a tricky one because you could have given us longer and some people could have absolutely flown through it. Or you could have gave us less time and some people still would have done it. I think it depends on more the computing skills than the mathematical skills and process, and I think probably the people that got through the problems quicker were the ones that were more confident using the software, they make animations and things like that rather than the actual maths behind it. I think the only issue that I had was the Wi-Fi […] because that was making the collaborative document really slow and cumbersome” (Teacher C, final interview)

Whilst it is perhaps important to note that Teacher J was less experienced than other participants, this perhaps reflects – as Teacher C observes – the different pace at which different individuals work, and the challenges incurred through attempting to gauge this when working across groups.

4. Discussion

To our knowledge, this is the first study to explore a fading programme design in the context of teacher PD. This article therefore contributes to the literature by providing an account of the original use of gradually fading worked examples to scaffold teachers’ understanding and application of metacognitive strategies for mathematical problem solving. Use of worked examples in our study was multi-layered, employed both as a pedagogic strategy to support pupils directly within sessions and, concurrently, through the broader Stepping Stones model whereby the programme materials themselves - including teacher scripts and pupil-facing session slides - formed a worked example for teachers to build familiarity with these techniques in action, before gradually fading this support over the final weeks of the programme. The data provided a nuanced consideration of how Stepping Stones and the associated PD offer impacted the teachers involved over the duration of delivery, focusing upon a central research question: how did the Stepping Stones programme influence teachers’ understanding and use of metacognitive strategies for mathematical problem solving? Further exploration considered two sub-questions: a) did teachers’ deployment of metacognitive strategies vary as the programme faded; and b) how did teachers perceive the acceptability of the fading programme design? In this section, we will discuss our results with reference to the wider literature.

Previous research notes the positive impact of metacognitive strategies upon competency for mathematics and mathematical problem solving [6,22,24,28,36] but also cautions that existing guidance and PD for teachers is insufficient [34,41] leading to weak implementation [6,7]. This study addresses these issues through demonstrating that adoption of the fading design inherent within Stepping Stones led to demonstrable gains in teachers’ knowledge and confidence. Furthermore, our results suggest that this fading approach was acceptable to teachers, leading to a sense of ownership and buy in which encouraged teachers’ participation in, and delivery of, Stepping Stones, alongside sensitive adjustments to tailor programme content according to the needs of pupils. We therefore advocate further examination of this fading PD model to explore its potential in serving as a template for teacher PD for mathematical problem solving, as well as possible applications in broader contexts.

The fading design deployed within this study was a deliberate choice, designed to support teachers’ knowledge and understanding in reference to existing understanding of mechanisms for effective teacher PD [42,43]. We believe that our results endorse its use in this novel context, resonating with wider research surrounding the use of fading worked examples within cognitive load theory [68], and the design of professional learning in other disciplines, such as health [79]. Worked examples are an effective means of scaffolding learning, reducing cognitive load, and supporting skill acquisition [68,80,81] and this was the case in our study. Teachers’ accounts indicated that use of worked examples developed their understanding of the programme format and structure, but also metacognition and how to teach it in relation to problem solving in mathematics.

Stepping Stones first focused upon building requisite knowledge of research around metacognition and mathematical problem solving within the initial PD session for teachers. Teachers’ accounts endorsed this approach, indicating that this increased motivation for participation. These accounts resonate with existing literature, reinforcing the value of presenting information from credible sources when seeking to influence behaviour change [42], as well as underscoring the need for clear communication of research evidence to build necessary understanding to appropriately translate and apply findings into practice [42,52,82]. Additionally, teachers’ knowledge was enhanced through engagement with programme materials, which were specifically designed as worked examples, modelling the desired metacognitive strategies within the first six weeks of the programme before fading throughout the final four weeks of delivery.

The success of this approach, evident in teachers’ later application of these same strategies in their own planning, reinforces existing literature regarding the importance of modelling and rehearsal to develop specific teacher techniques [42]. As well as this, managing cognitive load effectively through this faded programme ensured that teachers assimilated new knowledge without feeling overwhelmed, enabling them to gradually transition to independent application [83,84] and to grow in confidence even as the support offered to them reduced. Our results also connect with extensive findings regarding the importance of repetition in habit formation and sustaining behaviour change both specifically for teacher PD [42], as well as for behaviour change more generally [71].

Teachers’ accounts endorse the emphasis upon collaboration when designing the future programme materials, resonating with findings evident in the wider literature regarding the utility of peer-support between teachers in both implementing and sustaining new pedagogical approaches [54]. Teachers found collaboration - both among themselves and with members of the research team - valuable in deepening their understanding and use of the strategies and pedagogical approaches. This is reminiscent of the findings of Allen and Penuel [53] on the role of peer collaboration in sense-making and echoes broader research emphasising the pivotal role of developing understanding of underpinning rationale for changes as part of effective PD [43].

Collaborative planning appeared to play a particularly critical role in the fading model, as teachers transitioned from guided implementation to independent application and adaptation. By co-constructing materials, teachers not only reinforced their understanding but also developed a sense of ownership over the approach, which has been linked to greater application of teaching techniques [42,54]. This finding is of particular interest as it contrasts with previous studies maintaining the importance of absolute fidelity to the original design [74] to avoid lethal mutations which may lessen its effectiveness. Instead, our work demonstrates that teachers adhered to core programme principles, whilst also adapting to accommodate contextual factors [72,73]. This study therefore highlights the importance of promoting ownership to encourage intelligent adaptation of programme content and delivery, whilst maintaining alignment to central design principles.

It is important to acknowledge that, in this study, collaborative planning was curtailed by insufficient time to develop scripts and session slides for the final week of delivery, meaning that these remained incomplete. This highlights the importance of allocating adequate protected time for collaborative activity, and reinforces wider literature which emphasises that innovation can be inhibited, or that PD for teachers can often fail to become successfully embedded, due to a lack of time within already extensive workload demands [42,43,85]. To address this issue, in future iterations of Stepping Stones, we propose to extend both the duration of PD sessions to increase the amount of time allocated for collaborative planning, and the length of the programme itself.

4.1. Limitations

Although the results from this pilot study indicate positive impacts for participating teachers, as with all similar studies, they should be interpreted with some caution. Future research should build upon the results through further empirical work to explore the impacts of Stepping Stones across a larger sample of teachers and schools to better-understand the learning outcomes resulting from this innovative fading model.

Second, whilst we have taken steps to carefully interpret the multiple sources of data, the analytical procedures run on the quantitative data have some limitations. For example, the Goodman-Kruskal Gamma test [65] looks for associations of tied data and cannot determine causality. Research with larger samples will inevitably have more capacity to run parametric tests with greater power that can detect causality in carefully designed studies. Future research may consider adopting experimental designs with specific controls to determine which metacognitive strategies are preferred amongst teachers.

Third, we recognise the importance of having access to complete data. Due to teacher time constraints, data collected within this project included data from three out of four weeks of the fading phase, therefore any future programme scaling would benefit from a consistent availability of data, to include all weeks of programme delivery. We also contend that the fading design for PD may have wider applications beyond the context of metacognition and mathematical problem solving, and therefore advocate further exploration of this to scaffold teachers’ understanding and use of additional pedagogic approaches and in broader subject contexts.

4.2. Conclusions

In exploring the design and implementation of an innovative, fading model of teachers’ PD, this original study aims to enhance understanding and application of metacognitive strategies in mathematical problem solving. It offers a novel, insightful contribution to the existing body of evidence that are often overlooked and underrepresented. Overall, our results demonstrate that, when combined with peer-collaboration, our fading design was associated with improved knowledge and confidence for both metacognition and mathematical problem solving, alongside increased ownership and buy in. We therefore conclude that wider adoption of Stepping Stones provides a means of encouraging sustained behaviour change, prompting more frequent use of metacognitive strategies with increasing independence. Future research should build upon these results through empirical work to further explore the value of the Stepping Stones model – including in wider curriculum contexts – thereby extending our understanding of effective PD design.