Adsorption of Ternary Mixtures in the Presence of Multisite Occupancy: Theory and Monte Carlo Simulations

1. Introduction

Adsorption phenomena involving multicomponent mixtures on solid surfaces remain a central topic, not only due to their relevance in technological applications but also because of the fundamental insights they offer into surface interactions and structure formation [1,2,3,4]. While substantial progress has been made in the study of mixture adsorption, several important aspects remain unresolved. Experimental investigations of single-component adsorption are relatively straightforward and well-established, yet precise measurement techniques for gas mixtures often involve significant complexity and time investment [3,4,5,6].

From a theoretical perspective, a large proportion of existing models assume that each adsorbate species occupies a single adsorption site, thereby neglecting the possibility of multisite occupation in the adsorbed layer [5,6,7,8,9,10,11]. However, such simplifications can lead to inconsistencies when comparing theoretical predictions with experimental data. Crucial phenomena such as surface orientational phase transitions [12,13], or the displacement of one species by the other1 [14,15,16,17,18,19,20,21] cannot be adequately captured without including multisite occupancy effects.

The lattice gas model [22] provides a valuable framework to address these limitations by accommodating extended adsorbates, such as linear molecules that cover multiple sites upon adsorption, often referred to as k-mers. Building on this foundation, a variety of methods have been employed to analyze systems with extended particle sizes. One of the earliest approaches is the Flory–Huggins (FH) approximation, independently formulated by Flory [23] and Huggins [24], which generalized the Bragg–Williams theory originally used for binary mixtures on two-dimensional lattices [22]. Designed to account for chain-like molecules, the FH model has undergone numerous refinements aimed at enhancing its accuracy, with comprehensive discussions provided in works such as [22,25]. Guggenheim proposed an alternative route to evaluating the partition function in these systems [26], which was later refined by DiMarzio through the inclusion of corrections for rigid rod-like molecules [27]. This extended treatment is now known as the Guggenheim–DiMarzio (GD) approximation.

More recently, new theoretical formulations have emerged to better describe adsorption with multisite occupancy. The first, termed the Extension Ansatz (EA) approximation, uses analytically derived expressions for the thermodynamic properties of k-mers adsorbed on one-dimensional lattices and extends these results to more complex geometries [28,29,30]. A second approach, the Fractional Statistical Theory of Adsorption ($FSTA$) [31,32], is inspired by Haldane’s generalized exclusion statistics [33,34]. The third, the Occupation Balance ($OB$) method, employs a fugacity expansion to approximate adsorption thermodynamics [30,35,36]. Finally, the Semi-Empirical ($SE$) scheme combines exact 1D solutions with the GD framework to provide practical yet accurate predictions [37,38].

Despite the advances outlined above, most studies have concentrated on single-species adsorption, leaving the adsorption of k-mer mixtures relatively underexplored. Addressing this gap, our group has recently contributed a series of theoretical studies focused on polyatomic binary mixtures [39,40,41]. The first of these works [39] presents an exact statistical thermodynamic treatment for mixtures composed of s-mers and k-mers adsorbed on one-dimensional homogeneous substrates. This formalism, developed specifically for zeolite-like systems, was the first to rigorously model the adsorption of polyatomic mixtures and provided a clear theoretical explanation for the APR phenomenon. The analysis demonstrated that size asymmetry between adsorbed species plays a decisive role in driving APR and highlighted the risk of misinterpreting experimental data when the polyatomic nature of adsorbates is ignored.

A subsequent work [40] extended the analysis to two-dimensional lattices, using a generalized lattice gas approach informed by the classical GD approximation [26,27]. This framework enabled the exact solution in one dimension and yielded accurate approximations for higher dimensions, preserving the key effects of multisite occupation. In a third contribution [41], multicomponent adsorption of polyatomics was reframed within the language of fractional statistics, applying Haldane’s formulation [33,34] to model monomer–dimer mixtures and offering quantitative insight into methane–ethane adsorption in nanoporous materials such as zeolites.

The results presented in Refs. [39,40,41] are restricted to two-component systems. In this work, we extend the theoretical framework of multicomponent adsorption by analyzing the case of j distinct species adsorbing on triangular lattices. To this end, we employ the EA approximation as our core methodological approach [30,38]. This method begins with the exact calculation of the partition function for a multicomponent gas of polyatomic species adsorbed on a one-dimensional lattice [28,39]. Building on this foundation, we incorporate established theoretical arguments [22,23,25,28,43,44] to generalize the configurational entropy to systems with higher lattice connectivity. The key correction factor introduced in this generalization quantifies the number of possible configurations per site for placing a k-mer at zero coverage and explicitly depends on both the lattice topology and the geometry of the adsorbing species.

With the general theoretical framework in place, we focus on a specific case study: the adsorption of a ternary mixture consisting of dimers, linear trimers, and triangular trimers on triangular lattices (see molecular structures in Figure 1). Three main motivations drive this choice. First, (i) the dimer represents the simplest polyatomic adsorbate and captures the essential features of multisite occupancy; (ii) the trimer is the simplest species exhibiting multiple adsorption configurations on triangular lattices; and (iii) the difference in molecular size between dimers and trimers leads to competitive displacement effects, a hallmark of multicomponent adsorption phenomena.

Second, recent work by our group [45,46,47] introduced triangular lattice models to study the stability and distortion of sI clathrate hydrate structures formed by methane and carbon dioxide. In these models, methane is represented as triangular trimers and carbon dioxide as linear trimers, revealing lattice deformation mechanisms and free energy landscapes. Although prior investigations focused on single-component systems, practical scenarios often involve coadsorption. One of the key open questions is how carbon dioxide displaces methane during clathrate formation, a process of both theoretical and practical relevance.

Third, and equally important, triangular lattices are common in both natural and engineered materials. Therefore, adsorption studies on such geometries have significant theoretical and experimental implications, particularly for understanding surface phase transitions and for the structural characterization of solid surfaces [47,50,51,52,53].

Our approach combines analytical modeling with Monte Carlo (MC) simulations to test the theoretical predictions. This combined methodology enhances the robustness of our conclusions by allowing direct comparison between analytical results and computational data.

The present study represents a natural progression from our earlier work [39,40,41], which focused on simple multicomponent systems, including binary mixtures and linear molecules. As a precursor, the adsorption behavior of pure gases composed of dimers, linear trimers, and triangular trimers was analyzed in Ref. [42]. The problem becomes substantially more complex, and scientifically richer, when these three species are allowed to interact and adsorb concurrently.

The remainder of the paper is structured as follows: Section 2 presents the thermodynamic framework for multicomponent lattice gases with hard-core interactions. The Monte Carlo simulation methodology is detailed in Section 3. In Section 4, we present and discuss the results. Finally, Section 5 summarizes our main conclusions.

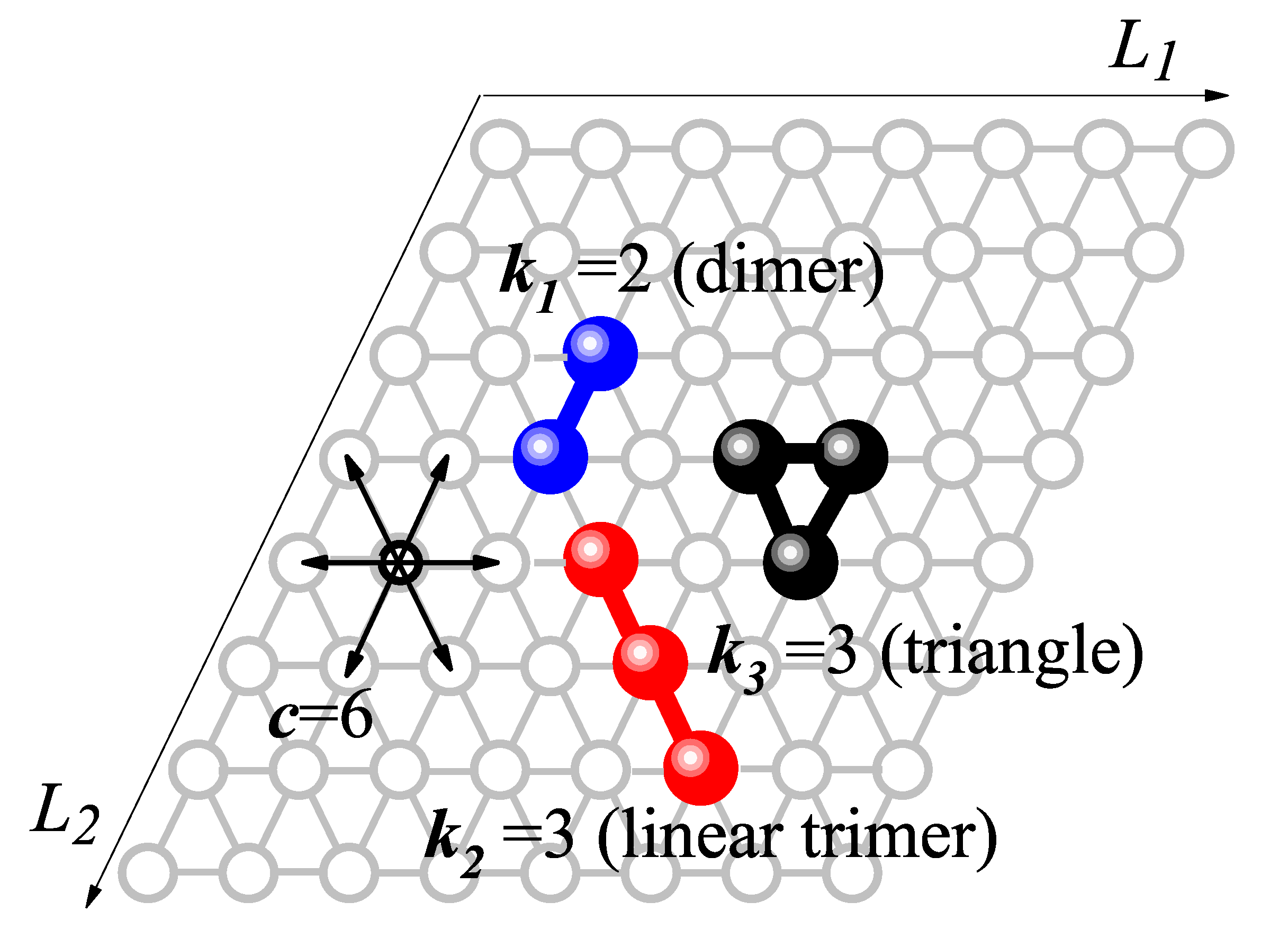
2. Thermodynamic Functions of Multicomponent Lattice Gases with Hard-Core Interactions

Consider a one-dimensional lattice composed of M sites, each separated by a constant distance a, under periodic boundary conditions. We assume $M\to \infty$. A monolayer adsorption scenario is examined, involving a j-component mixture, where the system contains $N_1$ molecules of type 1, $N_2$ of type 2, ..., and $N_j$ of type j. Each molecule of species i is a linear $k_i$-mer, meaning it is composed of $k_i$ identical segments, each occupying one lattice site; thus, a $k_i$-mer covers exactly $k_i$ consecutive lattice sites upon adsorption. Interactions are limited strictly to steric hindrance: no overlap between $k_i$-mers is permitted, ensuring that no site is shared by multiple adsorbed units. Under these assumptions, the canonical partition function $Q(M,N_1,N_2,\dots ,N_j,T)$ is expressed as:

$$Q(M,N_1,N_2,\dots ,N_j,T)=\Omega (M,N_1,N_2,\dots ,N_j)exp\left[-{\displaystyle \frac{E(M,N_1,N_2,\dots ,N_j)}{k_{B}T}}\right],$$

(1)

where $\Omega (M,N_1,N_2,\dots ,N_j)$ represents the total number of spatial arrangements consistent with the imposed constraints, $E(N_1,N_2,\dots ,N_j)$ denotes the total energy of interaction between the adsorbate molecules and the substrate, T is the absolute temperature, and $k_B$ is Boltzmann’s constant.

The term $\Omega (M,N_1,N_2,\dots ,N_j)$ can be derived as the total number of permutations of the $N_1$ indistinguishable $k_1$-mers, $N_2$ indistinguishable $k_2$-mers, …, and $N_j$ indistinguishable $k_j$-mers out of $n_e$ entities, where $n_e$ is given by:

$$\begin{array}{ccc}\hfill n_e& =& N_1+N_2+\dots +N_j+N_0\hfill \\ & =& \sum _{i=1}^j{N}_i+M-\sum _{i=1}^j{k}_i{N}_i=M-\sum _{i=1}^j\left(k_i-1\right)N_i,\hfill \end{array}$$

(2)

with $N_0$ denoting the number of vacant sites. Accordingly,

$$\Omega (M,N_1,N_2,\dots ,N_j)=\left(\begin{array}{c}{n}_e\\ N\end{array}\right)={\displaystyle \frac{\left[M-{\sum }_{i=1}^j(k_i-1)N_i\right]!}{N_1!N_2!\dots N_j!\left[M-{\sum }_{i=1}^j{k}_i{N}_i\right]!}}.$$

(3)

Let us now generalize this to a lattice of higher dimensionality characterized by a coordination number c (e.g., $c=3$ for a honeycomb structure, $c=4$ for a square lattice, and $c=6$ for a triangular one). In this case, the configurational contribution, denoted as ${\Omega }_c(M,N_1,N_2,\dots ,N_j)$, is approximated by considering a random, uncorrelated distribution of adsorbed species. Following methodologies proposed in prior studies [22,23,25,28,43,44], this multidimensional configurational factor is related to the one-dimensional result via:

$${\Omega }_c(M,N_1,N_2,\dots ,N_j)\approx {\left[K_1(c,k_1)\right]}^{N_1}{\left[K_2(c,k_2)\right]}^{N_2}\dots {\left[K_j(c,k_j)\right]}^{N_j}{\Omega }_{c=2}(M,N_1,N_2,\dots ,N_j)$$

(4)

where $K_i(c,k_i)$ corresponds to the number of configurations available per lattice site to a $k_i$-mer at zero surface coverage. The approximation presented in Equation 4 is known as the Extension Ansatz (EA) approximation [38]. This quantity generally depends on both the connectivity of the lattice and the geometric characteristics of the adsorbed molecule. For straight, rigid $k_i$-mers (linear particles with $k_i$ monomeric units), the available orientations reduce to $K_i(c,k_i)=c/2$ (this expression is only valid for $k_i\ge 2$; for monomer adsorption $K_i(c,k_i=1)=1$.

On the other hand, $E(M,N_1,N_2,\dots ,N_j)$ can be written as

$$E(M,N_1,N_2,\dots ,N_j)=\sum _{i=1}^j{ϵ}_i{N}_i,$$

(5)

where ${ϵ}_i$ denotes the binding energy between a $k_i$-mer and the surface.

The Helmholtz free energy $F(M,N_1,N_2,\dots ,N_j,T)$ is related to $Q(M,N_1,N_2,\dots ,N_j,T)$ through

$$\begin{array}{ccc}\hfill \beta F(M,N_1,N_2,\dots ,N_j,T)& =& -lnQ(M,N_1,N_2,\dots ,N_j,T)\hfill \\ & =& -ln{\Omega }_c(M,N_1,N_2,\dots ,N_j)+\beta \sum _{i=1}^j{ϵ}_i{N}_i,\hfill \end{array}$$

(6)

where $\beta ={(k_{B}T)}^{-1}$. From Equations (3), (4) and (6)

$$\begin{array}{ccc}\hfill \beta F(M,N_1,N_2,\dots ,N_j,T)& =& -\sum _{i=1}^j{N}_{i}ln\left[K_i(c,k_i)\right]-ln\left[M-\sum _{i=1}^j(k_i-1)N_i\right]!\hfill \\ & & +\sum _{i=1}^j\left[ln\left(N_i\right)!\right]+ln\left[M-\sum _{i=1}^j{k}_i{N}_i\right]!+\beta \sum _{i=1}^j{ϵ}_i{N}_i.\hfill \end{array}$$

(7)

Using the Stirling approximation

$$\begin{array}{ccc}\hfill \beta F(M,N_1,N_2,\dots ,N_j,T)& =& -\sum _{i=1}^j{N}_{i}ln\left[K_i(c,k_i)\right]\hfill \\ & & -\left[M-\sum _{i=1}^j(k_i-1)N_i\right]ln\left[M-\sum _{i=1}^j(k_i-1)N_i\right]\hfill \\ & & +\sum _{i=1}^j\left[N_{i}ln\left(N_i\right)\right]+\left[M-\sum _{i=1}^j{k}_i{N}_i\right]ln\left[M-\sum _{i=1}^j{k}_i{N}_i\right]\hfill \\ & & +\beta \sum _{i=1}^j{ϵ}_i{N}_i.\hfill \end{array}$$

(8)

The configurational entropy S, and the chemical potential corresponding to the i-species ${\mu }_{i,ads}$, can be calculated as [22]

$$S(M,N_1,N_2,\dots ,N_j,T)=-{\left({\displaystyle \frac{\partial F}{\partial T}}\right)}_{M,N_j^{\prime }s},$$

(9)

and

$${\mu }_{i,ads}={\left({\displaystyle \frac{\partial F}{\partial N_i}}\right)}_{T,M,N_j^{\prime }s(j\ne i)}(i=1,2,\dots ,j).$$

(10)

From Equations (8-10) it follows that

$$\begin{array}{ccc}\hfill {\displaystyle \frac{S(M,N_1,N_2,\dots ,N_j,T)}{k_B}}& =& +\sum _{i=1}^j{N}_{i}ln\left[K_i(c,k_i)\right]\hfill \\ & & +\left[M-\sum _{i=1}^j(k_i-1)N_i\right]ln\left[M-\sum _{i=1}^j(k_i-1)N_i\right]\hfill \\ & & -\sum _{i=1}^j\left[N_{i}ln\left(N_i\right)\right]-\left[M-\sum _{i=1}^j{k}_i{N}_i\right]ln\left[M-\sum _{i=1}^j{k}_i{N}_i\right],\hfill \end{array}$$

(11)

and

$$\begin{array}{ccc}\hfill \beta \left({\mu }_{i,ads}-{ϵ}_i\right)& =& -ln\left[K_i(c,k_i)\right]+(k_i-1)ln\left[M-\sum _{i=1}^j(k_i-1)N_i\right]\hfill \\ & & +ln\left(N_i\right)-k_{i}ln\left[M-\sum _{i=1}^j{k}_i{N}_i\right](i=1,2,\dots ,j).\hfill \end{array}$$

(12)

Then, by defining the partial coverage of the species i, ${\theta }_i=k_i{N}_i/M$, the free energy per site $f=F/M$ and the configurational entropy per site $s=S/M$, Equations (8), (11) and (12) can be rewritten in terms of the intensive variables ${\theta }_1$, ${\theta }_2$, …, ${\theta }_j$ and T,

$$\begin{array}{ccc}\hfill \beta f({\theta }_1,{\theta }_2,\dots ,{\theta }_j,T)& =& -\sum _{i=1}^j{\displaystyle \frac{{\theta }_i}{k_i}}ln\left[K_i(c,k_i)\right]\hfill \\ & & -\left[1-\sum _{i=1}^j\left({\displaystyle \frac{k_i-1}{k_i}}\right){\theta }_i\right]ln\left[1-\sum _{i=1}^j\left({\displaystyle \frac{k_i-1}{k_i}}\right){\theta }_i\right]\hfill \\ & & +\sum _{i=1}^j\left[{\displaystyle \frac{{\theta }_i}{k_i}}ln\left({\displaystyle \frac{{\theta }_i}{k_i}}\right)\right]+\left(1-\sum _{i=1}^j{\theta }_i\right)ln\left(1-\sum _{i=1}^j{\theta }_i\right)\hfill \\ & & +\beta \sum _{i=1}^j{ϵ}_i{\displaystyle \frac{{\theta }_i}{k_i}},\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{s({\theta }_1,{\theta }_2,\dots ,{\theta }_j,T)}{k_B}}& =& +\sum _{i=1}^j{\displaystyle \frac{{\theta }_i}{k_i}}ln\left[K_i(c,k_i)\right]\hfill \\ & & +\left[1-\sum _{i=1}^j\left({\displaystyle \frac{k_i-1}{k_i}}\right){\theta }_i\right]ln\left[1-\sum _{i=1}^j\left({\displaystyle \frac{k_i-1}{k_i}}\right){\theta }_i\right]\hfill \\ & & -\sum _{i=1}^j\left[{\displaystyle \frac{{\theta }_i}{k_i}}ln\left({\displaystyle \frac{{\theta }_i}{k_i}}\right)\right]-\left(1-\sum _{i=1}^j{\theta }_i\right)ln\left(1-\sum _{i=1}^j{\theta }_i\right),\hfill \end{array}$$

(14)

and

$$\begin{array}{ccc}\hfill \beta \left({\mu }_{i,ads}-{ϵ}_i\right)& =& -ln\left[K_i(c,k_i)\right]+(k_i-1)ln\left[1-\sum _{i=1}^j\left({\displaystyle \frac{k_i-1}{k_i}}\right){\theta }_i\right]\hfill \\ & & +ln\left({\displaystyle \frac{{\theta }_i}{k_i}}\right)-k_{i}ln\left[1-\sum _{i=1}^j{\theta }_i\right](i=1,2,\dots ,j).\hfill \end{array}$$

(15)

At equilibrium, the chemical potential of the adsorbed and gas phase are equal. Then,

$${\mu }_{i,ads}={\mu }_{i,gas}(i=1,2,\dots ,j),$$

(16)

where ${\mu }_{i,gas}$ corresponds to $k_i$-mers in the gas phase.

The chemical potential of each kind of molecule in an ideal gas mixture, at temperature T and pressure P, is

$$\beta {\mu }_{i,gas}=\beta {\mu }_i^0+ln{X}_{i}P(i=1,2,\dots ,j),$$

(17)

where ${\mu }_i^0$ and $X_i$ are the standard chemical potential and the mole fraction of $k_i$-mers, respectively. In addition, ${\sum }_{i=1}^j{X}_i=1$.

From Equations (15), (16) and (17), the partial adsorption isotherms can be obtained,

$$\begin{array}{c}-ln\left[K_i(c,k_i)\right]+(k_i-1)ln\left[1-\sum _{i=1}^j\left({\displaystyle \frac{k_i-1}{k_i}}\right){\theta }_i\right]+ln\left({\displaystyle \frac{{\theta }_i}{k_i}}\right)\\ -k_{i}ln\left[1-\sum _{i=1}^j{\theta }_i\right]+\beta \left({ϵ}_i-{\mu }_i^0\right)-ln{X}_i-lnP=0(i=1,2,\dots ,j).\end{array}$$

(18)

3. Monte Carlo Simulation Scheme

In order to model the adsorption process of the mixture, a general Monte Carlo (MC) scheme in the grand canonical ensemble was implemented [54,55]. The surface was represented by a triangular lattice of $M=L\times L$ adsorption sites, and a ternary (three-component) mixture was selected as the subject of study. The mixture consists of dimers (species 1, $k_1=2$), linear trimers (species 2, $k_2=3$), and triangular-shaped trimers (species 3, $k_3=3$). These species are adsorbed along three lattice directions and six possible orientations (connectivity $c=6$). Figure 1 provides a schematic representation of species 1 through 3. Blue spheres denote dimers, red spheres represent linear trimers, and black spheres correspond to triangular trimers. Unoccupied lattice sites are indicated by empty circles. The molar composition X of the ternary mixture satisfies the relation: $X_{\mathrm{Total}}=X_1+X_2+X_3$= 1.

As mentioned in previous section, the only interaction between different adsorbed particles is hard-core exclusion. In addition, since the lattice is assumed homogeneous, $E(M,N_1,N_2,N_3)$ (Equation (5)) can be arbitrarily chosen equal to zero without losing generality (i.e., the interaction energy between every $k_i$-mer and the substrate is set to be zero, ${ϵ}_i=0$ for $i=1,2,3$).

Then, given a lattice of M equivalent adsorption sites in contact with a ternary gas mixture at temperature T and pressure P, the state of the system may change through the adsorption or desorption of a $k_i$-uple ($k_i$-mer) of any of the three species. A elementary MC simulation step (MCS) proceeds as follows:

• Initialization:
  • Set temperature T, pressure P and molar compositions $X_1$, $X_2$ and $X_3$. Accordingly,

    $${\mu }_i={\mu }_i^0+ln{X}_{i}P[i=1(\mathrm{dimer}),i=2(\mathrm{linear}\mathrm{trimer})\mathrm{and}i=3(\mathrm{triangular}\mathrm{trimer})].$$

    (19)
• Random species selection:
  • Randomly select one of the three species.
• Random $k_i$-uple selection:
  • Randomly select a valid $k_i$-uple.

    -

    If the $k_i$-uple is empty: attempt to adsorb a $k_i$-mer of type selected in step 2 with probability $W_{\mathrm{ads}}$.

    -

    If the $k_i$-uple is fully occupied by a k-mer of type selected in step 2: attempt to desorb it with probability $W_{\mathrm{des}}$.

  • The probabilities $W_{\mathrm{ads}}$ and $W_{\mathrm{des}}$ are calculated according to the Metropolis criterion [54,55]:

    $$W_{\mathrm{ads}}=min\left[1,Pexp\left(-{\displaystyle \frac{\Delta E}{k_{B}T}}\right)\right],$$

    (20)

    and

    $$W_{\mathrm{des}}=min\left[1,{\displaystyle \frac{1}{P}}exp\left(-{\displaystyle \frac{\Delta E}{k_{B}T}}\right)\right],$$

    (21)

    where $\Delta E$ is the difference between the energies of the final (new) and initial (old) states.
• Repeat the simulation step:
  • Repeat steps 2–3 a total of M times to complete one MCS.

In our MC simulations, the equilibrium state can be well reproduced after discarding the first $m^{\prime }={10}^6$ MCS. Then, averages are taken over $m={10}^6$ MCS successive configurations. The initial configuration of the system is an empty triangular lattice, and the final configuration obtained for a given pressure is used as initial configuration for the next (higher) pressure.

Partial and total adsorption isotherms are obtained as simple averages

$${\theta }_i={\displaystyle \frac{k_i\langle N_i\rangle }{M}},$$

(22)

and

$$\theta =\sum _{i=1}^{i=j}{\theta }_i,$$

(23)

where $\langle \dots \rangle$ means the average over the MC simulation runs.

The use of MC techniques for computing thermal averages of thermodynamic quantities is a well-established and powerful approach [54,55]. Observables such as total energy, energy fluctuations, and correlation functions can be reliably estimated by averaging over a sufficiently large set of sampled configurations. In contrast, quantities like the free energy and entropy are more elusive, as they are not directly accessible through simple ensemble averages. To overcome this challenge, several indirect approaches have been introduced [55], with thermodynamic integration being among the most effective and commonly applied methods [35,36,56,57,58].

Within the grand canonical framework, thermodynamic integration involves evaluating the chemical potential $\mu$ as a function of surface coverage, tracing a reversible path from a known reference state to the target state of interest. This procedure also requires prior knowledge of the Helmholtz free energy $F_0$ associated with the reference condition. Accordingly, for a system consisting of a single component with N particles distributed over M lattice positions, the free energy can be determined from the following expression:

$$\mu ={\left({\displaystyle \frac{\partial F}{\partial N}}\right)}_{M,T},$$

(24)

and

$$F(M,N,T)=F_0(M,N_0,T)+{\int }_{N_0}^N\mu dN.$$

(25)

Using $F=E-TS$, the configurational entropy S can be written as,

$$S(M,N,T)=S_0(M,N_0,T)+{\displaystyle \frac{E(M,N,T)-E(M,N_0,T)}{T}}-{\displaystyle \frac{1}{T}}{\int }_{N_0}^N\mu dN.$$

(26)

In the case of a j-component mixture containing $N_1$ molecules of component 1, $N_2$ molecules of component 2, … , $N_j$ molecules of component j, the Equation (25) must be rewritten in terms of the chemical potentials of each adsorbed species ${\mu }_i$,

$${\mu }_i={\left({\displaystyle \frac{\partial F}{\partial N_i}}\right)}_{N_j,T,M}.$$

(27)

Integrating the last equation, we obtain,

$$F(M,N_1,N_2,\dots ,N_j,T)=F_0(M,N_{10},N_{20},\dots ,N_{j0},T)+\sum _{i=1}^j\left({\int }_{N_{i0}}^{N_i}{\mu }_{i}d{N}_i\right).$$

(28)

Accordingly, it follows that,

$$\begin{array}{ccc}\hfill S(M,N_1,N_2,\dots ,N_j,T)& =& S_0(M,N_{10},N_{20},\dots ,N_{j0},T)\hfill \\ & & +{\displaystyle \frac{E(M,N_1,N_2,\dots ,N_j,T)-E(M,N_{10},N_{20},\dots ,N_{j0},T)}{T}}\hfill \\ & & -{\displaystyle \frac{1}{T}}\left[\sum _{i=1}^j\left({\int }_{N_{i0}}^{N_i}{\mu }_{i}d{N}_i\right)\right].\hfill \end{array}$$

(29)

In our case $E(M,N_1,N_2,\dots ,N_j,T)=0$ and the determination of the entropy in the reference state, $S_0(M,N_{10},N_{20},\dots ,N_{j0},T)$, is trivial [$S_0(M,N_{10},N_{20},\dots ,N_{j0},T)=0$ for $N_{10}=N_{20}=\dots =N_{j0}=0$]. Then,

$$S(M,N_1,N_2,\dots ,N_j,T)=-{\displaystyle \frac{1}{T}}\left[\sum _{i=1}^j\left({\int }_0^{N_i}{\mu }_{i}d{N}_i\right)\right].$$

(30)

After writing the last equation in terms of intensive variables, the configurational entropy per site ($s=S/M$) results in

$${\displaystyle \frac{s(\theta ,T)}{k_B}}=-{\displaystyle \frac{1}{k_{B}T}}\left[\sum _{i=1}^j\left({\int }_0^{{\theta }_i}{\displaystyle \frac{{\mu }_i}{k_i}}d{\theta }_i\right)\right],$$

(31)

where ${\theta }_i=k_{i}N/M$ and $\theta ={\sum }_i{\theta }_i$.

The ${\mu }_i$ versus ${\theta }_i$ curves are determined by applying the adsorption-desorption methodology outlined earlier in this section. The integration involved in Eq. (31) is performed using the trapezoidal approximation, a standard numerical technique [59]. Since all chemical potentials are expressed in units of $k_{B}T$, all results will be independent of the temperature. Therefore, throughout the remainder of this work, we will refer to $s(\theta )$ as the configurational entropy per lattice site, omitting the explicit temperature reference (for simplicity we will drop the “T").

4. Results

In this section, the adsorption isotherm (i.e., surface coverage as a function of pressure) and the configurational entropy per site of the adsorbed layer, as predicted by the theoretical model introduced in Section 2, are compared with the results obtained from MC simulations, following the procedure outlined in Section 3.

Within the framework of the theoretical approach, it is important to emphasize that the use of the approximate configurational factor ${\Omega }_c(M,N_1,N_2,\dots ,N_j)$ (Equation (4)) enables a direct evaluation of the Helmholtz free energy. As a consequence, the partial and total thermodynamic functions of the ternary mixture, corresponding to different gas-phase compositions, can be consistently derived via Equation (17).

On the other hand, the numerical evaluation of the entropy per site, $s/k_B$, using Equation (31), is straightforward and computationally efficient, since the coverage dependence on $\mu /k_{B}T$ is computed according to the MC simulation protocol described in Section 3. In this approach, the partial chemical potentials are integrated as a function of the partial coverage of each species.

The simulations were carried out on triangular lattices of size $L\times L$, with $L/k=120$ ($L=240$ for dimers and $L=360$ for trimers). To minimize boundary effects, periodic boundary conditions were applied. Under these conditions, finite-size effects—which could influence adsorption isotherms in smaller systems—were found to be negligible. These findings are consistent with the results reported in a previous study by our research group (2023) [42], where a type-cluster approximation [60,61,62,63] was combined with MC simulations to analyze the configurational entropy per site of dimers and trimers on triangular lattices. It was observed that surface coverage values remain practically unchanged for $L/k>30$.

This section is organized into two main parts. In the first part (Section 4.1), a comprehensive comparison is made between the adsorption isotherms and configurational entropy per site obtained from the theoretical model (Section 2), the Ideal Adsorbed Solution Theory (IAST) [5,6], and the MC simulations (Section 3). Two representative cases are examined for (dimers-linear trimers-triangular trimers) ternary mixtures: an equimolar composition ($X_1=X_2=X_3=1/3$), and a diluted case for dimers ($X_1=0.10$) with equal fractions of linear and triangular trimers ($X_2=X_3=0.45$). This section also includes the study of the behavior of the partial configurational entropy per site, with particular emphasis on the role of this quantity in the displacement of larger species (trimers) due to the presence of smaller ones, specifically, dimers. The studied cases provide insights into the evolution of the partial entropy of each species and allow for a better understanding of their individual and collective contributions to the displacement process.

In the second part (Section 4.2), the total entropy of the mixture is examined as a function of different molar fractions of dimers ($k=2$). This analysis sheds light on how the total entropy landscape varies with composition, offering a broader perspective on the thermodynamic response of the system.

In all three parts of this study, the adsorbed species are treated as ideal, meaning that no lateral interactions between adsorbates are considered. The only interaction accounted for is excluded volume, which arises from the differences in size and shape among the species adsorbed on the lattice.

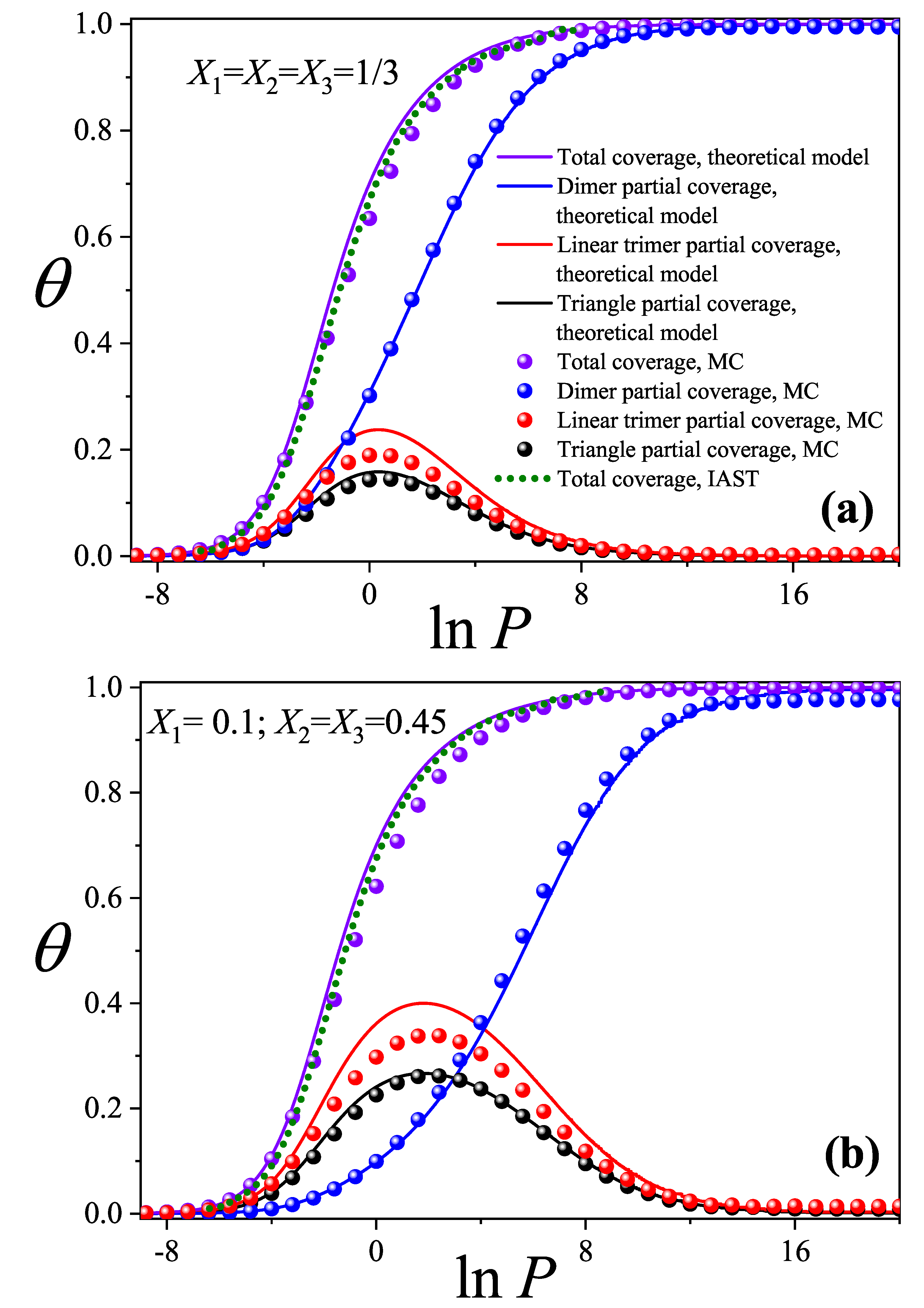
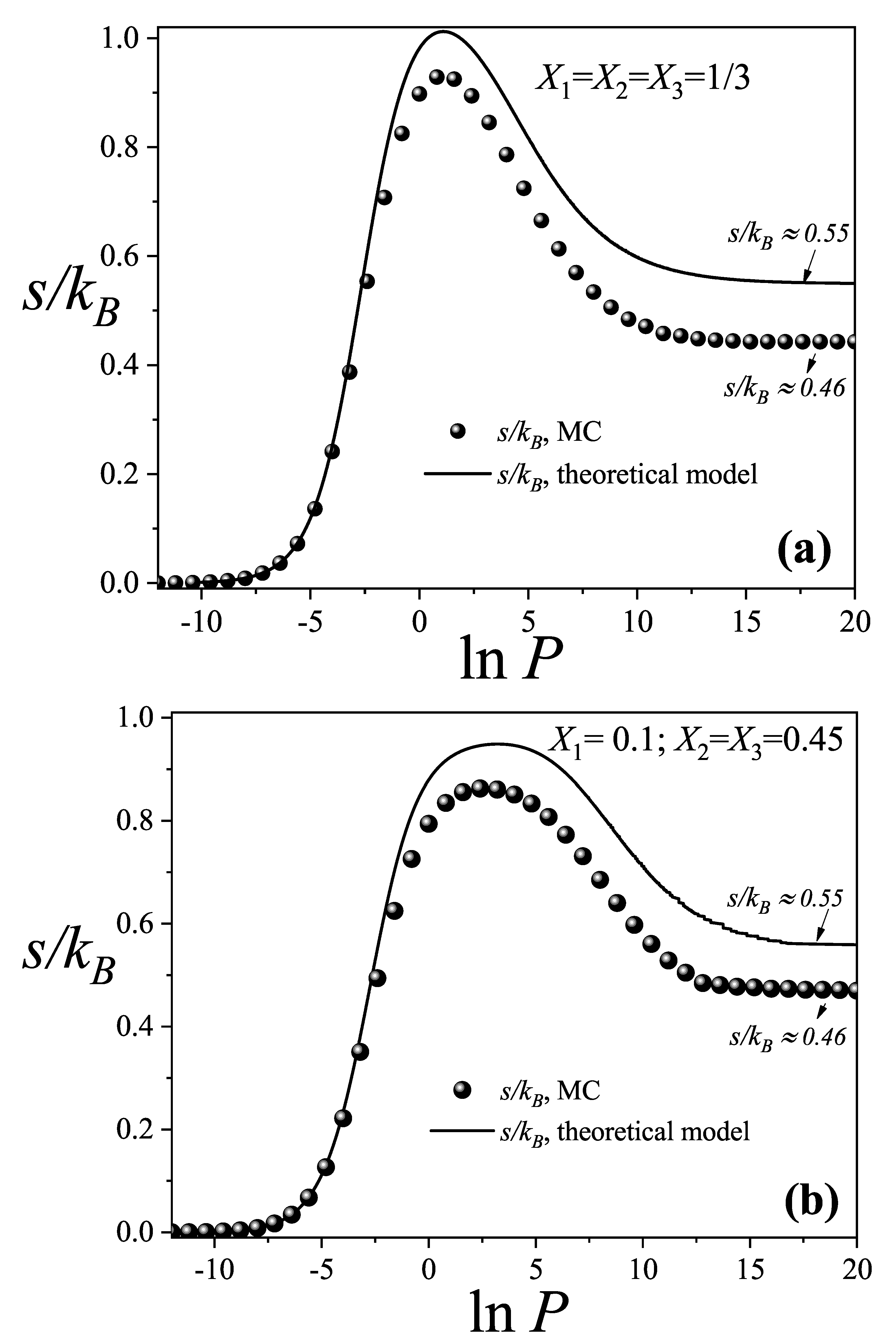
4.1. Adsorption Isotherms and Total Configurational Entropy per Site

We begin by analyzing a ternary mixture system by comparing results from the MC simulations described in Section 3 with predictions from the theoretical model in Section 2 and the well-established Ideal Adsorbed Solution Theory (IAST) for ideal mixtures [5,6].

Figure 2(a) and (b) display the total and partial adsorption isotherms for two different molar composition sets: (a) $X_1=X_2=X_3=1/3$ and (b) $X_1=0.10$, $X_2=X_3=0.45$. Solid lines correspond to theoretical predictions obtained from Equation (18); green dashed lines represent IAST results; and sphere-shaped markers indicate data from MC simulations. Curves for dimers are shown in blue, linear trimers in red, and triangular trimers in black.

For both composition sets $X_i$, the theoretical model shows excellent quantitative agreement with the MC simulations for both total and partial adsorption isotherms. However, a slight deviation is observed in the partial isotherms of the linear trimer species (red curves), relative to the MC results. This discrepancy arises from the configurational factor introduced in Equation (4), which accounts for the number of accessible configurations. This approximation tends to overestimate the adsorption of rigid rod-like molecules, particularly as their molecular size increases. In contrast, such deviations are not seen for dimers or triangular trimers, as both species occupy only two adjacent lattice sites, regardless of orientation.

Additionally, the total adsorption isotherms calculated using IAST show closer agreement with the theoretical model than with MC simulations. This behavior likely stems from the fact that IAST is constructed on ideal pure-component isotherms based on the configurational factors developed in Equation (4). For further details on the IAST approach, see Appendix A.

Moreover, for both cases studied (equimolar and asymmetric mixtures), a clear displacement of larger species (trimers) by smaller ones (dimers) is observed. As $lnP$ increases, species with $k_i=2$ dominate the adsorption process on the triangular lattice. In the high-pressure limit (large $lnP$), the total coverage $\theta$ is almost entirely due to dimer adsorption, with both linear and triangular trimers being nearly absent.

Figure 3 shows the total configurational entropy per site for the same systems analyzed in Figure 2. Solid lines represent theoretical predictions, while spheres correspond to MC results. In the theoretical model, the configurational entropy per site is calculated using Equation (14), with ${\theta }_i$ determined from Equation (15). In the MC approach, the total entropy of the mixture is obtained as the sum of the partial entropies of each species, given by:

$${\displaystyle \frac{s({\theta }_1,{\theta }_2,\dots ,{\theta }_j,T)}{k_B}}=\sum _{i=1}^j{\displaystyle \frac{s_i({\theta }_i,T)}{k_B}},$$

(32)

where $j=3$ in this case, and each ${\displaystyle \frac{s_i({\theta }_i,T)}{k_B}}$ is computed by integrating the partial chemical potential ${\mu }_i$ as a function of the partial coverage ${\theta }_i$ for species i.

Figure 3(a) and (b) reveal excellent qualitative agreement between the theoretical model and MC simulations across both molar composition sets $X_i$. However, at high pressures, a noticeable quantitative discrepancy emerges between the two approaches. In this context, we consider the MC results to better represent the true behavior of the system, whereas the discrepancies in the theoretical predictions highlight limitations arising from the approximations involved in the configurational factor.

As discussed earlier, the primary source of this discrepancy lies in the overestimation of accessible states for linear trimer species. As the occupancy of linear sites increases, the theoretical model tends to overcount configurations, particularly for larger species. This overcounting results from the breakdown of the approximations in ${\Omega }_c(M,N_1,N_2,\dots ,N_j)$, which fail to fully capture the geometric constraints that emerge with increasing molecular size. Despite these limitations, the theoretical predictions are considered highly satisfactory, especially given the significant complexity of modeling a ternary system composed of species with different sizes and multiple site occupancies.

The high-pressure regime is of particular interest, as the configurational entropy reaches a saturation value that becomes constant for the two studied cases. Within the theoretical model, the saturation entropy tends toward an approximate value of $s/k_B\approx 0.55$ for both compositions studied, whereas the numerical results obtained from Monte Carlo (MC) simulations yield a value close to $s/k_B\approx 0.46$. This latter result is especially significant, as it closely matches the value reported by other authors for a triangular lattice fully occupied by dimers, $s/k_B=0.4286$ [65]. This close agreement provides further evidence that, in the high-pressure regime, the lattice is effectively saturated by dimers.

The displacement of larger species (trimers) by smaller ones (dimers) has also been observed in studies of three-domain antifreeze proteins adsorbed on surfaces, where the molecules can bind via one, two, or all three domains—referred to as S1, S2, and S3 states, respectively [64]. The displacement of molecules in S2 and S3 by those in S1 is known as the APR phenomenon, previously reported in Refs. [14,15]. It is important to note that the partial coverage of the larger species tends toward zero but does not vanish entirely. In fact, a small residual adsorption of trimer species remains, on the order of $\theta \approx 1\times {10}^{-3}$. This minor contribution accounts for the observed discrepancy between our saturation entropy and the value reported in the literature, resulting in a deviation of $\Delta s=0.0314$.

To further investigate the behavior of the total configurational entropy of the mixture, it is useful to compare Figure 2 and Figure 3. As it can be observed from the figures, the partial adsorption isotherms of the larger species ($k_i=3$), namely, linear and triangular trimers, exhibit a maximum in coverage that coincides with the peak of the mixing entropy within the same $lnP$ interval. In this region, the coverage of the smallest species (dimers, $k_i=2$) begins to increase with $lnP$, indicating the onset of a displacement process. Beyond the entropy maximum, the smaller species progressively displace the larger ones, gaining occupancy on the lattice.

This maximum in the mixing entropy corresponds to a relative minimum in the Helmholtz free energy, establishing a favorable thermodynamic condition under constant volume M and temperature T. From this point onward, the adsorption of the smaller species proceeds in a spontaneous, natural, and thermodynamically viable manner.

In Figure 4, the behavior of the partial configurational entropies as a function of $lnP$ is presented, alongside the total configurational entropy of an equimolar ternary mixture ($X_1=X_2=X_3=1/3$). This figure illustrates how the overall entropy curve of the mixture arises from the combined contributions of each species across the entire pressure range. All curves were calculated from the theoretical model developed in Section 2. The total entropy of the mixture was computed using Equation (14), while the partial entropies for each component were obtained by integrating Equation (15).

At low pressures, the partial entropies of all three species increase with $lnP$, reflecting the progressive occupation of lattice sites. As pressure continues to rise and the total entropy approaches its maximum, inflection points emerge in the entropy curves of the linear trimers and triangular species. In contrast, the dimers, the smallest species, exhibit a slightly higher local maximum within this region, surpassing the individual contributions of the larger components.

This behavior indicates that dimers contribute most significantly to the total entropy maximum, as they access a greater number of configuations within this $lnP$ range. A comparison between Figure 2 and Figure 4 further reveals that beyond the entropy maximum, the dimers progressively displace the larger species.

A striking feature is observed in the dimer entropy at high total coverage. Although dimers dominate the lattice at elevated pressures, the limited available space severely restricts their configurational degrees of freedom, leading to a sharp decline in the number of accessible states. As a result, beyond the global maximum of the total entropy, their partial entropy decreases and eventually becomes negative as pressure increases. In contrast, the larger species, present in trace amounts, retain configurational freedom by occupying the voids left by the saturated dimers, and their partial entropies increase until reaching a constant positive value.

This phenomenon can be interpreted as a manifestation of what may be termed intelligent entropy: although the larger species are present in low concentrations, they contribute positively to the total entropy by efficiently utilizing the voids left by the saturation of dimers. Consequently, the total entropy of the ternary mixture remains positive. A comparable behavior has been reported in studies of random mixing in polymer solutions. When Flory’s approximation is applied [22,25,28], the entropy of the pure polymer can become negative, while the entropy of the mixture remains positive [22,25,28].

This behavior can be interpreted as a form of intelligent entropy: although present in small quantities, the larger species generate positive entropy by exploiting the voids left by the saturation of dimers. Thus, the total entropy of the ternary mixture remains positive. A similar behavior has been observed in the problem of random mixing of polymer solutions. When the Flory’s approximation is applied [22,25,28], the entropy of the pure polymer becomes negative while the entropy of the mixture is larger to 0 [22,25,28].

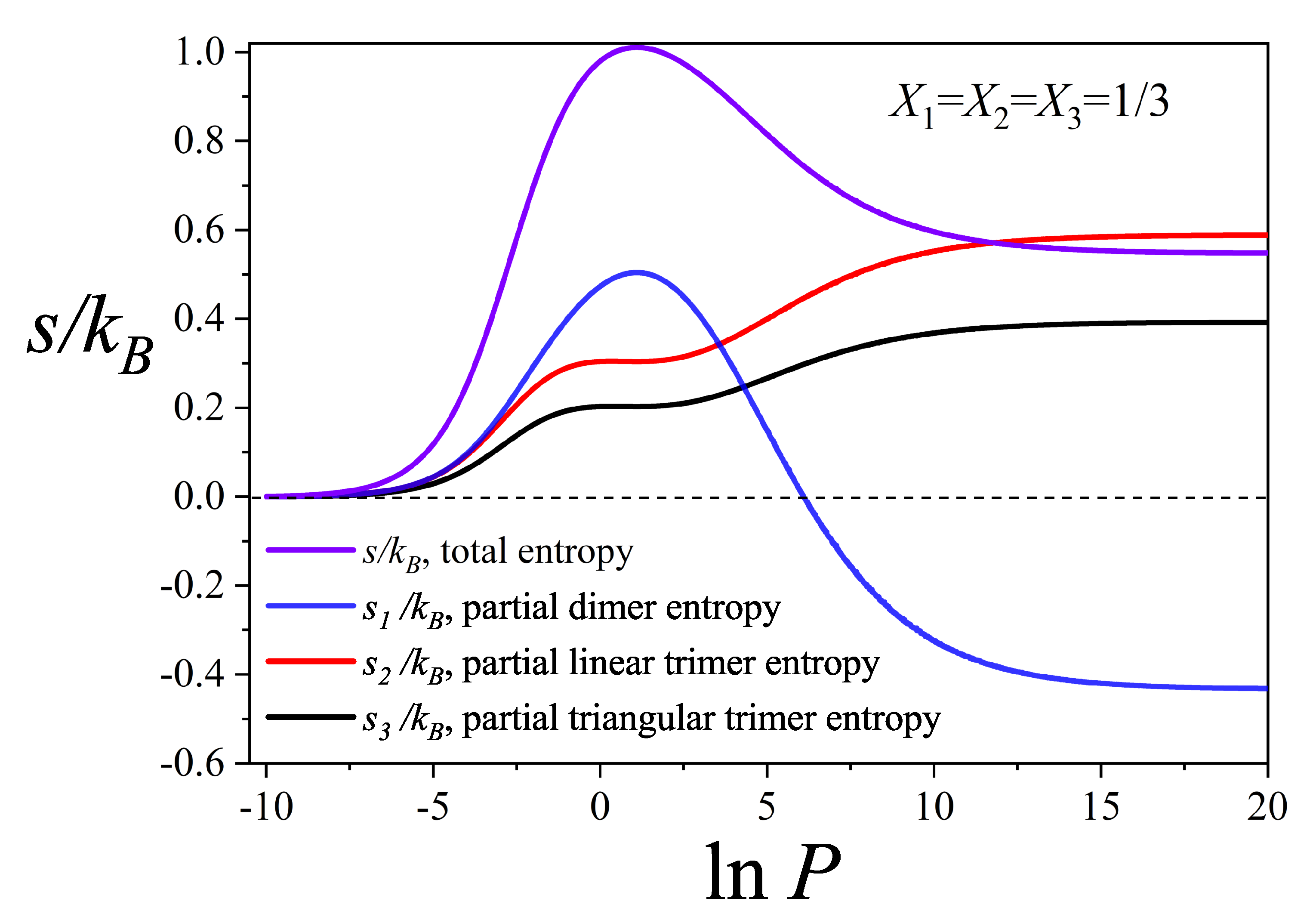
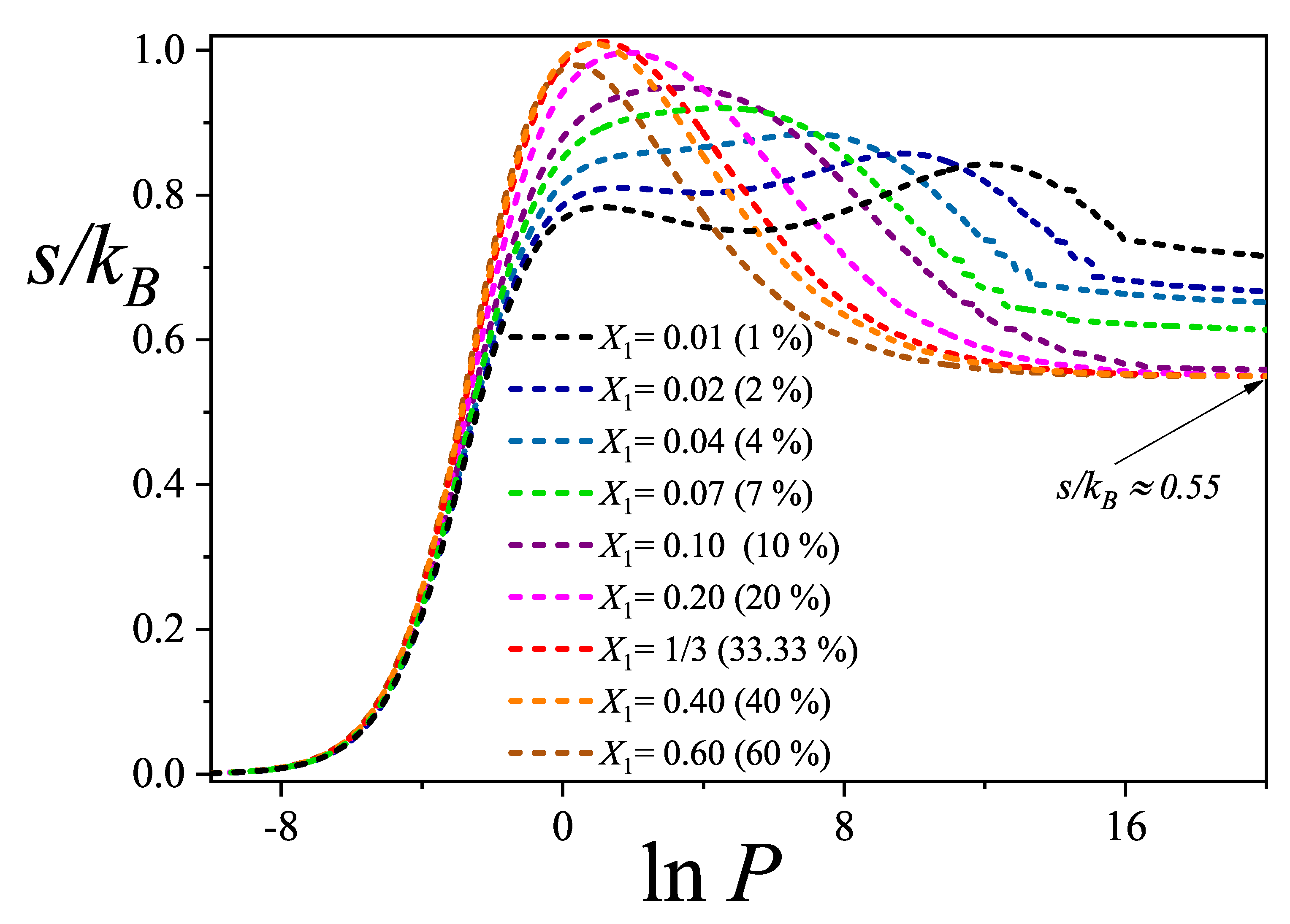
4.2. Configurational Entropy per Site for Different Molar Compositions

In this section, we examine the behavior of the total configurational entropy per site for varying dimer compositions $X_1$, based on the theoretical framework presented in Section 2. Our objective is to characterize the overall behavior of the mixing entropy in ternary systems. Figure 5 displays the evolution of the total entropy as a function of $lnP$, for dimer compositions ranging from highly dilute systems ($X_1=1/100$, i.e., 1 %) to highly concentrated ones ($X_1=3/5$, i.e., 60 %).

Each curve in Figure 5 exhibits a characteristic trend: the entropy increases with pressure, reaches a maximum, and subsequently decreases smoothly, eventually approaching a saturation plateau at high pressures. As discussed in Section 4.1, this saturation regime corresponds to a nearly fully occupied lattice, predominantly filled by dimers, with a small residual fraction of trimers. Despite their low coverage, these remaining trimers contribute positively to the entropy due to their configurational freedom. The cumulative effect of the larger species allows the total entropy to remain positive even under conditions of high pressure and coverage. It is worth noting, as previously reported in the literature [41], that the total mixing entropy remains positive in fully occupied lattices, reflecting the residual configurational complexity inherent in densely packed systems.

As shown in Figure 5, for the most dilute compositions ($X_1=1\%$ to $X_1=4\%$), the total configurational entropy exhibits two distinct maxima across the $lnP$ range. The first maximum occurs at low values of $lnP$, corresponding to a regime in which the partial coverage of the larger species, namely linear trimers and triangular clusters, increase rapidly, while the dimers accumulate more gradually. The second maximum, discussed in previous paragraphs, emerges at higher pressures and is associated with the gradual replacement of the larger species by dimers. This two-peak structure arises because, at such low dimer concentrations, higher pressures are required to initiate the displacement process.

In the high-pressure regime shown in Figure 5, it is further observed that variations in the saturation values of the total configurational entropy occur only in systems with very low dimer molar fractions. For compositions with $X_1\ge 1/10$, the saturation entropy converges to a nearly constant value of approximately $s/k_B\approx 0.55$. This trend is consistent with theoretical expectations: at lower dimer concentrations, the residual fraction of larger species, such as trimers and triangular clusters, remains higher, leading to an increase in configurational entropy due to their greater spatial and conformational flexibility on the lattice.

To complete the analysis, it is particularly insightful to examine the maximum values of the mixing entropy. As shown in previous figures, each entropy maximum corresponds to a specific pair of values: $lnP$ and the dimer composition $X_1$. This information is summarized in Figure 6(a), which presents a phase diagram involving three variables: the configurational entropy per site $s/k_B$ (plotted along the z-axis), the composition of the smallest species $X_1$ (on the x-axis), and the logarithm of pressure $lnP$ (on the y-axis), at which the entropy maximum occurs. The maximal values of the configurational entropy are represented by red spheres connected by lines. As illustrative examples, Figure 6(a) includes the configurational entropy $s/k_B$ as a function of $lnP$ for two fixed compositions: $X_1=1/3$ (black solid line) and $X_1=1/10$ (magenta solid line). The remaining entropy profiles are omitted for clarity. This representation enables clear identification of the different phases that arise in the system. Specifically: (i) a dimer-rich adsorbed phase at high values of $lnP$, (ii) a ternary mixture phase—comprising dimers, linear trimers, and triangular trimers—at intermediate pressures, and (iii) a nearly empty lattice at low values of $lnP$.

To better visualize the phase transitions, Figure 6(b) shows the projection of the entropy maxima onto the $X_1$–$lnP$ plane (i.e., the $xy$-plane), represented by blue spherical markers connected by solid lines. Three distinct regions can be distinguished in this projection. Around the curve of maximum entropy, the system behaves as a ternary mixture, while deviations from this region drive the system either toward a dimer-rich state or toward an almost empty lattice, depending on the trajectory in $lnP$ or $X_1$. As previously illustrated in Figure 5, the mixing entropy tends toward a finite constant as $lnP$ increases, corresponding to a nearly saturated lattice of dimers. Conversely, at low $lnP$, the entropy per site w approaches zero, indicating a dilute, nearly empty system.

Finally, it is worth noting that $lnP$ exhibits a nonlinear dependence on the dimer composition $X_1$: it decreases steeply at low concentrations ($X_1\le 1/10$), and more gradually at intermediate to high concentrations ($1/4\le X_1\le 1$). This suggests that, for dilute mixtures, significantly higher pressures are required to drive the system from the ternary mixture region into a dimer-rich adsorbed phase. In contrast, at higher concentrations, relatively small pressure changes suffice to induce this transition.

5. Conclusions

In this study, we developed and analyzed a theoretical framework to describe the adsorption of ternary mixtures of polyatomic molecules, specifically dimers, linear trimers, and triangular trimers, on triangular lattices, explicitly accounting for multisite occupancy and excluded volume effects. Our approach combines analytical statistical thermodynamics with grand canonical MC simulations, providing a detailed and consistent description of adsorption phenomena across a wide range of compositions and surface coverages. Several conclusions can be drawn from this study:

• The generalized lattice-gas model effectively captures the competitive adsorption behavior driven by molecular size and shape, illustrating the essential role of multisite occupation in realistic surface processes.
• Analytical expressions for thermodynamic quantities, Helmholtz free energy, configurational entropy per site, and total and partial coverage, were derived as functions of pressure. These predictions show excellent agreement with MC simulations for both total and partial isotherms, particularly for dimers and triangular trimers. Some deviations for linear trimers were observed, likely due to an overcounting of accessible configurations.
• A detailed entropy analysis reveals an entropy-driven displacement mechanism, where dimers progressively replace larger species at higher pressures, maximizing the system’s entropy prior to lattice saturation. In the high-coverage regime, entropy approaches a limiting value dominated by dimer adsorption, in line with previous studies on fully occupied lattices.
• Despite dimers playing a central role in the displacement process, larger molecules contribute cooperatively. Their ability to occupy residual voids left by smaller species supports the preservation of positive entropy and reinforces thermodynamic consistency, particularly in the behavior of mixing entropy.
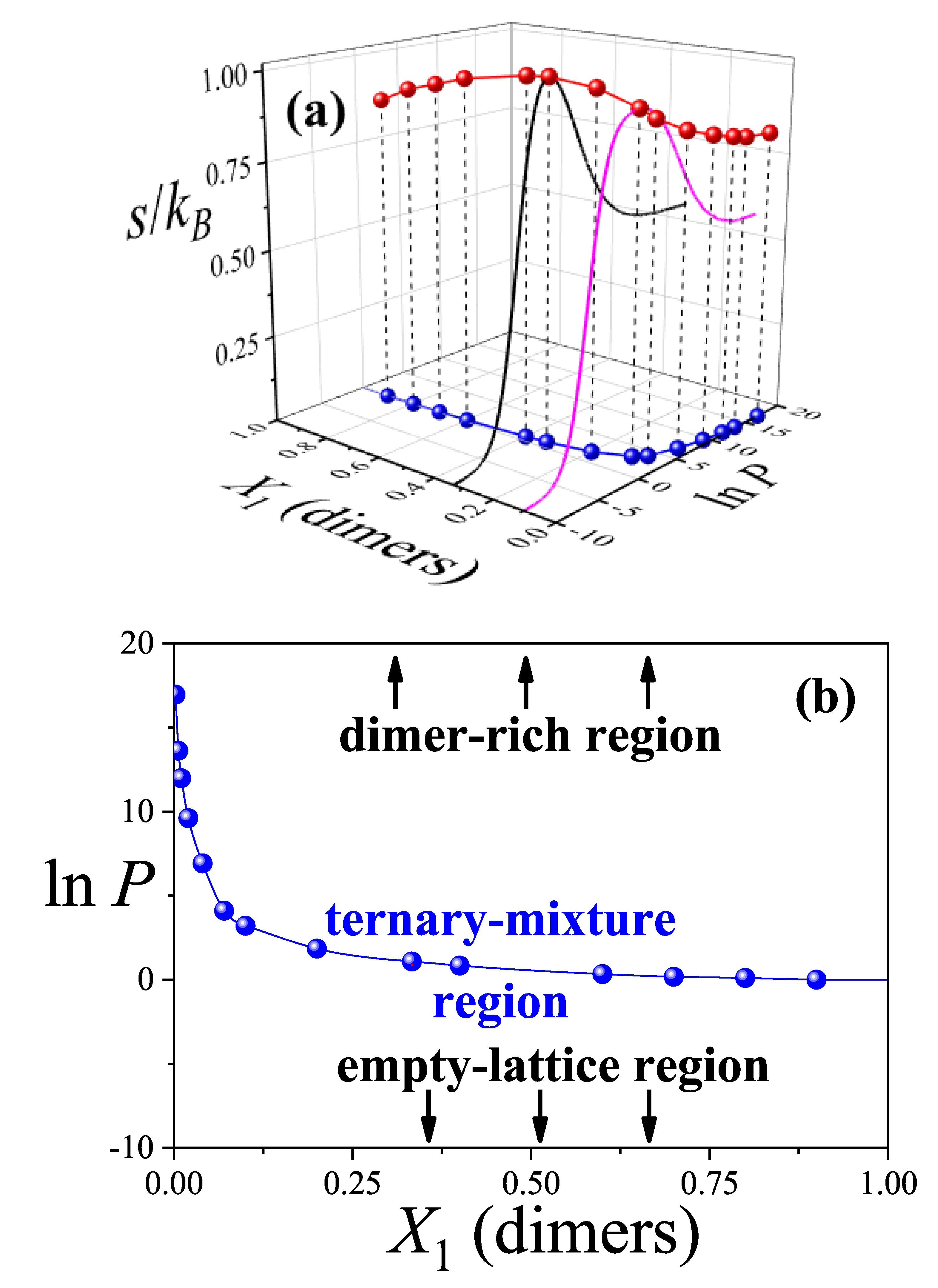
• The maximum entropy is attained for equimolar compositions, and the entropy landscape enables construction of an“entropic phase diagram" in the composition-pressure–maximum entropy space. This diagram delineates regions where competitive displacement is either enhanced or suppressed, offering a predictive tool for controlling surface composition, and illustrating the richness of configurational possibilities in such systems.

Overall, this study provides a comprehensive understanding of the role of entropy in multicomponent adsorption systems with multisite occupancy. The theoretical framework presented here not only aligns closely with simulation data but also provides predictive power for more complex scenarios. Future extensions may incorporate lateral interactions, surface heterogeneity, or more intricate lattice geometries, broadening the applicability of this approach to technologically relevant adsorption systems.