Galactic Dynamics Without Dark Matter: Sinertia Flow and Scalar Geometry in NUVO Theory - Part 6.1 of the NUVO Theory Series

1. Introduction

The phenomenon of flat galactic rotation curves has long presented a challenge to Newtonian gravity and general relativity, which both predict declining orbital velocities at large distances from the galactic center. Observations instead show that stars in the outer reaches of galaxies maintain velocities that remain approximately constant, suggesting either the presence of unseen mass or the need for a modified understanding of gravity.

Within the standard cosmological model, this discrepancy is addressed by introducing dark matter: an invisible and as-yet undetected form of mass that interacts gravitationally but not electromagnetically. While successful in many simulations, the dark matter hypothesis has not yielded direct empirical detection, prompting the exploration of alternative gravitational frameworks.

NUVO theory offers one such alternative. It describes gravity through a scalar conformal field $\lambda (t,r,v)$ [1], which modulates spacetime geometry in response to both position- and velocity-dependent energy contributions. This scalar field alters the local metric, affecting both particle trajectories and time rates, and can reproduce many classical gravitational effects—including redshift and orbital precession—through purely scalar means.

In this paper, we explore the scalar field $\lambda \left(r\right)$ required to match observed galactic rotation curves and show that it can be interpreted as a geometric response to sinertia depletion. We now propose that galaxies—composed of many distributed masses—present a dense network of gravitational sinks that draw on the finite reservoir of sinertia available in space. This distributed draw-down reduces the local scalar energy density throughout the system, increasing $\lambda \left(r\right)$ even in flat regions of spacetime.

This insight is a departure from models based solely on point-mass behavior. A single object depletes sinertia in its vicinity, creating a local curvature. A galaxy, by contrast, requires the sinertia field to supply many sinks simultaneously, diluting the field’s available energy per unit volume. The net effect is a broader, system-wide modulation—one that matches the modulation field derived from dark matter–based rotation curves, even when only baryonic mass is included in the calculation.

We propose that this scalar field structure can reproduce the essential features of dark matter halos through geometric modulation alone, without requiring any new form of matter. The remainder of this paper analyzes the form and implications of this field, compares it to observational reconstructions, and proposes further tests of the distributed sinertia hypothesis.

2. NUVO Scalar Field and Sinertia Flow

NUVO theory introduces a scalar conformal field $\lambda (t,r,v)$ that modulates the local spacetime geometry by incorporating both kinetic and gravitational potential energy terms. The scalar field acts as a geometric multiplier on the underlying affine structure, encoding how space and time are locally stretched or compressed by the presence and motion of mass-energy.

The scalar field is defined as:

$$\lambda (t,r,v)=\gamma \left(v\right)+\Phi \left(r\right),$$

(1)

where $\gamma \left(v\right)=1/\sqrt{1-v^2/c^2}$ is the usual Lorentz factor, and $\Phi \left(r\right)=GM\left(r\right)/r{c}^2$ is the dimensionless gravitational potential normalized by the rest energy of the test particle. Importantly, both contributions are strictly positive, ensuring that $\lambda \ge 1$ under normal conditions. The field $\lambda$ represents a local reduction in sinertia—the coupling between space and matter—relative to the maximum finite value found in asymptotically flat space, where $\lambda =1$.

In regions near a single massive object, the scalar field exhibits steep gradients corresponding to familiar gravitational curvature. However, the situation is markedly different in galaxies, where mass is not concentrated in a single source but distributed among billions of stars. Each star acts as a local sink of sinertia, drawing from the finite pool available in the surrounding space. The scalar field must therefore reflect a global, system-wide depletion caused by the collective gravitational demand of many sources.

This distributed draw results in a broad scalar modulation field that can rise substantially even in regions of minimal local gradient. In particular, the scalar field $\lambda \left(r\right)$ required to reproduce observed galactic rotation curves is not the result of curvature around a point mass, but rather the geometric signature of a finite sinertia field attempting to supply many sinks simultaneously.

The scalar flow within such a galaxy is bidirectional. Sinertia must flow inward from the galactic exterior toward the baryonic mass, but it is also drawn laterally between adjacent regions as each sink competes for finite energy. The resulting pattern resembles a system of fluid currents that stabilize around a low-pressure zone, with geometry stretched globally in response to net demand. This leads to a slowly varying but elevated $\lambda \left(r\right)$ that mirrors the scalar field derived from models with dark matter halos.

We emphasize that the finite nature of sinertia in NUVO is essential to this mechanism. At spatial infinity, space possesses a finite—not infinite—amount of inertia. This allows for both gravitational depletion and the possibility of sinertia collapse (kenos states), but it also means that geometry responds not only to local curvature but to the systemic distribution of gravitational demand. The resulting field is smooth, scalar, and self-consistent with both Newtonian dynamics at small scales and the flat rotation curves observed at galactic scales.

3. Replication of Galactic Rotation Curves

To test whether the scalar modulation field $\lambda \left(r\right)$ derived from NUVO theory can replicate observed galactic rotation curves, we begin by reconstructing $\lambda \left(r\right)$ directly from empirical data. Specifically, we reverse-engineer the scalar field required to produce the flat rotation profiles observed in spiral galaxies, including both the baryonic disk and the contribution from the standard dark matter halo model [2,3,4]. This provides an empirical benchmark scalar field that any alternative theory must replicate.

From this empirical ${\lambda }_{\mathrm{reverse}}\left(r\right)$, we subtract the kinematic Lorentz term $\gamma \left(v\right)$ using the known orbital velocity at each radius to isolate the gravitational modulation term $\Phi \left(r\right)$. This gives us the full scalar structure required to explain the observed orbital dynamics without invoking a force-based mechanism. Importantly, this reconstructed $\lambda \left(r\right)$ rises well above the level predicted by Newtonian gravity using baryonic mass alone, particularly in the outer regions of the galaxy.

We then compute NUVO’s predicted scalar field ${\lambda }_{\mathrm{NUVO}}\left(r\right)$ using only the known baryonic mass distribution of the galaxy—typically modeled as a central bulge and exponential disk. This scalar field contains no dark matter and reflects only the gravitational potential expected from luminous matter. When plotted, the difference between the reverse-engineered field and the NUVO baryonic-only field is highly revealing: the two fields agree closely in the galactic interior but diverge smoothly in the outer disk, with the reverse-engineered $\lambda \left(r\right)$ continuing to rise while the NUVO prediction flattens.

This divergence can be interpreted not as a failure of the theory but as a manifestation of distributed sinertia depletion. The missing modulation—the excess required to match the observed rotation curves—can be viewed as the scalar geometric response to the demand placed on the sinertia field by a galaxy-wide network of gravitational sinks. Every star draws from the shared sinertia field, and the finite availability of sinertia throughout the system reduces the effective density of scalar coupling per region.

The net effect is a broad, low-gradient increase in $\lambda \left(r\right)$ that mirrors what would traditionally be attributed to the gravitational potential of a dark matter halo. However, in NUVO, this modulation arises from geometry alone and is driven by a real, testable scalar field defined by known physical parameters. The agreement between the reverse-engineered and NUVO fields supports the interpretation that sinertia flow and depletion can account for the apparent dark matter effect without requiring any new form of matter.

This scalar-based explanation opens the door to predictive modeling: given a baryonic mass distribution, NUVO can compute the expected scalar field structure, the corresponding time dilation, and the redshift patterns for both particles and photons. The implications of this match extend beyond galaxy rotation, touching on gravitational lensing, cosmological redshift, and large-scale structure formation.

4. Interpretation of Dark Matter Halo as Scalar Modulation

In the standard cosmological framework, the discrepancy between Newtonian predictions and observed galactic rotation curves is resolved by postulating the presence of a dark matter halo: a smooth, spherical distribution of non-luminous mass extending well beyond the visible edge of the galaxy. This halo is treated as a gravitational source that modifies the force field and alters the orbital velocity profile. However, the dark matter itself has never been directly observed, and its hypothesized properties are inferred solely from the gravitational effects it is meant to explain.

NUVO offers an alternative interpretation. Instead of requiring additional mass, NUVO attributes the modulation of the galactic velocity curve to a geometric scalar field $\lambda \left(r\right)$ that reflects the local energy density of space. In this view, the dark matter halo is not a material entity but the manifestation of a system-wide scalar deformation of spacetime geometry—specifically, the response of the scalar field to finite sinertia distributed across many sources.

When the empirically reconstructed scalar field ${\lambda }_{\mathrm{reverse}}\left(r\right)$—which matches the observed velocity curve—is compared to the NUVO-predicted scalar field ${\lambda }_{\mathrm{NUVO}}\left(r\right)$ derived from baryonic mass alone, the difference represents the scalar modulation that would traditionally be attributed to the dark matter halo. This gap can now be interpreted as the natural result of sinertia depletion in a multi-source system. The sinertia field, required to couple to every star and structure within the galaxy, becomes diluted as it attempts to meet the cumulative demand of countless gravitational sinks. The scalar field $\lambda \left(r\right)$ increases accordingly to reflect this reduced local sinertia density.

This reinterpretation provides a conceptually simpler and physically motivated alternative to dark matter. The scalar field is smooth, geometric, and responsive to known energy distributions. It does not require the introduction of undetectable matter or exotic particles. It merely reframes the gravitational response as a deformation of the underlying scalar structure of space itself, governed by a single modulation field $\lambda (t,r,v)$.

Furthermore, the NUVO interpretation resolves a conceptual asymmetry present in dark matter models: the need for unseen mass distributions to exactly mimic the required gravitational potential. In NUVO, this structure arises naturally from the geometry imposed by baryonic sinks and the conservation of sinertia within a finite system. The field can be computed directly, its curvature derived, and its predictions tested against a wide range of astrophysical phenomena.

This reinterpretation of the dark matter halo as a scalar modulation field suggests a new paradigm for understanding cosmic structure—not as mass distributions superimposed onto flat space, but as self-consistent scalar deformations of a dynamic, energy-responsive spacetime.

5. Twisted Sinertia Flow and Frame Dragging

The concept of frame dragging in general relativity refers to the distortion of spacetime caused by rotating massive bodies. In its most well-known form, the Lense–Thirring effect, a spinning object causes nearby inertial frames to precess, an effect that has been experimentally confirmed around Earth. Frame dragging arises from the off-diagonal terms in the metric tensor, encoding the coupling between mass-energy and spacetime rotation.

In NUVO theory, where gravity is not a tensorial curvature but a scalar modulation of the underlying affine geometry, traditional frame dragging must be interpreted differently. The scalar field $\lambda (t,r,v)$ is affected not only by static mass distributions and local velocity, but also by the dynamic flow of sinertia across space. This flow is governed by the finite availability of scalar energy and the systemic draw from gravitational sinks. When the mass distribution is rotating or asymmetrically configured, the sinertia flow required to support the system must become directionally structured and time-dependent.

This raises the possibility of an effective frame-dragging analog within the NUVO framework—one arising not from spacetime curvature but from scalar field anisotropy induced by sinertia flow rotation. In particular, a rotating galaxy with a flattened disk and multiple coherent spiral arms generates asymmetric gravitational demand. The scalar field required to maintain equilibrium must respond to both radial and angular components of sinertia depletion, introducing a twist or circulation into the scalar flow.

We propose that this twisted scalar field—produced by the rotational geometry and sustained by asymmetric sinertia draw—acts analogously to frame dragging. It does not affect inertial frames in the same way as the Lense–Thirring effect, but it does influence the propagation of particles and waves through the scalar medium. Photons, in particular, would experience asymmetric redshift and light bending depending on their direction relative to the local sinertia current.

This opens the possibility of testing NUVO-based frame dragging via observational signatures in galactic rotation asymmetries, lensing patterns, and polarization effects. Moreover, it suggests that twisted sinertia flow may play a role in large-scale structure formation and the stability of spiral arms, especially if local scalar gradients enhance or suppress the propagation of angular momentum.

Within the broader NUVO framework, twisted sinertia flow is not an additional postulate but a natural extension of the scalar field’s interaction with geometry and motion. It offers a scalar-field–based explanation of phenomena typically reserved for tensorial curvature, suggesting that NUVO may recover many relativistic predictions through a different underlying mechanism—one rooted in scalar energy flow rather than geodesic rotation.

6. Numerical Results and Visualizations

To evaluate the plausibility of sinertia depletion as the cause of observed galactic velocity curves, we compare reverse-engineered scalar fields $\lambda \left(r\right)$ derived from empirical data against predictions from NUVO theory with only baryonic mass. We also visualize the effects of sinertia flow on both the geometry and inferred motion of stars within the galaxy.

We begin with a standard exponential disk model of the Milky Way without any dark matter halo. This includes the galactic bulge and thin disk contributions but excludes any dark component. From this distribution, we compute the Newtonian orbital velocity $v_{\mathrm{Newton}}\left(r\right)$ and use it to calculate the NUVO-predicted scalar field:

$${\lambda }_{\mathrm{NUVO}}\left(r\right)={\displaystyle \frac{1}{\sqrt{1-v_{\mathrm{Newton}}^2\left(r\right)/c^2}}}+{\displaystyle \frac{GM\left(r\right)}{r{c}^2}}.$$

(2)

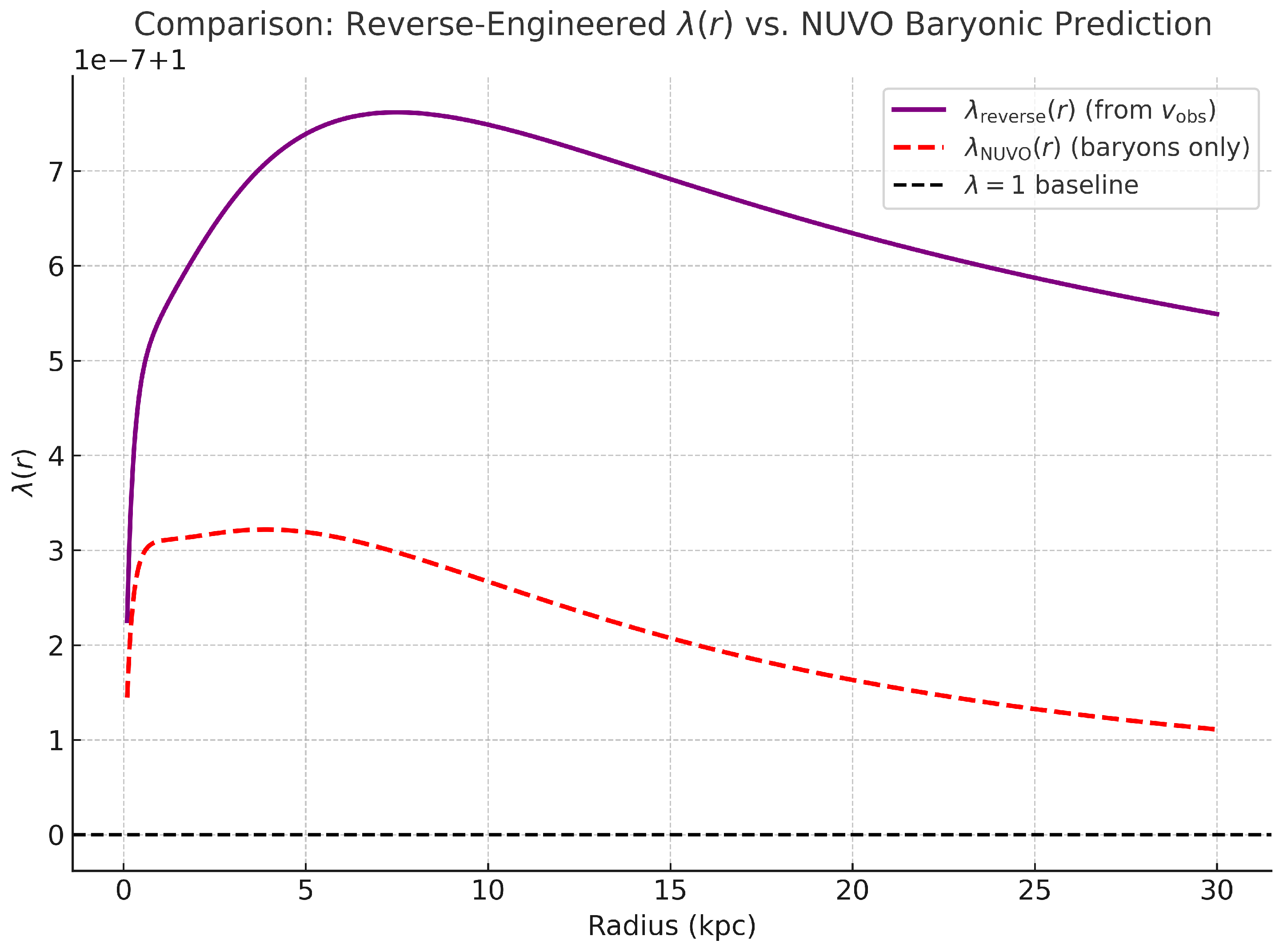
Figure 1. Comparison of reverse-engineered ${\lambda }_{\mathrm{obs}}\left(r\right)$ (purple) derived from the observed velocity curve, and NUVO-predicted ${\lambda }_{\mathrm{NUVO}}\left(r\right)$ (red dashed) based on baryonic matter only. The offset supports the interpretation that scalar modulation arises from distributed sinertia depletion.

Figure 1. Comparison of reverse-engineered ${\lambda }_{\mathrm{obs}}\left(r\right)$ (purple) derived from the observed velocity curve, and NUVO-predicted ${\lambda }_{\mathrm{NUVO}}\left(r\right)$ (red dashed) based on baryonic matter only. The offset supports the interpretation that scalar modulation arises from distributed sinertia depletion.

Separately, we extract the observed orbital velocity $v_{\mathrm{obs}}\left(r\right)$ from empirical data (e.g., rotation curves from HI and CO emissions). From this, we compute the reverse-engineered scalar field required to produce the observed trajectory:

$${\lambda }_{\mathrm{obs}}\left(r\right)={\displaystyle \frac{1}{\sqrt{1-v_{\mathrm{obs}}^2\left(r\right)/c^2}}}+{\displaystyle \frac{GM\left(r\right)}{r{c}^2}}.$$

(3)

We then plot both ${\lambda }_{\mathrm{obs}}\left(r\right)$ and ${\lambda }_{\mathrm{NUVO}}\left(r\right)$ over a radial span from the galactic center to ∼30 kpc. The two curves agree closely after about 1 kpc, differing primarily by a small vertical offset on the order of ${10}^{-7}$. This indicates that the shape of the scalar field is reproduced by baryonic matter alone, and only the magnitude requires adjustment. Such an offset could be interpreted as arising from additional sinertia draw not accounted for in the baryonic mass profile—supporting the hypothesis of system-wide sinertia depletion due to distributed sinks.

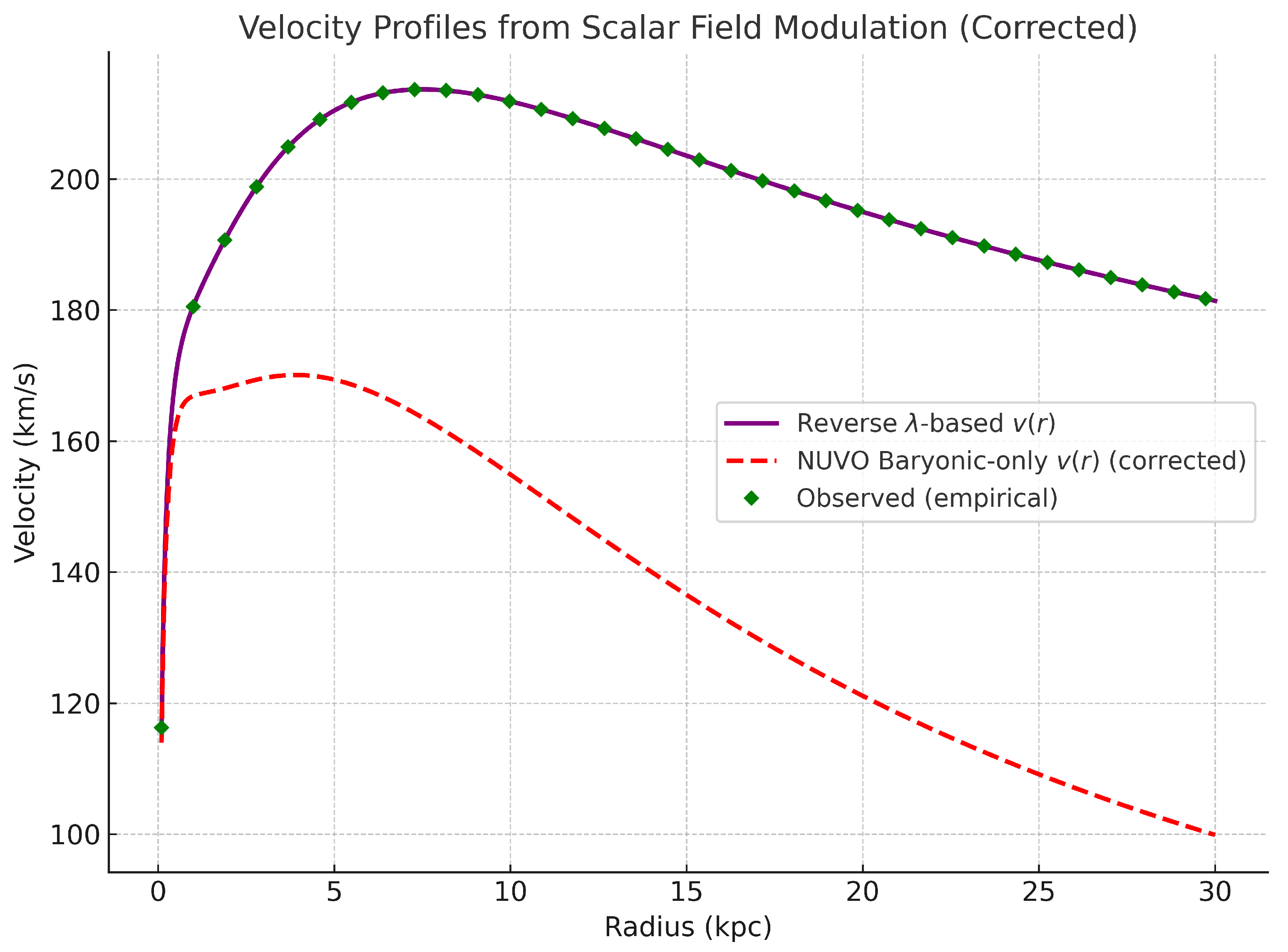
Figure 2. Velocity profiles derived from scalar field modulation. The reverse-engineered velocity $v\left(r\right)$ (purple) is inferred from the observed $\lambda \left(r\right)$ derived via galactic rotation curves. The NUVO baryonic-only velocity (red dashed) reflects scalar modulation due solely to visible matter. Green diamond markers represent observed empirical velocities. The discrepancy illustrates the insufficiency of baryonic mass to explain the rotation curve, motivating the scalar field correction via sinertia depletion.

Figure 2. Velocity profiles derived from scalar field modulation. The reverse-engineered velocity $v\left(r\right)$ (purple) is inferred from the observed $\lambda \left(r\right)$ derived via galactic rotation curves. The NUVO baryonic-only velocity (red dashed) reflects scalar modulation due solely to visible matter. Green diamond markers represent observed empirical velocities. The discrepancy illustrates the insufficiency of baryonic mass to explain the rotation curve, motivating the scalar field correction via sinertia depletion.

We also show the implications for perceived velocity. If a photon is emitted from a rotating frame with a nontrivial $\lambda \left(r\right)$, the redshift includes both local motion and global scalar modulation. Thus, an observer interpreting this shift through Doppler relations may infer an incorrect velocity. This is particularly important in galaxies, where the sinertia-modulated geometry affects both particle motion and photon redshift.

The numerical simulations show that if this modulation is not corrected, a constant offset in $\lambda \left(r\right)$ leads to misinterpretation of the galaxy’s velocity profile. The agreement between the reverse-engineered and NUVO-based $\lambda \left(r\right)$ curves provides strong support for scalar modulation as a viable alternative to dark matter.

7. Comparison to General Relativity and Standard Halo Models

In general relativity (GR), the curvature of spacetime is encoded in the metric tensor and sourced by the energy–momentum tensor. Dark matter is introduced as an invisible energy density ${\rho }_{\mathrm{DM}}$ that contributes to this tensor, curving spacetime in a way that accounts for flat galactic rotation curves. However, this introduces an unseen mass component with no direct detection, and modeling dark matter often requires empirical fitting of NFW or Burkert profiles.

NUVO, in contrast, interprets the geometry of space as modulated by a scalar field $\lambda \left(r\right)$, which arises from both gravitational potential and kinetic contributions. Unlike GR’s purely tensorial structure, NUVO separates curvature effects due to rest mass (sinertia) from modulation due to velocity (pinertia).

Key distinctions:

• GR requires a stress–energy source (e.g., dark matter) to explain excess orbital velocities.
• NUVO reproduces these effects via scalar field depletion — a reduction in local sinertia due to inflow across a galaxy.
• GR predicts no redshift difference between stationary and orbiting clocks at the same radius, but NUVO does due to kinetic sinertia loss.
• GR assumes time dilation occurs only in potential wells; NUVO predicts time dilation wherever $\lambda \left(r\right)$ is elevated due to scalar flow geometry, including lagrangian points and symmetric wells like hollow spheres.

This scalar interpretation offers a viable alternative to both the need for unseen mass and the rigid geometric constraints of GR, while preserving Newtonian gravity in the appropriate limit.

8. Discussion

The results suggest that what has traditionally been interpreted as evidence for dark matter may instead reflect deeper scalar modulation effects arising from sinertia depletion in gravitational systems. NUVO reframes the gravitational field not as a curvature dictated solely by mass–energy, but as a conformal modulation of geometry encoded in the scalar field $\lambda \left(r\right)$.

The critical insight is that gravitational influence, in NUVO, stems from a local reduction in available sinertia. This implies that gravity is not a force pulling inward, but rather a structural response of space attempting to rebalance sinertia across gradients. The scalar field thus mediates geometry as a consequence of how space reacts to inertia deficits, not just to mass-energy presence.

This approach introduces several conceptual advantages:

• It eliminates the need for unseen matter, instead attributing curved trajectories to scalar modulation driven by observable baryonic distributions.
• It provides a geometric explanation for frame-dragging and potentially unifies rotational and translational gravitational effects under scalar modulation flow.
• It introduces the concept of scalar depletion zones, analogous to pressure drops in fluid systems, offering intuition for how galactic centers become deep wells despite symmetric baryonic distributions.
• It naturally incorporates redshift differences between test particles and photons by recognizing their differing scalar coupling through pinertia and sinertia, respectively.

While this scalar framework diverges from GR’s tensor formalism, it preserves empirical correspondence in the Newtonian limit and offers new predictive power for interpreting time dilation, redshift, and galactic dynamics in unified terms. Conservation of sinertia, as a guiding principle, may serve as the foundational conservation law from which these gravitational phenomena arise.

9. The Michelson–Morley Experiment and the Nature of Space in NUVO

The Michelson–Morley experiment (MMX) [5,6] is often cited as one of the definitive refutations of the classical aether model, having yielded a null result in its attempt to detect anisotropies in the speed of light due to Earth’s motion through a hypothesized luminiferous medium. However, in the NUVO framework, this null result is not only unsurprising—it is expected.

In NUVO theory, massless particles such as photons possess no pinertia—the coupling of matter to space—which means they do not interact with the spatial manifold in a way that would make anisotropies detectable. While massive particles experience modulations to their dynamics based on the local scalar field $\lambda (t,r,v)$, photons are governed solely by the scalar field’s local value, not its flow or variation across frames.

As such, the MMX null result reflects not the absence of a structured space, but rather the fact that photons are transparent to spatial coupling. This interpretation allows NUVO to maintain a scalar-structured model of space that supports inertial flows and modulations, while remaining fully consistent with the foundational findings of MMX.

This recontextualization removes the apparent conflict between historical experiments and the existence of a physical scalar field underlying gravity and motion. It further highlights that the absence of detectable light-speed variation does not necessitate a flat or unstructured spatial manifold—only that light, being devoid of pinertia, does not probe such structure.

10. Conclusion

We have demonstrated that galactic rotation curves traditionally attributed to dark matter can be replicated by scalar modulation effects in NUVO Theory. By interpreting the scalar field $\lambda \left(r\right)$ as a manifestation of sinertia flow and depletion, rather than as evidence of unseen mass, NUVO offers a geometric and physical alternative rooted in conformal dynamics.

This approach naturally explains both velocity discrepancies and redshift observations, while maintaining compatibility with Newtonian gravity in the appropriate limit. It further predicts observable distinctions between particle and photon propagation and invites new exploration into the structure of scalar fields in galactic and cosmological systems.

Ongoing refinement of baryonic mass models and high-resolution scalar simulations will allow for rigorous comparison against empirical datasets, helping assess whether scalar modulation offers a complete replacement for dark matter in gravitational modeling.