Submitted:
04 June 2025
Posted:
04 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
- (1)
- The proposed admissibility criteria are different from all existing criteria. Unlike in [21], which involves an excessive number of decision variables, the proposed admissibility criterion uses only a single LMI variable. This paper not only reduces computational complexity but also extends the results of [11] from IOSs to singular fractional-order systems with orders in .
- (2)
- These criteria provide several advantageous characterizations of existing results. The proposed approach avoids the use of complex variables [17,18,19], making it well-suited for handling eigenvalues of system matrices with positive real parts; it does not involve a large number of LMI variables [20] and does not contain equality constraints [22,23], making it easy to both for controller design and numerical simulation.
- (3)
- Admissibility and stabilization problems for singular FOSs with orders in the interval solved. Equality constraints and non-strict linear matrix inequalities have been removed in all admissibility conditions to facilitate checking. A BBA was devised to solve the bilinear problem [24,25] arising in stabilization criterion.
2. Problem Statements and Preliminaries
- (1)
- for , there exist dimensional real square matrices X and Y such that
- (2)
- for , there exist dimensional real square matrices X and Y, and dimensional real matrix Q, such thatwhere S is an dimensional matrix characterized by full column rank, such that .
- (1)
- (2)
- (3)
3. Main Results
3.1. Novel Admissibility Conditions for Singular FOSs
3.2. Novel Stabilization Conditions for Singular FOSs
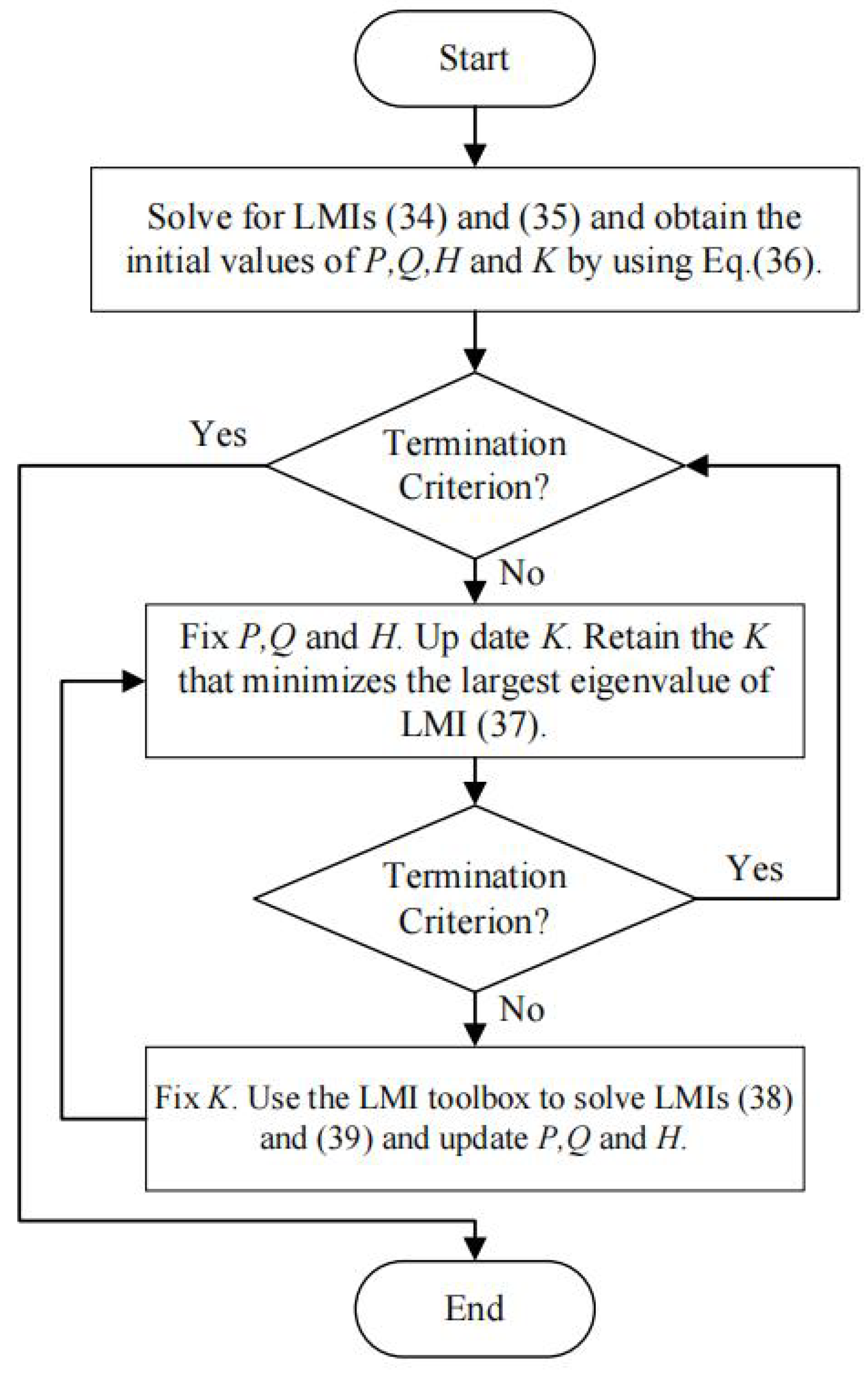
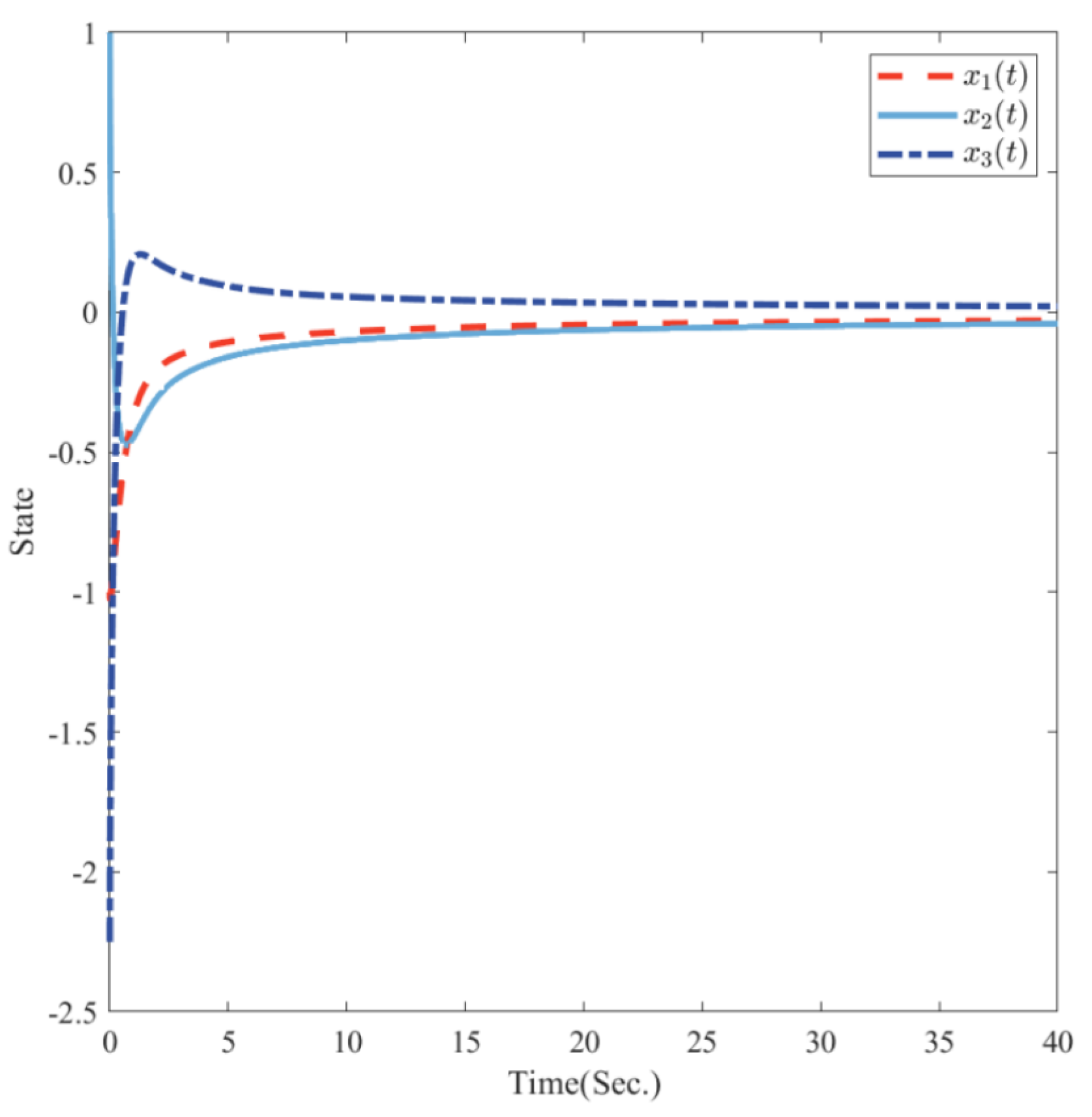
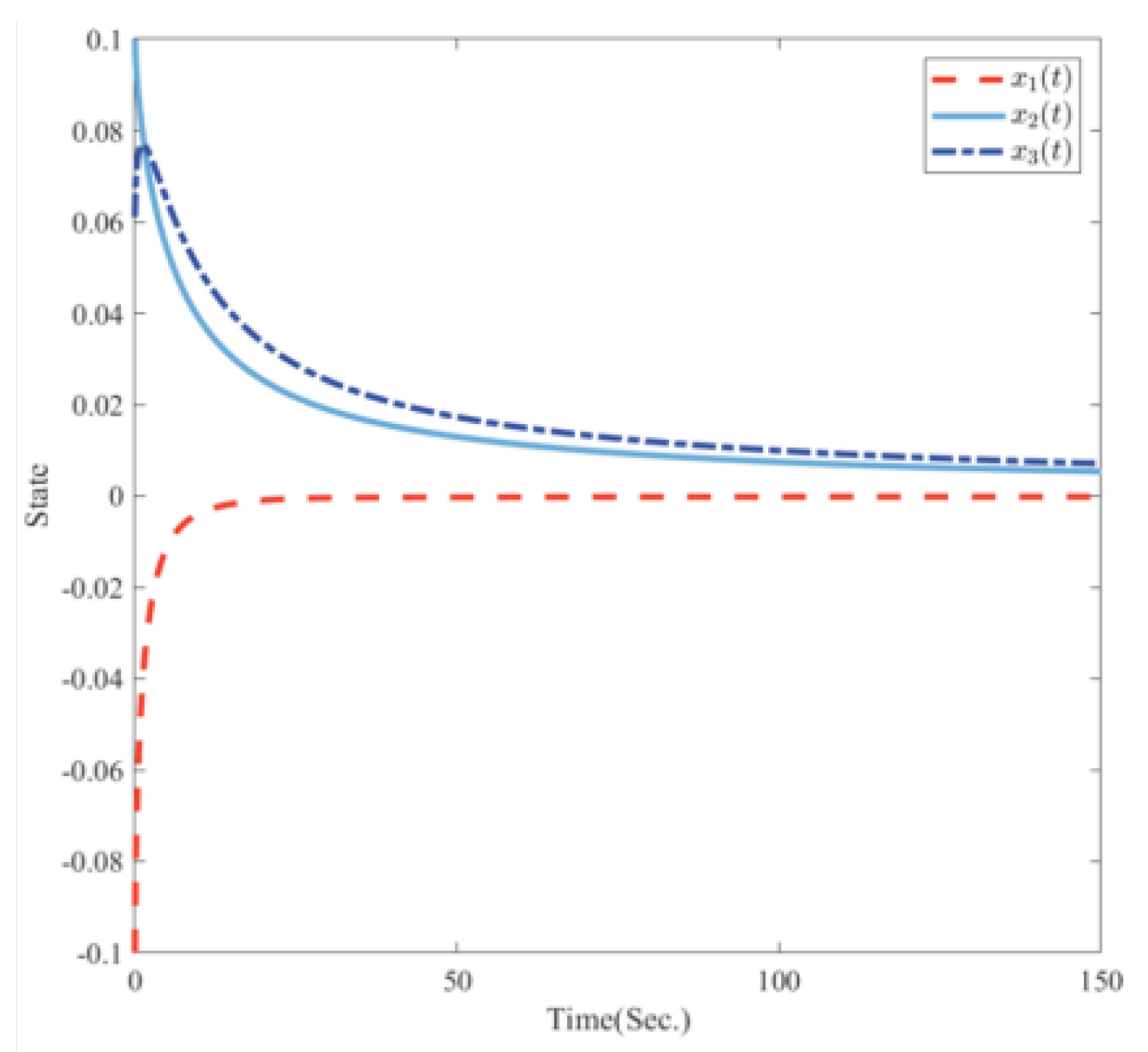
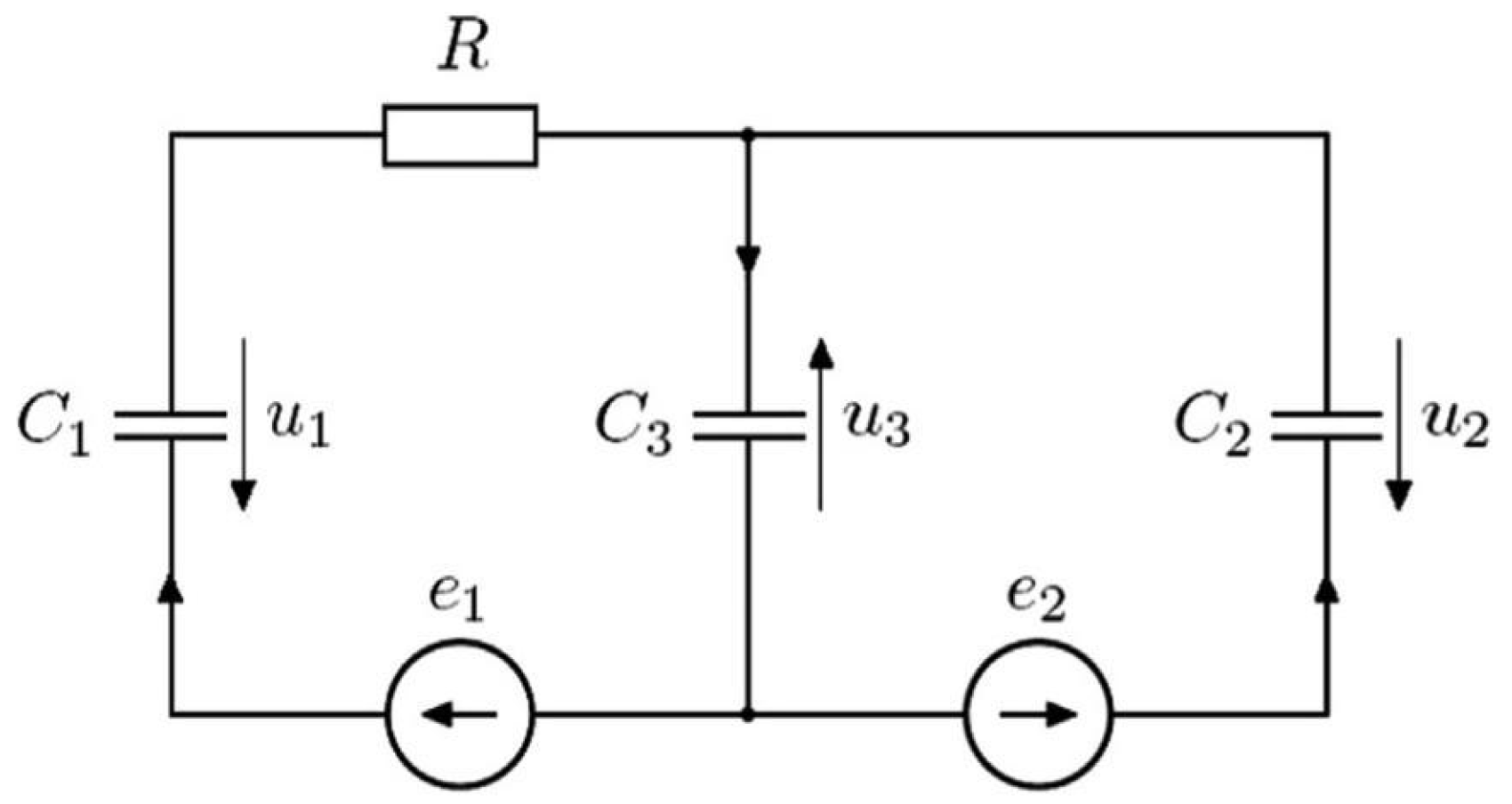
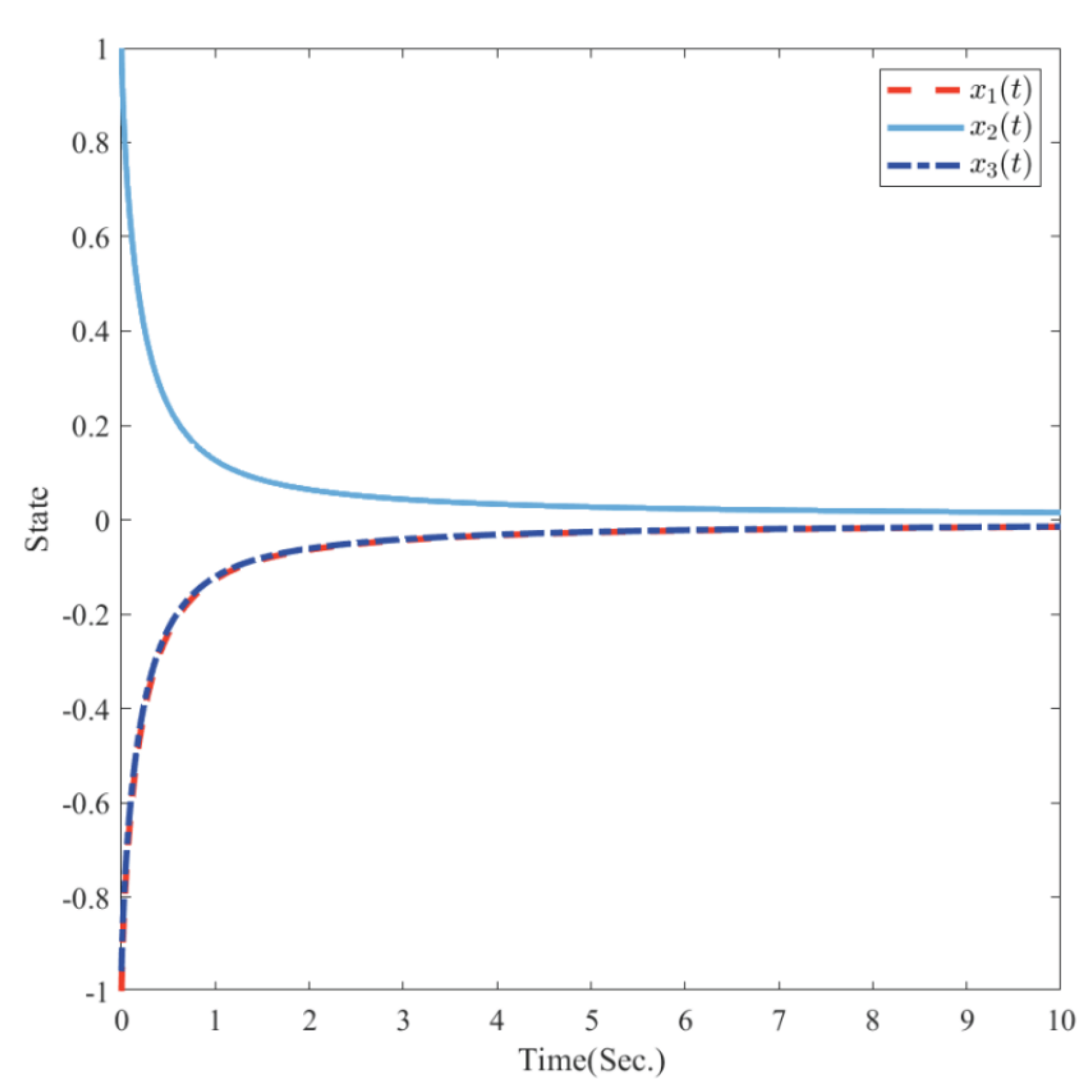
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lim, Y.; Oh, M.; Ahn, H. Stability and stabilization of fractional-order linear systems subject to input saturation. IEEE Trans. Autom. Control, 2013, 58, 1062–1067. [CrossRef]
- Zhang, X.F.; Liu, R.; Ren, J.X.; Cui, Q.L. Adaptive fractional image enhancement algorithm based on rough set and particle swarm optimization. Fractal Fract., 2022, 6, 100. [CrossRef]
- Zhang, J.-X.; Zhang, X.F.; Boutat, D.; Liu, D.Y. Fractional-order complex systems: Advanced control, intelligent estimation and reinforcement learning image-processing algorithms. Fractal Fract., 2025, 7, 67. [CrossRef]
- Huang, L.; Wu, G.; Baleanu, D.; Wang, H. Discrete fractional calculus for interval-valued systems. Fuzzy Sets Syst., 2021, 404, 141–158. [CrossRef]
- Gong, P.; Lan, W.; Han, Q. Robust adaptive fault-tolerant consensus control for uncertain nonlinear fractional-order multi-agent systems with directed topologies. Automatica, 2020, 117, 109011. [CrossRef]
- Zhang, J.-X.; Ding, J.; Chai, T. Fault-tolerant prescribed performance control of wheeled mobile robots: A mixed-gain adaption approach. IEEE Trans. Autom. Control, 2024, 69, 5500–5507. [CrossRef]
- Zhang, J.-X.; Xu, K.; Wang, Q. Prescribed performance tracking control of time-delay nonlinear systems with output constraints. IEEE/CAA J. Autom. Sin., 2024, 11, 1557–1565. [CrossRef]
- Zhang, J.-X.; Ding, J.; Chai, T. Cyclic performance monitoring-based fault-tolerant funnel control of unknown nonlinear systems with actuator failures. IEEE Trans. Autom. Control, 2025. [CrossRef]
- Zhang, J.-X.; Cui, E.-Y.; Shi, P. Low-complexity high-performance control of unknown block-triangular MIMO nonlinear systems. IEEE Trans. Ind. Electron., 2024, doi:10.1109/TIE.2024.3515269. [CrossRef]
- Zhang, J.-X.; Yang, G.-H. Low-complexity tracking control of strict-feedback systems with unknown control directions. IEEE Trans. Autom. Control, 2019, 64(12), 5175–5182. [CrossRef]
- Wu, J.; Yung, C. A new generalized bounded real lemma for continuous-time descriptor systems. Asian J. Control, 2022, 24, 2729–2737. [CrossRef]
- Feng, Z.; Shi, P. Two equivalent sets: Application to singular systems. Automatica, 2017, 77, 198–205. [CrossRef]
- Tavazoei, M.; Haeri, M. A note on the stability of fractional order systems. Math. Comput. Simul., 2009, 79, 1566–1576. [CrossRef]
- Matignon, D. Stability result on fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl., 1996, 2, 963–968.
- Amini, A.; Azarbahram, A.; Sojoodi, M. H∞ consensus of nonlinear multi-agent systems using dynamic output feedback controller: An LMI approach. Nonlinear Dyn., 2016, 85, 1865–1886. [CrossRef]
- El-Khazali, R.; Momani, S. Stability analysis of composite fractional systems. Int. J. Appl. Math., 2003, 12, 73–85.
- Sabatier, J.; Moze, M.; Farges, C. LMI stability conditions for fractional order systems. Comput. Math. Appl., 2010, 59, 1594–1609. [CrossRef]
- Ahn, H.; Chen, Y. Necessary and sufficient stability condition of fractional-order interval linear systems. Automatica, 2008, 44, 2985–2988. [CrossRef]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo-state feedback stabilization of commensurate fractional order systems. Automatica, 2010, 46, 1730–1734. [CrossRef]
- Jiao, Z.; Zhong, Y. Robust stability for fractional-order systems with structured and unstructured uncertainties. Comput. Math. Appl., 2012, 3258–3266.
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional-order interval systems with the fractional order α: The 0 < α < 1 Case. IEEE Trans. Autom. Control, 2009, 152–158.
- Marir, S.; Chadli, M.; Basin, M. Necessary and sufficient admissibility conditions of dynamic output feedback for singular linear fractional-order systems. Asian J. Control, 2023, 25, 2439–2450. [CrossRef]
- Liu, Y.; Cui, L.; Duan, D. Dynamic output feedback stabilization of singular fractional-order systems. Math. Probl. Eng., 2016, 9694780.
- Marir, S.; Chadli, M.; Bouagada, D. A novel approach of admissibility for singular linear continuous-time fractional-order systems. Int. J. Control Autom. Syst., 2017, 15, 959–964. [CrossRef]
- Marir, S.; Chadli, M. Robust admissibility and stabilization of uncertain singular fractional-order linear time-invariant systems. IEEE/CAA J. Autom. Sin., 2019, 6, 685–692. [CrossRef]
- Ji, Y.; Qiu, J. Stabilization of fractional-order singular uncertain systems. ISA Trans., 2015, 56, 53–643. [CrossRef]
- N’Doye, I.; Darouach, M.; Zasadzinski, M.; Radhy, N. Robust stabilization of uncertain descriptor fractional-order systems. Automatica, 2013, 49, 1907–1913. [CrossRef]
- Wei, Y.; Tse, P.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Trans., 2017, 69, 1–9. [CrossRef]
- Zhang, X.F.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0 < α < 2. IEEE Trans. Circuits Syst. II Express Briefs, 2020, 67, 3237–3241.
- Shen, J.; Lam, J. State feedback H∞ control of commensurate fractional-order systems. Int. J. Syst. Sci., 2014, 45, 363–372. [CrossRef]
- Zhang, X.; Chen, Y. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0 < α < 1 case. ISA Trans., 2018, 82, 42–50.
- Marir, S.; Chadli, M.; Basin, M. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica, 2022, 135, 109962. [CrossRef]
- Di, Y.; Zhang, J.; Zhang, X. Robust stabilization of descriptor fractional-order interval systems with uncertain derivative matrices. Appl. Math. Comput., 2023, 453, 128076. [CrossRef]
- Zhang, L.; Zhang, J.; Zhang, X. Generalized criteria for admissibility of singular fractional order systems. Fractal Fract., 2023, 7, 363. [CrossRef]
| Ref. | System type | Fractional order field |
Variables | No equality constraints |
No bilinear problem |
|---|---|---|---|---|---|
| Theorem 3 in [24] | Singular FOSs | 6 | × | ||
| Theorem 2 in [25] | Singular FOSs | 5 | × | ||
| Theorem 1 in [22] | Singular FOSs | 4 | × | ||
| Theorem 1 in [21] | FOSs | 4 | |||
| Our Theorems 1 and 2 | Singular FOSs | 2/3 | |||
| Our Corollary 1 | Singular FOSs | 1 | |||
| Our Theorem 3 | Singular FOSs | 3 | × |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





