Submitted:
30 September 2024
Posted:
03 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Problem Formulation and Preliminaries
3. Main Results
3.1. ILMI Algorithm for Output Feedback Consensus with
3.2. ILMI Algorithm for Output Feedback Consensus with
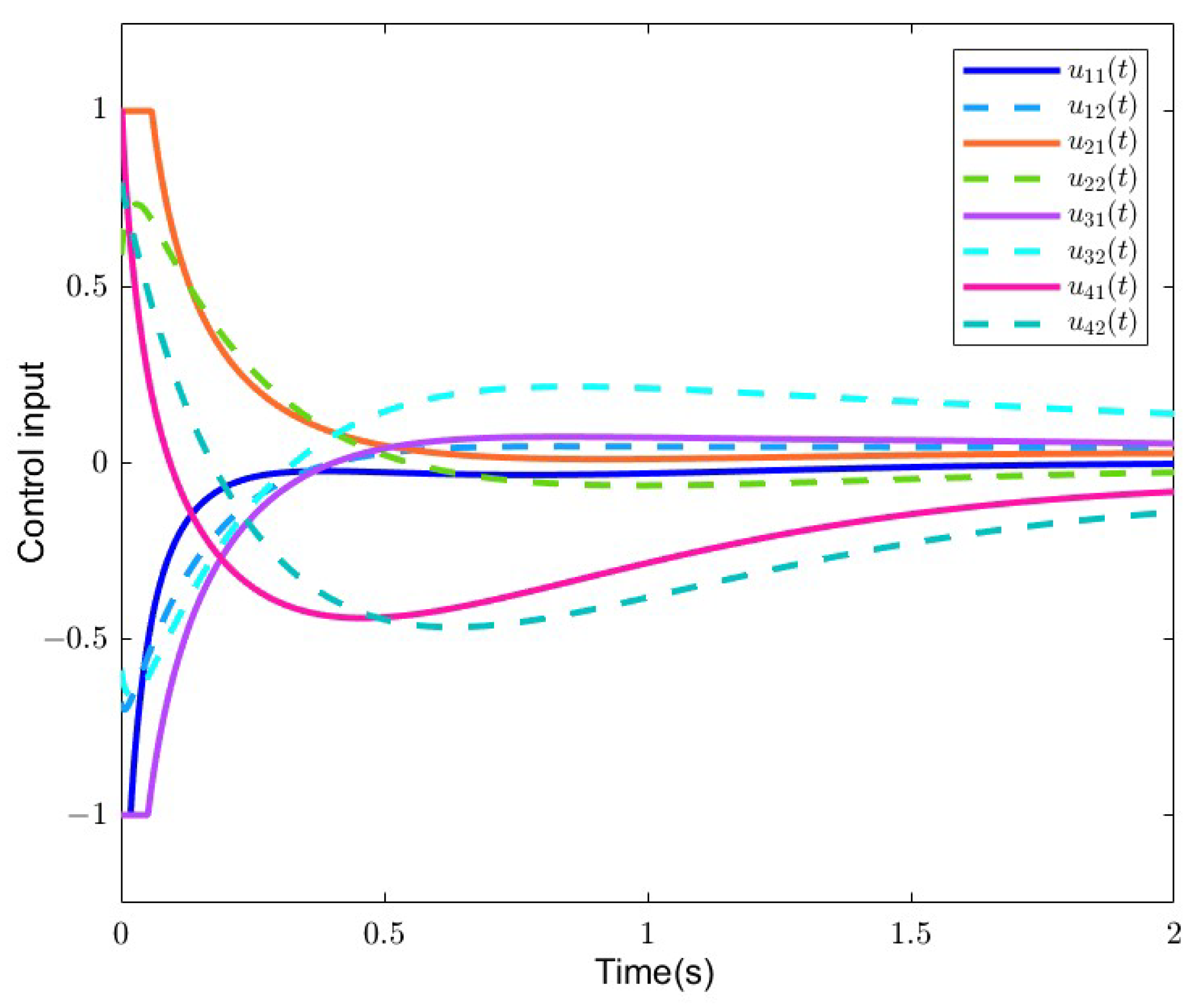
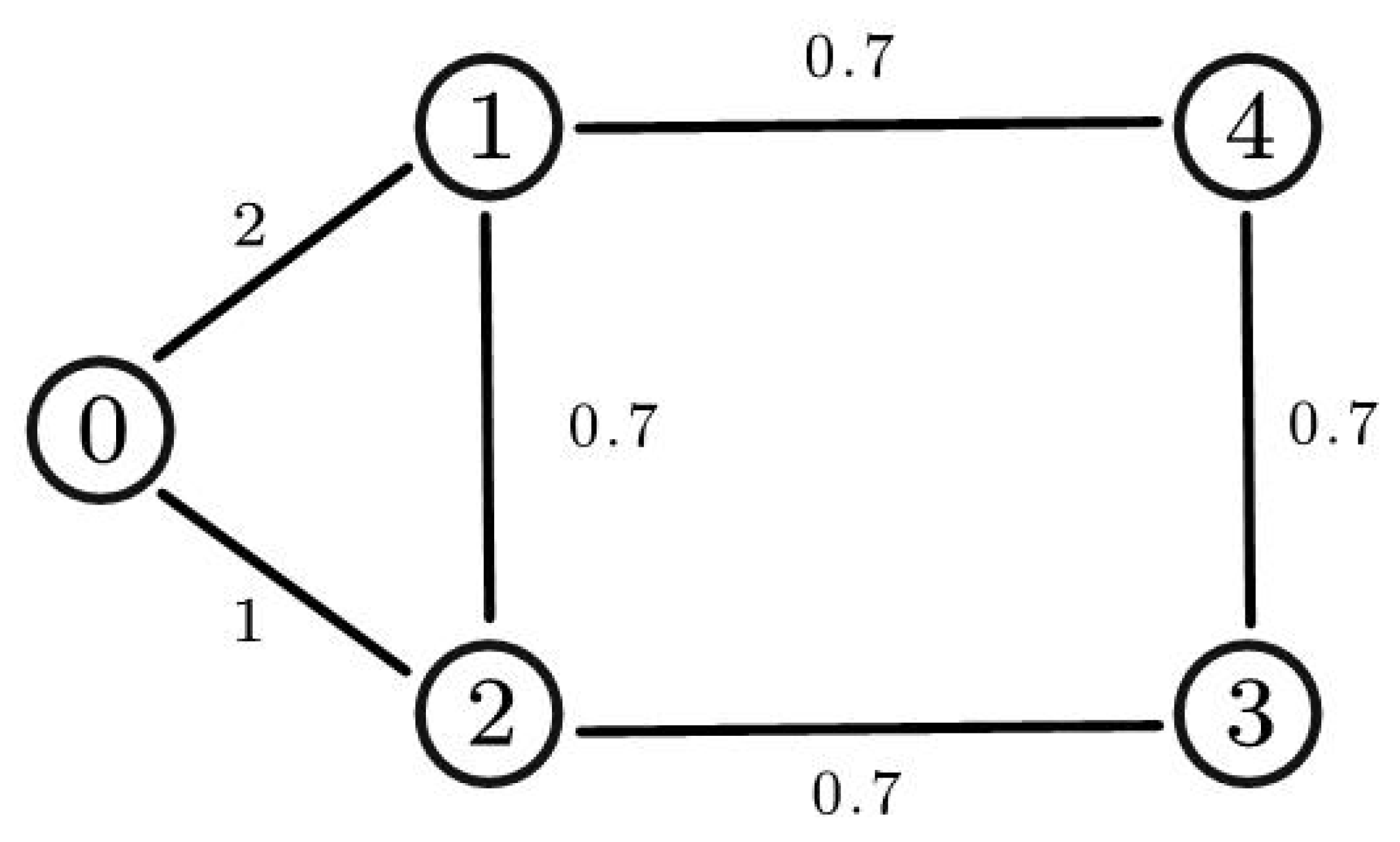
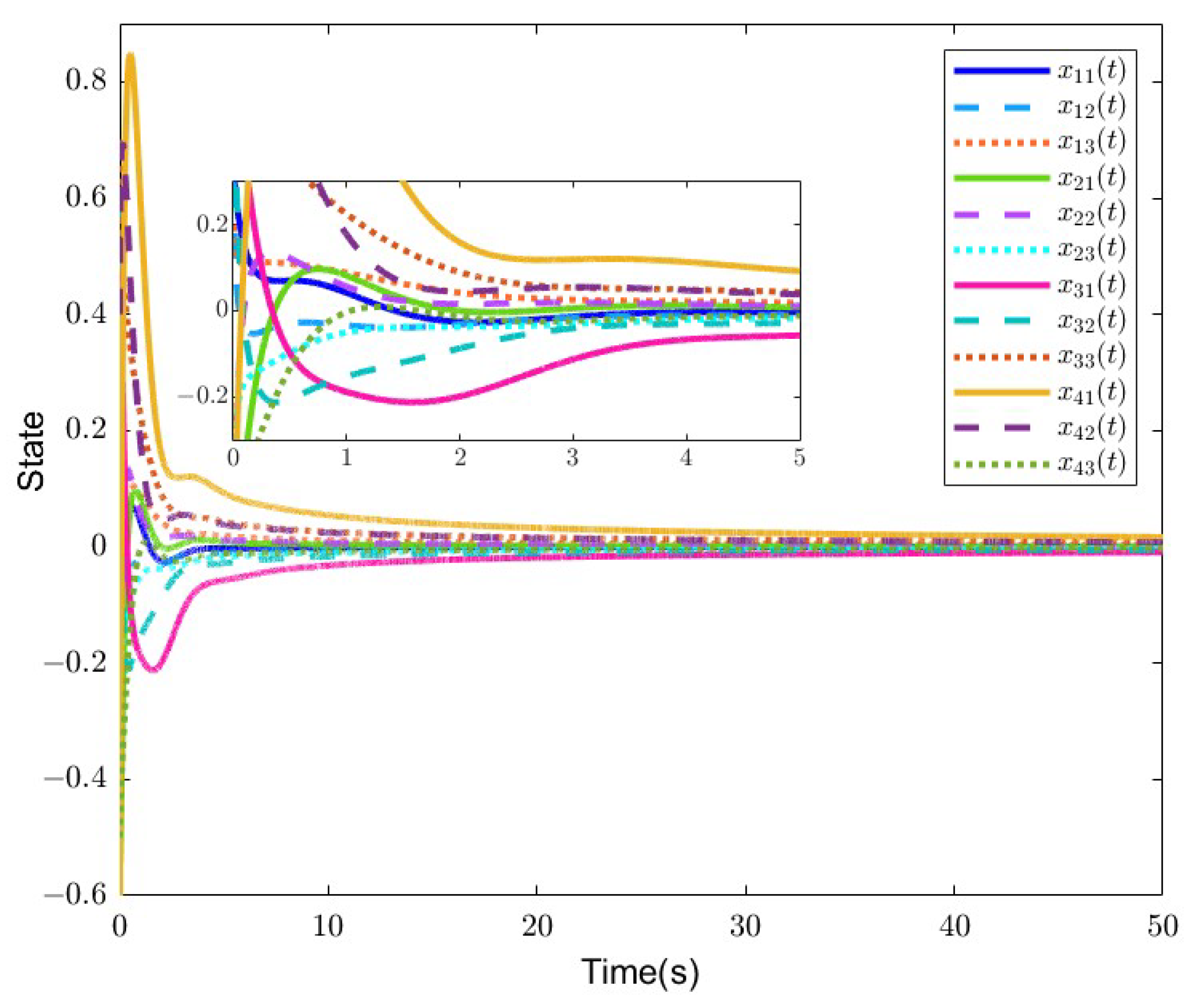
4. Numerical Examples
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Zhang, J.; Wang, H. Urban traffic control in software defined internet of things via a multi-agent deep reinforcement learning approach. IEEE Transactions on Intelligent Transportation Systems 2020, 22, 3742–3754. [Google Scholar] [CrossRef]
- Yan, Z.; Xu, Y. A multi-agent deep reinforcement learning method for cooperative load frequency control of a multi-area power system. IEEE Transactions on Power Systems 2020, 35, 4599–4608. [Google Scholar] [CrossRef]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A multi-agent reinforcement learning-based data-driven method for home energy management. IEEE Transactions on Smart Grid 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Amirkhani, A.; Barshooi, A.H. Consensus in multi-agent systems: A review. Artificial Intelligence Review 2022, 55, 3897–3935. [Google Scholar] [CrossRef]
- Zhang, J.X.; Ding, J.; Chai, T. Fault-tolerant prescribed performance control of wheeled mobile robots: A mixed-gain adaption approach. IEEE Transactions on Automatic Control 2024. [Google Scholar] [CrossRef]
- Zhang, J.X.; Wang, Q.G.; Ding, W. Global output-feedback prescribed performance control of nonlinear systems with unknown virtual control coefficients. IEEE Transactions on Automatic Control 2021, 67, 6904–6911. [Google Scholar] [CrossRef]
- Zhang, J.X.; Xu, K.D.; Wang, Q.G. Prescribed performance tracking control of time-delay nonlinear systems with output constraints. IEEE/CAA Journal of Automatica Sinica 2024, 11, 1557–1565. [Google Scholar] [CrossRef]
- Rana, M.; Pande, R.; Kukreti, K. Design of RF MEMS piezoelectric disk resonator for 5G communication. Materials Today: Proceedings 2023, 73, 13–17. [Google Scholar] [CrossRef]
- Radwan, A.G.; Emira, A.A.; AbdelAty, A.M.; Azar, A.T. Modeling and analysis of fractional order DC-DC converter. ISA Transactions 2018, 82, 184–199. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Z.; Khan, M.A. Fractional investigation of bank data with fractal-fractional Caputo derivative. Chaos, Solitons & Fractals 2020, 131, 109528. [Google Scholar]
- Yang, F.; Wang, P.; Wei, K.; Wang, F. Investigation on nonlinear and fractional derivative Zener model of coupled vehicle-track system. Vehicle System Dynamics 2020, 58, 864–889. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos, Solitons & Fractals 2020, 135, 109811. [Google Scholar]
- Ghanbari, B. A fractional system of delay differential equation with nonsingular kernels in modeling hand-foot-mouth disease. Advances in Difference Equations 2020, 2020, 536. [Google Scholar] [CrossRef]
- Farges, C.; Moze, M.; Sabatier, J. Pseudo state feedback stabilization of commensurate fractional order systems. In Proceedings of the 2009 European Control Conference (ECC). IEEE; 2009; pp. 3395–3400. [Google Scholar]
- Zhang, X.; Lin, C.; Chen, Y.Q.; Boutat, D. A unified framework of stability theorems for LTI fractional order systems with 0< α < 2. IEEE Transactions on Circuits and Systems II: Express Briefs 2020, 67, 3237–3241. [Google Scholar]
- Cheng, Y.; Hu, T.; Li, Y.; Zhang, X.; Zhong, S. Delay-dependent consensus criteria for fractional-order Takagi-Sugeno fuzzy multi-agent systems with time delay. Information Sciences 2021, 560, 456–475. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.X.; Zhang, X. Fuzzy control of singular fractional order multi-agent systems with actuator saturation. Information Sciences 2024, 665, 120397. [Google Scholar] [CrossRef]
- Zamani, H.; Khandani, K.; Majd, V.J. Fixed-time sliding-mode distributed consensus and formation control of disturbed fractional-order multi-agent systems. ISA Transactions 2023, 138, 37–48. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Pedrycz, W.; Yang, S.H.; Boutat, D. Consensus of TS fuzzy fractional-Order, singular perturbation, multi-agent systems. Fractal and Fractional 2024, 8, 523. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Wang, Y.; Zhang, K. Leader-following consensus conditions for fractional-order descriptor uncertain multi-agent systems with 0< α< 2 via output feedback control. Journal of the Franklin Institute 2020, 357, 2263–2281. [Google Scholar]
- Zhang, X.; Han, Z. Static and dynamic output feedback control for polytopic uncertain fractional order systems with 0< μ< 1. International Journal of Control, Automation and Systems 2023, 21, 52–60. [Google Scholar]
- N’doye, I.; Voos, H.; Darouach, M.; Schneider, J.G. Static output feedback H∞ control for a fractional-order glucose-insulin system. International Journal of Control, Automation and Systems 2015, 13, 798–807. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Peaucelle, D. From static output feedback to structured robust static output feedback: A survey. Annual reviews in control 2016, 42, 11–26. [Google Scholar] [CrossRef]
- Wei, Y.; Peter, W.T.; Yao, Z.; Wang, Y. The output feedback control synthesis for a class of singular fractional order systems. ISA Transactions 2017, 69, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, D.; Pan, F. Output consensus for fuzzy singular multi-agent fractional order systems with actuator saturation. IEEE Transactions on Circuits and Systems II: Express Briefs 2022, 69, 3465–3469. [Google Scholar] [CrossRef]
- Liang, S.; Wei, Y.H.; Pan, J.W.; Gao, Q.; Wang, Y. Bounded real lemmas for fractional order systems. International Journal of Automation and Computing 2015, 12, 192–198. [Google Scholar] [CrossRef]
- Padula, F.; Alcántara, S.; Vilanova, R.; Visioli, A. H∞ control of fractional linear systems. Automatica 2013, 49, 2276–2280. [Google Scholar] [CrossRef]
- Li, H.; Yang, G.H. Dynamic output feedback H∞ control for fractional-order linear uncertain systems with actuator faults. Journal of the Franklin Institute 2019, 356, 4442–4466. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Basin, M.V. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
- Wang, Z.; Xue, D.; Pan, F. Admissible H∞ control of fuzzy singular fractional order multi-agent systems with external disturbances. IEEE Transactions on Automation Science and Engineering 2023. [Google Scholar] [CrossRef]
- An, C.; Su, H.; Chen, S. H∞ consensus for discrete-time fractional-order multi-agent systems with disturbance via Q-learning in zero-sum games. IEEE Transactions on Network Science and Engineering 2022, 9, 2803–2814. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, Z.; Yu, Y.; Guo, L.; Yang, H. Active disturbance rejection control for a pneumatic motion platform subject to actuator saturation: An extended state observer approach. Automatica 2019, 107, 353–361. [Google Scholar] [CrossRef]
- Selvaraj, P.; Sakthivel, R.; Ahn, C.K. Observer-based synchronization of complex dynamical networks under actuator saturation and probabilistic faults. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2018, 49, 1516–1526. [Google Scholar] [CrossRef]
- Yan, Y.; Zhang, H.; Mu, Y.; Sun, J. Fault-tolerant fuzzy-resilient control for fractional-order stochastic underactuated system with unmodeled dynamics and actuator saturation. IEEE Transactions on Cybernetics 2023, 54, 988–998. [Google Scholar] [CrossRef]
- Pan, H.; Yu, X.; Guo, L. Admissible leader-following consensus of fractional-order singular multiagent system via observer-based protocol. IEEE Transactions on Circuits and Systems II: Express Briefs 2018, 66, 1406–1410. [Google Scholar] [CrossRef]
- Fang, H.; Lin, Z.; Hu, T. Analysis of linear systems in the presence of actuator saturation and L2-disturbances. Automatica 2004, 40, 1229–1238. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. In Proceedings of the Computational engineering in systems applications. Lille, France, 1996, Vol. 2, pp. 963–968.
- Lim, Y.H.; Oh, K.K.; Ahn, H.S. Stability and stabilization of fractional-order linear systems subject to input saturation. IEEE Transactions on Automatic Control 2013, 58, 1062–1067. [Google Scholar] [CrossRef]
- Marir, S.; Chadli, M.; Basin, M.V. Bounded real lemma for singular linear continuous-time fractional-order systems. Automatica 2022, 135, 109962. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.X.; Zhang, X. Generalized criteria for admissibility of singular fractional order systems. Fractal and Fractional 2023, 7, 363. [Google Scholar] [CrossRef]
- Xiong, M.; Tan, Y.; Du, D.; Zhang, B.; Fei, S. Observer-based event-triggered output feedback control for fractional-order cyber–physical systems subject to stochastic network attacks. ISA Transactions 2020, 104, 15–25. [Google Scholar] [CrossRef]
- Jin, K.; Zhang, X. Output feedback stabilization of type 2 fuzzy singular fractional-order systems with mismatched membership functions. Soft Computing 2023, 27, 4917–4929. [Google Scholar] [CrossRef]
- Ji, Y.; Qiu, J. Stabilization of fractional-order singular uncertain systems. ISA Transactions 2015, 56, 53–64. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, W. Robust H∞ adaptive output feedback sliding mode control for interval type-2 fuzzy fractional-order systems with actuator faults. Nonlinear Dynamics 2021, 104, 537–550. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z.; Chen, G. On H∞ and H2 performance regions of multi-agent systems. Automatica 2011, 47, 797–803. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





