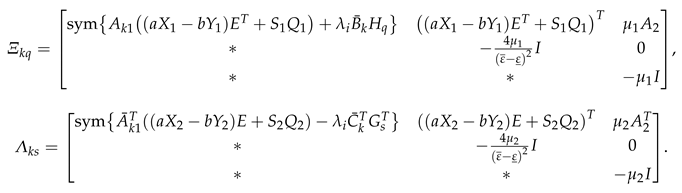Submitted:
29 July 2024
Posted:
31 July 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
- To provide a more accurate portrayal of complex systems in practice, a T-S fuzzy FOSPMAS with is formulated to reduce the difficulty of directly studying nonlinear systems. Compared to integer order systems, the constructed model exhibits more enhanced accuracy and complexity. A fuzzy FOSPS with error as a variable is derived by designing a fuzzy observer-based controller.
- The fuzzy FOSPS is analyzed by transforming it into a fuzzy SFOS using the system augmentation method. In comparison to the existing work [41], the proposed approach not only relaxes the assumption that the fast subsystem matrix must be nonsingular, but also avoids the ill-conditioned issue arising from the parameter .
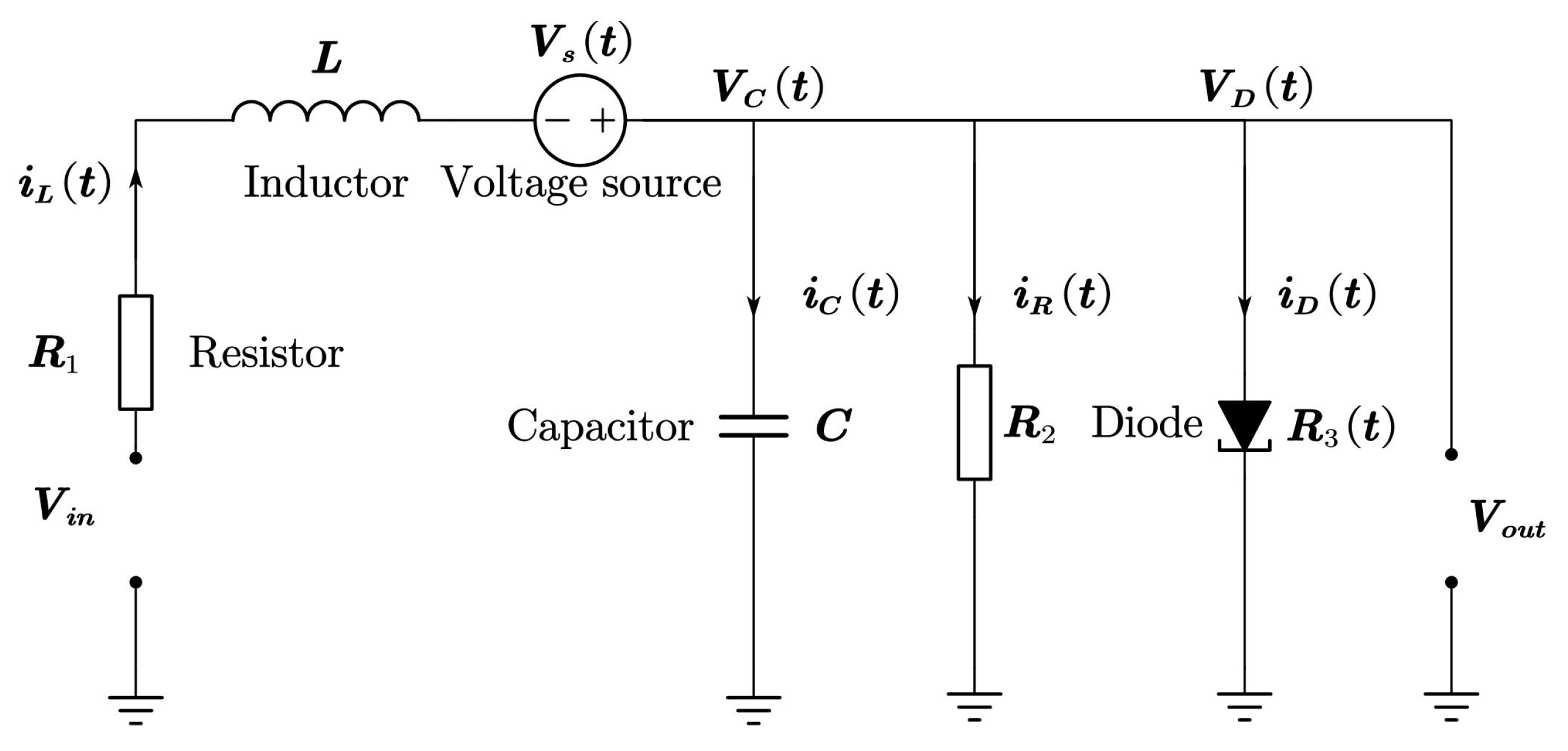
- The consensus conditions for fuzzy FOSPMASs with and are formulated in this study for any , where and are given lower and upper boundaries, respectively. The results are presented based on LMIs without equality constraints, reducing solution difficulties. It is demonstrated through an RLC circuit model that the proposed methods are effective in practice.
2. Preliminaries
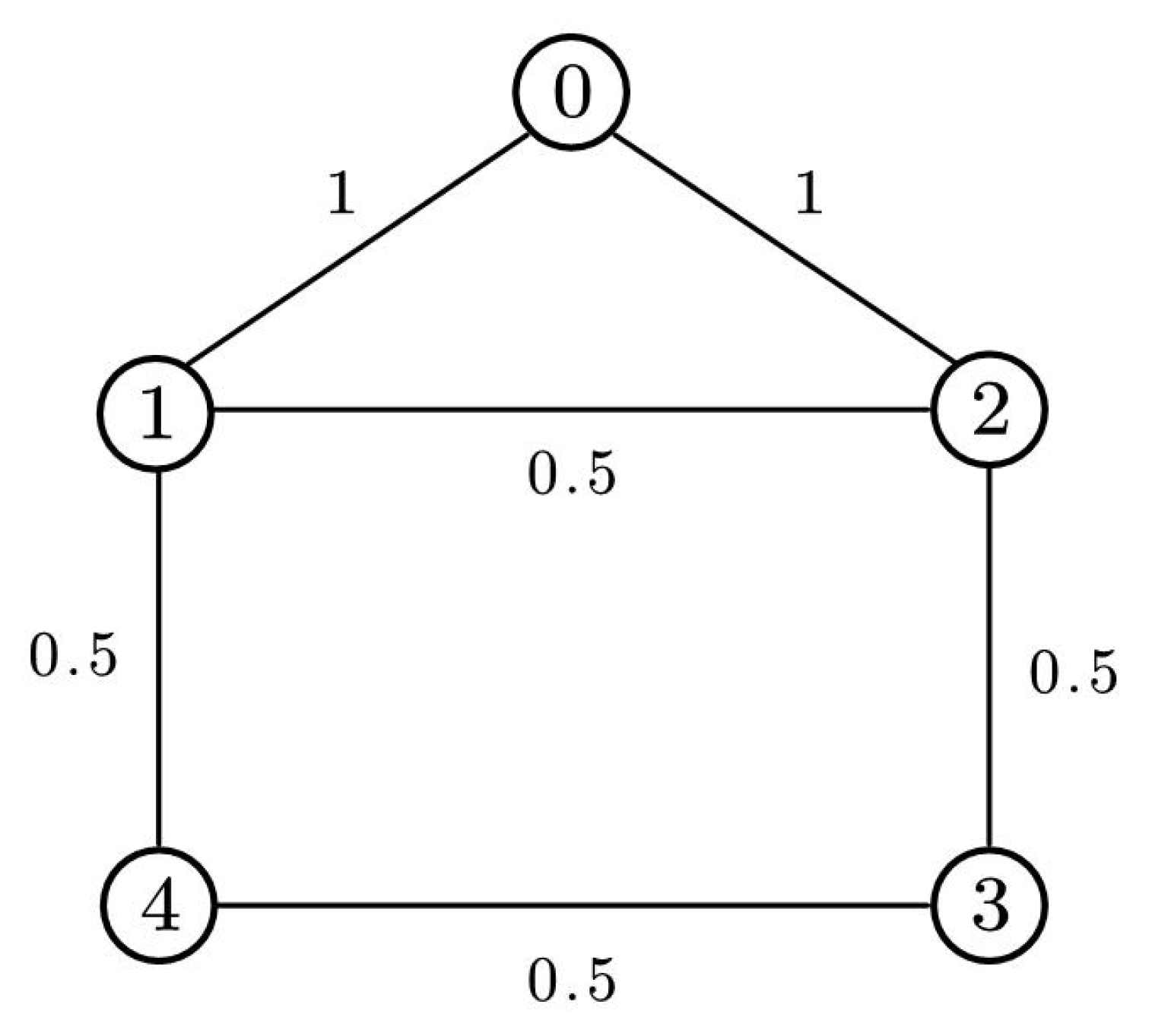
2.1. Graph Theory
2.2. Preliminary Lemmas
3. Main Results
3.1. System Model Description
3.2. Equivalent Transformations
3.3. Consensus Conditions of T-S Fuzzy FOSPMAS


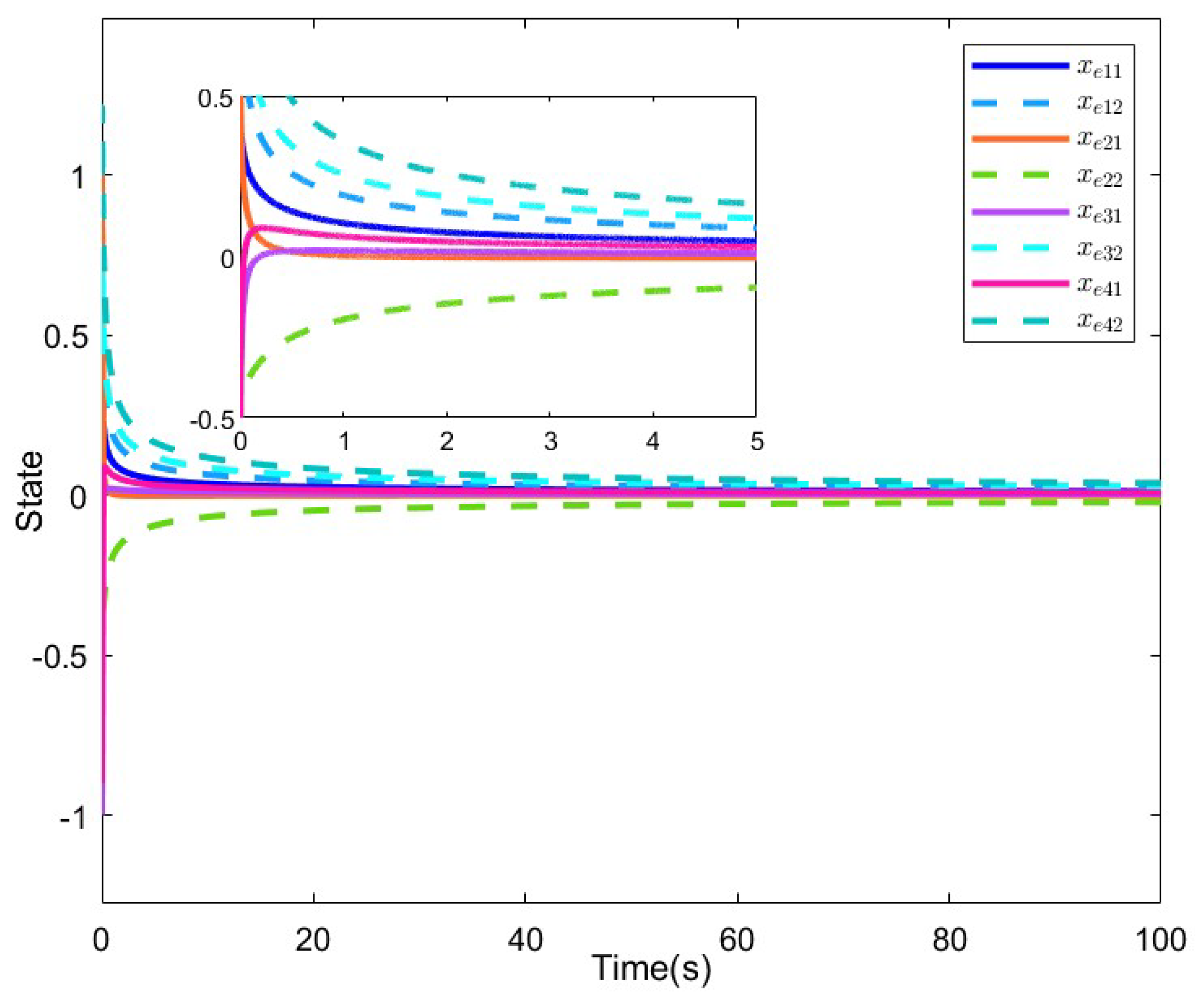
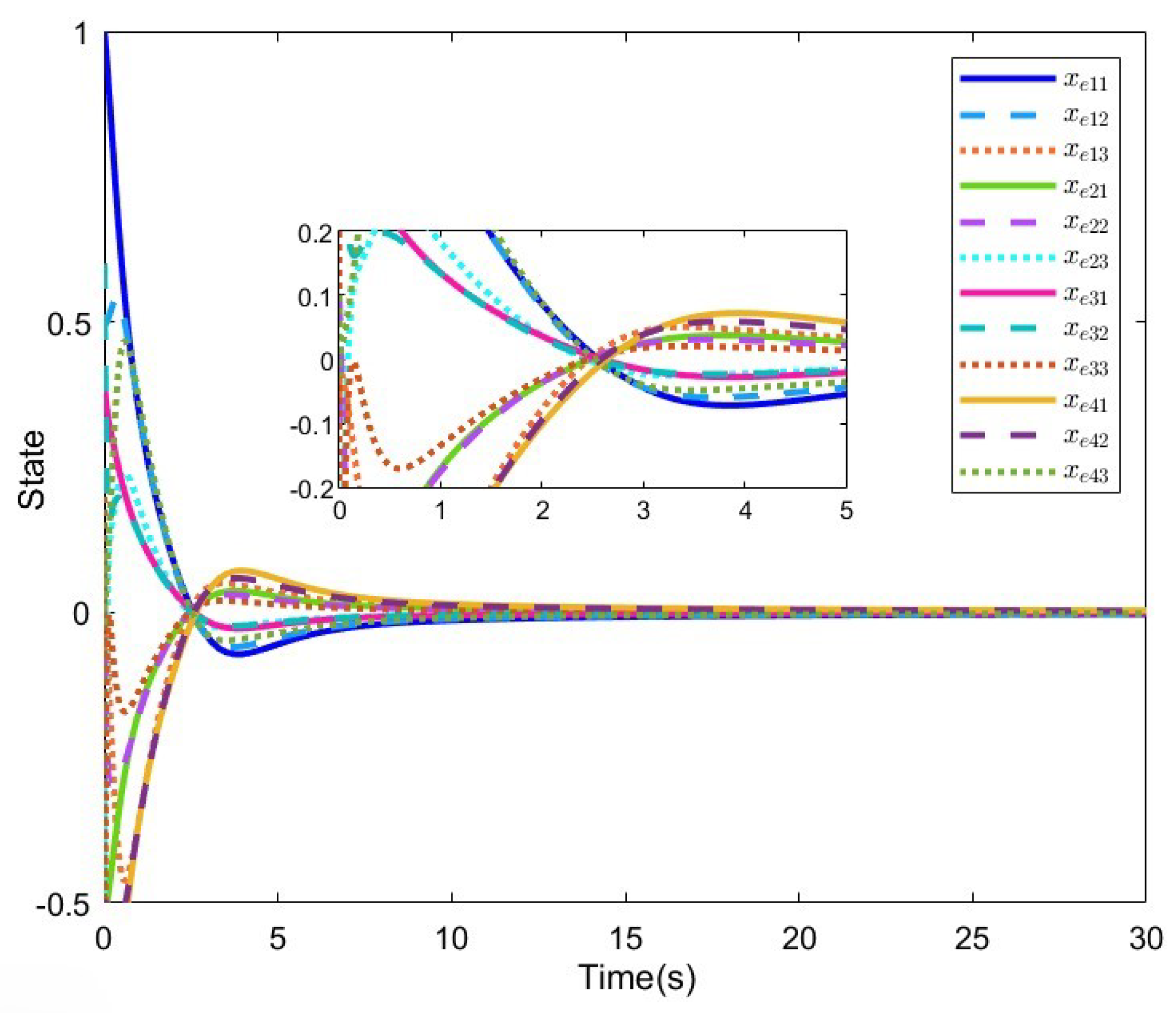
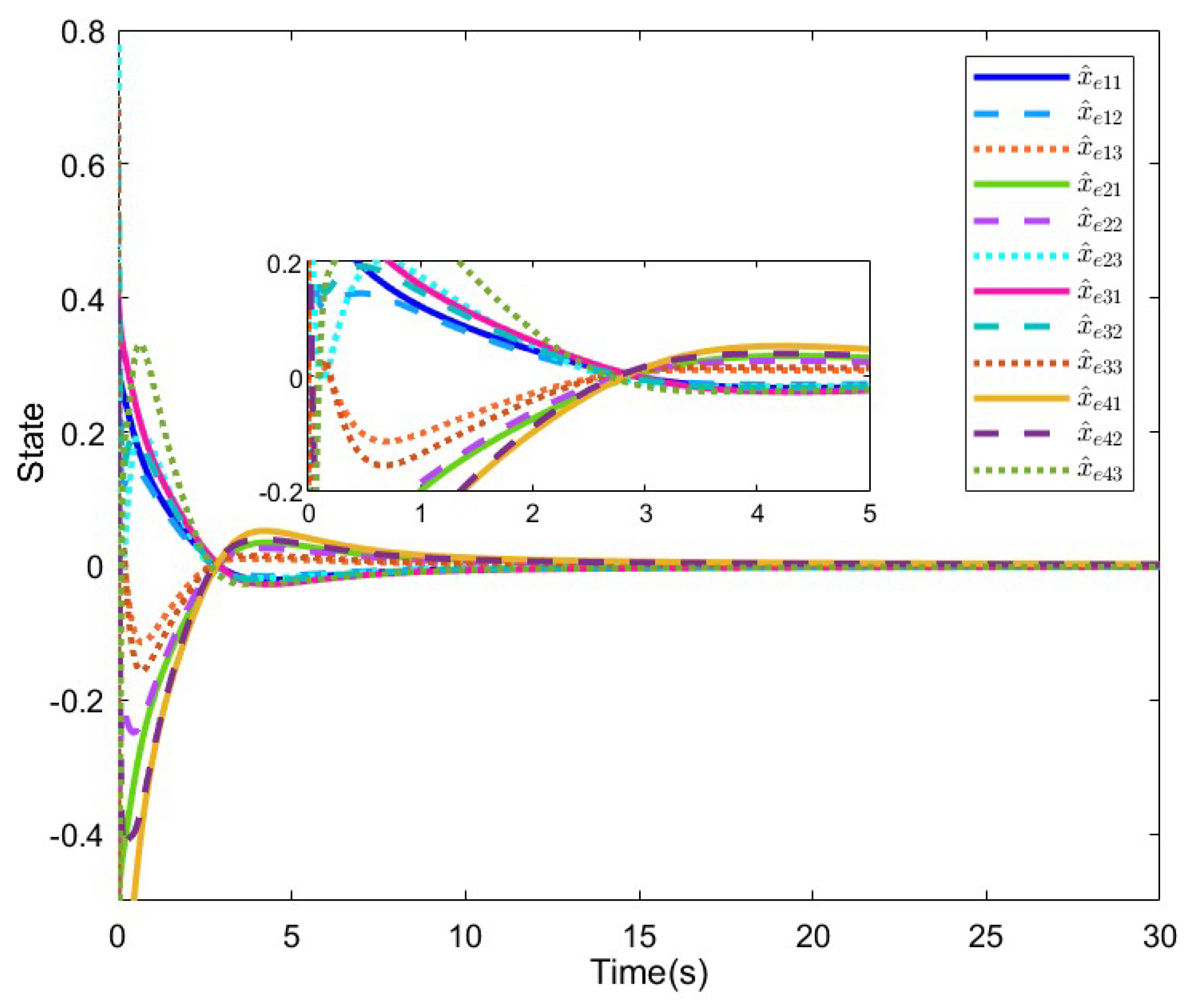
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Santos, G.; Pinto, T.; Praça, I.; Vale, Z. MASCEM: Optimizing the performance of a multi-agent system. Energy 2016, 111, 513–524. [Google Scholar] [CrossRef]
- Jiménez, A.C.; García-Díaz, V.; Bolaños, S. A decentralized framework for multi-agent robotic systems. Sensors 2018, 18, 417. [Google Scholar] [CrossRef] [PubMed]
- Iñigo-Blasco, P.; Diaz-del-Rio, F.; Romero-Ternero, M.C.; Cagigas-Muñiz, D.; Vicente-Diaz, S. Robotics software frameworks for multi-agent robotic systems development. Robotics and Autonomous Systems 2012, 60, 803–821. [Google Scholar] [CrossRef]
- Florez-Lozano, J.; Caraffini, F.; Parra, C.; Gongora, M. Cooperative and distributed decision-making in a multi-agent perception system for improvised land mines detection. Information Fusion 2020, 64, 32–49. [Google Scholar] [CrossRef]
- Yan, Z.W.; Han, L.; Li, X.D.; Dong, X.W.; Li, Q.D.; Ren, Z. Event-triggered formation control for time-delayed discrete-time multi-agent system applied to multi-UAV formation flying. Journal of the Franklin Institute 2023, 360, 3677–3699. [Google Scholar] [CrossRef]
- Zhang, J.X.; Xu, K.D.; Wang, Q.G. Prescribed Performance Tracking Control of Time-Delay Nonlinear Systems With Output Constraints. IEEE/CAA Journal of Automatica Sinica 2024, 11, 1557–1565. [Google Scholar] [CrossRef]
- Zhang, J.X.; Yang, G.H. Low-Complexity Tracking Control of Strict-Feedback Systems With Unknown Control Directions. IEEE Transactions on Automatic Control 2019, 64, 5175–5182. [Google Scholar] [CrossRef]
- Ren, W. On Consensus Algorithms for Double-Integrator Dynamics. IEEE Transactions on Automatic Control 2008, 53, 1503–1509. [Google Scholar] [CrossRef]
- Tian, Y.P.; Liu, C.L. Consensus of Multi-Agent Systems With Diverse Input and Communication Delays. IEEE Transactions on Automatic Control 2008, 53, 2122–2128. [Google Scholar] [CrossRef]
- Wen, G.H.; Duan, Z.S.; Yu, W.W.; Chen, G.R. Consensus in multi-agent systems with communication constraints. International Journal of Robust and Nonlinear Control 2012, 22, 170–182. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, G.; Yan, H.C.; Chen, Q.J. Observer-Based Output Feedback Event-Triggered Control for Consensus of Multi-Agent Systems. IEEE Transactions on Industrial Electronics 2014, 61, 4885–4894. [Google Scholar] [CrossRef]
- Tan, M.C.; Song, Z.Q.; Zhang, X.M. Robust leader-following consensus of cyber-physical systems with cyber attack via sampled-data control. ISA Transactions 2021, 109, 61–71. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of fractional calculus in physics; World scientific, 2000.
- Ye, Y.Y.; Su, H.S. Leader-following consensus of general linear fractional-order multiagent systems with input delay via event-triggered control. International Journal of Robust and Nonlinear Control 2018, 28, 5717–5729. [Google Scholar] [CrossRef]
- Ye, Y.Y.; Su, H.S. Leader-following consensus of nonlinear fractional-order multi-agent systems over directed networks. Nonlinear Dynamics 2019, 96, 1391–1403. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Tan, Y.Y.; Zhang, Y.J.; Jiang, W. Consensus analysis of fractional-order nonlinear multi-agent systems with distributed and input delays. Neurocomputing 2019, 329, 46–52. [Google Scholar] [CrossRef]
- Yang, R.; Liu, S.; Li, X.Y.; Zhao, X.W.; Pan, G. Consensus of fractional-order delayed multi-agent systems in Riemann-Liouville sense. Neurocomputing 2020, 396, 123–129. [Google Scholar] [CrossRef]
- Hu, T.T.; He, Z.; Zhang, X.J.; Zhong, S.M. Leader-following consensus of fractional-order multi-agent systems based on event-triggered control. Nonlinear Dynamics 2020, 99, 2219–2232. [Google Scholar] [CrossRef]
- Bahrampour, E.; Asemani, M.H.; Dehghani, M.; Tavazoei, M. Consensus control of incommensurate fractional-order multi-agent systems: An LMI approach. Journal of the Franklin Institute 2023, 360, 4031–4055. [Google Scholar] [CrossRef]
- Fridman, E. Robust sampled-data H∞ control of linear singularly perturbed systems. IEEE Transactions on Automatic control 2006, 51, 470–475. [Google Scholar] [CrossRef]
- Yang, C.Y.; Zhang, L.L.; Sun, J. Anti-windup controller design for singularly perturbed systems subject to actuator saturation. IET Control Theory & Applications 2016, 10, 469–476. [Google Scholar]
- Saksena, V. R; O’reilly, J.; Kokotovic, P.V. Singular perturbations and time-scale methods in control theory: survey 1976-1983. Automatica 1984, 20, 273–293. [Google Scholar] [CrossRef]
- Naidu, D. Singular perturbations and time scales in control theory and applications: An overview. Dynamics of Continuous Discrete and Impulsive Systems Series B 2002, 9, 233–278. [Google Scholar]
- Wang, Y.Y.; Shi, P.; Yan, H.C. Reliable control of fuzzy singularly perturbed systems and its application to electronic circuits. IEEE Transactions on Circuits and Systems I: Regular Papers 2018, 65, 3519–3528. [Google Scholar] [CrossRef]
- Munje, R.; Patre, B.; Tiwari, A.; Munje, R.; Patre, B.; Tiwari, A. State feedback control using linear quadratic regulator. Investigation of Spatial Control Strategies with Application to Advanced Heavy Water Reactor 2018, 61–77. [Google Scholar]
- Xia, G.Q.; Zhang, Y.; Zhang, W.; Chen, X.M.; Yang, H.Y. Multi-time-scale 3-D coordinated formation control for multi-underactuated AUV with uncertainties: Design and stability analysis using singular perturbation methods. Ocean Engineering 2021, 230, 109053. [Google Scholar] [CrossRef]
- Nagarale, R.M.; Patre, B.M. Composite fuzzy sliding mode control of nonlinear singularly perturbed systems. ISA Transactions 2014, 53, 679–689. [Google Scholar] [CrossRef]
- Litkouhi, B.; Khalil, H. Multirate and composite control of two-time-scale discrete-time systems. IEEE Transactions on Automatic Control 1985, 30, 645–651. [Google Scholar] [CrossRef]
- Yang, C.Y.; Che, Z.Y.; Shen, L.P. Integral sliding mode control for singularly perturbed systems with matched disturbances. 2017 Chinese Automation Congress (CAC), 2017, pp. 2452-2456. [CrossRef]
- Gao, Y.B.; Sun, B.H.; Lu, G.P. Passivity-Based Integral Sliding-Mode Control of Uncertain Singularly Perturbed Systems. IEEE Transactions on Circuits and Systems II: Express Briefs 2011, 58, 386–390. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Y.Y.; Wang, Z.M. H∞ observer-based sliding mode control for singularly perturbed systems with input nonlinearity. Nonlinear Dynamics 2016, 85, 573–582. [Google Scholar] [CrossRef]
- Fridman, E. Effects of small delays on stability of singularly perturbed systems. Automatica 2002, 38, 897–902. [Google Scholar] [CrossRef]
- Ben Rejeb, J.; Morărescu, I.-C.; Daafouz, J. Control design with guaranteed cost for synchronization in networks of linear singularly perturbed systems. Automatica 2018, 91, 89–97. [Google Scholar] [CrossRef]
- Tognetti, E.S.; Calliero, T. R; Morărescu, I.-C.; Daafouz, J. Synchronization via output feedback for multi-agent singularly perturbed systems with guaranteed cost. Automatica 2021, 128, 109549. [Google Scholar] [CrossRef]
- Xu, J.; Niu, Y.G.; Zou, Y.Y. Finite-time consensus for singularity-perturbed multiagent system via memory output sliding-mode control. IEEE Transactions on Cybernetics 2021, 52, 8692–8702. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Q.; Wu, H.Q.; Cao, J.D. Global Mittag-Leffler consensus for fractional singularly perturbed multi-agent systems with discontinuous inherent dynamics via event-triggered control strategy. Journal of the Franklin Institute 2021, 358, 2086–2114. [Google Scholar] [CrossRef]
- Yang, C.Y.; Zhang, Q.L. Multiobjective Control for T-S Fuzzy Singularly Perturbed Systems. IEEE Transactions on Fuzzy Systems 2009, 17, 104–115. [Google Scholar] [CrossRef]
- Chen, J.X.; Sun, Y.G.; Min, H.B.; Sun, F.C.; Zhang, Y.G. New results on static output feedback H∞ control for fuzzy singularly perturbed systems: a linear matrix inequality approach. International Journal of Robust and Nonlinear Control 2013, 23, 681–694. [Google Scholar] [CrossRef]
- Visavakitcharoen, A.; Assawinchaichote, W.; Shi, Y.; Angeli, C. Event-triggered fuzzy integral control for a class of nonlinear singularly perturbed systems. ISA Transactions 2023, 139, 71–85. [Google Scholar] [CrossRef]
- Zhang, X.F.; Han, Z.R. Output feedback control of fractional order Takagi-Sugeno fuzzy singularly perturbed systems. Journal of Vibration and Control 2022, 28, 3162–3172. [Google Scholar] [CrossRef]
- Koskie, S.; Coumarbatch, C.; Gajic, Z. Exact slow-fast decomposition of the singularly perturbed matrix differential Riccati equation. Applied Mathematics and Computation 2010, 216, 1401–1411. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Computational engineering in systems applications. Lille, France, 1996, Vol. 2, pp. 963-968.
- Zhang, X.F.; Chen, Y.Q. Admissibility and robust stabilization of continuous linear singular fractional order systems with the fractional order α: The 0<α<1 case. ISA Transactions 2018, 82, 42–50. [Google Scholar]
- Marir, S.; Chadli, M.; Bouagada, D. New admissibility conditions for singular linear continuous-time fractional-order systems. Journal of the Franklin Institute 2017, 354, 752–766. [Google Scholar] [CrossRef]
- Lee, H.J.; Park, J.B.; Chen, G.R. Robust fuzzy control of nonlinear systems with parametric uncertainties. IEEE Transactions on fuzzy systems 2001, 9, 369–379. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).