1. Introduction
In the universe, it is very common to collide and influence between galaxies. A galaxy consists of approximately 100 billion planets. Therefore, it is generally believed that in a frontal impact between galaxies, countless interplanetary collisions will occur. In fact, in such an impact, the probability of two planets colliding is almost zero. This is because although there are countless planets in a galaxy, the density of the planet is actually very small due to its huge size. That is, the diameter of the planet is very small relative to the average distance between the planets. This means that when two galaxies collide, the planets in their respective galaxies will pass through each other without having a big impact on each other! However, the space between planets in ordinary galaxies is not empty, but is filled with gas and dust. These matter will affect each other under the action of gravity during galaxy collisions. The collision galaxy will continuously draw gas and dust in the other galaxy. During this process, there will also be friction between the gases, resulting in shock waves. This process will usually last for millions of years. When we catch up with the two galaxies in the fusion process, we can capture a moment at a certain stage of the entire process. In collision galaxies, galaxies only occupy a small part of the total mass of the galaxy cluster, and the main components that make up the total mass of the galaxy cluster are huge dark matter halos and hot gas clouds. The thermal radiation of the gas cloud can reach hundreds of millions of degrees Celsius, which makes the X-rays it emits very strong. These X-rays can be observed through specialized x-ray telescopes. For the visible light band, most collision galaxies have lens phenomena. The traditional view believes that the mass distribution of intermediate celestial bodies can be calculated based on the degree of bend of the gravitational lens on the light of the source celestial body. Generally, in collision galaxies, the mass distribution of intermediate celestial bodies inverted by gravitational lenses is separated from the distribution of hot gases observed through x-rays [
1]. This is the problem of the separation of the distribution center of matter inverted by the hot gas as the main substance in galaxy collisions and the gravitational lens.
2. Common Collision Galaxy Examples
2.1. Bullet Galaxy
Bullet galaxy cluster [
2](1E0657-56) is a high-speed head-on collision between two galaxy clusters. In the figure, the blue color represents the distribution of matter (dark matter) measured by a gravitational lens, and the red color shows the spatial distribution of non-luminescent hot gas measured by the Chandra X-ray space telescope. It can be clearly seen that the distribution of matter (dark matter) observed in the gravitational lens is significantly different from the distribution of hot gas substances that do not emit light.
Figure 1.
The collision of the Bullet Cluster (1E0657-558).
Figure 1.
The collision of the Bullet Cluster (1E0657-558).
2.2. MACS J0025.4-1222 Galaxy
MACS J 0025.4-1222is a galaxy cluster formed by the collision of two galaxy clusters and is part of the Large-scale Galaxy Cluster Survey (MACS). The images shown are taken by the Hubble Space Telescope ACS and WFPC 2 detectors and the Chandra ACIS detectors respectively. The visible light image from Hubble shows gravitational lenses, which allow astronomers to infer the distribution of total mass (dark matter and normal matter) (in blue). In X-rays, the distribution of normal substances mainly occurs in the form of hot gases (pink). Its distribution is mapped accurately from Chandra's data. From the figure, we can see that the center of mass inversion of gravitational lenses is separated from the center of distribution of non-luminescent hot gas material that is the main material of the galaxy.
Figure 2.
Collision between MACS J0025.4-1222.
Figure 2.
Collision between MACS J0025.4-1222.
2.3. Abell 2744: Pandora Cluster
Figure 3.
Abell 2744: Pandora Galaxy Cluster.
Figure 3.
Abell 2744: Pandora Galaxy Cluster.
Abell 2744is one of the Pandora galaxies, connected with galaxies. The X-rays (labeled in red) emitted by the hot gases of the galaxies are different from those of dark matter. Using the gravity lens effect to distort the image background galaxy, it was concluded that dark matter (labeled as blue) accounts for 75% of the mass in this galaxy cluster. The chaos originated from the slow collision of at least four galaxies over the past billions of years. This image combines the optical data of the Huber Space Telescope and the super-large telescope, as well as the X-ray images of the Qianzhuo Observatory. The researchers found that in the visible light band, the mass of member galaxies in images observed by the Very Large Telescope and the Hubble Space Telescope accounted for less than 5% of the total mass of the Abel-2744 galaxy. About 20% of the other mass is diffuse gaseous substances, which are in high temperatures and
emit strong X-ray radiation, thus being observed by Chandra X-ray telescope. What remains is dark matter. The researchers said that it appears that the separation of hot gas and dark matter was caused during the impact, so they were temporarily in separate positions. The impact also causes these matter to separate from galaxy matter. A shock shock wave area can be observed near the center of the galaxy group, which is the area where the hot gases of the two original galaxy groups collide with each other at high speed. It was obvious that dark matter passed through without any effect during this impact. In other locations of this galaxy cluster, galaxies and dark matter can be seen, but hot gases cannot be seen. The gas here may have been stripped off during the impact, leaving only some thin marks. And outside the galaxy group, there are more special clues. There is a large amount of dark matter here, but there is very little visible matter. It can be seen that all matter is ejected further out of the outer edge position, away from the evenly distributed area.
2.4. Abell 520 galaxy cluster
Figure 4.
Abell 520 galaxy cluster.
Figure 4.
Abell 520 galaxy cluster.
Multi-band synthetic images of Abell 520galaxy clusters, color matching: green, X-ray (high temperature plasma); orange: photometric distribution (low temperature matter); white, visible light image of galaxy; blue, dark matter distribution.
2.5. NGC 6338
Using optical observations from NASA's Chandra X-ray Observatory, ESA's XMM-Newton, the Giant meter-wave radio telescope (GMRT), and the Apache Point Observatory in New Mexico, a team of astronomers discovered two groups of galaxies at alarming speeds, about 4 million miles per hour. This is probably the most violent collision between two galaxy groups so far. The system is called NGC 6338and is about 380 million light-years away from the Earth. This composite image contains X-ray data from Chandra (shown in red), showing hot gases at temperatures up to about 20 million degrees Celsius, and cooler gases detected with Chandra and XMM (shown in blue), which also emit X-rays. Chandra data combines optical data from Sloan Digital Survey to show galaxies and stars in white. Researchers estimate that the total mass contained in NGC 6338 is about 100 trillion times the mass of the sun. This significant weight, about 83% is dark matter, 16% is hot gas, and 1% is stars. New Chandra and XMM-Newton data also show that the left and right sides of the cold core and the gas between them appear to have been heated by the shock wave front to form due to the collision of two galaxy clusters.
There are many similar practical observation examples, and these phenomena reflect a common problem: the center of mass inversion of gravitational lenses and the center of distribution of non-luminescent hot gases that are the main matter of galaxy.
3. The meaning of separation of mass centers in galaxy collisions
The mass center of matter inversion by gravitational lenses is separated from the distribution center of non-luminescent hot gas material that is the main matter of the galaxy. This shows that the mass of the celestial body inversion by the gravitational lens does not include the mass of the hot gas, that is, the hot gas as the main mass in the collision galaxy has not contributed to the formation of the gravitational lens. To be honest, a large number of non-luminescent hot gas (pre-shaped celestial bodies) do not bend the visible light passing by it, that is, the hot gas as the main mass in the collision galaxy has not bend the space-time around it. This is inconsistent with the conjecture of the general theory of space-time view. A reasonable explanation is: gravity bends the direction of movement of massed objects. When massless visible light passes by the massive luminous planet, it continuously acts with the electromagnetic waves emitted by the massive luminous planet, bends the visible light. Such a large amount of non-luminescent gas is reasonable to not bend visible light.
3.1. Einstein did not describe the space-time structure in detail when he published the general theory of relativity.
When Einstein published the general theory of relativity, he did not describe the structure of space-time in detail, nor did he describe how gravity bends space-time in detail. Therefore, Einstein's general theory of relativity can only be used as a hypothesis. In recent years, the research on space-time structure has been more in-depth in the circle quantum theory [
7]. Under this theory, space-time is described as a space-time geometry paved with a spin network woven in a contextually independent and woven by a relational cycle.
3.2. The microscopic mechanism of gravitational lens cannot be explained
For mass objects, gravity deflects the direction of movement of the object. But for visible light, light is propagated by photons, and photons have no mass; gravity is propagated by gravitons, and gravitons and photons basically do not act, so gravity and light do not act. Gravitational bending light cannot be explained by microscopic mechanism. We know that light can interfere, diffraction, and interfere with the same frequency, so light will have mutual influence when intersect. "Explanation of the concurrent frequency interfering of light bending" believes that intersecting light will interact with each other and affect the propagation direction of light. Generally speaking, the degree of light deflection is too small, and we cannot observe that only when light passes by a large-scale luminous planet, the visible light is continuously affected by the electromagnetic waves emitted by the luminous planet, and will form an arc around the luminous planet. This arc is just like gravitational curved light, which is why people form gravitational curved light. "Same-frequency mutual interference explanation of light bending" believes that when visible light passes by the luminous planet, its bending degree is proportional to the planet's luminous brightness and is inversely proportional to the square of the distance from the center of the planet.
3.3. Gravitational lens inversion of dark matter in collision galaxies
Astronomical observations show that collision galaxies are generally far away from the Earth. The reason we can observe these galaxies is because the brightness of the planets in these galaxies is much higher than that of the sun. Statistics on some planets show that the brightness/mass ratio of long-distance planets is tens of thousands of times that of the sun. The brightness of distant galaxies is 10 billion times brighter than that of the sun. In this way, the degree of bending of the light passing by these planets is explained by the inter-light interference, which is equivalent to the use of a "gravity lens" to explain by tens of thousands of times larger. The material inverted by the curved light is explained by tens of thousands of times less than that in the use of a "gravity lens", and there are fewer in the distant galaxies. In this way, there is no dark matter in the principle of "gravity lens". The inter-interference explanation of light interfering in long-distance galaxy collision observations will not invert dark matter, which is in line with the reality of astronomical observations. The low proportion of dark matter in multi-star systems also illustrates this problem.
4. Interpretation of the co-interference of light bending
We know that gravity is propagated by gravitons, and light is propagated by photons. Gravitational and photons basically do not act, so gravity does not bend light. Light can interfere, diffraction, and homofrequency interference, which means that photons and photons can act, and photons and photons scattering (collision) can change the propagation direction of photons. Generally speaking, this change is too small and we cannot observe it at all. When a column of visible light passes next to a massive luminous planet, it is subject to the continuous action of electromagnetic waves emitted by the massive luminous planet, and it will form an arc around the massive luminous planet, which is exactly the "gravity curved light", which is why people form the impression of "gravity curved light" and "gravity lens".
Traditional photons are defined as fh, where f is the frequency of electromagnetic waves and h is the Planck constant. In this article, we regard a wave packet of electromagnetic waves as a photon, and photon scattering (collision) as the collision of two completely elastic spheres. The properties of photons and photons are exactly the same as kinetic energy. Therefore, photons and photons are scattering (collision) are equivalent to interchange photons. After interchange, other properties of photons remain unchanged, but the propagation direction of photons will change. Detailed analysis of the changes in the direction after the scattering (collision) between photons and photons and the average magnitude of the deflection angle involves the analysis and probability of various collision situations. Here (reverse) analysis is performed based on the bending of light when it passes by the sun.
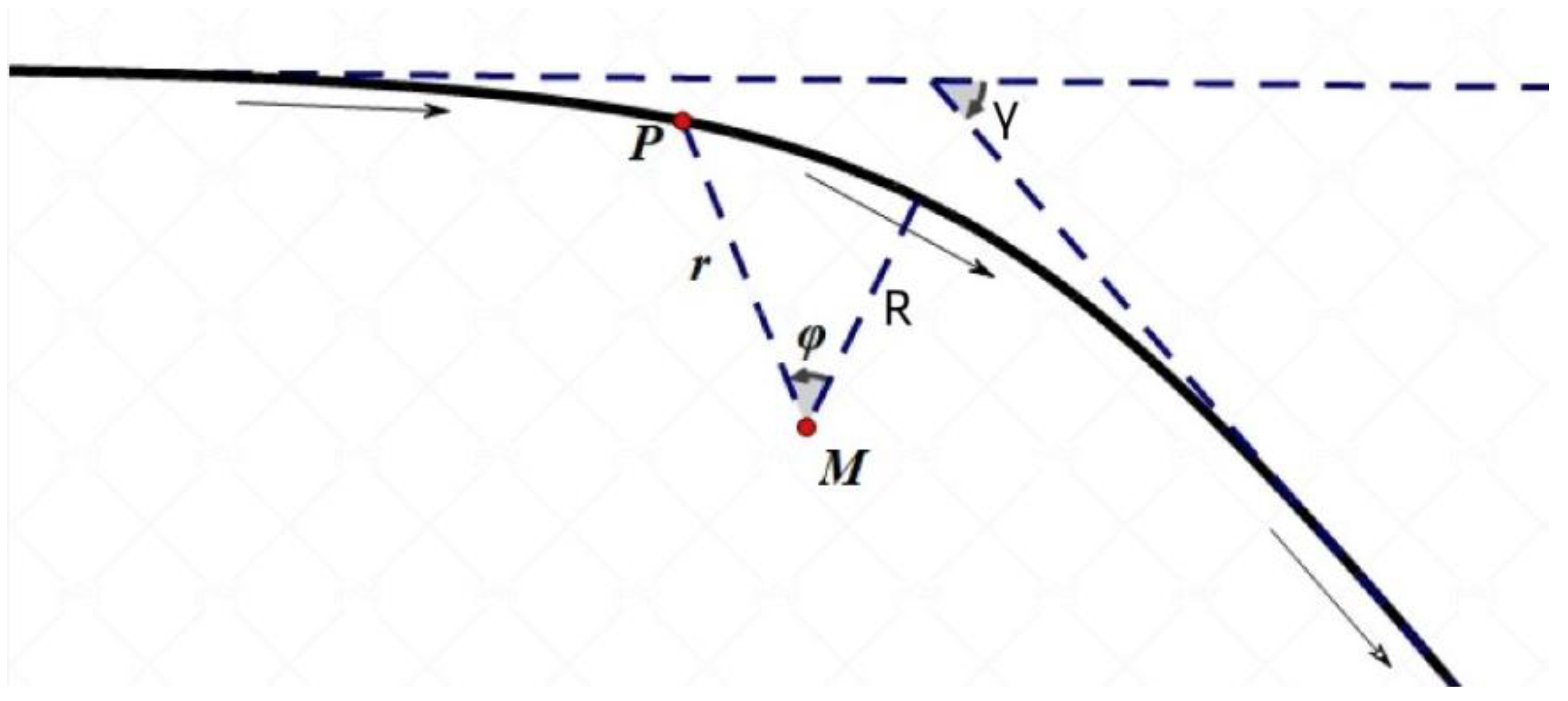
Figure 6 is a schematic diagram of the sun's curved light. Visible light comes toward the sun from infinite distance. Suppose the closest distance between the visible light and the sun is R, and the deflection angle after passing through the sun is γ. The polar coordinates (r,φ) are established with the sun as the pole and the rays pointed from the sun to the closest visible light to the celestial body as the polar axis. Suppose the speed of light is c and the Planck constant is h.
The number of photons passed by light per unit time is related to the luminous flux. Treat light particles as mass particles. Assume that the equivalent mass of particles passing by visible light per unit time is m0, and the number of photons passing by visible light per unit time is N0. The energy (kinetic energy) carried by these photons is E0, the brightness of sunlight is Es, the number of photons at the intersection of visible light per unit time is Nsi, and the energy (kinetic energy) carried by the sunlight photon is Esi. Obviously:
When visible light intersects sunlight, the force of photons interacting at the intersection is proportional to the number of photons interacting:
In the above formula, k1 is the coefficient between the number of photons acting and the force, and k2 is the coefficient between the energy carrying of photons and the force.
Newton's second law points out that the rate of change of the momentum of an object is equal to the combined force of all external forces acting on the object, i.e.
Assume that the momentum perpendicular to the direction of light propagation is ,
Angular momentum of a particle
Here w is the angular velocity. Since the angular momentum L is conserved, the
The combination (5) (8) formula and the deflection angle γ is used as a small amount to obtain
Einstein's mass-energy equation has
Get the deflection angle:
In the process of light coming from infinity to infinity, points are
In the formula, the deflection angle of γ light, the coefficients related to the wavelength, Es is the brightness (luminescence intensity) of the sun, and R is the shortest distance between the visible light and the center of the planet when the light passes by the planet. This conclusion can be generalized to any planet in the universe. The factors that affect the degree of light bending can be seen from the formula: (1) the wavelength of visible light, (2) the luminous intensity of the corresponding wavelength of the front celestial body, and (3) the distance between the visible light and the front celestial body.
The total amount of radiation of the sun (photometric) is about 3.845×10^26 watts (W). The brightness is the amount of radiation in a single direction, and the brightness E = luminosity L/sphere area 4πr^2. The solar radiation energy is within the entire electromagnetic spectrum region from cosmic rays, X-rays to infinite radio waves, and more than 99% is between 0.15 and 4.0 microns in wavelength. About 50% of the solar radiation energy is in the visible spectrum region (wavelength 0.4 to 0.76 microns), 7% is in the ultraviolet spectrum region (wavelength <0.4 microns), 43% is in the infrared spectrum region (wavelength >0.76 microns), and the maximum energy is at the wavelength 0.475 microns. The radius of the sun is 6.955×10^5 km (as for the photosphere). Considering the distance between visible light and the sun, R is 697,000 km. During the total solar eclipse in 1919, the observation results of two observation teams led by Eddington and others were 1.61″ and 1.98″ respectively, with an average of 1.795″. 1 watt = 1 joule/second = 1 Newton meter/second, so the coefficient of visible light is:
Bring (14) into (13), calculate the angle of the planet's luminous intensity to the visible light deflection is approximately:
Planet brightness E (luminous intensity) unit: watts (joules/second), distance R unit: meters, γ is the light deflection angle, unit: ″.
The explanation of the co-frequency mutual interference of light curves does not invert dark matter in collision galaxies, and this result is consistent with astronomical observations.
5. Non-distance redshift of lens galaxies
In 1923, when studying the experiment of scattering x-rays through physical matter, American physicist Compton discovered a new phenomenon, that is, in addition to the x-ray with the original wavelength λ0, the scattered light also produces x-ray with the wavelength λ≧λ0, and the increment of its wavelength varies with the scattering angle. This phenomenon is called the Compton effect [
10]. Compton used Einstein's photon theory to fully explain this experimental phenomenon from the perspective of photons and electrons collision based on energy conservation and momentum conservation.
Figure 7 is a schematic diagram of the bending analysis of visible light passing by a large-scale luminous planet. In
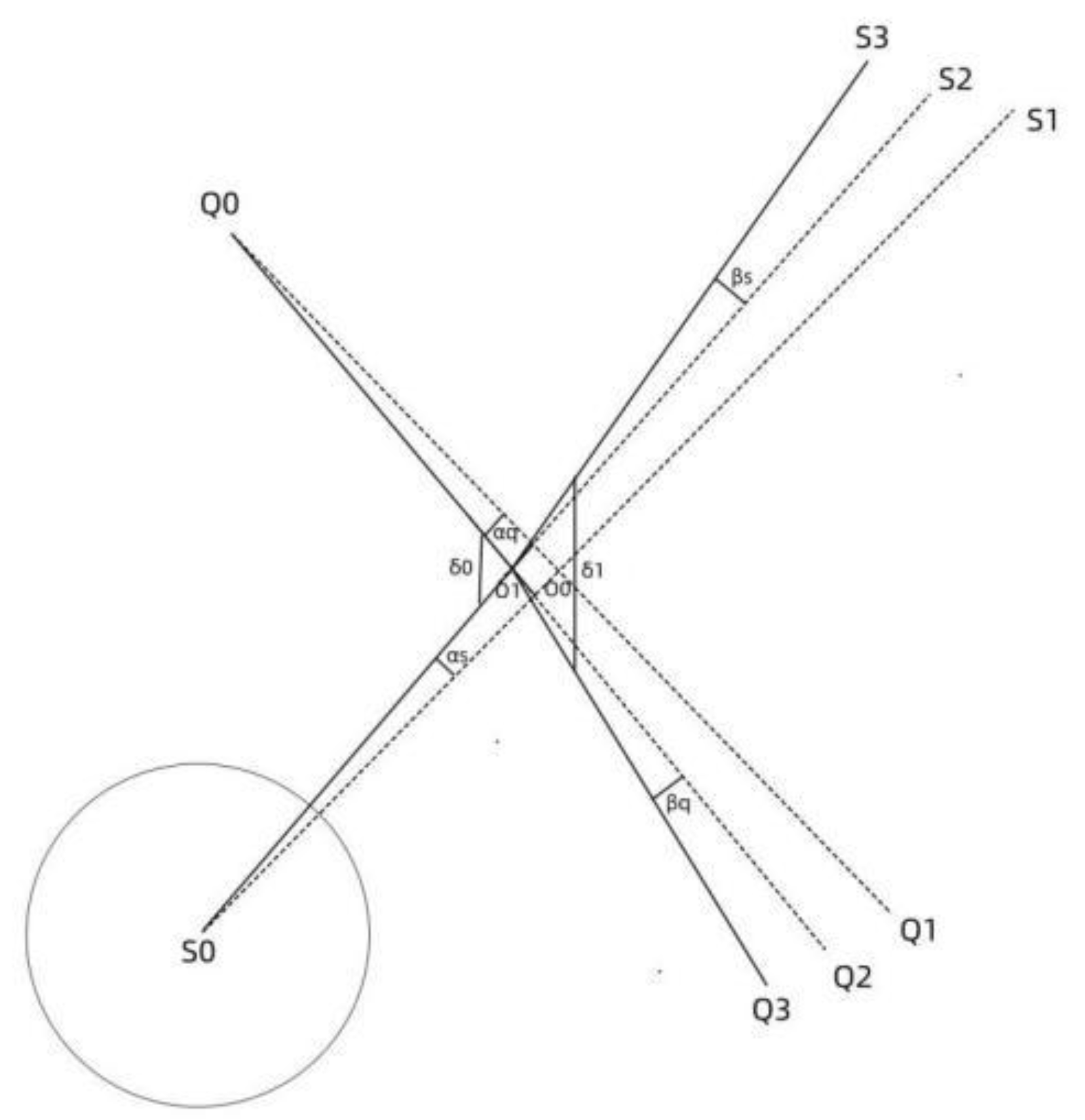
the figure, Q0Q1 is a light that spreads in the universe. S0 is a planet encountered during the light propagation process. S0 will emit light in all directions. The light emitted by S0 will have many lights intersecting with Q0Q1. These intersecting lights will have an impact on Q0Q1, but the biggest impact is S0S1 perpendicular to Q0Q1. We use the impact of S0S1 on Q0Q1 to represent the impact of S0 on the light Q0Q1 of the entire planet. Before Q0Q1 and S0S1 intersect, Q0Q1 is affected by S0 and actually propagates along Q0Q2. The deflection angle between Q0Q2 and Q0Q1 is αq. Before S0S1 and Q0Q1 intersect, S0S1 is affected by Q0 and actually propagates along S0S2. The deflection angle between S0 and S0S1 is αs. After Q0Q2 and S0S2 intersect, Q0Q2 is affected by S0 and actually propagates along O1Q3. The deflection angle between O1Q3 and Q0Q2 is βq. After S0S2 and Q0Q2 intersect, S0S2 is affected by Q0 and actually propagates along O1S3. The deflection angle between O1S2 and O1S3 is βs.
Taking the bending of the light in
Figure 7 as a whole, represented by the middle box in
Figure 8, we do not discuss the specific bending process of the light, but only discuss the changes in the incident light before the intersecting and the outgoing light after the intersecting.
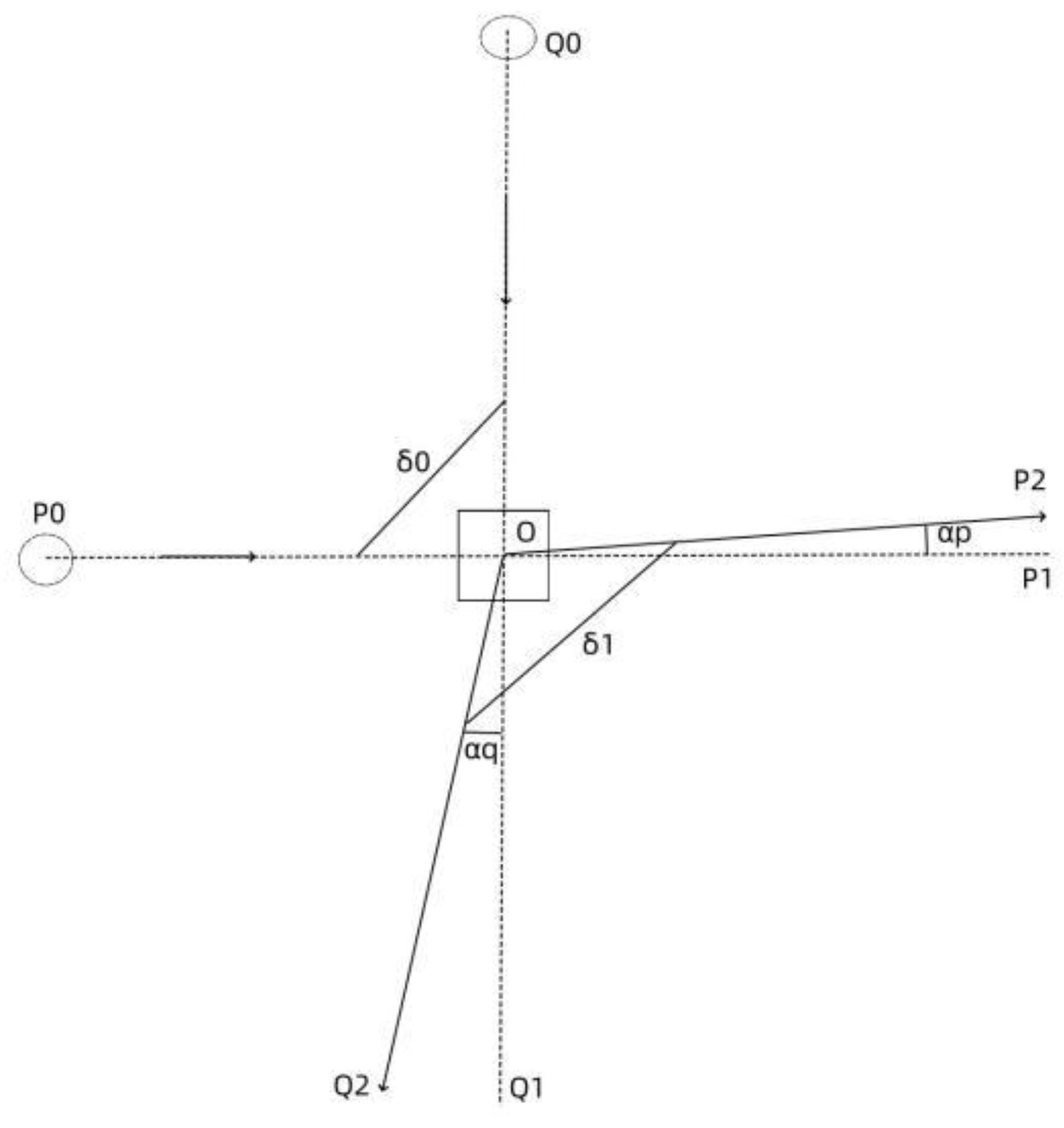
Figure 8 is the photon photon scattering analysis diagram. In the figure, δ0 is the incident angle between the two incident lights, and δ1 is the exit angle between the two outgoing lights. For individual photons propagating light, referring to the Compton effect, momentum during the collision should be conserved. Here we obtain from E=mc², the momentum of the photon is p=mc=E/c=hv/c. Because the wavelength λ=c/v, the momentum can also be written as p=h/λ:
Here h is the Planck constant, λ00, λ10 is the wavelength of two incident waves, λ01, λ11 is the wavelength of two outgoing waves. It is known from the same frequency interference of the light. When the two beams of light are the same frequency, the two beams of light have the greatest impact on each other. For light Q0Q1, the light emitted by planet S0 always has the same component as its wavelength. Suppose λ10=λ00=λ0, λ11=λ01=λ1, the above formula is simplified to
Generally speaking, αp and αq are very small, and the influence of light Q on S<< the influence of light S on Q, so
The red shift caused by the bending of the light by the planet is:
The red shift formed by the bending visible light of the sun is:
Astronomically, the distance of celestial bodies can generally be calculated based on the Hubble Redshift. For lens galaxies, when calculating the distance of the galaxy by redshift, the non-distance redshift of the light bending should be reduced [
11].
6. Conclusion
The phenomenon of separation of the mass center of gravitational lens in a collision galaxy from the mass distribution center of the hot gas as the main matter of the galaxy shows that the hot gas as the main matter has not contributed to the gravitational lens, that is, the hot gas does not bend the light around it, and does not bend the space-time around it. This paper proposes the same frequency mutual inclination explanation of light bending, indicating that when light passes by a large-mass luminous planet, the degree of bending of light is proportional to the brightness of the large-mass luminous planet and inversely proportional to the shortest distance between visible light and the center of the planet. This article believes that there is no dark matter in collision galaxies, and the view of space-time in general relativity is worth discussing. In addition, this article believes that there is a slight non-distance redshift in lens galaxies.
References
- A scientific theory of competition: Dark matter and modified gravity theory [EB/OL].[2024-12-04],http://news.sohu.com/a/500038284_136745.
- Bullet galaxy cluster [EB/OL].[2024-12-04], https://baike.baidu.com/item/%E5%AD%90%E5%BC%B9%E6%98%9F%E7%B3%BB%E5%9B%A2/19525045?fr=ge_ala.
- MACS J 0025.4-1222,[EB/OL].[2024-12-04],https://baike.baidu.com/item/MACS%20J0025.4-1222/23119373?fr=ge_ala.
- Babyk I , Elyiv A , Melnyk O ,et al.The mass distribution in the galaxy cluster Abell 2744[J],Kinematics & Physics of Celestial Bodies, 2012, 28(2):69-76. [CrossRef]
- Clowe D , Markevitch M , Bradac M ,et al.On Dark Peaks and Missing Mass: A Weak Lensing Mass Reconstruction of the Merging Cluster System Abell 520[J].Physics, 2012, 758(2):-. [CrossRef]
- Wang Y , Lui F , Shen Z ,et al.Revealing A Head-on Major Merger in the Nearby NGC 6338 Group with Chandra and VLA observations[J].The Astrophysical Journal, 2019, 870(2):132-. [CrossRef]
- Xu Jun. Introduction to the quantum gravity of the ring circle [J]. Physics Bulletin, 2007(3): 53-55.
- Chen Junli. Interpretation of the co-frequency mutual interference of light bending—dark matter deduced by "gravity lens" in collision galaxy clusters[J]. Astronomy and Astrophysics, 2024, 12(3): 44-55. [CrossRef]
- Baidu Encyclopedia, Solar Radiation [EB/OL].[2024-12-04,https://baike.baidu.com/item/%E5%A4%AA%E9%98%B3%E8%BE%90%E5%B0%84/5211804?fr=ge_ala.
- Generation wave. Further discussion of Compton effect [J]. University Physics, 2010, 29(9): 30-32.
- Chen Junli. Non-distance redshift of lens galaxies[J]. Astronomy and Astrophysics, 2024, 12(4): 72-85. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).