Submitted:
27 May 2025
Posted:
28 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Study Species and Study Area
2.2. Input Data
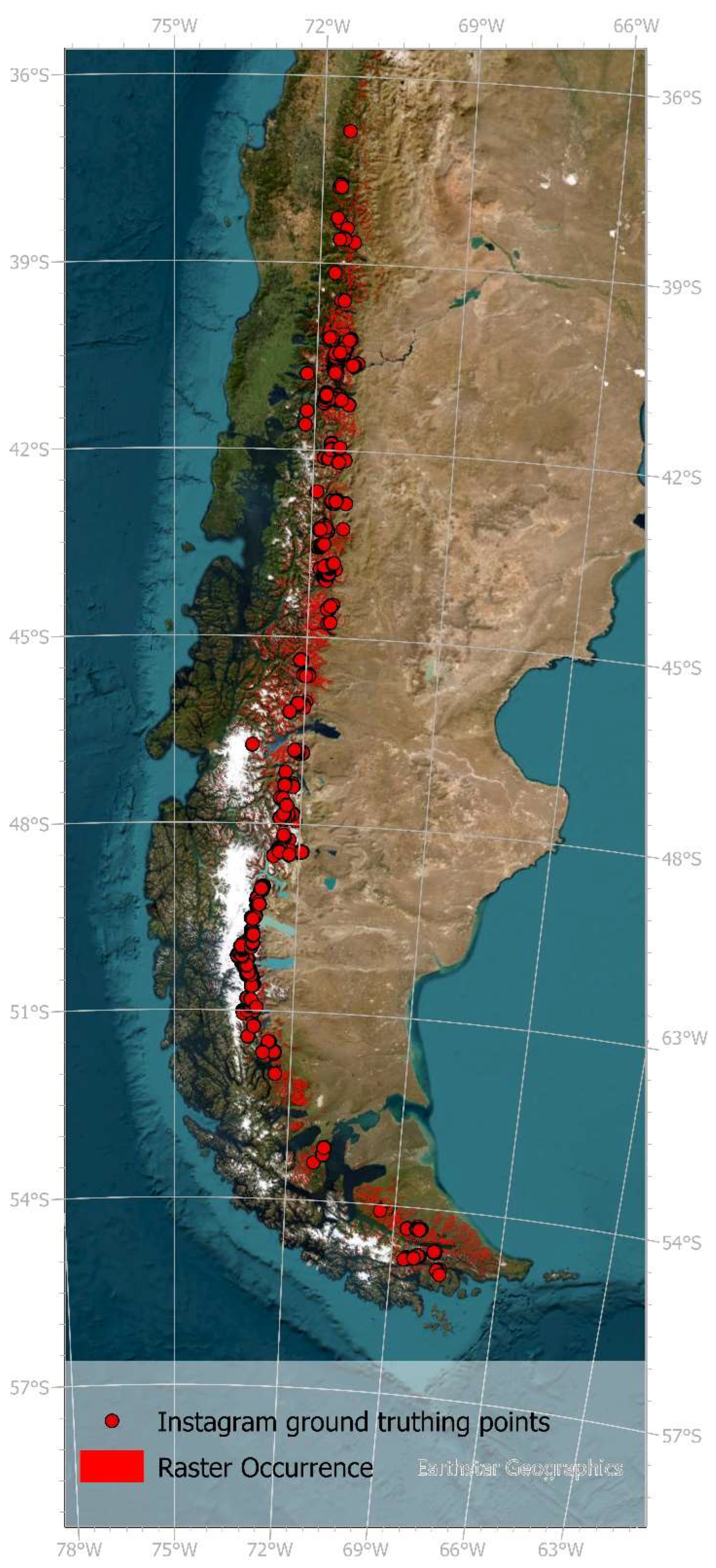
2.2.1. Species Data
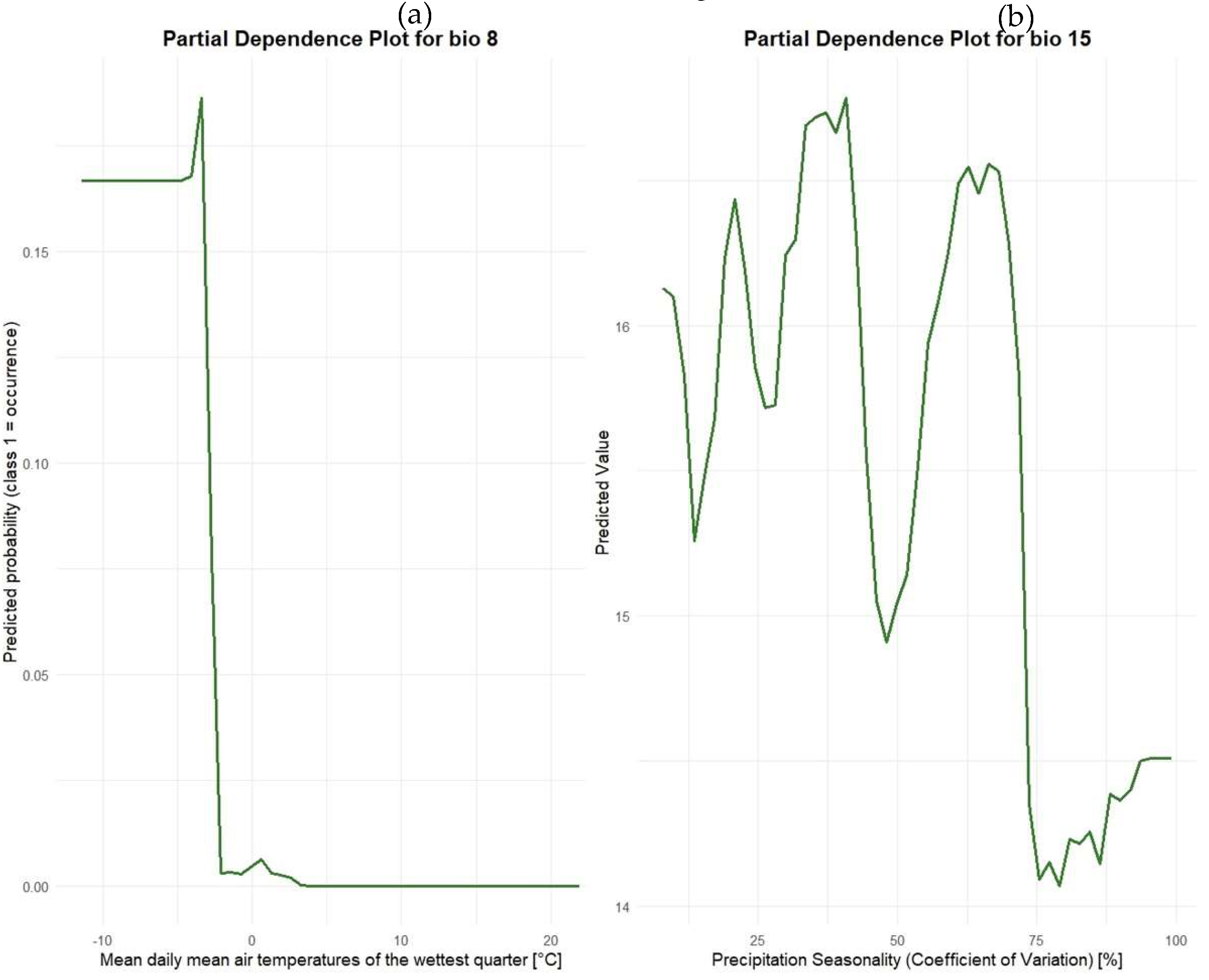
2.2.2. Bioclimatic Predictors
2.3. Model Approach and Model Algorithm
2.4. Model Calibration and Evalution
3. Results
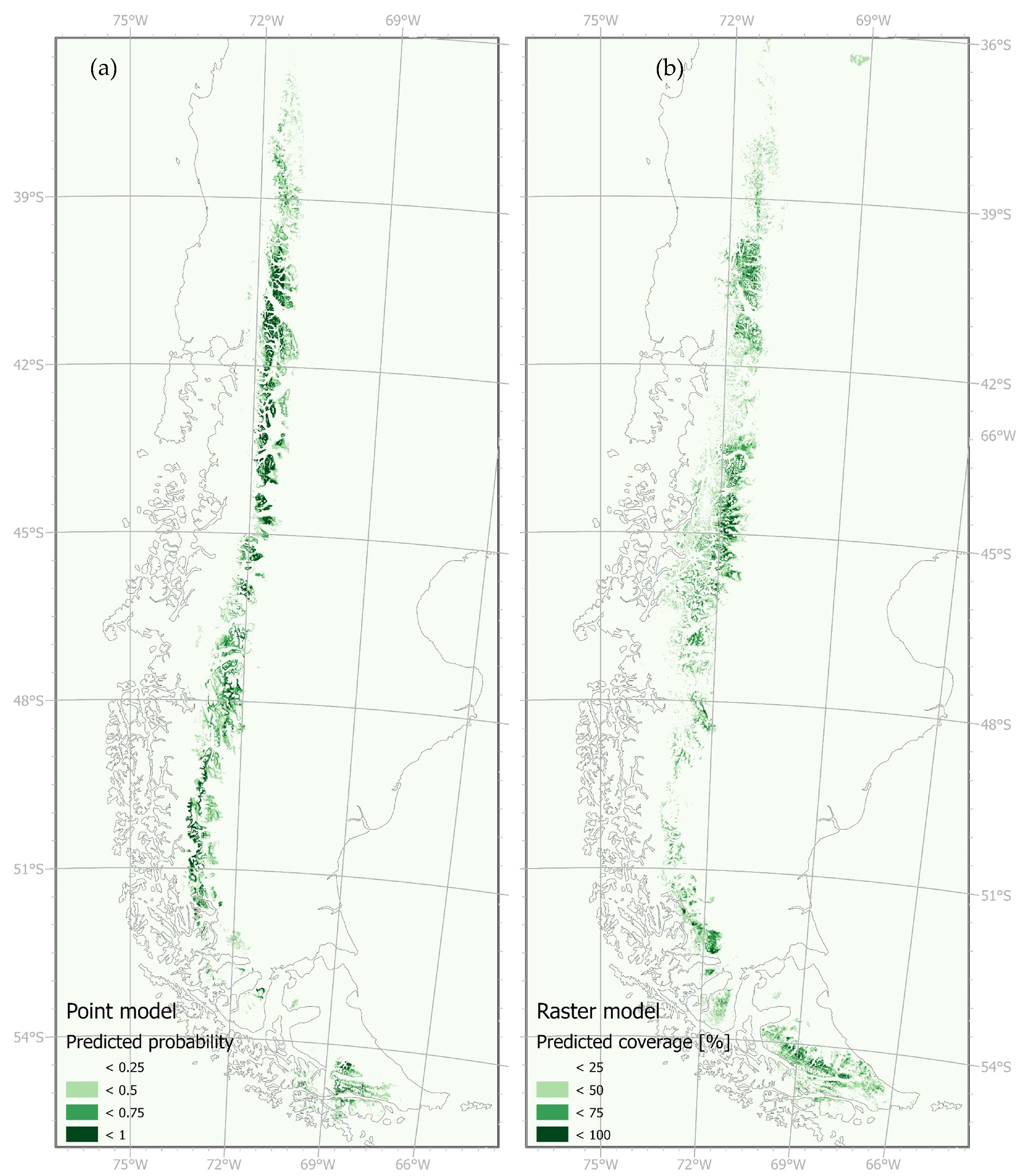
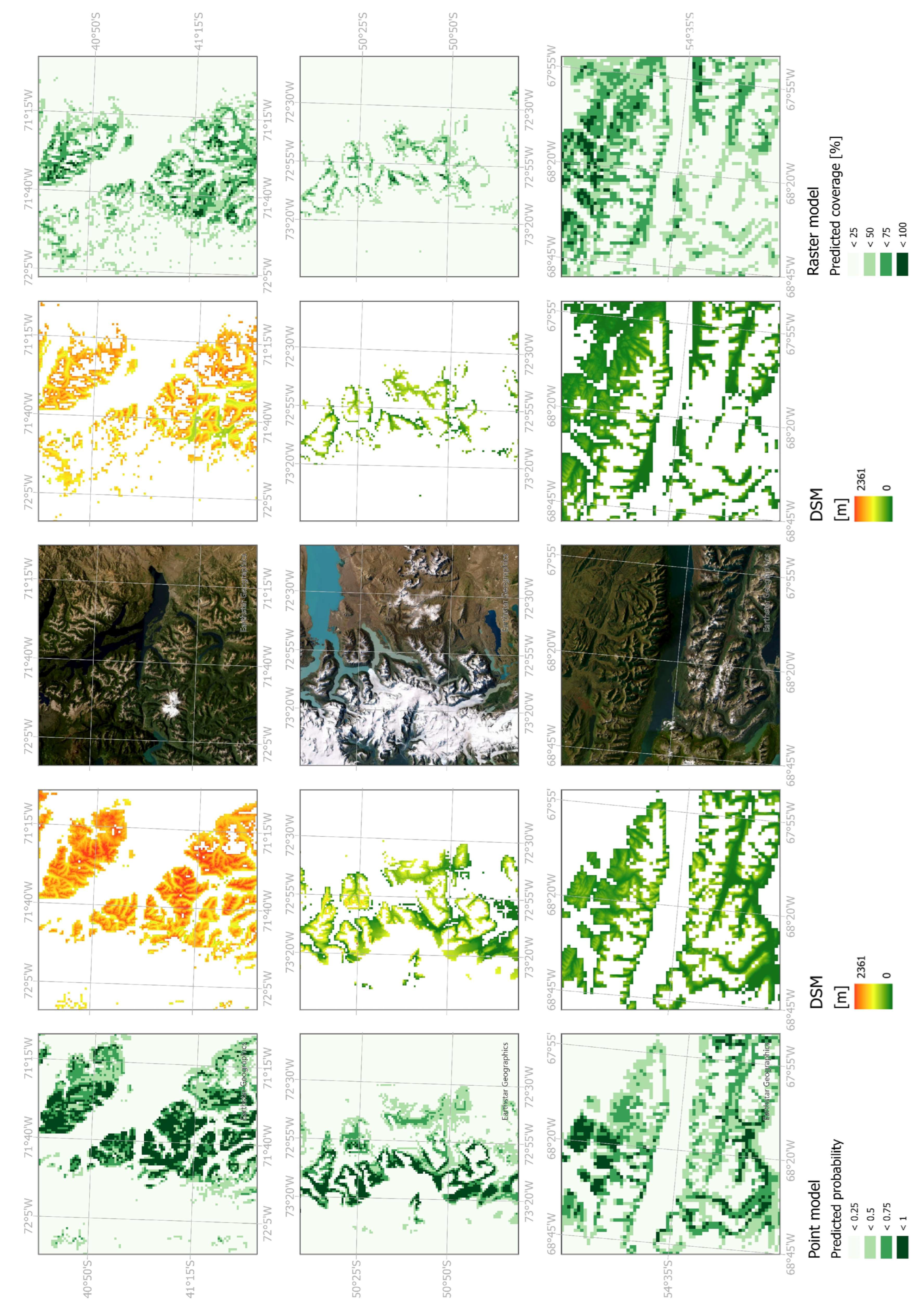
3.1. Current Distribution Range of N. pumilio
3.2. Future Distribution Range of N. pumilio
4. Discussion
4.1. Current Distribution Range of N. pumilio
4.2. Future Distribution Range of N. pumilio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1

Appendix A.2
| No | set.seed | cfm (train) (00, 01, 10, 11) | cfm (test) (00, 01, 10, 11) | Accuracy (test) [%] | AUC | TSS (test, without threshold) |
|---|---|---|---|---|---|---|
| 1 | 123 | 7774, 105, 152, 645 | 1936, 36, 31, 166 | 0.9691 | 0.9866 | 0.8060 |
| 2 | 321 | 7736, 106, 154, 680 | 1977, 29, 27, 136 | 0.9742 | 0.9928 | 0.8108 |
| 3 | 456 | 7762, 115, 154, 645 | 1946, 30, 23, 170 | 0.9756 | 0.9922 | 0.8383 |
| 4 | 654 | 7736, 118, 158, 664 | 1968, 25, 24, 152 | 0.9774 | 0.9919 | 0.8467 |
| 5 | 789 | 7790, 104, 159, 623 | 1926, 38, 26, 179 | 0.9705 | 0.9929 | 0.8116 |
| 6 | 987 | 7768, 112, 157, 639 | 1939, 39, 27, 164 | 0.9696 | 0.9900 | 0.7941 |
| 7 | 111 | 7774, 105, 151, 646 | 1945, 42, 22, 160 | 0.9705 | 0.9894 | 0.7809 |
| 8 | 222 | 7757, 110, 163, 646 | 1954, 38, 25, 152 | 0.9710 | 0.9868 | 0.7874 |
| 9 | 333 | 7755, 103, 143, 675 | 1958, 33, 30, 148 | 0.9710 | 0.9886 | 0.8026 |
| 10 | 444 | 7731, 122, 154, 669 | 1969, 36, 24, 140 | 0.9723 | 0.9890 | 0.7834 |
| No. | set.seed | explained var. (train) | RMSE1 (train) | RMSE1 (test) | R2 (test) |
|---|---|---|---|---|---|
| 1 | 123 | 65.44 | 147.24 | 141.76 | 0.661 |
| 2 | 321 | 65.53 | 146.12 | 146.27 | 0.657 |
| 3 | 456 | 65.38 | 147.02 | 141.42 | 0.666 |
| 4 | 654 | 65.51 | 146.32 | 145.14 | 0.659 |
| 5 | 789 | 65.43 | 146.34 | 146.30 | 0.659 |
| 6 | 987 | 65.57 | 145.74 | 145.31 | 0.661 |
| 7 | 111 | 65.52 | 146.38 | 142.82 | 0.663 |
| 8 | 222 | 65.29 | 147.30 | 140.92 | 0.668 |
| 9 | 333 | 65.48 | 146.72 | 143.09 | 0.661 |
| 10 | 444 | 65.47 | 146.46 | 142.80 | 0.664 |
References
- Holtmeier, F.-K.; Broll, G. Treeline Research—From the Roots of the Past to Present Time. A Review. Forests 2020, 11, 38. [Google Scholar] [CrossRef]
- Schickhoff, U.; Bobrowski, M.; Mal, S.; Schwab, N.; Singh, R.B. The World’s Mountains in the Anthropocene. In Mountain Landscapes in Transition; Schickhoff, U., Singh, R.B., Mal, S., Eds.; Springer International Publishing: Cham, 2022; pp. 1–144. ISBN 978-3-030-70237-3. [Google Scholar]
- Körner, C. Climatic Controls of the Global High Elevation Treelines. In Encyclopedia of the World's Biomes; Elsevier, 2020; pp. 275–281. ISBN 9780128160978. [Google Scholar]
- Paulsen, J.; Körner, C. A climate-based model to predict potential treeline position around the globe. Alp Botany 2014, 124, 1–12. [Google Scholar] [CrossRef]
- Qiu, J.; Feng, S.; Yuan, W. Upward-moving mountain treelines: An indicator of changing climate. Glob. Chang. Biol. 2023, 29, 6832–6833. [Google Scholar] [CrossRef] [PubMed]
- Schickhoff, U.; Bobrowski, M.; Böhner, J.; Bürzle, B.; Chaudhary, R.P.; Gerlitz, L.; Heyken, H.; Lange, J.; Müller, M.; Scholten, T.; et al. Do Himalayan treelines respond to recent climate change? An evaluation of sensitivity indicators. Earth Syst. Dynam. 2015, 6, 245–265. [Google Scholar] [CrossRef]
- Schickhoff, U.; Bobrowski, M.; Böhner, J.; Bürzle, B.; Chaudhary, R.P.; Müller, M.; Scholten, T.; Schwab, N.; Weidinger, J. The Treeline Ecotone in Rolwaling Himal, Nepal: Pattern-Process Relationships and Treeline Shift Potential. In Ecology of Himalayan Treeline Ecotone; Singh, S.P., Reshi, Z.A., Joshi, R., Eds.; Springer Nature Singapore: Singapore, 2023; pp. 95–145. ISBN 978-981-19-4475-8. [Google Scholar]
- Harsch, M.A.; Hulme, P.E.; McGlone, M.S.; Duncan, R.P. Are treelines advancing? A global meta-analysis of treeline response to climate warming. Ecol. Lett. 2009, 12, 1040–1049. [Google Scholar] [CrossRef]
- Hansson, A.; Dargusch, P.; Shulmeister, J. A review of modern treeline migration, the factors controlling it and the implications for carbon storage. J. Mt. Sci. 2021, 18, 291–306. [Google Scholar] [CrossRef]
- Hansson, A.; Shulmeister, J.; Dargusch, P.; Hill, G. A review of factors controlling Southern Hemisphere treelines and the implications of climate change on future treeline dynamics. Agricultural and Forest Meteorology 2023, 332, 109375. [Google Scholar] [CrossRef]
- Lu, X.; Liang, E.; Wang, Y.; Babst, F.; Camarero, J.J. Mountain treelines climb slowly despite rapid climate warming. Global Ecology and Biogeography 2021, 30, 305–315. [Google Scholar] [CrossRef]
- Harsch, M.A.; Bader, M.Y. Treeline form - a potential key to understanding treeline dynamics. Global Ecology and Biogeography 2011, 20, 582–596. [Google Scholar] [CrossRef]
- Bader, M.Y.; Llambí, L.D.; Case, B.S.; Buckley, H.L.; Toivonen, J.M.; Camarero, J.J.; Cairns, D.M.; Brown, C.D.; Wiegand, T.; Resler, L.M. A global framework for linking alpine-treeline ecotone patterns to underlying processes. Ecography 2021, 44, 265–292. [Google Scholar] [CrossRef]
- Körner, C. Alpine Treelines; Springer Basel: Basel, 2012; ISBN 978-3-0348-0395-3. [Google Scholar]
- Tovar, C.; Carril, A.F.; Gutiérrez, A.G.; Ahrends, A.; Fita, L.; Zaninelli, P.; Flombaum, P.; Abarzúa, A.M.; Alarcón, D.; Aschero, V.; et al. Understanding climate change impacts on biome and plant distributions in the Andes: Challenges and opportunities. Journal of Biogeography 2022, 49, 1420–1442. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, J.G. Tree recruitment at the Nothofagus pumilio alpine timberline in Tierra del Fuego, Chile. Journal of Ecology 2000, 88, 840–855. [Google Scholar] [CrossRef]
- Holtmeier, F.-K. Mountain timberlines: Ecology, patchiness, and dynamics; Springer: Dordrecht, 2009; ISBN 978-1-4020-9704-1. [Google Scholar]
- Fajardo, A.; Piper, F.I. An experimental approach to explain the southern Andes elevational treeline. Am. J. Bot. 2014, 101, 788–795. [Google Scholar] [CrossRef] [PubMed]
- Bozkurt, D.; Rojas, M.; Boisier, J.P.; Valdivieso, J. Projected hydroclimate changes over Andean basins in central Chile from downscaled CMIP5 models under the low and high emission scenarios. Climatic Change 2018, 150, 131–147. [Google Scholar] [CrossRef]
- Pessacg, N.; Flaherty, S.; Solman, S.; Pascual, M. Climate change in northern Patagonia: critical decrease in water resources. Theor Appl Climatol 2020, 140, 807–822. [Google Scholar] [CrossRef]
- Álvarez, C.; Veblen, T.T.; Christie, D.A.; González-Reyes, Á. Relationships between climate variability and radial growth of Nothofagus pumilio near altitudinal treeline in the Andes of northern Patagonia, Chile. Forest Ecology and Management 2015, 342, 112–121. [Google Scholar] [CrossRef]
- Srur, A.M.; Villalba, R.; Rodríguez-Catón, M.; Amoroso, M.M.; Marcotti, E. Establishment of Nothofagus pumilio at Upper Treelines Across a Precipitation Gradient in the Northern Patagonian Andes. Arctic, Antarctic, and Alpine Research 2016, 48, 755–766. [Google Scholar] [CrossRef]
- Srur, A.M.; Villalba, R.; Rodríguez-Catón, M.; Amoroso, M.M.; Marcotti, E. Climate and Nothofagus pumilio Establishment at Upper Treelines in the Patagonian Andes. Front. Earth Sci. 2018, 6. [Google Scholar] [CrossRef]
- Brand, R.; Srur, A.M.; Villalba, R. Contrasting growth trends in Nothofagus pumilio upper-elevation forests induced by climate warming in the Southern Andes. Agricultural and Forest Meteorology 2022, 323, 109083. [Google Scholar] [CrossRef]
- Reiter, E.J.; Weigel, R.; Walentowski, H.; Loguercio, G.A.; Fierke, J.; Winter, A.F.N.; Simon, A.; Kotowska, M.M.; Joelson, N.Z.; Caselli, M.; et al. Climate vulnerability of Nothofagus pumilio, Nothofagus dombeyi and Austrocedrus chilensis in northern Patagonia’s temperate forests. Forest Ecology and Management 2024, 572, 122261. [Google Scholar] [CrossRef]
- Rodriguez-Souilla, J.; Cellini, J.M.; Roig, F.A.; Lencinas, M.V.; Chaves, J.E.; Peri, P.L.; Martínez Pastur, G.J. Climate influence seed production in managed and unmanaged Nothofagus pumilio forests of Southern Patagonia. NZJFS 2024, 54. [Google Scholar] [CrossRef]
- Pissolito, C. Sucesión Primaria de la Vegetación en Bosques de Nothofagus spp. en los Andes Patagónicos: Patrones Espacio Temporales de Establecimiento de Plantas e Implicancias Para la Restauración. Ph.D. Dissertation, Universidad Nacional de Cuyo, Mendoza, 2016. [Google Scholar]
- Feng, X.; Park, D.S.; Walker, C.; Peterson, A.T.; Merow, C.; Papeş, M. A checklist for maximizing reproducibility of ecological niche models. Nat. Ecol. Evol. 2019, 3, 1382–1395. [Google Scholar] [CrossRef] [PubMed]
- Karger, D.N.; Conrad, O.; Böhner, J.; Kawohl, T.; Kreft, H.; Soria-Auza, R.W.; Zimmermann, N.E.; Linder, H.P.; Kessler, M. Climatologies at high resolution for the earth's land surface areas. Sci. Data 2017, 4, 170122. [Google Scholar] [CrossRef] [PubMed]
- Karger, D.N.; Wilson, A.M.; Mahony, C.; Zimmermann, N.E.; Jetz, W. Global daily 1 km land surface precipitation based on cloud cover-informed downscaling. Sci. Data 2021, 8, 307. [Google Scholar] [CrossRef] [PubMed]
- Beck, J.; Böller, M.; Erhardt, A.; Schwanghart, W. Spatial bias in the GBIF database and its effect on modeling species' geographic distributions. Ecological Informatics 2014, 19, 10–15. [Google Scholar] [CrossRef]
- Marcer, A.; Chapman, A.D.; Wieczorek, J.R.; Xavier Picó, F.; Uribe, F.; Waller, J.; Ariño, A.H. Uncertainty matters: ascertaining where specimens in natural history collections come from and its implications for predicting species distributions. Ecography 2022, 2022. [Google Scholar] [CrossRef]
- Werner, M.; Weidinger, J.; Böhner, J.; Schickhoff, U.; Bobrowski, M. Instagram data for validating Nothofagus pumilio distribution mapping in the Southern Andes: A novel ground truthing approach. biogeography 2024, 17. [Google Scholar] [CrossRef]
- Amigo Vázquez, F.J.; Rodríguez Guitián, M.A. Bioclimatic and phytosociological diagnosis of the species of the Nothofagus genus (Nothofagaceae) in South America. IJGR 2011, 1, 1–20. [Google Scholar] [CrossRef]
- Soliani, C.; Tsuda, Y.; Bagnoli, F.; Gallo, L.A.; Vendramin, G.G.; Marchelli, P. Halfway encounters: meeting points of colonization routes among the southern beeches Nothofagus pumilio and N. antarctica. Mol. Phylogenet. Evol. 2015, 85, 197–207. [Google Scholar] [CrossRef]
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-Scale Control on the Patagonian Climate. Journal of Climate 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Cameron, S.E.; Parra, J.L.; Jones, P.G.; Jarvis, A. Very high resolution interpolated climate surfaces for global land areas. Intl Journal of Climatology 2005, 25, 1965–1978. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas. Intl Journal of Climatology 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- Soria-Auza, R.W.; Kessler, M.; Bach, K.; Barajas-Barbosa, P.M.; Lehnert, M.; Herzog, S.K.; Böhner, J. Impact of the quality of climate models for modelling species occurrences in countries with poor climatic documentation: a case study from Bolivia. Ecological Modelling 2010, 221, 1221–1229. [Google Scholar] [CrossRef]
- Bobrowski, M.; Weidinger, J.; Schickhoff, U. Is New Always Better? Frontiers in Global Climate Datasets for Modeling Treeline Species in the Himalayas. Atmosphere 2021, 12, 543. [Google Scholar] [CrossRef]
- Jentsch, H.; Weidinger, J.; Werner, M.; Bobrowski, M. ClimDatDownloadR: Accessing Climate Data Respositories for Modelling manuscript in preparation.
- Jentsch, H.; Weidinger, J.; Bobrowski, M. ClimDatDownloadR: Downloads Climate Data from Chelsa and WorldClim; Zenodo, 2023. [Google Scholar]
- Genuer, R.; Poggi, J.-M.; Tuleau-Malot, C. VSURF: An R Package for Variable Selection Using Random Forests. The R Journal 2015, 7, 19–33. [Google Scholar] [CrossRef]
- Franklin, J. Mapping Species Distributions; Cambridge University Press, 2012; ISBN 9780521876353. [Google Scholar]
- Miller, J. Species Distribution Modeling. Geography Compass 2010, 4, 490–509. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y. Applying various algorithms for species distribution modelling. Integr. Zool. 2013, 8, 124–135. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Leo Breiman. Statistical Modeling: The Two Cultures. Statistical Science 2001, 16, 199–215. [Google Scholar] [CrossRef]
- Bobrowski, M.; Gerlitz, L.; Schickhoff, U. Modelling the potential distribution of Betula utilis in the Himalaya. Global Ecology and Conservation 2017, 11, 69–83. [Google Scholar] [CrossRef]
- R Core Team. A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/.
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]
- ESRI. ArcGIS Pro (Version 2.7.0). Available online: https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview.
- Andy Liaw; Matthew Wiener. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Aschero, V.; Srur, A.M.; Guerrido, C.; Villalba, R. Contrasting climate influences on Nothofagus pumilio establishment along elevational gradients. Plant Ecol 2022, 223, 369–380. [Google Scholar] [CrossRef]
- Toro-Manríquez, M.D.; Huertas Herrera, A.; Soler, R.M.; Lencinas, M.V.; Martínez Pastur, G.J. Combined effects of tree canopy composition, landscape location, and growing season on Nothofagus forest seeding patterns in Southern Patagonia. Forest Ecology and Management 2023, 529, 120708. [Google Scholar] [CrossRef]
- Elith, J.; Franklin, J. Species Distribution Modeling. In Encyclopedia of Biodiversity; Elsevier, 2013; ISBN 9780123847201. [Google Scholar]
- Stecconi, M.; Puntieri, J.G.; Barthélémy, D. An architectural approach to the growth forms of Nothofagus pumilio (Nothofagaceae) along an altitudinal gradient. Botany 2010, 88, 699–709. [Google Scholar] [CrossRef]
- Körner, C. Alpine Plant Life; Springer International Publishing: Cham, 2021; ISBN 978-3-030-59537-1. [Google Scholar]
- Hertel, D.; Therburg, A.; Villalba, R. Above- and below-ground response by Nothofagus pumilio to climatic conditions at the transition from the steppe–forest boundary to the alpine treeline in southern Patagonia, Argentina. Plant Ecology & Diversity 2008, 1, 21–33. [Google Scholar] [CrossRef]
- Daniels, L.D.; Veblen, T.T. SPATIOTEMPORAL INFLUENCES OF CLIMATE ON ALTITUDINAL TREELINE IN NORTHERN PATAGONIA. Ecology 2004, 85, 1284–1296. [Google Scholar] [CrossRef]
- Villalba, R.; BONINSEGNA, J.A.; Veblen, T.T.; SCHMELTER, A.; RUBULIS, S. RECENT TRENDS IN TREE-RING RECORDS FROM HIGH ELEVATION SITES IN THE ANDES OF NORTHERN PATAGONIA. Climatic Change 1997, 36, 425–454. [Google Scholar] [CrossRef]
- Lara, A.; Aravena, J.C.; Villalba, R.; Wolodarsky-Franke, A.; Luckman, B.; Wilson, R. Dendroclimatology of high-elevation Nothofagus pumilio forests at their northern distribution limit in the central Andes of Chile. Can. J. For. Res. 2001, 31, 925–936. [Google Scholar] [CrossRef]
- Fajardo, A.; Gazol, A.; Mayr, C.; Camarero, J.J. Recent decadal drought reverts warming-triggered growth enhancement in contrasting climates in the southern Andes tree line. Journal of Biogeography 2019, 46, 1367–1379. [Google Scholar] [CrossRef]
- Batllori, E.; Camarero, J.J.; Ninot, J.M.; Gutiérrez, E. Seedling recruitment, survival and facilitation in alpine Pinus uncinata tree line ecotones. Implications and potential responses to climate warming. Global Ecology and Biogeography 2009, 18, 460–472. [Google Scholar] [CrossRef]
- Bürzle, B.; Schickhoff, U.; Schwab, N.; Wernicke, L.M.; Müller, Y.K.; Böhner, J.; Chaudhary, R.P.; Scholten, T.; Oldeland, J. Seedling recruitment and facilitation dependence on safe site characteristics in a Himalayan treeline ecotone. Plant Ecol 2018, 219, 115–132. [Google Scholar] [CrossRef]
- Karger, D.N.; Schmatz, D.R.; Dettling, G.; Zimmermann, N.E. High-resolution monthly precipitation and temperature time series from 2006 to 2100. Sci. Data 2020, 7, 248. [Google Scholar] [CrossRef] [PubMed]

| Short Name | Long Name | Used in Analysis |
|---|---|---|
| bio 4 | temperature seasonality [°C/100] 1 | X |
| bio 8 | mean daily mean air temperatures of the wettest quarter [°C] | X |
| bio 9 | mean daily mean air temperatures of the driest quarter [°C] | excluded by VSURF |
| bio 10 | mean daily mean air temperatures of the warmest quarter [°C] | X |
| bio 11 | mean daily mean air temperatures of the coldest quarter [°C] | X |
| bio 15 | precipitation seasonality [kg m-2] 2 | X |
| bio 16 | mean monthly precipitation amount of the wettest quarter [kg m-2 month-1] | excluded by VSURF |
| bio 17 | mean monthly precipitation amount of the driest quarter [kg m-2 month-1] | X |
| bio 18 | mean monthly precipitation amount of the warmest quarter [kg m-2 month-1] | X |
| bio 19 | mean monthly precipitation amount of the coldest quarter [kg m-2 month-1] | X |
| time span 2041 - 2070 | time span 2071 - 2100 | ||||
| model | area [km2] | area [%] | area [km2] | area [%] | |
| point model | SSP126 | 14916.48 | 37.54 | 14794.67 | 37.24 |
| SSP370 | 9594.11 | 24.15 | 7856.97 | 19.77 | |
| SSP585 | 11527.92 | 29.01 | 6206.62 | 15.62 | |
| raster model | SSP126 | 30143.13 | 75.06 | 28893.18 | 71.95 |
| SSP370 | 22077.23 | 54.97 | 17090.35 | 42.56 | |
| SSP585 | 27348.67 | 68.10 | 15758.20 | 39.24 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





