A Photon-Based Vector Particle Model for Proton and Neutron Masses

1. Introduction

Quantum Chromodynamics (QCD) describes nucleon masses via quark-gluon interactions, but its computational complexity motivates alternative models to explore underlying principles. Thomas N. Lockyer’s Vector Particle Physics [1] proposes that nucleons are lepton-based, with mass arising from photon momentum stored in spinning, nested square layers rotated by ${45}^{\circ }$. This paper formalizes the model, verifies its high-precision predictions for $m_p/m_e$ and $m_n/m_e$, and discusses its potential to illuminate symmetries in the Standard Model.

2. Model Description

The proton is modeled as a positron (mass $m_e$, charge $+e$) forming a base level (level 0), with 18 energy layers (levels 1–18). Each layer is an idealized square with side length tied to the rationalized Compton wavelength (${\lambda }_e^{\prime }=\hslash /\left(m_{e}c\right)\approx 3.8615932\times {10}^{-13}\mathrm{m}$). The inner square, rotated ${45}^{\circ }$, has corners at the midpoints of the outer square’s sides, yielding a $\sqrt{2}$ scaling:

$$L_{\mathrm{inner}}={\displaystyle \frac{L_{\mathrm{outer}}}{\sqrt{2}}}.$$

(1)

The neutron adds an electron (mass $m_e$, charge $-e$) sharing level 0 and doubles level 1 for binding energy. Rest mass arises from photon momentum ($p=h/\lambda$) confined in spinning layers, with energy contributions:

$$m={\displaystyle \frac{e^2}{m_{e}4\pi c^2{\lambda }_e^{\prime }d{ϵ}_0}},d={\displaystyle \frac{1-\sqrt{2}/2}{2}}-{\displaystyle \frac{a_u}{\sqrt{2}}},a_u=2\left(\sqrt{1+{\displaystyle \frac{\alpha }{2\pi }}}-1\right).$$

(2)

Mass contributions per level i (1 to 19) are:

$$m_1\left[i\right]={\displaystyle \frac{{\left(\sqrt{2}\right)}^{i-1}}{1-\sqrt{2}{a}_u}},m_2\left[i\right]=m·{\displaystyle \frac{{\left(\sqrt{2}\right)}^{i-1}}{1-\sqrt{2}{a}_u}}.$$

(3)

3. Calculations

The proton mass ratio is:

$$m_p/m_e=\sum _{i=1}^{19}(m_1\left[i\right]+m_2\left[i\right]).$$

(4)

The neutron mass ratio includes doubled first two levels:

$$m_n/m_e=\sum _{i=1}^{19}(m_1\left[i\right]+m_2\left[i\right])+\sum _{i=1}^2(m_1\left[i\right]+m_2\left[i\right]).$$

(5)

Implementation details are in Appendix A.

4. Results and Discussion

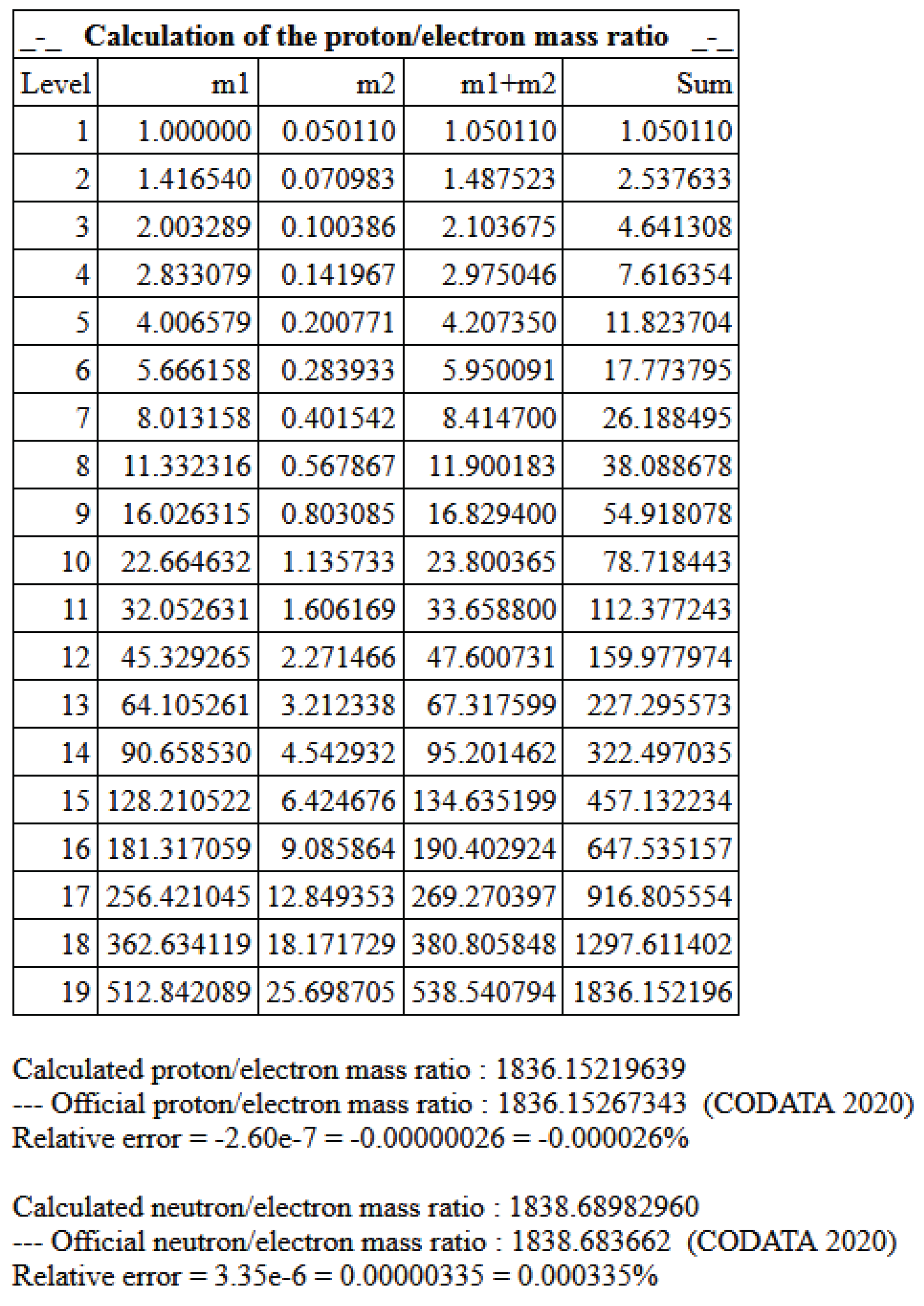
The JavaScript implementation yields:

• Proton: $m_p/m_e=1836.1521964$, error $-2.6\times {10}^{-7}$ vs. CODATA’s 1836.15267343 (seven significant figures).
• Neutron: $m_n/m_e=1838.6898296$, error $3.35\times {10}^{-6}$ vs. CODATA’s 1838.68366173 (six significant figures).

Figure 1. Output of the JavaScript code, showing mass contributions per level.

Figure 1. Output of the JavaScript code, showing mass contributions per level.

• Note: The total mass contribution of each row ($m_1\left[i\right]+m_2\left[i\right]$) is exactly equal to the total of the previous multiplied by $\sqrt{2}$, reflecting the geometric scaling of the nested square layers rotated by ${45}^{\circ }$.

The model’s precision, using only fundamental constants and a $\sqrt{2}$ factor from ${45}^{\circ }$-rotated square geometry, suggests a physical basis. The photon momentum stored in spinning layers offers a lepton-centric alternative to QCD. The 19 levels may reflect an energy quantization (∼52 MeV per layer) related to cosmological conditions.

The model’s inclusion of an electron-like contribution in the first layer of the neutron raises the possibility of exploring connections to the strong force that binds nucleons, though such an extension requires further theoretical development.

5. Implications and Future Work

Lockyer’s model challenges QCD by prioritizing photon-based electromagnetic interactions. Its precision suggests a semi-classical approximation of strong force effects or a new symmetry. Future work could:

• Derive the 19-level energy condition.
• Model the spinning-photon mechanism as charge loops.
• Attempt to further improve accuracy with CODATA constants.
• Extend the model to derive the masses of the muon and tauon, adapting the summation framework to account for their mass ratios.

6. Conclusions

QCD no longer needs to prove its computational capabilities. Lockyer’s photon-based model, with no reference to quarks, raises questions and invites us to try to understand and possibly reconcile the two approaches.