A Geometric Model for the Proton and Neutron

1. Introduction

Quantum Chromodynamics (QCD) describes nucleon masses through quark-gluon interactions, at the cost of significant computational complexity. Vector Particle Physics by Thomas N. Lockyer [1] proposes nucleons based on leptons, whose masses originate from the momentum of photons trapped in a layered structure of increasing energies nested like Russian dolls. This article formalizes and simplifies Lockyer’s model by eliminating a corrective term, deemed unnecessary and ad hoc, inspired by quantum electrodynamics (QED). This simplification improves the accuracy of the proton-to-electron mass ratio calculation from six to seven significant digits.

2. Brief Description of Lockyer’s Model

Lockyer’s model conceptualizes the positron as a cube whose edges have a length based on the reduced Compton wavelength (${\lambda }_e^{\prime }=\hslash /\left(m_{e}c\right)\approx 3.8615932\times {10}^{-13}\mathrm{m}$). The proton is modeled as a positron (level 0) containing 18 nested energy layers (levels 1–18). The edge of the positron ’cube’ has a length shortened by a factor deduced from the electron’s magnetic moment, using only physical constants. For the complete description of Lockyer’s original model, refer to the bibliography [1,2].

Projected onto a plane perpendicular to the rotation axis giving the magnetic moment, the cube appears as a square. Each ’square’ of the inner layers is inscribed with a 45° rotation relative to its containing square, and consequently sees its dimensions reduced by a factor of $\sqrt{2}$:

$$L_{\mathrm{inner}}={\displaystyle \frac{L_{\mathrm{outer}}}{\sqrt{2}}}.$$

(1)

The rest mass originates from the momentum of photons ($p=h/\lambda$) confined in the rotating layers, with energy contributions:

$$m={\displaystyle \frac{e^2}{m_{e}4\pi c^2{\lambda }_e^{\prime }d{ϵ}_0}},d={\displaystyle \frac{1-\sqrt{2}/2}{2}}-{\displaystyle \frac{a_u}{\sqrt{2}}},a_u=2\left(\sqrt{1+{\displaystyle \frac{\alpha }{2\pi }}}-1\right).$$

(2)

  The mass contributions per level i (1 to 19) are:

$$m_1\left[i\right]={\displaystyle \frac{{\left(\sqrt{2}\right)}^{i-1}}{1-\sqrt{2}{a}_u}},m_2\left[i\right]=m·{\displaystyle \frac{{\left(\sqrt{2}\right)}^{i-1}}{1-\sqrt{2}{a}_u}}.$$

(3)

  The neutron, in turn, adds an electron (mass $m_e$, charge $-e$) sharing level 0 with the positron (mass $m_e$, charge $+e$), and doubles the energy of level 1.

3. Calculations

The proton mass ratio is:

$$m_p/m_e=\sum _{i=1}^{19}(m_1\left[i\right]+m_2\left[i\right]).$$

(4)

The neutron mass ratio includes the doubling of the first two levels:

$$m_n/m_e=\sum _{i=1}^{19}(m_1\left[i\right]+m_2\left[i\right])+\sum _{i=1}^2(m_1\left[i\right]+m_2\left[i\right]).$$

(5)

Implementation details are in Appendix A.

4. Results and Discussion

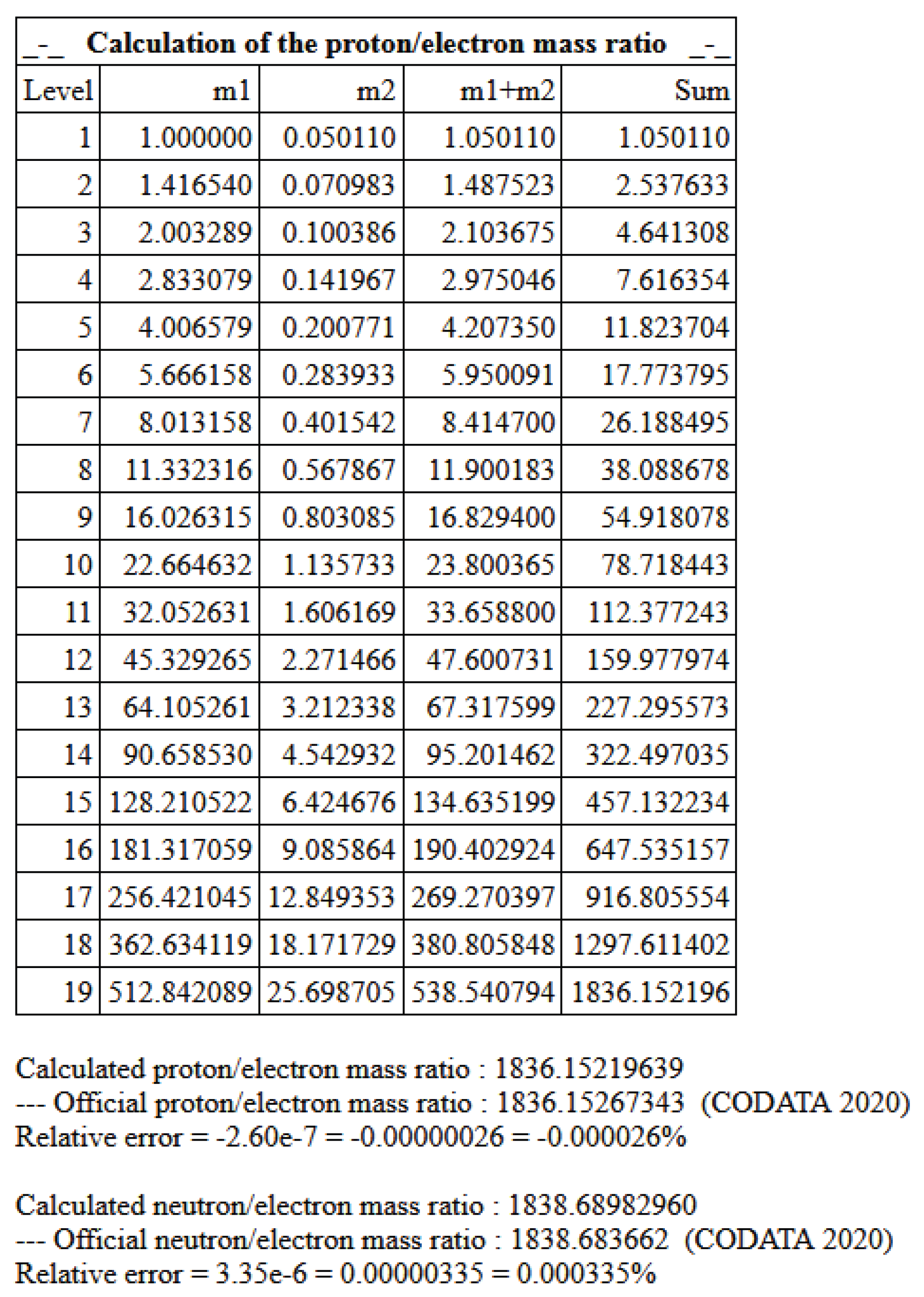
The JavaScript implementation yields:

• Proton: $m_p/m_e=1836.1521964$, error $-2.6\times {10}^{-7}$ relative to CODATA 1836.15267343 (seven significant digits).
• Neutron: $m_n/m_e=1838.6898296$, error $3.35\times {10}^{-6}$ relative to CODATA 1838.68366173 (six significant digits).

Figure 1. JavaScript code result, showing mass contributions per level.

Figure 1. JavaScript code result, showing mass contributions per level.

Note: The contribution of each line ($m_1\left[i\right]+m_2\left[i\right]$) is exactly equal to the previous one multiplied by $\sqrt{2}$.

5. Implications and Future Work

The model’s accuracy, using only fundamental constants and a factor of $\sqrt{2}$, suggests a physical basis. The geometric structure of this model is an idealization and is not the most important aspect to retain, as other structures, and other theoretical explanations, could lead to this same calculation. What should be thought-provoking is that a very simple calculation, using only physical constants and no ad hoc parameters, can achieve a result of extreme accuracy. This simplicity indicates to us that the complexity of our models might emerge from an underlying, simpler physics.

Furthermore, the model’s inclusion of an electron-like contribution in the neutron’s first layer opens the possibility of exploring links with the strong force that binds nucleons, but such an extension requires further theoretical development.

Future work should:

• Explore a semi-classical approximation of the strong force.
• Derive the condition for the 18 nested energy levels.
• Explain the energy ratio of $\sqrt{2}$ between successive levels.
• Attempt to extend the model to calculate the masses of the muon and tauon.

6. Conclusion

QCD has long proven its computational capabilities. Lockyer’s model, favoring electromagnetic interactions based on photons, without reference to quarks, raises questions and invites us to push reflection further to reconcile the two approaches.