1. Introduction
Biometric systems, which emerged in the early 1960s with the first semi-automated face recognition system and fingerprint verification in the 1970s, represent a significant advancement in biometric authentication technology. These solutions exploit intrinsic physiological or behavioral attributes of individuals for identification and verification purposes. The field gained substantial momentum in the 1990s with the development of more sophisticated algorithms and improved sensor technologies, leading to widespread adoption across various sectors contemporary biometric systems offer several distinct advantages over traditional authentication methods such as passwords, PINs, or ID cards. Unlike knowledge-based authentication (passwords) or token-based systems (ID cards) that can be forgotten, stolen, or shared, biometric traits are inherently linked to an individual, providing stronger binding between the authenticator and the person’s true identity. Moreover, biometric characteristics cannot be easily transferred between individuals and generally require the physical presence of the person being authenticated, significantly enhancing security against impersonation attacks.
The applications of biometric systems have expanded significantly, now encompassing law enforcement, border control, healthcare, financial services, and consumer electronics. For instance, smartphones increasingly incorporate fingerprint and facial recognition for device unlock and payment authorization, while governments employ biometric passports and national ID systems for enhanced security. In healthcare, biometric systems ensure accurate patient identification and secure access to medical records, while financial institutions utilize them for secure transactions and fraud prevention. However, despite these advantages, biometric systems face unique challenges, including privacy concerns, template security, and the irrevocability of biometric traits [
1,
2]. Unlike passwords that can be changed if compromised, biometric characteristics are permanent and cannot be reset, necessitating robust security measures for template protection and storage. These challenges have driven continuous innovation in the field, leading to the development of more sophisticated multimodal systems and advanced security frameworks.
The remainder of this paper is structured as follows:
Section 2 provides a comprehensive review of extant literature, examining the inherent vulnerabilities in both unimodal and multimodal biometric systems, while emphasizing the pivotal role of cryptographic security in enhancing system robustness.
Section 3 delineates the methodological framework, focusing on the analytical characterization of Qi Hyperchaotic systems and their application in encryption-decryption protocols.
Section 4 presents empirical findings, including comparative analyses against state-of-the-art algorithms and offers a fair discussion of the results, while in Section 6, we present conclusive insights and directions for future research endeavors.
2. Related Works
In this section, we briefly introduced a short literature survey on the related biometric security works. The landscape of biometric authentication systems presents complex security challenges that demand sophisticated solutions. This review examines the evolution, challenges, and emerging solutions in multimodal biometric security, with particular emphasis on the integration of cryptographic techniques and advanced security frameworks. Biometric authentication systems face vulnerabilities at four critical junctures that fundamentally impact their security architecture: sensor-level susceptibility to presentation attacks utilizing synthetic biometrics, data transmission vulnerability between system components, template database exposure to unauthorized access, and decision module vulnerability to result falsification [
1,
2]. Building upon the aforementioned elements, we can categorize the attacks on biometric authentication systems into two major classifications: unauthorized acquisition of raw biometric data and malicious attempts to manipulate the templates databases. To mitigate these vulnerabilities, robust cryptographic mechanisms must be integrated into the biometric system architecture, ensuring protection against both biometric data falsification and stored templates tampering. The complexity of these challenges necessitates comprehensive security measures to maintain system integrity while ensuring practical usability in real-world applications.
The vulnerability of biometric systems to presentation attacks represents a particularly significant challenge in authentication security. Contemporary research demonstrates that sensor-level susceptibility to synthetic biometric presentations can fundamentally compromise system integrity, especially when sophisticated counterfeit characteristics circumvent traditional detection mechanisms [
1,
3,
4]. This vulnerability becomes more pronounced when attackers possess detailed knowledge of system architecture, enabling them to exploit inherent limitations in distinguishing between genuine and fraudulent or fake biometric presentations.
Contemporary unimodal biometric authentication systems, despite their recent development, demonstrate significant vulnerabilities to sophisticated spoofing attacks. Modern attackers have developed techniques to generate false positive authentications, fundamentally compromising these systems’ accuracy and reliability in user verification, thus undermining the core integrity of the authentication mechanism. A fundamental question that one might ask is how vulnerable are biometric systems to fake biometric information, and how is it accomplished? A targeted review of recent literature examines the scope and implications of biometric spoofing techniques.
For example, facial recognition systems and fingerprint authentication mechanisms exhibit significant vulnerabilities to presentation attacks (spoofing). While numerous scholars have advanced liveness detection protocols to mitigate face-based spoofing threats [
3,
4,
5], the susceptibility of fingerprint biometric systems to artificial reproductions remains a pressing concern [
6,
7,
8,
9]. This vulnerability has catalyzed extensive research into countermeasure development, particularly focusing on the detection, identification, and prevention of synthetic fingerprint attacks [
6,
9,
10]. The proliferation of these security challenges underscores the critical importance of robust anti-spoofing mechanisms in biometric authentication systems.
Although iris patterns offer unique identification markers independent of genetic factors, making them among the most reliable biometric identifiers, they remain susceptible to spoofing attacks. Recent research has explored various methodologies for both detecting and counterfeiting iris biometrics during authentication procedures. Notable contributions include Saranya et al. (2016) [
9] who developed an Image Quality Assessment (IQA) framework to enhance biometric security systems, particularly for iris and fingerprint verification. Building on this foundation, He et al. (2008) [
10] integrated Fast Fourier Transform (FFT) analysis with IQA techniques to detect fake iris data. Their research specifically addressed photographic and printed iris replicas, employing IQA to filter low-quality forgeries while utilizing Fourier frequency patterns to detect sophisticated fake iris samples.
In response to the inherent limitations of unimodal biometric systems, multimodal biometric authentication has emerged as a sophisticated countermeasure. These systems integrate multiple biometric modalities—either heterogeneous (combining different biometric traits) or homogeneous (utilizing multiple instances of the same trait, such as bilateral iris patterns or multiple fingerprints). The integration of multiple modalities substantially elevates the system’s security threshold, as it necessitates the successful spoofing of multiple independent biometric traits simultaneously. Recent scholarly work has demonstrated that this architectural approach significantly mitigates the vulnerabilities inherent in single-modal systems while enhancing authentication robustness [
11,
12,
13,
14,
15].
A novel authentication mechanism leveraging multiple biometric traits—face, eye region, and iris patterns—was introduced in [
16]. The researchers successfully adapted the OSIRIS v4.1 segmentation framework for smartphone implementation, with experimental validation confirming its viability on Android smart devices.
Smartphone-based recognition solutions incorporating face, iris, and periocular characteristics have achieved Equal Error Rates (EER) of 0.68% [
14], demonstrating the potential for highly accurate multimodal authentication. Similarly, Research by Raj G et al. [
17] introduced a comprehensive biometric authentication system that synthesizes three distinct modalities - facial features, iris patterns, and palm vein characteristics. Their implementation in banking environments demonstrated heightened security measures while yielding improved identification precision. These advancements highlight the practical viability of multimodal approaches in real-world applications. However, research has shown that even multimodal systems are not impervious to sophisticated attacks, particularly when attackers can simultaneously compromise multiple biometric modalities [
18,
19].
Research by Rodrigues et al. [
18] explored vulnerabilities in dual-trait authentication systems combining facial recognition and fingerprint analysis. Their investigation across four distinct attack scenarios revealed that even combined biometric measures remain susceptible to sophisticated spoofing attempts. These findings highlight the necessity of integrating cryptographic protocols with multi-factor biometric systems to achieve comprehensive security.
The security and data protection paradigm represents a fundamental consideration in biometric solution architectures. While multimodal biometric systems inherently incorporate security enhancement through their multifaceted nature, the implementation of robust cryptographic frameworks becomes imperative to fortify these systems against presentation attacks and ensure data privacy preservation. The system’s capability to discriminate between genuine and fraudulent or fake biometric presentations is particularly crucial, given that contemporary spoofing methodologies can produce highly convincing synthetic biometric artifacts [
11,
12]. The rising frequency of cyberattacks has accelerated the adoption of biometric security measures, offering enhanced protection for enterprises and individuals in today’s digital ecosystem. The integration of cryptographic techniques with multimodal biometric systems has emerged as a crucial development in enhancing security frameworks.
Researchers have proposed various approaches to secure biometric data both at rest and in transit. Notable among these is the implementation of DNA QR coding combined with face and fingerprint authentication, achieving detection performance rates of 98.58% while significantly enhancing resistance to identity compromise attempts [
44]. This approach demonstrates the potential for innovative security solutions that combine traditional biometric methods with advanced cryptographic techniques.
The fundamental challenges in biometric security extend beyond mere technical vulnerabilities. The intrinsic nature of biometric data presents unique privacy and security considerations that traditional authentication methods do not encounter [
32,
33]. Unlike passwords or security tokens, biometric characteristics cannot be revoked or replaced if compromised, creating a permanent security vulnerability. This irrevocability of biometric data necessitates exceptionally robust protection mechanisms from the outset of system design and implementation.
Contemporary research has identified multiple attack vectors that must be addressed in comprehensive security solutions. These include presentation attacks at the sensor level, replay attacks utilizing previously captured legitimate signals, feature extraction compromise, and template storage attacks [
34]. Each of these vulnerability points requires specific security measures, leading to the development of layered security approaches that combine multiple protection mechanisms. However, they have overlooked the practicability of the multistage encryption in real-work applications.
In their research, [
20] A. Rahik and C. Priya developed an integrated authentication framework combining DNA QR encoding with EXOR operations, utilizing DNA sequences as cryptographic keys. This system incorporates facial and fingerprint biometrics for enhanced cybersecurity. Their novel fusion methodology achieved 98.58% accuracy while strengthening defenses against identity theft.
In [
21], Eid and Mohamed developed a multimodal biometric system integrating iris and facial recognition, secured through 2D Henon chaotic mapping. Their approach implemented encryption at three critical stages: pre-feature extraction, pre-matching, and database storage. The combination of Henon and 2D Logistic maps provided efficient encryption, while fuzzy logic fusion of face and iris matching scores achieved a FAR of 0.0345% and FRR of 0.001%.
Singh K et al. in [
22] developed a multimodal biometric framework for cloud security, integrating steganographic and cryptographic techniques in a triple-authentication system. Their approach enables secure smartphone-based file operations while mitigating unauthorized access risks
Arulalan et al. in [
23] proposed a multi-modal biometric encryption framework, integrating palmprint and fingerprint characteristics to generate 256-bit cryptographic keys for document security. The system’s strength lies in leveraging physiological traits, making key prediction computationally infeasible for adversaries. While their empirical validation demonstrated system effectiveness, the research notably omitted crucial randomness assessments of the biometric-derived bit sequences through standardized testing protocols such as FIPS or NIST suites.
Yagiz S. et al. in [
24] propose a biometrics-based cryptography scheme for E-Health systems that has two main components: Biometrics-based Fuzzy Authentication and Key Negotiation (BFAKN) for secure authentication and key exchange between system components, and Fingerprint-based Authority Access Mechanism (FAAM) for managing access control and data permissions. The key particularity is that it leverages biological signals and fingerprint biometrics to establish secure communications and granular access control within E-Health systems, achieving high security (99.6% impostor rejection) while maintaining usability for legitimate users (93.5% acceptance rate).
The work in [
25] introduced a cryptographic system combining facial and iris biometrics, utilizing dual chaos mechanics through 2G Logistic Sine-coupling and Tent Logic Cosine maps. Their adaptive approach implements six rotation diffusion techniques that vary based on input images, enhancing resistance to plaintext attacks. The system demonstrated robust security metrics with entropy exceeding 7.99, NPCR >99.6%, and UACI >33.4%.
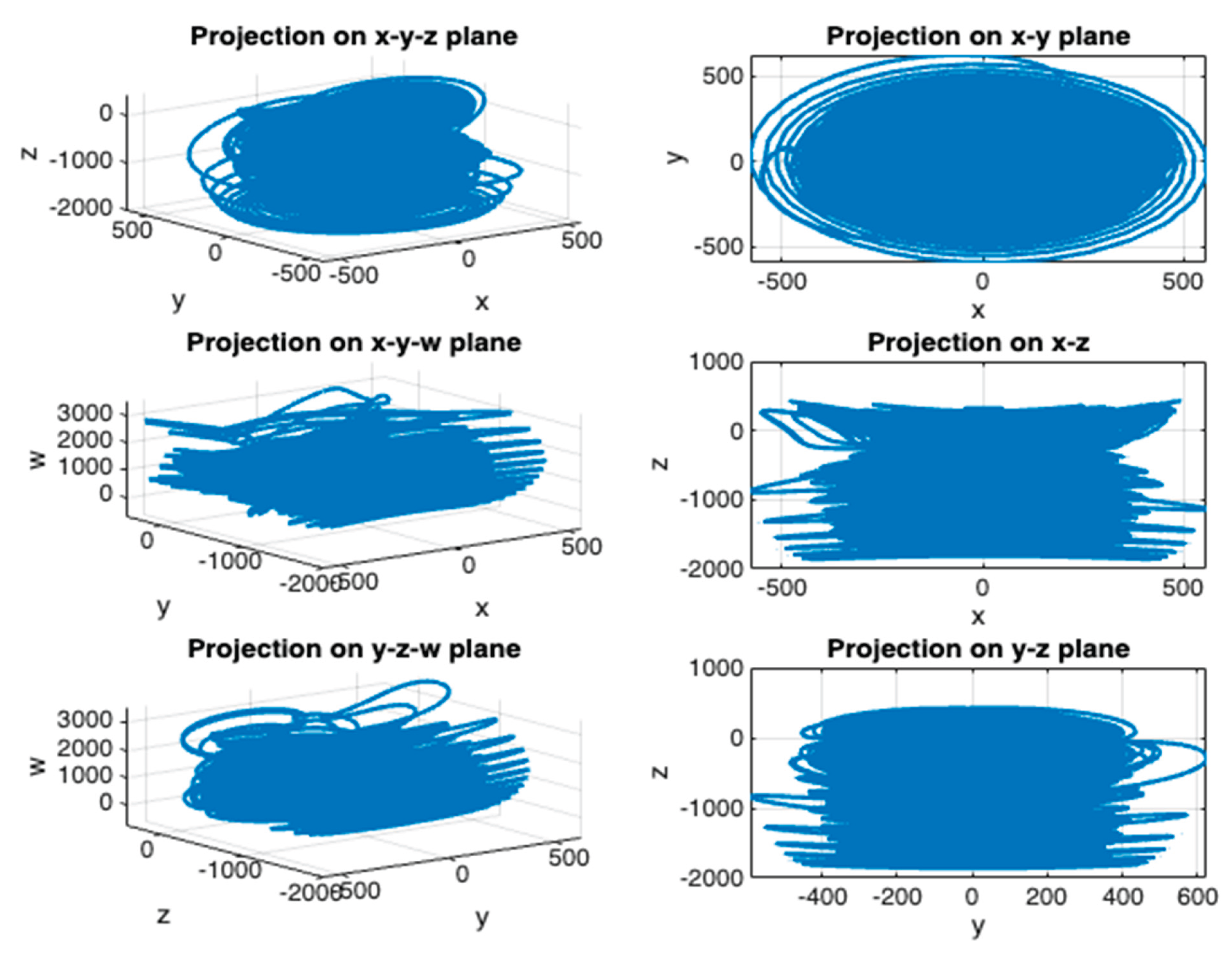
Figure 1.
Qi Hyperchaos attractors.
Figure 1.
Qi Hyperchaos attractors.
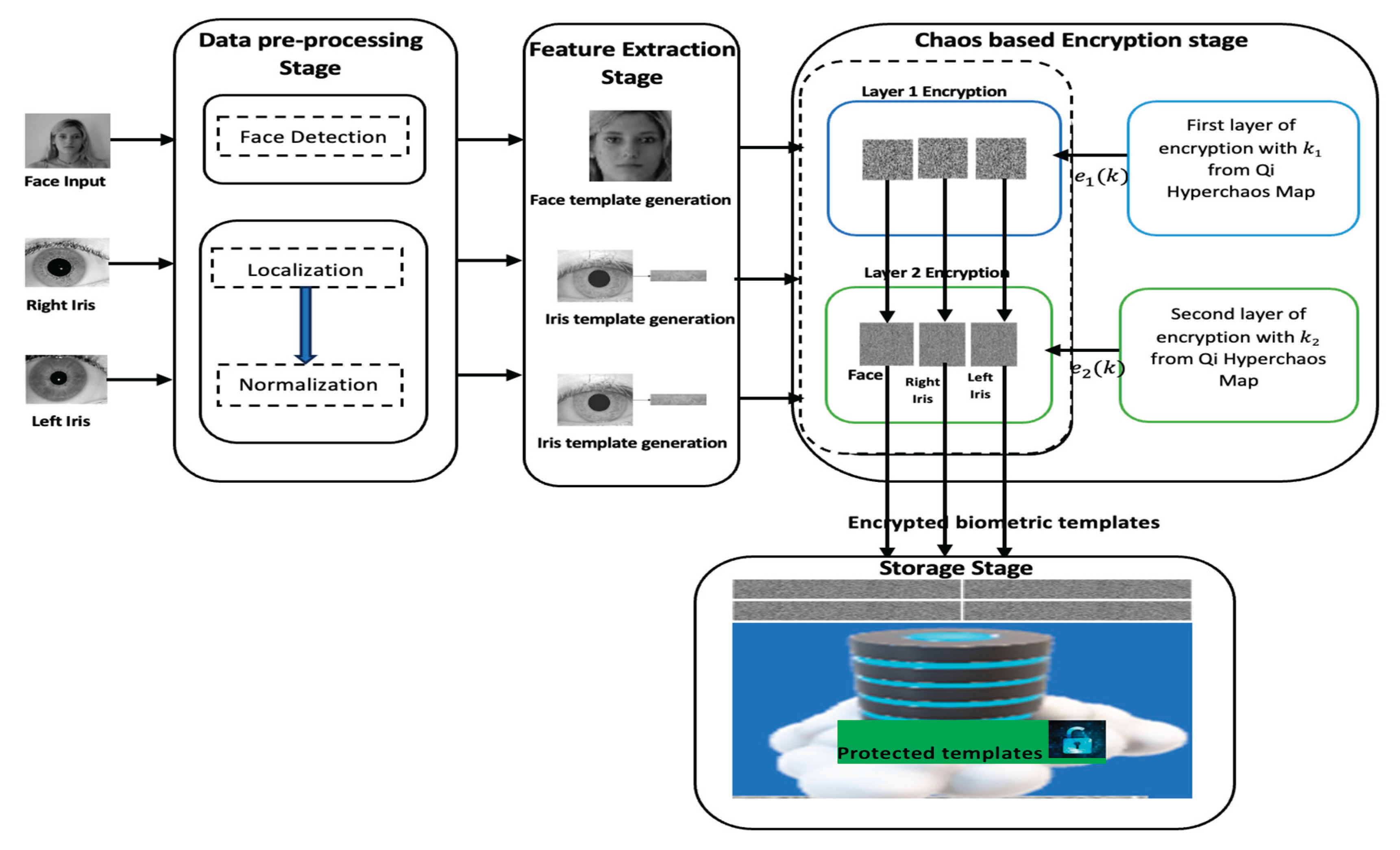
Figure 2.
Multimodal Biometric enrollment framework.
Figure 2.
Multimodal Biometric enrollment framework.
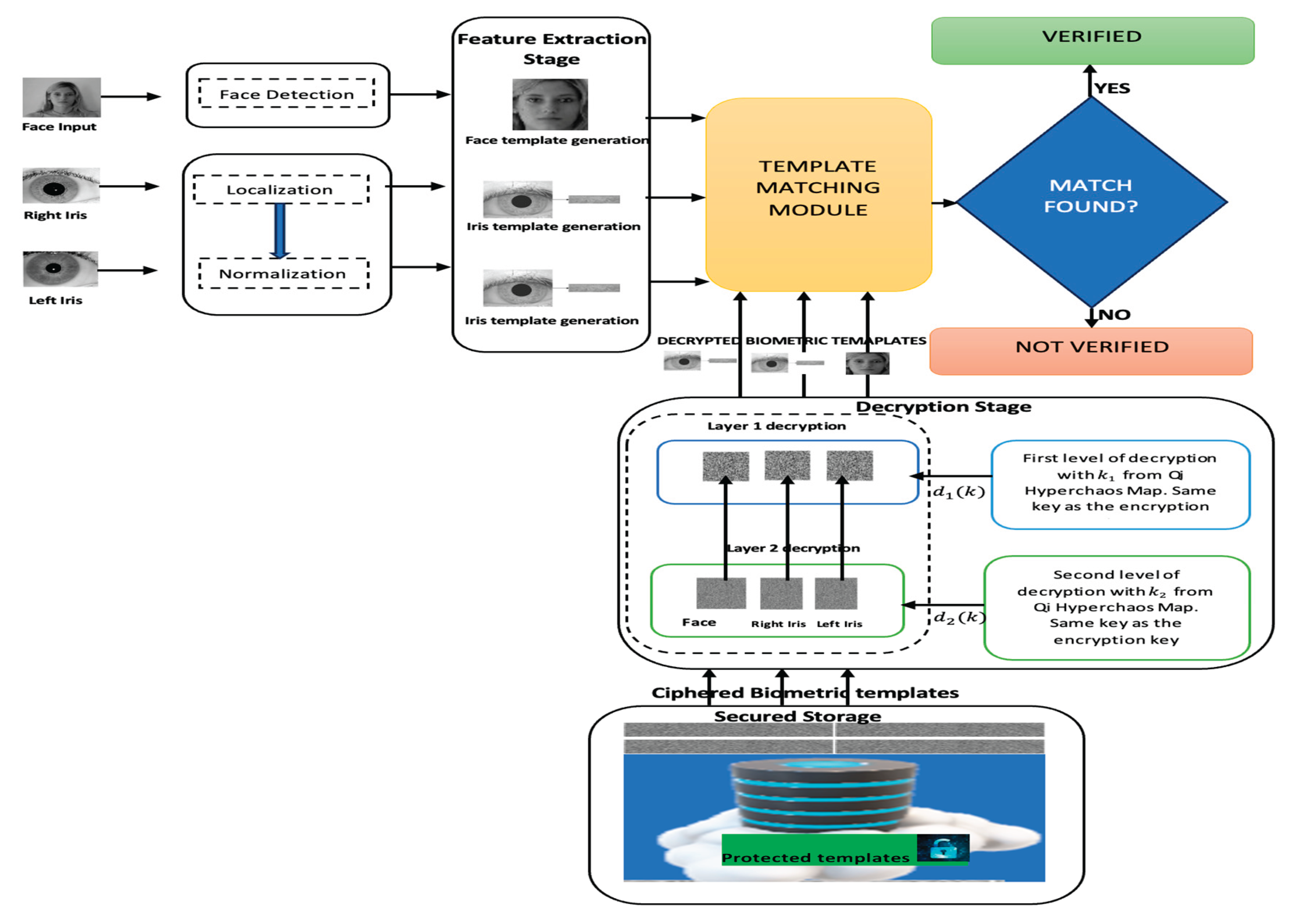
Figure 3.
Biometric Verification framework.
Figure 3.
Biometric Verification framework.
Figure 4.
Biometric encryption stages for Left Iris, Right Iris, and Face images. (a)(d)(g) Original plaintext images; (b)(e)(h) First-layer encryption results using key1; (c)(f)(i) Second-layer encryption results using key2.
Figure 4.
Biometric encryption stages for Left Iris, Right Iris, and Face images. (a)(d)(g) Original plaintext images; (b)(e)(h) First-layer encryption results using key1; (c)(f)(i) Second-layer encryption results using key2.
Figure 5.
Two-layer decryption process using encryption-corresponding keys: (a)(d)(g) Second-layer encrypted images; (b)(e)(h) First-layer decryption results using key2; (c)(f)(i) Complete decryption results using key1.
Figure 5.
Two-layer decryption process using encryption-corresponding keys: (a)(d)(g) Second-layer encrypted images; (b)(e)(h) First-layer decryption results using key2; (c)(f)(i) Complete decryption results using key1.
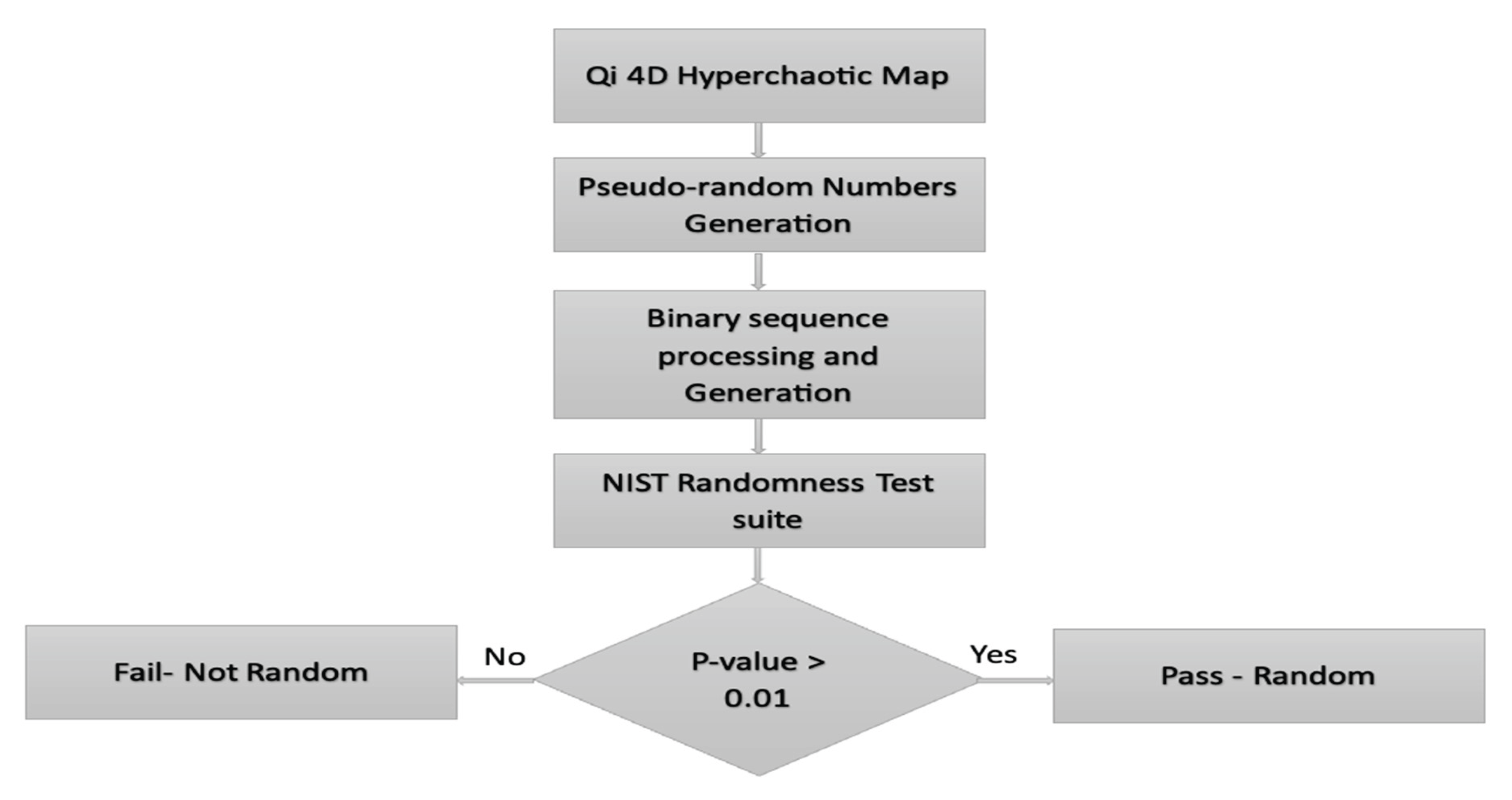
Figure 6.
Framework for Randomness Evaluation.
Figure 6.
Framework for Randomness Evaluation.
Figure 7.
key sensitivity original key, slightly modified key and the difference between the encrypted images with original and the modified ones.
Figure 7.
key sensitivity original key, slightly modified key and the difference between the encrypted images with original and the modified ones.
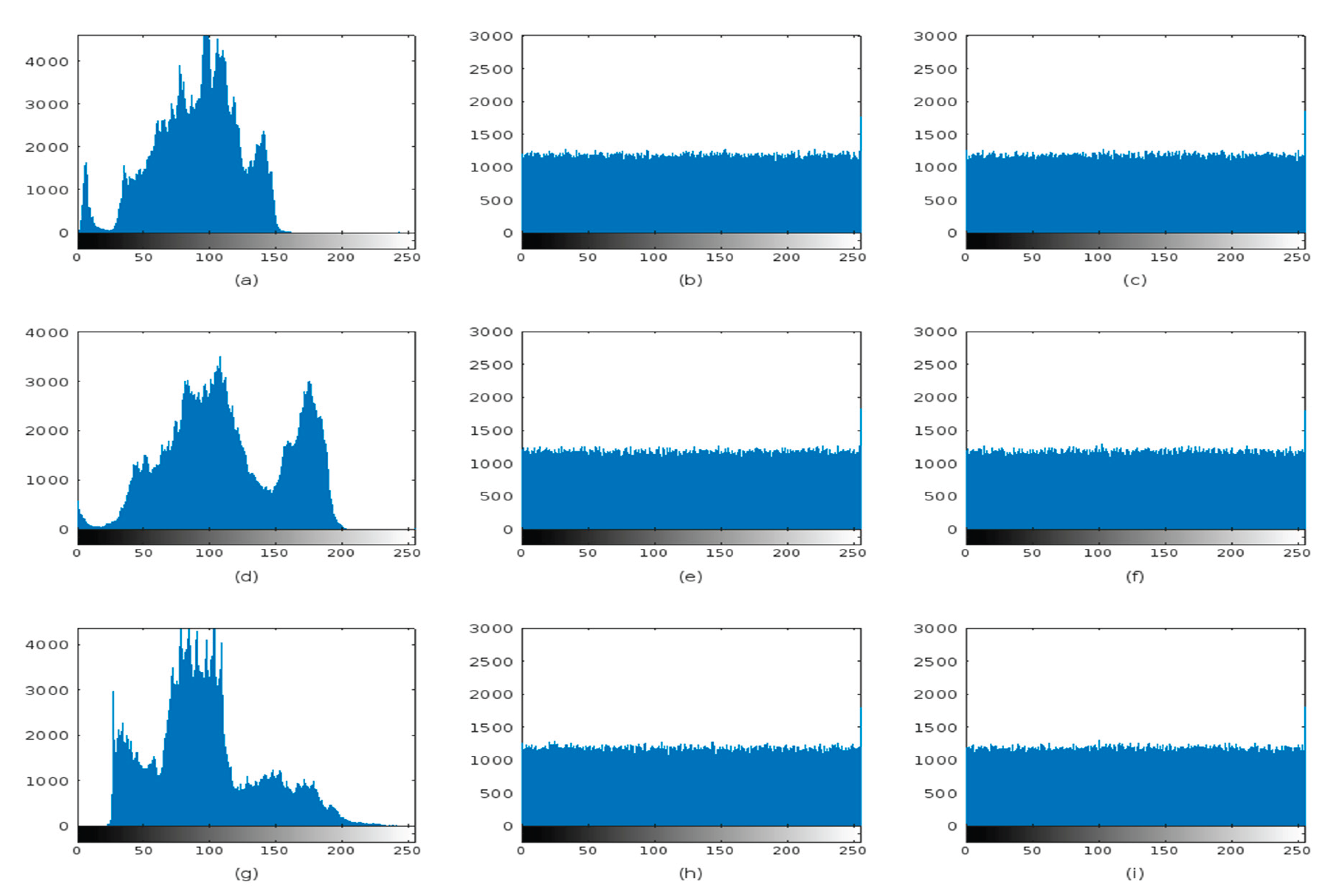
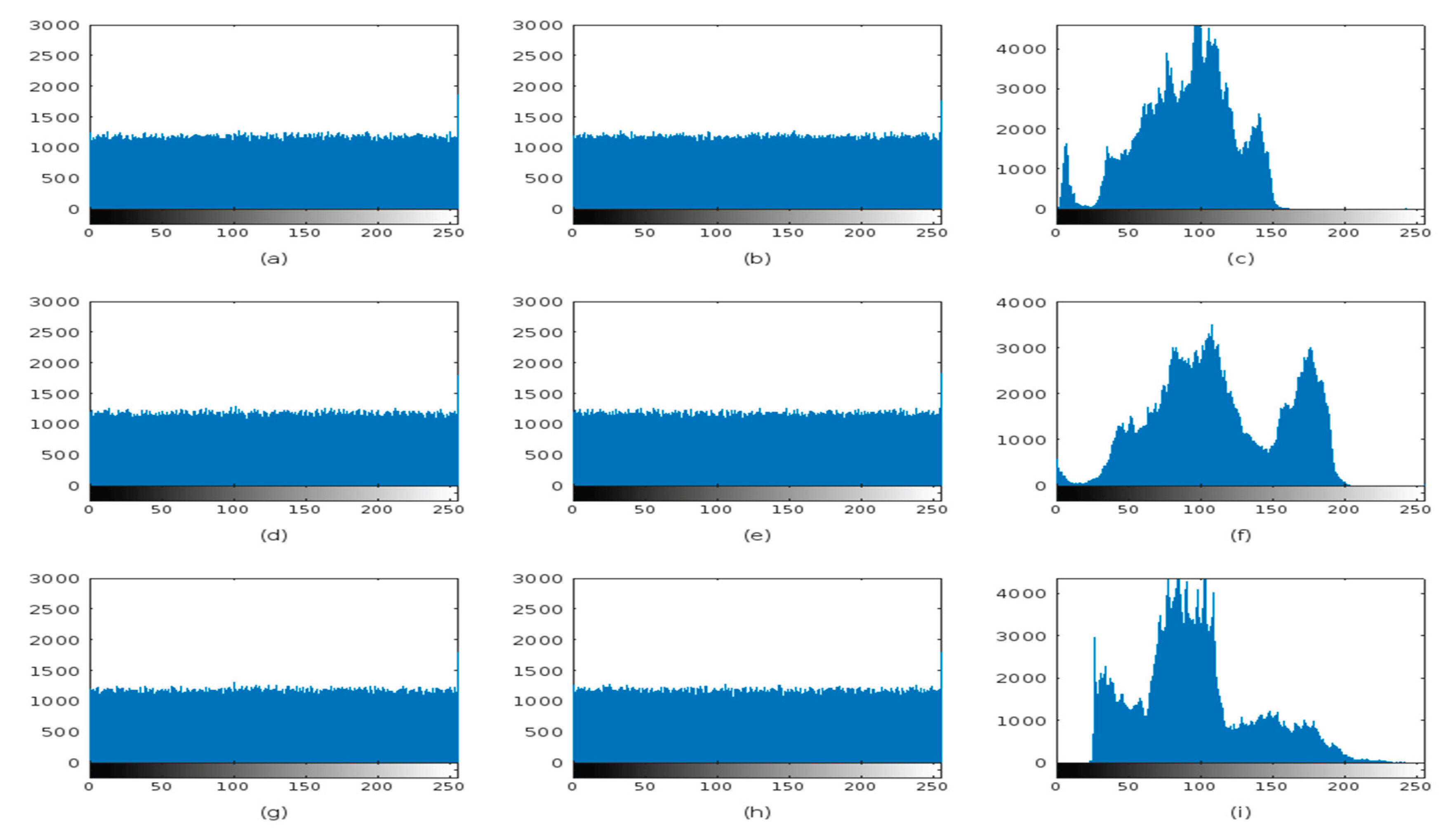
Figure 8.
Histograms of Original Plaintext image, first layer encryption and second layer encryption for Left Iris, Right Iris and Face images respectively.
Figure 8.
Histograms of Original Plaintext image, first layer encryption and second layer encryption for Left Iris, Right Iris and Face images respectively.
Figure 9.
Decryption process using the same set of keys used for encryption process.
Figure 9.
Decryption process using the same set of keys used for encryption process.
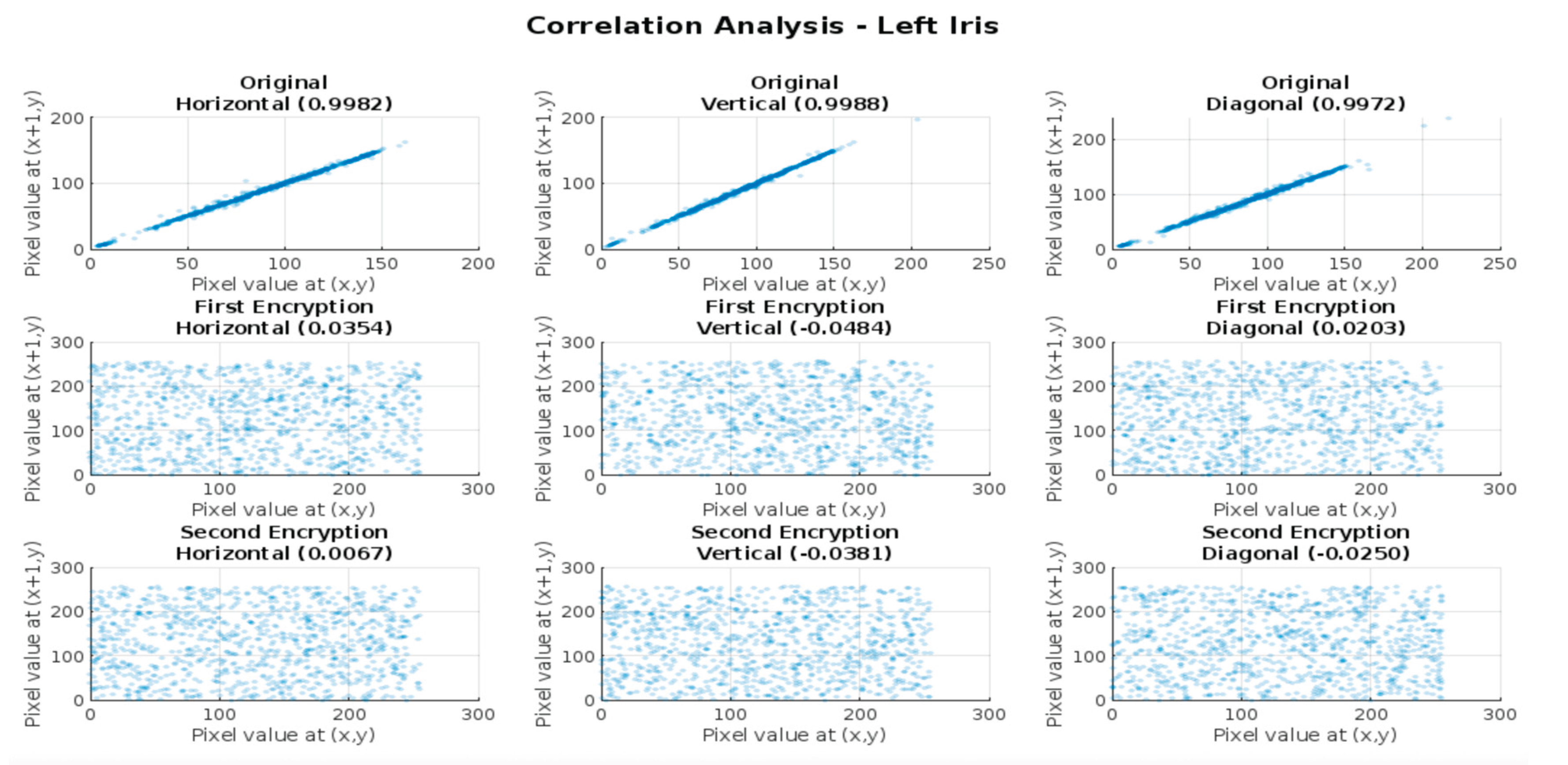
Figure 10.
Adjacent pixel correlations in (a) original left iris image, (b) first-level encrypted image, and (c) second-level encrypted image, shown in horizontal, vertical, and diagonal directions.”.
Figure 10.
Adjacent pixel correlations in (a) original left iris image, (b) first-level encrypted image, and (c) second-level encrypted image, shown in horizontal, vertical, and diagonal directions.”.
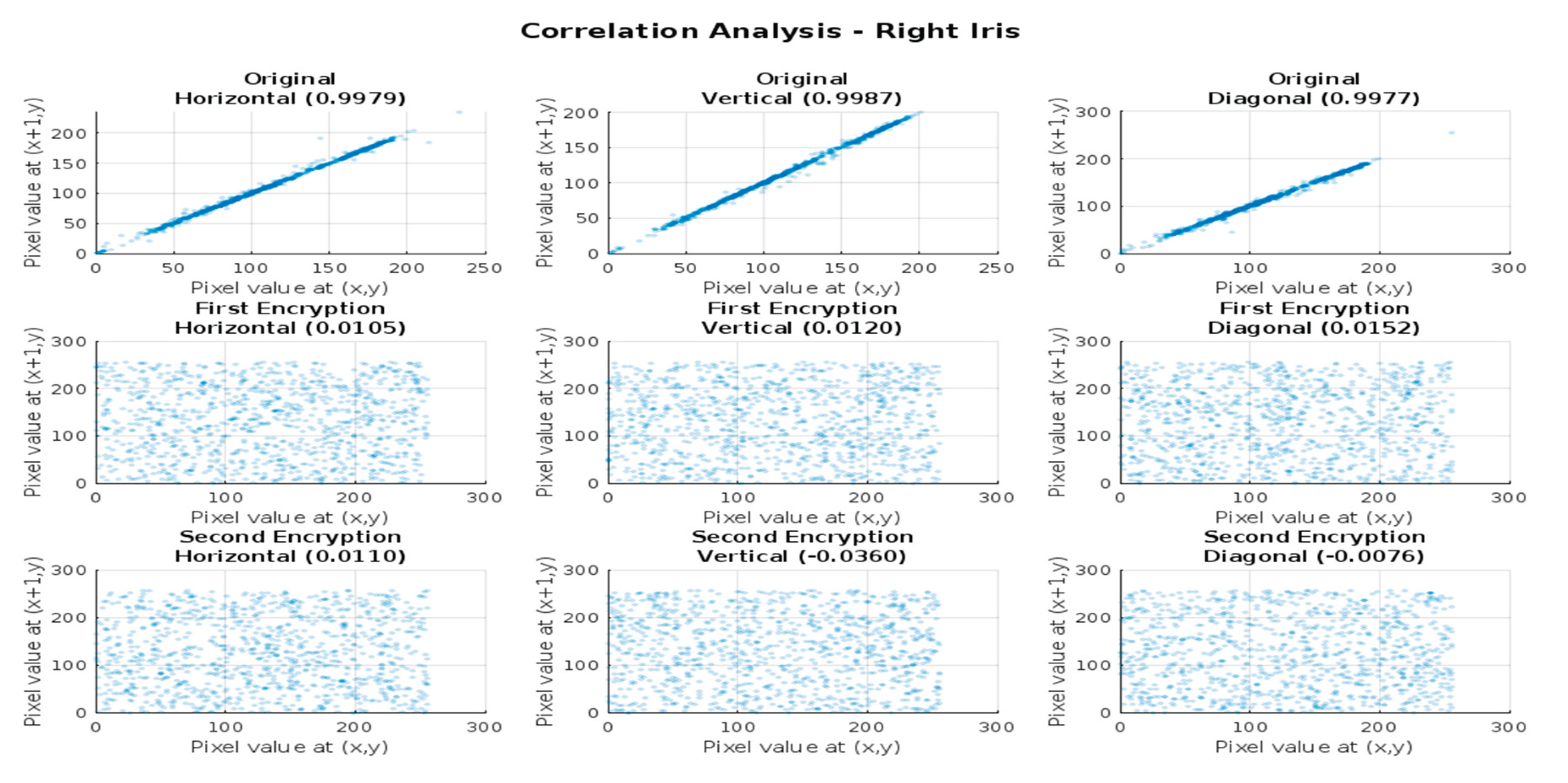
Figure 11.
Adjacent pixel correlations in (a) First row - original Right iris image, (b)middle row - first-level encrypted image, and (c) bottom row - second-level encrypted image, shown in horizontal, vertical, and diagonal directions.
Figure 11.
Adjacent pixel correlations in (a) First row - original Right iris image, (b)middle row - first-level encrypted image, and (c) bottom row - second-level encrypted image, shown in horizontal, vertical, and diagonal directions.
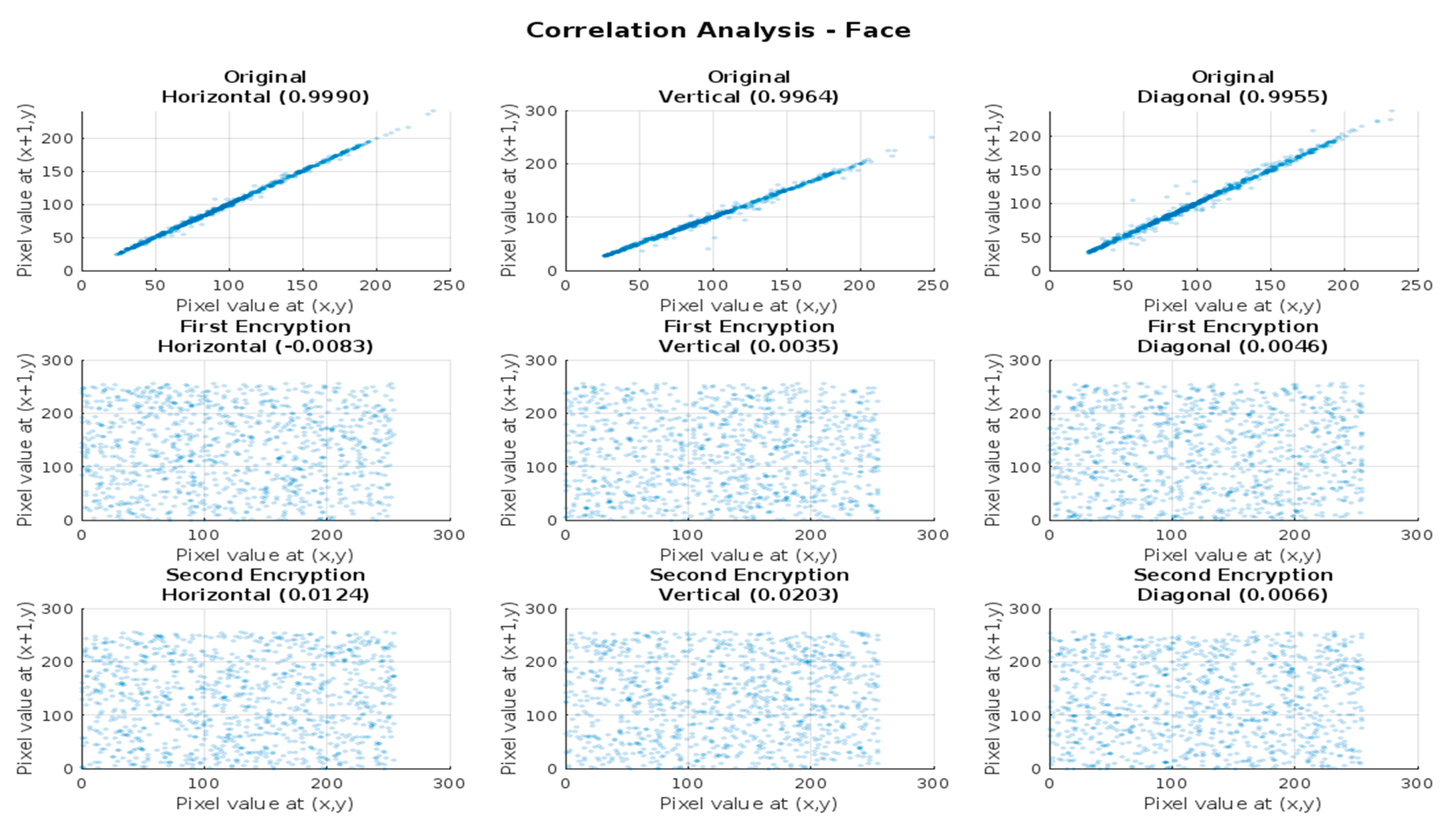
Figure 12.
Adjacent pixel correlation distributions in horizontal, vertical, and diagonal directions for: Top row (a): Original face image; middle row (b): First-level encrypted image; bottom row (c): Second-level encrypted image. Correlations shown in horizontal, vertical, and diagonal directions.
Figure 12.
Adjacent pixel correlation distributions in horizontal, vertical, and diagonal directions for: Top row (a): Original face image; middle row (b): First-level encrypted image; bottom row (c): Second-level encrypted image. Correlations shown in horizontal, vertical, and diagonal directions.
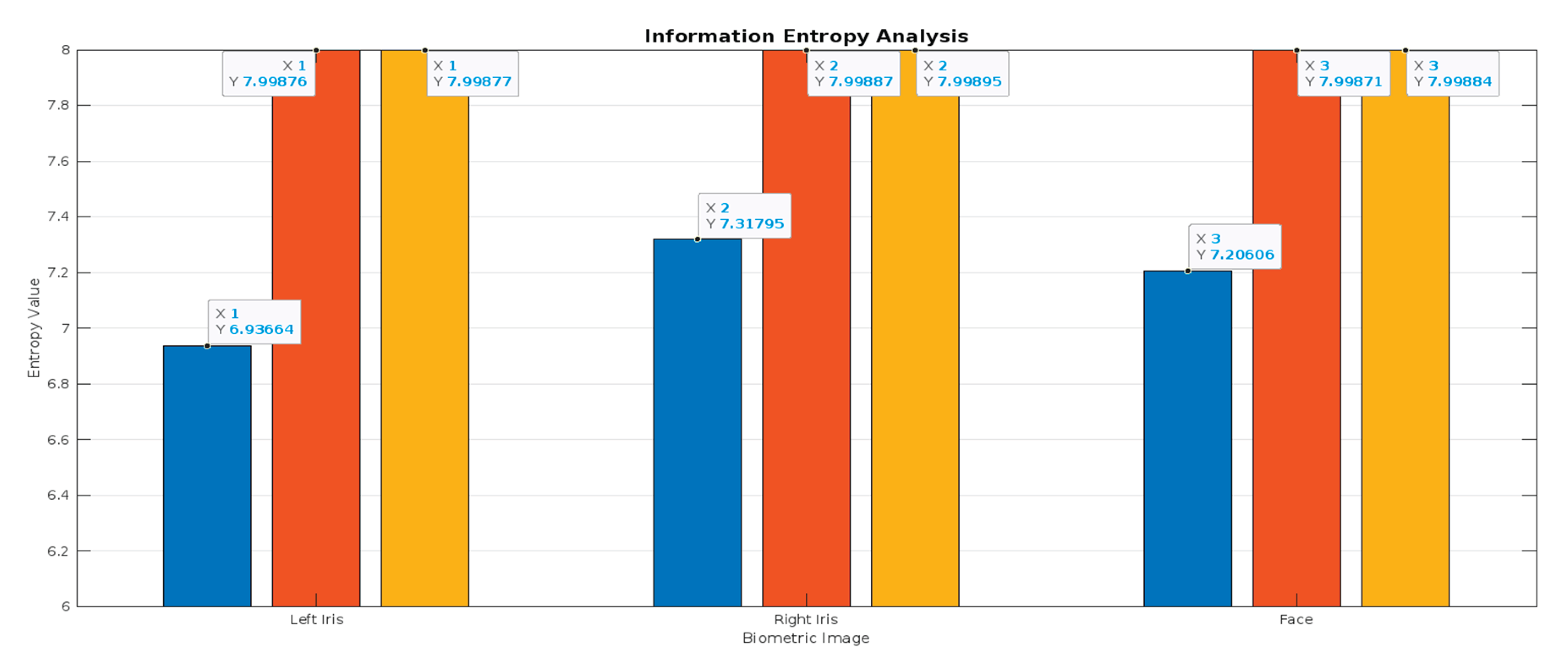
Figure 13.
Information Entropy for Biometric Left Iris, Right Iris and Face, plaintext, Ciphertext level1 and Ciphertext level2.
Figure 13.
Information Entropy for Biometric Left Iris, Right Iris and Face, plaintext, Ciphertext level1 and Ciphertext level2.
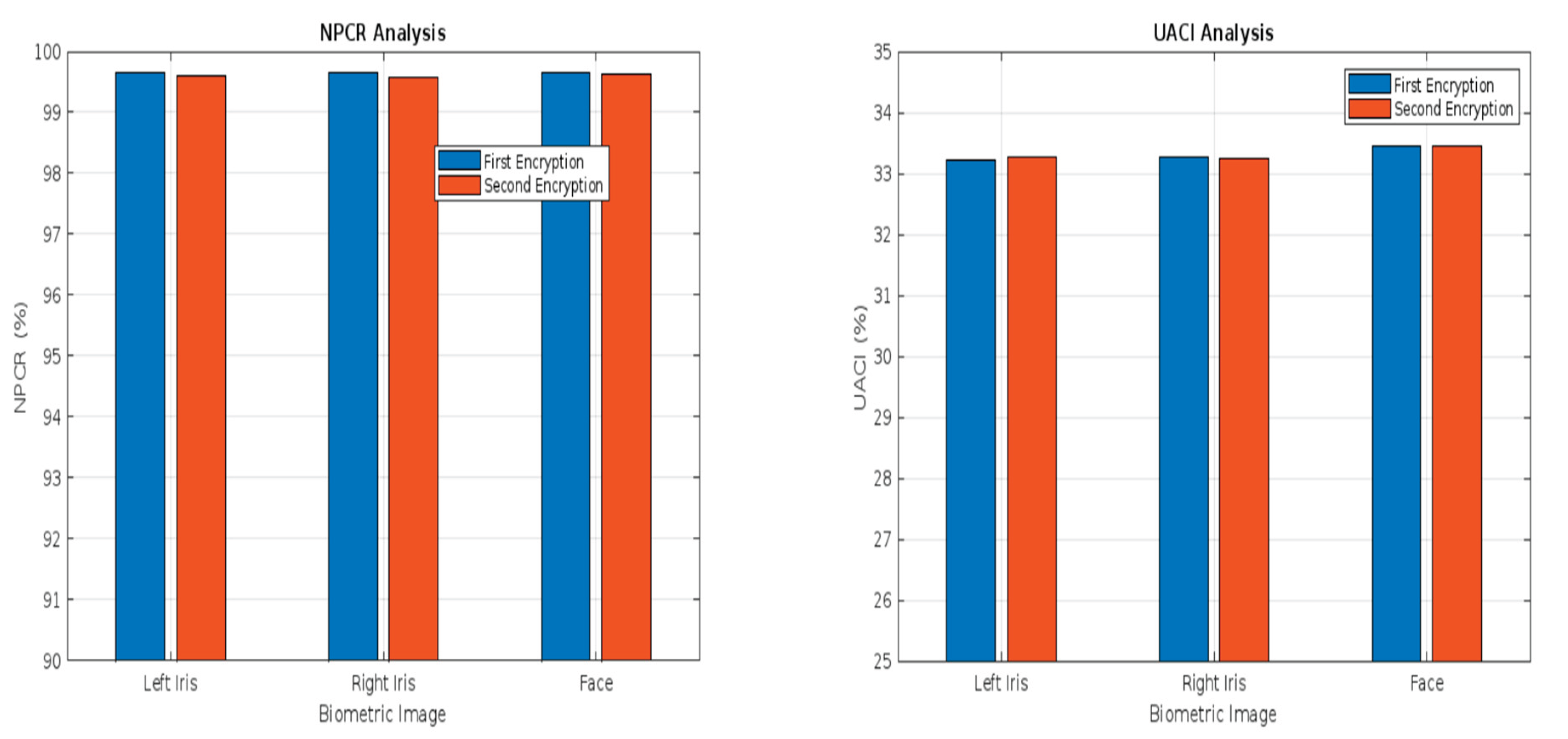
Figure 14.
NPCR and UACI performance Analysis for Left iris, Right Iris and Face biometric images.
Figure 14.
NPCR and UACI performance Analysis for Left iris, Right Iris and Face biometric images.
Table 1.
NIST 800-22 Test Results for Qi Hyoerchaos System.
Table 1.
NIST 800-22 Test Results for Qi Hyoerchaos System.
| Test Name |
|
|
Result |
| Frequency (Monobit) Test |
0.0375 |
0.8103 |
Pass - Random |
| Block Frequency Test |
0.7509 |
0.3084 |
Pass - Random |
| Runs Test |
0.7632 |
0.4023 |
Pass - Random |
| Longest Run of Ones in a Block Test |
0.4252 |
0.0215 |
Pass - Random |
| Binary Matrix Rank Test |
0.6883 |
0.5895 |
Pass - Random |
| Discrete Fourier Transform (Spectral) Test |
0.5318 |
0.7420 |
Pass - Random |
| Non-overlapping Template Matching Test |
0.4654 |
0.8026 |
Pass - Random |
| Overlapping Template Matching Test |
0.6917 |
0.9102 |
Pass - Random |
| Maurer’s Universal Statistical Test |
0.4965 |
0.5782 |
Pass - Random |
| Linear Complexity Test |
0.8346 |
0.7831 |
Pass - Random |
| Serial Test |
0.0491 |
0.1749 |
Pass - Random |
| Approximate Entropy Test |
0.9704 |
0.1690 |
Pass - Random |
| Cumulative Sums (Cusum) Test |
0.9998 |
0.1045 |
Pass - Random |
| Random Excursions Test |
0.9992 |
0.0916 |
Pass - Random |
| Random Excursions Variant Test |
0.9985 |
0.8342 |
Pass - Random |
Table 2.
Key Space performance Analysis.
Table 2.
Key Space performance Analysis.
| Chaotic System |
Precision |
Number of parameter and Initial conditions |
Key Space |
| Ours |
|
20 |
|
| Ref-[37] |
|
8 |
|
| Ref-[27] |
|
10 |
|
| Ref-[25] |
|
5 |
|
| Ref-[38] |
|
14 |
|
Table 3.
Comparative Analysis of Adjacent Pixel Correlation Coefficients Across Three Directional Planes with Existing Cryptographic Schemes.
Table 3.
Comparative Analysis of Adjacent Pixel Correlation Coefficients Across Three Directional Planes with Existing Cryptographic Schemes.
| Chaotic System |
Correlation Coefficients |
| |
Horizontal |
Vertical |
Diagonal |
| Ours |
0.0072 |
0.0046 |
0.0063 |
| Ref-[27] |
0.0105 |
-0.0019 |
-0.0019 |
| Ref-[37] |
0.0206 |
0.0003 |
-0.0141 |
| Ref-[38] |
-0.0082 |
0.0073 |
0.0089 |
| Ref-[44] |
0.0003 |
0.0009 |
0.019 |
| Ref-[45] |
0.0011 |
0.0012 |
0.016 |
| Ref-[46] |
0.004 |
0.007 |
0.037 |
Table 4.
Performance Analysis of Entropy of Encrypted with Lena Image by existing schemes.
Table 4.
Performance Analysis of Entropy of Encrypted with Lena Image by existing schemes.
| Proposed |
Ref-[27] |
Ref-[37] |
Ref-[42] |
Ref-[47] |
Ref-[48] |
Ref-[49] |
| 7.9988 |
7.9983 |
7.9998 |
7.9996 |
7.9993 |
7.9971 |
7.7795 |
Table 5.
NPCR and UACI performance and comparison with existing Methods using Lena image.
Table 5.
NPCR and UACI performance and comparison with existing Methods using Lena image.
| |
Proposed |
Ref-[25] |
Ref-[27] |
Ref-[37] |
Ref-[44] |
Ref-[45] |
Ref-[47] |
Ref-[49] |
Ref-[52] |
| NPCR (%) |
99.629 |
99.658 |
99.810 |
99.715 |
99.603 |
99.611 |
99.614 |
99.510 |
99.630 |
| UACI (%) |
33.441 |
33.459 |
33.400 |
33.511 |
33.692 |
33.692 |
33.466 |
33.160 |
33.480 |
Table 6.
Comparison analysis of encryption time with existing algorithms with Lena image.
Table 6.
Comparison analysis of encryption time with existing algorithms with Lena image.
| Algorithms |
Image size |
Encryption time in s |
Decryption time in s |
| Ours |
512x512 |
2.1439 |
2.1081 |
| 256x256 |
0.61158 |
0.6094 |
| Ref-[25] |
512x512 |
2.727 |
2.708 |
| 256x256 |
0.941 |
0.902 |
| Ref-[37] |
512x512 |
3.17 |
-- |
| 256x256 |
1.23 |
-- |
| Ref-[44] |
512x512 |
0.5156 |
-- |
| 256x256 |
0.1272 |
-- |
| Ref-[45] |
512x512 |
25.3077 |
-- |
| 256x256 |
6.3849 |
-- |
| Ref-[54] |
512x512 |
16.43 |
-- |
| 256x256 |
8.2 |
-- |
| Ref-[55] |
512x512 |
25.867 |
24.564 |
| 256x256 |
6.494 |
6.471 |